Probabilistic Analysis of Floods from Tailings Dam Failures: A Method to Analyze the Impact of Rheological Parameters on the HEC-RAS Bingham and Herschel-Bulkley Models
Abstract
:1. Introduction
2. Materials and Methods
2.1. Mathematical Rheological Models and Parameterization
2.2. Parameter Intervals and Sampling
2.3. Automation of Sensitivity Analysis in HEC-RAS
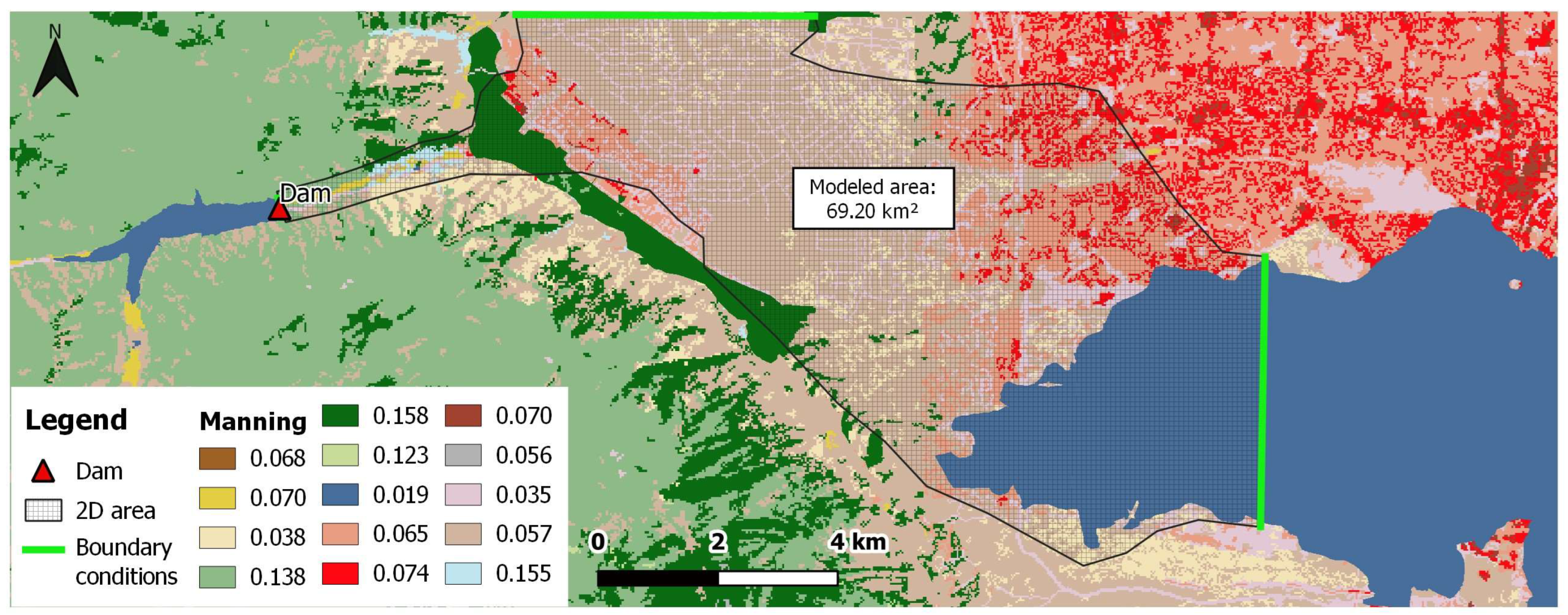
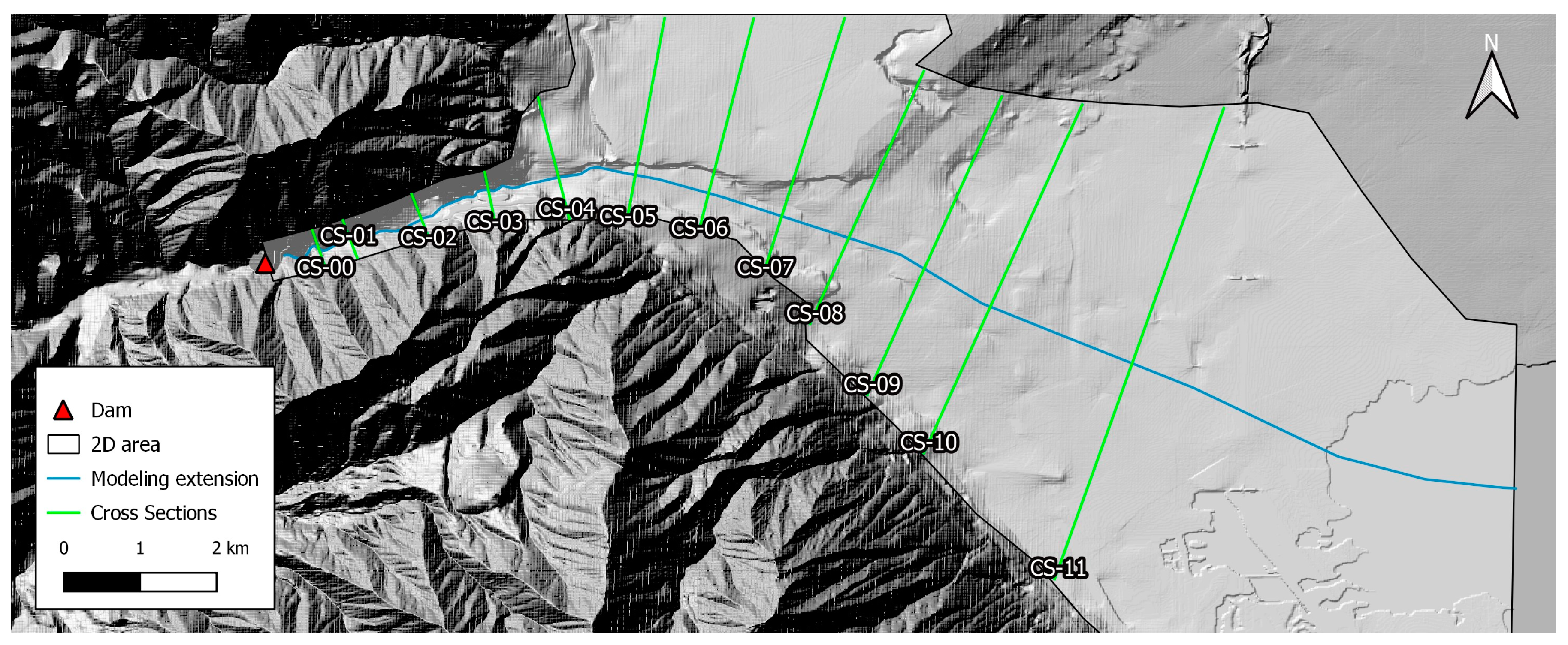
2.4. Case Study: The Hydrodynamic Model
| Parameters | Data | Froehlich [64] |
|---|---|---|
| Failure Mode | Overflow | |
| Total volume (Vw) (1.000 m3) | 38,276.34 | |
| Average breach width (Bm) (m) | 116.27 | |
| Minimum breach width (m) | 55.27 | |
| Elevation of the dam crest (m) | 272.00 | |
| Elevation of the base of the dam (m) | 211.00 | |
| Elevation of the bottom of the breach (m) | 211.00 | |
| Dam height (m) | 61.0 | |
| Height of the breach (Hb) (m) | 61.0 | |
| Time of breach formation (h) | 0.54 | |
| Left Lateral Slope (H:1V) | 1.0 | |
| Right Side Slope (H:1V) | 1.0 | |
| Mode of progression | Sine Curve |
3. Results
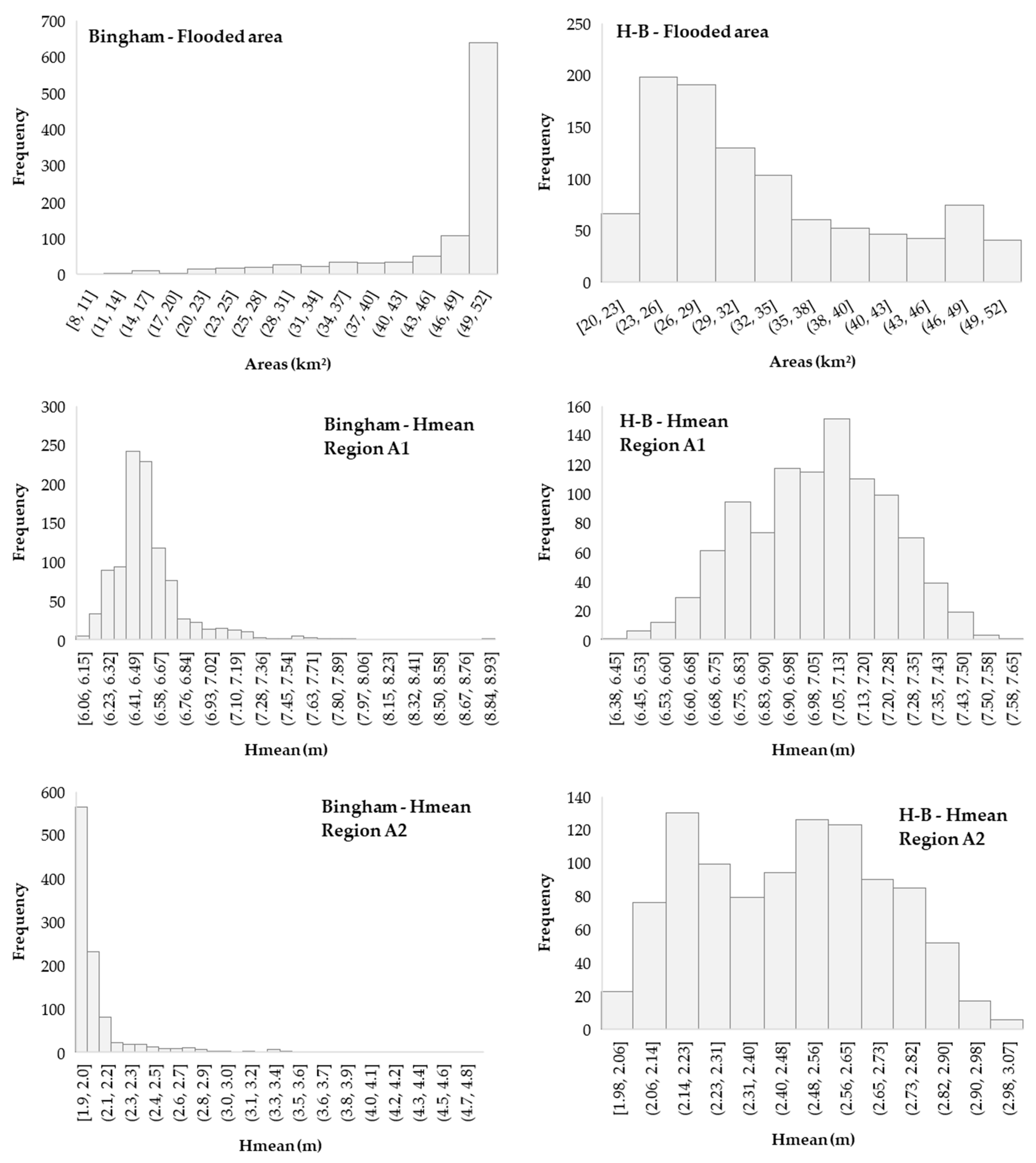
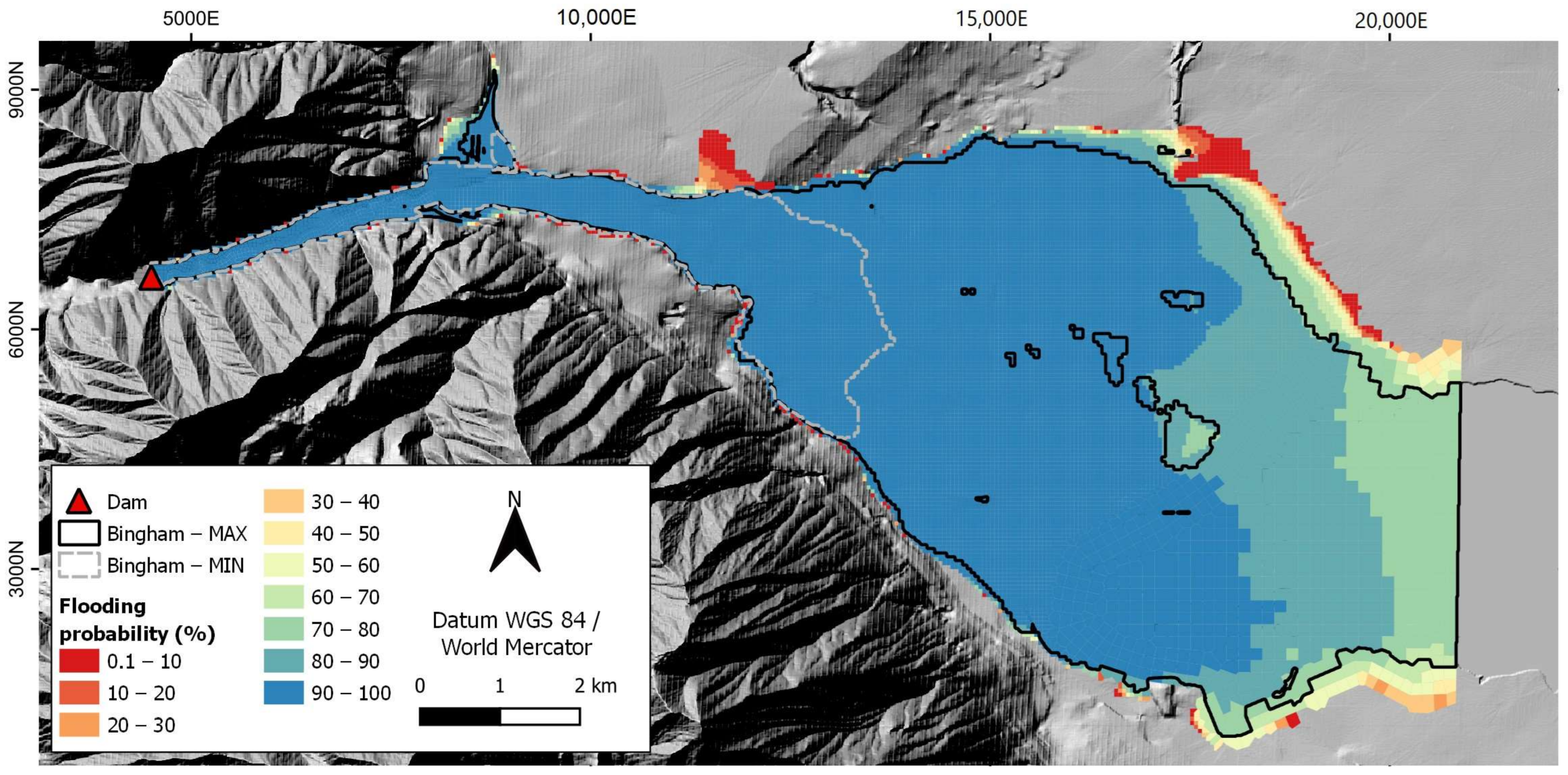
3.1. Probabilistic Maps Related to Flooded Areas
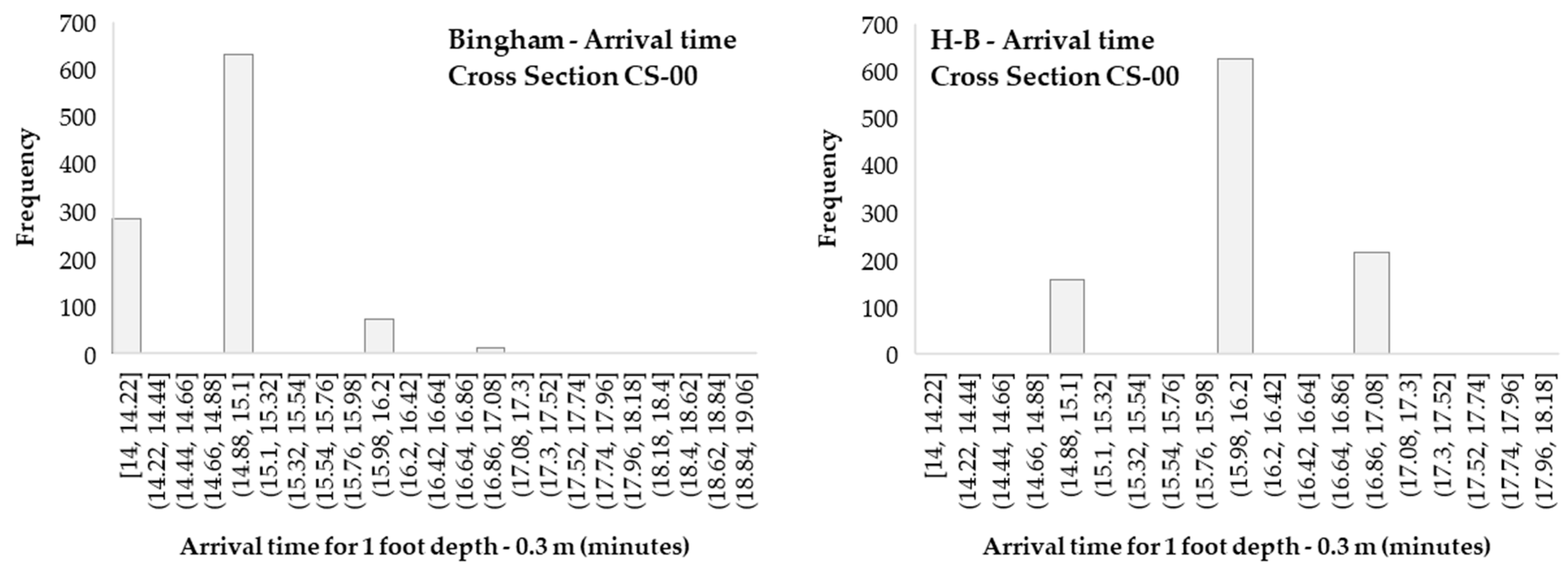
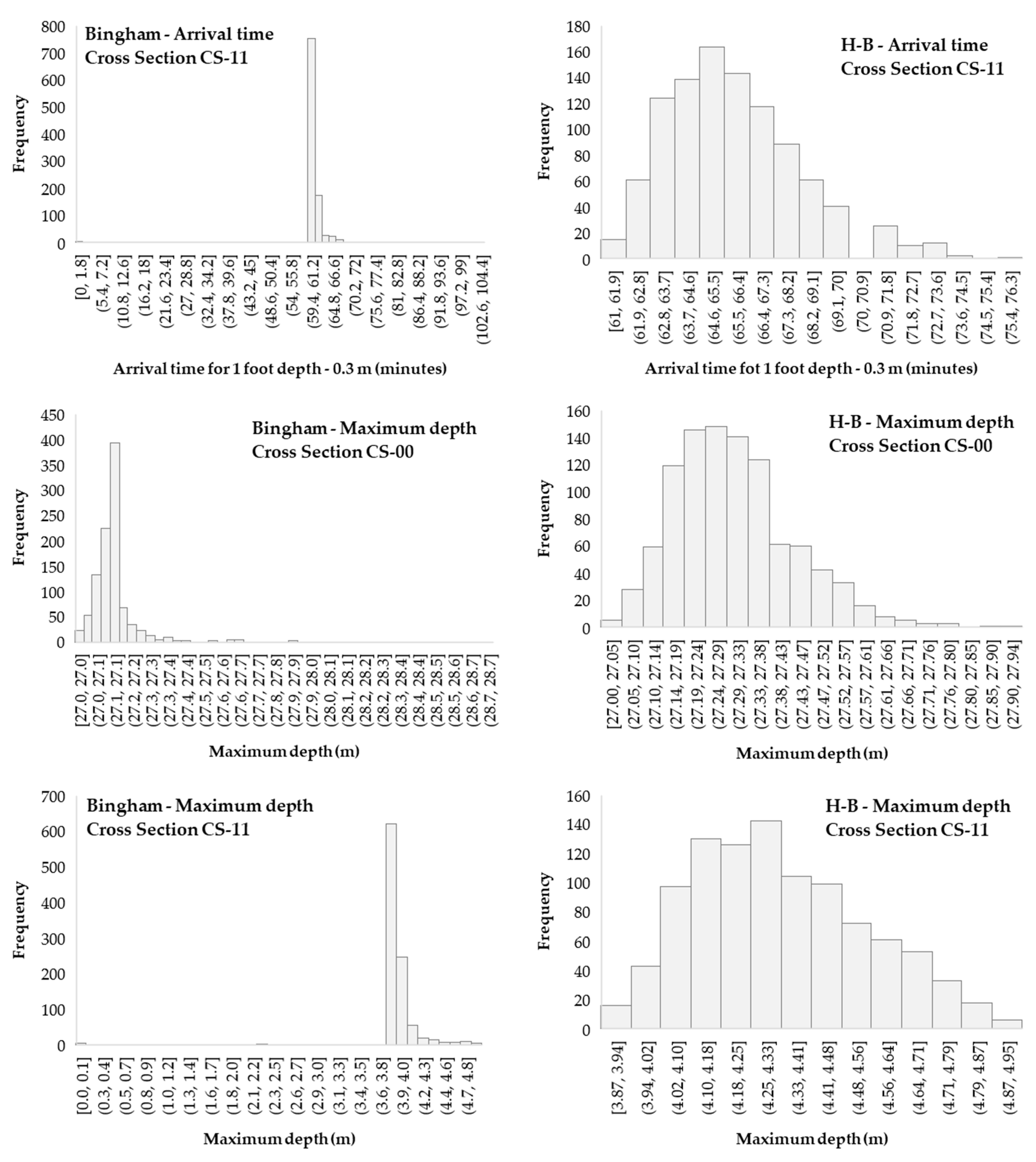
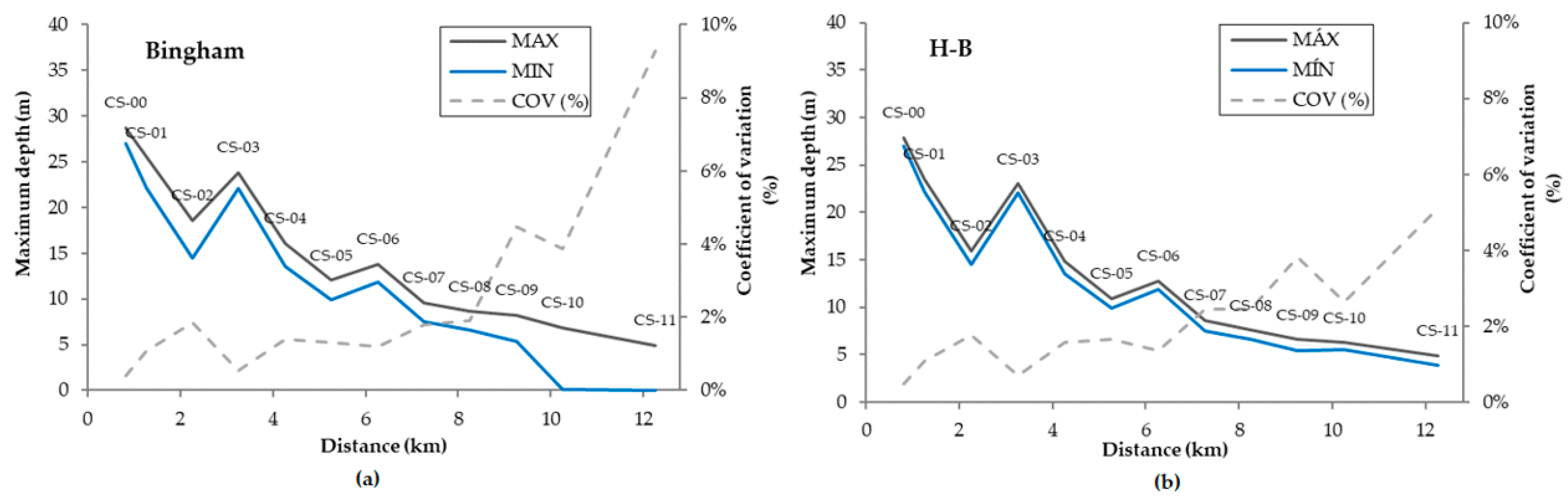
3.2. Arrival Times and Maximum Depth Variation along the Valley
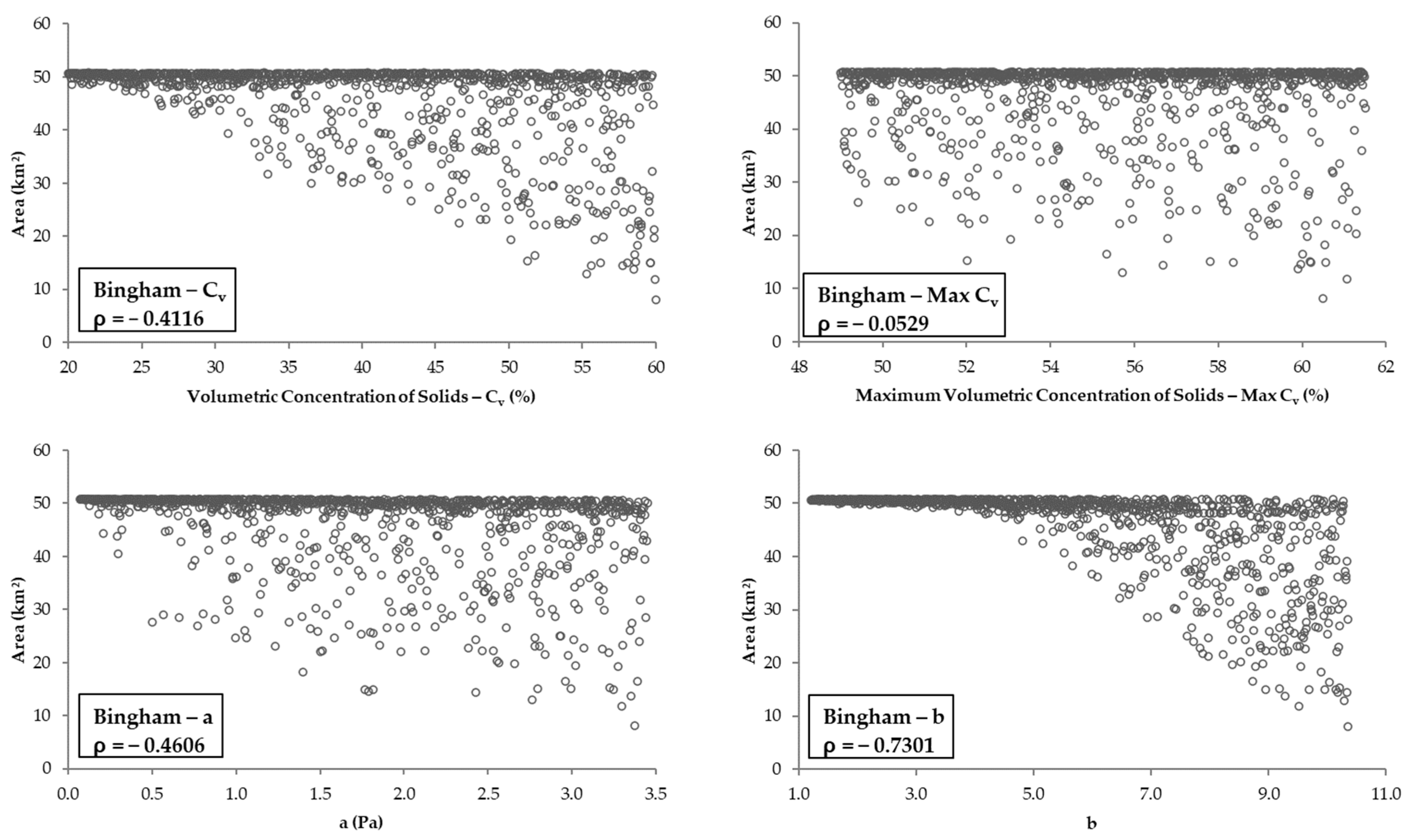
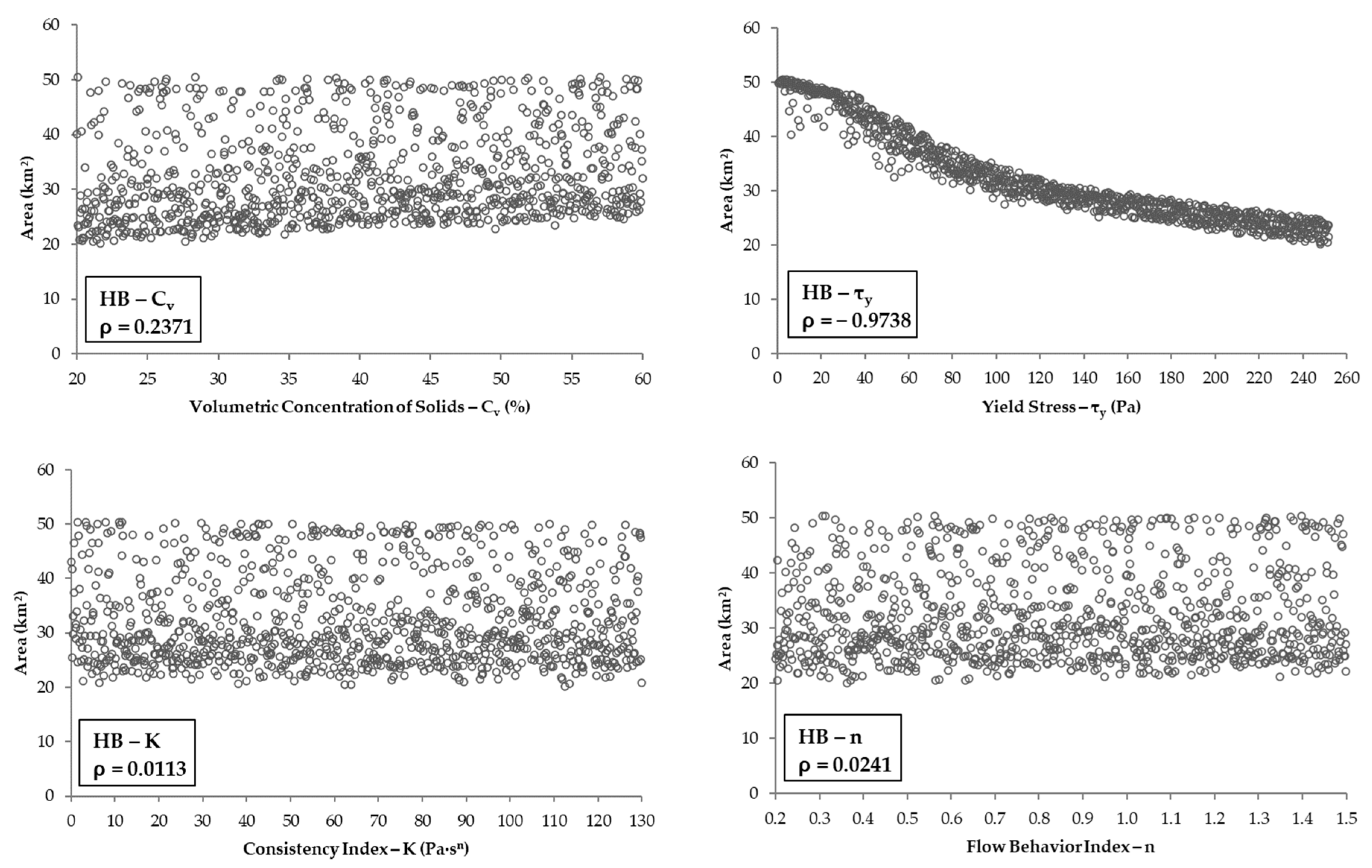
3.3. Rheological Parameters vs. Simulated Areas
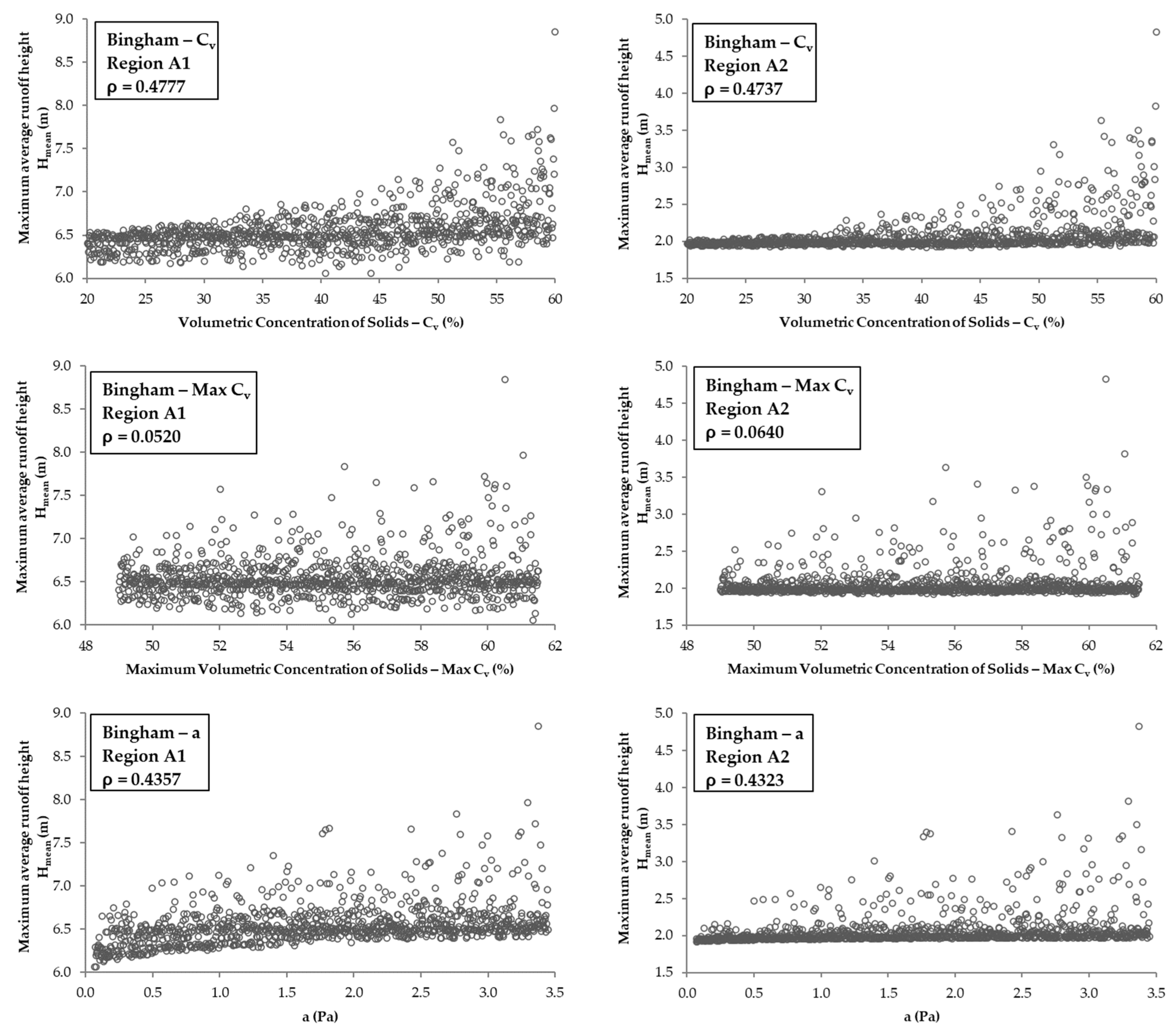
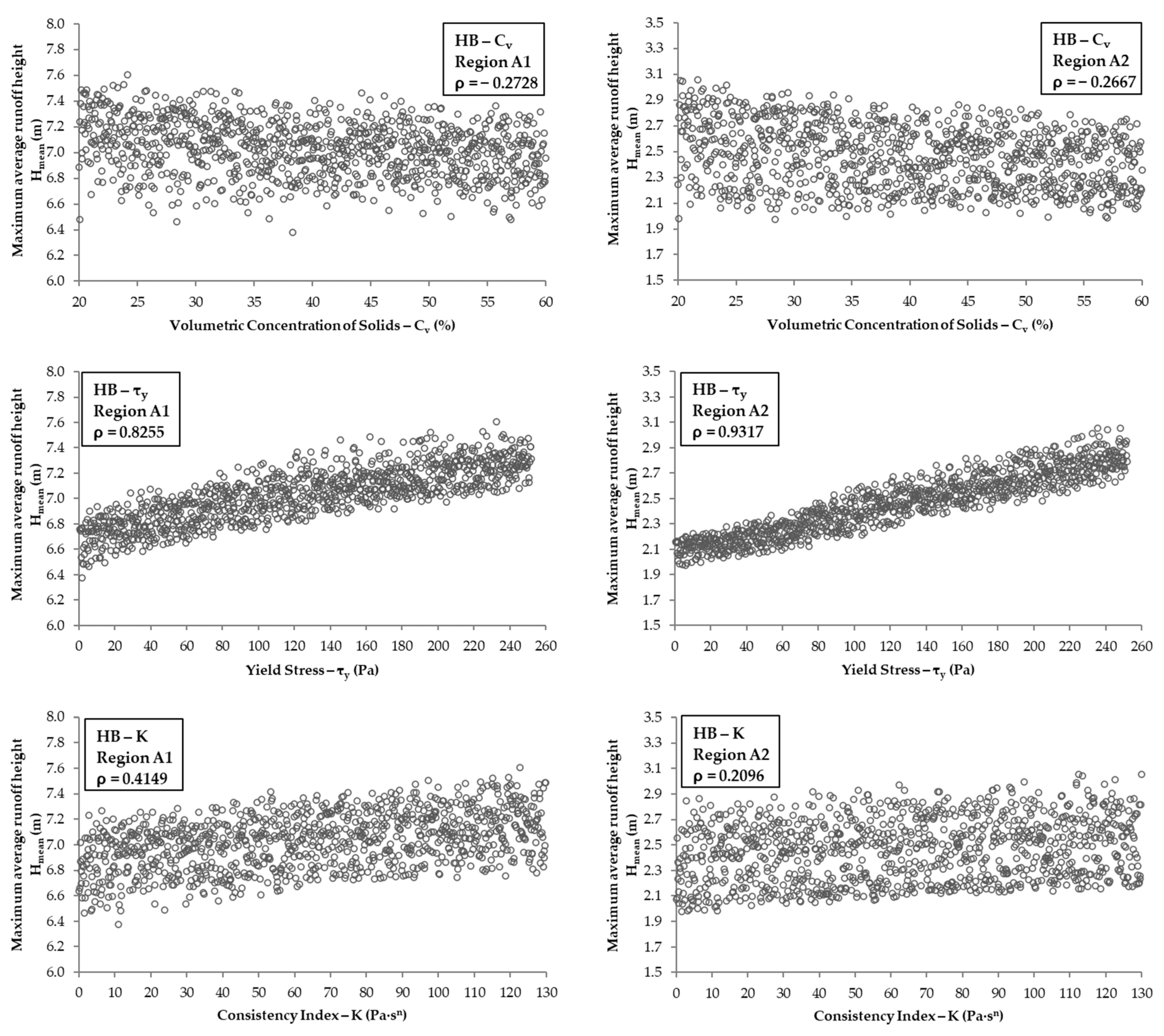
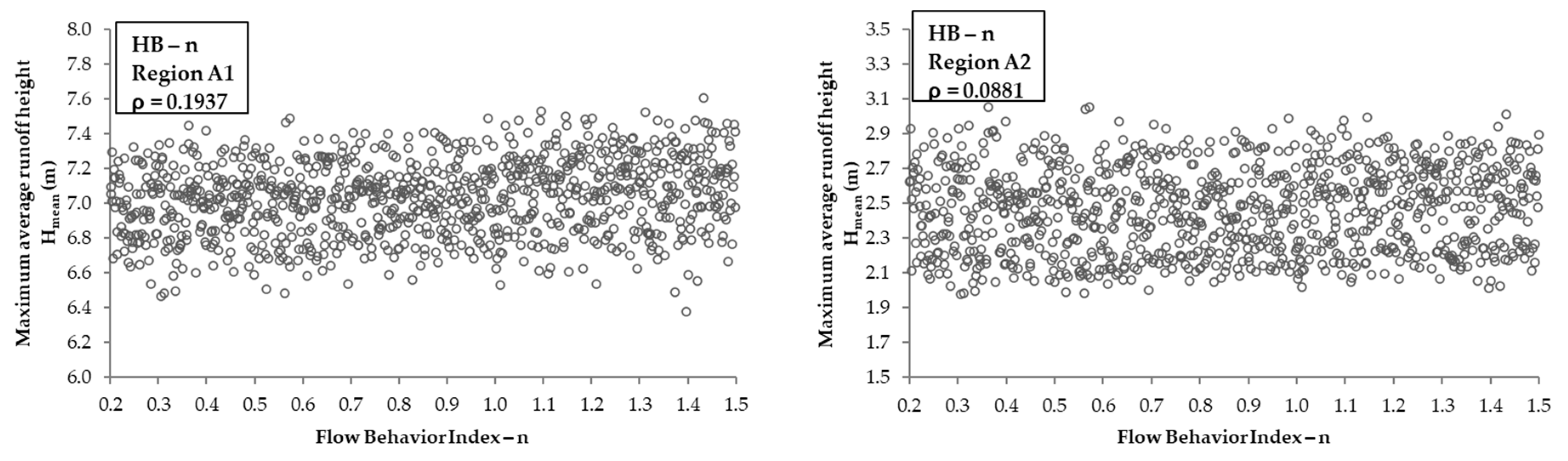
3.4. Rheological Parameters vs. Hmean
4. Discussion
5. Conclusions and Recommendations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Parameter [Unit] | Parameter Range | Reference | Tailings | Test/Method | Rheological Model/Fitted Equation |
|---|---|---|---|---|---|
| Volumetric concentration of solids (Cv) [%] | 21.21–35.78 | [47] | Coal | n.a. | n.a. |
| 27.98–46.65 | [47] | Copper | |||
| 36.50–38.62 | [47] | Gold | |||
| 36.34–44.62 | [47] | Lithium | |||
| 11.09–19.66 | [47] | Nickel | |||
| 25.48–31.25 | [47] | Uranium | |||
| 11.82–50.11 | [47] | Zinc | |||
| 18.0–52.5 | [7] | Base metal | |||
| 21.8–55.3 | [48] | Iron | |||
| 32.5–65.0 | [48] | Iron | |||
| 9.3–48.4 | [9] | Gold | |||
| 34.75–57.14 | [49] | Iron | |||
| 58 | [2] | Iron | |||
| 47 | [37] | Iron | |||
| 23 | [52] | Iron | |||
| Maximum volumetric concentration of solids (Max Cv) [%] | 61.5 | [53] | - | - | n.a. |
| 53 | [7] | Base metal | - | ||
| 49.0–62.0 * | [50] | Copper | [67] ** | ||
| 59.9–76.5 * | [51] | Iron | [67] ** | ||
| 57.3–68.0 * | [51] | Gold | [67] ** | ||
| Dynamic viscosity (μ) [Pa∙s] | 0.03–0.49 | [7] | Base metal | Viscometer | Bingham |
| 0.15–2.69 | [48] | Iron | Viscometer | Bingham | |
| 0.002–0.311 | [9] | Gold | Viscometer | Bingham | |
| 0.0071–0.4457 | [49] | Iron | Rheometer | Quadrática | |
| 1.09–1.46 | [8] | Pyrophyllite | Rheometer | Bingham | |
| 50 | [37] | Iron | Calibration | Bingham | |
| 30.0–100.0 | [38] | Iron | Calibration | Full Bingham | |
| Yield stress (τy) [Pa] | 2.122–48.535 | [47] | Coal | Viscometer | Herschel-Bulkley |
| 0.641–93.50 | [47] | Copper | Viscometer | Herschel-Bulkley | |
| 0.6–1.5 | [47] | Gold | Viscometer | Herschel-Bulkley | |
| 1.048–11.165 | [47] | Lithium | Viscometer | Herschel-Bulkley | |
| 1.564–37.110 | [47] | Nickel | Viscometer | Herschel-Bulkley | |
| 2.769–9.411 | [47] | Uranium | Viscometer | Herschel-Bulkley | |
| 0.652–100.260 | [47] | Zinc | Viscometer | Herschel-Bulkley | |
| 26.0–638.0 | [7] | Base metal | Viscometer | Bingham | |
| 19.36–602.82 | [48] | Iron | Viscometer | Bingham | |
| 59.59–2396.53 *** | [48] | Iron | Slump test | Bingham | |
| 0.5–181.0 | [9] | Gold | Viscometer | Bingham | |
| 0.085–118.0 | [49] | Iron | Rheometer | Quadrática | |
| 12.0–23.0 | [8] | Pyrophyllite | Rheometer | Herschel-Bulkley | |
| 9.7–251.9 | [27] | Synthetic | Rheometer | Herschel-Bulkley | |
| 100.0–1000.0 | [37] | Iron | Calibration | Bingham | |
| 750.0–1000.0 | [38] | Iron | Calibration | Full Bingham | |
| a [Pa] | 1 | [7] | Base metal | Viscometer | Exponential |
| 21.381 | [48] | Iron | Viscometer | ||
| 0.0065 | [48] | Iron | Slump test | ||
| 0.08 | [52] | Iron | Calibration | ||
| 1.00 × 10−7 | [49] | Iron | Rheometer | ||
| ~0.04–3.40 | [10] | Copper | Rheometer | ||
| ~0.40–3.45 | [10] | Iron | Rheometer | ||
| b [-] | 12.2 | [7] | Base metal | Viscometer | Exponential |
| 90.874 | [48] | Iron | Viscometer | ||
| 20.47 | [48] | Iron | Slump test | ||
| 40 | [52] | Iron | Calibration | ||
| 39.278 | [49] | Iron | Rheometer | ||
| ~1.2–5.0 | [10] | Copper | Rheometer | ||
| ~1.2–5.5 | [10] | Iron | Rheometer | ||
| Consistency index (K) [Pa∙sn] | 0.034–6.409 | [47] | Coal | Viscometer | Herschel-Bulkley |
| 0.008–130.0 | [47] | Copper | Viscometer | ||
| 0.108–0.221 | [47] | Gold | Viscometer | ||
| 0.222–1.515 | [47] | Lithium | Viscometer | ||
| 0.154–2.001 | [47] | Nickel | Viscometer | ||
| 0.065–0.097 | [47] | Uranium | Viscometer | ||
| 0.428–14.720 | [47] | Zinc | Viscometer | ||
| 0.69–1.96 | [8] | Pyrophyllite | Rheometer | ||
| Flow behavior index (n) [-] | 0.4–1.0 | [47] | Coal | Viscometer | Herschel-Bulkley |
| 0.192–1.347 | [47] | Copper | Viscometer | ||
| 0.705–0.744 | [47] | Gold | Viscometer | ||
| 0.766–1.020 | [47] | Lithium | Viscometer | ||
| 0.450–0.602 | [47] | Nickel | Viscometer | ||
| 0.742–0.913 | [47] | Uranium | Viscometer | ||
| 0.306–0.577 | [47] | Zinc | Viscometer | ||
| 0.84–1.14 | [8] | Pyrophyllite | Rheometer | ||
| 0.50–1.50 | [37] | Teórico | Calibration |
Appendix B







Appendix C
| Specification | Bingham | Herschel-Bulkley H-B |
|---|---|---|
| Model area | 69.8 km2 | |
| 2D mesh resolution | 40 m on the slope centerline in the embedded valley 100 m in the downstream lake 50 m for the rest of the model | |
| Number of template cells | 21,148 | |
| Equation | Shallow Water Equations | |
| Simulation time frame | 20 h | |
| Maximum number of computational iterations | 20 | |
| Computational Interval | Adjustable based on Courant: maximum = 1.0; minimum = 0.45 1.0–16.0 s | |
| Machine used | Processor AMD Ryzen 7 3700X. 8-Core. 3.6 GHz processing speed (4.4 GHz Turbo). 16 GB DDR4 RAM and 4 GB/s M,2 SSD | AMD Ryzen 3 3200G. 4-Core. 3.6 GHz processing speed. 8 GB DDR4 RAM and 6 GB/s Sata SSD |
| Average time per simulation | 3.233 min/simulation | 5.284 min/simulation |
Appendix D
References
- Davies, M.P. Tailings Impoundment Failures: Are Geotechnical Engineers Listening? Geotech. News 2002, 20, 31–36. [Google Scholar]
- Robertson, P.K.; de Melo, L.; Williams, D.J.; Wilson, G.W. Report of the Expert Panel on the Technical Causes of the Failure of Feijão Dam I. Available online: http://www.b1technicalinvestigation.com/ (accessed on 19 February 2022).
- Morgenstern, N.R. et al Fundão Tailings Dam Review Panel. Available online: https://pedlowski.files.wordpress.com/2016/08/fundao-finalreport.pdf (accessed on 5 February 2022).
- Julien, P.Y. Erosion and Sedimentation; Cambridge University Press: Cambridge, UK; New York, NY, USA, 1995; ISBN 978-0-521-44237-4. [Google Scholar]
- Mezger, T. The Rheology Handbook: For Users of Rotational and Oscillatory Rheometers. In The Rheology Handbook; Vincentz Network: Hannover, Germany, 2020; ISBN 978-3-7486-0370-2. [Google Scholar]
- O’Brien, J.S.; Julien, P.Y. Laboratory Analysis of Mudflow Properties. J. Hydraul. Eng. 1988, 114, 877–887. [Google Scholar] [CrossRef] [Green Version]
- Faitli, J.; Gombkötő, I. Some Technical Aspects of the Rheological Properties of High Concentration Fine Suspensions to Avoid Environmental Disasters. J. Environ. Eng. Landsc. Manag. 2015, 23, 129–137. [Google Scholar] [CrossRef]
- Jeong, S.-W. Shear Rate-Dependent Rheological Properties of Mine Tailings: Determination of Dynamic and Static Yield Stresses. Appl. Sci. 2019, 9, 4744. [Google Scholar] [CrossRef] [Green Version]
- Zengeni, B.T. Bingham Yield Stress and Bingham Plastic Viscosity of Homogeneous Non-Newtonian Slurries. Ph.D. Thesis, Cape Peninsula University of Technology, Cape Town, South Africa, 2016. [Google Scholar]
- Wang, X.; Wei, Z.; Li, Q.; Chen, Y. Experimental Research on the Rheological Properties of Tailings and Its Effect Factors. Environ. Sci. Pollut. Res. 2018, 25, 35738–35747. [Google Scholar] [CrossRef]
- Jeyapalan, J.K.; Duncan, J.M.; Seed, H.B. Investigation of Flow Failures of Tailings Dams. J. Geotech. Eng. 1983, 109, 172–189. [Google Scholar] [CrossRef]
- Yu, D.; Tang, L.; Chen, C. Three-Dimensional Numerical Simulation of Mud Flow from a Tailing Dam Failure across Complex Terrain. Nat. Hazards Earth Syst. Sci. 2020, 20, 727–741. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.-H.; Pan, Y.-W.; Dong, J.-J.; Yeh, K.-C.; Liao, J.-J. A Systematic Approach for the Assessment of Flooding Hazard and Risk Associated with a Landslide Dam. Nat Hazards 2013, 65, 41–62. [Google Scholar] [CrossRef]
- O’ Brien, J.S.; Julien, P.Y. Physical Properties and Mechanics of Hyperconcentrated Sediment Flows; Bowles, D.D., Ed.; Delineation of Landslide, Flash Flood, and Debris-Flow Hazards in Utah; Utah Water Research Laboratory: Logan, UT, USA, 1985; pp. 260–279. [Google Scholar]
- D’Agostino, V.; Tecca, P.R. Some Considerations On The Application Of The FLO-2D Model For Debris Flow Hazard Assessment. In Monitoring, Simulation, Prevention and Remediation of Dense and Debris Flows; WIT Press: The New Forest, UK, 2006; Volume 90, pp. 159–170. [Google Scholar]
- Naef, D.; Rickenmann, D.; Rutschmann, P.; McArdell, B.W. Comparison of Flow Resistance Relations for Debris Flows Using a One-Dimensional Finite Element Simulation Model. Nat. Hazards Earth Syst. Sci. 2006, 6, 155–165. [Google Scholar] [CrossRef] [Green Version]
- Sosio, R.; Crosta, G.; Frattini, P. Field Observations, Rheologucal Testing and Numerical Modeling of a Debris-Flow Event. Earth Surf. Process. Landf. 2007, 32, 290–306. [Google Scholar] [CrossRef]
- Rickenmann, D.; Laigle, D.; McArdell, B.W.; Hübl, J. Comparison of 2D Debris-Flow Simulation Models with Field Events. Comput Geosci 2006, 10, 241–264. [Google Scholar] [CrossRef] [Green Version]
- Cesca, M.; D’Agostino, V. Comparison between FLO-2D and RAMMS in Debris-Flow Modelling: A Case Study in the Dolomites. In Monitoring, Simulation, Prevention and Remediation of Dense Debris Flows II; WIT Press: The New Forest, UK, 2008; Volume 60, pp. 197–206. ISBN 978-1-84564-118-4. [Google Scholar]
- Lin, J.-Y.; Yang, M.-D.; Lin, B.-R.; Lin, P.-S. Risk Assessment of Debris Flows in Songhe Stream, Taiwan. Eng. Geol. 2011, 123, 100–112. [Google Scholar] [CrossRef]
- Hungr, O. A Model for the Runout Analysis of Rapid Flow Slides, Debris Flows, and Avalanches. Can. Geotech. J. 1995, 32, 610–623. [Google Scholar] [CrossRef]
- Arattano, M.; Franzi, L.; Marchi, L. Influence of Rheology on Debris-Flow Simulation. Nat. Hazards Earth Syst. Sci. 2006, 6, 519–528. [Google Scholar] [CrossRef]
- Coussot, P.; Meunier, M. Recognition, Classification and Mechanical Description of Debris Flows. Earth-Sci. Rev. 1996, 40, 209–227. [Google Scholar] [CrossRef]
- Zegers, G.; Mendoza, P.A.; Garces, A.; Montserrat, S. Sensitivity and Identifiability of Rheological Parameters in Debris Flow Modeling. Nat. Hazards Earth Syst. Sci. 2020, 20, 1919–1930. [Google Scholar] [CrossRef]
- Iaccarino, G. Quantification of Uncertainty in Flow Simulations Using Probabilistic Methods. In Proceedings of the Non-Equilibrium Gas Dynamics from Physical Models to Hypersonic Flights, Rhode St. Genèse, Belgium, 8 September 2008. [Google Scholar]
- Cepeda, J.; Quan Luna, B.; Nadim, F. Assessment of Landslide Run-out by Monte Carlo Simulations. In Proceedings of the Landslides, Risk & Reliability, Paris, France, 2 September 2013; pp. 2157–2160. [Google Scholar]
- Contreras, S.; Castillo, C.; Olivera-Nappa, Á.; Townley, B.; Ihle, C.F. A New Statistically-Based Methodology for Variability Assessment of Rheological Parameters in Mineral Processing. Miner. Eng. 2020, 156, 106494. [Google Scholar] [CrossRef]
- Kameda, J.; Okamoto, A. 1-D Inversion Analysis of a Shallow Landslide Triggered by the 2018 Eastern Iburi Earthquake in Hokkaido, Japan. Earth Planets Space 2021, 73, 116. [Google Scholar] [CrossRef]
- Stowe, J.; Farrell, I.; Wingeard, E. Tailings Transport System Design Using Probabilistic Methods. Min. Metall. Explor. 2021, 38, 1289–1296. [Google Scholar] [CrossRef]
- De La Rosa, Á.; Ruiz, G.; Castillo, E.; Moreno, R. Calculation of Dynamic Viscosity in Concentrated Cementitious Suspensions: Probabilistic Approximation and Bayesian Analysis. Materials 2021, 14, 1971. [Google Scholar] [CrossRef]
- Quan Luna, B.; Blahut, J.; van Westen, C.J.; Sterlacchini, S.; van Asch, T.W.J.; Akbas, S.O. The Application of Numerical Debris Flow Modelling for the Generation of Physical Vulnerability Curves. Nat. Hazards Earth Syst. Sci. 2011, 11, 2047–2060. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.-H.; Liu, K.-F.; Chen, Y.-C. Comparison between FLO-2D and Debris-2D on the Application of Assessment of Granular Debris Flow Hazards with Case Study. J. Mt. Sci. 2013, 10, 293–304. [Google Scholar] [CrossRef]
- Pasculli, A.; Cinosi, J.; Turconi, L.; Sciarra, N. Learning Case Study of a Shallow-Water Model to Assess an Early-Warning System for Fast Alpine Muddy-Debris-Flow. Water 2021, 13, 750. [Google Scholar] [CrossRef]
- Fallas Salazar, S.; Rojas González, A.M. Evaluation of Debris Flows for Flood Plain Estimation in a Small Ungauged Tropical Watershed for Hurricane Otto. Hydrology 2021, 8, 122. [Google Scholar] [CrossRef]
- Bingham, E.C. Fluidity and Plasticity.; McGraw-Hill: New York, NY, USA, 1922. [Google Scholar]
- Herschel, W.H.; Bulkley, R. Konsistenzmessungen von Gummi-Benzollösungen. Kolloid-Z. 1926, 39, 291–300. [Google Scholar] [CrossRef]
- Ligier, P.-L. Implementation of Non-Newtonian Rheological Models in TELEMAC-2D. In Proceedings of the 2020 TELEMAC-MASCARET, Online, 15 October 2020; pp. 14–25. [Google Scholar]
- Lumbroso, D.; Davison, M.; Body, R.; Petkovšek, G. Modelling the Brumadinho Tailings Dam Failure, the Subsequent Loss of Life and How It Could Have Been Reduced. Nat. Hazards Earth Syst. Sci. 2021, 21, 21–37. [Google Scholar] [CrossRef]
- Da Silva, A.; Eleutério, J. Effectiveness of Dam-Breach Flood Alert in Mitigating Life-Losses—A Spatiotemporal Sectorisation Analysis in a High-Density Urban Area in Brazil. Water, 2023; under review. [Google Scholar]
- Zenz, G.; Goldgruber, M. ICOLD Proceeding, 12th International Benchmark Workshop on Numerical Analysis of Dams. In Proceedings of the ICOLD Proceedings, Gerald Zenz and Markus Goldgruber, Graz, Austria, 2 October 2013; Volume 12, p. 210. [Google Scholar]
- Waele, A. Viscometry and Plastometry; Oil and Colour Chemists’ Association: Manchester, UK, 1923. [Google Scholar]
- Ostwald, W. Ueber die Geschwindigkeitsfunktion der Viskosität disperser Systeme. II. Kolloid-Z. 1925, 36, 157–167. [Google Scholar] [CrossRef]
- Qian, N.; Wan, Z. A Critical Review of the Research on the Hyperconcentrated Flow in China; International Research and Training Centre on Erosion and Sedimentation: Beijing, China, 1986. [Google Scholar]
- de Ferreira, F.O. Abordagem Matemática de Roll Waves em Escoamentos Hiperconcentrados Com Superfície Livre. Mater’s Thesis, Universidade Estadual Paulista, Faculdade de Engenharia de Ilha Solteira, Ilha Solteira, Brazil, 2007. [Google Scholar]
- Tarcha, B.A. Desafios na Medição da Tensão Limite de Escoamento de óleos Parafínicos. Mater’s Thesis, Universidade Federal do Espírito Santo, Centro Tecnológico, Vitória, Espírito Santo, Brazil, 2014. [Google Scholar]
- USACE (U. S. Army Corps of Engineers) HEC-RAS Mud and Debris Flow: Non-Newtonian User’s Manual. Available online: https://www.hec.usace.army.mil/confluence/rasdocs/rasmuddebris (accessed on 5 June 2022).
- Fitton, T.G.; Seddon, K.D. Relating Atterberg Limits to Rheology. In Proceedings of the Paste 2012, Australian Centre for Geomechanics, Perth, Australia, 16 April 2012; pp. 273–284. [Google Scholar]
- Ribeiro, V.Q.F. Proposta de Metodologia para Avaliação do Efeito de Rupturas de Estruturas de Contenção de Rejeitos. Master’s Thesis, Universidade Federal de Minas Gerais, Belo Horizonte, Brazil, 2015. [Google Scholar]
- Machado, N.C. Retroanálise da propagação decorrente da ruptura da barragem do fundão com diferentes modelos numéricos e hipóteses de simulação. Master’s Thesis, Universidade Federal de Minas Gerais, Belo Horizonte, Brazil, 2017. [Google Scholar]
- Gitari, W.M.; Thobakgale, R.; Akinyemi, S.A. Mobility and Attenuation Dynamics of Potentially Toxic Chemical Species at an Abandoned Copper Mine Tailings Dump. Minerals 2018, 8, 64. [Google Scholar] [CrossRef] [Green Version]
- Mahmood, A.A.; Elektorowicz, M. An Investigation of the Porosity Dependent Strength and Leachability of Mine Tailings Matrices Containing Heavy Metals. Cogent Environ. Sci. 2020, 6, 1743626. [Google Scholar] [CrossRef]
- Gibson, S.; Moura, L.Z.; Ackerman, C.; Ortman, N.; Amorim, R.; Floyd, I.; Eom, M.; Creech, C.; Sánchez, A. Prototype Scale Evaluation of Non-Newtonian Algorithms in HEC-RAS: Mud and Debris Flow Case Studies of Santa Barbara and Brumadinho. Geosciences 2022, 12, 134. [Google Scholar] [CrossRef]
- Bagnold, R.A. Experiments on a Gravity-Free Dispersion of Large Solid Spheres in a Newtonian Fluid under Shear. Proc. R. Soc. Lond. A 1954, 225, 49–63. [Google Scholar] [CrossRef]
- Rickenmann, D. Hyperconcentrated Flow and Sediment Transport at Steep Slopes. J. Hydraul. Eng. 1991, 117, 1419–1439. [Google Scholar] [CrossRef]
- Olsson, A.; Sandberg, G.; Dahlblom, O. On Latin Hypercube Sampling for Structural Reliability Analysis. Struct. Saf. 2003, 25, 47–68. [Google Scholar] [CrossRef]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code. Technometrics 1979, 21, 239–245. [Google Scholar] [CrossRef]
- Pirouz, B.; Javadi, S.; Seddon, K. Thickener Performance Variability: Underflow Solids Concentration and Flowrate. In Proceedings of the Paste 2017, University of Science and Technology Beijing, Beijing, China, 16 June 2017; pp. 29–40. [Google Scholar]
- Bezerra, R.; Eleutério, J. A Novel Full 2D Probabilistic Hydrodynamic Approach to Model and Map Floods from Dam Failures Considering Breach Parameters Uncertainty. Water, 2023; under review. [Google Scholar]
- Goodell, M.C.R. Breaking the HEC-RAS Code: A User’s Guide to Automating HEC-RAS, 1st ed.; H2ls: Portland, OR, USA, 2014; ISBN 978-0-9908918-0-2. [Google Scholar]
- Dysarz, T. Application of Python Scripting Techniques for Control and Automation of HEC-RAS Simulations. Water 2018, 10, 1382. [Google Scholar] [CrossRef] [Green Version]
- Papaioannou, G.; Vasiliades, L.; Loukas, A.; Aronica, G.T. Probabilistic Flood Inundation Mapping at Ungauged Streams Due to Roughness Coefficient Uncertainty in Hydraulic Modelling. Adv. Geosci. 2017, 44, 23–34. [Google Scholar] [CrossRef] [Green Version]
- Hamouda, T. Impact of Micro-Topography and Bathymetry Modification on Inundation Modelling with Different Magnitudes Based on SRTM Data. Master’s Thesis, UNESCO-IHE Institute for Water Education, Delft, The Netherlands, 2018. [Google Scholar]
- Da Silva, A.Â.C.L.; Eleutério, J.C. Identifying and Testing the Probability Distribution of Earthfill Dam Breach Parameters for Probabilistic Dam Breach Modeling. J. Flood Risk Manag. 2023, e12900. [Google Scholar] [CrossRef]
- Froehlich, D. Empirical Model of Embankment Dam Breaching. In Proceedings of the River Flow 2016, St. Louis, MO, USA, 11–14 July 2016; CRC Press: Boca Raton, FL, USA, 2016; pp. 1821–1826. [Google Scholar]
- FEMA (Federal Emergency Management Agency). Federal Guidelines for Inundation Mapping of Flood Risks Associated with Dam Incidents and Failures; FEMA: Washington, DC, USA, 2013; p. 145.
- Hussin, H.Y. Probabilistic Run-out Modeling of a Debris Flow in Barcelonnette, France. Thesis, ITC: Faculty of Geo-Information Science and Earth Observation, Enschede, The Netherlands, 2011. Available online: http://essay.utwente.nl/84877/ (accessed on 30 July 2023).
- Wooster, J.K.; Dusterhoff, S.R.; Cui, Y.; Sklar, L.S.; Dietrich, W.E.; Malko, M. Sediment Supply and Relative Size Distribution Effects on Fine Sediment Infiltration into Immobile Gravels. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef] [Green Version]




| Rheological Model | Varied Parameters | Literature Value Ranges | Adopted Interval |
|---|---|---|---|
| Bingham | Cv (%) | 9.3–65.0 | 20.0–60.0 |
| Max Cv (%) | 49.9–76.5 | 49.0–61.5 | |
| a (Pa) | 0.0000001–3.45 | 0.067–3.450 | |
| b | 1.2–40.0 | 1.2–10.359 | |
| Herschel-Bulkley (H-B) | Cv (%) | 20.0–60.0 | |
| τy (Pa) | 0.6–251.9 | ||
| K (Pa∙sn) | 0.008–130.0 | ||
| n | 0.192–1.5 | ||
| Results/Parameters | Bingham | Herschel H-B | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Cv | Max Cv | a | b | Cv | τy | K | n | ||
| Hmean | Region A1 | 0.4777 | 0.052 | 0.4357 | 0.6902 | −0.2728 | 0.8255 | 0.4149 | 0.1937 |
| Region A2 | 0.4737 | 0.064 | 0.4323 | 0.6896 | −0.2667 | 0.9317 | 0.2096 | 0.0881 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Melo, M.; Eleutério, J. Probabilistic Analysis of Floods from Tailings Dam Failures: A Method to Analyze the Impact of Rheological Parameters on the HEC-RAS Bingham and Herschel-Bulkley Models. Water 2023, 15, 2866. https://doi.org/10.3390/w15162866
Melo M, Eleutério J. Probabilistic Analysis of Floods from Tailings Dam Failures: A Method to Analyze the Impact of Rheological Parameters on the HEC-RAS Bingham and Herschel-Bulkley Models. Water. 2023; 15(16):2866. https://doi.org/10.3390/w15162866
Chicago/Turabian StyleMelo, Malena, and Julian Eleutério. 2023. "Probabilistic Analysis of Floods from Tailings Dam Failures: A Method to Analyze the Impact of Rheological Parameters on the HEC-RAS Bingham and Herschel-Bulkley Models" Water 15, no. 16: 2866. https://doi.org/10.3390/w15162866
APA StyleMelo, M., & Eleutério, J. (2023). Probabilistic Analysis of Floods from Tailings Dam Failures: A Method to Analyze the Impact of Rheological Parameters on the HEC-RAS Bingham and Herschel-Bulkley Models. Water, 15(16), 2866. https://doi.org/10.3390/w15162866









