Skip to Content
MDPIMDPI
WaterWater
PDF
  • Article
  • Open Access

31 July 2023

Understanding the Challenges of Hydrological Analysis at Bridge Collapse Sites

and
1
Department of Civil Engineering and Construction, Bradley University, Peoria, IL 61625, USA
2
Illinois Department of Transportation, Peoria, IL 61602, USA
*
Author to whom correspondence should be addressed.
Water2023, 15(15), 2772;https://doi.org/10.3390/w15152772
This article belongs to the Special Issue A Safer Future—Prediction of Water-Related Disasters
Version Notes
Order Reprints
Review Reports

Abstract

There is a crucial need for modeling hydrological extremes in order to optimize hydraulic system safety. It is often perceived that the best-fitted distribution accurately captures the intricacies of the hydrological extremes, particularly for the least disturbed watersheds. Thirty collapse sites with the least disturbed watersheds within the Appalachian Highland region in the U.S. are identified and used to test this perception. Goodness-of-fit tests, time series analysis, and comparison of predictor variables are carried out to find out the best-fitted distribution, identify trends and seasonal variation, and assess site variability. The study results are found to be inconclusive and sometimes contradictory; sometimes even complex distribution models do not provide better results. For most sites, the historic peak flow data are best-fitted with multiple distributions, including heavy and light tails. For monthly flow data, seasonal variation and trend cannot be categorized since no definitive, distinct tendency can be identified. When comparing sites best-fitted with a single distribution to sites best-fitted with multiple distributions, significant differences in certain geospatial characteristics are identified. However, these characteristics at the watershed scale are claimed to be less important in predicting the behavior of a flood event. All of these results capture the difficulties and inconsistencies in interpreting the results of hydrologic analysis, potentially reducing the robustness of the hydrologic tools used in the design and risk assessment of bridges.

1. Introduction

In the U.S., the hydraulic collapse frequency is estimated at 0.02% per year for a total population of about 504,000 bridges [1,2]. Hydraulic collapses include those induced by flood, scour, debris flow, and others [3]. Flooding is identified as one of the common reasons for total or partial bridge collapse [4,5,6]. Floods and scour are claimed to have caused 53% of collapses in the U.S. for the period of 1989 to 2000 [3] and 47% for the period of 1980 to 2012 [7]. Most of the flood- and scour-induced collapses are associated with steel bridges in the U.S. [7]. In a number of studies, the changing climate together with land use changes are linked with the increasing rate of extreme floods [8,9,10], and the increasing flood risk is linked with the increasing rate of hydraulic bridge collapse in the upcoming decades [11,12,13,14,15]. Whereas a number of studies predicted the severe impact of climate change on bridges with aging infrastructure in the U.S., one study predicted the direct cost of the climate impact would be about $140–$250 billion [11]. Another study predicted an increased loss of resources of 17% due to the anticipated increase in bridge collapses [14].
In climate risk studies and standard bridge design procedures, the derived return periods of chosen extreme flood events are frequently used [16,17]. In the U.S., the bridge design guidelines specify the use of a 100-year flood [18], whereas values between 50 and 100 years for flood design [19,20] and 100 to 500 years for scour design are common [5]. Methods for estimating the return period of a flood event include the block maxima approach, developed by an inter-agency committee led by the United States Geological Survey (USGS) and frequently referenced in bridge design manuals [17]. In the block maxima approach, a series of annual peak flows is used to define an extreme value distribution. The generalized extreme value distribution (GEV) is a widely used block maxima approach for extreme events that envelopes three types of distributions: Frechet, Gumbel, and Weibull distributions [21]. Nonetheless, given the changing climate and land use conditions, the selection of the most appropriate distribution to describe the phenomena under study is an ever-growing concern of modern science [22,23].
Many statistical tools for identifying the best-fitted model among a set of candidates have been suggested in the literature [24,25]. A good distribution model is expected to be simple, best-fitted to the data, and easily generalizable. Two of the most widely used model selection indicators are the Akaike information criterion (AIC) [26] and the Bayesian information criterion (BIC) [27]. The AIC and BIC include both the goodness-of-fit and the penalty term, which penalizes the selection as the complexity of the model grows [26,27]. Other goodness-of-fit tests, including Cramer-con Mises (CVM) and Anderson Darling (AD), are commonly used to test data-model differences [28]. However, the proliferation of efforts focusing on fitting data to a distribution, which is presented as proof of the model’s soundness and a justification for using the probabilistic distribution, might not have the required practical utility for hydraulic extrapolations [29].
More than three decades ago, a paper on hydrology [29] discussed the misconceptions common in hydrology and their consequences. With altering hydrologic conditions due to climate and land use change [17], the hydrologic challenges are becoming more intensified, particularly for investigating extreme events. Case studies [3,7,30,31,32] have investigated specific bridge collapses during extreme events, focusing on hydrology, hydraulics, and/or structural analyses with the goal of identifying design elements that should be improved. There is also a proliferation of studies focusing on the development of numerical and physical lab models [33]. The Federal Highway Administration (FHWA) in the U.S. suggested the use of mathematical and physical model studies as the highest level of evaluation since they are usually more expensive and time-consuming [33]. Regardless of the existence of these wide ranges of studies, most of them are site-specific and carried out independently with varying goals, scopes, and datasets. Therefore, it is difficult to integrate these study results into any universally robust methodology and/or tool. In fact, there is a lack of integrated large-scale studies analyzing hydrology, hydraulics, and structural interactions in relation to the tools and methodologies used. It should be noted that depending on the type of approach and statistical tools used in the bridge analysis, the results might be quite different. Sometimes the study results are also mixed and/or contradictory. For instance, current hydrologic studies of historical streamflow data have yielded mixed results in terms of current trends in annual peak flows and the existence of abrupt changes [34,35,36,37,38]. These mixed results obtained in recent hydrologic studies, together with the evolution of standards and studies in relation to confounding hydraulic factors (e.g., debris jam, river meandering, scour), suggest the possibility of a lack of uniformity in the statistical tools used in hydraulic design. Nonetheless, the engineering understanding and application of hydrology are often rather simplistic.
The goal of the paper is to identify the increased sophistication in understanding the challenges of hydrologic extremes in relation to commonly used statistical tools in hydraulics and related river engineering. To achieve the goal, three new objectives are identified: (1) detect the inadequacy and/or limitations of widely used model selection criteria and/or goodness-of-fit tests for annual peak flow data; (2) categorize trend and seasonal variation to provide additional insights into the underlying physical processes and site characteristics; and (3) compare predictor variables (watershed, climate, topography, human intervention, and other variables) to inform assessments of collapse risk in relation to the impact of climate and land use change on bridges. Analyses undertaken include the selection of best-fitted models for annual peak flow data, time series analysis of monthly flow data, and comparison of predictor variables. Thirty USGS stations within the Appalachian Highland (with the least disturbed watersheds) at or near which partial or complete collapse events occurred were selected for the study. These collapse sites represent 3% of the collapses linked to hydraulic causes as reported in the New York State Department of Transportation (NYSDOT) Failure Database [19]. The results of this set of sites can be used to evaluate and/or modify the approaches used in hydraulic design and hydraulic risk assessment, as well as to provide a more inclusive account of the performance of statistical tools as used in hydrology, hydraulics, and river engineering.

2. Methods

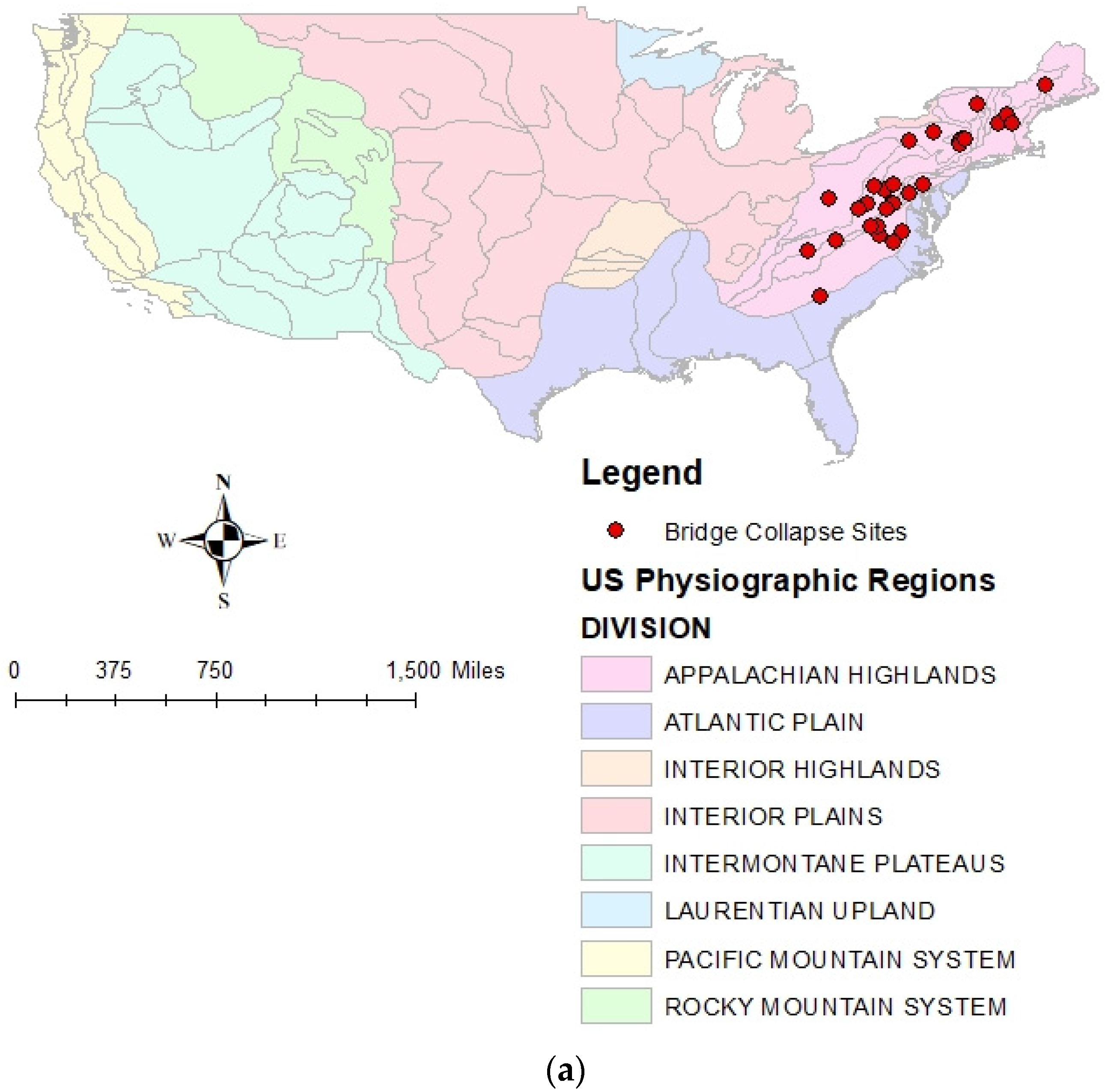
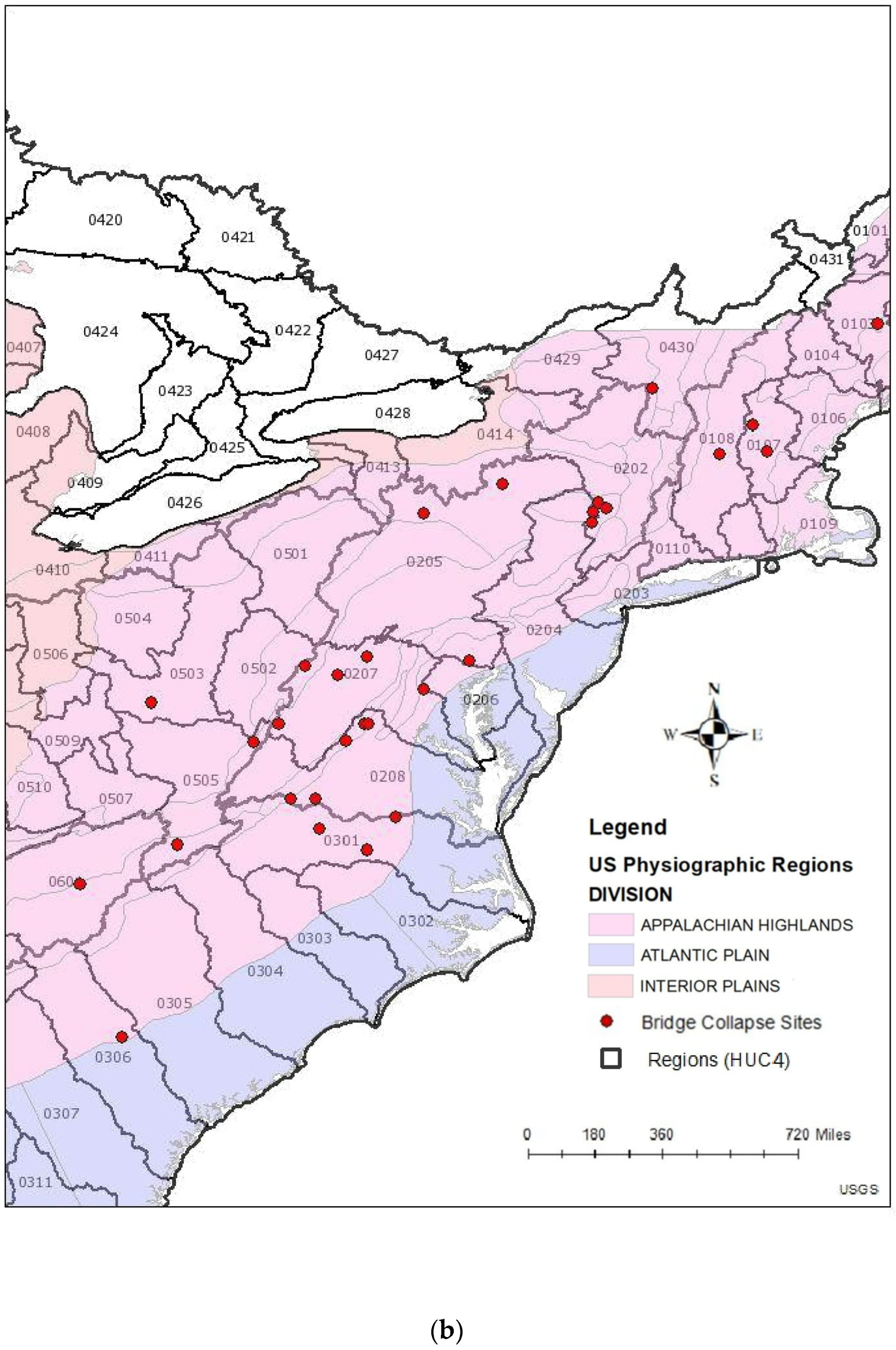
2.1. Selection of Sites

Thirty USGS stations were selected for the study (Figure 1). Seven out of thirty sites have flow records of less than fifty years, with six sites having a flow record of less than thirty years. A record of forty to fifty years is, in general, claimed to be satisfactory for extreme precipitation frequency analysis [39]. In other studies, it is argued that a twenty-five-year period of record is sufficient for extreme precipitation frequency analysis in humid regions [40]. For trend analysis, fifty years is typically named as the criteria for robustness [36]. The World Meteorological Organization (WMO) recommends a thirty-year period for the purpose of comparing hydrological and climatic characteristics [41]. According to guidelines developed by the Interagency Advisory Committee on Water Data in the U.S., at least ten years of records are required for flood frequency and other statistical analysis [42]. For the current study, twenty-two sites have more than fifty years of record, four sites have at least twenty-five years of record, two sites have at least twenty years of record, and two sites have at least fifteen years of record.
Figure 1. Thirty bridge collapse sites within the Appalachian Highland region in the U.S. (a) Location of sites in the U.S.; (b) Location of sites within the Appalachian Highland region with watershed boundaries (with HUC 04 ID).
In the current study, all available flow data are used for the analysis since all available annual peak flow data are being used to predict the probability of the design flood [42,43]. Available flow data with different lengths and periods have been used for trend analysis, retrospective studies, and/or comparison studies [17,44]. Since consistent flow records of the same length and period are difficult to obtain, the approach of using all available data is also being used in risk assessment tools [44]. Several State Departments of Transportation (DOTs) in the U.S. have used the risk assessment tool HyRisk, incorporating available data of different lengths and periods in relation to hydrology, hydraulics, and structure [45]. In the current study, since the hydrological regimes are least affected by human activities, the adopted approach is also similar to the approach of using ‘normal’, ‘quasi-periodicities’, or ‘potential’ cycles for hydrologic analysis [46]. Quasi-periodicities or potential cycles imply specific periods for which the watersheds are least disturbed [46]; therefore, such periods can be different across watersheds.
All of the selected USGS stations satisfy some specific criteria for inclusion in the study. Firstly, all of the sites chosen are classified as ‘reference’ sites by the USGS, which indicates that the sites possess the least altered hydrologic conditions [47]. The performance of hydrologic models in altered conditions is somewhat uncertain [48]. However, it is often assumed that the widely used statistical tools would be effective in analyzing hydrologic data within watersheds with minimal alterations. The selection of ‘reference’ sites within the least altered watersheds would help test such an assumption.
Secondly, the inclusion criteria for the study require the occurrence of partial or complete bridge collapse events at or near the USGS stations due to hydraulic reasons. The selected collapse sites are derived from the New York Department of Transportation Failure Database [19]. The inclusion of collapse sites in the study ensures that the results obtained are noteworthy and applicable for reducing future collapse risk and ensuring the safety of the hydraulic system.
Finally, all 30 sites selected for the study are located within the Appalachian Highland physiographic region. The Appalachian Highland region possesses intrinsic risk conditions, including high erosion at bed and bank and/or debris jams [45,49]. In a recent study on 147 collapse sites within the Appalachian Highland region, including the current study sites, it was found that the region exhibits the characteristics of hydrologic heterogeneity [50]. For the Appalachian Highland region, forty predictor variables are identified, and among them, certain climate and topography variables are found to be the most important variables (ranking 1 to 10) in predicting flood behavior [50]. Although relatively less important, anthropogenic conditions (i.e., dam density and road density) are also found to be associated with flood flow behavior [50]. In the current study, sites with specific best-fit distributions would be compared in relation to the forty predictor variables [50] as identified for the Appalachian Highland region.
Table 1 includes the information for the thirty selected USGS stations and the associated collapse sites within the Appalachian Highland region. The information about the station and related flow values is collected from the USGS. The related collapse site information is collected from the NYSDOT Failure Database [19].
Table 1. Information for thirty selected USGS stations and the associated collapse sites within the Appalachian Highland region.

2.2. Analysis of Annual Peak Flow Data

The methodology in the analysis of annual peak flow data as derived from the USGS is aimed at selecting the best-fitted distribution and identifying contradictory results. In the study, GEV is used to fit the annual peak flow data, and the derived shape parameter value is used to identify the specific type of distribution. GEV is a widely used model for extreme events due to its flexibility, interpretability, and theoretical justification for fitting to block maxima of data enveloping three types of extreme value behavior: Weibull, Gumbel, and Frechet distributions [21]. The location parameter (μ) of the GEV distribution implies the central tendency of the distribution. The scale parameter (σ) of the GEV implies the scale or spread of the distribution. The shape parameter (k) of the GEV is a measure of the tail behavior of the distribution. The heavy-tailed Frechet results from the shape parameter (k) being greater than 0, and the upper-bounded Weibull results from the shape parameter (k) being less than 0 [51]. The Gumbel distribution is obtained when the shape parameter (k) tends to be zero or close to zero [51]. The annual peak flow data are also fitted with other widely accepted extreme value distributions, such as Lognormal and Pareto. The Log-Person Type III distribution is excluded from the study since the interpretation of the physical mechanism in relation to the fitted Log-Person Type III distribution, with two interacting shape parameters, is complicated [52].
The AIC [26] and BIC [27] values are utilized to compare the fitted distributions and/or select the best-fitted models. The AIC provides a measure of the relative quality of a statistical model by evaluating the balance between goodness-of-fit and model complexity [26]. The BIC is similar to the AIC but places a stronger penalty on models with a large number of parameters [27]. Other goodness-of-fit tests, including the Likelihood Ratio test [51], the AD test [28], and the CVM test [28], are also conducted. The Likelihood Ratio test is used to compare the fit of two nested models (GEV and Gumbel), where one model (Gumbel) is a simplified or restricted version of the other (GEV) [51]. The AD test provides goodness-of-fit by evaluating whether the data fit the assumptions of the fitted statistical model [28]. The test statistic used in the CVM is less sensitive to the tails of the distribution compared to the AD test [28], making it more appropriate when the interest is in testing the overall fit of the distribution to the bulk of the data. The extReme R [51], ismev R [53], fitdistrplus R [54], gnfit R [55], and goftest R [56] packages are used to fit multiple distributions to the annual peak flow data and conduct goodness-of-fit tests.
Finally, both the Pettitt-Mann-Whitney (PMW) [57] and Mann-Kendall (MK) [58] tests are used to detect abrupt changes and trends in annual peak flow data. The PMW test is primarily used to detect a change or abrupt shift in the data, and it assumes that the data before and after the change point have different distribution functions [57]. On the other hand, the MK test is used to detect a monotonic trend in time series data [58]. The trend R package [59] and the kendall R package [60] are used to conduct PMW and MK tests. The annual peak data used in the study can be accessed at https://github.com/fahmidah/Challenges-in-Hydrologic-Extremes/tree/main/Annual%20Peak%20FLow (accessed on 20 January 2023).

2.3. Analysis of Monthly Flow Data

The methodology in the analysis of monthly flow data is aimed at identifying the correlation, seasonal variation, and trend. Correlation measures the linear association between a pair of variables (x, y), and it takes a value between −1 and +1, with a value of 0 indicating no linear association. For the study, the correlation between the values of monthly flow data at different lags (time intervals) is measured and presented in the correlogram. To identify the type of seasonal variation and any apparent trend, the X11 decomposition model [61], developed by the U.S. Census Bureau and Statistics Canada, is used. A decomposition model is a statistical technique used to break down a time series into its constituent components, including trend, seasonality, and irregularity. The X11 decomposition envelops both additive (constant over time) and multiplicative (changing over time) time series [61], and it tends to be highly robust to outliers and level shifts in the time series [61]. To gain a clearer view of the seasonal variation, including outliers, a summary of the values for each season is also viewed using a boxplot. Because of the possibility of exhibiting trend and seasonal effects, the Augmented Dickey–Fuller (ADF) test is conducted to check the stationarity of the data. The seasonal R package [62] is used to implement the X11 decomposition.
To check whether the monthly flow data follows a deterministic or stochastic (random) trend, the correlogram of the series of differences is derived and analyzed for each site [63]. The first-order differences of a random walk are a white noise series, so the correlogram of the series of differences can be used to assess whether a given series is a random walk or not [63]. Finally, for a better approximation of the series, the Holt-Winters (HW) model [63] is used to fit the monthly flow data and is compared to the Random Walk (RW) model. The parameters of the Holt-Winters model take into account three components of a time series: level (α), changing trend (β), and changing seasonality (γ) [63].
The parameters of the Holt-Winters (HW) model as derived for each site are compared using the hypsometric curves [64]. The hypsometric curves illustrate the distribution of normalized model parameters. The model parameters at each site are normalized with the mean value of the model parameters [65]. The normalized (or scaled) model parameters are defined as α* (α/Average α), β* (β/Average β), and γ* (γ/Average γ). The normalized hypsometric curves of α*, β*, and γ* can be used to assess the variation in level (α), changing trend (β), and changing seasonality (γ) across different sites. The monthly flow data used in the study can be accessed at https://github.com/fahmidah/Challenges-in-Hydrologic-Extremes/tree/main/Monthly%20Flow%20Data (accessed on 20 January 2023).

2.4. Analysis of Predictor Variables

The methodology is aimed at identifying any significant differences among geospatial characteristics by comparing two types of collapse sites. The first comparison is between sites where peak flow data is best-fitted with a single distribution versus sites where peak flow data is best-fitted with multiple distributions. The second comparison is between sites best-fitted with heavy tail distributions versus sites best-fitted with light tail distributions.
The geospatial characteristics used for the comparison study were retrieved from the “GAGES II dataset” [47]. The dataset includes watershed characteristics, including environmental features (e.g., climate—including precipitation, geology, soils, and topography) and anthropogenic influences (e.g., land use, road density, or presence of dams) [47]. For all selected variables, the extent scale is watershed [47]. All these variables are also continuous and have physical meaning [47,50].
In a recent study [50], the importance levels are derived for the geospatial variables (from the GAGES II dataset) in relation to their capability in predicting the flood behavior at the bridge collapse sites. In the referred study [50], forty variables are ranked (from one to forty) in relation to their predicting ability within different regions, including the Appalachian Highland region. Among the forty predictor variables, fifteen are related to climate, seven are related to watershed, six are related to soil, five are related to topography, three are related to population infrastructure, and four are related to dam infrastructure [50]. Only the ranked (one to forty) predictor variables from the referred study [50] are used here for the comparison of the collapse sites. The goal is to identify specific important predictor variables (or geospatial characteristics) that are significantly different when comparing two types of collapse sites as fitted with single versus multiple and heavy versus light tail distributions. Such findings can help us further investigate specific geospatial characteristics that might lead to specific peak flow distributions, that is, specific flood behavior. In the current study, forty predictor variables, ranking from one to forty [50], are compared using the t-test [66]. Details about the forty predictor variables within the Appalachian Highland region can be found at https://github.com/fahmidah/Challenges-in-Hydrologic-Extremes/blob/main/Predictor%20Variables%20of%20Collapse%20Sites.xlsx (accessed on 20 January 2023).

3. Results

3.1. Annual Peak Flows

A majority of the sites (60%; eighteen out of thirty) exhibit a heavy tail distribution for the annual peak flow data. Sites with heavy-tailed distributions tend to exhibit a large number of small samples, with a few very large samples that can significantly impact the overall behavior of the distribution [67]. However, none of the sites exhibit a heavy-tailed Pareto distribution as best-fitted; that is, none of the sites exhibit an infinite mean and/or variance [67]. Additionally, no sites exhibit any significant abrupt change in the flow data except for two (USGS stations #01662800 and #01665500), although for the majority of sites (seventeen out of thirty), the annual peak flow data is best-fitted with multiple distributions. The AIC and BIC values for all fitted distributions, including the results of Mann-Kendall and Pettitt’s tests, can be accessed at https://github.com/fahmidah/Challenges-in-Hydrologic-Extremes (accessed on 20 January 2023).

3.1.1. Best-Fitted with Heavy Tail Distributions

About 13% of the sites (four out of thirty) exhibit consistent statistical results for the best-fitted distribution (Table 2). At these four sites, the Frechet distribution (GEV shape parameter > 0) is found to be the best-fitted distribution with minimum AIC/BIC values (Table 2). The goodness-of-fit tests (AD and CVM tests) fail to reject the GEV–Frechet distribution (Table 2), and the Likelihood Ratio test rejects the light tail (Gumbel) in favor of the heavy tail distribution (GEV–Frechet) (Table 2). For the Frechet distribution, a higher probability is assigned to the occurrence of rare extreme events as compared to other distributions except for Pareto. The data fitted with the Frechet distribution is also claimed to have two distinct characteristics: (a) regularly varying and (b) a decreasing hazard rate (DHR) [67]. If a dataset is regularly varying, then the tail of the distribution closely follows a power law [67]. A power law represents a relationship between two quantities where a relative change in one quantity results in a relative proportional change in the other quantity [67]. On the other hand, a DHR implies that there is a decreasing likelihood of observing an extreme value as time passes in consecutive years; one example of a DHR is the decreasing likelihood of receiving a response to an email as time passes [67]. All of the four sites modeled with Frechet distribution exhibit positive trends, but none of the trends are found to be significant.
Table 2. Sites best-fitted with the GEV–Frechet distribution with minimum AIC and BIC values.
At nine sites, the Lognormal distribution is found to be the best-fitted distribution with minimum AIC/BIC values (Table 3). The Lognormal distribution is intimately tied to the growth of multiplicative processes [67]. However, the fitted Lognormal distribution is rejected by the CVM test, whereas the AD test fails to reject the Lognormal distribution (Table 3). The AD test is more sensitive to deviations in the tails of the distribution [68,69]; this might explain the discrepancies in the test results. On the other hand, both the CVM and AD tests fail to reject the GEV–Frechet distribution (shape parameter > 0) (Table 3) as fitted with higher AIC/BIC values compared to Lognormal. Here, the Likelihood Ratio test rejects the light tail (Gumbel distribution) in favor of the heavy-tailed GEV. For these nine sites, five are exhibiting positive trends (two significant trends), while four are displaying negative ones.
Table 3. Sites best-fitted with the Lognormal distribution with minimum AIC and BIC values.
At five sites, the annual peak flow is well-fitted with two heavy-tailed distributions, GEV–Frechet and Lognormal, with minimum AIC or BIC values (Table 4). Both AD and CVM tests fail to reject the fitted GEV–Frechet distribution except for site #1644000. For the Lognormal distribution, the AD test also fails to reject the fitted distribution except for site #1644000, whereas the CVM test rejects the Lognormal for all considered sites. For site #1644000, the goodness-of-fit test results are, therefore, inconclusive since both fitted distributions are rejected. Among the five sites, four are exhibiting positive trends (insignificant), while one is exhibiting a significant negative trend.
Table 4. Sites best-fitted with the GEV–Frechet and Lognormal distributions with minimum AIC or BIC values.

3.1.2. Best-Fitted with Heavy and Light Tail Distributions

For twelve sites considered, the fitted GEV and Gumbel distributions are found to be not significantly different from each other as evidenced by the Log-Likelihood Ratio test results (Table 5); that is, there is no strong evidence to suggest that the more complex model (GEV) provides a better fit compared to Gumbel (light tail). At eleven sites, the annual peak flow data is best-fitted with both heavy (Frechet, Weibull, or Lognormal) and light tail (Gumbel) distributions with minimum AIC or BIC values (Table 5). The AD and CVM test results also do not provide evidence to reject the hypothesis of a light-tailed distribution (Gumbel) in favor of heavy-tailed distributions (Frechet or Weibull). However, the CVM test rejects the Lognormal distribution. For the sites considered, the statistical results are, therefore, inconclusive and/or contradictory, fitting with both heavy and light tails. Selecting the heavy tail distribution suggests that extreme flow events are more likely to occur, while opting for the light (Gumbel) tail distribution suggests the opposite, that extreme flow events are less likely to occur. In such cases, the underlying physical processes must be evaluated before selecting a single distribution. A mixed distribution can be used since the available data is fitted with multiple distributions, implying a mixed population. Here it should be noted that water management decisions are increasingly being made through a consensual approach, including relevant stakeholders, expert opinions, and peer review [39]. Regardless of the approach used in decision-making, the selection should be governed by the quality and quantity of data as retrieved from a highly variable environment in terms of weather, climate, land use, human intervention, and/or natural vegetation. Among the considered sites, six are exhibiting positive trends (insignificant), while five are exhibiting negative trends (insignificant).
Table 5. Sites best-fitted with heavy and light tail distributions.

3.2. Monthly Flows

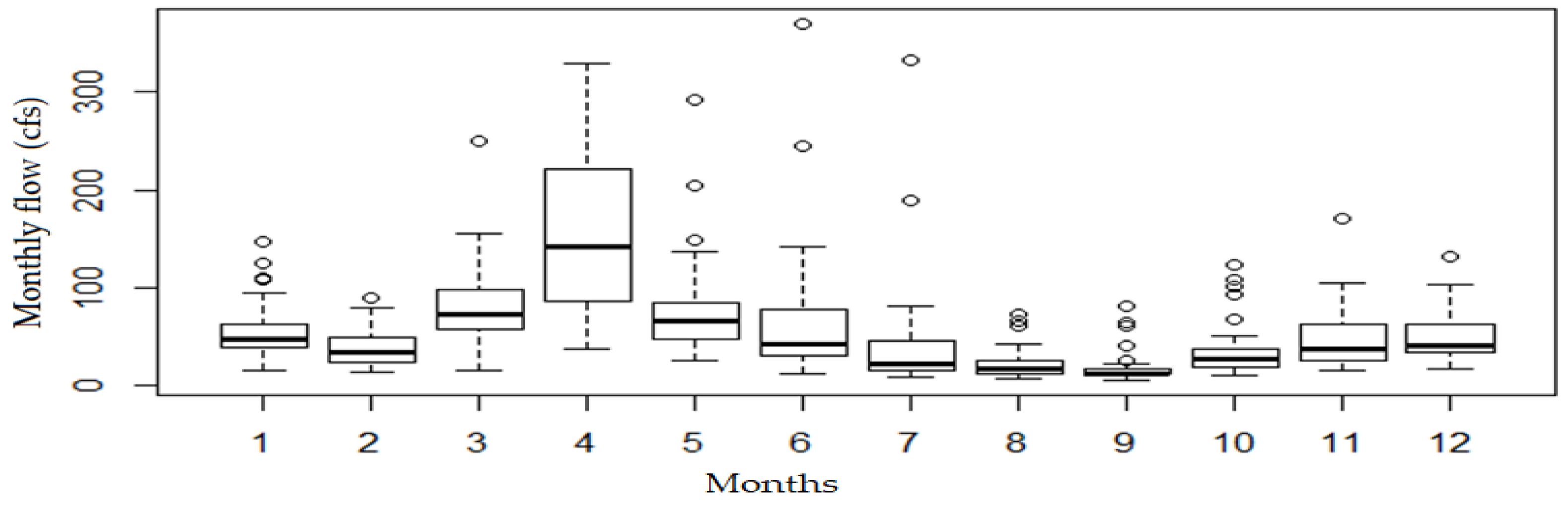
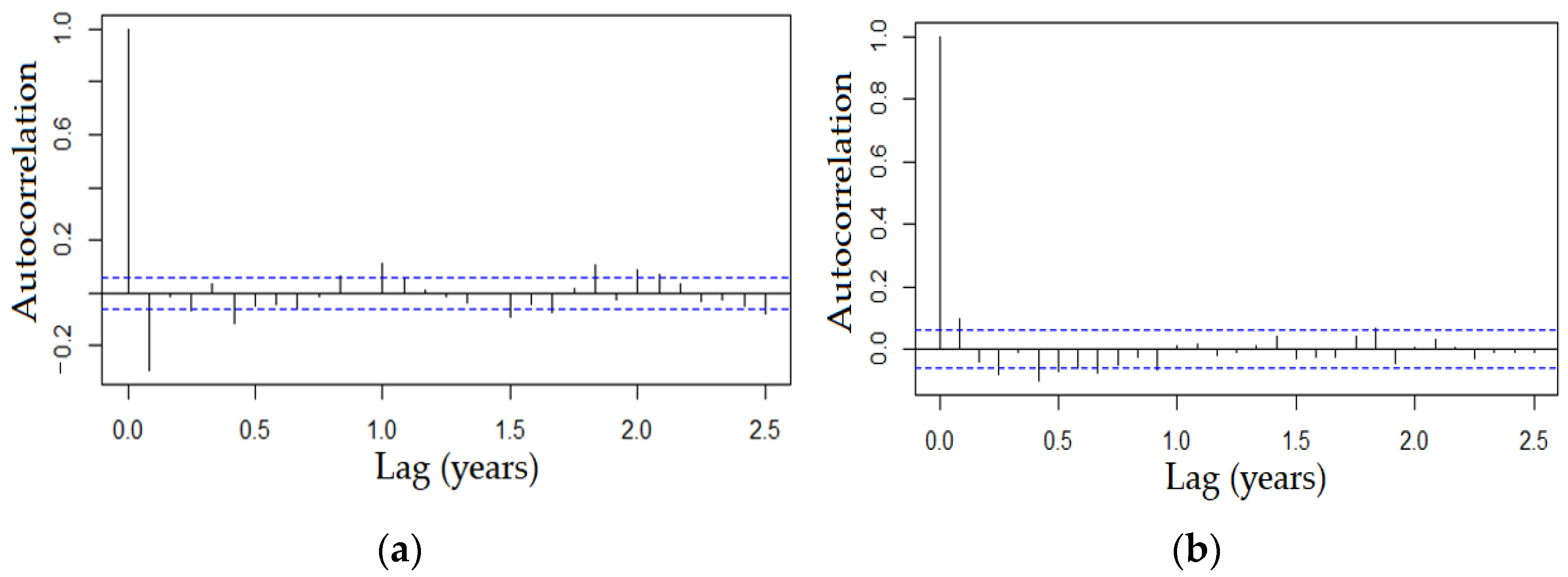
3.2.1. Correlogram and Boxplot

Examples of derived correlograms are provided in Figure 2. In Figure 2, the x-axis gives the lag (in years), and the y-axis gives the autocorrelation at each lag. There are no units for the y-axis since the correlation is dimensionless. The dotted lines in Figure 2 represent the 5% significance level for the statistical test. Any correlations that fall outside these lines are ‘significantly’ different from zero. The lag 0 autocorrelation in Figure 2 is always 1, and it provides an indicator of the relative values of the other autocorrelations.
Figure 2. Examples of correlograms for the monthly flow data. (a) USGS station #03164000; (b) USGS station #01362370.
For all sites, significant autocorrelations are found at multiple lags (Figure 2), which can be expected for monthly flow data. For most of the sites (twenty out of thirty sites), the derived autocorrelations reflect both significant positive and negative linear relationships between pairs of variables separated by different lags (Figure 2a, Table 6), which implies that higher flows tend to occur in the specific months followed by lower flows in the consecutive months. It is worth looking for significant values at significant lags (Table 6), i.e., the annual cycle (lag 1 or twelve months) and seasonal period (lag 0.5 or six months). For all sites except one, the annual cycle appears with a significant positive correlation at one year in the correlogram (Table 6). This reflects a significant positive linear relationship between pairs of flow values (xt, xt+12) separated by twelve-month periods. Conversely, values separated by a period of six months tend to have a significant negative relationship for most sites (twenty out of thirty sites) (Table 6). Higher values tend to occur in the summer months, followed by lower values in the winter months. A significant negative correlation, therefore, occurs at a lag of six months (or 0.5 years). The maximum significant correlation is found at lag 0.1 (1 month) for twenty-five out of thirty sites. The significant autocorrelation at one month (Table 6, Figure 2a,b), which is found for all sites, generally implies an increasing trend over the period of the flow data [63]. Another marginal piece of evidence of a trend can be discerned from the correlogram. If a trend is present in the data, it will show as a slow decay in the autocorrelations in the correlogram [63]. The data in Figure 2a provides somewhat marginal evidence of the slow decay in the autocorrelations, which holds true for most of the sites. The available monthly flow data at all sites are found to be stationary, rejecting the null hypothesis of non-stationary data (p-value < 0.1) (Table 6).
Table 6. Analysis results for monthly flow data.
The boxplot summarizes the observed values for each season; an example is provided in Figure 3. The presence of outliers for both summer and winter months is evident in the derived boxplot (Figure 3). A tendency for higher flows over the summer months is also evident in the boxplot (Figure 3). The presence of outliers over several months holds true for all of the studied sites. The derived correlograms and boxplots for all sites can be accessed at https://github.com/fahmidah/Challenges-in-Hydrologic-Extremes/tree/main/Correlogram%20and%20Boxplot (accessed on 20 January 2023).
Figure 3. Seasonal boxplot of the monthly flow data (cfs) at USGS station #04273800. On the x-axis, the numbers represent consecutive months (January, February, March, etc.).

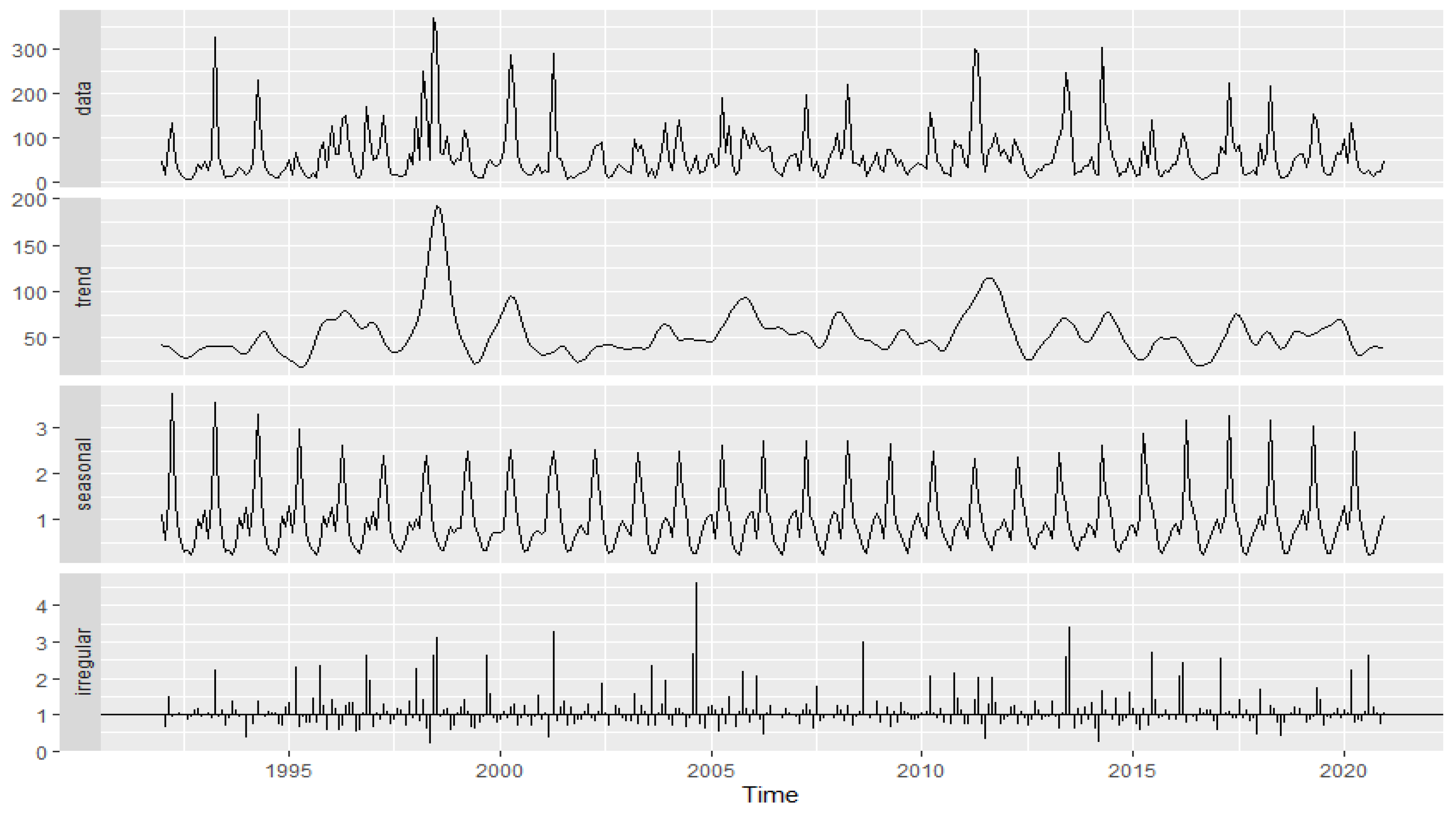
3.2.2. Decomposition

An example of a decomposition model is provided in Figure 4. It is a common practice not to include units in the y-axis of the decomposition series [63] since the goal of the decomposition series is to highlight the qualitative characteristics of the data, including significant shifts and the overall trend. For the current study, the decomposition series is retrieved based on the monthly flow values (in cfs).
Figure 4. Decomposition of the monthly flow data (in cfs) at USGS station #04273800.
In Figure 4, the trend cycle has captured the peak in the data that occurred in the month of June 1998. No obvious deterministic trend (upward or downward) is detected for the data series (Figure 4). For the seasonal component, it decreases at the beginning of the period, then remains somewhat constant for some period of time, and finally increases at the end of the time period (Figure 4). The constancy of the seasonal component implies additives, and variation in the seasonal component implies a multiplicative process. For all sites, the decomposed series reveals the absence of any monotonic deterministic trend and the presence of both additive and multiplicative seasonal variation. An additive process is one in which the effect of one variable on another is constant or fixed. A multiplicative process, on the other hand, is one in which the effect of one variable on another is proportional or changes with the level of the variable. A physical system with both additive and multiplicative processes can possess a combination of phenomena that have different effects on the output or behavior of the system. For the decomposition series in Figure 4, the unusual observation (peak flow) in 1998 can be clearly seen in the irregular component of the decomposition. Each irregular monthly observation requires a detailed investigation, which is outside the scope of the current study. The derived decomposed series for all sites can be accessed at https://github.com/fahmidah/Challenges-in-Hydrologic-Extremes/tree/main/Decomposition (accessed on 20 January 2023).

3.2.3. Random Walk and Holt-Winter Models

The monthly flow data is better fitted with the Holt-Winters (HW) model as compared to the Random Walk (RW) model. In Figure 5a, no obvious patterns in the correlogram are detected, implying the absence of any significant deterministic trend in favor of the random walk trend [63]. However, significant values at different lags are present in the correlogram, particularly at lag 0.1 (Figure 5a). The Holt-Winters (HW) model with additional parameters (change in trend, β, and change in seasonality, γ) provides a better fit (Figure 5b). For the HW model, the ‘significant’ values, as obtained for sites, can be ignored because they are small in magnitude (<5%) (Figure 5b), and about 5% of the values are expected to be statistically significant even when the underlying correlation values are zero. The results provided in Figure 5 are typical for all stations in that the significance of existing correlations decreased as the data was fitted with the HW model as opposed to the RW model. The derived correlograms for RW and HW models for all sites can be accessed at https://github.com/fahmidah/Challenges-in-Hydrologic-Extremes/tree/main/Random%20Walk%20and%20Holt%20Winters%20Model (accessed on 20 January 2023).
Figure 5. The correlograms for fitting monthly flow data with the Random Walk versus Holt-Winters model at USGS station #03164000. (a) Correlogram of the Random Walk model; (b) Correlogram of the Holt-Winters model.
Most of the sites exhibit both changes in trend and changes in seasonality, as evidenced by the derived HW model parameters (Table 6). There are a few sites for which the value of beta (β) is found to be zero, which implies that there is no change in trend for these sites. Hypsometric curves for the model parameters are plotted in Figure 6. If there is no variation in model parameters across different sites, the plotted line would appear as a vertical line at Model parameter* = 1 with a standard deviation equal to 0. It is apparent that a wider variation is found for β across different sites (Figure 6), with a standard deviation of about 1.24. The standard deviation for α* is calculated as 0.67, and the standard deviation for γ* is calculated as 0.61. The derived α, β, and γ values are provided in Table 5, including the maximum linear dependency as obtained for RW and HW models.
Figure 6. Hypsometric curves of normalized Holt-Winters model parameters (α, β, and γ).

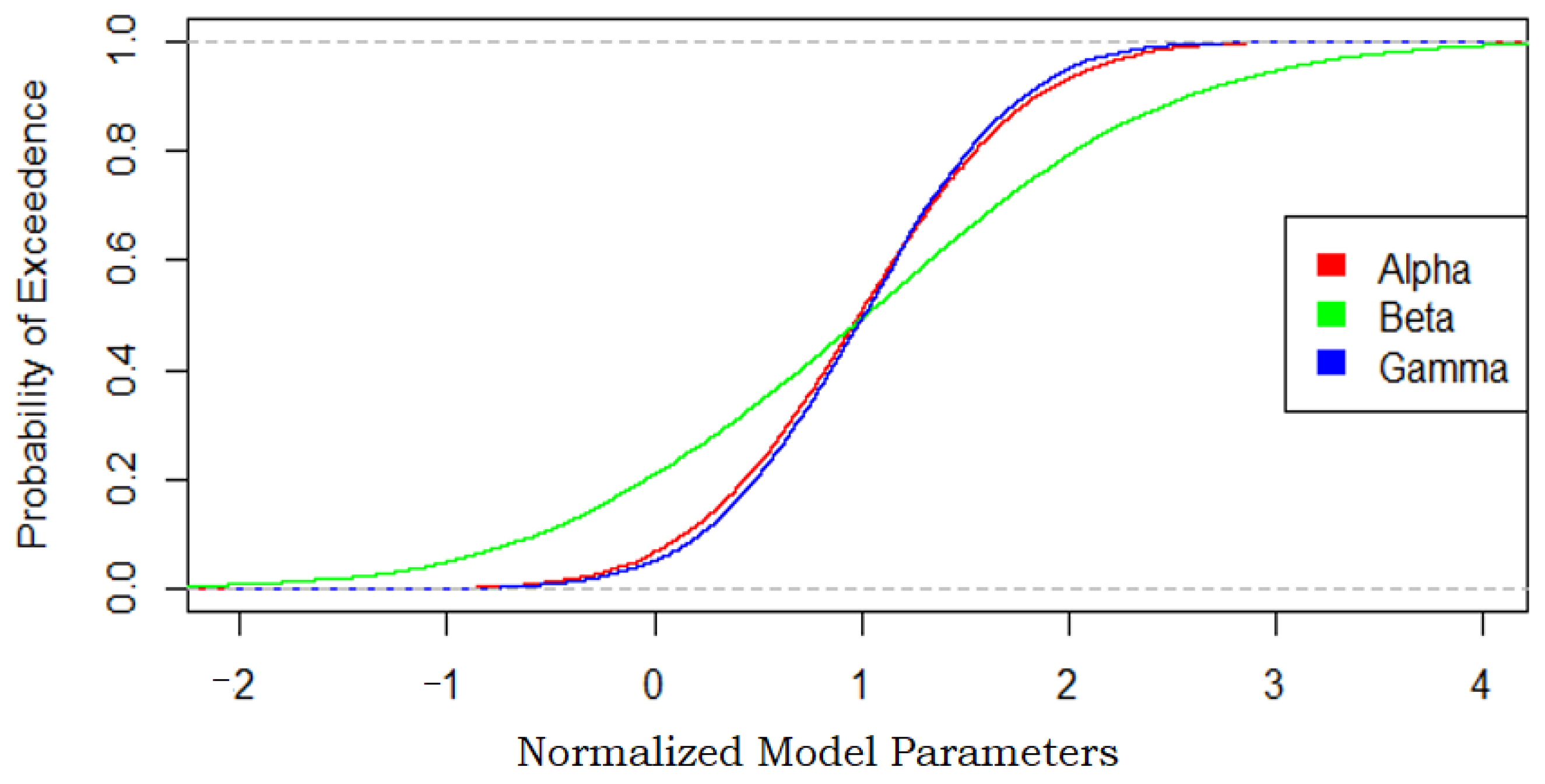
3.3. Predictor Variables

Few predictor variables are found to be significantly different when comparing two types of collapse sites in relation to the fitted distributions. When comparing sites where peak flow data is best-fitted with a single distribution with sites where peak flow data is best-fitted with multiple distributions, four variables are found to be significantly different: two variables are related to topography, one is related to population infrastructure, and one is related to climate (Table 7). When comparing sites best-fitted with heavy tail distributions with sites best-fitted with light tail distributions, six variables are found to be significantly different: three variables are related to topography, one variable is related to climate, one variable is related to watershed, and one is related to dams (Table 7). Two common predictor variables that are found to be significantly different for both comparisons are (a) the standard deviation of elevation (meters) across the watershed and (b) the standard deviation of the maximum monthly air temperature (degrees C). Attention should be given to the anthropogenic changes (percent of impervious changes and dam density), which are found to be significantly different (Table 7), in order to investigate their effect on the behavior of the flood flow. Such investigation is essential since the collapse sites are referred to as reference sites by the USGS with the least disturbed watersheds, that is, the flow is claimed to be least affected by anthropogenic changes [47].
Table 7. Significantly different predictor variables in relation to the comparisons of best-fitted distributions.
Based on a recent study [50], the predictor variables, which were found to be significantly different (Table 7), are comparatively less important (ranking between eleven and forty) for their ability to predict the behavior of a flood. That is, the most important predictor variables, ranking one to ten [50], are not significantly different (Table 8) across the study sites regardless of the difference in the fitted distributions. The absence of any significant difference among the most important variables can be expected since all sites are located within the same physiographic region. However, it should also be noted that the extent scale of all predictor variables considered is watershed, that is, they are not site-specific.
Table 8. Important predictor variables that are not significantly different across the study sites.

4. Discussion

In the current study, the potency of the results can be justified through the following factors: (a) use of all available data, which is a common practice for flood frequency analysis [42,43], (b) stationarity of the flow data, (c) absence of any significant abrupt change in annual peak flow data, and (d) presence of the least anthropogenic changes [47]. Nonetheless, there can be many wrong reasons why models may work well for different datasets [70]. Additionally, it is imperative that analysis time periods be chosen selectively, for instance, using change point detection methods [71], which is upheld in the current study. However, the five sites with the best multiple distributions have datasets of less than 50 years, and the studied time periods are of various lengths and periods. As more data become available for the studied sites, analysis can be focused on the development of 50-, 100-, and 150-year studies. The key findings of the study are discussed here:
(a)
Annual peak flow data is best-fit with multiple distributions. For seventeen out of thirty of the collapse sites (56%), the annual peak flow data is best-fitted with multiple distributions. For eleven out of thirty collapse sites (36%), the annual peak flow data is best-fitted with both heavy and light tail distributions with minimum AIC/BIC values, and the goodness-of-fit tests also fail to reject the fitted distributions. Such a finding implies discrepancies or complexity in the dataset studied. It might also suggest that there might be distinct groups or modes within the data, and each group may have its own underlying distribution. Whereas one specific distribution might be reasonable for modeling the central tendency (or concentrated values), another distribution might be more reasonable to model the tail behavior (extreme values). Each best-fitted distribution may help uncover the underlying patterns and provide a more nuanced understanding of the distinct low, medium, and/or high flow values. Finally, site-specific, rigorous investigation is essential, invoking analysis of hydrologic, climatic, geologic, or other hydraulic conditions so that the background physics can be relatively well understood.
(b)
There is a discrepancy between the model selection criteria and the goodness-of-fit tests. At about 76% of sites (23 out of 30 sites), the annual peak flow data is best-fitted with a Lognormal distribution with minimum AIC and/or BIC values. However, for all of these sites, the fitted distribution is rejected by the CVM test, whereas for two sites, the distribution is rejected by both the AD and CVM tests. The AIC/BIC and the goodness-of-fit tests are based on different statistical principles and have different underlying assumptions. The AIC/BIC favor models with a high likelihood but implement a penalty for complexity [26,27]. The AD test (a weighted version of the CVM statistic) emphasizes differences near the ends, that is, differences between actual high values and predicted high values [72]. As the Lognormal distribution is not rejected by the AD test, it implies that it can capture the high values relatively well. The CVM statistic is favorable for models regardless of the large-scale or small-scale confidence intervals as retrieved for the shape of the distribution [72]. The CVM statistic also gives equal weight to all observations, including very low and very high values [72]. Therefore, the Lognormal distribution as rejected by the CVM test implies that it cannot capture all observations, including very low and very high values. It is apparent that when the interest is on the tail of the distribution, particularly for heavy tails, adopting certain standard statistical procedures (in reference to the hydraulic design manual) might not be a reasonable choice.
(c)
Complex models do not provide significantly better results. For the majority of the sites (87%), a simple model such as Gumbel and/or a Lognormal distribution provides a reasonable fit to the dataset with minimum AIC and/or BIC values. A complex model such as GEV does not improve the fit significantly. Additionally, for GEV, the exact type of enveloped distribution (Gumbel, Weibull, or Frechet) cannot be determined decisively for 40% of the sites (twelve out of thirty). Nonetheless, the diminishing credibility of complex hydrologic models is not acknowledged in current hydraulic design approaches; a number obtained from a complex distribution (i.e., GEV) with no clearly defined physical process seems to be taken with the same consideration as one obtained from a simple model (i.e., Lognormal) with a clearly defined physical process (i.e., multiplicative).
(d)
The trend and seasonal variation in the time series data cannot be identified decisively. For monthly flow data, the derived trend does not fit into either a deterministic trend or a random walk trend decisively. Across all sites, the trend is also changing to a wide variety of degrees. For annual peak flow data, no trend is found to be statistically significant at most of the sites. These findings in the preliminary analysis might exclude the collapse sites from further investigation in relation to risk prioritization and resource allocation since linking the collapse risk to the identification of significant positive trends is a common practice in risk studies [17]. Whereas identification of a specific type of trend provides insights into long-term patterns or changes to assess possible changes to collapse risk, the intricacy of pattern recognition in relation to complex hydraulic systems (i.e., debris jams) cannot be performed only using standard trend recognition approaches, at least for the studied collapse sites. In fact, the results of the trend analysis in this study are consistent with other studies in that statistically significant trends were not found at the majority of sites, with mixed results in terms of current trends (positive or negative) [9,35,36,37,38].
(e)
Local site characteristics should be considered in relation to fitted distributions. All the studied sites are located within the Appalachian Highland region and are associated with different watersheds. Most of the geospatial characteristics (at the watershed scale) are not significantly different in relation to the comparison of the fitted distributions (i.e., single versus multiple distributions). On the other hand, significantly different characteristics (at the watershed scale) are claimed to be less important in predicting flood behavior [50]. Such a result implies that the spatial scale might need to be narrowed down to identify site-specific differences that lead to specific probabilistic distributions, at least for the studied collapse sites. Recent studies on the collapse sites do reveal specific characteristics for the collapse sites within different physiographic regions, including the Appalachian Highland, such as (a) the presence of very high and very low flows [73], (b) debris jams [45,73], (c) high erosion at bed and bank [45,73], (d) the presence of other in-stream structures [45,73], and (e) the removal of vegetation and other human interference [45]. Such site-specific characteristics are typically included in the hydraulic analysis. In fact, hydraulic analysis is mainly focused on a local scale, whereas hydrologic analysis is mainly focused on a watershed scale. Therefore, rigorous scientific research should be carried out to integrate specific local characteristics within the extreme hydrologic flow analysis, which is commonly performed at the watershed or regional scale.

5. Conclusions

In the study, thirty USGS stations within the Appalachian Highland region with the least altered watersheds are studied to identify challenges/drawbacks in relation to the widely used tools in hydrologic analysis. The study sites are of key importance since partial or complete hydraulic bridge collapse events occurred at or near the selected stations. Analyses undertaken include selecting a model using widely used flood distributions, conducting goodness-of-fit tests to aid the model selection, conducting statistical analyses to identify trend, seasonality, and stationarity, and comparing geospatial characteristics at the watershed scale in order to assess the site variability linked to specific flood behavior. The key findings are (a) multiple best-fitted distributions for annual peak flow data; (b) inconclusive and/or contradictory results for the model selection criteria; (c) the absence of any specific single trend and/or seasonal variation for monthly flow data; and (d) the potential role of local site-specific characteristics in relation to the fitted flood distribution models. The results reveal the lack of robustness of the widely used hydrologic tools in relation to their inability to identify the background physics of the system, even for the least disturbed watersheds. Such findings also imply the reduced capability of the hydrologic tools as linked to different spatial scales, including physiography, watershed, and/or local scale. Rigorous scientific research needs to be carried out to link these different spatial scales in order to develop robust models/tools for sites with unique characteristics, such as the studied collapse sites. It should be noted that hydraulic engineers do need models/tools to estimate the probability of a chosen large flood (typically a 50- or 100-year flood) to optimize the design of the hydraulic structure. However, selecting a single best-fitted distribution (among multiple best-fitted) to derive the design flow may not matter much in design optimization given that the background physics is not well understood. Whenever a mathematical procedure (geometrical or statistical) embedded within a hydrologic model leads to a number (i.e., design flow), the model should underline a clearly defined physical process.

Author Contributions

Conceptualization, F.U.A.; methodology, F.U.A.; formal analysis, F.U.A. and M.H.I.; data curation, M.H.I.; writing—original draft preparation, F.U.A.; writing—review and editing, M.H.I.; supervision, F.U.A.; funding acquisition, F.U.A. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: https://github.com/fahmidah/Challenges-in-Hydrologic-Extremes/tree/main (accessed on 20 January 2023).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Cook, W.; Barr, P.J.; Halling, M.W. Segregation of Bridge Failure Causes and Consequences. In Proceedings of the Transportation Research Board 93rd Annual Meeting, Washington, DC, USA, 12–16 January 2014. [Google Scholar]
  2. Nowak, A.S.; Collins, K.R. Reliability of Structures, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
  3. Wardhana, K.; Hadipriono, F.C. Analysis of Recent Bridge Failures in the United States. J. Perform. Constr. Facil. 2003, 17, 144–150. [Google Scholar] [CrossRef]
  4. Cook, W.; Barr, P.J.; Halling, M.W. Bridge Failure Rate. J. Perform. Constr. Facil. 2013, 29, 4014080. [Google Scholar] [CrossRef]
  5. Arneson, L.; Zevenbergen, L.; Lagasse, P.; Clopper, P. Evaluating Scour at Bridges, 5th ed.; FHWA: Washington, DC, USA, 2012.
  6. Kattell, J.; Eriksson, M. Bridge Scour Evaluation: Screening, Analysis, and Countermeasures; Report No. 9877; USDA: Washington, DC, USA, 1998.
  7. Lee, G.C.; Mohan, S.B.; Huang, C.; Fard, B.N. A Study of U.S. Bridge Failures; MCEER: Buffalo, NY, USA, 2013. [Google Scholar]
  8. Singh, D.; Tsiang, M.; Rajaratnam, B.; Dienbaugh, N.S. Precipitation extremes over the continental United States in a transient, high-resolution, ensemble climate model experiment. J. Geophys. Res. Atmos. 2013, 118, 7063–7086. [Google Scholar] [CrossRef]
  9. Milillo, J.M.; Richmond, T.C.; Yohe, G.W. Climate Change Impacts in the United States: The Third National Climate Assessment; US Global Change Research Program: Washington DC, USA, 2014.
  10. Meyer, M.D.; Flood, M.; Keller, J.; Lennon, J.; McVoy, G.; Dorney, C.; Leonard, K.; Hyman, R.; Smith, J. Strategic Issues Facing Transportation Volume 2: Climate Change, Extreme Weather Events and the Highway System: A Practitioner’s Guide; Report No. 750; NCHRP: Washington, DC, USA, 2013. [Google Scholar]
  11. Wright, L.; Chinowsky, P.; Strzepek, K.; Jones, R.; Streeter, R.; Smith, J.B.; Mayotte, J.M.; Powell, A.; Jantarasami, L.; Perkins, W. Estimated effects of climate change on flood vulnerability of U.S. bridges. Mitig. Adapt. Strateg. Glob. Chang. 2012, 17, 939–955. [Google Scholar] [CrossRef]
  12. Neumann, J.E.; Price, J.; Chinowsky, P.; Wright, L.; Ludwig, L.; Streeter, R.; Jones, R.; Smith, J.B.; Perkins, W.; Jantarasami, L.; et al. Climate change risks to US infrastructure: Impacts on roads, bridges, coastal development, and urban drainage. Clim. Chang. 2014, 131, 97–109. [Google Scholar] [CrossRef]
  13. Meyer, M.D.; Weigel, B. Climate change and transportation engineering: Preparing for a sustainable future. J. Transp. Eng. 2011, 137, 393–403. [Google Scholar] [CrossRef]
  14. Khelifa, A.; Garrow, L.A.; Higgins, M.J.; Meyer, M.D. Impacts of climate change on scour-vulnerable bridges: Assessment based on HYRISK. J. Infrastruct. Syst. 2013, 19, 138–146. [Google Scholar] [CrossRef]
  15. Suarez, P.; Anderson, W.; Mahal, V.; Lakshmanan, T.R. Impacts of flooding and climate change on urban transportation: A system wide performance assessment of the Boston Metro Area. Transp. Res. Part D Transp. Environ. 2005, 10, 231–244. [Google Scholar] [CrossRef]
  16. USDOT Center for Climate Change and Environmental Forecasting. Impacts of Climate Change and Variability on Transportation Systems and Infrastructure: The Gulf Coast Study, Phase 2; Report No. FHWA-HEP-15-004; FHWA: Washington, DC, USA, 2013.
  17. Flint, M.M.; Fringer, O.; Billington, S.L.; Freyberg, D. Historical analysis of hydraulic bridge collapses in the continental United States. J. Infrastruct. Syst. 2017, 23, 04017005. [Google Scholar] [CrossRef]
  18. US Code of Federal Regulations. Bridges, Structures and Hydraulics; US Code of Federal Regulations: Washington, DC, USA, 2009. [Google Scholar]
  19. NYSDOT. Highway Drainage, Highway Design Manual; NYSDOT: Albany, NY, USA, 2014.
  20. CDOT. Drainage Design Manual; Colorado Department of Transportation: Denver, CO, USA, 2004.
  21. Eljabri, S.S.M. New Statistical Models for Extreme Values. Ph.D. Thesis, The University of Manchester, Manchester, UK, 2013. [Google Scholar]
  22. Bailly, F.; Longo, G. Mathematics and the Natural Sciences; Imperial College Press: London, UK, 2011. [Google Scholar]
  23. D’Espargnat, B. On Physics and Philosophy; Princeton University Press: Oxford, UK, 2002. [Google Scholar]
  24. Claeskens, G. Statistical model choice. Annu. Rev. Stat. Its Appl. 2016, 3, 233–256. [Google Scholar] [CrossRef]
  25. Corder, G.W.; Foreman, D.I. Nonparametric Statistics for Non-Statisticians: A Step-by-Step Approach; Wiley: Hoboken, NJ, USA, 2009; ISBN 978-0-470-45461-9. [Google Scholar]
  26. Akaike, H. Information Theory and an Extension of the Maximum Likelihood Principle. In Selected Papers of Hirotugu Akaike; Parzen, E., Tanabe, K., Kitagawa, G., Eds.; Springer: New York, NY, USA, 1973; pp. 267–281. [Google Scholar] [CrossRef]
  27. Schwarz Gideon, E. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
  28. Babu, G.J.; Feigelson, E.D. Astrostatistics: Goodness of Fit and All That. Astron. Data Anal. Softw. Syst. XV 2006, 351, 127. [Google Scholar]
  29. Klemes, V. Dilettantism in Hydrology: Transition or Destiny. Water Resour. Res. 1986, 22, 177–188. [Google Scholar] [CrossRef]
  30. Ario, I.; Yamashita, T.; Tsubaki, R.; Kawamura, S.; Uchida, T.; Watanabe, G.; Fujiwara, A. Investigation of bridge collapse phenomena due to heavy rain floods: Structural, hydraulic, and hydrological analysis. J. Bridge Eng. 2022, 27, 04022073. [Google Scholar] [CrossRef]
  31. Maddison, B. Scour failure of bridges. Proc. Inst. Civ. Eng.-Forensic Eng. 2012, 165, 39–52. [Google Scholar] [CrossRef]
  32. Zhang, G.; Liu, Y.; Liu, J.; Lan, S.; Yang, J. Causes and statistical characteristics of bridge failures: A review. J. Traffic Transp. Eng. 2022, 9, 388–406. [Google Scholar] [CrossRef]
  33. Liu, X.; Ashraf, F.U.; Strom, K.B.; Wang, K.H.; Briaud, J.L.; Sharif, H.; Shafique, S.B. Assessment of the Effects of Regional Channel Stability and Sediment Transport on Roadway Hydraulic Structures: Final Report; Texas Department of Transportation: Austin, TX, USA, 2014.
  34. Lins, H.; Slack, J. Streamflow trends in the United States. Geophys. Res. Lett. 1999, 26, 227–230. [Google Scholar] [CrossRef]
  35. Mallakpour, I.; Villarini, G. The changing nature of flooding across the central United States. Nat. Clim. Chang. 2015, 5, 250–254. [Google Scholar] [CrossRef]
  36. Hirsch, R.M.; Ryberg, K.R. Has the magnitude of floods across the USA changed with global CO2 levels? Hydrol. Sci. J. 2012, 57, 1–9. [Google Scholar] [CrossRef]
  37. Villarini, G.; Serinaldi, F.; Smith, J.; Krajewski, W.F. On the stationarity of annual flood peaks in the continental United States during the 20th century. Water Resour. Res. 2009, 45, W08417. [Google Scholar] [CrossRef]
  38. Kundzewicz, Z.W.; Kanae, S.; Seneviratne, S.I.; Handmer, J.; Nicholls, N.; Peduzzi, P.; Mechler, R.; Bouwer, L.M.; Arnell, N.; Mach, K.; et al. Flood risk and climate change: Global and regional perspectives. Hydrol. Sci. J. 2014, 59, 1–28. [Google Scholar] [CrossRef]
  39. Stewart, B. Measuring What We Manage—The Importance of Hydrological Data to Water Resources Management. In Hydrological Sciences and Water Security: Past, Present, and Future; International Association of Hydrological Sciences: Paris, France, 2014. [Google Scholar]
  40. Sevruk, B.; Geiger, H. Selection of Distribution Types for Extremes of Precipitation; World Meteorological Organization: Geneva, Switzerland, 1981. [Google Scholar]
  41. World Meteorological Organization. Statement on the Term Hydrological Normal; Hydrological Coordination Panel: Prague, Czech Republic, 2023; Available online: https://community.wmo.int/activity-areas/hydrology-and-water-resources/hydrological-coordination-panel (accessed on 27 January 2023).
  42. Bulletin 17B Hydrology Subcommittee. Guidelines for Determining Flood Flow Frequency; USGS Interagency Advisory Committee on Water Data: Reston, VA, USA, 1982.
  43. England, J.F.; Cohn, T.A.; Faber, B.A.; Stedinger, J.R.; Thomas, W.O.; Veilleux, A.G.; Kiang, J.E.; Mason, R.R. Guidelines for Determining Flood Flow Frequency—Bulletin 17C; U.S. Geological Survey: Reston, VA, USA, 2019.
  44. Stein, S.; Sedmera, K. Risk-Based Management Guidelines for Scour at Bridges with Unknown Foundations; National Academic Press: Washington, DC, USA, 2007. [Google Scholar]
  45. Ashraf, F.; Flint, M.M. Retrospective analysis of U.S. hydraulic bridge collapse sites to assess HYRISK performance. In Proceedings of the ASCE World Environmental and Water Resources Congress, Virtual, 7–11 June 2021. [Google Scholar]
  46. Poórová, J.; Jeneiová, K.; Blaškovičová, L.; Danáčová, Z.; Kotríková, K.; Melová, K.; Paľušová, Z. Effects of the Time Period Length on the Determination of Long-Term Mean Annual Discharge. Hydrology 2023, 10, 88. [Google Scholar] [CrossRef]
  47. Falcone, J. GAGES-II: Geospatial Attributes of Gages for Evaluating Streamflow; U.S. Geological Survey: Reston, VA, USA, 2011.
  48. Bloschl, G.; Montanari, A. climate change impacts—Throwing the dice. Hydrol. Process. 2010, 24, 374–381. [Google Scholar] [CrossRef]
  49. Johnson, P.A. Physiographic Characteristics of Bridge-Stream Intersections. River Res. Appl. 2006, 22, 617–630. [Google Scholar] [CrossRef]
  50. Ashraf, F.; Tyralis, H.; Papacharalampous, G. Explaining the Flood Behavior for the Bridge Collapse Sites. J. Mar. Sci. Eng. 2022, 10, 1241. [Google Scholar] [CrossRef]
  51. Gilleland, E.; Katz, R.W. extRemes 2.0: An Extreme Value Analysis Package in R. J. Stat. Softw. 2016, 72, 1–39. [Google Scholar] [CrossRef]
  52. Webster, V.; Stedinger, J. Log-Pearson Type 3 Distribution and Its Application in Flood Frequency Analysis. I: Distribution Characteristics. J. Hydrol. Eng. 2007, 12, 482–491. [Google Scholar] [CrossRef]
  53. Coles, S.G. An Introduction to Statistical Modelling of Extreme Values; Springer: London, UK, 2001. [Google Scholar]
  54. Delignette-Muller, M.L.; Dutang, C. fitdistrplus: An R Package for Fitting Distributions. J. Stat. Softw. 2015, 64, 1–34. [Google Scholar] [CrossRef]
  55. Saeb, A. Goodness of Fit Test for Continuous Distribution Functions; R Package Version 0.2.0. 2018. Available online: https://cran.r-project.org/web/packages/gnFit/index.html (accessed on 20 January 2023).
  56. R Core Team. Classical Goodness of Fit Tests for Univariate Distributions; R Package Version 1.2-3. 2022. Available online: https://cran.r-project.org/web/packages/goftest/index.html (accessed on 20 January 2023).
  57. Pettitt, A. A non-parametric approach to the change-point problem. J. R. Stat. Soc. Ser. C 1979, 28, 126–135. [Google Scholar] [CrossRef]
  58. Mann, H.B. Nonparametric tests against trend. Econ. J. Econ. Soc. 1945, 13, 245–259. [Google Scholar] [CrossRef]
  59. Pohlert, T. Trend: Non-Parametric Trend Tests and Change-Point Detection; R Package Version 1.1.2. 2020. Available online: https://cran.r-project.org/web/packages/trend/index.html (accessed on 20 January 2023).
  60. McLeod, A.I. Trend: Non-Parametric Trend Tests and Change-Point Detection; R Package Version 2.2.1. 2022. Available online: https://cran.r-project.org/web/packages/Kendall/index.html (accessed on 20 January 2023).
  61. Dagum, E.B.; Bianconcini, S. Seasonal Adjustment Methods and Real Time Trend-Cycle Estimation, 1st ed.; Springer: Berlin, Germany, 2016. [Google Scholar]
  62. Sax, C.; Eddelbuettel, D. R Interface to X-13-ARIMA-SEATS; R Package Version 1.9.0. 2022. Available online: https://cran.r-project.org/web/packages/seasonal/index.html (accessed on 20 January 2023).
  63. Cowpertwait, P.S.P.; Metcalfe, A. Introductory Time Series with R; Springer: Berlin, Germany, 2009. [Google Scholar] [CrossRef]
  64. Scheer, J. Failed Bridges: Case Studies, Causes and Consequences; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar] [CrossRef]
  65. Czapiga, M.J.; Smith, V.B.; Nittrouer, J.A.; Mohrig, D.; Parker, G. Internal connectivity of meandering rivers: Statistical generalization of channel hydraulic geometry. Water Resour. Res. 2015, 51, 7485–7500. [Google Scholar] [CrossRef]
  66. Kim, T.K. T test as a parametric statistic. Korean J. Anesthesiol. 2015, 68, 540–546. [Google Scholar] [CrossRef] [PubMed]
  67. Nair, J.; Wierman, A.; Zwart, B. The Fundamentals of Heavy Tails: Properties, Emergence, and Estimation (Cambridge Series in Statistical and Probabilistic Mathematics); Cambridge University Press: Cambridge, UK, 2022. [Google Scholar] [CrossRef]
  68. Stephens, M.A. EDF Statistics for Goodness of Fit and Some Comparisons. J. Am. Stat. Assoc. 1974, 69, 730–737. [Google Scholar] [CrossRef]
  69. Laio, F. Cramer–von Mises and Anderson-Darling goodness of fit tests for extreme value distributions with unknown parameters. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
  70. Klemes, V. Scientific Basis of Water Resource Management; National Academy Press: Washington, DC, USA, 1982. [Google Scholar]
  71. Myers, D.T.; Ficklin, D.L.; Robeson, S.M.; Neupane, R.P.; Botero-Acosta, A.; Avellaneda, P.M. Choosing an arbitrary calibration period of hydrologic models: How much does it influence water balance simulations? Hydrol. Process. 2021, 35, e14045. [Google Scholar] [CrossRef]
  72. Babu, G.J.; Toreti, A. A Goodness-of- fit test for heavy tailed distributions with unknown parameters and its application to simulated precipitation extremes in the Euro-Mediterranean region. J. Stat. Plan. Inference 2016, 174, 11–19. [Google Scholar] [CrossRef]
  73. Ashraf, F.; Spaunhorst, M. At a station hydraulic geometry for reaches with bridge collape events. River Res. Appl. 2023, 39, 108–121. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Article Metrics

Citations

Article Access Statistics

Journal Statistics
Multiple requests from the same IP address are counted as one view.
Experimental Study of Flow Kinematics and Impacting Pressures on a Suspended Horizontal Plate by Extreme Waves
Previous
Photodegradation of Rhodamine B and Phenol Using TiO2/SiO2 Composite Nanoparticles: A Comparative Study
Next