Research on a Prediction Model of Water Quality Parameters in a Marine Ranch Based on LSTM-BP
Abstract
:1. Introduction
2. Data Source and Data Processing
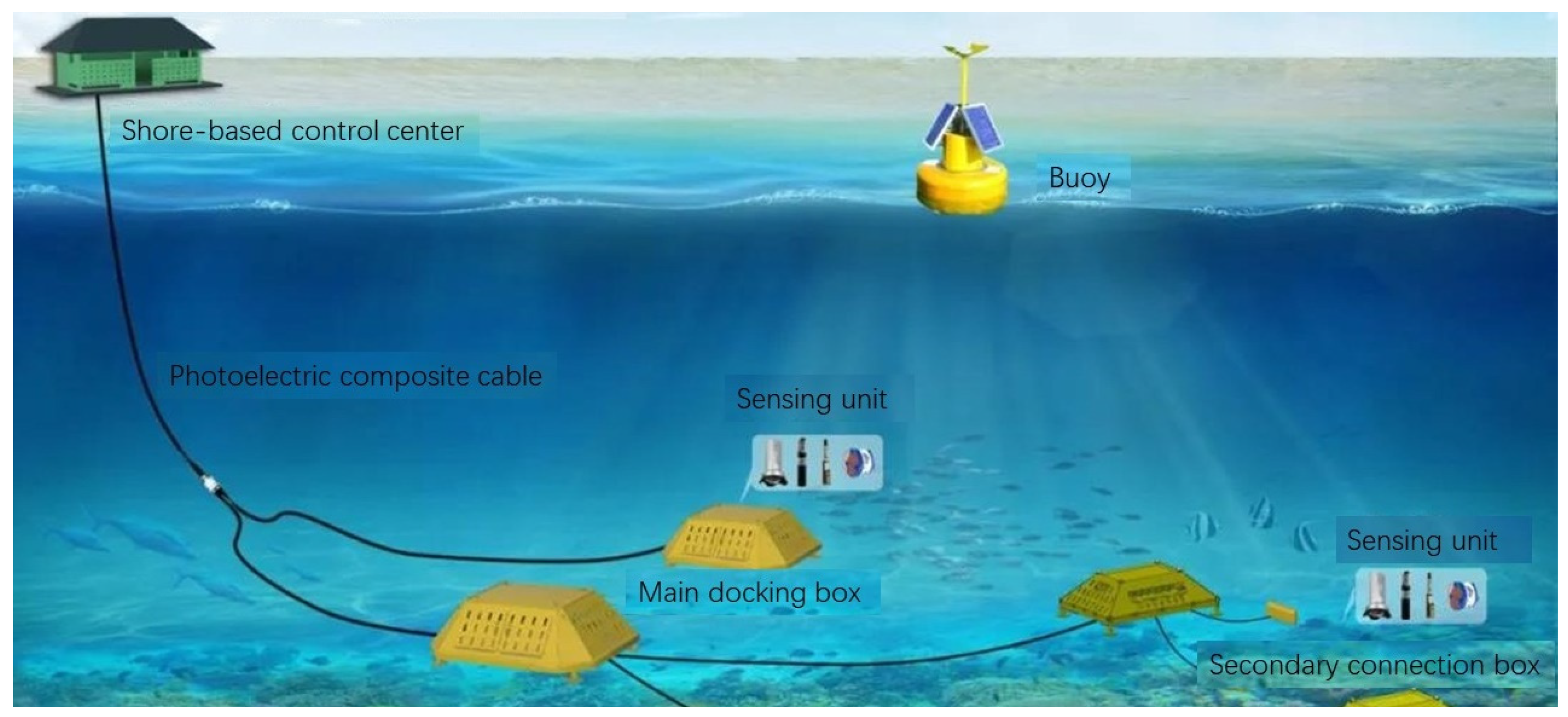
2.1. Monitoring System Structure and Data Acquisition
2.2. Data Processing
3. Build Models and Evaluation Indicators
3.1. Predictive Model Evaluation Index
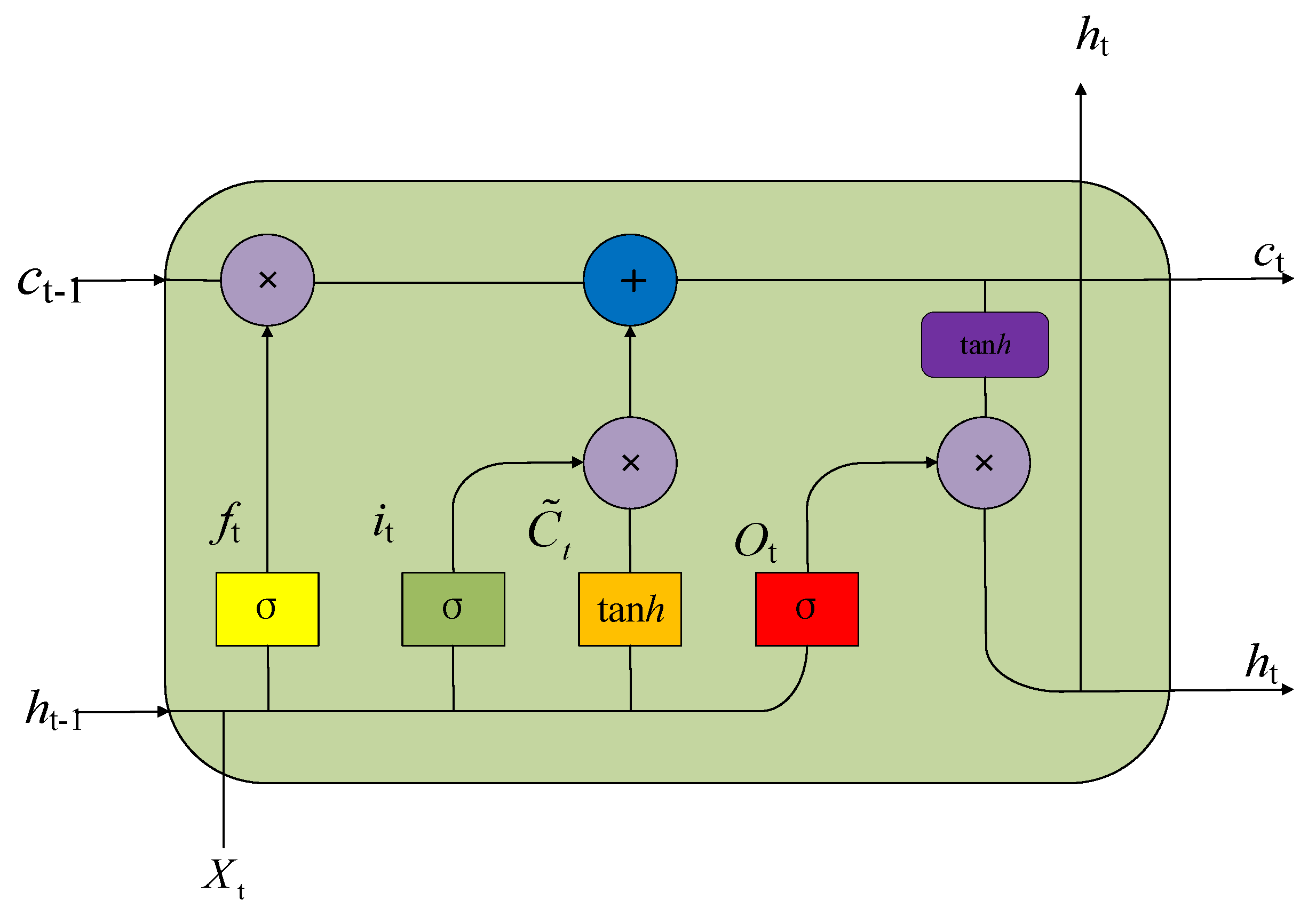
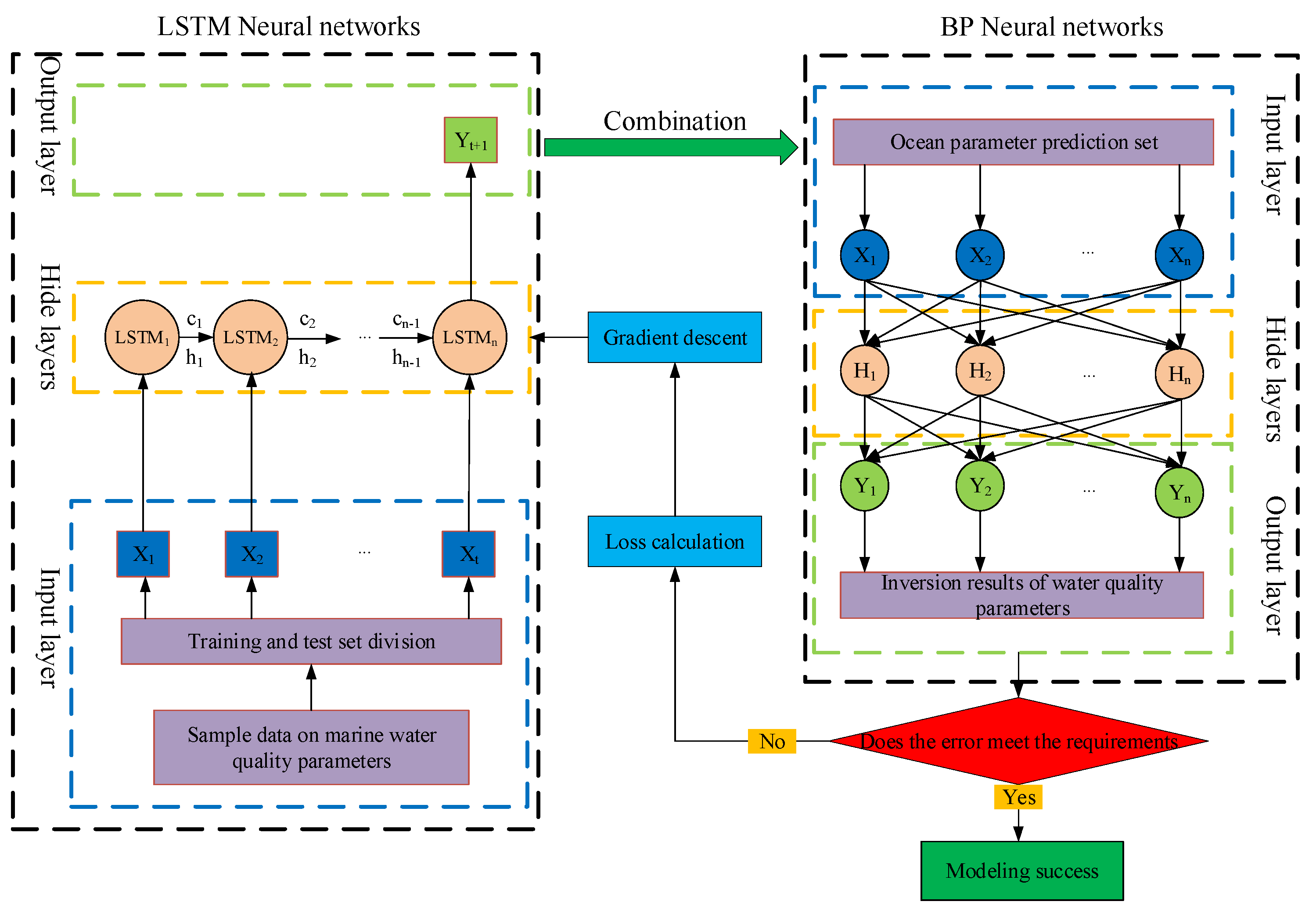
3.2. LSTM-BP Combination Model Construction
3.3. Comparison of Model Settings
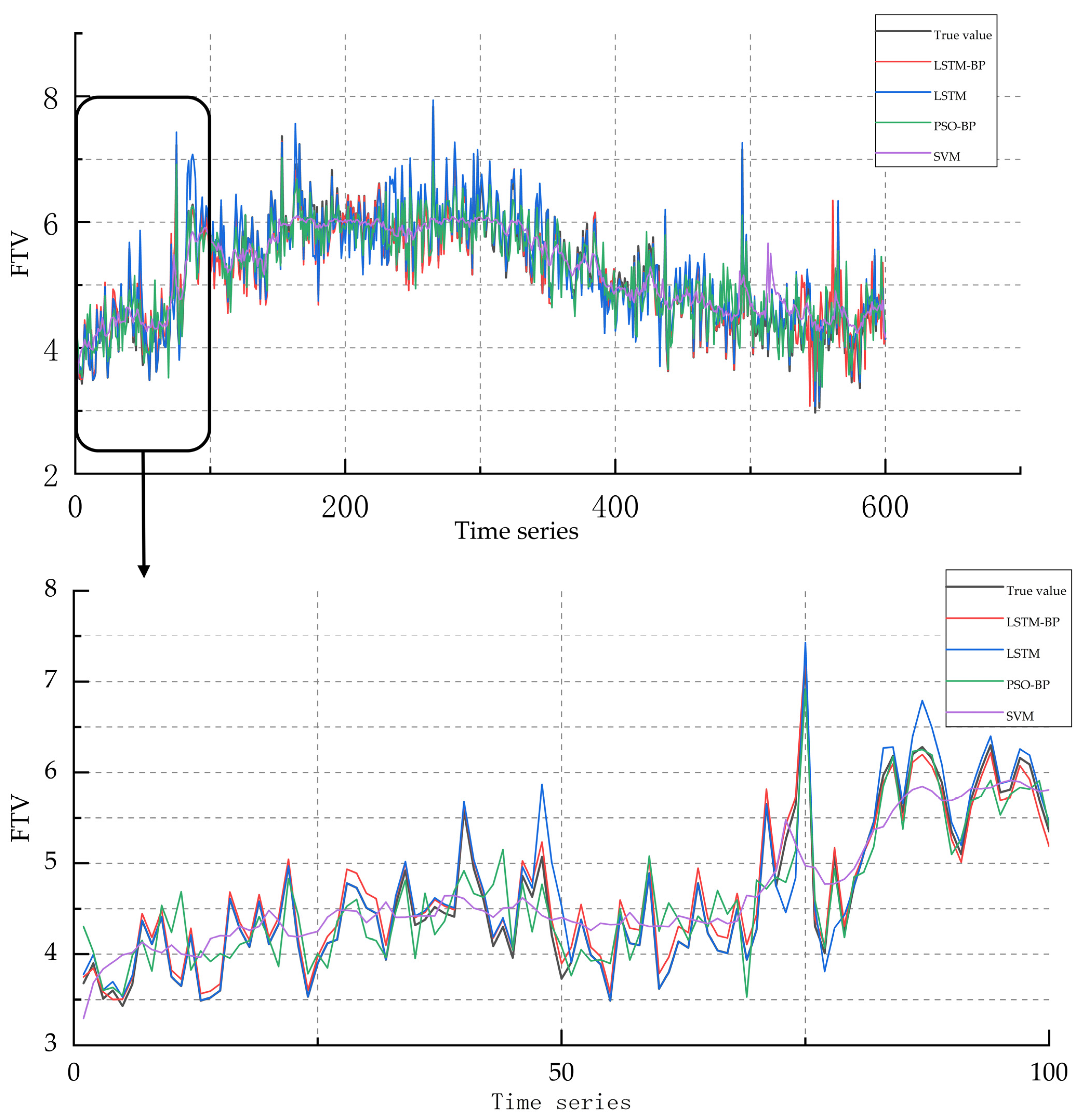
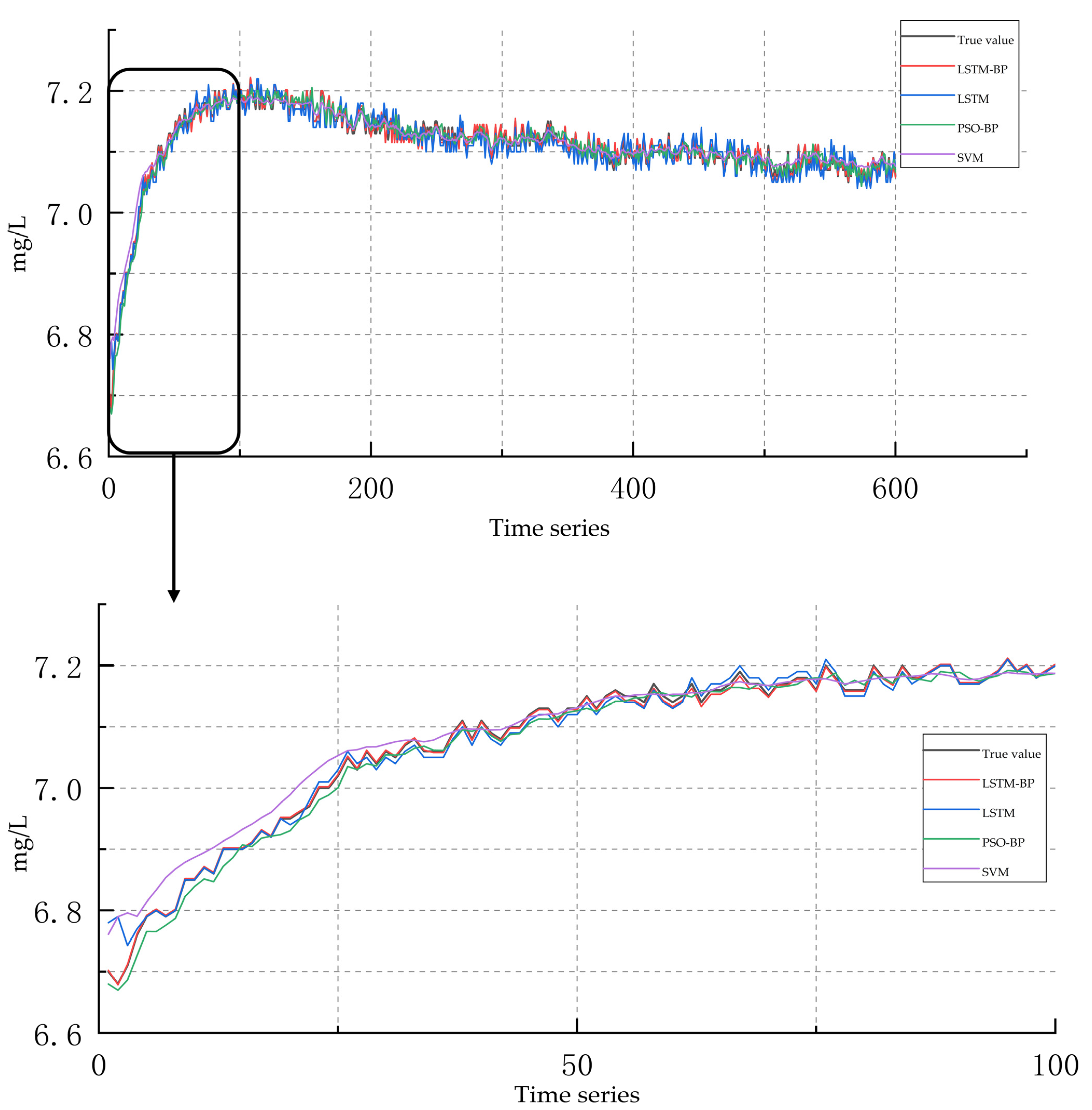
4. Analysis and Discussion of Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hartman, S.E.; Bett, B.J.; Durden, J.M.; Henson, S.A.; Iversen, M.; Jeffreys, R.M.; Horton, T.; Lampitt, R.; Gates, A.R. Enduring science: Three decades of observing the northeast Atlantic from the Porcupine Abyssal Plain Sustained Observatory (PAP-SO). Prog. Oceanogr. 2021, 191, 102508. [Google Scholar] [CrossRef]
- Chen, G.; Huang, B.X.; Chen, X.Y.; Ge, L.Y.; Radenkovic, M.; Ma, Y. Deep Blue AI: A new bridge from data to knowledge for the ocean science. Deep Sea Res. Part I Oceanogr. Res. Pap. 2022, 190, 103886. [Google Scholar] [CrossRef]
- Tian, C.P.; Xu, Z.Y.; Wang, L.K.; Liu, Y.J. Arc fault detection using artificial intelligence: Challenges and benefits. Math. Biosci. Eng. 2023, 20, 12404–12432. [Google Scholar] [CrossRef] [PubMed]
- Bartsev, S.; Saltykov, M.; Belolipetsky, P.; Pianykh, A. Imperfection of the convergent cross-mapping method. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1047, 012081. [Google Scholar] [CrossRef]
- Graf, R.; Zhu, S.L.; Sivakumar, B. Forecasting river water temperature time series using a wavelet–neural network hybrid modelling approach. J. Hydrol. 2019, 578, 124115. [Google Scholar] [CrossRef]
- Wen, X.H.; Feng, Q.; Deo, R.C.; Wu, M.; Si, J.H. Wavelet analysis–artificial neural network conjunction models for multi-scale monthly groundwater level predicting in an arid inland river basin, Northwestern China. Hydrol. Res. 2016, 48, 1710–1729. [Google Scholar] [CrossRef]
- Zhang, S.T.; Wu, J.R.; Jia, Y.G.; Wang, Y.G.; Zhang, Y.Q.; Duan, Q.B. A temporal LASSO regression model for the emergency forecasting of the suspended sediment concentrations in coastal oceans: Accuracy and Interpretability. Eng. Appl. Artif. Intell. 2021, 100, 104206. [Google Scholar] [CrossRef]
- Gauch, M.; Kratzert, F.; Klotz, D.; Nearing, G.; Lin, J.; Hochreiter, S. Rainfall–runoff prediction at multiple timescales with a single long short-term Memory Network. Hydrol. Earth Syst. Sci. 2021, 25, 2045–2062. [Google Scholar] [CrossRef]
- Chen, X.Y.; Chau, K.W. Uncertainty analysis on hybrid double feedforward neural network model for sediment load estimation with Lube Method. Water Resour. Manag. 2016, 33, 3563–3577. [Google Scholar] [CrossRef]
- Clark, S.R.; Pagendam, D.; Ryan, L. Forecasting multiple groundwater time series with local and Global Deep Learning Networks. Int. J. Environ. Res. Public Health 2022, 19, 5091. [Google Scholar] [CrossRef]
- Tang, Y.W.; Qiu, F.; Wang, B.J.; Wu, D.; Jing, L.H.; Sun, Z.C. A deep relearning method based on the recurrent neural network for land cover classification. GISci. Remote Sens. 2022, 59, 1344–1366. [Google Scholar] [CrossRef]
- Song, W.; Fujimura, S. Capturing combination patterns of long- and short-term dependencies in Multivariate Time Series forecasting. Neurocomputing 2021, 464, 72–82. [Google Scholar] [CrossRef]
- Guo, D.L.; Lintern, A.; Webb, J.A.; Ryu, D.; Bende-Michl, U.; Liu, S.C.; Western, A.W. A data-based predictive m-odel for spatiotemporal variability in stream water quality. Hydrol. Earth Syst. Sci. 2020, 24, 827–847. [Google Scholar] [CrossRef] [Green Version]
- Lu, H.F.; Ma, X. Hybrid decision tree-based machine learning models for short-term water quality prediction. Chemosphere 2020, 249, 126169. [Google Scholar] [CrossRef]
- Wang, H.; Wang, W.J.; Cui, Z.H.; Zhou, X.Y.; Zhao, J.; Li, Y. A new dynamic Firefly algorithm for demand estimation of water resources. Inf. Sci. 2018, 438, 95–106. [Google Scholar] [CrossRef]
- Green, M.B.; Pardo, L.H.; Bailey, S.W.; Campbell, J.L.; McDowell, W.H.; Bernhardt, E.S.; Rosi, E.J. Predicting high-frequency variation in stream solute concentrations with water quality sensors and machine learning. Hydrol. Process. 2020, 35, 14000. [Google Scholar] [CrossRef]
- Willard, J.D.; Read, J.S.; Appling, A.P.; Oliver, S.K.; Jia, X.W.; Kumar, V. Predicting water temperature dynamics of unmonitored lakes with meta-transfer learning. Water Resour. Res. 2021, 57, WR029579. [Google Scholar] [CrossRef]
- Kargar, K.; Samadianfard, S.; Parsa, J.; Nabipour, N.; Shamshirband, S.; Mosavi, A.; Chau, K.W. Estimating longitudinal dispersion coefficient in natural streams using empirical models and machine learning algorithms. Eng. Appl. Comput. Fluid Mech. 2020, 14, 311–322. [Google Scholar] [CrossRef]
- Ikotun, A.M.; Ezugwu, A.E.; Abualigah, L.; Abuhaija, B.; Heming, J. K-means Clustering Algorithms: A comprehensive review, variants analysis, and advances in the era of Big Data. Inf. Sci. 2023, 622, 178–210. [Google Scholar] [CrossRef]
- Ismkhan, H.; Izadi, M. K-means-G*: Accelerating K-means clustering algorithm utilizing primitive geometric concepts. Inf. Sci. 2022, 618, 298–316. [Google Scholar] [CrossRef]
- Dorabiala, O.; Kutz, J.N.; Aravkin, A.Y. Robust trimmed K-means. Pattern Recognit. Lett. 2022, 161, 9–16. [Google Scholar] [CrossRef]
- Husein, M.; Chung, I.Y. Day-ahead solar irradiance forecasting for microgrids using a long short-term memory recurrent neural network: A deep learning approach. Energies 2019, 12, 1856. [Google Scholar] [CrossRef] [Green Version]
- Aydın, H.; Orman, Z.; Aydın, M.A. A long short-term memory (LSTM)-based distributed denial of service (DDoS) detection and defense system design in Public Cloud Network Environment. Comput. Secur. 2022, 118, 102725. [Google Scholar] [CrossRef]
- Tang, Y.Y.; Wang, Y.L.; Liu, C.L.; Yuan, X.F.; Wang, K.; Yang, C.H. Semi-supervised LSTM with historical feature fusion attention for temporal sequence dynamic modeling in Industrial Processes. Eng. Appl. Artif. Intell. 2023, 117, 105547. [Google Scholar] [CrossRef]
- Ismael, M.; Mokhtar, A.; Farooq, M.; Lv, X. Assessing drinking water quality based on physical, chemical and microbial parameters in the Red Sea State, Sudan using a combination of water quality index and Artificial Neural Network Model. Groundw. Sustain. Dev. 2021, 14, 100612. [Google Scholar] [CrossRef]
- Mouloodi, S.; Rahmanpanah, H.; Gohari, S.; Burvill, C.; Davies, H. Feedforward backpropagation artificial neural networks for predicting mechanical responses in complex nonlinear structures: A study on a long bone. J. Mech. Behav. Biomed. Mater. 2022, 128, 105079. [Google Scholar] [CrossRef] [PubMed]
- Bogard, N.; Linder, J.; Rosenberg, A.B.; Seelig, G. A deep neural network for predicting and engineering alternative polyadenylation. Cell 2019, 178, 91–106.e23. [Google Scholar] [CrossRef]


| Serial Number | LSTM Network Layers | LSTM Number of Neurons | BP Network Layers | BP Number of Neurons | MAE |
|---|---|---|---|---|---|
| 1 | 2 | 10 | 2 | 20 | 0.0131 |
| 2 | 2 | 10 | 2 | 24 | 0.0097 |
| 3 | 2 | 10 | 3 | 20 | 0.0065 |
| 4 | 2 | 10 | 3 | 24 | 0.0039 |
| 5 | 2 | 12 | 2 | 20 | 0.0026 |
| 6 | 2 | 12 | 2 | 24 | 0.0016 |
| 7 | 2 | 12 | 3 | 20 | 0.0054 |
| 8 | 2 | 12 | 3 | 24 | 0.0058 |
| 9 | 3 | 10 | 2 | 20 | 0.0068 |
| 10 | 3 | 10 | 2 | 24 | 0.0072 |
| 11 | 3 | 10 | 3 | 20 | 0.0061 |
| 12 | 3 | 10 | 3 | 24 | 0.0146 |
| 13 | 3 | 12 | 2 | 20 | 0.0076 |
| 14 | 3 | 12 | 2 | 24 | 0.0153 |
| 15 | 3 | 12 | 3 | 20 | 0.0086 |
| 16 | 3 | 12 | 3 | 24 | 0.0073 |
| Lab Environment | Specific Information |
|---|---|
| operating system | Windows10 |
| processor | Intel(R) Pentium(R) CPU G3220 @ 3.00 GHz |
| Onboard RAM | 8 G |
| programming language | Python3.6 |
| development environment | Keras + TensorFlow/scikit-learn |
| development tools | Pycharm |
| Chlorophyll | Turbidity | Dissolved Oxygen | |||||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | NSE | RMSE | MAE | NSE | RMSE | MAE | NSE | |
| LSTM-BP | 36.64 | 23.50 | 0.967 | 2042.92 | 1214.25 | 0.876 | 52.69 | 38.28 | 0.971 |
| LSTM | 75.63 | 56.74 | 0.896 | 2578.36 | 1274.41 | 0.739 | 113.63 | 96.25 | 0.903 |
| PSO-BP | 125.26 | 87.63 | 0.853 | 2753.76 | 2003.65 | 0.686 | 119.45 | 101.62 | 0.874 |
| SVM | 157.16 | 114.58 | 0.761 | 4617.01 | 3275.73 | 0.577 | 151.40 | 112.75 | 0.765 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Lv, B.; Chen, J.; Kou, L.; Liu, H.; Liu, M. Research on a Prediction Model of Water Quality Parameters in a Marine Ranch Based on LSTM-BP. Water 2023, 15, 2760. https://doi.org/10.3390/w15152760
Xu H, Lv B, Chen J, Kou L, Liu H, Liu M. Research on a Prediction Model of Water Quality Parameters in a Marine Ranch Based on LSTM-BP. Water. 2023; 15(15):2760. https://doi.org/10.3390/w15152760
Chicago/Turabian StyleXu, He, Bin Lv, Jie Chen, Lei Kou, Hailin Liu, and Min Liu. 2023. "Research on a Prediction Model of Water Quality Parameters in a Marine Ranch Based on LSTM-BP" Water 15, no. 15: 2760. https://doi.org/10.3390/w15152760
APA StyleXu, H., Lv, B., Chen, J., Kou, L., Liu, H., & Liu, M. (2023). Research on a Prediction Model of Water Quality Parameters in a Marine Ranch Based on LSTM-BP. Water, 15(15), 2760. https://doi.org/10.3390/w15152760








