Water Renewal Simulation in Two Flow-Through Water Bodies in Western Greece

Abstract

The basic hydrodynamic characteristics and water renewal of two flow-through water bodies in Western Greece, the Gulf of Patras and Lysimachia Lake, are studied via numerical simulations. The currents on the northern coasts of the Gulf are much stronger compared with the southern region, and rapid water renewal is achieved in the area of the Rio–Antirio strait (<1 month). In the northern part of the Gulf, the residence time varies from 1 to 4 months, while in the central and southern parts, it is estimated to exceed 6 months. Regarding the water renewal of deep waters (>60 m), which are enclosed between sills, the same pattern was observed, with residence times exceeding 6 months. In Lysimachia Lake, the effect of inflow waters from surrounding water bodies was analyzed over a time period of approximately 2 months. Gyres formation was observed due to local topography, and the numerically predicted results for water renewal were found to be in good agreement with those in the literature. Specifically, Lysimachia Lake seems to be replenished approximately 13 times per year.

1. Introduction

During the last decades, environmental issues like eutrophication and water pollution have been in the spotlight. The environmental condition of many water bodies has degraded significantly as a result of both natural and anthropogenic contribution. The water quality of these water bodies is highly dependent on hydrodynamic circulation and the water renewal rate. Hence, water renewal constitutes one of the most crucial factors for the management and restoration of aquatic ecosystems.

The water renewal of a water body is achieved via different mechanisms. In the marine environment, water renewal is mainly achieved under the combined action of the wind and the tide. Regardless of the wind effect, water renewal is achieved and enhanced due to the tidal forcing in a gulf or a coastal water body, i.e., a lagoon or a lake. This is accomplished by the exchange of a water quantity equal to the tidal prism with the open sea during each tidal cycle. This mechanism is significantly enhanced under wind action and the associated wind-induced flow, leaving the pure tide-induced water renewal to be the most adverse condition in terms of water replenishment. In many marine water bodies, the tidal prism mechanism is the main cause for tide-induced water renewal. However, in other cases, a flow-through mechanism is developed, which greatly improves water circulation, notably reducing the water renewal time [1,2]. Regarding freshwater bodies, i.e., lakes or reservoirs, water renewal remains nearly seasonal, due to the river or stream inflow that feeds the water body. The generation of flow-through conditions in these water bodies can substantially affect water renewal, giving rise to a fast replenishment mechanism.

During the last decades, both computer technology and computing power have advanced significantly. As a result, numerical modeling has become increasingly popular in coastal and ocean research. Computational fluid dynamics (CFD) is a field of science that produces quantitative predictions of fluid flow phenomena, utilizing the governing fluid motion equations and with the potential to fully exploit modern computer capabilities [3]. As a result, several numerical studies have focused on water circulation and renewal rate in lakes, lagoons and bays. These smaller or larger water bodies can suffer eutrophication problems when characterized by negligible inflow–outflow and stagnant waters, which results in accumulation of nutrients such as nitrogen and phosphorus [4]. Problems of eutrophication due to stagnant waters are obviously quite common in hydrodynamic systems like lakes [5], and even in lagoons [6] and bays [7].

Ribbe et al. [8] assessed the water renewal time scales of Hervey Bay in Australia using the code COHERENS. Due to wind- and tide-induced renewal pathways, more than 85% of the entire water volume is replenished within a period of 50–80 days. Cavalcante et al. [9] focused on the basin formed by the Palm Jumeirah in Dubai and computed the tide-induced current fields utilizing the software DHI MIKE 21. They found that the residence time (defined as the 37% threshold of the initial value) is unequally distributed in the bay, ranging from 7 to 20 days, due to the great depths and the tide asymmetry. Ranjbar and Zaker [7] numerically studied the water circulation and residence time of Gorgan Bay in Iran, utilizing DHI MIKE 3. They concluded that the circulation was driven mainly by the wind, producing a two-gyre circulation during all seasons. Due to the presence of one primary inlet on the northeastern side of the bay, a spatially varying residence time was observed, with values of more than 100 days far from the inlet, which poses a risk of eutrophication problems.

Using the three-dimensional (3D) code PANORMUS, the wind- and tide-induced hydrodynamic circulation in the Stagnone di Marsala lagoon in Italy was modeled by De Marchis et al. [10]. Their main conclusion is that the wind force is more dominant than the effect of the tide for the generation of the current field. Mahanty et al. [11] investigated the residence time of tracer concentrations in Chilika lagoon in India using DHI MIKE 21. They noticed a seasonal variation of wind, tide and river influx, which significantly affects the water circulation. The residence time (defined as the 50% threshold in this case) was found to vary spatially and seasonally, ranging from 4 to 5 days to even 132 days in specific parts of the lagoon. Montano-Ley et al. [12] performed numerical simulations for the time evolution of a tracer concentration in a coastal lagoon in Mexico, using an inhouse depth-averaged numerical model. They considered both wind and tidal forcing, and their results indicated that the residence time fluctuated from a few days (in proximity to the inlets) up to four months (deep inside the lagoon). Umgiesser et al. [13] analyzed the exchange rates due to tide and wind, by means of the SHYFEM 3D numerical model, for 10 Mediterranean lagoons. The renewal time ranged from a few days up to even 1 year, depending on the lagoon, and based on this time, they categorized the 10 lagoons as leaky, restricted, choked and intermediate. The water renewal inside the Venice lagoon, which is a tidally flushed basin with negligible freshwater inflow, was studied by Viero et al. [14], using a two-dimensional inhouse numerical model. The time series of concentration levels were used for the estimation of the 1/e threshold (37%) residence time at different locations inside the lagoon. Similar time series were analyzed by Atoui et al. [15] for the Boughara lagoon in Tunisia, using the Delft-Flow hydrodynamic model. They considered only the effect of tidal forcing, and residence time was found to vary spatially inside the lagoon, ranging from 1 week up to 6.5 months [14].

Water mass transport is an important factor for the behavior of chemical and biological variables of an ecosystem. Consequently, water renewal is a main indicator for management bodies against the degradation of water quality [16]. Water renewal is mainly controlled by the flow field and the generated currents, and hence, a detailed analysis of the flow field is needed.

The aim of this work is the understanding of the spatial distribution of water renewal in two water bodies in Western Greece, as well as the identification of areas where weak circulation exists, giving rise to high residence times and making these areas highly vulnerable to marine pollution and/or litter accumulation. These water bodies are the Gulf of Patras and Lysimachia Lake, which have been mentioned to suffer from natural or anthropogenic pollution and/or high litter densities. The Gulf of Patras has been characterized in the literature as polluted by wastewaters and toxic metals [17,18]. Ioakeimidis et al. [19] state that marine litter densities in the Gulf of Patras are higher than would be expected based on the population density, the sea traffic, and the outflow of rivers in the area, which is attributed to the enclosed character of the Gulf and the steep bottom topography. Koutsodendris et al. [20] and Stefatos et al. [21] also mention high litter and debris densities in the Gulf of Patras, which are attributed to the densely populated southern coastline of the Gulf. Based on the abovementioned studies, it is concluded that the distribution and accumulation of litter is influenced by the oceanographic–hydrodynamic conditions as well as by the associated transport phenomena. In areas with weak currents and low water renewal, litter accumulation is influenced by parameters such as distance from coasts and estuaries, population centers and distance from shipping routes. As far as Lake Lysimachia is concerned, the Lake is characterized as eutrophic in the literature [22,23], mainly due to the chronic inflow of urban sewage from the city of Agrinio during the past decades. Furthermore, Avramidis et al. [24] found high values of total organic carbon (TOC) and total nitrogen (TN) in the northern part of the Lake, which are used as an indicator of pollution and eutrophication rate according to the USA Environmental Protection Agency.

The assessment of the hydrodynamic behavior, as well as the associated water renewal, is achieved via numerical simulations of the hydrodynamic circulation and advection–dispersion processes in these water bodies. Both of them have a nearly elongated shape and communicate with other larger and much deeper water bodies that seem to determine their flow field and their renewal times, generating flow-through conditions. The worst-case scenario in terms of water renewal was examined for both water bodies. This scenario includes minimal freshwater inflow for Lysimachia Lake, while for the Gulf of Patras, the worst-case scenario involves pure tidal flow under windless conditions.

The Study Areas

The Gulf of Patras (the “Gulf” hereafter for brevity) is located in the region of Western Greece, between Central Greece and the Peloponnese (Figure 1a). It is a relatively shallow flow-through gulf with a maximum depth of 135 m and an average depth of ~56.5 m [25], connecting the deeper Gulf of Corinth at the east with the Ionian Sea at the west, exchanging water masses under the effect of tide and wind. The bathymetry of the Gulf shows a strong marine relief with significant depths. Specifically, the Gulf basin is bounded between two transverse sills, one to the west at the Tourlida–Papas border and one to the east in the area of the Rio–Antirio strait (Figure 1a). The transverse sills formed to a depth of ~40–50 m, keeping the deeper Gulf’s waters, which are enclosed between these, nearly isolated from the coastal waters.

Lysimachia Lake is located to the south of Aetoloakarnania prefecture in Western Greece and is approximately 5 km away from the city of Agrinio (Figure 1b). It is formed between mounts Panetolikos and Arakynthos, by which the water is supplied. More specifically, it is fed by the Ermitsa stream, which outflows in the northeastern part of the Lake and constitutes the main freshwater input. Lysimachia is only 2 km away from the largest and deeper Lake Trichonida, as they are only separated by a strip of land. It is also linked to Lake Trichonida by a connecting channel (~2.7 km). The two lakes along with the connecting channel constitute a single ecosystem. Surplus water, i.e., winter floodwaters from Trichonida, is drained via the connecting channel to Lysimachia and subsequently channeled by the “Dimikos” channel to the Acheloos River, in the west of the Lake (Figure 1b). The Lake has a nearly elongated shape with low banks, its maximum length is 6 km, its width is about 3 km, and it has a maximum depth of around 7.5 m, while its surface covers an area up to 13.2 km².

2. Methodology

2.1. Hydrodynamic Formulation

The numerical simulations were performed utilizing the CFD code MIKE 3 Flow Model FM (Flexible Mesh), which is a 3D numerical modelling system developed by the Danish Hydraulic Institute (DHI). MIKE 3 FM Hydrodynamic Module (HD) was used for the numerical simulation of unsteady 3D flows, taking into consideration complex bathymetry data, variations in water density as well as environmental forcings. A cell-centered finite volume approach was used for spatial discretization, with a triangular unstructured mesh applied in the horizontal direction, while in the vertical direction, an orthogonal structured mesh was used. In the present work, MIKE 3 FM Transport Module (TR) was also utilized, for the numerical simulation of the spreading and fate of dissolved or suspended substances in an aquatic environment under the influence of fluid movement and the associated diffusion processes. More specifically, the advection and diffusion of a conservative tracer, applied in the Gulf´s waters as well as in Lysimachia Lake, was simulated utilizing the TR module. For the details of the codes, the interested reader is referred to [27,28]. The simulations are based on the solution of the Reynolds-averaged Navier–Stokes (RANS) equations for 3D unsteady and incompressible flow, considering the hydrostatic pressure in the vertical direction. A sigma-coordinate transformation approach was used for the evolution of the free surface in the model. Concerning the turbulence closure, an eddy viscosity concept was used, described individually for the horizontal and vertical transport. More specifically, the Smagorinsky [29] model was used for horizontal subgrid-scale transport, while the standard k-ε turbulence model [30] was used for vertical eddy viscosity. An approximate Riemann solver scheme [31] was applied for spatial discretization. In this specific scheme, the convective fluxes in the horizontal plane are calculated at the vertical interface of the cells, while in the vertical plane, the convective fluxes are calculated at the horizontal interfaces using an upwinding scheme.

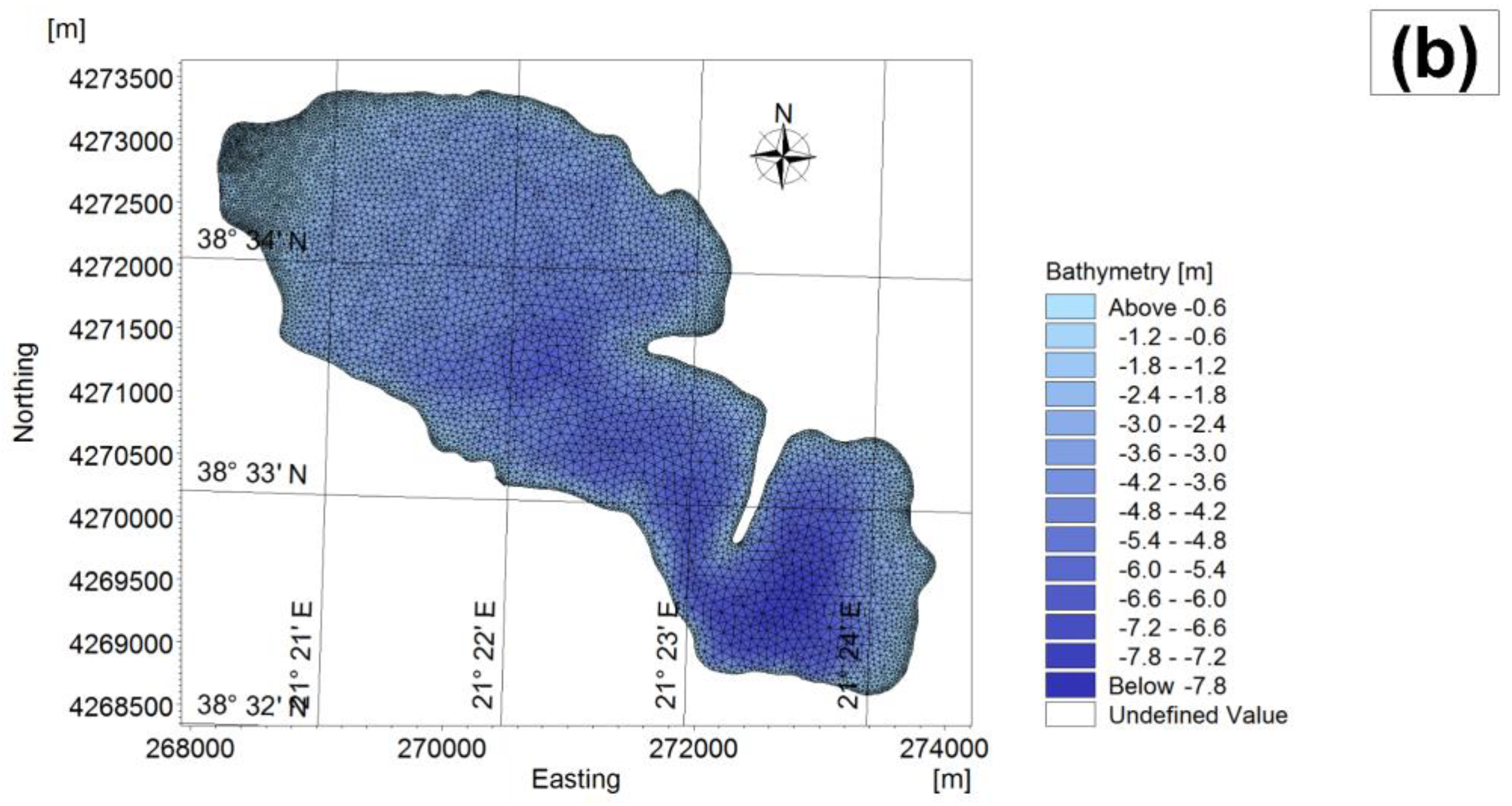
2.2. Computational Domain and Grid

For the Gulf’s basin, the computational domain, the open boundaries formation and the application of the initial and boundary conditions were specified in [32], based on numerical simulations for many combinations of forcing of the hydrodynamic system. More specifically, in the horizontal plane, an unstructured mesh was applied, consisting of 23,197 triangular cells (Figure 2a). In the vertical direction, a hybrid grid-building system was chosen by applying 10 σ-layers from the free surface to the depth of 30 m, while for the rest of the water column, a Cartesian computational grid was applied, with a uniform cell height of 3 m. This discretization was implemented in order to maintain a tolerable computational cell height-to-width ratio, given the steep, large gradients found between the two transverse sills that bound the Gulf’s basin. The numerical time step was appropriately chosen in order not to violate the CFL criterion (CFLmax = 0.8) and to achieve convergence. It is noteworthy that for coupled hydrodynamic and transport simulation of a 6-month period, about 1 month was required on an Intel core i7, 3.4 GHz PC.

The numerical domain for the 3D simulations of Lysimachia Lake is presented in Figure 2b, which covers the Lake’s waters and the adjacent open boundaries. The bathymetric data for Lysimachia Lake were received from [33]. In the vicinity of the freshwater inlets/outlets, i.e., northeasterly and easterly (inflow from the Ermitsa stream and the connecting channel) and westerly and southerly (outflow to the Acheloos River via the “Dimikos” channel and Lysimachia tunnel), a finer discretization is required for adequate simulation of the freshwater plume propagation from the stream or connecting channel to the Lake’s body. Thus, a non-uniform computational mesh was generated (Figure 2b). In the vicinity of the open boundaries, i.e., inlets and outlets of the Lake, the area consists of cells with a characteristic dimension of ~10 m, gradually increasing outwards. Adjacent to this area lies a greater zone covering the Lake’s main body, where the grid size gradually increases from ~10 m near the shore to ~50 m inside the Lake’s body. The total number of computational cells in the horizontal plane is 14,416 (7738 nodes). Using the specific discretization, an overall satisfactory accuracy is achieved, while the computational cost is maintained at a reasonable level. In the vertical plane, 10 σ-layers were used over the depth. The accuracy of the numerical model was assessed by performing a mesh sensitivity analysis, using 10 and 20 computational cells for vertical discretization. The vertical profile of the flow velocity is presented in Figure 3b for both mesh cases in front of the connecting channel (Figure 3a) in the eastern part of the Lake. The numerical results indicate that the vertical discretization of 10 cells is sufficient to capture well the flow development in the Lake.

The suitable locations chosen as inflow freshwater boundaries are the main inflows from Lysimachia Lake, one of which, i.e., the eastern open boundary, is close to the outflow of the connecting channel between the two lakes. The second inflow boundary is located in the northeastern part of the Lake where the Ermitsa stream outflows (Figure 1b). Furthermore, two outflow open boundaries were chosen, one in the western part of the Lake, close to the outflow of the drainage channel “Dimikos” to the Acheloos River. The second outflow boundary is located in the south of the Lake where the Lysimachia tunnel outflows (Figure 1b).

2.3. Boundary and Initial Conditions

The hydrodynamic circulation in the Gulf of Patras under the combined action of tides and wind has been thoroughly studied in previous works [32,34]. The goal of these simulations was to understand the flow structure in the Gulf, as well as to numerically calculate the exchange flow between the Gulf of Patras and Corinth in the Rio–Antirio strait. In this work, the tidal effect on the Gulf of Patras under windless conditions was studied numerically during the winter season, when the Gulf was found to be homogeneous [35]. The initial and boundary conditions used for the simulations reported below were identical to those used to simulate tidal hydrodynamics in the same Gulf [32].

Regarding the case of Lysimachia Lake, the bank of the Lake has been defined as an impermeable boundary with zero normal velocity, while the bottom is a no-slip (via wall functions), impermeable boundary. Mean annual values of inflow and outflow discharge that derived from the literature [23,36] were used as open boundary conditions in the following simulations. The inflow forcing, i.e., the discharge from the connecting channel between the two lakes as well as freshwater inflow discharged from the Ermitsa stream, was imposed as a specified discharge value which is constant along the open boundary. More specifically, a mean value of ≈22 m³/s was considered representative for the eastern open boundary, while the freshwater discharge from the Ermitsa stream was imposed as equal to ≈1.5 m³/s. In the south open boundary, where the Lysimachia tunnel is located, a mean outflow discharge of ≈18 m³/s was used, while in the western boundary of the Lake, free outflow condition was taken into account. The bed roughness height was set equal to 0.01 m. Special focus was given to the geometry of the bottom cell, to ensure its compatibility with fully rough flow requirements, based on the assumption of a minimum water depth equal to 0.2 m. Concerning the initial conditions, all simulations were initiated from the state of rest. In addition, barotropic flow was taken into account, as the Lake was found to be nearly homogeneous, without crucial stratification in the water column [23,37].

Regarding the water renewal simulations, various time scales have been reported in the literature for the quantifications of water renewal in natural systems [38]. In the present study, residence time is defined as the time needed for the concentration of a conservative, passive tracer to fall to 1/e (~37%) of its initial value [39]. The initial concentration of the conservative numerical tracer is equal to 1 inside and 0 outside the Gulf or Lysimachia Lake, respectively. Thus, the residence time is calculated everywhere inside the water body by following the evolution of the numerical tracer concentration. Based on this method, the analysis of the complex water renewal problem is performed on the abovementioned water bodies. Furthermore, the estimation of low water renewal areas inside their basins is examined.

3. Results and Discussion

3.1. The Gulf of Patras

In this section, basic flow characteristics in the Gulf of Patras under the effect of tides are briefly summarized. During the transition phase from flood to ebb and vice versa, the circulation pattern in the Gulf changes visibly. In particular, in the wider area of the Rio–Antirio strait, cyclonic and anticyclonic gyres are formed under tidal action. Based on the numerical simulations of the tidal circulation, it is shown that the tide determines the water circulation in the main body of the Gulf and in the wider area of the Rio–Antirio strait, causing strong tidal currents and leaving the coasts nearly unaffected. More specifically, the tidal action causes stronger currents near the northern part of the Gulf of Patras and weaker ones in the southern part, as predicted by the numerical simulation and illustrated in Figure 4. In Figure 5, time series of the surface currents during a one-month (30 days) simulation are given for two points selected near the northern (p₁) and southern (p₂) parts of the Gulf, the locations of which are illustrated in Figure 4. It is noteworthy that the current values were calculated to be in the same phase but show significant differences in intensity, with the strongest currents affecting the northern areas of the Gulf of Patras, reaching current speed values twice as large.

Regarding the Gulf’s water renewal, in Figure 6, the concentration fields of a conservative numerical tracer applied to the numerical domain of the Gulf are contrasted as they occurred after 1.5 months (45 days), 3 months (90 days), 4.5 months (135 days) and 6 months (180 days) from the start of the simulation. The comparison shows that the effect of the tide is crucial for the renewal of the waters in the northern part of the Gulf, where lower concentration values are observed. The phenomenon is associated with the strongest tidal currents that arise for the northern part of the Gulf. Furthermore, based on the simulations, the evolution of the concentration in the northern part of the Gulf highlights a quasi-dominant direction of the tidal flow from east to west, which gradually leads to enhanced flushing of the waters of the northern part of the Gulf, achieving shorter residence times for these areas. On the contrary, in the central and southern parts of the Gulf, the waters are almost stagnant, leading to significant residence times, exceeding 6 months.

Figure 7a shows the spatial distribution of the residence time of the Gulf’s waters for a period of 6 months based on the numerical simulations. The numerically predicted results highlight the short residence times (<1 month) and the rapid renewal of waters in the area of the Rio–Antirio strait. This is due to the rapid mixing of the waters of the Gulf with those of the deeper Gulf of Corinth, which is achieved under the effect of strong tidal currents generated in the wider area of the strait. Residence times ranging from 1 to 4 months are estimated for the northern area of the Gulf, while in the central and southern areas, the waters show stagnation, with renewal times estimated to exceed 6 months. The same pattern of water renewal occurs for the deeper parts of the Gulf, especially at depths greater than 60 m.

In Figure 7b, the residence time distribution is presented for the deeper bottom waters of the Gulf. It is shown that the Gulf’s bottom waters, enclosed between the two sills, remain nearly isolated, achieving high residence times. More specifically, in this case, the calculated residence times exceed 6 months in the central deepest part, while lower values (<4 months) were obtained for the northern parts of the Gulf’s basin. Therefore, also in the case of deep waters (>60 m), the central and southern part of the Gulf of Patras basin shows a weakness in water renewal, leading to significant residence times as well as an inability to replenish bottom waters. These results seem to be related to the results of Kalpaxis et al. [17], who mentioned that the degree of organic pollution in the southern Gulf of Patras varies between different coastal locations. More specifically, they found enhanced organic pollution in a location close to the city of Patras (Figure 1), while no organic pollution was found close to Rio (Figure 1), which is in accordance with the present numerical results.

3.2. Lysimachia Lake

The horizontal geometric length scale of Lysimachia Lake basin is in the order of 5 × 10³ m. The Rossby (Ro) number value of the freshwater-plume-generated flow as well as the wind-driven flow is expected to be less than 1, approaching a value of 1 for strong winds, so that Coriolis force is expected to affect the flow field. However, the Lake is restricted and variable in depth, mainly in the central part of the basin due to the Ermitsa stream outflows. Thus, the effect of rotation is expected to be reduced with increasing wind speed, in the case of wind-induced flow, which is outside the scope of this paper. More specifically, the Lake consists of two sub-basins, one in the eastern part of the Lake, and the other in the west. The maximum depth of the former basin is ≈7.5 m and that of the latter ≈ 6 m. Thus, the formation of the shape of the Lake is expected to have a crucial role in water renewal. Another important characteristic of the Lake’s basin is that the smaller sub-basin on the east has a horizontal length scale of ~1.5 km, whereas the central part of the Lake, a nearly restricted area due to the sedimentation from the Ermitsa stream outflows, is only approximately 1 km. Thus, the importance of the Coriolis force is anticipated to be suppressed in these areas, the overall Ro value notwithstanding. In this area, the behavior of the wind-induced flow seems to resemble that of a classical hydraulic behavior rather than a geophysical flow. Herein, the Lake hydrodynamics is considered under windless conditions, which remain the most adverse case for water mixing as well as the associated water replenishment of the Lake.

In Figure 8, the numerically predicted surface current field is depicted. The flow is driven by freshwater plumes, i.e., the outflow of the Ermitsa stream as well as the inflow discharge from the connecting channel. In general terms, the salient features of the flow are preserved during steady inflow/outflow discharges: the currents in the near-field region of the freshwater inflows/outflows are substantially stronger than currents in the central parts of the Lake. The hydrodynamic circulation of the Lake seems to be affected by the presence of the sand spit formed in the northeastern part due to Ermitsa stream outflows, which poses an obstacle to the inflow discharge drained from the connecting channel to the Lake. Under these conditions, a cyclonic eddy is formed in the southeastern part of the Lake (red dashed line in Figure 8), leaving the waters nearly isolated and leading to water entrapment and recirculation in this area of the Lake (Figure 9, see at t = 5 days). The phenomenon appears to persist during the simulations, with residence time slightly increased in the vicinity of the connecting channel inflow to the Lake (Figure 10). The eddy is formed by the end of the first 24 h of the simulation. Eventually, a steady-state condition is reached, despite the fact that, in reality, it is seldom approached.

In the main part of the Lake, the formation of a main flow path is observed (blue dashed line in Figure 8), which is dictated by the freshwater plumes. Furthermore, a flow-through hydrodynamic regime is formed that substantially affects the water renewal (Figure 9, see at t = 10, 20 days). The incoming floodwaters from Trichonida Lake significantly improve the renewal of the Lysimachia waters, regardless of the local effect of the Ermitsa stream inflow.

More specifically, a considerable inflow (~22 m³/s) from Trichonida Lake generates a flow-through regime from east to west, which is the main reason for the Lake´s replenishment. In this case, the residence (e-folding) time of the main body of the Lake varies from 20 to 40 days (Figure 10). These values are consistent with findings in the literature, mentioning that the Lake appears to be replenished approximately 13 times a year, i.e., every 28 days [23]. Moreover, the resulting simulated spatial variation of water renewal is in fair agreement with the results of Avramidis et al. [24] for the organic pollution at characteristic sites in the Lake. More specifically, they found higher values of TOC and TN in the northern part of the Lake.

4. Conclusions

In this work, basic flow characteristics and water renewal in the Gulf of Patras as well as in Lysimachia Lake were studied numerically. Based on the numerical simulations, the following conclusions are drawn:

• Water renewal is controlled by the hydrodynamic conditions, and it is an important mechanism against the degradation of water quality. The generated flow field can result in an increased water renewal rate locally, thus reducing the probability of organic pollution or litter accumulation in these areas.
• Tidal circulation has a critical effect in the vicinity of the Rio–Antirio strait, causing strong tidal currents. The tide determines the circulation of water in the main body of the Gulf as well as in the wider area of the strait, leaving the coasts almost unaffected. Current speeds between the northern and southern parts of the Gulf show significant differences, with the strongest currents affecting the northern area of the Gulf.
• Relatively rapid water renewal is achieved in the wider area of the Rio–Antirio strait (<1 month). Residence times ranging from 1 to 4 months are numerically calculated for the northern part of the Gulf, while in the central and southern part, the renewal times are estimated to exceed 6 months.
• Significant renewal times also occur for the deeper parts of the Gulf (>60 m). The same renewal pattern is also reflected in the deeper water area, where the water renewal time was found to exceed 6 months.
• The spatially varying water renewal predicted by the numerical results for the Gulf of Patras seems to be related to findings in the literature reporting different values of organic pollution in two locations in the southern part of the Gulf.
• The geometry of Lysimachia Lake, under the freshwater inflows, generates a characteristic flow-through hydrodynamic function of the water body. It has been shown that a main flow path is formed, generating a nearly unidirectional flow within the Lake’s basin. In the southeastern part of the Lake, a cyclonic eddy is formed, leading to water entrapment and recirculation in the area.
• The resulting flow regime, dictated by the main flow path, enhances the mechanism of the Lake’s replenishment, leading to residence times of less than a month.
• The numerical results for the Lake’s water renewal are consistent with the relevant literature, which mentions that the Lake’s waters are renewed approximately 13 times a year, as well as that higher values of TOC and TN are observed in the northern part of the Lake.