Surrogate-Based Multiobjective Optimization of Detention Pond Volume in Sponge City
Abstract
:1. Introduction
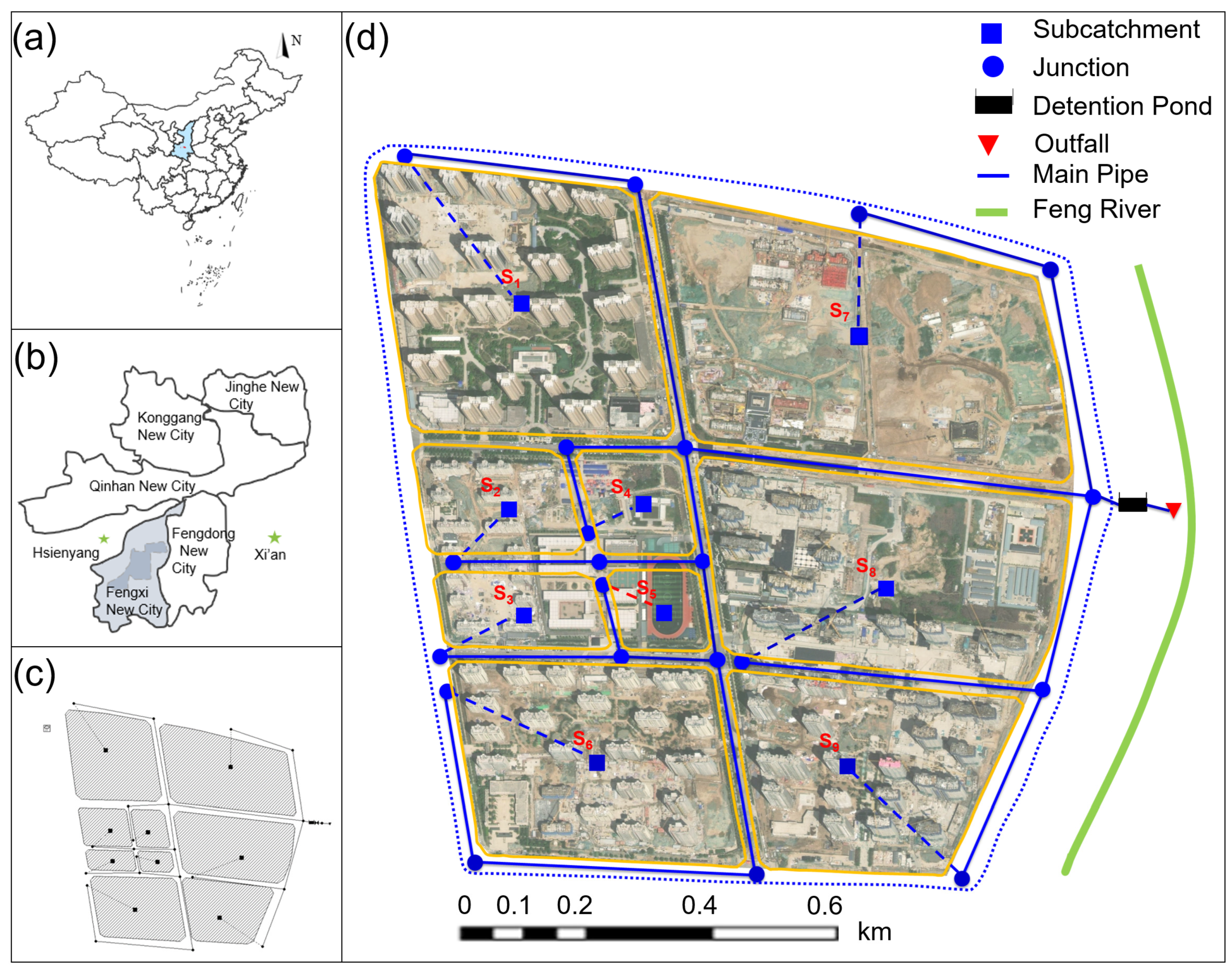
2. Study Area and Data
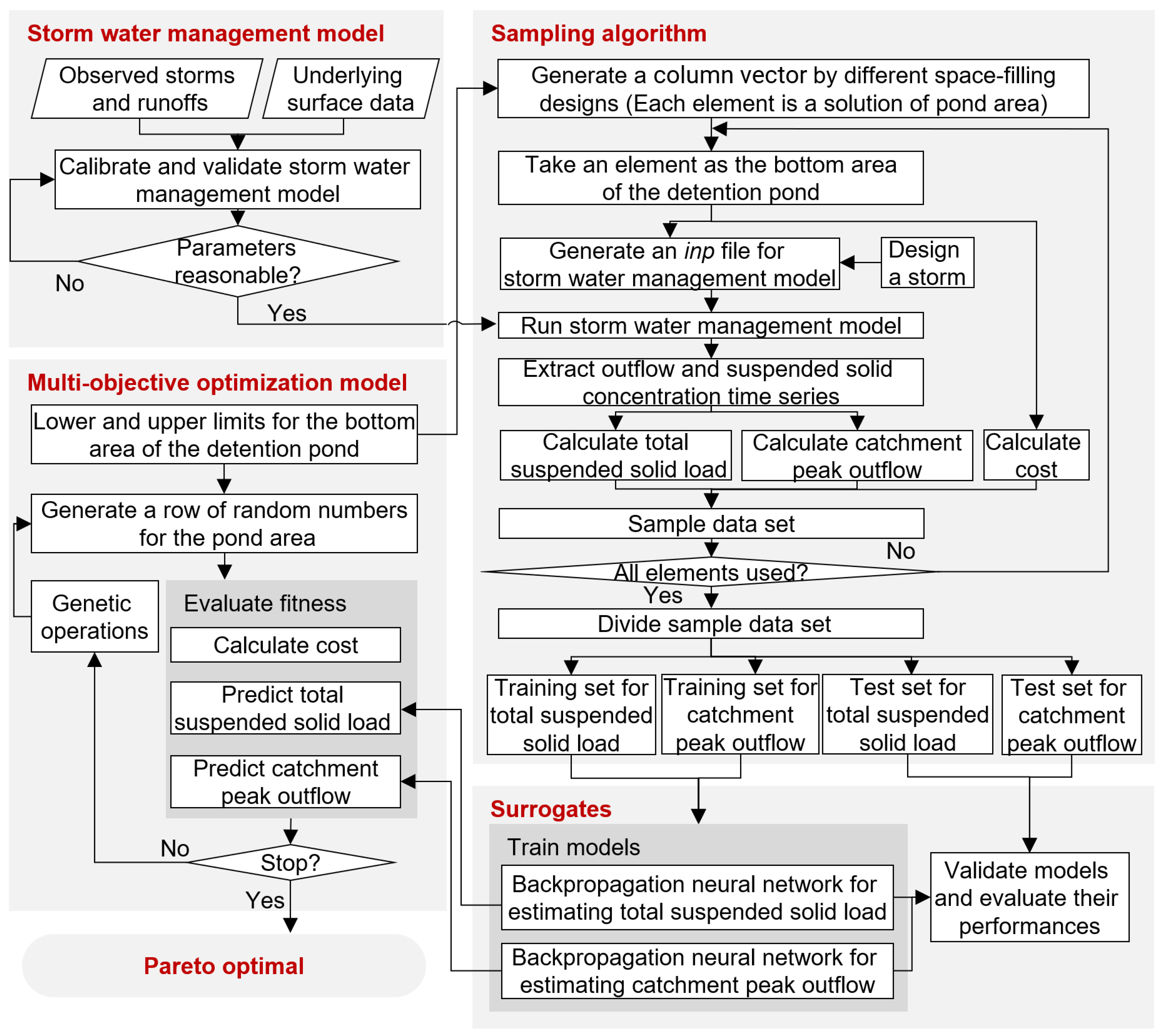
3. Methodology
3.1. Chicago Design Storm
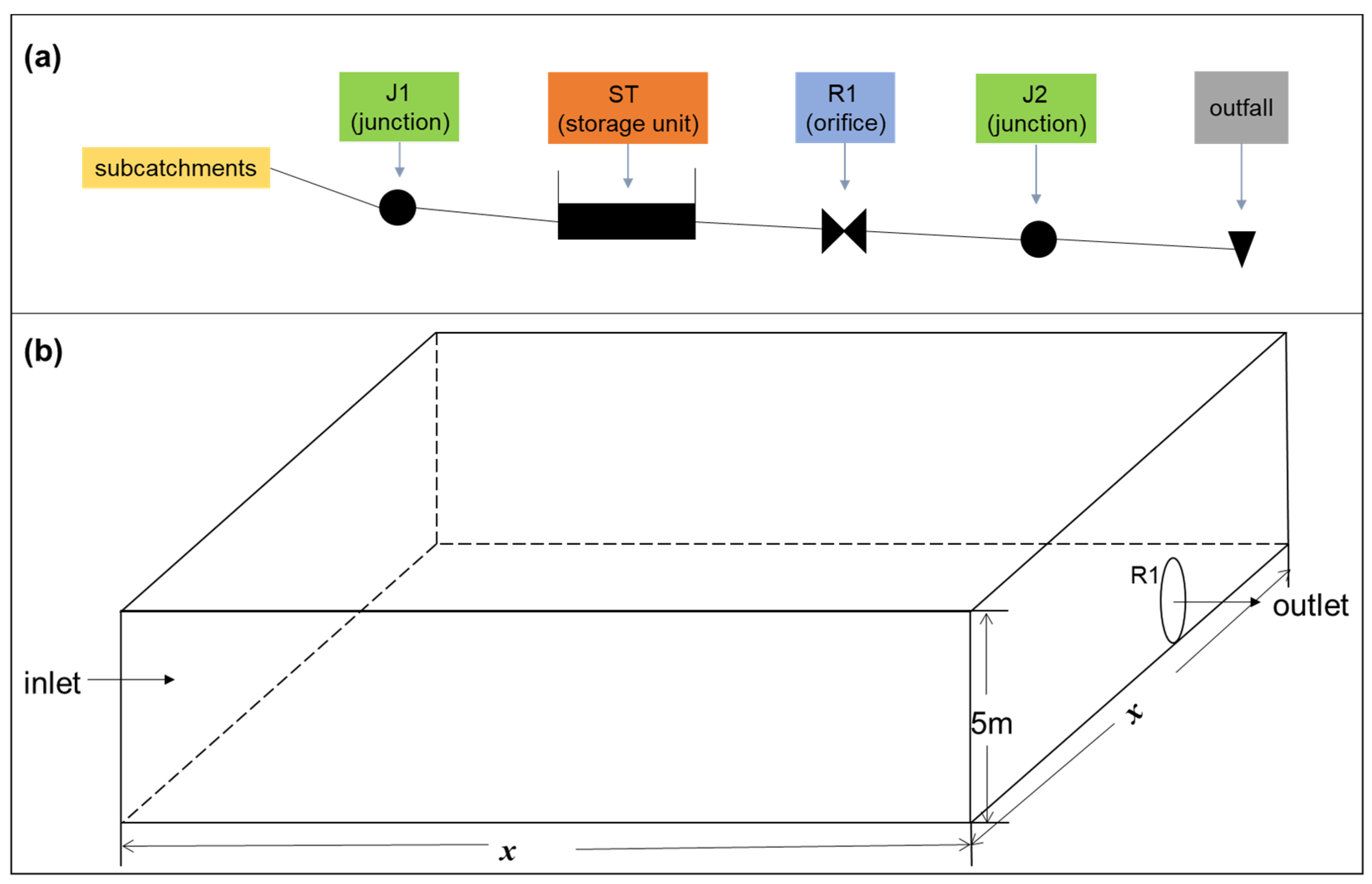
3.2. Detention Pond Simulation in Stormwater Management Model
| Algorithm 1. Control rule of detention pond in storm water management model. | |
| 1 | RULE 1 |
| 2 | IF NODE ST DEPTH > 0 |
| 3 | AND NODE ST DEPTH ≤ 0.5 |
| 4 | THEN ORIFICES R1 SETTING = 0 |
| 5 | RULE 2 |
| 6 | IF NODE ST DEPTH > 0.5 |
| 7 | AND NODE ST DEPTH ≤ 2 |
| 8 | THEN ORIFICES R1 SETTING = 0.2 |
| 9 | RULE 3 |
| 10 | IF NODE ST DEPTH > 2 |
| 11 | AND NODE ST DEPTH ≤ 4 |
| 12 | THEN ORIFICES R1 SETTING = 0.4 |
| 13 | RULE 4 |
| 14 | IF NODE ST DEPTH > 4 |
| 15 | AND NODE ST DEPTH ≤ 4.5 |
| 16 | THEN ORIFICES R1 SETTING = 0.6 |
| 17 | RULE 5 |
| 18 | IF NODE ST DEPTH > 4.5 |
| 19 | AND NODE ST DEPTH ≤ 4.8 |
| 20 | THEN ORIFICES R1 SETTING = 0.8 |
| 21 | RULE 6 |
| 22 | IF NODE ST DEPTH > 4.8 |
| 23 | AND NODE ST DEPTH ≤ 5 |
| 24 | THEN ORIFICES R1 SETTING = 1 |
3.3. Multiobjective Optimization
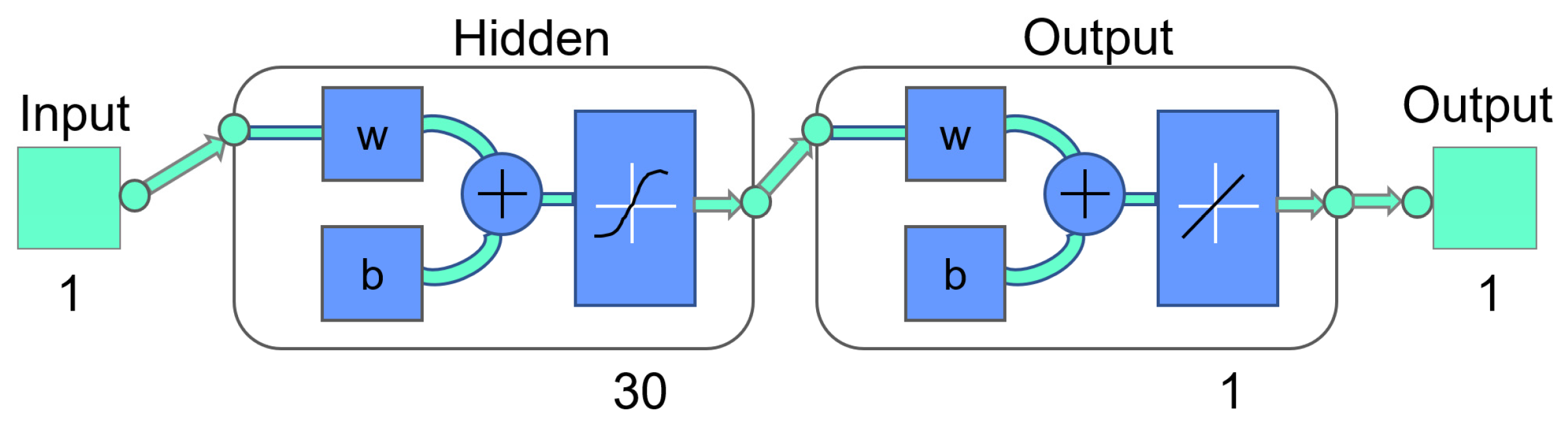
3.4. Surrogate Model
| Algorithm 2. Pseudocode of sampling algorithm. nsam is the number of samples. LB and UB are the lower and upper boundaries for the pond area, respectively. P(t) is the rainfall depth during time ∆t. inp and out are the input and output files for the SWMM, respectively. xk is the pond area for the k-th sample. COSTk, TSSk, and CPOk are the life-cycle cost, TSS, and CPO for the k-th sample. C(k,t) is the average pollutant concentration and the average outflow rate at the outfall in t-th time step for the k-th sample, respectively. SAMk is the data point for the k-th sample. | |
| 1 | Specify nsam, LB, and UB. |
| 2 | Get P(t) |
| 3 | Load inp |
| 4 | for k = 1 to nsam do |
| 5 | Randomly generate xk between LB and UB. |
| 6 | Calculate COSTk |
| 7 | Update the pond area in the CURVE section of inp with xk |
| 8 | Save the updated file as kth inp |
| 9 | Drive MatSWMM with kth inp |
| 10 | Save simulation results into kth out |
| 11 | Load kth out |
| 12 | end for |
| 13 | for k = 1 to nsam do |
| 14 | Get C(k,t) and Q(k,t) |
| 15 | Calculate TSSk |
| 16 | Calculate CPOk |
| 17 | Do SAMk = [xk, COSTk, TSSk, CPOk] |
| 18 | end for |
4. Results and Discussion
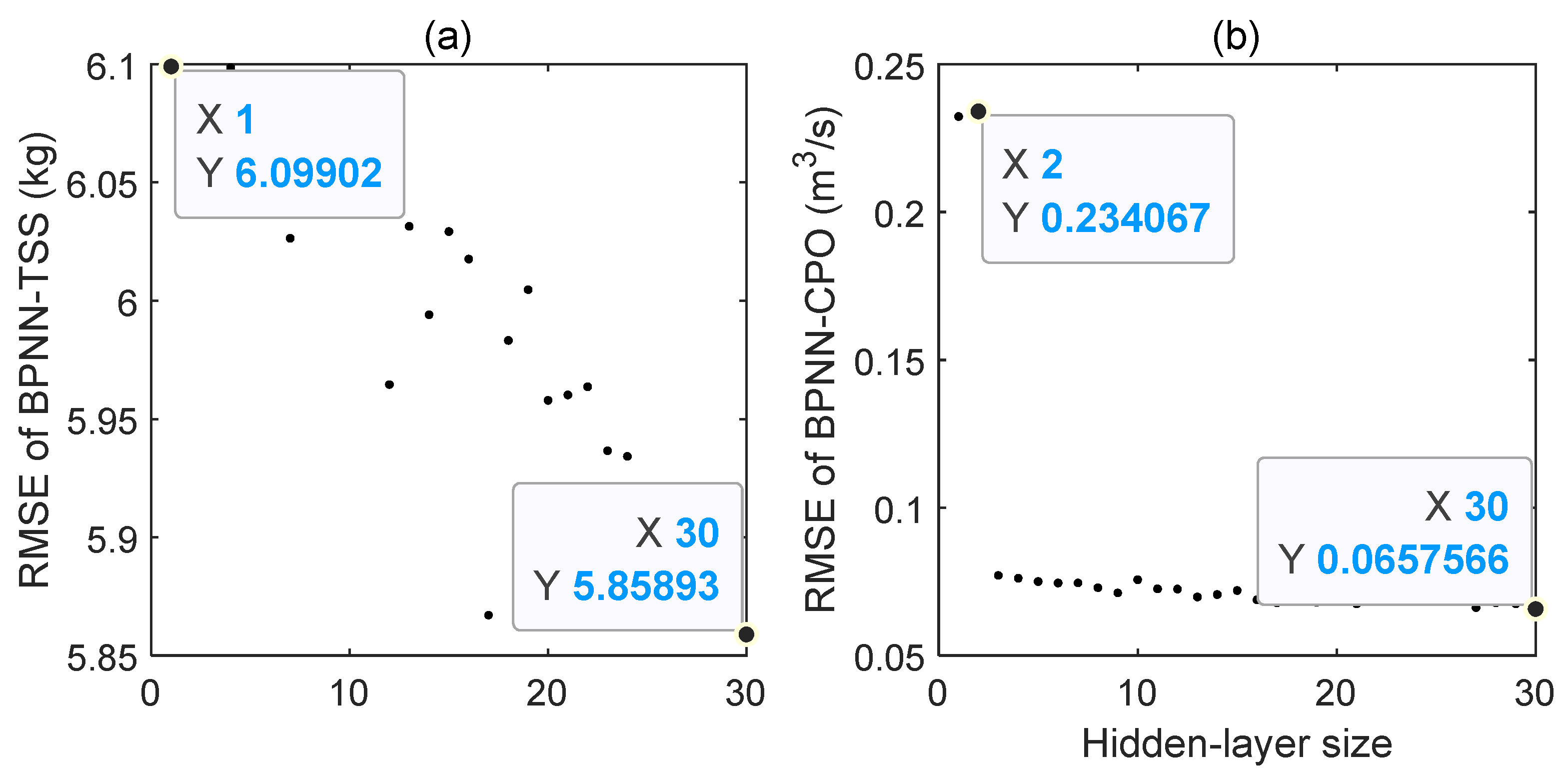
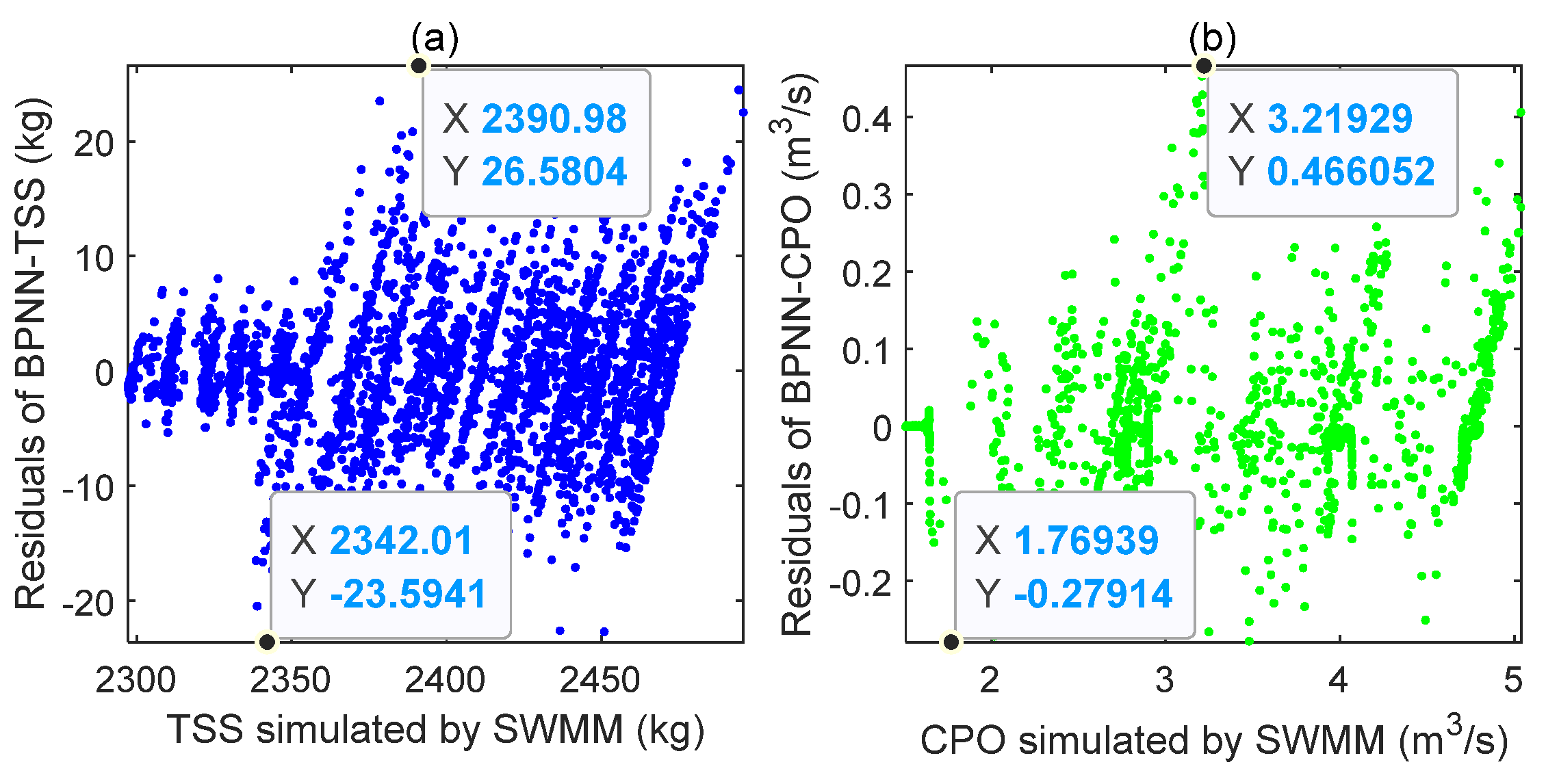
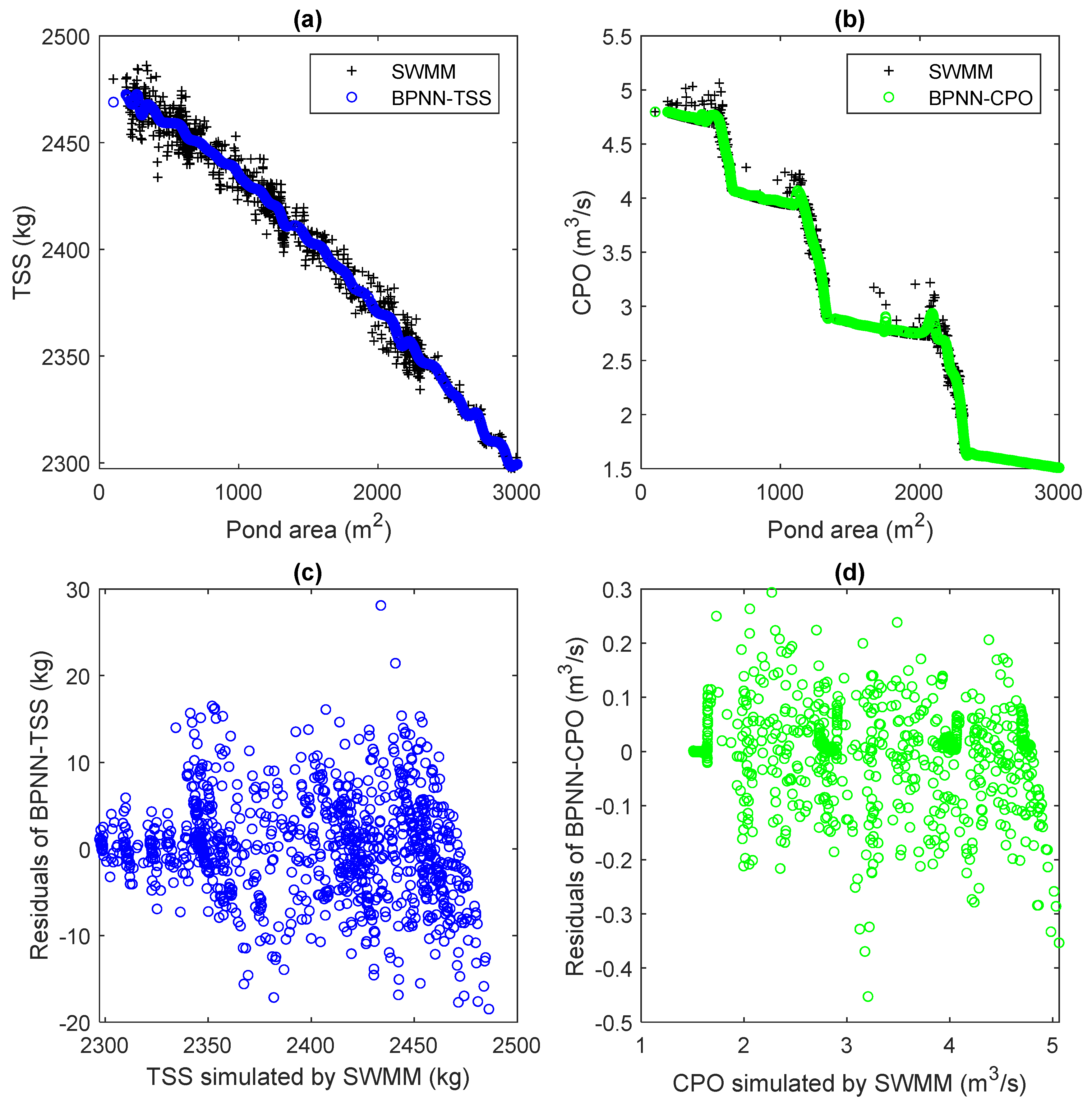
4.1. Performance of Surrogate Models
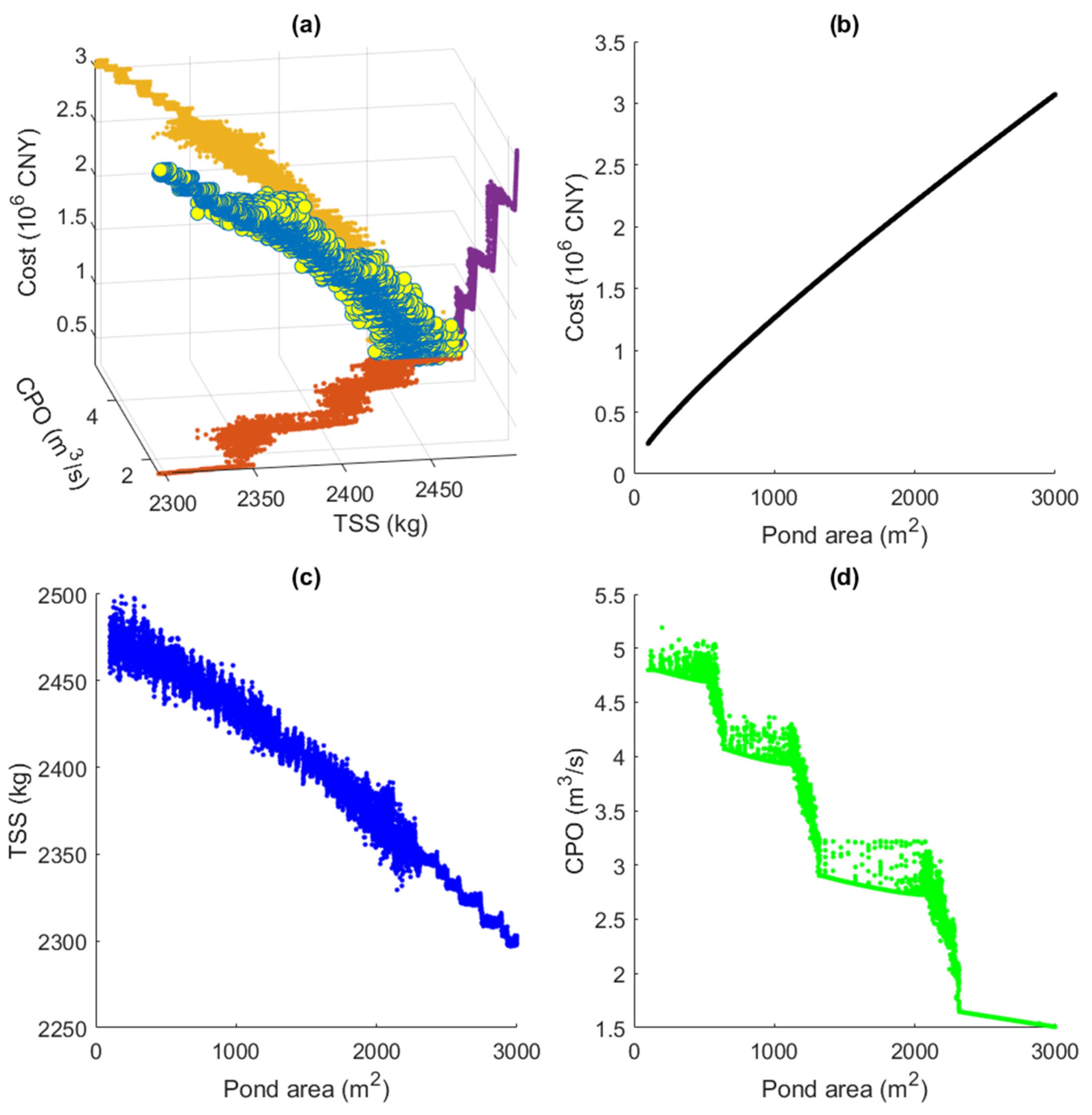
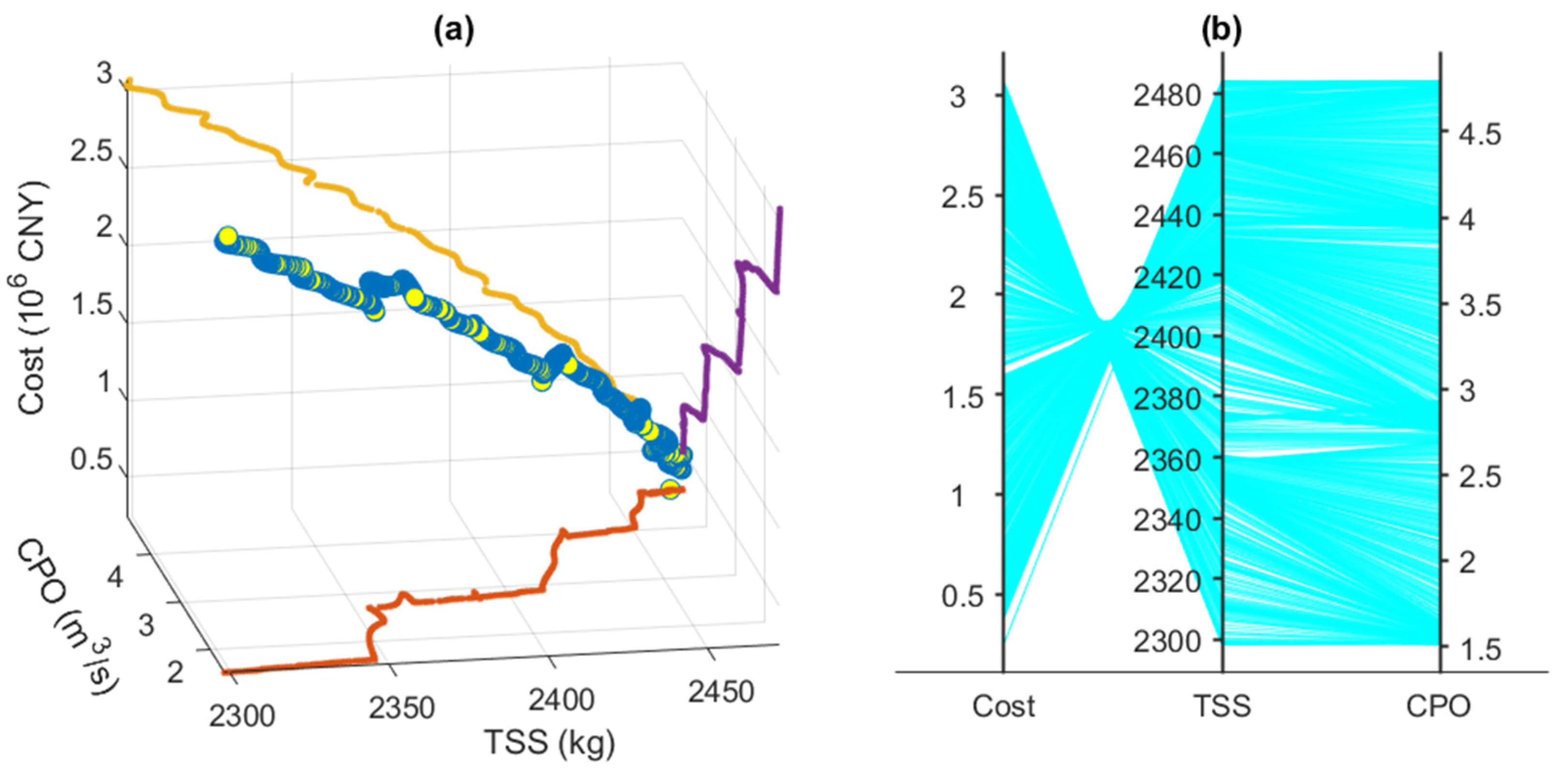
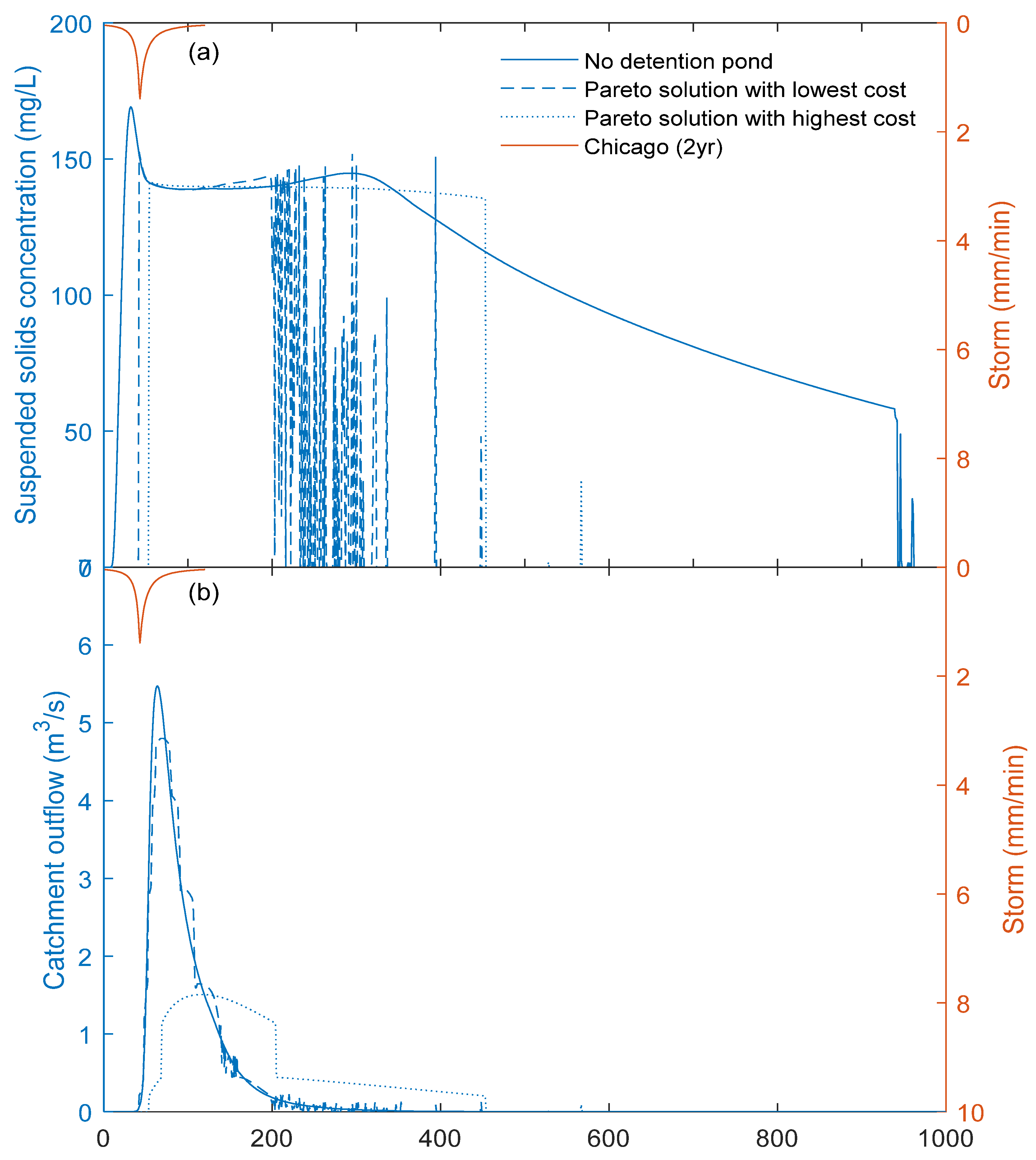
4.2. Effectiveness of Pareto Solutions
4.3. Computational Efficiency
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cheng, M.; Qin, H.; Fu, G.; He, K. Performance evaluation of time-sharing utilization of multi-function sponge space to reduce waterlogging in a highly urbanizing area. J. Environ. Manag. 2020, 269, 110760. [Google Scholar] [CrossRef] [PubMed]
- Gold, A.C.; Thompson, S.P.; Piehler, M.F. Seasonal Variation in Nitrate Removal Mechanisms in Coastal Stormwater Ponds. Water Resour. Res. 2021, 57, e2021WR029718. [Google Scholar]
- Eckart, K.; McPhee, Z.; Bolisetti, T. Performance and implementation of low impact development—A review. Sci. Total Environ. 2017, 607–608, 413–432. [Google Scholar] [CrossRef] [PubMed]
- Aldrees, A.; Dan’azumi, S. Application of Analytical Probabilistic Models in Urban Runoff Control Systems’ Planning and Design: A Review. Water 2023, 15, 1640. [Google Scholar]
- Sharior, S.; McDonald, W.; Parolari, A.J. Improved reliability of stormwater detention basin performance through water quality data-informed real-time control. J. Hydrol. 2019, 573, 422–431. [Google Scholar] [CrossRef] [Green Version]
- Behera, P.K.; Teegavarapu, R.S.V. Optimization of a Stormwater Quality Management Pond System. Water Resour. Manag. 2015, 29, 1083–1095. [Google Scholar]
- Szeląg, B.; Kiczko, A.; Musz-Pomorska, A.; Widomski, M.K.; Zaburko, J.; Łagód, G.; Stránský, D.; Sokáč, M. Advanced Graphical–Analytical Method of Pipe Tank Design Integrated with Sensitivity Analysis for Sustainable Stormwater Management in Urbanized Catchments. Water 2021, 13, 1035. [Google Scholar]
- Yang, S.N.; Chang, L.C.; Chang, F.J. AI-based design of urban stormwater detention facilities accounting for carryover storage. J. Hydrol. 2019, 575, 1111–1122. [Google Scholar] [CrossRef]
- Yang, Y.Y.; Zhang, W.H.; Liu, Z.; Liu, D.F.; Huang, Q.; Xia, J. Coupling a Distributed Time Variant Gain Model into a Storm Water Management Model to Simulate Runoffs in a Sponge City. Sustainability 2023, 15, 3804. [Google Scholar] [CrossRef]
- Zhang, G.S.; Hamlett, M.J.; Reed, P.; Tang, Y. Multi-Objective Optimization of Low Impact Development Designs in an Urbanizing Watershed. Open J. Optim. 2013, 2, 95–108. [Google Scholar] [CrossRef] [Green Version]
- Oxley, R.L.; Mays, L.W. Optimization—Simulation Model for Detention Basin System Design. Water Resour. Manag. 2014, 28, 1157–1171. [Google Scholar] [CrossRef]
- Tian, W.C.; Liao, Z.L.; Zhang, Z.Y.; Wu, H.; Xin, K.L. Flooding and Overflow Mitigation Using Deep Reinforcement Learning Based on Koopman Operator of Urban Drainage Systems. Water Resour. Res. 2022, 58, e2021WR030939. [Google Scholar]
- Lund, N.S.V.; Borup, M.; Madsen, H.; Mark, O.; Mikkelsen, P.S. CSO Reduction by Integrated Model Predictive Control of Stormwater Inflows: A Simulated Proof of Concept Using Linear Surrogate Models. Water Resour. Res. 2020, 56, e2019WR026272. [Google Scholar]
- Yang, Y.Y.; Li, J.; Huang, Q.; Xia, J.; Li, J.K.; Liu, D.F.; Tan, Q.T. Performance assessment of sponge city infrastructure on stormwater outflows using isochrone and SWMM models. J. Hydrol. 2021, 597, 126151. [Google Scholar] [CrossRef]
- Duan, H.F.; Li, F.; Yan, H.X. Multi-Objective Optimal Design of Detention Tanks in the Urban Stormwater Drainage System: LID Implementation and Analysis. Water Resour. Manag. 2016, 30, 4635–4648. [Google Scholar]
- Yang, Y.Y.; Li, Y.B.; Huang, Q.; Xia, J.; Li, J.K. Surrogate-based multiobjective optimization to rapidly size low impact development practices for outflow capture. J. Hydrol. 2023, 616, 128848. [Google Scholar] [CrossRef]
- Liang, R.J.; Thyer, M.A.; Maier, H.R.; Dandy, G.C.; Di Matteo, M. Optimising the design and real-time operation of systems of distributed stormwater storages to reduce urban flooding at the catchment scale. J. Hydrol. 2021, 602, 126787. [Google Scholar]
- Jefferson, A.J.; Bhaskar, A.S.; Hopkins, K.G.; Fanelli, R.; Avellaneda, P.M.; McMillan, S.K. Stormwater management network effectiveness and implications for urban watershed function: A critical review. Hydrol. Process 2017, 31, 4056–4080. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar]
- Liu, D.; Huang, Q.; Yang, Y.Y.; Liu, D.F.; Wei, X.T. Bi-objective algorithm based on NSGA-II framework to optimize reservoirs operation. J. Hydrol. 2020, 585, 124830. [Google Scholar] [CrossRef]
- Yang, Y.Y.; Xu, X.Y.; Liu, D.F. An Event-Based Stochastic Parametric Rainfall Simulator (ESPRS) for Urban Stormwater Simulation and Performance in a Sponge City. Water 2023, 15, 1561. [Google Scholar] [CrossRef]
- Riaño-Briceño, G.; Barreiro-Gomez, J.; Ramirez-Jaime, A.; Quijano, N.; Ocampo-Martinez, C. MatSWMM—An open-source toolbox for designing real-time control of urban drainage systems. Environ. Modell Softw. 2016, 83, 143–154. [Google Scholar] [CrossRef] [Green Version]
- Yu, J.J.; Qin, X.S.; Chiew, Y.M.; Min, R.; Shen, X.L. Stochastic Optimization Model for Supporting Urban Drainage Design under Complexity. J. Water Res. Plan Man 2017, 143, 05017008. [Google Scholar] [CrossRef]
- Chaudhary, S.; Chua, L.H.C.; Kansal, A. The uncertainity in stormwater quality modelling for temperate and tropical catchments. J. Hydrol. 2023, 617, 128941. [Google Scholar] [CrossRef]
- Rossman, L.A. Storm Water Management Model User’s Manual, Version 5.1; United States Environmental Protection Agency: Westlake, OH, USA, 2015.
- Liang, R.J.; Maier, H.R.; Thyer, M.A.; Dandy, G.C.; Tan, Y.H.; Chhay, M.; Sau, T.; Lam, V. Calibration-free approach to reactive real-time control of stormwater storages. J. Hydrol. 2022, 614, 128559. [Google Scholar] [CrossRef]
- Yazdi, J. Optimal Operation of Urban Storm Detention Ponds for Flood Management. Water Resour. Manag. 2019, 33, 2109–2121. [Google Scholar] [CrossRef]
- Saadatpour, M.; Delkhosh, F.; Afshar, A.; Solis, S.S. Developing a simulation-optimization approach to allocate low impact development practices for managing hydrological alterations in urban watershed. Sustain. Cities Soc. 2020, 61, 102334. [Google Scholar] [CrossRef]
- Luan, B.; Yin, R.X.; Xu, P.; Wang, X.; Yang, X.M.; Zhang, L.; Tang, X.Y. Evaluating Green Stormwater Infrastructure strategies efficiencies in a rapidly urbanizing catchment using SWMM-based TOPSIS. J. Clean. Prod. 2019, 223, 680–691. [Google Scholar] [CrossRef]
- Li, F.; Duan, H.F.; Yan, H.X.; Tao, T. Multi-Objective Optimal Design of Detention Tanks in the Urban Stormwater Drainage System: Framework Development and Case Study. Water Resour. Manag. 2015, 29, 2125–2137. [Google Scholar]
- Verma, S.; Pant, M.; Snasel, V. A Comprehensive Review on NSGA-II for Multi-Objective Combinatorial Optimization Problems. IEEE Access 2021, 9, 57757–57791. [Google Scholar] [CrossRef]
- Lu, W.; Xia, W.; Shoemaker, C.A. Surrogate Global Optimization for Identifying Cost-Effective Green Infrastructure for Urban Flood Control With a Computationally Expensive Inundation Model. Water Resour. Res. 2022, 58, e2021WR030928. [Google Scholar] [CrossRef]
- Zhang, W.; Li, J.; Chen, Y.H.; Li, Y. A Surrogate-Based Optimization Design and Uncertainty Analysis for Urban Flood Mitigation. Water Resour. Manag. 2019, 33, 4201–4214. [Google Scholar] [CrossRef]
- Huang, C.L.; Hsu, N.S.; Wei, C.C.; Luo, W.J. Optimal Spatial Design of Capacity and Quantity of Rainwater Harvesting Systems for Urban Flood Mitigation. Water 2015, 7, 5173–5202. [Google Scholar] [CrossRef] [Green Version]
- Zhang, P.P.; Cai, Y.P.; Wang, J.L. A simulation-based real-time control system for reducing urban runoff pollution through a stormwater storage tank. J. Clean. Prod. 2018, 183, 641–652. [Google Scholar] [CrossRef]
- Stajkowski, S.; Hotson, E.; Zorica, M.; Farghaly, H.; Bonakdari, H.; McBean, E.; Gharabaghi, B. Modeling stormwater management pond thermal impacts during storm events. J. Hydrol. 2023, 620, 129413. [Google Scholar] [CrossRef]
- Wang, J.; Guo, Y.P. Stochastic analysis of storm water quality control detention ponds. J. Hydrol. 2019, 571, 573–584. [Google Scholar] [CrossRef]
- Lu, W.; Qin, X.S.; Yu, J.J. On comparison of two-level and global optimization schemes for layout design of storage ponds. J. Hydrol. 2019, 570, 544–554. [Google Scholar] [CrossRef]
- Raei, E.; Alizadeh, M.R.; Nikoo, M.R.; Adamowski, J. Multi-objective decision-making for green infrastructure planning (LID-BMPs) in urban storm water management under uncertainty. J. Hydrol. 2019, 579, 124091. [Google Scholar] [CrossRef]
- Liu, Y.Z.; Cibin, R.; Bralts, V.F.; Chaubey, I.; Bowling, L.C.; Engel, B.A. Optimal selection and placement of BMPs and LID practices with a rainfall-runoff model. Environ. Modell Softw. 2016, 80, 281–296. [Google Scholar] [CrossRef] [Green Version]
- Yazdi, J.; Neyshabouri, S.A.A.S. Adaptive surrogate modeling for optimization of flood control detention dams. Environ. Modell Softw. 2014, 61, 106–120. [Google Scholar] [CrossRef]
| Parameter | Value |
|---|---|
| Catchment-related | |
| Catchment slope (%) | 0.5 |
| Imperviousness (%) | 0.76 |
| Manning’s n for overland flow in impervious area | 0.013 |
| Manning’s n for overland flow in pervious area | 0.15 |
| Depression storage in impervious areas (mm) | 1 |
| Depression storage in pervious areas (mm) | 3.2 |
| Maximum infiltration rate of Horton curve (mm/h) | 25.4 |
| Minimum infiltration rate of Horton curve (mm/h) | 3.56 |
| Decay rate constant of Horton curve (1/h) | 2 |
| Last swept | 1 |
| Detention pond-related | |
| Invert elevation (m) | 380.58 |
| Maximum depth (m) | 5 |
| Detention pond shape | Cube |
| Storage curve | TABULAR |
| Orifice type | SIDE |
| Orifice shape | CIRCULAR |
| Orifice diameter (m) | 1 |
| Discharge coefficient | 0.65 |
| Parameter | Residence | Commercial Land | Greenbelt | Road |
|---|---|---|---|---|
| Area of land surface type (m2) | 84,534 | 50,720 | 439,574 | 270,507 |
| Proportion of the area of land use type to the total area | 10% | 6% | 52% | 32% |
| Maximum buildup possible (kg/hm2) | 70 | 80 | 70 | 140 |
| Days to reach half of the maximum buildup (day) | 10 | 8 | 10 | 10 |
| Washoff coefficient | 0.001 | 0.001 | 0.050 | 0.001 |
| Runoff exponent in washoff function | 0.5 | 0.5 | 0.3 | 0.6 |
| Water Depth in the Detention Pond (m) | Orifice Opening Percentage |
|---|---|
| (0, 0.5] | 0 (Fully close) |
| (0.5, 2] | 20% |
| (2, 4] | 40% |
| (4, 4.5] | 60% |
| (4.5, 4.8] | 80% |
| (4.8, 5] | 100% (Fully open) |
| Option | Value |
|---|---|
| Distance measure function | phenotype |
| Pareto fraction | 0.35 |
| Selection function | @selectiontournament |
| Constraint tolerance | 10−3 |
| Creation function | @gacreationuniform |
| Cross function | @crossoverintermediate |
| Cross fraction | 0.8 |
| Max generations | 200 |
| Function tolerance | 10−4 |
| Max stall generations | 100 |
| Max time (seconds) | Inf |
| Mutation function | @mutationadaptfeasible |
| Population size | 1000 |
| Indicators 1 | MAE | MAPE | RMSE | DC | NSE | PBIAS |
|---|---|---|---|---|---|---|
| Training phase of BPNN-TSS | 4.323 | 0.00179 | 5.859 | 0.990 | 0.988 | −0.00003 |
| Test phase of BPNN-TSS | 4.392 | 0.00182 | 5.931 | 0.988 | 0.987 | −0.00007 |
| Training phase of BPNN-CPO | 0.033 | 0.01017 | 0.066 | 0.996 | 0.997 | −0.00002 |
| Test phase of BPNN-CPO | 0.034 | 0.01038 | 0.068 | 0.992 | 0.996 | 0.00041 |
| Scheme | Pond Area (m2) | Cost (106 CNY) | Total Suspended Solids | Catchment Peak Outflow | |||
|---|---|---|---|---|---|---|---|
| Mass (kg) | Reduction Rate | Reduction Unit Cost (106 CNY/kg) | Reduction Rate | Reduction Unit Cost (106 CNY/(m3/s)) | |||
| 0 | 0 | 0 | 2507.96 | N/A | N/A | N/A | N/A |
| 1 | 100 | 0.25 | 2479.77 | 1.12% | 0.0089 | 12.29% | 0.37 |
| 2 | 3000 | 3.07 | 2298.94 | 8.33% | 0.0147 | 72.44% | 0.78 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Xin, Y.; Li, J. Surrogate-Based Multiobjective Optimization of Detention Pond Volume in Sponge City. Water 2023, 15, 2705. https://doi.org/10.3390/w15152705
Yang Y, Xin Y, Li J. Surrogate-Based Multiobjective Optimization of Detention Pond Volume in Sponge City. Water. 2023; 15(15):2705. https://doi.org/10.3390/w15152705
Chicago/Turabian StyleYang, Yuanyuan, Yanfei Xin, and Jiake Li. 2023. "Surrogate-Based Multiobjective Optimization of Detention Pond Volume in Sponge City" Water 15, no. 15: 2705. https://doi.org/10.3390/w15152705
APA StyleYang, Y., Xin, Y., & Li, J. (2023). Surrogate-Based Multiobjective Optimization of Detention Pond Volume in Sponge City. Water, 15(15), 2705. https://doi.org/10.3390/w15152705







