Comparative Analysis of Tree-Based Ensemble Learning Algorithms for Landslide Susceptibility Mapping: A Case Study in Rize, Turkey
Abstract
:1. Introduction
2. Materials and Methods
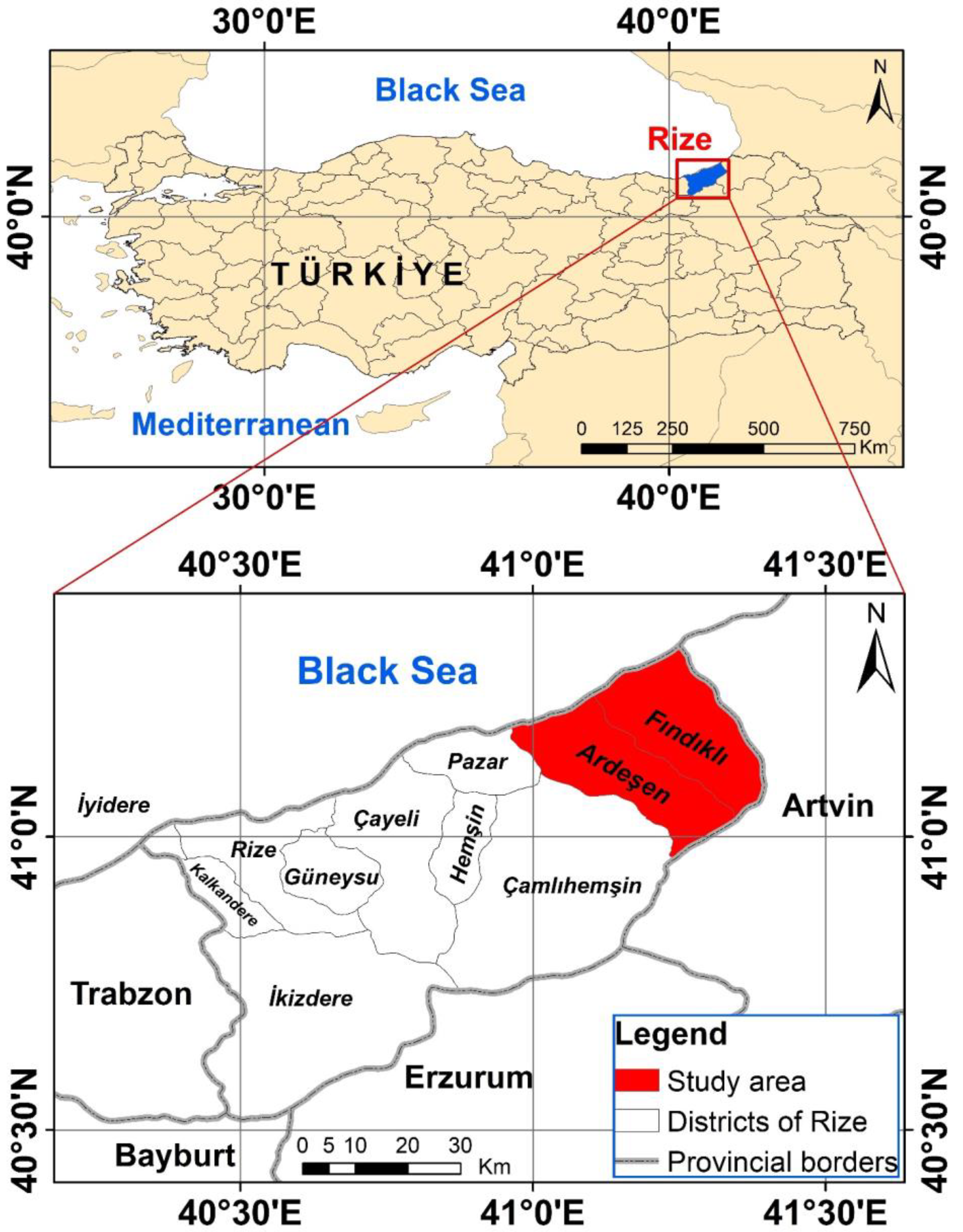
2.1. Study Area
2.2. Landslide Inventory Map
2.3. Data Preparation for Landslide Conditioning Factors
2.4. Multicollinearity Analysis
2.5. Model Validation
2.6. Machine Learning Methods
2.6.1. Random Forest (RF)
2.6.2. Gradient Boosting Machine (GBM)
2.6.3. Extreme Gradient Boosting (XGBoost)
2.6.4. Categorical Boosting (CatBoost)
3. Results and Discussion
3.1. Multicollinearity Analysis of Conditioning Factors
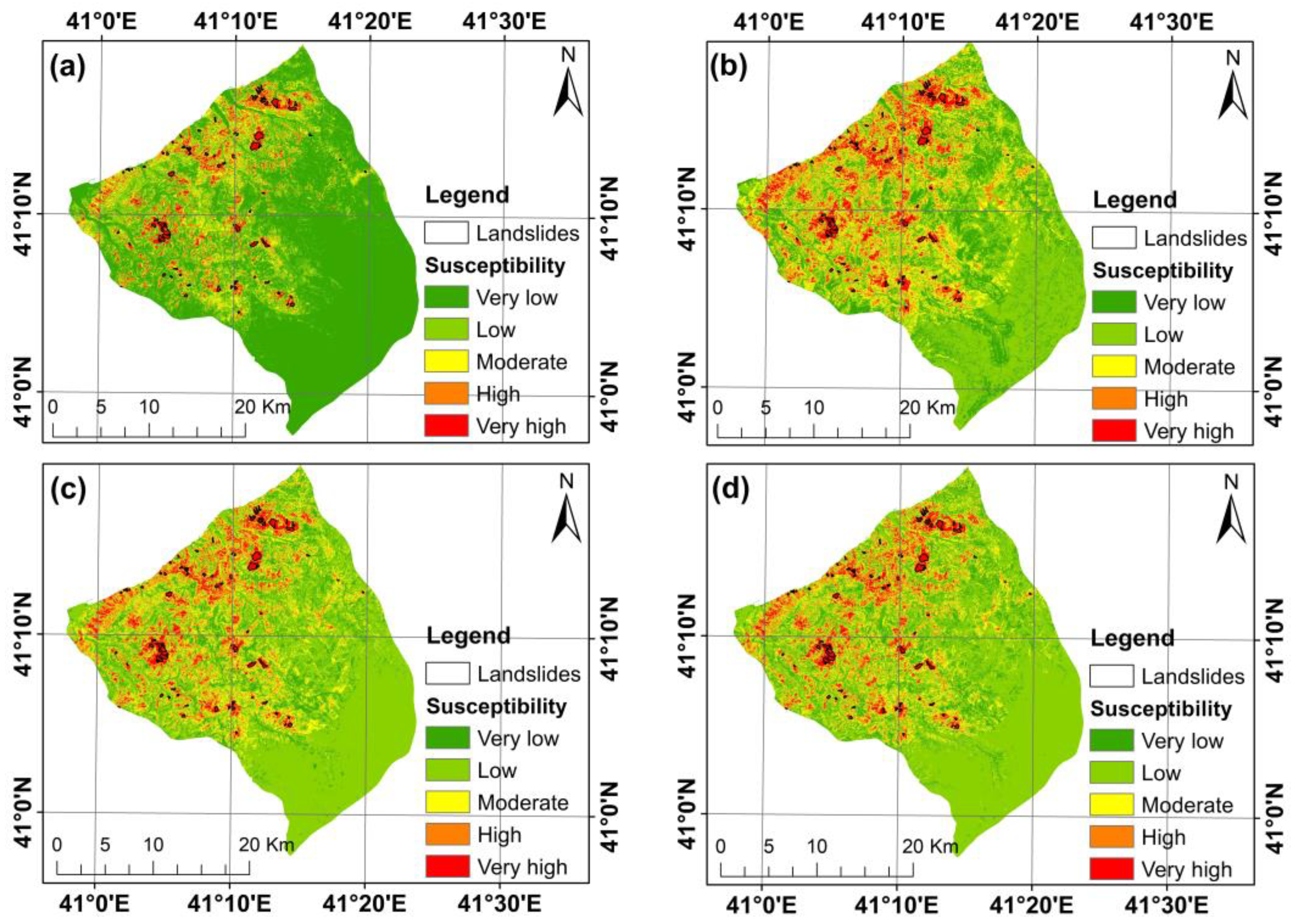
3.2. Landslide Susceptibility Maps
3.3. Landslide Susceptibility Map Rationality
3.4. Landslide Conditioning Factors Analysis
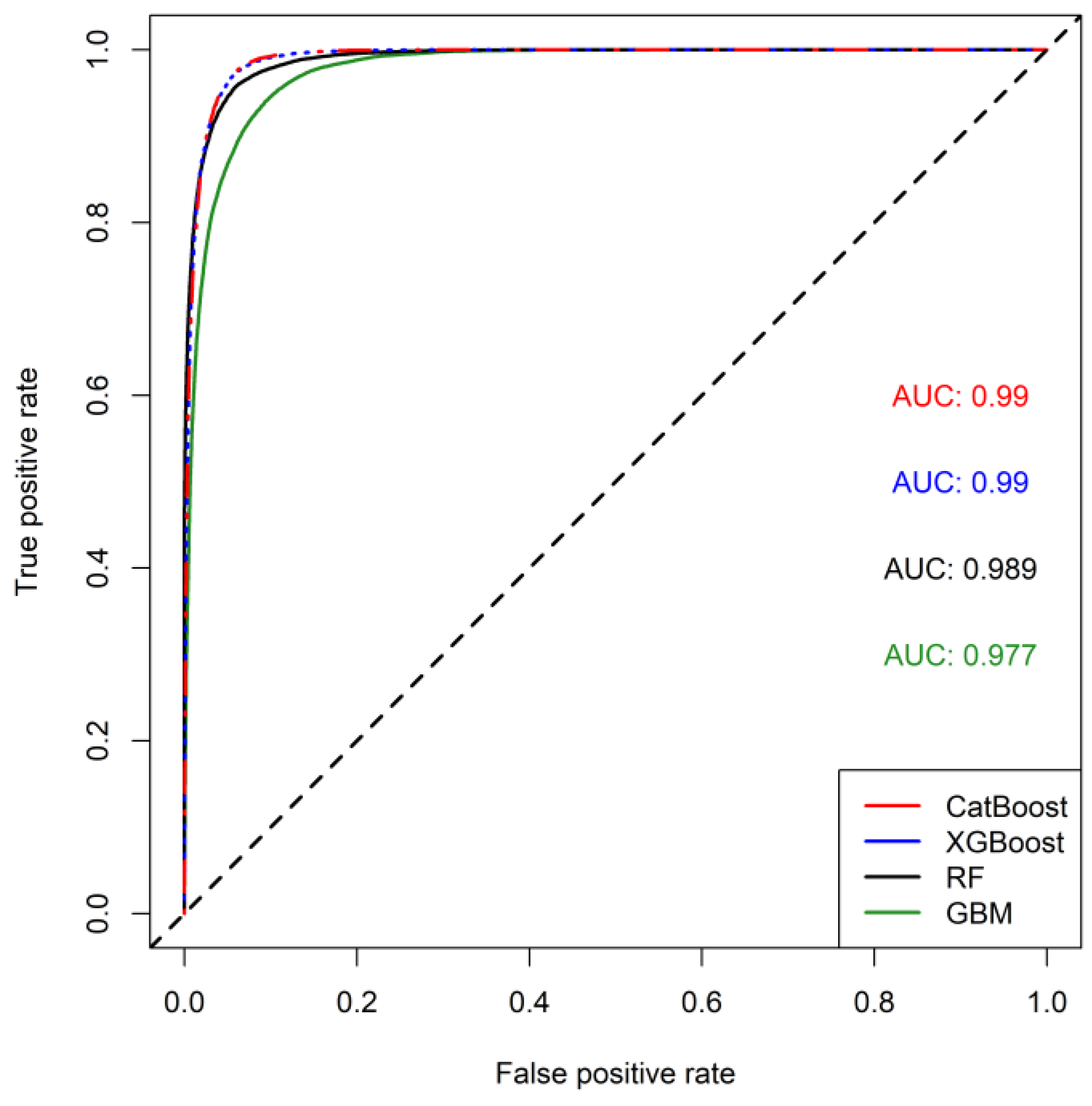
3.5. Models Validation and Comparison
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gökçe, O.; Özden, S.; Demir, A. Türkiye’de Afetlerin Mekânsal ve İstatistiksel Dağılımı Afet Bilgileri Envanteri; Bayındırlık ve İskân Bakanlığı Afet İşleri Genel Müdürlüğü, Afet Etüt ve Hasar Tespit Daire Başkanlığı: Ankara, Turkey, 2008. [Google Scholar]
- Aydoğan, E.; Dağ, S. Landslide susceptibility analysis of the northeastern part of the upper Karasu Basin (Erzurum) using statistical methods. Turk. J. Remote Sens. GIS 2023, 4, 64–82. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Teke, A. Predictive performances of ensemble machine learning algorithms in landslide susceptibility mapping using random forest, extreme gradient boosting (XGBoost) and natural gradient boosting (NGBoost). Arab. J. Sci. Eng. 2022, 47, 7367–7385. [Google Scholar] [CrossRef]
- IPCC. Climate change 2022: Impacts, adaptation and vulnerability. In Contribution of Working Group II to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Pörtner, H.-O., Roberts, D.C., Tignor, M., Poloczanska, E.S., Mintenbeck, K., Alegría, A., Craig, M., Langsdorf, S., Löschke, S., Möller, V., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2022; p. 3056. [Google Scholar] [CrossRef]
- Demirağ Turan, İ.; Özkan, B.; Türkeş, M.; Dengiz, O. Landslide susceptibility mapping for the Black Sea Region with spatial fuzzy multi-criteria decision analysis under semi-humid and humid terrestrial ecosystems. Theor. Appl. Climatol. 2020, 140, 1233–1246. [Google Scholar] [CrossRef]
- Pardeshi, S.D.; Autade, S.E.; Pardeshi, S.S. Landslide hazard assessment: Recent trends and techniques. SpringerPlus 2013, 2, 523. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tien Bui, D.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2016, 13, 361–378. [Google Scholar] [CrossRef]
- Ullah, I.; Aslam, B.; Shah, S.H.I.A.; Tariq, A.; Qin, S.; Majeed, M.; Havenith, H.-B. An integrated approach of machine learning, remote sensing, and GIS data for the landslide susceptibility mapping. Land 2022, 11, 1265. [Google Scholar] [CrossRef]
- Das, S.; Sarkar, S.; Kanungo, D.P. A critical review on landslide susceptibility zonation: Recent trends, techniques, and practices in Indian Himalaya. Nat. Hazards 2023, 115, 23–72. [Google Scholar] [CrossRef]
- Taalab, K.; Cheng, T.; Zhang, Y. Mapping landslide susceptibility and types using random forest. Big Earth Data 2018, 2, 159–178. [Google Scholar] [CrossRef]
- Shahzad, N.; Ding, X.; Abbas, S. A comparative assessment of machine learning models for landslide susceptibility mapping in the rugged terrain of northern Pakistan. Appl. Sci. 2022, 12, 2280. [Google Scholar] [CrossRef]
- Pradhan, A.M.S.; Kim, Y.T. Rainfall-induced shallow landslide susceptibility mapping at two adjacent catchments using advanced machine learning algorithms. ISPRS Int. J. Geo-Inf. 2020, 9, 569. [Google Scholar] [CrossRef]
- He, Q.; Shahabi, H.; Shirzadi, A.; Li, S.; Chen, W.; Wang, N.; Chai, H.; Bian, H.; Ma, J.; Chen, Y.; et al. Landslide spatial modelling using novel bivariate statistical based Naïve Bayes, RBF Classifier, and RBF Network machine learning algorithms. Sci. Total Environ. 2019, 663, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Mutlu, B.; Nefeslioglu, H.A.; Sezer, E.A.; Akcayol, M.A.; Gokceoglu, C. An experimental research on the use of recurrent neural networks in landslide susceptibility mapping. ISPRS Int. J. Geo-Inf. 2019, 8, 578. [Google Scholar] [CrossRef] [Green Version]
- Shahri, A.A.; Spros, J.; Johasson, F.; Larsson, S. Landslide susceptibility hazard map in southwest Sweden using artificial neural network. Catena 2019, 183, 104225. [Google Scholar] [CrossRef]
- Akinci, H.; Kilicoglu, C.; Dogan, S. Random Forest-Based Landslide Susceptibility Mapping in Coastal Regions of Artvin, Turkey. ISPRS Int. J. Geo-Inf. 2020, 9, 553. [Google Scholar] [CrossRef]
- Can, R.; Kocaman, S.; Gokceoglu, C. A Comprehensive assessment of XGBoost algorithm for landslide susceptibility mapping in the upper basin of Ataturk Dam, Turkey. Appl. Sci. 2021, 11, 4993. [Google Scholar] [CrossRef]
- Cao, J.; Zhang, Z.; Du, J.; Zhang, L.; Song, Y.; Sun, G. Multi-geohazards susceptibility mapping based on machine learning—A case study in Jiuzhaigou, China. Nat. Hazards 2020, 102, 851–871. [Google Scholar] [CrossRef]
- Akinci, H.; Zeybek, M. Comparing classical statistic and machine learning models in landslide susceptibility mapping in Ardanuc (Artvin), Turkey. Nat. Hazards 2021, 108, 1515–1543. [Google Scholar] [CrossRef]
- Ajim Ali, S.; Parvin, F.; Pham, Q.B.; Khedher, K.M.; Dehbozorgi, M.; Rabby, Y.W.; Anh, D.T.; Nguyen, D.H. An ensemble random forest tree with SVM, ANN, NBT, and LMT for landslide susceptibility mapping in the Rangit River watershed, India. Nat. Hazards 2022, 113, 1601–1633. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Sahin, E.K.; Colkesen, I. Landslide susceptibility mapping using GIS-based multi-criteria decision analysis, support vector machines, and logistic regression. Landslides 2014, 11, 425–439. [Google Scholar] [CrossRef]
- Colkesen, I.; Sahin, E.K.; Kavzoglu, T. Susceptibility mapping of shallow landslides using kernel-based Gaussian process, support vector machines and logistic regression. J. Afr. Earth Sci. 2016, 118, 53–64. [Google Scholar] [CrossRef]
- Merghadi, A.; Yunus, A.P.; Dou, J.; Whiteley, J.; ThaiPham, B.; Bui, D.T.; Avtar, R.; Abderrahmane, B. Machine learning methods for landslide susceptibility studies: A comparative overview of algorithm performance. Earth Sci. Rev. 2020, 207, 103225. [Google Scholar] [CrossRef]
- Abu El-Magd, S.; Ali, S.A.; Pham, Q.B. Spatial modeling and susceptibility zonation of landslides using random forest, naïve bayes and K-nearest neighbor in a complicated terrain. Earth Sci. Inform. 2021, 14, 1227–1243. [Google Scholar] [CrossRef]
- Tsangaratos, P.; Ilia, I. Comparison of a logistic regression and Naïve Bayes classifier in landslide susceptibility assessments: The influence of models complexity and training dataset size. Catena 2016, 145, 164–179. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Gayen, A.; Park, S.; Lee, C.W.; Lee, S. Assessment of landslide-prone areas and their zonation using logistic regression, LogitBoost, and NaïveBayes machine-learning algorithms. Sustainability 2018, 10, 3697. [Google Scholar] [CrossRef] [Green Version]
- Tsangaratos, P.; Benardos, A. Estimating landslide susceptibility through a artificial neural network classifier. Nat. Hazards 2014, 74, 1489–1516. [Google Scholar] [CrossRef]
- Akinci, H. Assessment of rainfall-induced landslide susceptibility in Artvin, Turkey using machine learning techniques. J. Afr. Earth Sci. 2022, 191, 104535. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, Q.; Liu, Y. Mapping landslide susceptibility using machine learning algorithms and GIS: A case study in Shexian county, Anhui province, China. Symmetry 2020, 12, 1954. [Google Scholar] [CrossRef]
- Youssef, A.M.; Pourghasemi, H.R.; Pourtaghi, Z.S.; Al-Katheeri, M.M. Landslide susceptibility mapping using random forest, boosted regression tree, classification and regression tree, and general linear models and comparison of their performance at Wadi Tayyah Basin, Asir Region, Saudi Arabia. Landslides 2016, 13, 839–856. [Google Scholar] [CrossRef]
- Chen, W.; Xie, X.; Wang, J.; Pradhan, B.; Hong, H.; Tien Bui, D.; Duan, Z.; Ma, J. A comparative study of logistic model tree, random forest, and classification and regression tree models for spatial prediction of landslide susceptibility. Catena 2017, 151, 147–160. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Zhang, S.; Li, R.; Shahabi, H. Performance evaluation of the GIS-based data mining techniques of best-first decision tree, random forest, and naïve Bayes tree for landslide susceptibility modeling. Sci. Total Environ. 2018, 644, 1006–1018. [Google Scholar] [CrossRef]
- Nhu, V.; Mohammadi, A.; Shahabi, H.; Ahmad, B.B.; Al-Ansari, N.; Shirzadi, A.; Clague, J.J.; Jaafari, A.; Chen, W.; Nguyen, H. Landslide susceptibility mapping using machine learning algorithms and remote sensing data in a tropical environment. Int. J. Environ. Res. Public Health 2020, 17, 4933. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Pei, W.; Zhang, J.; Chen, G. Landslide susceptibility mapping and driving mechanisms in a vulnerable region based on multiple machine learning models. Remote Sens. 2023, 15, 1886. [Google Scholar] [CrossRef]
- Sahin, E.K. Assessing the predictive capability of ensemble tree methods for landslide susceptibility mapping using XGBoost, gradient boosting machine, and random forest. SN Appl. Sci. 2020, 2, 1308. [Google Scholar] [CrossRef]
- Sahin, E.K. Comparative analysis of gradient boosting algorithms for landslide susceptibility mapping. Geocarto Int. 2022, 37, 2441–2465. [Google Scholar] [CrossRef]
- Song, Y.; Yang, D.; Wu, W.; Zhang, X.; Zhou, J.; Tian, Z.; Wang, C.; Song, Y. Evaluating landslide susceptibility using sampling methodology and multiple machine learning models. ISPRS Int. J. Geo-Inf. 2023, 12, 197. [Google Scholar] [CrossRef]
- Ye, P.; Yu, B.; Chen, W.; Liu, K.; Ye, L. Rainfall-induced landslide susceptibility mapping using machine learning algorithms and comparison of their performance in Hilly area of Fujian Province, China. Nat. Hazards 2022, 113, 965–995. [Google Scholar] [CrossRef]
- Wei, A.; Yu, K.; Dai, F.; Gu, F.; Zhang, W.; Liu, Y. Application of tree-based ensemble models to landslide susceptibility mapping: A comparative study. Sustainability 2022, 14, 6330. [Google Scholar] [CrossRef]
- Hong, H.; Pourghasemi, H.R.; Pourtaghi, Z.S. Landslide susceptibility assessment in Lianhua County (China): A comparison between a random forest data mining technique and bivariate and multivariate statistical models. Geomorphology 2016, 259, 105–118. [Google Scholar] [CrossRef]
- Aditian, A.; Kubota, T.; Shinohara, Y. Comparison of GIS-based landslide susceptibility models using frequency ratio, logistic regression, and artificial neural network in a tertiary region of Ambon, Indonesia. Geomorphology 2018, 318, 101–111. [Google Scholar] [CrossRef]
- Merghadi, A.; Abderrahmane, B.; Tien Bui, D. Landslide susceptibility assessment at Mila basin (Algeria): A comparative assessment of prediction capability of advanced machine learning methods. ISPRS Int. J. Geo-Inf. 2018, 7, 268. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Fang, Z.; Hong, H. Comparison of convolutional neural networks for landslide susceptibility mapping in Yanshan County, China. Sci. Total Environ. 2019, 666, 975–993. [Google Scholar] [CrossRef] [PubMed]
- Thi Ngo, P.T.; Panahi, M.; Khosravi, K.; Ghorbanzadeh, O.; Kariminejad, N.; Cerda, A.; Lee, S. Evaluation of deep learning algorithms for national scale landslide susceptibility mapping of Iran. Geosci. Front. 2021, 12, 505–519. [Google Scholar] [CrossRef]
- Lv, L.; Chen, T.; Dou, J.; Plaza, A. A hybrid ensemble-based deep-learning framework for landslide susceptibility mapping. Int. J. Appl. Earth Obs. Geoinf. 2022, 108, 102713. [Google Scholar] [CrossRef]
- Aslam, B.; Zafar, A.; Khalil, U. Comparative analysis of multiple conventional neural networks for landslide susceptibility mapping. Nat. Hazards 2023, 115, 673–707. [Google Scholar] [CrossRef]
- Sameen, M.I.; Pradhan, B.; Lee, S. Application of convolutional neural networks featuring Bayesian optimization for landslide susceptibility assessment. Catena 2020, 186, 104249. [Google Scholar] [CrossRef]
- Mandal, K.; Saha, S.; Mandal, S. Applying deep learning and benchmark machine learning algorithms for landslide susceptibility modelling in Rorachu river basin of Sikkim Himalaya, India. Geosci. Front. 2021, 12, 101203. [Google Scholar] [CrossRef]
- Akgun, A.; Dag, S.; Bulut, F. Landslide susceptibility mapping for a landslide-prone area (Findikli, NE of Turkey) by likelihood-frequency ratio and weighted linear combination models. Environ. Geol. 2008, 54, 1127–1143. [Google Scholar] [CrossRef]
- Yalcin, A. GIS-based landslide susceptibility mapping using analytical hierarchy process and bivariate statistics in Ardesen (Turkey): Comparisons of results and confirmations. Catena 2008, 72, 1–12. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- General Directorate of Meteorology. Climate Classification Rize. 2023. Available online: https://www.mgm.gov.tr/iklim/iklim-siniflandirmalari.aspx?m=RIZE, (accessed on 11 April 2023).
- General Directorate of Meteorology. General Statistical Data of Our Provinces. 2023. Available online: https://www.mgm.gov.tr/veridegerlendirme/il-ve-ilceler-istatistik.aspx?k=A&m=RIZE (accessed on 11 April 2023).
- Karsli, F.; Atasoy, M.; Yalcin, A.; Reis, S.; Demir, O.; Gokceoglu, C. Effects of land-use changes on landslides in a landslide-prone area (Ardesen, Rize, NE Turkey). Environ. Monit. Assess. 2009, 156, 241–255. [Google Scholar] [CrossRef]
- Dağ, S.; Bulut, F. An example for preparation of GIS-based landslide susceptibility maps: Çayeli (Rize, NE Türkiye). J. Eng. Geol. 2012, 36, 35–62. (In Turkish) [Google Scholar]
- Keskin, I. 1:100,000 Scale Geological Map of Turkey, No:178 Artvin-F46 Map Sheet; General Directorate of Mineral Research and Exploration, Geological Research Department: Ankara, Turkey, 2013. (In Turkish) [Google Scholar]
- Parise, M. Landslide mapping techniques and their use in the assessment of the landslide hazard. Phys. Chem. Earth C 2001, 26, 697–703. [Google Scholar] [CrossRef]
- Varnes, D.J. Slope movement types and processes. In Landslides Analysis and Control; Schuster, R.L., Krizek, R.J., Eds.; Special Report; Transportation Research Board, National Academy of Sciences: New York, NY, USA, 1978; Volume 176, pp. 12–33. [Google Scholar]
- Yalçın, A. Use of analytical hierarchy method and GIS in the production of landslide susceptibility maps. J. Fac. Eng. Arch. Selcuk. Univ. 2007, 22, 1–14. (In Turkish) [Google Scholar]
- Vakhshoori, V.; Pourghasemi, H.R.; Zare, M.; Blaschke, T. Landslide susceptibility mapping using GIS-based data mining algorithms. Water 2019, 11, 2292. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Chen, W. Landslide susceptibility evaluation using hybrid integration of evidential belief function and machine learning techniques. Water 2020, 12, 113. [Google Scholar] [CrossRef] [Green Version]
- Pourghasemi, H.R.; Sadhasivam, N.; Amiri, M.; Eskandari, S.; Santosh, M. Landslide susceptibility assessment and mapping using state-of-the art machine learning techniques. Nat. Hazards 2021, 108, 1291–1316. [Google Scholar] [CrossRef]
- Arca, D.; Keskin Citiroglu, H.; Tasoglu, I.K. A comparison of GIS-based landslide susceptibility assessment of the Satuk village (Yenice, NW Turkey) by frequency ratio and multi-criteria decision methods. Environ. Earth Sci. 2019, 78, 81. [Google Scholar] [CrossRef]
- Shahabi, H.; Hashim, M.; Ahmad, B.B. Remote sensing and GIS-based landslide susceptibility mapping using frequency ratio, logistic regression, and fuzzy logic methods at the central Zab basin, Iran. Environ. Earth Sci. 2015, 73, 8647–8668. [Google Scholar] [CrossRef]
- Dağ, S.; Akgün, A.; Kaya, A.; Alemdağ, S.; Bostancı, H.T. Medium scale earthflow susceptibility modelling by remote sensing and geographical information systems based multivariate statistics approach: An example from Northeastern Turkey. Environ. Earth Sci. 2020, 79, 468. [Google Scholar] [CrossRef]
- Youssef, A.M.; Pourghasemi, H.R. Landslide susceptibility mapping using machine learning algorithms and comparison of their performance at Abha Basin, Asir Region, Saudi Arabia. Geosci. Front. 2021, 12, 639–655. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Pradhan, B.; Gokceoglu, C.; Moezzi, K.D. A comparative assessment of prediction capabilities of Dempster–Shafer and Weights-of-evidence models in landslide susceptibility mapping using GIS. Geomat. Nat. Hazards Risk 2013, 4, 93–118. [Google Scholar] [CrossRef]
- Ding, Q.; Chen, W.; Hong, H. Application of frequency ratio, weights of evidence and evidential belief function models in landslide susceptibility mapping. Geocarto Int. 2017, 32, 619–639. [Google Scholar] [CrossRef]
- Kilicoglu, C. Investigation of the effects of approaches used in the production of training and validation data sets on the accuracy of landslide susceptibility mapping models: Samsun (Turkey) example. Arab. J. Geosci. 2021, 14, 2106. [Google Scholar] [CrossRef]
- Erener, A.; Mutlu, A.; Düzgün, H.S. A comparative study for landslide susceptibility mapping using GIS-based multi-criteria decision analysis (MCDA), logistic regression (LR) and association rule mining (ARM). Eng. Geol. 2016, 203, 45–55. [Google Scholar] [CrossRef]
- Feizizadeh, B.; Blaschke, T.; Nazmfar, H. GIS based ordered weighted averaging and Dempster–Shafer methods for landslide susceptibility mapping in the Urmia Lake Basin, Iran. Int. J. Digit. Earth. 2014, 7, 688–708. [Google Scholar] [CrossRef]
- Shahabi, H.; Khezri, S.; Ahmad, B.B.; Hashim, M. Landslide susceptibility mapping at central Zab basin, Iran: A comparison between analytical hierarchy process, frequency ratio and logistic regression models. Catena 2014, 115, 55–70. [Google Scholar] [CrossRef]
- Ba, Q.; Chen, Y.; Deng, S.; Wu, Q.; Yang, J.; Zhang, J. An improved information value model based on gray clustering for landslide susceptibility mapping. ISPRS Int. J. Geoinf. 2017, 6, 18. [Google Scholar] [CrossRef]
- Du, G.L.; Zhang, Y.S.; Iqbal, J.; Yang, Z.; Yao, X. Landslide susceptibility mapping using an integrated model of information value method and logistic regression in the Bailongjiang watershed, Gansu Province, China. J. Mt. Sci. 2017, 14, 249–268. [Google Scholar] [CrossRef]
- Roy, D.; Sarkar, A.; Kundu, P.; Paul, S.; Sarkar, B.C. An ensemble of evidence belief function (EBF) with frequency ratio (FR) using geospatial data for landslide prediction in Darjeeling Himalayan region of India. Quat. Sci. Adv. 2023, 11, 100092. [Google Scholar] [CrossRef]
- Hong, H.; Xu, C.; Tien Bui, D. Landslide susceptibility assessment at the Xiushui area (China) using frequency ratio model. Procedia Environ. Sci. 2015, 15, 513–517. [Google Scholar] [CrossRef] [Green Version]
- Ghasemian, B.; Shahabi, H.; Shirzadi, A.; Al-Ansari, N.; Jaafari, A.; Kress, V.R.; Geertsema, M.; Renoud, S.; Ahmad, A. A robust deep-learning model for landslide susceptibility mapping: A case study of Kurdistan Province, Iran. Sensors 2022, 22, 1573. [Google Scholar] [CrossRef] [PubMed]
- Trigila, A.; Iadanza, C.; Esposito, C.; Scarascia-Mugnozza, G. Comparison of logistic regression and random forests techniques for shallow landslide susceptibility assessment in Giampilieri (NE Sicily, Italy). Geomorphology 2015, 249, 119–136. [Google Scholar] [CrossRef]
- Yilmaz, I. Landslide susceptibility mapping using frequency ratio, logistic regression, artificial neural networks and their comparison: A case study from Kat landslides (Tokat—Turkey). Comput. Geosci. 2009, 35, 1125–1138. [Google Scholar] [CrossRef]
- Guillard, C.; Zezere, J. Landslide susceptibility assessment and validation in the framework of municipal planning in Portugal: The case of Loures municipality. Environ. Manag. 2012, 50, 721–735. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Ryu, J.H.; Kim, L.S. Landslide susceptibility analysis and its verification using likelihood ratio, logistic regression, and artificial neural network models: Case study of Youngin, Korea. Landslides 2007, 4, 327–338. [Google Scholar] [CrossRef]
- Son, J.; Suh, J.; Park, H.D. GIS-based landslide susceptibility assessment in Seoul, South Korea, applying the radius of influence to frequency ratio analysis. Environ. Earth Sci. 2016, 75, 310. [Google Scholar] [CrossRef]
- Arabameri, A.; Saha, S.; Roy, J.; Chen, W.; Blaschke, T.; Tien Bui, D. Landslide susceptibility evaluation and management using different machine learning methods in the Gallicash river watershed, Iran. Remote Sens. 2020, 12, 475. [Google Scholar] [CrossRef] [Green Version]
- Sahin, E.K.; Colkesen, I. Performance analysis of advanced decision tree-based ensemble learning algorithms for landslide susceptibility mapping. Geocarto Int. 2021, 36, 1253–1275. [Google Scholar] [CrossRef]
- Chen, X.; Chen, W. GIS-based landslide susceptibility assessment using optimized hybrid machine learning methods. Catena 2021, 196, 104833. [Google Scholar] [CrossRef]
- Nohani, E.; Moharrami, M.; Sharafi, S.; Khosravi, K.; Pradhan, B.; Pham, B.T.; Lee, S.; Melesse, A.M. Landslide susceptibility mapping using different GIS-based bivariate models. Water 2019, 11, 1402. [Google Scholar] [CrossRef] [Green Version]
- Akinci, H.; Yavuz Ozalp, A. Landslide susceptibility mapping and hazard assessment in Artvin (Turkey) using frequency ratio and modified information value model. Acta Geophys. 2021, 69, 725–745. [Google Scholar] [CrossRef]
- Hong, H.; Tsangaratos, P.; Ilia, I.; Loupasakis, C.; Wang, Y. Introducing a novel multi-layer perceptron network based on stochastic gradient descent optimized by a meta-heuristic algorithm for landslide susceptibility mapping. Sci. Total Environ. 2020, 742, 140549. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Fu, Q.; Li, C.; Liu, F.; Wang, H.; Han, L.; Quevedo, R.P.; Chen, T.; Lei, N. Modeling landslide susceptibility using data mining techniques of kernel logistic regression, fuzzy unordered rule induction algorithm, SysFor and random forest. Nat. Hazards 2022, 114, 3327–3358. [Google Scholar] [CrossRef]
- Jiao, Y.; Zhao, D.; Ding, Y.; Liu, Y.; Xu, Q.; Qiu, Y.; Liu, C.; Liu, Z.; Zha, Z.; Li, R. Performance evaluation for four GIS-based models purposed to predict and map landslide susceptibility: A case study at a World Heritage site in Southwest China. Catena 2019, 183, 104221. [Google Scholar] [CrossRef]
- Wu, Y.; Ke, Y.; Chen, Z.; Liang, S.; Zhao, H.; Hong, H. Application of alternating decision tree with AdaBoost and bagging ensembles for landslide susceptibility mapping. Catena 2020, 187, 104396. [Google Scholar] [CrossRef]
- Althuwaynee, O.F.; Pradhan, B.; Lee, S. Application of an evidential belief function model in landslide susceptibility mapping. Comput. Geosci. 2012, 44, 120–135. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Mohammady, M.; Pradhan, B. Landslide susceptibility mapping using index of entropy and conditional probability models in GIS: Safarood Basin, Iran. Catena 2012, 97, 71–84. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Akıncı, H.A.; Akıncı, H. Machine learning based forest fire susceptibility assessment of Manavgat district (Antalya), Turkey. Earth Sci. Inform. 2023, 16, 397–414. [Google Scholar] [CrossRef]
- Costache, R.; Arabameri, A.; Elkhrachy, I.; Ghorbanzadeh, O.; Pham, Q.B. Detection of areas prone to flood risk using state-of-the-art machine learning models. Geomat. Nat. Hazards Risk 2021, 12, 1488–1507. [Google Scholar] [CrossRef]
- Kuhn, M. Building predictive models in R using the caret package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef] [Green Version]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. In Proceedings of the 32nd Conference on Neural Information Processing Systems (NeurIPS 2018), Montréal, QC, Canada, 2–8 December 2018. [Google Scholar]
- Huang, G.; Wu, L.; Ma, X.; Zhang, W.; Fan, J.; Yu, X.; Zeng, W.; Zhou, H. Evaluation of CatBoost method for prediction of reference evapotranspiration in humid regions. J. Hydrol. 2019, 574, 1029–1041. [Google Scholar] [CrossRef]
- Kang, Y.; Jang, E.; Im, J.; Kwon, C.; Kim, S. Developing a new hourly forest fire risk index based on Catboost in South Korea. Appl. Sci. 2020, 10, 8213. [Google Scholar] [CrossRef]
- Catboost. Available online: https://catboost.ai/en/docs/concepts/r-installation (accessed on 2 April 2023).
- Jenks, G.F. The data model concept in statistical mapping. Int. Yearb. Cartogr. 1967, 7, 186–190. [Google Scholar]
- Guo, X.; Fu, B.; Du, J.; Shi, P.; Chen, Q.; Zhang, W. Applicability of Susceptibility Model for Rock and Loess Earthquake Landslides in the Eastern Tibetan Plateau. Remote Sens. 2021, 13, 2546. [Google Scholar] [CrossRef]
- Kasahara, N.; Gonda, Y.; Huvaj, N. Quantitative land-use and landslide assessment: A case study in Rize, Türkiye. Water 2022, 14, 1811. [Google Scholar] [CrossRef]
- Chen, W.; Zhao, X.; Shahabi, H.; Shirzadi, A.; Khosravi, K.; Chai, H.; Zhang, S.; Zhang, L.; Ma, J.; Chen, Y.; et al. Spatial prediction of landslide susceptibility by combining evidential belief function, logistic regression, and logistic model tree. Geocarto Int. 2019, 34, 1177–1201. [Google Scholar] [CrossRef]
- Achour, Y.; Pourghasemi, H.R. How do machine learning techniques help in increasing accuracy of landslide susceptibility maps? Geosci. Front. 2020, 11, 871–883. [Google Scholar] [CrossRef]
- Chen, T.; Zhu, L.; Niu, R.-q.; Trinder, C.J.; Peng, L.; Lei, T. Mapping landslide susceptibility at the Three Gorges Reservoir, China, using gradient boosting decision tree, random forest, and information value models. J. Mt. Sci. 2020, 17, 670–685. [Google Scholar] [CrossRef]
- Rabby, Y.W.; Li, Y. Landslide Susceptibility Mapping Using Integrated Methods: A Case Study in the Chittagong Hilly Areas, Bangladesh. Geosciences 2020, 10, 483. [Google Scholar] [CrossRef]
- Wubalem, A. Landslide susceptibility mapping using statistical methods in Uatzau catchment area, northwestern Ethiopia. Geoenviron. Disasters. 2021, 8, 1. [Google Scholar] [CrossRef]
- Dorogush, A.V.; Ershov, V.; Gulin, A. CatBoost: Gradient boosting with categorical features support. arXiv 2018, arXiv:1810.11363. [Google Scholar] [CrossRef]



| Factors | Source | Scale/Resolution | Sub-Classes | Reference | |||
|---|---|---|---|---|---|---|---|
| Altitude (m) | DEM | 10 m | 1 | 0–300 | 6 | 1500–1800 | [31,67,68] |
| 2 | 300–600 | 7 | 1800–2100 | ||||
| 3 | 600–900 | 8 | 2100–2400 | ||||
| 4 | 900–1200 | 9 | 2400–2700 | ||||
| 5 | 1200–1500 | 10 | 2700–3497.38 | ||||
| Aspect | DEM | 10 m | 1 | Flat | 6 | South | [16,29,36,69] |
| 2 | North | 7 | South West | ||||
| 3 | North East | 8 | West | ||||
| 4 | East | 9 | North West | ||||
| 5 | South East | ||||||
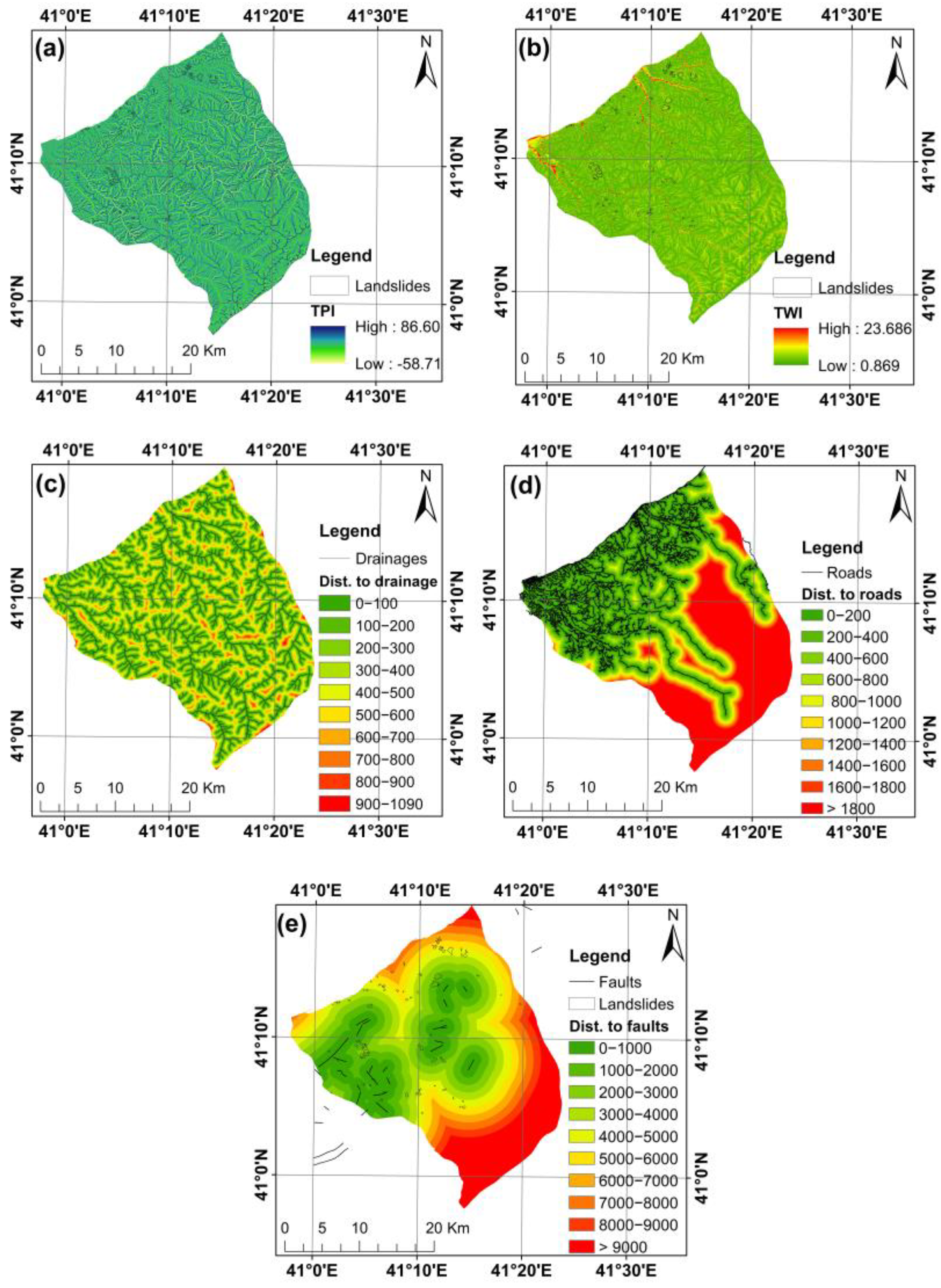
| Distance to drainage (m) | DEM | 10 m | 1 | 0–100 | 6 | 500–600 | [16,19,35,70] |
| 2 | 100–200 | 7 | 600–700 | ||||
| 3 | 200–300 | 8 | 700–800 | ||||
| 4 | 300–400 | 9 | 800–900 | ||||
| 5 | 400–500 | 10 | 900–1090.18 | ||||
| Distance to faults (m) | GDMRE, Türkiye | 1:100,000 | 1 | 0–1000 | 6 | 5000–6000 | [16,19,71,72] |
| 2 | 1000–2000 | 7 | 6000–7000 | ||||
| 3 | 2000–3000 | 8 | 7000–8000 | ||||
| 4 | 3000–4000 | 9 | 8000–9000 | ||||
| 5 | 4000–5000 | 10 | 9000–16,500.94 | ||||
| Distance to roads (m) | digital road network (Basarsoft Inc., Ankara, Turkey) | 10 m | 1 | 0–200 | 6 | 1000–1200 | [16,19,73,74] |
| 2 | 200–400 | 7 | 1200–1400 | ||||
| 3 | 400–600 | 8 | 1400–1600 | ||||
| 4 | 600–800 | 9 | 1600–1800 | ||||
| 5 | 800–1000 | 10 | 1800–8658.22 | ||||
| Land cover | ESRI Land Cover | 10 m | 1 | Water | 7 | Built Area | [23,34,46,75] |
| 2 | Trees | 8 | Bare ground | ||||
| 3 | Grass (Rangeland) | 9 | Snow/ice | ||||
| 5 | Crops | ||||||
| 6 | Scrub/shrub | ||||||
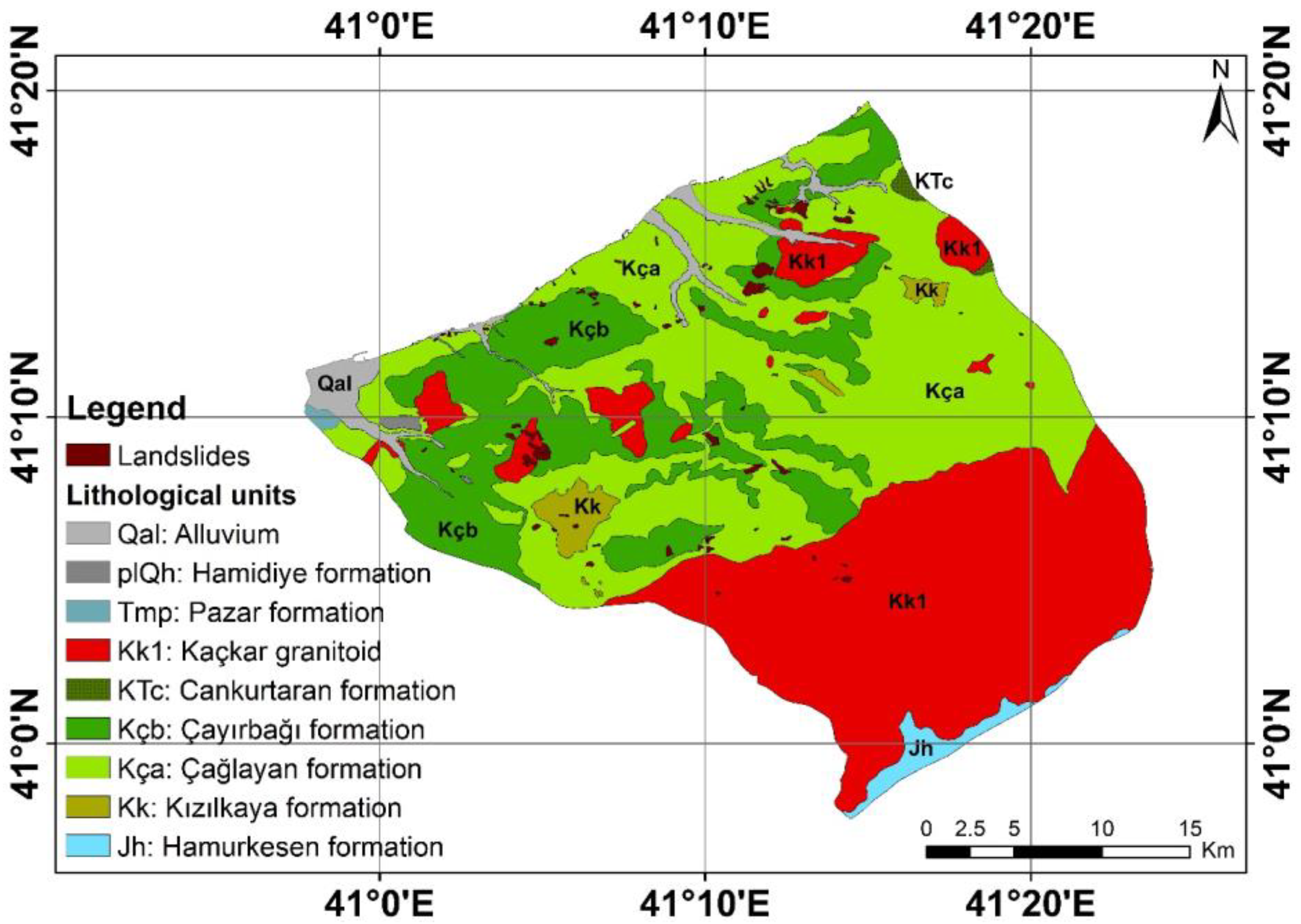
| Lithology | GDMRE, Türkiye | 1:100,000 | Presented in Figure 2. | [56] | |||
| LS-factor | DEM | 10 m | 1 | 0.003–13.938 | 5 | 76.648–118.455 | [40,67,76,77] |
| 2 | 13.938–30.196 | 6 | 118.455–190.456 | ||||
| 3 | 30.196–48.777 | 7 | 190.456–592.265 | ||||
| 4 | 48.777–76.648 | ||||||
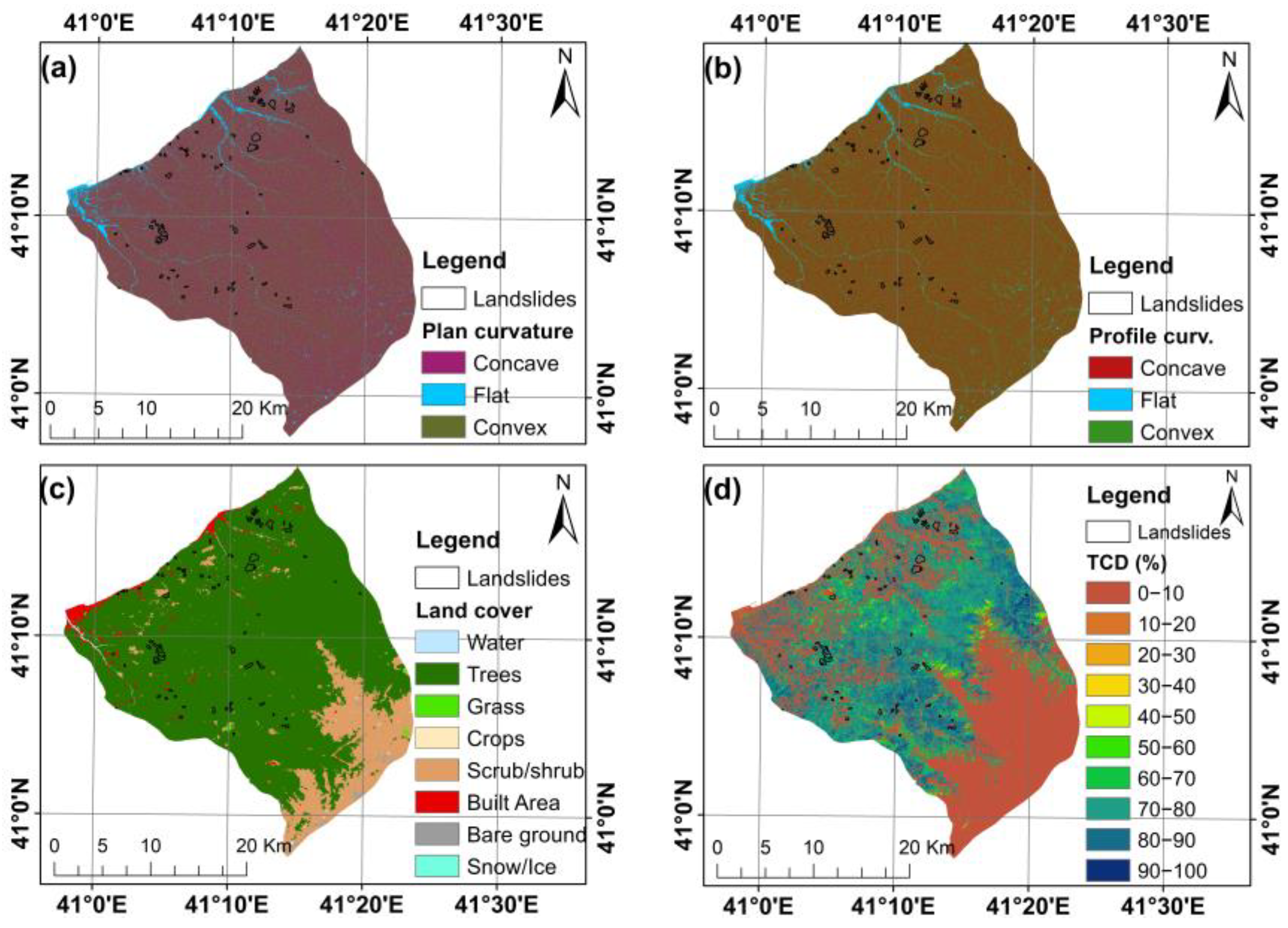
| Plan curvature | DEM | 10 m | 1 | <0 (concave) | [3,69,78] | ||
| 2 | 0 (flat) | ||||||
| 3 | >0 (convex) | ||||||
| Profile curvature | DEM | 10 m | 1 | <0 (concave) | [3,69,78] | ||
| 2 | 0 (flat) | ||||||
| 3 | >0 (convex) | ||||||
| Slope (°) | DEM | 10 m | 1 | 0–5 | 6 | 25–30 | [16,69,79,80] |
| 2 | 5–10 | 7 | 30–35 | ||||
| 3 | 10–15 | 8 | 35–40 | ||||
| 4 | 15–20 | 9 | 40–45 | ||||
| 5 | 20–25 | 10 | 45–75.82 | ||||
| TCD (%) | Copernicus Land Monitoring Service | 10 m | 1 | 0–10 | 6 | 50–60 | [26,81,82] |
| 2 | 10–20 | 7 | 60–70 | ||||
| 3 | 20–30 | 8 | 70–80 | ||||
| 4 | 30–40 | 9 | 80–90 | ||||
| 5 | 40–50 | 10 | 90–100 | ||||
| TPI | DEM | 10 m | 1 | −58.711–15.402 | 5 | 5.113–11.381 | [3,35,83] |
| 2 | −15.402–6.854 | 6 | 11.381–20.499 | ||||
| 3 | −6.854–0.586 | 7 | 20.499–86.602 | ||||
| 4 | −0.586–5.113 | ||||||
| TWI | DEM | 10 m | 1 | 0.869–4.627 | 5 | 9.548–12.591 | [19,35,84] |
| 2 | 4.627–5.880 | 6 | 12.591–16.796 | ||||
| 3 | 5.880–7.401 | 7 | 16.796–23.686 | ||||
| 4 | 7.401–9.548 | ||||||
| Conditioning Factors | VIF | TOL |
|---|---|---|
| Altitude (m) | 2.29424 | 0.43587 |
| Aspect | 1.04426 | 0.95762 |
| Distance to drainage (m) | 1.10645 | 0.90379 |
| Distance to faults (m) | 1.18195 | 0.84606 |
| Distance to roads (m) | 2.25385 | 0.44369 |
| Land cover | 1.17820 | 0.84875 |
| Lithology | 1.11000 | 0.90090 |
| LS-factor | 3.01434 | 0.33175 |
| Plan curvature | 1.31931 | 0.75797 |
| Profile curvature | 1.15036 | 0.86929 |
| Slope (°) | 3.61071 | 0.27695 |
| TCD | 1.13473 | 0.88126 |
| TPI | 1.85399 | 0.53938 |
| TWI | 3.13184 | 0.31930 |
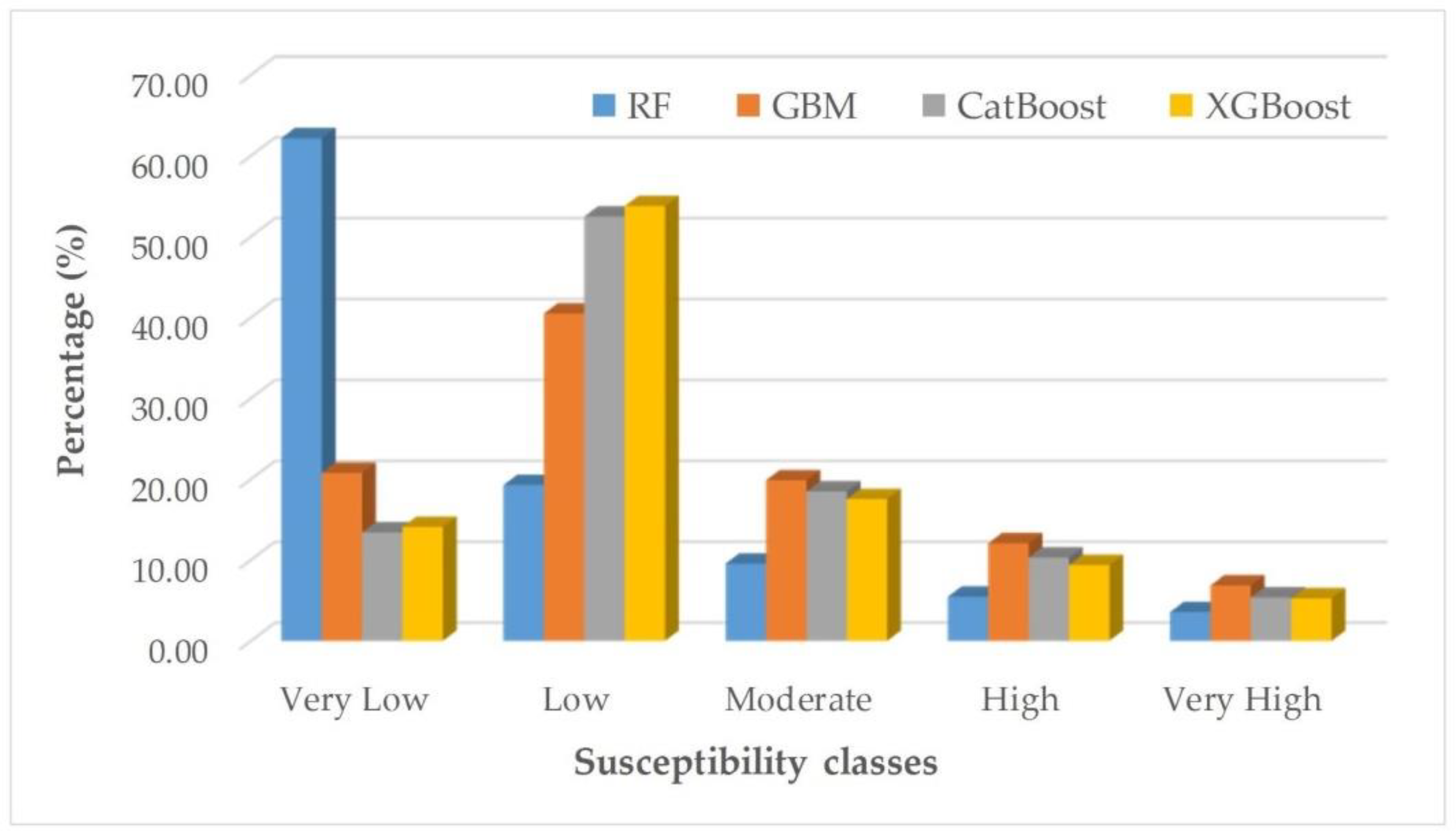
| ML Model | Susceptibility Level | Area Percentage (%) | Landslide Pixel | Landslide Percentage (%) | Frequency Ratio |
|---|---|---|---|---|---|
| RF | Very low | 62.17 | 31 | 0.049 | 0.0008 |
| Low | 19.27 | 501 | 0.807 | 0.0419 | |
| Moderate | 9.55 | 1695 | 2.729 | 0.2858 | |
| High | 5.45 | 5988 | 9.646 | 1.7699 | |
| Very high | 3.56 | 53,874 | 86.769 | 24.3733 | |
| GBM | Very low | 20.76 | 2 | 0.003 | 0.0001 |
| Low | 40.48 | 47 | 0.076 | 0.0019 | |
| Moderate | 19.85 | 960 | 1.546 | 0.0779 | |
| High | 12.06 | 5906 | 9.512 | 0.7887 | |
| Very high | 6.85 | 55,174 | 88.863 | 12.9727 | |
| XGBoost | Very low | 14.08 | 0 | 0 | 0 |
| Low | 53.77 | 7 | 0.011 | 0.0002 | |
| Moderate | 17.53 | 306 | 0.493 | 0.0281 | |
| High | 9.36 | 3383 | 5.449 | 0.5822 | |
| Very high | 5.26 | 58,393 | 94.047 | 17.8796 | |
| CatBoost | Very low | 13.40 | 0 | 0 | 0 |
| Low | 52.48 | 5 | 0.008 | 0.0001 | |
| Moderate | 18.47 | 219 | 0.353 | 0.0191 | |
| High | 10.29 | 3328 | 5.360 | 0.5209 | |
| Very high | 5.36 | 58,537 | 94.279 | 17.5894 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yavuz Ozalp, A.; Akinci, H.; Zeybek, M. Comparative Analysis of Tree-Based Ensemble Learning Algorithms for Landslide Susceptibility Mapping: A Case Study in Rize, Turkey. Water 2023, 15, 2661. https://doi.org/10.3390/w15142661
Yavuz Ozalp A, Akinci H, Zeybek M. Comparative Analysis of Tree-Based Ensemble Learning Algorithms for Landslide Susceptibility Mapping: A Case Study in Rize, Turkey. Water. 2023; 15(14):2661. https://doi.org/10.3390/w15142661
Chicago/Turabian StyleYavuz Ozalp, Ayse, Halil Akinci, and Mustafa Zeybek. 2023. "Comparative Analysis of Tree-Based Ensemble Learning Algorithms for Landslide Susceptibility Mapping: A Case Study in Rize, Turkey" Water 15, no. 14: 2661. https://doi.org/10.3390/w15142661
APA StyleYavuz Ozalp, A., Akinci, H., & Zeybek, M. (2023). Comparative Analysis of Tree-Based Ensemble Learning Algorithms for Landslide Susceptibility Mapping: A Case Study in Rize, Turkey. Water, 15(14), 2661. https://doi.org/10.3390/w15142661









