A Bilevel Optimal Water Allocation Model Considering Water Users’ Satisfaction Degree and Water Rights Transaction: A Case Study in Qingzhang River Basin, China
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Definition and Principles of Water Users’ Satisfaction Degree
2.1.1. Definition of Water Users’ Satisfaction Degree
2.1.2. Principles of Water Users’ Satisfaction Degree
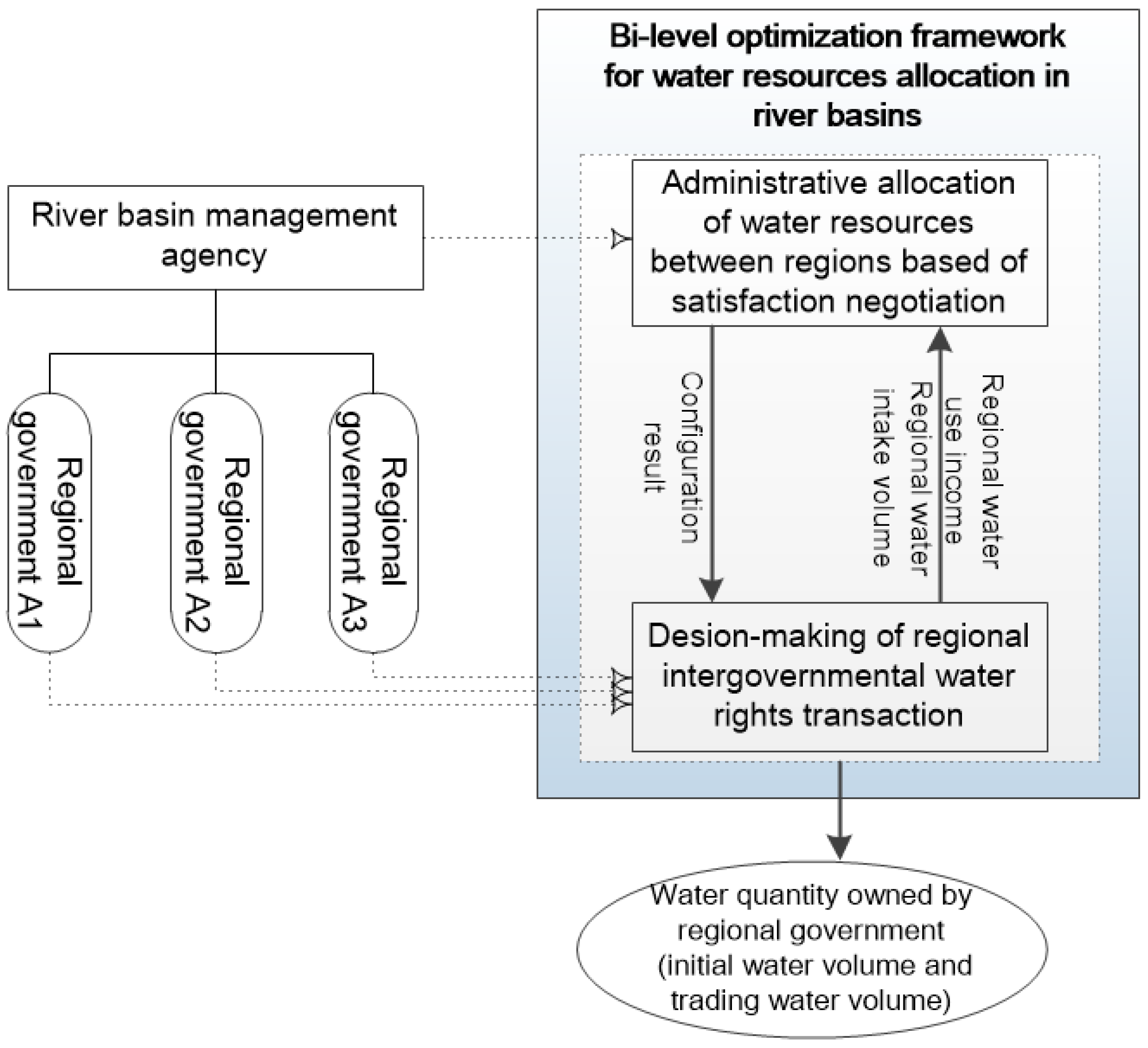
2.2. A Bilevel Optimization Model for Basin Water Resources Allocation
2.2.1. Model Framework
2.2.2. Model Assumptions
2.2.3. Model Construction
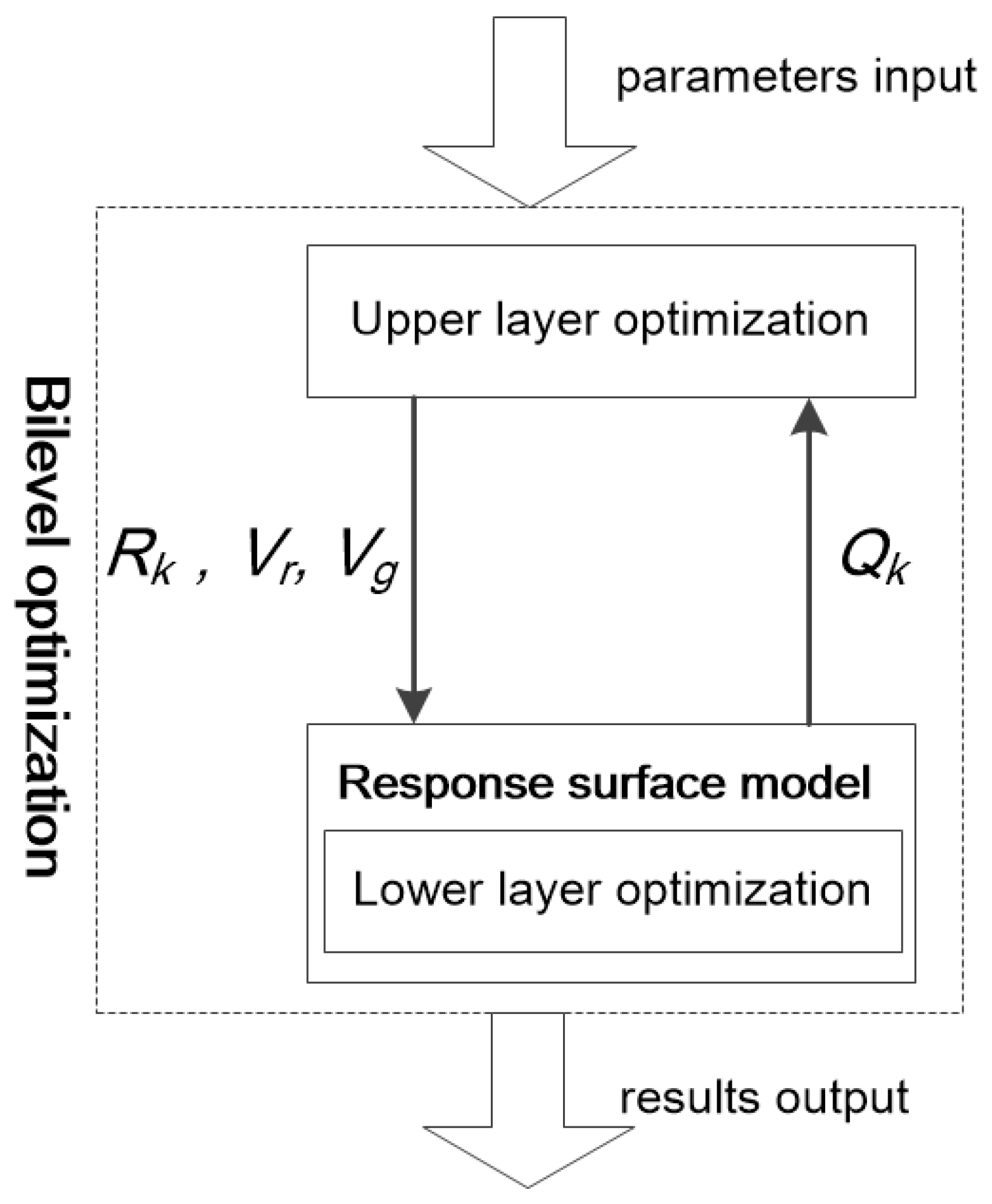
2.3. Solution to the Bilevel Optimization Model for Water Basin Resource Allocation
2.3.1. Solution Ideas
2.3.2. Algorithm Design Based on Response Surface Methodology
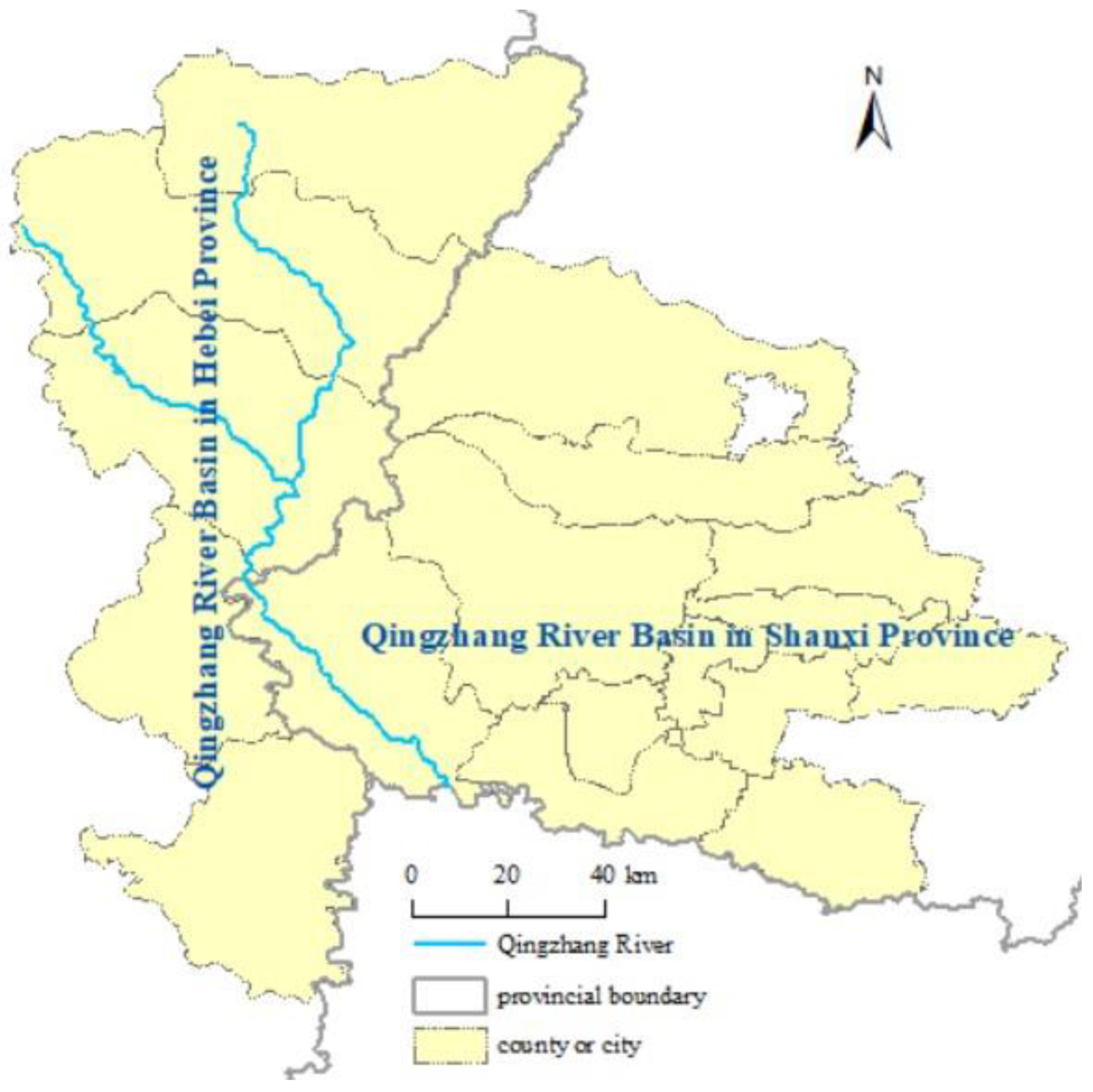
3. Case Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yan, Q.; Zhang, Y.; Wang, Q. Analysis of Demand and Structural Changes in China’s Water Resources over the Next 30 Years. Water 2023, 15, 745. [Google Scholar] [CrossRef]
- Roson, R.; Damania, R. The macroeconomic impact of future water scarcity: An assessment of alternative scenarios. J. Policy Model. 2017, 39, 1141–1162. [Google Scholar] [CrossRef]
- Wu, N.; Xu, Y.; Kilgour, D.M. Water allocation analysis of the Zhanghe River basin using the Graph Model for Conflict Resolution with incomplete fuzzy preferences. Sustainability 2019, 11, 1099. [Google Scholar] [CrossRef] [Green Version]
- Yuan, L.; He, W.; Degefu, D.M.; Wan, Z.; Ramsey, T.S.; Wu, X. A system dynamics simulation model for water conflicts in the Zhanghe River Basin, China. Int. J. Water Resour. Dev. 2021, 6, 1–17. [Google Scholar] [CrossRef]
- Wang, J.; Wu, T.; Li, Q.; Wang, S. Quantifying the effect of environmental drivers on water conservation variation in the eastern Loess Plateau, China. Ecol. Indic. 2021, 125, 107493. [Google Scholar] [CrossRef]
- Chu, Y.; Hipel, K.W.; Fang, L.; Wang, H. Systems methodology for resolving water conflicts: The Zhanghe River water allocation dispute in China. Int. J. Water Resour. Dev. 2015, 31, 106–119. [Google Scholar] [CrossRef]
- Luo, Y.; Sha, J.; Liu, B.; Zhang, Y.; Yang, J. Optimal Allocation of Water Resources Based on GWAS Model in Handan, China. Water 2023, 15, 1090. [Google Scholar] [CrossRef]
- Chu, Y. Optimal Water Resource Allocation of the River Basin Considering the Water Body Satisfaction Degree. Resour. Sci. 2018, 40, 8. [Google Scholar] [CrossRef] [Green Version]
- Ma, J.; Liu, H.; Wu, W.; Zhang, Y.; Dong, S. Research on Optimal Allocation of Water Resources in Handan City Based on the Refined Water Resource Allocation Model. Water 2023, 15, 154. [Google Scholar] [CrossRef]
- Tian, J.; Guo, S.; Liu, D.; Pan, Z.; Hong, X. A Fair Approach for Multi-Objective Water Resources Allocation. Water Resour. Manag. 2019, 33, 3633–3653. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, L.; Cheng, L.; Liu, K.; Wei, Y.M. Basin-Wide Initial Water Rights Allocation Model Considering Both the Quantity and Quality of Water. Environ. Model. Assess. 2020, 25, 581–589. [Google Scholar] [CrossRef]
- Ge, M.; Wu, F.P.; You, M. Initial Provincial Water Rights Dynamic Projection Pursuit Allocation Based on the Most Stringent Water Resources Management: A Case Study of Taihu Basin, China. Water 2017, 9, 35. [Google Scholar] [CrossRef] [Green Version]
- Delorit, J.D.; Block, P.J. Promoting Competitive Water Resource Use Efficiency at the Water-Market Scale: An Intercooperative Demand Equilibrium-Based Approach to Water Trading. Water Resour. Res. 2018, 54, 5394–5421. [Google Scholar] [CrossRef]
- He, Y.; Yang, J.; Chen, X. Allocating river water in a cooperative way: A case study of the Dongjiang River Basin, South China. Stoch. Environ. Res. Risk Assess. 2018, 32, 3083–3097. [Google Scholar] [CrossRef]
- Wang, L.; Fang, L.; Hipel, K.W. Basin-wide cooperative water resources allocation. Eur. J. Oper. Res. 2008, 190, 798–817. [Google Scholar] [CrossRef]
- Zeng, X.T.; Li, Y.P.; Huang, G.H.; Liu, J. Modeling of Water Resources Allocation and Water Quality Management for Supporting Regional Sustainability under Uncertainty in an Arid Region. Water Resour. Manag. 2017, 31, 3699–3721. [Google Scholar] [CrossRef]
- Pienaar, G.W.; Hughes, D.A. Linking Hydrological Uncertainty with Equitable Allocation for Water Resources Decision-Making. Water Resour. Manag. 2017, 31, 269–282. [Google Scholar] [CrossRef]
- Zheng, H.; Wang, Z.; Hu, S.; Wei, Y. A Comparative Study of the Performance of Public Water Rights Allocation in China. Water Resour. Manag. 2012, 26, 1107–1123. [Google Scholar] [CrossRef]
- Yao, L.; Xu, Z.; Chen, X. Sustainable water allocation strategies under various climate scenarios: A case study in China. J. Hydrol. 2019, 574, 529–543. [Google Scholar] [CrossRef]
- Zheng, H.; Liu, Y.; Zhao, J. Understanding water rights and water trading systems in China: A systematic framework. Water Secur. 2021, 13, 100094. [Google Scholar] [CrossRef]
- Zhou, Y.; Guo, S.; Xu, C.Y.; Liu, D.; Chen, L.; Wang, D. Integrated optimal allocation model for complex adaptive system of water resources management (II): Case study. J. Hydrol. 2015, 531, 977–991. [Google Scholar] [CrossRef]
- Hung, M.F.; Shaw, D.; Chie, B.T. Water Trading: Locational Water Rights, Economic Efficiency, and Third-Party Effect. Water 2014, 6, 723–744. [Google Scholar] [CrossRef] [Green Version]
- Yan, S.; Wang, L.; Li, T. An Agricultural Interval Two-Stage Fuzzy Differential Water Price Model (ITS-DWPM) for Initial Water Rights Allocation in Hulin, China. Water 2020, 12, 221. [Google Scholar] [CrossRef] [Green Version]
- He, Y.; Chen, X.; Sheng, Z.; Lin, K.; Gui, F. Water allocation under the constraint of total water-use quota: A case from Dongjiang River Basin, South China. Hydrol. Sci. J. 2018, 63, 154–167. [Google Scholar] [CrossRef]
- Zhang, J.; Meng, C.; Hu, S.; Li, W. Optimal allocation model for water resources coupled with ecological value factors—A case study of Dalian, China. Water 2022, 14, 266. [Google Scholar] [CrossRef]
- Wu, D.; Wu, F. The coupling allocation of initial two-dimensional water rights in basin based on the bi-hierarchy optimal model. China Popul. Resour. Environ. 2012, 22, 26–34. (In Chinese) [Google Scholar] [CrossRef]
- Lizhong, W.; Liping, F. WHK Mathematical Programming Approaches for Modeling Water Rights Allocation. J. Water Resour. Plan. Manag. 2007, 133, 50–59. [Google Scholar] [CrossRef]
- Congleton, R.D. The Logic of Collective Action and beyond. Public. Choice 2015, 164, 217–234. [Google Scholar] [CrossRef] [Green Version]
- Tian, G.L.; Liu, J.N.; Li, X.Y.; Li, Y.Q.; Yin, H. Water rights trading: A new approach to dealing with trans-boundary water conflicts in river basins. Water Policy 2020, 22, 133–152. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Mao, H.; Yin, H.; Guo, X. A pricing model for water rights trading between agricultural and industrial water users in China. J. Water Supply Res. Technol. 2018, 67, 347–356. [Google Scholar] [CrossRef]
- Zhang, G.Z.; Liu, H.; Jia, D.W. River Basin Management Based on the Mechanisms of Water Rights Trading. Procedia Environ. Sci. 2010, 2, 665–673. [Google Scholar] [CrossRef] [Green Version]
- Degefu, D.M.; He, W.; Yuan, L. Monotonic Bargaining Solution for Allocating Critically Scarce Transboundary Water. Water Resour. Manag. 2017, 31, 2627–2644. [Google Scholar] [CrossRef]
- Huangg; Loucks, P. An Inexact Two-Stage Stochastic Programming Model for Water Resources Management Under Uncertainty. Civ. Eng. Environ. Syst. 2000, 17, 95–118. [Google Scholar] [CrossRef]
- Li, T.; Zeng, X.; Chen, C.; Kong, X.; Zhang, J.; Zhu, Y.; Zhang, F.; Dong, H. Scenario Analysis of Initial Water-Rights Allocation to Improve Regional Water Productivities. Water 2019, 11, 1312. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; He, W.; Yuan, L.; Kong, Y.; Li, R.; Qi, Y.; Yang, D.; Degefu, D.M.; Ramsey, T.S. Two-stage water resources allocation negotiation model for transboundary rivers under scarcity. Front. Environ. Sci. 2022, 10, 900854. [Google Scholar] [CrossRef]
- Yuan, L.; He, W.; Liao, Z.; Degefu, D.; An, M.; Zhaofang, Z. Simulating Water Resource Disputes of Transboundary River: A Case Study of the Zhanghe River Basin, China. In IOP Conference Series: Earth and Environmental Science, Proceedings of the 2017 International Conference on Advanced Environmental Engineering (ICAEE2017), Shenzen, China, 15–17 December 2017; IOP Publishing Ltd.: Bristol, UK, 2018; Volume 111, p. 12001. [Google Scholar] [CrossRef] [Green Version]
| Subregion | Total Water Supply (108 m3) | Current Water Consumption (108 m3) | Irrigated Area (104 mu) | Agricultural Water Quota (m3/mu) | Industrial Water Quota (m3/104 CNY) | Total Water Demand (108 m3) |
|---|---|---|---|---|---|---|
| Qingzhang in Shanxi | 0.50 | 0.50 | 14.69 | 300 | 73.8 | 0.52 |
| Qingzhang in Hebei | 1.18 | 1.17 | 18.5 | 548 | 43 | 1.20 |
| Subregion | Urban Population (Hundred Million) | Urban Water Use Quota (L/Person-Day) | Rural Population (Hundred Million) | Rural Water Use Quota (L/Person-Day) | Large Livestock (Hundred Million) | Small livestock (Hundred Million) | Water for Large Livestock (L/Person-Day) | Water for Small Livestock (L/Person-Day) |
|---|---|---|---|---|---|---|---|---|
| Qingzhang in Shanxi | 9.12 | 121.27 | 29.78 | 56.58 | 8.41 | 71.99 | 35 | 15 |
| Qingzhang in Hebei | 10.12 | 142 | 35.46 | 45 | 5.26 | 41.23 | 35 | 15 |
| Provinces | Water Demand (Million m3) | Initial Water Distribution (Million m3) | Water Shortage Rate | Satisfaction Degrees of Water Users | Decision Weight | Economic Benefit (Hundred Million CNY) |
|---|---|---|---|---|---|---|
| Shanxi | 36.60 | 34.36 | 0.06 | 0.88 | 0.35 | 39.17 |
| Hebei | 106.33 | 103.43 | 0.02 | 0.95 | 0.65 | 240.99 |
| Provinces | Water Demand (Million m3) | Initial Water Distribution (Million m3) | Water Intake (Million m3) | Water Resource Fee (CNY) | Trading Benchmark Price(CNY) | Satisfaction of Water Users | Decision Weight | Pre-transaction Benefit (Hundred Million CNY) | Post-transaction Benefit (Hundred Million CNY) |
|---|---|---|---|---|---|---|---|---|---|
| Shanxi | 36.60 | 34.58 | 34.03 | 0.54 | 0.75 | 0.89 | 0.35 | 39.23 | 50.24 |
| Hebei | 106.33 | 103.21 | 103.76 | 0.54 | 0.75 | 0.94 | 0.65 | 239.92 | 289.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, Y.; Xiao, Y.; Zhu, J. A Bilevel Optimal Water Allocation Model Considering Water Users’ Satisfaction Degree and Water Rights Transaction: A Case Study in Qingzhang River Basin, China. Water 2023, 15, 2650. https://doi.org/10.3390/w15142650
Chu Y, Xiao Y, Zhu J. A Bilevel Optimal Water Allocation Model Considering Water Users’ Satisfaction Degree and Water Rights Transaction: A Case Study in Qingzhang River Basin, China. Water. 2023; 15(14):2650. https://doi.org/10.3390/w15142650
Chicago/Turabian StyleChu, Yu, Yi Xiao, and Jiulong Zhu. 2023. "A Bilevel Optimal Water Allocation Model Considering Water Users’ Satisfaction Degree and Water Rights Transaction: A Case Study in Qingzhang River Basin, China" Water 15, no. 14: 2650. https://doi.org/10.3390/w15142650




