1. Introduction
The interdependence and response processes of runoff and sediment elements in river basins have always been the focus of water science research [
1,
2,
3]. Runoff and sediment are carriers of material transport in river systems and outputs of runoff and sediment production processes in river basins [
4,
5,
6]; their relationship and synergistic evolution play an irreplaceable role in the function of watershed systems [
7]. The research of the joint probability of runoff and sediment is a prerequisite for realizing the scientific management scheme of runoff and sediment, which is of great importance in the utilization of water resources, sustainable development of the river basin, flood control, soil and water conservation, and ecological construction [
8,
9,
10,
11].
Hydrological events are complex stochastic events coupled with multiple factors, and correlations commonly exist among their internal variables. The use of traditional univariate hydrological frequency analysis is difficult to fully reflect the dependencies among the variables of hydrological events and has limitations [
12,
13,
14]. Traditional multivariate hydrological analysis calculations also mainly tend to adopt linear correlation multivariate distribution models with the same marginal distribution [
15,
16], limiting the accuracy of their results. Copula function is a breakthrough method for establishing multivariate joint distributions [
17], which can connect two or more correlated variables [
18] and study the marginal distribution and correlation structure, respectively, without restricting the type of marginal distributions. It has high adaptability and is widely used in hydrological and water resources application fields, such as frequency analysis, risk analysis, stochastic simulation of rainfall, floods, droughts, etc. [
19,
20,
21,
22,
23] Golian et al. employed the copula method to study the joint probability distribution of rainfall depth and peak flow [
24]; Bacchi and Balistrocchi proposed a criterion for deriving flood frequency curves from rainfall and duration distribution, and evaluated the return period of bivariate rainfall events [
25]; Zhang et al. utilized copula functions to focus on the relationship between groundwater depth changes and three selected control factors from a probability perspective, and compared the differences between the results of the two-dimensional and three-dimensional copula functions [
18]; Requena et al. applied the copula approach to perform multivariate flood frequency analyses, and the uncertainty involved in selecting copula to characterize the dependency structure of short data sequences is analyzed [
26]; Chang et al. constructed a two-dimensional copula drought risk model of drought duration and severity, and the drought risk of Weihe River Basin was fully assessed [
27]; Li et al. constructed a model of runoff and sediment over two stations in the Anning watershed 2010~2015 using the copula analysis method, analyzing the synchronous and asynchronous probabilities of runoff and sediment from both time and space perspectives [
28]; Dodangeh et al. established a joint probabilistic model of the extreme rainfall–runoff, using annual maximum precipitation, corresponding historical and simulated runoff data [
29]; Salvadori et al. introduced a framework for multivariate copula for handing multivariate disaster scenarios and evaluated the threat probability of natural disasters [
30].
Due to its complex physical mechanisms and numerous influencing factors (including climate, meteorology, topography, geomorphology, underlying surface, etc.,), uncertainties in hydrological processes are prevalent, and the degree of uncertainty is directly related to the complexity of the system [
31]. Uncertainties in the framework of multidimensional variable models based on copula theory include the uncertainty in the marginal distribution, the uncertainty in the selection of copula functions, and the uncertainties in sample sampling and parameter estimation [
32,
33]. The uncertainty in the process of constructing the copula joint distribution model has a significant impact on the accuracy of the conclusion and the correctness of the decision. Comprehensive assessment of uncertainty in joint distribution models has complexity, and the quantitative analysis of uncertainty has rarely been addressed in previous studies, and related research is currently at the initial stage.
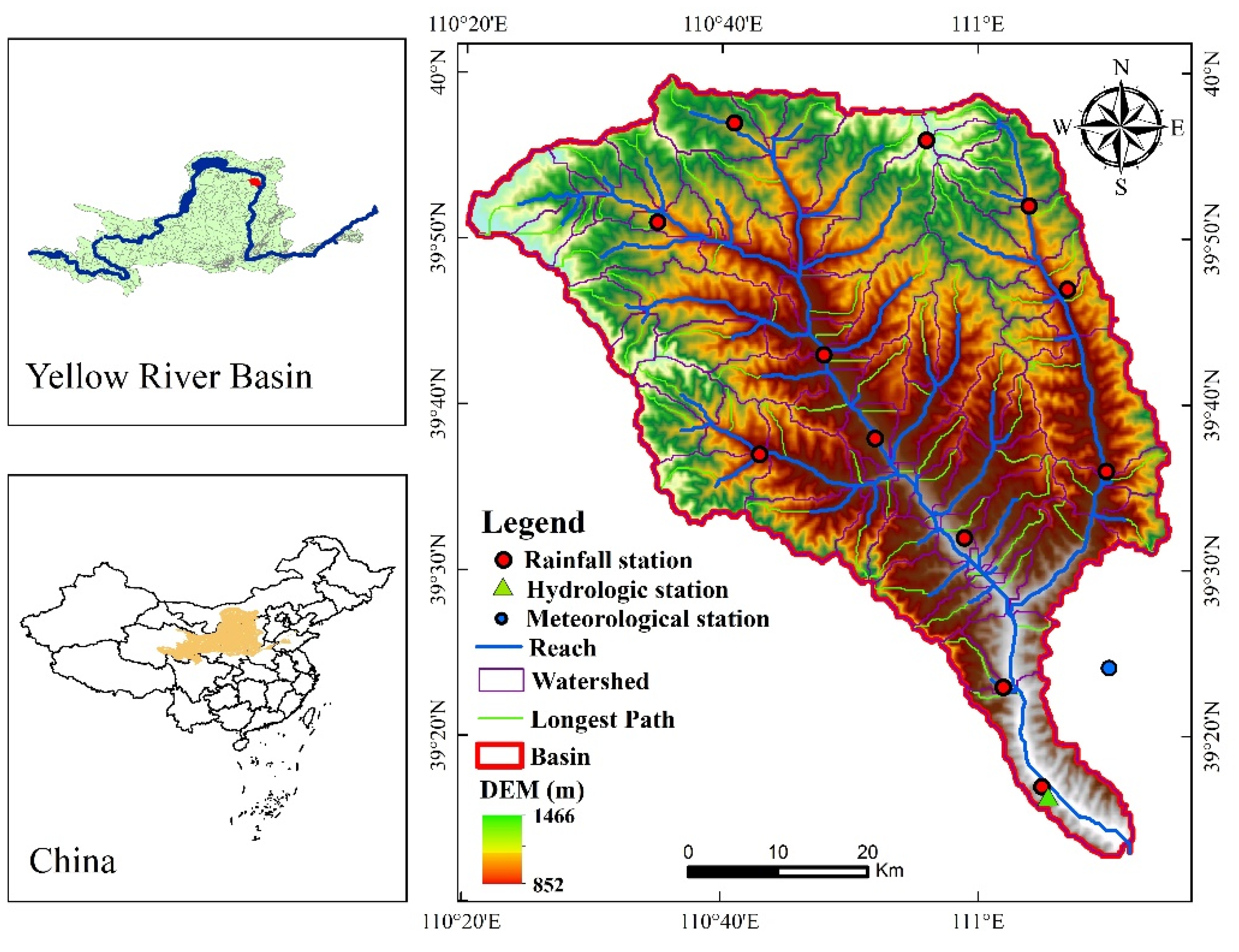
The Yellow River has the highest sediment concentration in the world and is the world’s most famous sandy river. In recent years, under the combined influence of climate change and human activities, the runoff–sediment process of the Yellow River has changed significantly [
34]. The Huangfuchuan River basin is a typical basin in the concentrated source area of sandy and coarse sediment in the middle reaches of the Yellow River (Heilong interval), which is one of the main production areas of coarse sediment in the Yellow River and the basin with the highest erosion intensity among the tributaries of the Yellow River. Since the 20th century, due to the over-exploitation of coal resources in the Huangfuchuan River basin, the groundwater level has continued to decline, runoff has shown a decreasing trend, and droughts have continued to occur in the arid zone. In addition, arsenic sandstone has been exposed in a large area in the basin, and the original vegetation has been severely damaged. These features are extremely rare in China and even around the world. Under the changing environment, the modeling and analysis of the synergistic evolution of runoff and sediment in the Huangfuchuan River basin can help clarify the runoff-sediment relationship and the change patterns in the Yellow River basin and help guide watershed management planning and soil erosion control. It is the theoretical basis for establishing a runoff-sediment regulation system for the harmonious development of man and nature. It provides the scientific basis and data support for runoff-sediment resource utilization in the region, is theoretical support for the formulation of regional sustainable development countermeasures, and is of practical significance for the ecological environment construction of the Loess Plateau, the healthy management of the Yellow River, and the high-quality development of the Yellow River basin.
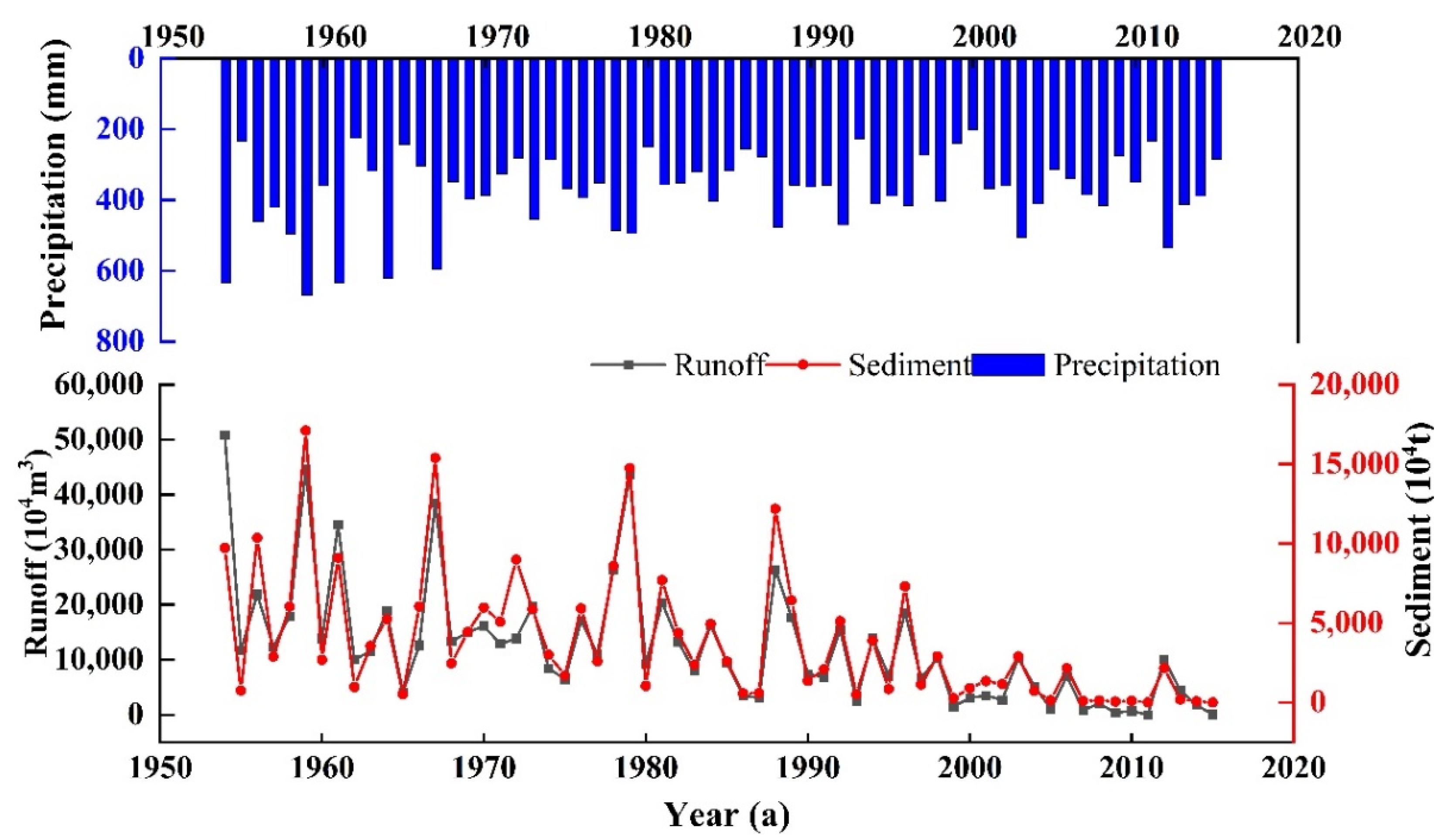
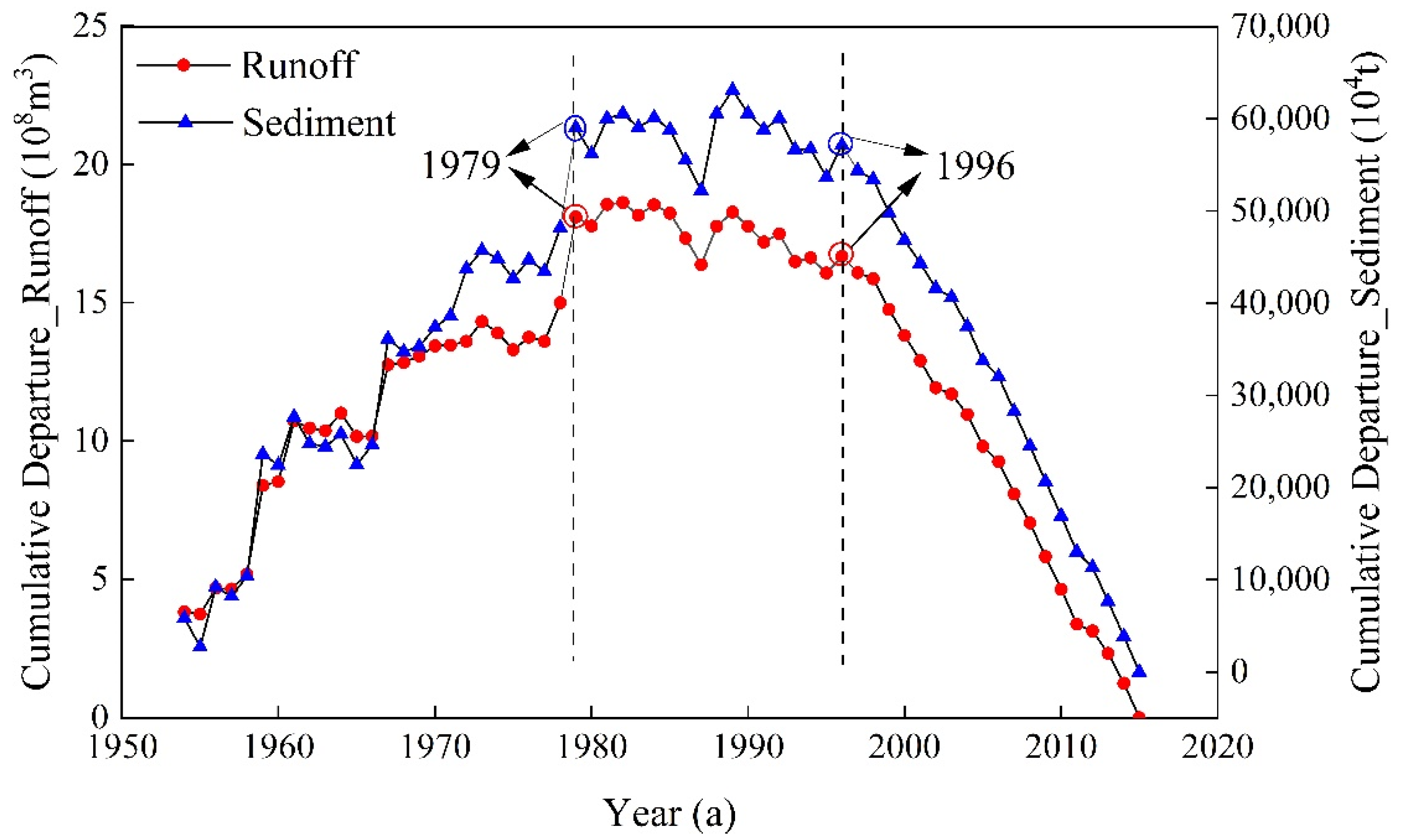
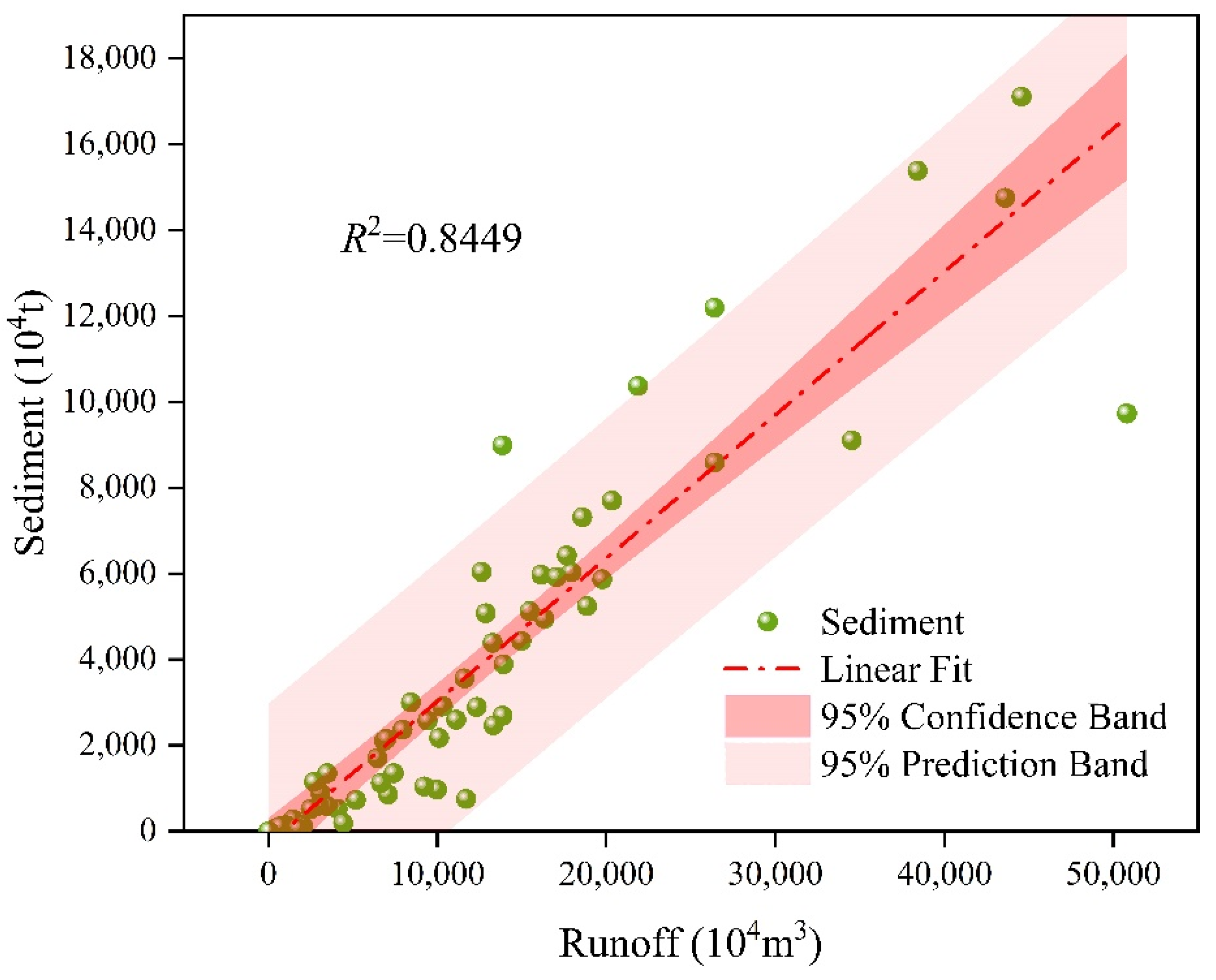
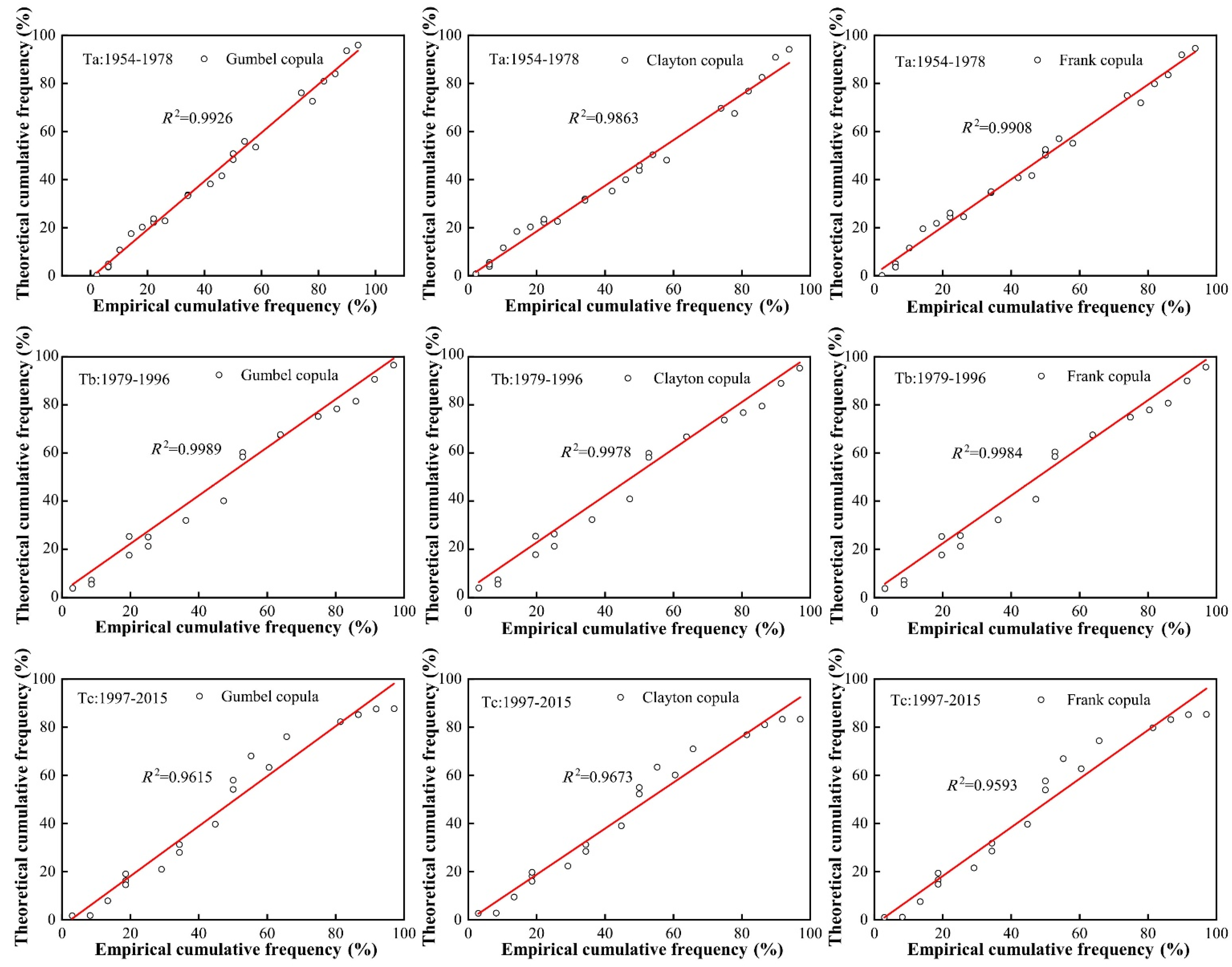
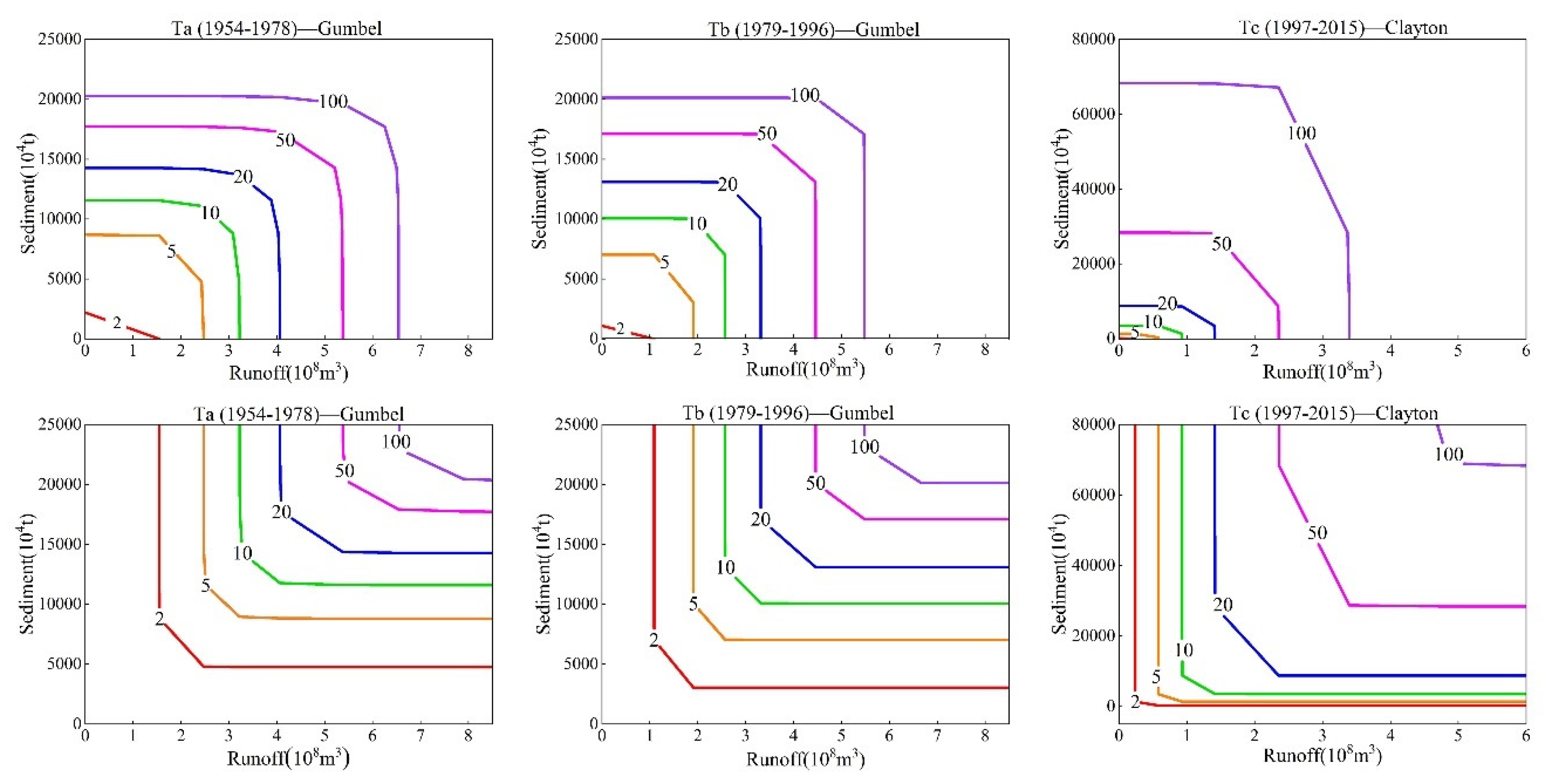
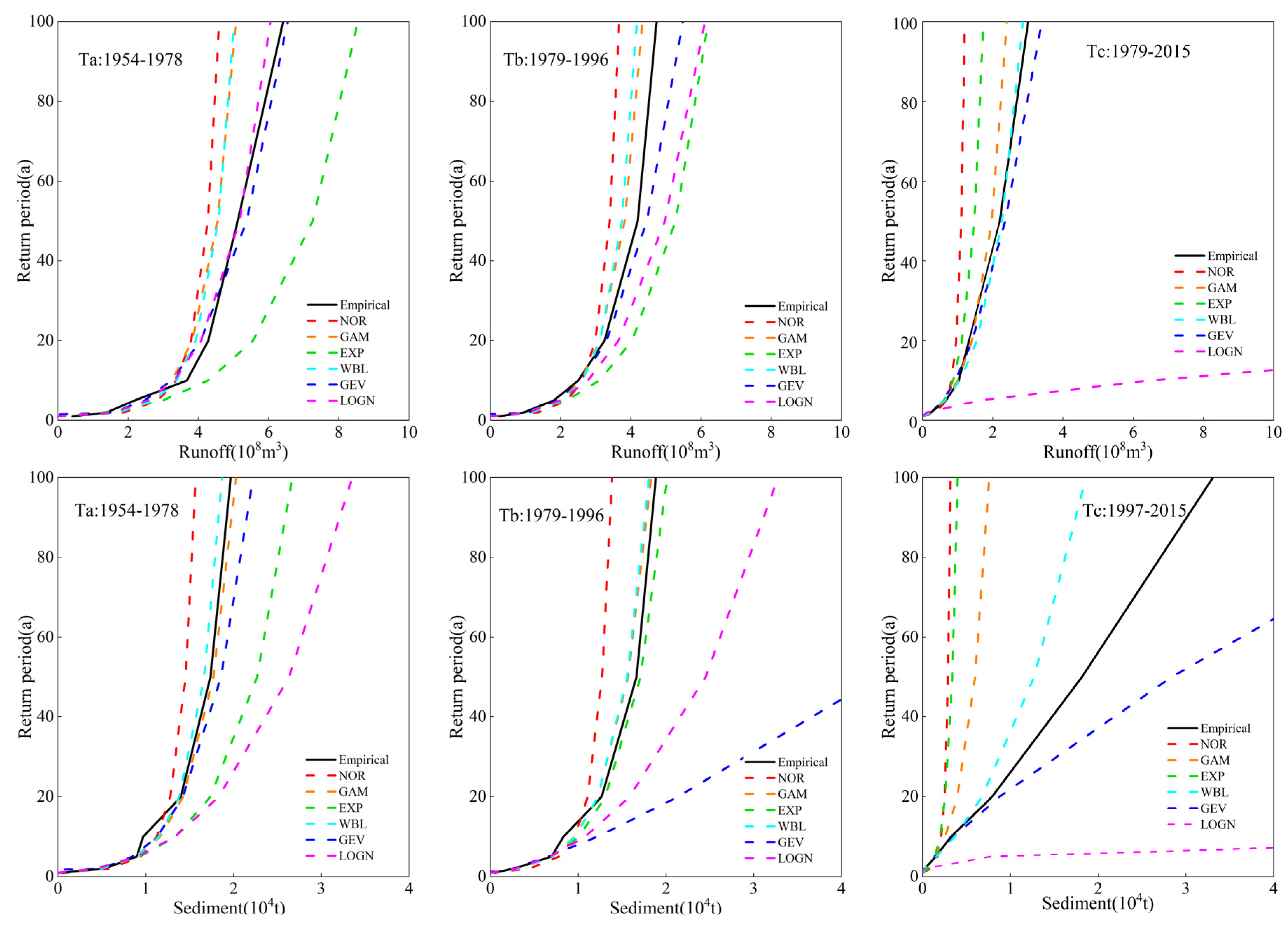
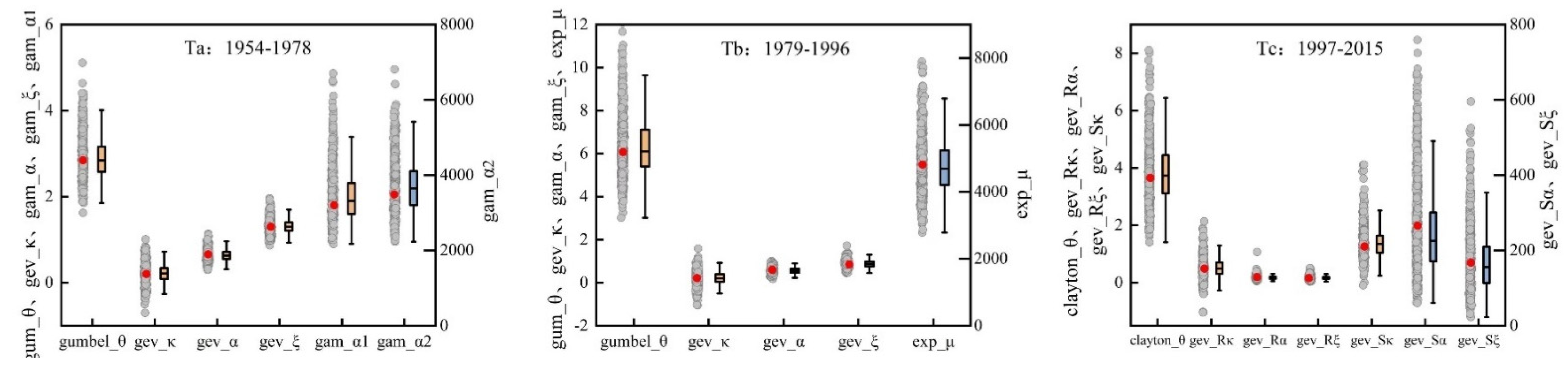
In this paper, the Huangfuchuan River basin is taken as the research object, the joint probability distribution model of runoff and sediment in a sandy area is constructed, and the uncertainties in the process of constructing the copula joint distribution function are analyzed. Firstly, the cumulative anomaly method, the double mass curve (DMC) method, and the Mann-Kendall test are used to analyze the runoff and sediment discharge series from 1954 to 2015, determine the mutation points, and divide them into three stages; the copula function is introduced to construct the joint distribution model of runoff and sediment in each stage, calculate the synchronous and asynchronous encounter probabilities of runoff and sediment, and analyze the joint return period and the co-occurrence return period. Finally, the uncertainties of the marginal distribution, parameters estimation, and the copula function are analyzed.
5. Discussions
Many studies have shown that climate change and human activities are important factors that cause changes in runoff and sediment, as well as changes in the runoff–sediment relationship. Therefore, it is necessary to study the response of runoff and sediment to climate and human activities. Many meteorological factors are closely related to changes in runoff and sediment. Precipitation and temperature are selected as representatives of meteorological factors, which act on hydrological cycles and directly or indirectly affect the process of runoff and sediment. It is important to calculate the Pearson correlation coefficient between runoff (sediment) and selected meteorological factors and analyze the impact of climate change (precipitation and temperature) on runoff and sediment changes and runoff-sediment relationships in the Huangfuchuan River basin. The calculation results are shown in
Table 9.
As shown in
Table 9, there are significant differences in the impact factors on runoff and sediment at each stage, but there are still certain regularities. Among them, precipitation in each stage has a strong correlation with runoff and sediment, but the correlation gradually weakens over time, and the correlation between runoff (sediment) and temperature in each stage is relatively small. In other words, the dynamic change of runoff and sediment is mainly driven by precipitation, and temperature is also one of the indispensable reasons for the change of runoff and sediment. In recent decades, the climate in the Huangfuchuan River basin has shown a relatively obvious trend of warming and drying, which is one of the important reasons for the reduction of runoff and sediment in the Huangfuchuan River basin.
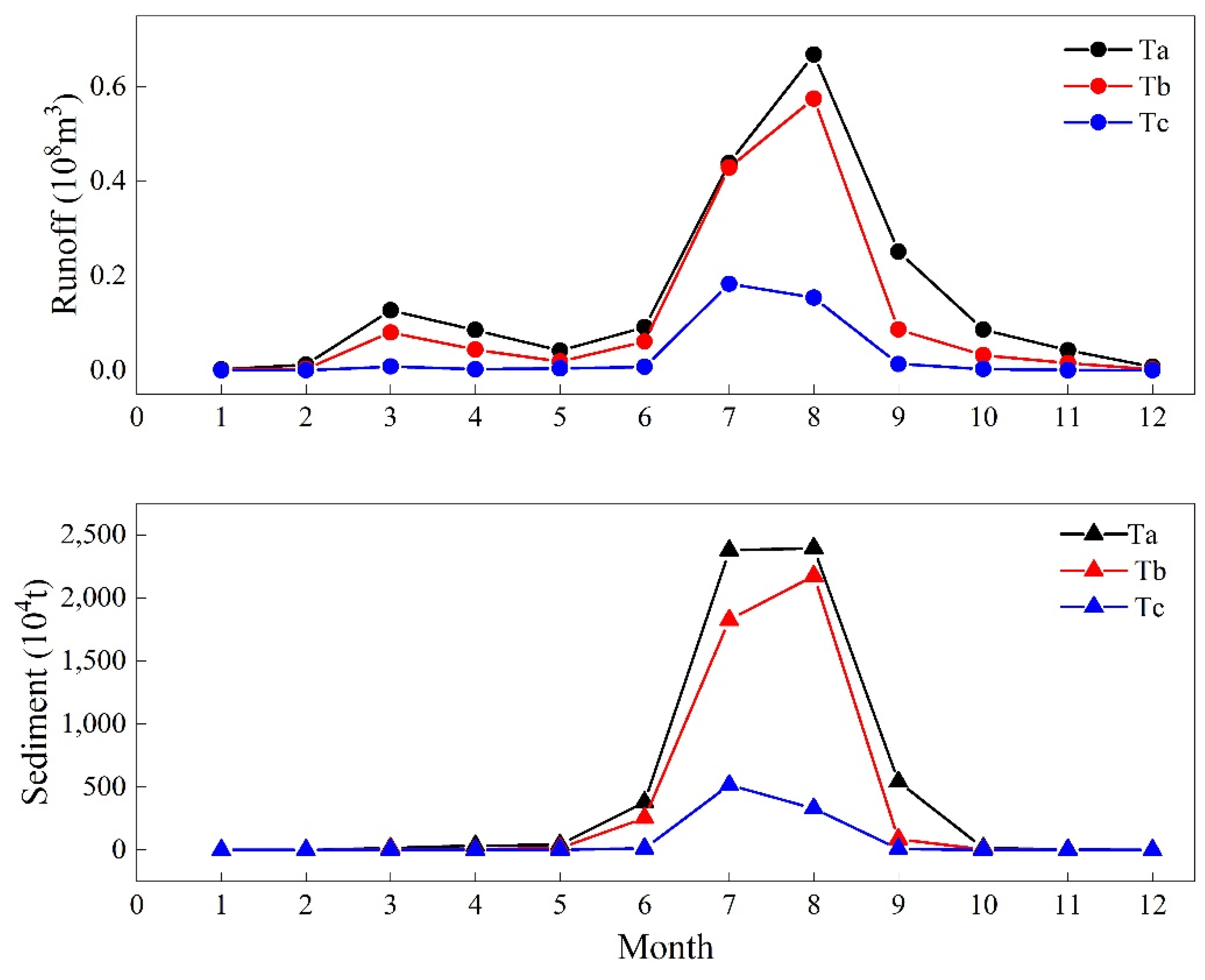
Human activities usually have an impact on the underlying surface of a watershed through methods such as soil and water conservation, urban construction, and domestic production water use. The changes in underlying surface conditions are mainly reflected in land use methods, vegetation cover changes, and water conservancy engineering measures. The construction of check dams is one of the important measures for soil erosion control in the Huangfuchuan River basin. The check dam project can effectively regulate runoff and play a role in reducing flood and sediment. Since the 1950s, soil and water conservation management has been carried out in the Huangfuchuan River basin, with the construction of check dams. However, due to the use of traditional farming methods and the small proportion of remaining storage capacity of check dams before 2000, most of them have already been silted and become ineffective. Therefore, the control speed is relatively slow, and the effect is not significant. Compared with the base period, the synchronous frequency of runoff and sediment increased, while the asynchronous frequency decreased in the stage
. The frequency of rich runoff and rich sediment, normal runoff and normal sediment, poor runoff and poor sediment all increased, indicating that although soil and water conservation measures at this stage have played a role in reducing runoff and sediment to a certain extent (
Table 4), they have not made a contribution to regulating the coupling relationship between water and sediment.
Vegetation can intercept precipitation, increase infiltration, and play a role in reducing flood peaks and erosion. In 1999, the Huangfuchuan River basin started a large-scale project of returning cropland to forests and grassland. The normalized vegetation index (NDVI) showed an upward trend, with an increase rate of 0.095/10a. After 2000, the construction of check dams was further strengthened. By 2015, the number of check dams in the Huangfuchuan River basin had increased to 886, with a total storage capacity of 493 million m3, and the proportion of dam-controlled area in the basin reached 70%. Therefore, compared with the stage , the synchronous frequency of runoff-sediment (especially the frequency of the same rich and same normal) in stage significantly decreased, while the asynchronous frequency of runoff–sediment increased during the same period, indicating that soil and water conservation measures in this stage not only reduced runoff and sediment, but also effectively reduced the sediment content of rich runoff, reduced co-occurrence probability, and adjusted the probability of extreme runoff and sediment events.