Intensity–Duration–Frequency Curves for Dependent Datasets
Abstract
:1. Introduction
2. Classical Models and Vine Copula Approach
- Rainfall intensity sample definition;
- Determination and estimation of the marginal distributions and, for the sampled series, estimation of the copula parameters and construction of the joint distribution;
- Estimation of the quantiles corresponding to specified return periods;
- Adjustment of an IDF relationship to the estimated quantiles;
2.1. GEV-Distribution-Based Rainfall Quantiles
2.2. Vine-Copula-Based Rainfall Quantiles
- 1.
- .
- 2.
- is a tree of nodes and a set of edges denoted by .
- 3.
- For , is a tree of nodes and a set of edges denoted by .
2.3. IDF Curve Formulation
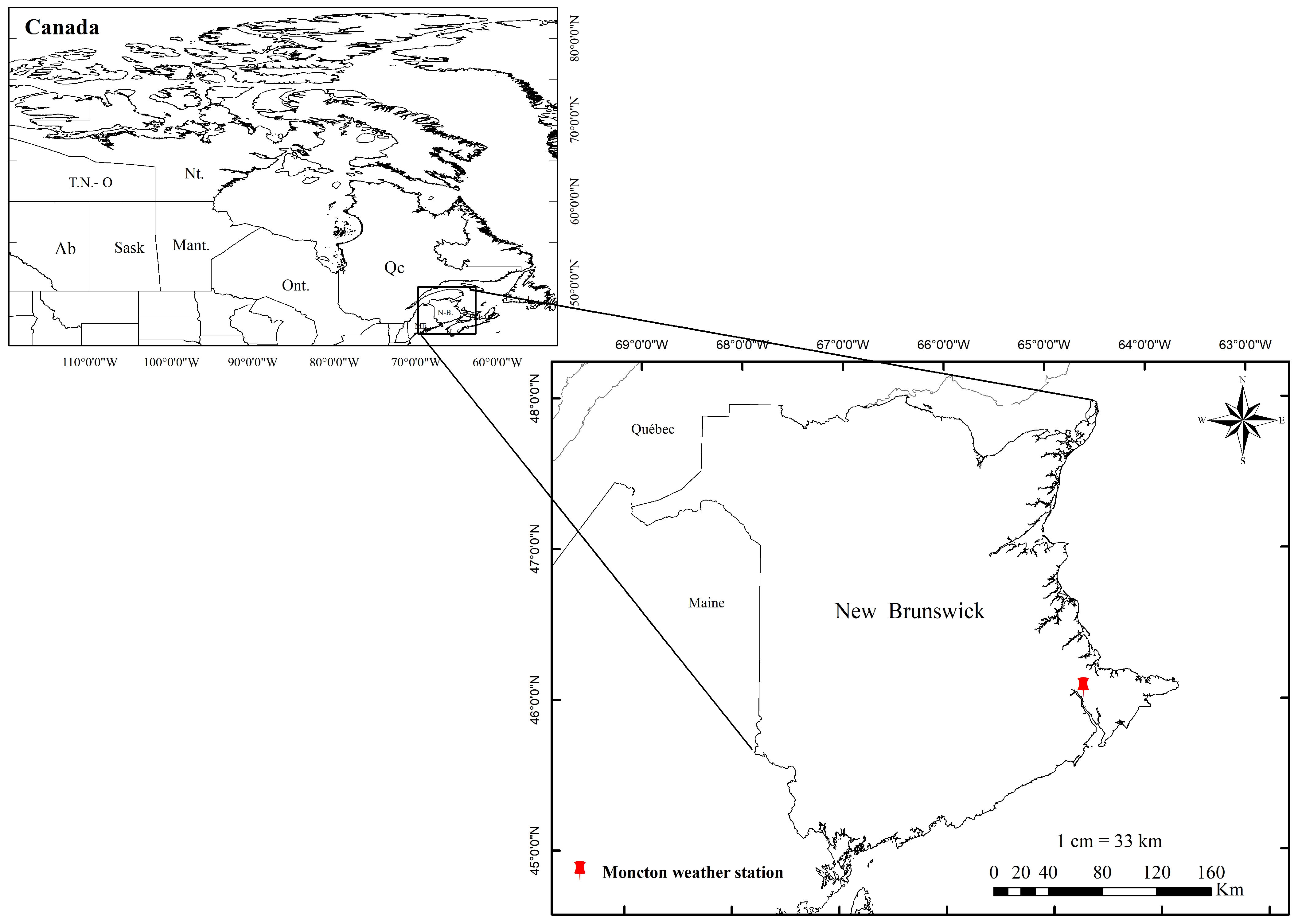
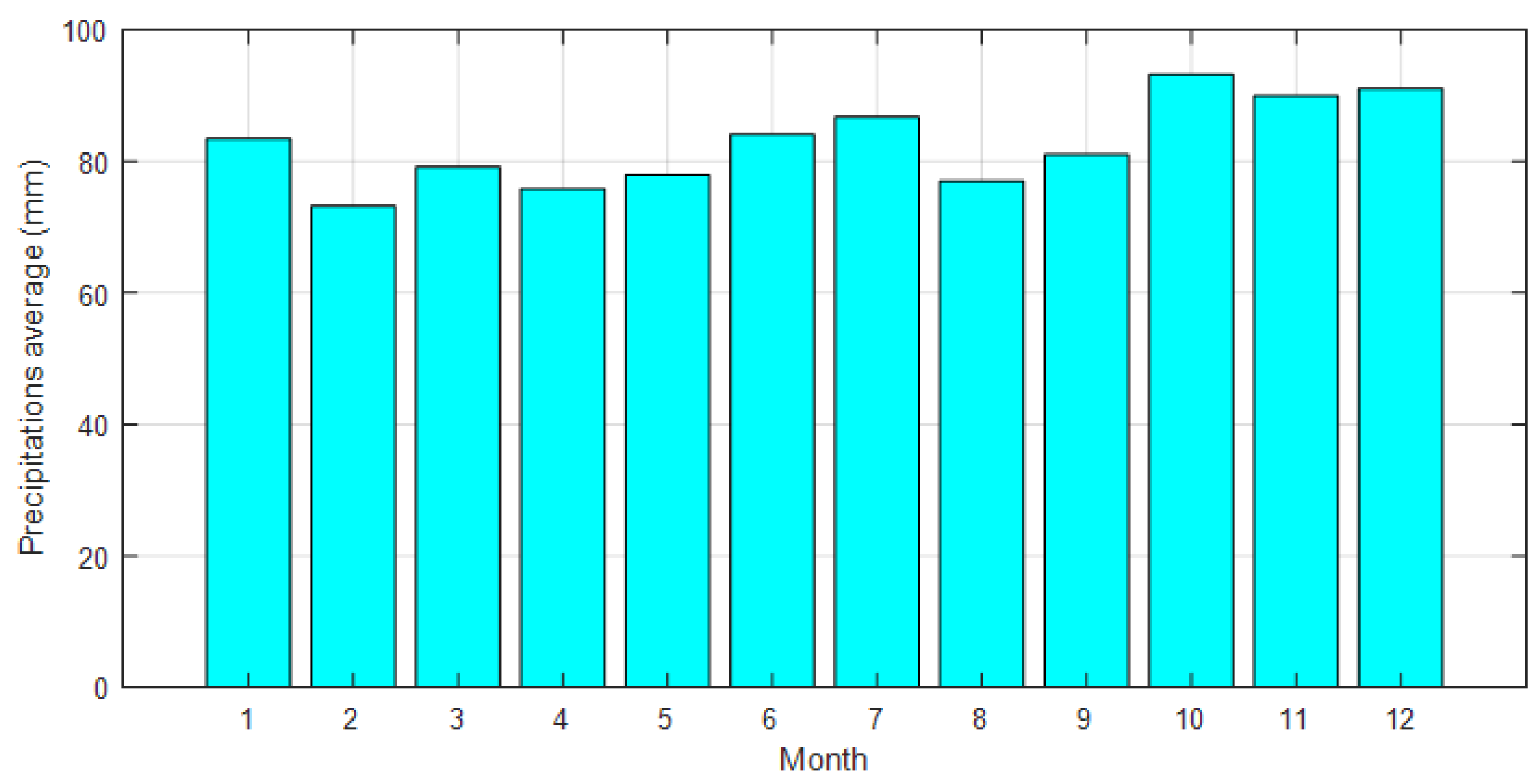
3. Study Area and Dataset
4. Results and Discussion
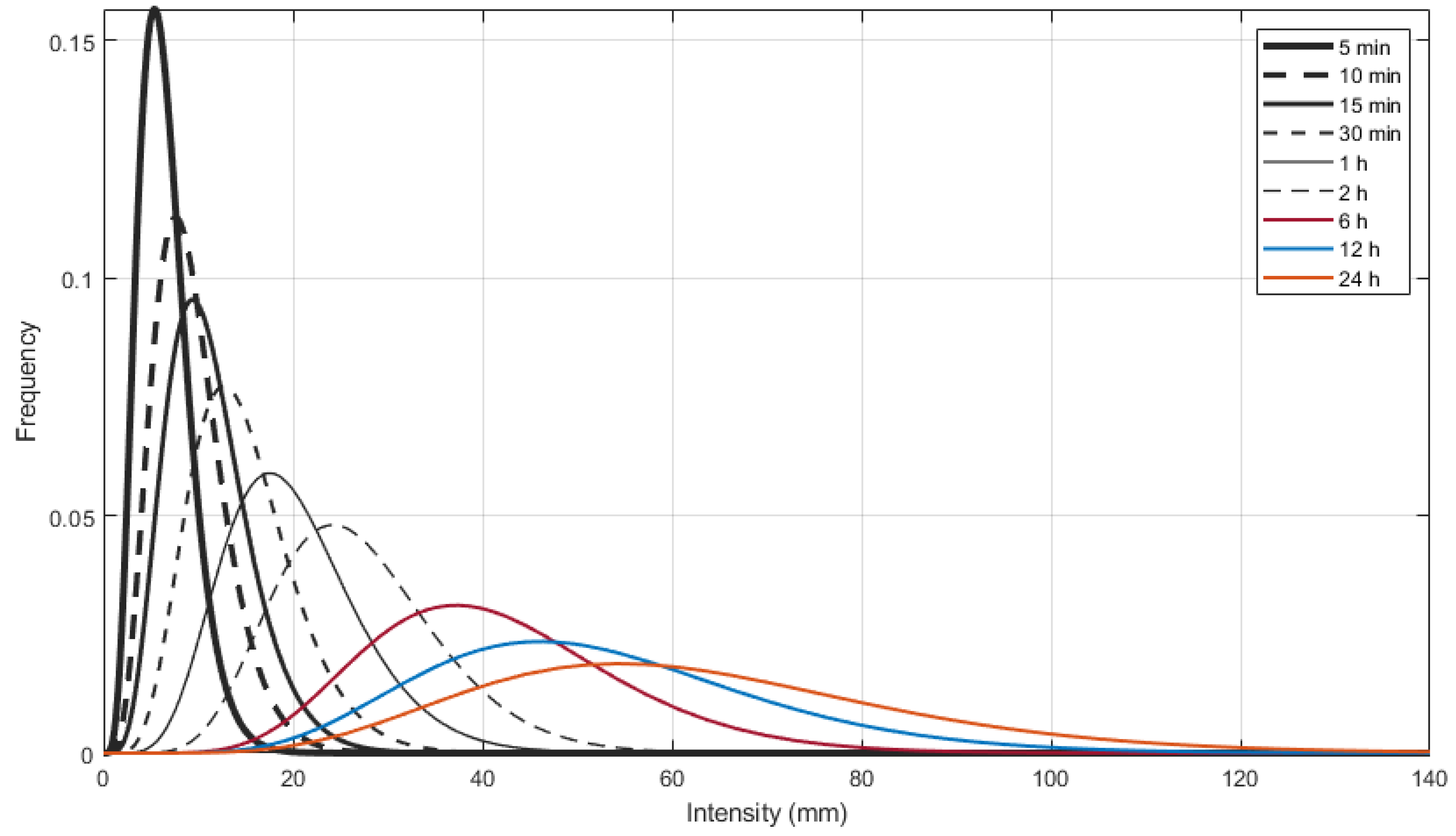
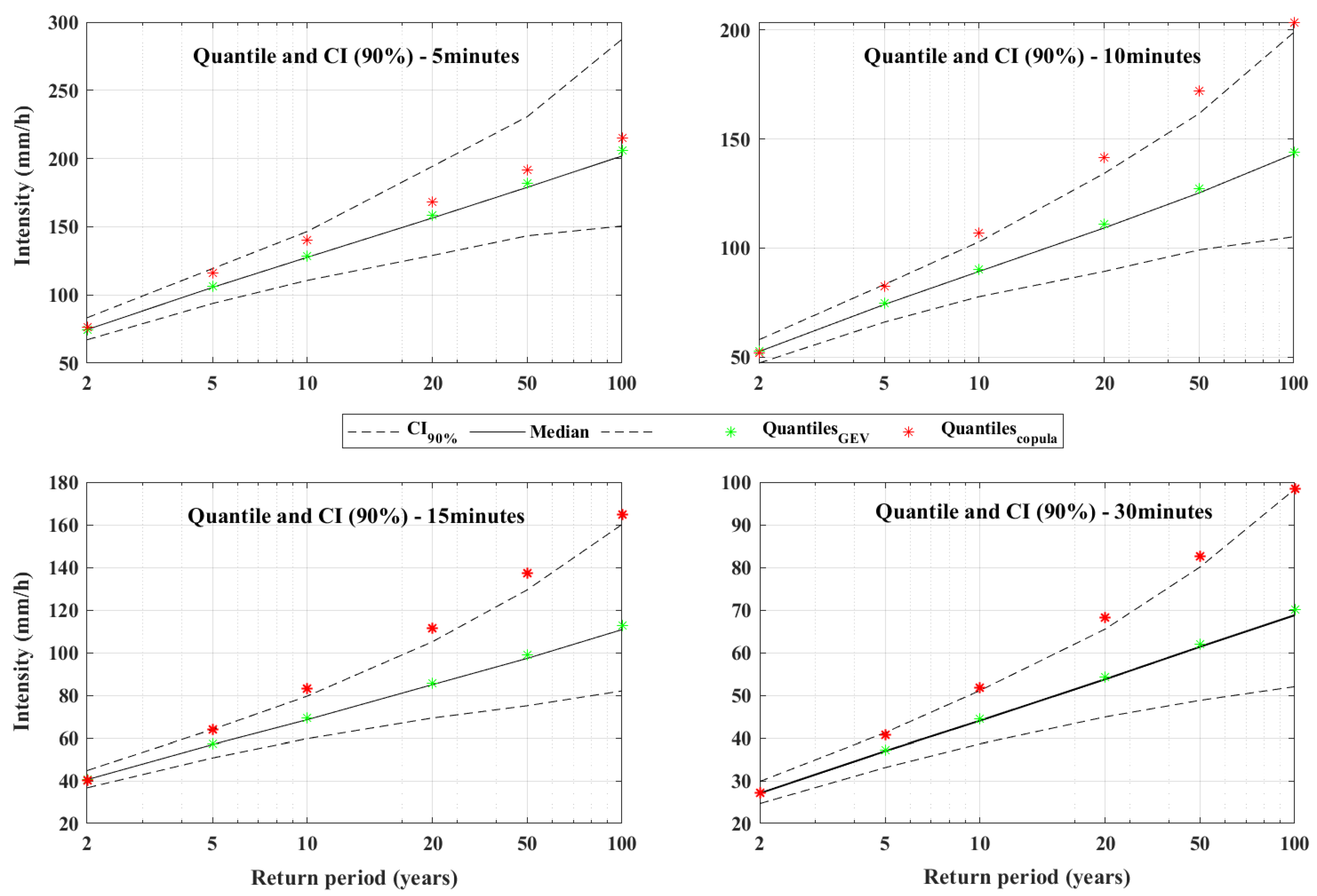
4.1. Quantile Estimation and Comparison
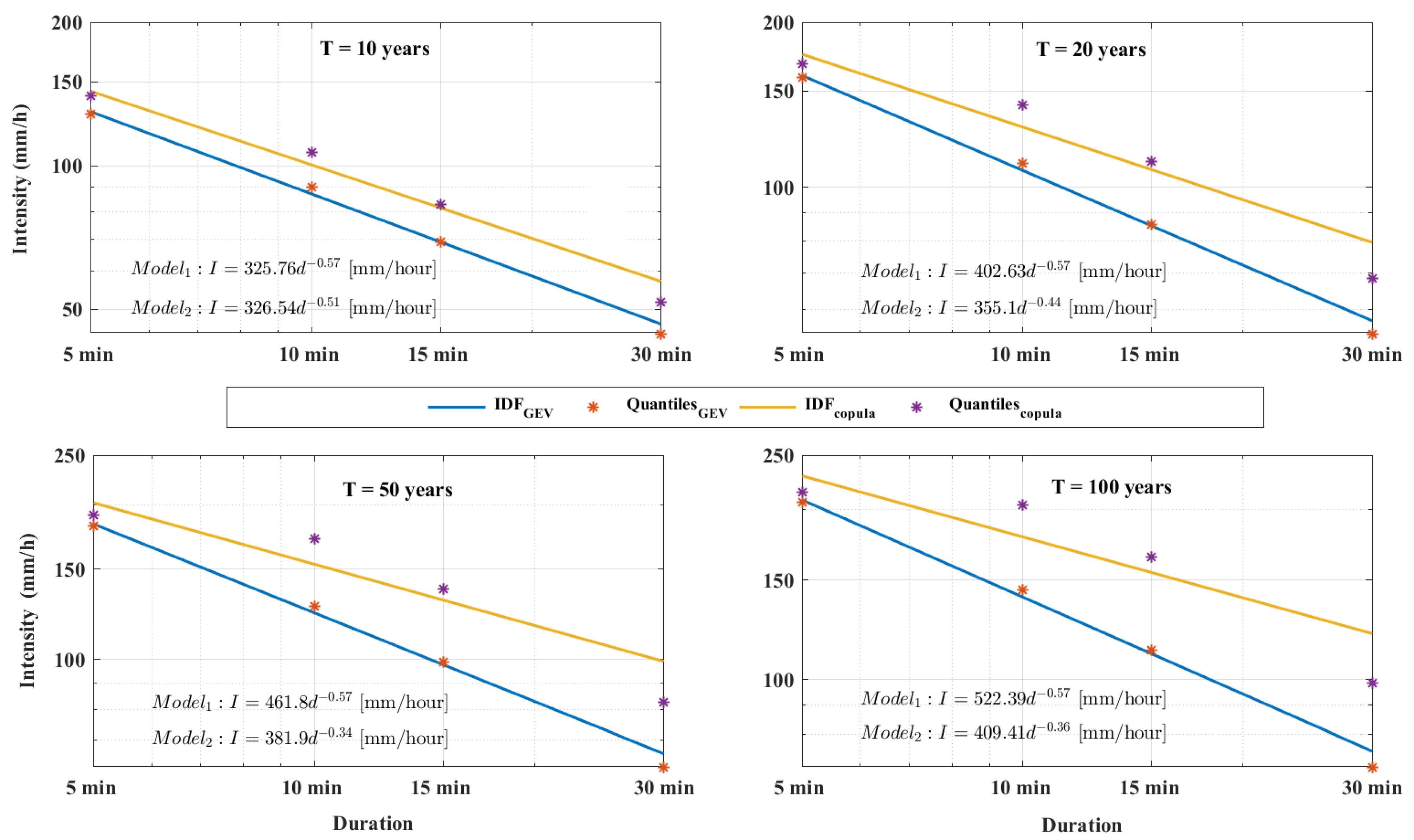
4.2. IDF Curve Estimation and Comparison
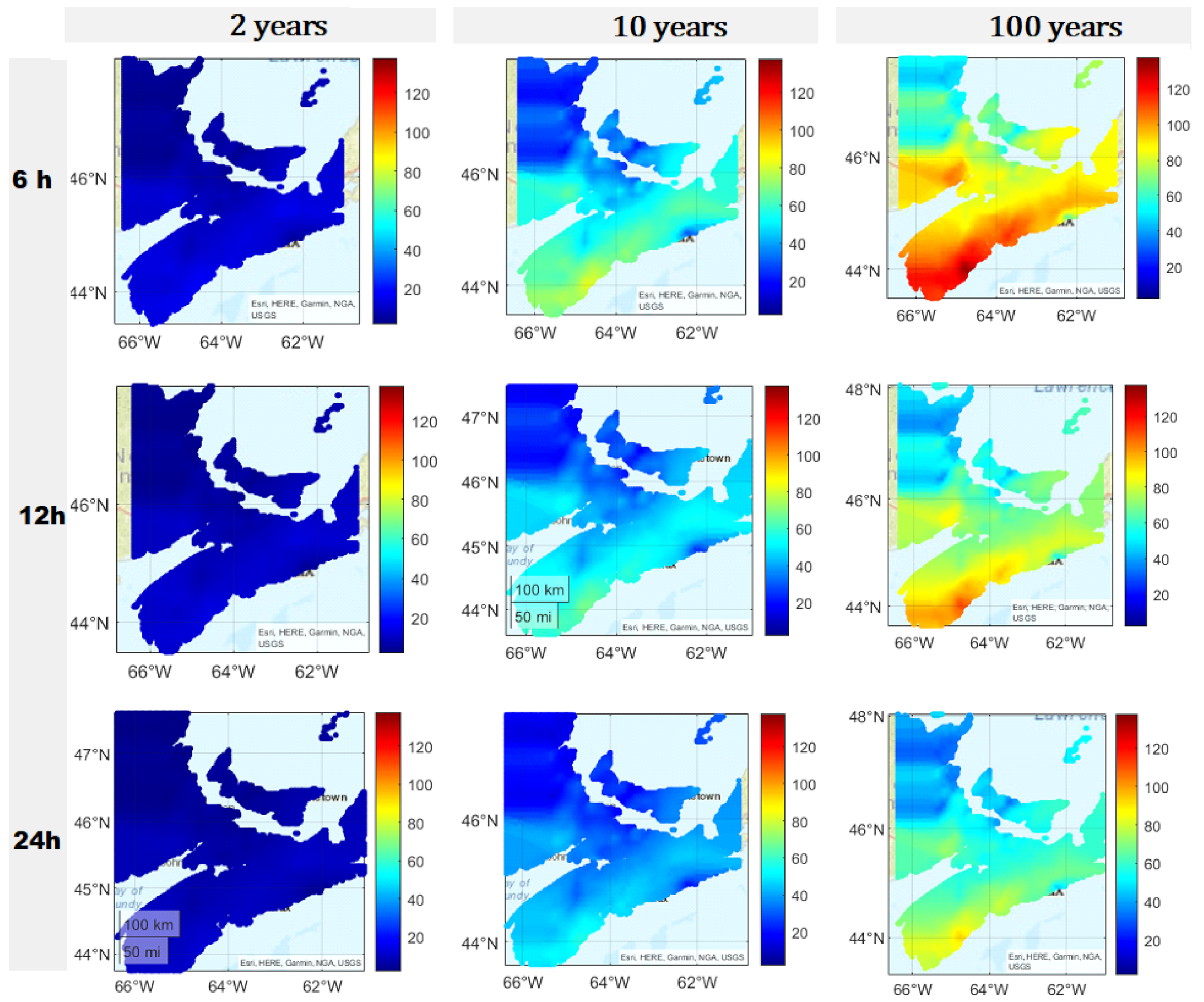
5. IDF Projections for Global Climate Models (GCMs)
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Miller, J.; Taylor, C.; Guichard, F.; Peyrillé, P.; Vischel, T.; Fowe, T.; Panthou, G.; Visman, E.; Bologo, M.; Traore, K.; et al. High-impact weather and urban flooding in the West African Sahel–A multidisciplinary case study of the 2009 event in Ouagadougou. Weather. Clim. Extrem. 2022, 36, 100462. [Google Scholar] [CrossRef]
- Kouassi, A.; Nassa, R.; Yao, K.; Kouame, K.; Biemi, J. Modélisation statistique des pluies maximales annuelles dans le District d’Abidjan (Sud de la Côte d’Ivoire). Rev. Des Sci. L’Eau/J. Water Sci. 2018, 31, 147–160. [Google Scholar] [CrossRef] [Green Version]
- Kingumbi, A.; Mailhot, A. Intensity-duration-frequency (IDF) curves: Comparison of annual maximum and partial duration estimators. Hydrol. Sci. J. 2010, 55, 162–176. [Google Scholar] [CrossRef]
- Gu, X.; Ye, L.; Xin, Q.; Zhang, C.; Zeng, F.; Nerantzaki, S.D.; Papalexiou, S.M. Extreme precipitation in China: A review. Adv. Water Resour. 2022, 163, 104144. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Kozonis, D.; Manetas, A. A mathematical framework for studying rainfall intensity-duration-frequency relationships. J. Hydrol. 1998, 206, 118–135. [Google Scholar] [CrossRef]
- Reder, A.; Raffa, M.; Padulano, R.; Rianna, G.; Mercogliano, P. Characterizing extreme values of precipitation at very high resolution: An experiment over twenty European cities. Weather. Clim. Extrem. 2022, 35, 100407. [Google Scholar] [CrossRef]
- Mohymont, B.; Demarée, G.; Faka, D. Establishment of IDF-curves for precipitation in the tropical area of Central Africa-comparison of techniques and results. Nat. Hazards Earth Syst. Sci. 2004, 4, 375–387. [Google Scholar] [CrossRef]
- Mohymont, B.; Demarée, G.R. Courbes intensité-durée-fréquence des précipitations à Yangambi, Congo, au moyen de différents modèles de type Montana. Hydrol. Sci. J. 2006, 51, 239–253. [Google Scholar] [CrossRef]
- Van de Vyver, H. Bayesian estimation of rainfall intensity–duration–frequency relationships. J. Hydrol. 2015, 529, 1451–1463. [Google Scholar] [CrossRef]
- Zahiri, E.P.; Bamba, I.; Famien, A.M.; Koffi, A.K.; Ochou, A.D. Mesoscale extreme rainfall events in West Africa: The cases of Niamey (Niger) and the Upper Ouémé Valley (Benin). Weather. Clim. Extrem. 2016, 13, 15–34. [Google Scholar] [CrossRef] [Green Version]
- Ouarda, T.B.; Yousef, L.A.; Charron, C. Non-stationary intensity-duration-frequency curves integrating information concerning teleconnections and climate change. Int. J. Climatol. 2019, 39, 2306–2323. [Google Scholar] [CrossRef] [Green Version]
- Moujahid, M.; Stour, L.; Agoumi, A.; Saidi, A. Regional approach for the analysis of annual maximum daily precipitation in northern Morocco. Weather. Clim. Extrem. 2018, 21, 43–51. [Google Scholar] [CrossRef]
- Muller, A.; Bacro, J.N.; Lang, M. Bayesian comparison of different rainfall depth–duration–frequency relationships. Stoch. Environ. Res. Risk Assess. 2008, 22, 33–46. [Google Scholar] [CrossRef] [Green Version]
- Gräler, B. Joint modeling of annual maximum precipitation across different duration levels. 2016. Available online: https://www.researchgate.net/publication/311230602_Joint_modeling_of_annual_maximum_precipitation_across_different_duration_levels (accessed on 17 June 2023).
- Mazo, G.; Girard, S.; Forbes, F. A flexible and tractable class of one-factor copulas. Stat. Comput. 2016, 26, 965–979. [Google Scholar] [CrossRef] [Green Version]
- Stephenson, A.G.; Lehmann, E.A.; Phatak, A. A max-stable process model for rainfall extremes at different accumulation durations. Weather. Clim. Extrem. 2016, 13, 44–53. [Google Scholar] [CrossRef] [Green Version]
- Gargouri-Ellouze, E.; Chebchoub, A. Modelling the dependence structure of rainfall depth and duration by Gumbel’s copula. Hydrol. Sci. J.-J. Sci. Hydrol. 2008, 53, 802–817. [Google Scholar] [CrossRef] [Green Version]
- Ariff, N.; Jemain, A.; Ibrahim, K.; Zin, W.W. IDF relationships using bivariate copula for storm events in Peninsular Malaysia. J. Hydrol. 2012, 470, 158–171. [Google Scholar] [CrossRef]
- Bezak, N.; Šraj, M.; Mikoš, M. Copula-based IDF curves and empirical rainfall thresholds for flash floods and rainfall-induced landslides. J. Hydrol. 2016, 541, 272–284. [Google Scholar] [CrossRef]
- Sklar, A. Fonctions de Répartition à n Dimensions et Leurs Marges; Publications of the Institute of Statistics of the University of Paris: Paris, France, 1959; Volume 8, pp. 229–231. [Google Scholar]
- Singh, V.P. Entropy Theory and Its Application in Environmental and Water Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Eschenburg, P. Properties of Extreme-Value Copulas. Ph.D. Thesis, Technische Universitat Munchen Fakultat fur Mathematik, Munchen, Germany, 2013. [Google Scholar]
- Hutchinson, T.P. Continuous Bivariate Distributions Emphasising Applications; Technical report; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar]
- Joe, H. Families of m-Variate Distributions with Given Margins and m (m-1)/2 Bivariate Dependence Parameters; Lecture Notes-Monograph Series; Institute of Mathematical Statistics: Beachwood, OH, USA, 1996; pp. 120–141. [Google Scholar]
- Nelsen, R.B. Properties and applications of copulas: A brief survey. In Proceedings of the First Brazilian Conference on Statistical Modeling in Insurance and Finance; Citeseer: Princeton, NJ, USA, 2003; pp. 10–28. [Google Scholar]
- Chebana, F. Multivariate Frequency Analysis of Hydro-Meteorological Variables: A Copula-Based Approach; Elsevier: Amsterdam, The Netherlands, 2022. [Google Scholar]
- Aas, K.; Czado, C.; Frigessi, A.; Bakken, H. Pair-copula constructions of multiple dependence. Insur. Math. Econ. 2009, 44, 182–198. [Google Scholar] [CrossRef] [Green Version]
- Cooke, R.M.; Joe, H.; Aas, K. Vines arise. In Dependence Modeling: Vine Copula Handbook; World Scientific: Singapore, 2010; pp. 37–71. [Google Scholar]
- Joe, H. Multivariate extreme-value distributions with applications to environmental data. Can. J. Stat. 1994, 22, 47–64. [Google Scholar] [CrossRef]
- Xiong, L.; Yu, K.x.; Gottschalk, L. Estimation of the distribution of annual runoff from climatic variables using copulas. Water Resour. Res. 2014, 50, 7134–7152. [Google Scholar] [CrossRef]
- El Adlouni, S. Quantile regression C-vine copula model for spatial extremes. Nat. Hazards 2018, 94, 299–317. [Google Scholar] [CrossRef]
- Aas, K.; Berg, D. Models for construction of multivariate dependence–a comparison study. Eur. J. Financ. 2009, 15, 639–659. [Google Scholar] [CrossRef]
- Adlouni, S.; Ouarda, T. Comparaison des méthodes d’estimation des paramètres du modèle GEV non stationnaire. Rev. Sci. L’Eau/J. Water Sci. 2008, 21, 35–50. [Google Scholar] [CrossRef] [Green Version]
- Bedford, T.; Cooke, R.M. Vines: A new graphical model for dependent random variables. Ann. Stat. 2002, 30, 1031–1068. [Google Scholar] [CrossRef]
- Shlef, K.E.; Kunkel, K.E.; Brown, C.; Demissie, Y.; Lettenmaier, D.P.; Wagner, A.; Wigmosta, M.S.; Karl, T.R.; Easterling, D.R.; Wang, K.J.; et al. Incorporating non-stationarity from climate change into rainfall frequency and intensity-duration-frequency (IDF) curves. Journal of Hydrology 2022, 616, 128757. [Google Scholar] [CrossRef]
- Campos, J.N.B.; de Studart, T.M.C.; de Assis de Souza Filho, F.; Porto, V.C. On the rainfall intensity–duration–frequency curves, partial-area effect and the rational method: Theory and the engineering practice. Water 2020, 12, 2730. [Google Scholar] [CrossRef]
- Grace, A. Optimization Toolbox. In The MathWorks; Cochituate Place, Inc.: Natick, MA, USA, 1994. [Google Scholar]
- Konapala, G.; Mishra, A.K.; Wada, Y.; Mann, M.E. Climate change will affect global water availability through compounding changes in seasonal precipitation and evaporation. Nat. Commun. 2020, 11, 3044. [Google Scholar] [CrossRef]
- Tabari, H.; Madani, K.; Willems, P. The contribution of anthropogenic influence to more anomalous extreme precipitation in Europe. Environ. Res. Lett. 2020, 15, 104077. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef] [Green Version]
- Silva, D.F.; Simonovic, S.P.; Schardong, A.; Goldenfum, J.A. Assessment of non-stationary IDF curves under a changing climate: Case study of different climatic zones in Canada. J. Hydrol. Reg. Stud. 2021, 36, 100870. [Google Scholar] [CrossRef]
- Martel, J.L.; Brissette, F.; Troin, M.; Arsenault, R.; Chen, J.; Su, T.; Lucas-Picher, P. CMIP5 and CMIP6 model projection comparison for hydrological impacts over North America. Geophys. Res. Lett. 2022, 49, e2022GL098364. [Google Scholar] [CrossRef]
- Kraus, D.; Czado, C. D-vine copula based quantile regression. Comput. Stat. Data Anal. 2017, 110, 1–18. [Google Scholar] [CrossRef] [Green Version]
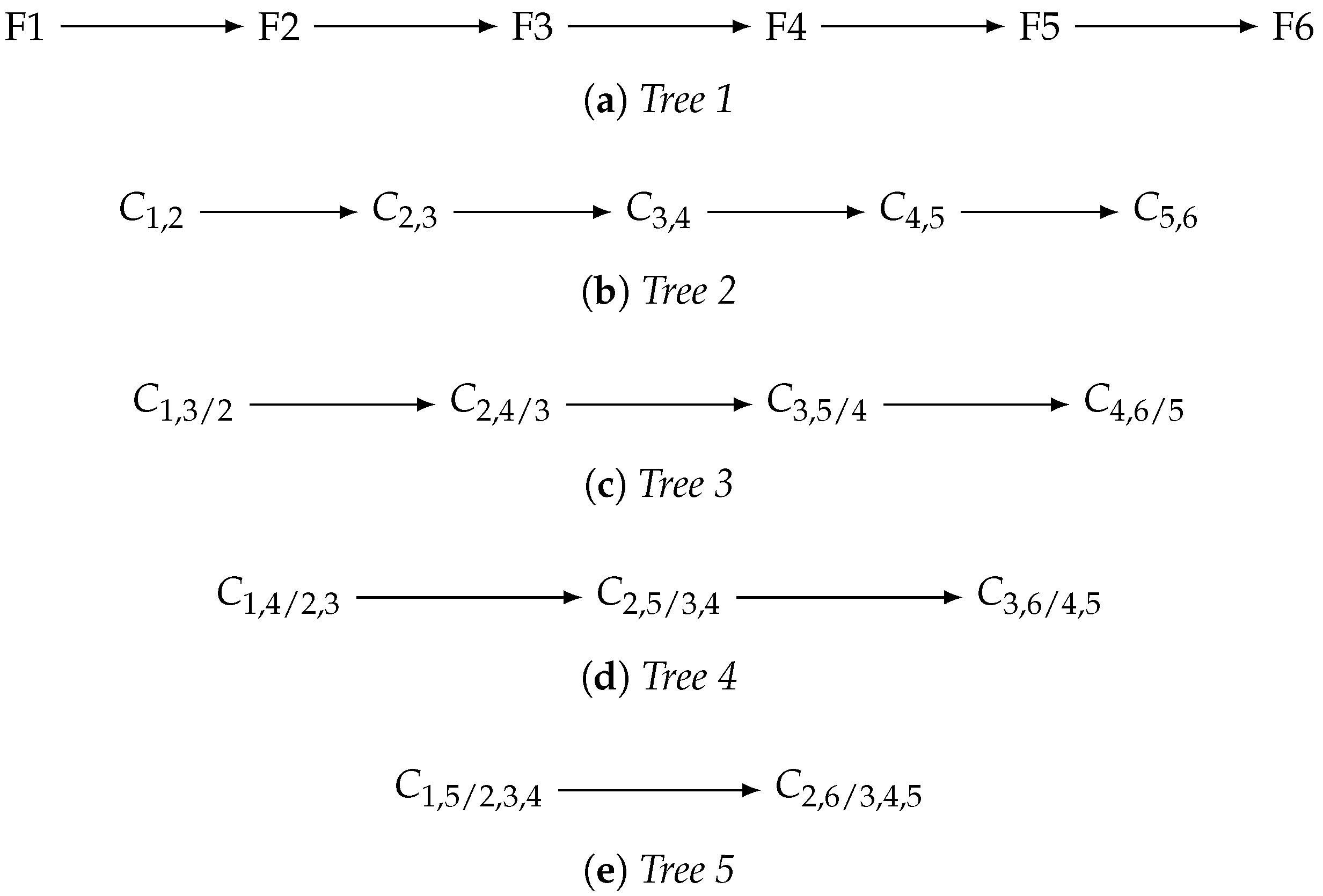
| Station | ID | Lat. | Long. | Alt (m) | Years | Start | End |
|---|---|---|---|---|---|---|---|
| Moncton Int A | NB- 103201 | 46 7 N | 64 41 W | 70 | 67 | 1946 | 2016 |
| Tree | Edge | ||||
|---|---|---|---|---|---|
| 1 | 2,1 | Sur BB8 (6, 0.57) | N (0.7) | N (0.76) | N (0.88) |
| 3,2 | Gumbel (2.57) | Gumbel (2.57) | Gumbel (2.57) | Gumbel (2.57) | |
| 4,3 | N (0.76) | N (0.76) | N (0.76) | N (0.76) | |
| 5,4 | N (0.90) | N (0.90) | N (0.90) | N (0.90) | |
| 6,5 | N (0.92) | N (0.92) | N (0.92) | N (0.92) | |
| 2 | 3,1;2 | I (0) | I (0) | I (0) | I (0) |
| 4,2;3 | r270 BB7 () | r270 BB7 () | r270 BB7 () | r270 BB7 () | |
| 5,3;4 | r90 Joe () | r90 Joe () | r90 Joe () | r90 Joe () | |
| 6,4;5 | Frank () | Frank () | Frank () | Frank () | |
| 3 | 4,1;3,2 | I (0) | I (0) | I (0) | I (0) |
| 5,2;4,3 | Frank (1.5) | Frank (1.5) | Frank (1.5) | Frank (1.5) | |
| 6,3;5,4 | I (0) | I (0) | I (0) | I (0) | |
| 4 | 5,1;4,3,2 | I (0) | I (0) | I (0) | I (0) |
| 6,2;5,4,3 | I (0) | I (0) | I (0) | I (0) | |
| 5 | 6,1;5,4,3,2 | Frank () | r90 Clayton () | r90 Clayton () | Frank () |
| Intensities over the Different Durations | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T (Years) | min | min | min | min | ||||||||
| 2 | 74.6 | 76.6 | 2.7 | 52.5 | 51.8 | 40.7 | 40.2 | 27.1 | 27.2 | 0.3 | ||
| 5 | 106.2 | 115.9 | 8.4 | 74.5 | 82.6 | 9.8 | 57.3 | 63.8 | 10.2 | 37.2 | 40.7 | 8.7 |
| 10 | 128.5 | 140.2 | 8.3 | 90.1 | 106.8 | 15.7 | 69.3 | 82.9 | 16.5 | 44.4 | 51.7 | 14.1 |
| 25 | 158.4 | 168.2 | 5.8 | 110.8 | 141.6 | 21.7 | 85.7 | 111.6 | 23.2 | 54.2 | 68.2 | 20.6 |
| 50 | 181.7 | 191.4 | 5.0 | 127.1 | 172.1 | 26.1 | 98.9 | 137.4 | 28.0 | 61.9 | 82.5 | 25.0 |
| 100 | 206.0 | 215.2 | 4.3 | 144.1 | 203.6 | 29.2 | 112.9 | 165.0 | 31.6 | 70.1 | 98.5 | 28.9 |
| Intensities over the Different Durations | |||||
|---|---|---|---|---|---|
| T (Years) | h | h | h | h | h |
| 2 | 18.0 | 12.2 | 6.6 | 4.1 | 2.4 |
| 5 | 24.4 | 16.2 | 8.6 | 5.4 | 3.3 |
| 10 | 29.6 | 19.5 | 9.9 | 6.4 | 3.9 |
| 25 | 37.6 | 24.5 | 11.6 | 7.6 | 4.7 |
| 50 | 44.7 | 29.1 | 12.8 | 8.5 | 5.3 |
| 100 | 52.9 | 34.4 | 14.0 | 9.4 | 5.9 |
| Duration | RCP2.6 | RCP4.5 | RCP8.5 | Observations | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 Years | 10 Years | 100 Years | 2 Years | 10 Years | 100 Years | 2 Years | 10 Years | 100 Years | 2 Years | 10 Years | 100 Years | |
| 5 min | 119 | 178.8 | 260 | 129.4 | 198.7 | 293.2 | 126.4 | 188.6 | 273.1 | 71.3 | 113.1 | 155.3 |
| 10 min | 72.2 | 108.6 | 157.8 | 78.6 | 120.6 | 178 | 76.7 | 114.5 | 165.8 | 50.2 | 79.2 | 108.4 |
| 15 min | 53.9 | 81.1 | 117.9 | 58.7 | 90.1 | 132.9 | 57.3 | 85.5 | 123.8 | 40.5 | 62.7 | 85.1 |
| 30 min | 32.8 | 49.2 | 71.6 | 35.6 | 54.7 | 80.7 | 34.8 | 51.9 | 75.2 | 27 | 40.7 | 54.5 |
| 1 h | 19.9 | 29.9 | 43.4 | 21.6 | 33.2 | 49 | 21.1 | 31.5 | 45.6 | 17.9 | 25.5 | 33.2 |
| 2 h | 12.1 | 18.1 | 26.4 | 13.1 | 20.2 | 29.7 | 12.8 | 19.1 | 27.7 | 12.1 | 16.8 | 21.5 |
| 6 h | 5.5 | 8.2 | 12 | 6 | 9.1 | 13.5 | 5.8 | 8.7 | 12.6 | 6.5 | 9.6 | 12.7 |
| 12 h | 3.3 | 5 | 7.3 | 3.6 | 5.5 | 8.2 | 3.5 | 5.3 | 7.6 | 4.1 | 6 | 8 |
| 24 h | 2 | 3 | 4.4 | 2.2 | 3.4 | 5 | 2.1 | 3.2 | 4.6 | 2.4 | 3.6 | 4.8 |
| Duration | RCP2.6 | RCP4.5 | RCP8.5 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 2 Years | 10 Years | 100 Years | 2 Years | 10 Years | 100 Years | 2 Years | 10 Years | 100 Years | |
| 5 min | 67 | 58 | 67 | 82 | 76 | 89 | 77 | 67 | 76 |
| 10 min | 44 | 37 | 46 | 56 | 52 | 64 | 53 | 45 | 53 |
| 15 min | 33 | 29 | 39 | 45 | 44 | 56 | 41 | 36 | 46 |
| 30 min | 21 | 21 | 31 | 32 | 34 | 48 | 29 | 28 | 38 |
| 1 h | 11 | 17 | 31 | 21 | 30 | 48 | 18 | 24 | 38 |
| 2 h | 0 | 8 | 23 | 8 | 20 | 38 | 6 | 14 | 29 |
| 6 h | −16 | −14 | −6 | −9 | −5 | 6 | −11 | −10 | −1 |
| 12 h | −18 | −17 | −10 | −11 | −8 | 2 | −13 | −13 | −5 |
| 24 h | −16 | −16 | −9 | −9 | −7 | 3 | −11 | −11 | −4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Hannoun, W.; Boukili Makhoukhi, A.; Zoglat, A.; El Adlouni, S.-E. Intensity–Duration–Frequency Curves for Dependent Datasets. Water 2023, 15, 2641. https://doi.org/10.3390/w15142641
El Hannoun W, Boukili Makhoukhi A, Zoglat A, El Adlouni S-E. Intensity–Duration–Frequency Curves for Dependent Datasets. Water. 2023; 15(14):2641. https://doi.org/10.3390/w15142641
Chicago/Turabian StyleEl Hannoun, Wafaa, Anas Boukili Makhoukhi, Abdelhak Zoglat, and Salah-Eddine El Adlouni. 2023. "Intensity–Duration–Frequency Curves for Dependent Datasets" Water 15, no. 14: 2641. https://doi.org/10.3390/w15142641





