Deep-Learning-Enhanced CT Image Analysis for Predicting Hydraulic Conductivity of Coarse-Grained Soils
Abstract
:1. Introduction
2. Materials and Methods
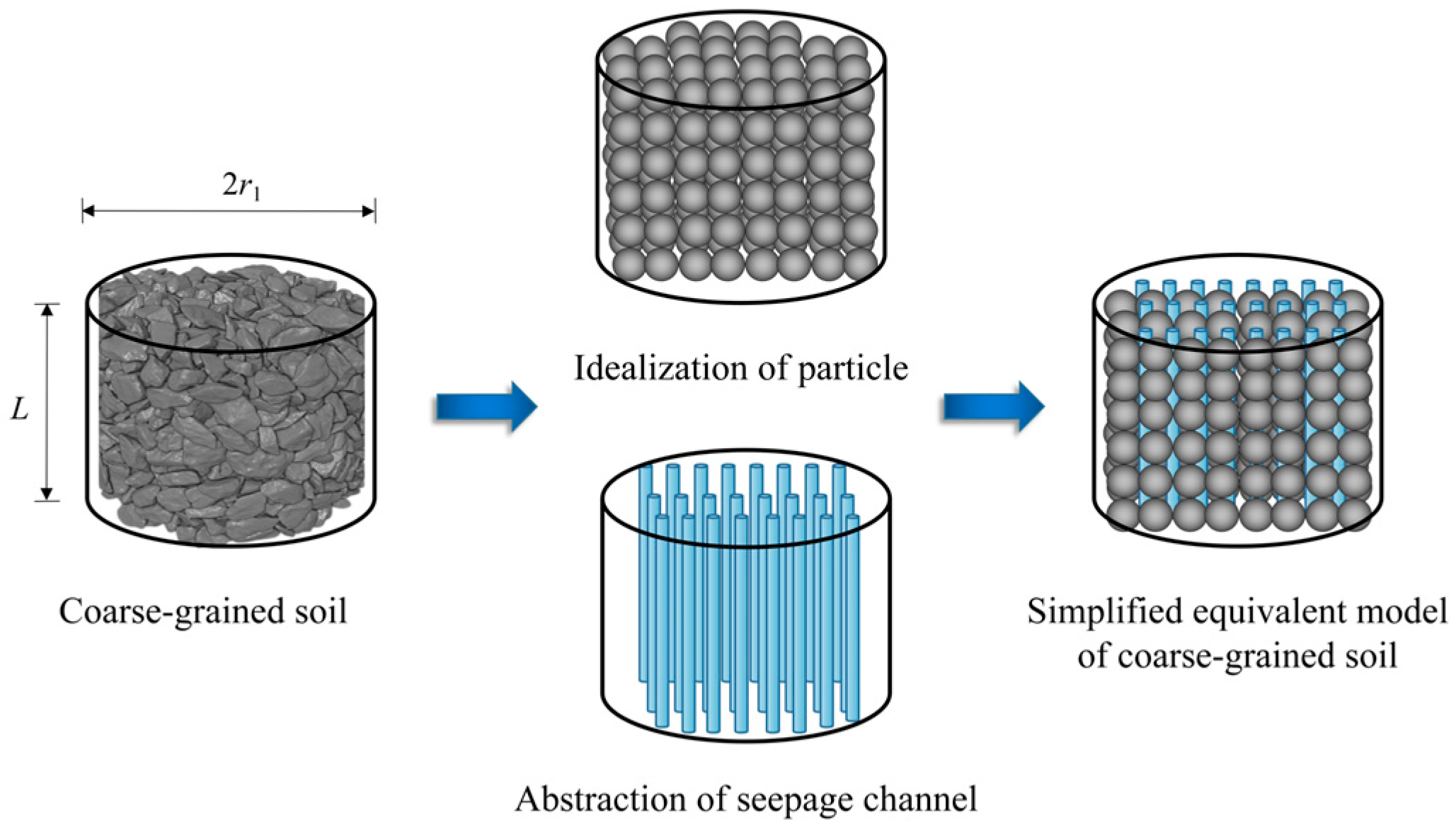
2.1. Hydraulic Conductivity Calculation Model for Coarse-Grained Soil Based on Equivalent Simplified Model and Poiseuille’s Law
2.2. Materials
2.3. Laboratory Test
- A settlement measurement device was installed at the top of the coarse-grained soil specimens to prevent seepage deformation during the test.
- Aerated water was used to negate the impact of air bubbles on the percolation volume.
- Before the test, the specimen was saturated with bottom-up exhaust under a lower head and soaked for over 8 h to eliminate the influence of non-saturation on the permeability test results.
- The test head from the starting hydraulic slope dropped from 0.05 to 0.30, loaded step by step, with each head level loaded for 20 min before measuring the overflow in the permeameter and recording it.
- The next level of head was loaded only when the overflow in the unit time remained unchanged. This process continued until the test concluded.
2.4. Coarse-Grained Soil CT Image Segmentation Method Based on Convolutional Neural Network
2.4.1. U-Net Structured Convolutional Neural Network
2.4.2. Loss Function
2.4.3. Workflow of Convolutional Neural Network Segmentation Model
2.5. Geometric Characterization of Coarse Soil Particles via CT Image Analysis
2.6. Data Analysis
3. Results
3.1. Accuracy Verification of CT Image-Segmentation Program Based on Convolutional Neural Network
3.1.1. Verification of CT Image-Segmentation Accuracy Based on Convolutional Neural Networks
3.1.2. Comparison of Segmentation Results between CNN Model and Traditional Methods for CT Images of Coarse-Grained Soil
3.2. Equivalent Simplified Model of Ideal Particle Diameter in Coarse-Grained Soil
3.2.1. Three-Dimensional Model Reconstruction of Coarse-Grained Soil Based on CT Image Segmentation Results
3.2.2. Empirical Formula for the Ideal Particle Size of Coarse Soil Particles
3.3. Prediction Formula for Permeability Coefficient of Coarse-Grained Soil Based on CT Image Analysis
3.3.1. Constant-Head Permeability Test Results
3.3.2. Empirical Formula for Discount Factor
3.3.3. Prediction Formula and Accuracy Verification of Hydraulic Conductivity of Coarse-Grained Soil
4. Discussion
5. Conclusions
- The implementation of the CNN model demonstrates unparalleled precision in the segmentation of coarse-grained soil CT images, ascertaining the model’s superiority over traditional segmentation methods. The accuracy of the 3D models reconstructed from these segmented images corroborates the effectiveness of this approach and broadens the prospects of automation and precision in soil particle segmentation.
- We established and validated empirical formulae for the ideal particle size of coarse-grained soil and the discount factor, both predicated on a robust linear correlation found in the study. These novel formulae contribute significantly to understanding the granulometric characteristics of soils and predicting their behavior under various hydraulic gradients, thus providing valuable insights for soil-related engineering and hydraulic applications.
- Our research underlines the strong influence of the granular composition, especially the concentration of fine particles, on the tortuosity of water flow paths and the discount factor. These findings highlight the potential of the CNN model in soil hydrodynamics research and its implications for a variety of fields, including water conservancy and geotechnical engineering.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nam, S.; Gutierrez, M.; Diplas, P.; Petrie, J. Laboratory and in Situ Determination of Hydraulic Conductivity and Their Validity in Transient Seepage Analysis. Water 2021, 13, 1131. [Google Scholar] [CrossRef]
- Shaker, A.A.; Dafalla, M.; Al-Mahbashi, A.M.; Al-Shamrani, M.A. Predicting Hydraulic Conductivity for Flexible Wall Conditions Using Rigid Wall Permeameter. Water 2022, 14, 286. [Google Scholar] [CrossRef]
- Yoon, S.; Lee, S.R.; Kim, Y.T.; Go, G.H. Estimation of Saturated Hydraulic Conductivity of Korean Weathered Granite Soils Using a Regression Analysis. Geomech. Eng. 2015, 9, 101–113. [Google Scholar] [CrossRef]
- Edeh, I.G.; Mašek, O. The Role of Biochar Particle Size and Hydrophobicity in Improving Soil Hydraulic Properties. Eur. J. Soil Sci. 2022, 73, e13138. [Google Scholar] [CrossRef]
- Liu, Z.R.; Cui, Y.J.; Ye, W.M.; Chen, B.; Wang, Q.; Chen, Y.G. Investigation of the Hydro-Mechanical Behaviour of GMZ Bentonite Pellet Mixtures. Acta Geotech. 2020, 15, 2865–2875. [Google Scholar] [CrossRef]
- Mijic, Z.; Dayioglu, A.Y.; Hatipoglu, M.; Aydilek, A.H. Hydraulic and Environmental Impacts of Using Recycled Asphalt Pavement on Highway Shoulders. Constr. Build. Mater. 2020, 234, 117226. [Google Scholar] [CrossRef]
- Hatipoglu, M.; Cetin, B.; Aydilek, A.H. Effects of Fines Content on Hydraulic and Mechanical Performance of Unbound Granular Base Aggregates. J. Transp. Eng. Part B Pavements 2020, 146, 04019036. [Google Scholar] [CrossRef]
- Wang, J.P.; Zhuang, P.Z.; Luan, J.Y.; Liu, T.H.; Tan, Y.R.; Zhang, J. Estimation of Unsaturated Hydraulic Conductivity of Granular Soils from Particle Size Parameters. Water 2019, 11, 1826. [Google Scholar] [CrossRef] [Green Version]
- Wang, T.; Yan, C.; Zheng, Y.; Jiao, Y.-Y.; Zou, J. Numerical Study on the Effect of Meso-Structure on Hydraulic Conductivity of Soil-Rock Mixtures. Comput. Geotech. 2022, 146, 104726. [Google Scholar] [CrossRef]
- Huang, L.; He, R.; Yang, Z.; Tan, P.; Chen, W.; Li, X.; Cao, A. Exploring Hydraulic Fracture Behavior in Glutenite Formation with Strong Heterogeneity and Variable Lithology Based on DEM Simulation. Eng. Fract. Mech. 2023, 278, 109020. [Google Scholar] [CrossRef]
- Tseng, C.-Y.; Ghadiri, M.; Kumar, P.; Meidani, H. Estimation of Hydraulic Conductivity in a Watershed Using Sparse Multi-Source Data via Gaussian Process Regression and Bayesian Experimental Design. Adv. Water Resour. 2023, 178, 104489. [Google Scholar] [CrossRef]
- Luo, M.; Ye, C.; Wang, X.; Huang, E.; Yan, X. Analytical Model of Flow Velocity in Gravel-Bed Streams under the Effect of Gravel Array with Different Densities. J. Hydrol. 2022, 608, 127581. [Google Scholar] [CrossRef]
- An, R.; Wang, Y.; Zhang, X.; Chen, C.; Liu, X.; Cai, S. Quantitative Characterization of Drying-Induced Cracks and Permeability of Granite Residual Soil Using Micron-Sized X-Ray Computed Tomography. Sci. Total Environ. 2023, 876, 163213. [Google Scholar] [CrossRef] [PubMed]
- Lin, S.; Zheng, H.; Zhang, Z.; Li, W. Evaluation of Permeability of Soil & Rock Aggregate Using Meshless Numerical Manifold Method. Comput. Geotech. 2022, 151, 104953. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, L.; Su, X.; Zhao, L.; Wang, Y. Micro-CT Characterization on Pore Structure Evolution of Low-Permeability Sandstone under Acid Treatment. Appl. Geochem. 2023, 152, 105633. [Google Scholar] [CrossRef]
- Ferreira, T.R.; Archilha, N.L.; Cássaro, F.A.M.; Pires, L.F. How Can Pore Characteristics of Soil Aggregates from Contrasting Tillage Systems Affect Their Intrinsic Permeability and Hydraulic Conductivity? Soil Tillage Res. 2023, 230, 105704. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, J. Prediction of the Soil Saturated Hydraulic Conductivity in a Mining Area Based on CT Scanning Technology. J. Clean. Prod. 2023, 383, 135364. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, C.; Li, C.; Cheng, J.; Zhang, Y.; Xu, H.; Song, T.; Zhao, L.; Chen, X. A Practical PET/CT Data Visualization Method with Dual-Threshold PET Colorization and Image Fusion. Comput. Biol. Med. 2020, 126, 104050. [Google Scholar] [CrossRef]
- Zhang, J.; Yan, C.-H.; Chui, C.-K.; Ong, S.-H. Fast Segmentation of Bone in CT Images Using 3D Adaptive Thresholding. Comput. Biol. Med. 2010, 40, 231–236. [Google Scholar] [CrossRef]
- Mat Jais, I.S.; Liu, X.; An, K.-N.; Tay, S.C. A Method for Carpal Motion Hysteresis Quantification in 4-Dimensional Imaging of the Wrist. Med. Eng. Phys. 2014, 36, 1699–1703. [Google Scholar] [CrossRef]
- Peter, Z.; Bousson, V.; Bergot, C.; Peyrin, F. A Constrained Region Growing Approach Based on Watershed for the Segmentation of Low Contrast Structures in Bone Micro-CT Images. Pattern Recognit. 2008, 41, 2358–2368. [Google Scholar] [CrossRef]
- Cristoforetti, A.; Faes, L.; Ravelli, F.; Centonze, M.; Del Greco, M.; Antolini, R.; Nollo, G. Isolation of the Left Atrial Surface from Cardiac Multi-Detector CT Images Based on Marker Controlled Watershed Segmentation. Med. Eng. Phys. 2008, 30, 48–58. [Google Scholar] [CrossRef]
- Minnema, J.; Wolff, J.; Koivisto, J.; Lucka, F.; Batenburg, K.J.; Forouzanfar, T.; van Eijnatten, M. Comparison of Convolutional Neural Network Training Strategies for Cone-Beam CT Image Segmentation. Comput. Methods Programs Biomed. 2021, 207, 106192. [Google Scholar] [CrossRef]
- Roslin, A.; Marsh, M.; Provencher, B.; Mitchell, T.R.; Onederra, I.A.; Leonardi, C.R. Processing of Micro-CT Images of Granodiorite Rock Samples Using Convolutional Neural Networks (CNN), Part II: Semantic Segmentation Using a 2.5D CNN. Miner. Eng. 2023, 195, 108027. [Google Scholar] [CrossRef]
- Dong, Y.; Su, C.; Qiao, P.; Sun, L. Microstructural Crack Segmentation of Three-Dimensional Concrete Images Based on Deep Convolutional Neural Networks. Constr. Build. Mater. 2020, 253, 119185. [Google Scholar] [CrossRef]
- Nguyen, T.; Truong, T.T.; Nguyen-Thoi, T.; Van Hong Bui, L.; Nguyen, T.-H. Evaluation of Residual Flexural Strength of Corroded Reinforced Concrete Beams Using Convolutional Long Short-Term Memory Neural Networks. Structures 2022, 46, 899–912. [Google Scholar] [CrossRef]
- Mirbod, M.; Shoar, M. Intelligent Concrete Surface Cracks Detection Using Computer Vision, Pattern Recognition, and Artificial Neural Networks. Procedia Comput. Sci. 2023, 217, 52–61. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, J.; Zhao, T.; Wang, Z.; Wang, Z. Reconstruction of the Meso-Scale Concrete Model Using a Deep Convolutional Generative Adversarial Network (DCGAN). Constr. Build. Mater. 2023, 370, 130704. [Google Scholar] [CrossRef]
- Tian, W.; Cheng, X.; Liu, Q.; Yu, C.; Gao, F.; Chi, Y. Meso-Structure Segmentation of Concrete CT Image Based on Mask and Regional Convolution Neural Network. Mater. Des. 2021, 208, 109919. [Google Scholar] [CrossRef]
- Zhang, W.; Shi, D.; Shen, Z.; Zhang, J.; Zhao, S.; Gan, L.; Li, Q.; Chen, Y.; Tang, P. Influence of Chopped Basalt Fibers on the Fracture Performance of Concrete Subjected to Calcium Leaching. Theor. Appl. Fract. Mech. 2023, 125, 103934. [Google Scholar] [CrossRef]
- Zhang, W.; Shi, D.; Shen, Z.; Wang, X.; Gan, L.; Shao, W.; Tang, P.; Zhang, H.; Yu, S. Effect of Calcium Leaching on the Fracture Properties of Concrete. Constr. Build. Mater. 2023, 365, 130018. [Google Scholar] [CrossRef]
- Zhang, W.; Shi, D.; Shen, Z.; Shao, W.; Gan, L.; Yuan, Y.; Tang, P.; Zhao, S.; Chen, Y. Reduction of the Calcium Leaching Effect on the Physical and Mechanical Properties of Concrete by Adding Chopped Basalt Fibers. Constr. Build. Mater. 2023, 365, 130080. [Google Scholar] [CrossRef]
- Roslin, A.; Marsh, M.; Piché, N.; Provencher, B.; Mitchell, T.R.; Onederra, I.A.; Leonardi, C.R. Processing of Micro-CT Images of Granodiorite Rock Samples Using Convolutional Neural Networks (CNN), Part I: Super-Resolution Enhancement Using a 3D CNN. Miner. Eng. 2022, 188, 107748. [Google Scholar] [CrossRef]
- Dawson, H.L.; Dubrule, O.; John, C.M. Impact of Dataset Size and Convolutional Neural Network Architecture on Transfer Learning for Carbonate Rock Classification. Comput. Geosci. 2023, 171, 105284. [Google Scholar] [CrossRef]
- Roslin, A.; Lebedev, M.; Mitchell, T.R.; Onederra, I.A.; Leonardi, C.R. Processing of Micro-CT Images of Granodiorite Rock Samples Using Convolutional Neural Networks (CNN). Part III: Enhancement of Scanco Micro-CT Images of Granodiorite Rocks Using a 3D Convolutional Neural Network Super-Resolution Algorithm. Miner. Eng. 2023, 195, 108028. [Google Scholar] [CrossRef]
- Karimpouli, S.; Faraji, A.; Balcewicz, M.; Saenger, E.H. Computing Heterogeneous Core Sample Velocity Using Digital Rock Physics: A Multiscale Approach. Comput. Geosci. 2020, 135, 104378. [Google Scholar] [CrossRef]
- Wang, Y.D.; Shabaninejad, M.; Armstrong, R.T.; Mostaghimi, P. Deep Neural Networks for Improving Physical Accuracy of 2D and 3D Multi-Mineral Segmentation of Rock Micro-CT Images. Appl. Soft Comput. 2021, 104, 107185. [Google Scholar] [CrossRef]
- Dobry, R. Simplified Methods in Soil Dynamics. Soil Dyn. Earthq. Eng. 2014, 61–62, 246–268. [Google Scholar] [CrossRef]
- Sutera, S.P.; Skalak, R. The History of Poiseuille’s Law. Annu. Rev. Fluid Mech. 1993, 25, 1–20. [Google Scholar] [CrossRef]
- Whitaker, S. Flow in Porous Media I: A Theoretical Derivation of Darcy’s Law. Transp. Porous Media 1986, 1, 3–25. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, Munich, Germany, 5–9 October 2015; Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Ho, Y.; Wookey, S. The Real-World-Weight Cross-Entropy Loss Function: Modeling the Costs of Mislabeling. IEEE Access 2020, 8, 4806–4813. [Google Scholar] [CrossRef]
- Petrou, M.M.P.; Petrou, C. Image Processing: The Fundamentals; John Wiley & Sons: New York, NY, USA, 2010. [Google Scholar]
- Björck, Å. Least Squares Methods. In Handbook of Numerical Analysis; Elsevier: Amsterdam, The Netherlands, 1990; Volume 1, pp. 465–652. ISBN 1570-8659. [Google Scholar]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson Correlation Coefficient. In Noise Reduction in Speech Processing; Cohen, I., Huang, Y., Chen, J., Benesty, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. ISBN 978-3-642-00296-0. [Google Scholar]
- Chan, F.H.Y.; Lam, F.K.; Zhu, H. Adaptive Thresholding by Variational Method. IEEE Trans. Image Process. 1998, 7, 468–473. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gostick, J.T. Versatile and Efficient Pore Network Extraction Method Using Marker-Based Watershed Segmentation. Phys. Rev. E 2017, 96, 23307. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kozeny, J. Unber Kapillare Leitung Des Wassers Im Boden. Sitz. Akad. Wiss WIEN 1927, 136, 271–306. [Google Scholar]
- Xu, P.; Yu, B. Developing a New Form of Permeability and Kozeny–Carman Constant for Homogeneous Porous Media by Means of Fractal Geometry. Adv. Water Resour. 2008, 31, 74–81. [Google Scholar] [CrossRef]
- Henderson, N.; Brêttas, J.C.; Sacco, W.F. A Three-Parameter Kozeny–Carman Generalized Equation for Fractal Porous Media. Chem. Eng. Sci. 2010, 65, 4432–4442. [Google Scholar] [CrossRef]
- Javad Azarhoosh, M.; Koohmishi, M. Prediction of Hydraulic Conductivity of Porous Granular Media by Establishment of Random Forest Algorithm. Constr. Build Mater. 2023, 366, 130065. [Google Scholar] [CrossRef]
- Terzaghi, K.; Peck, R.B.; Mesri, G. Soil Mechanics in Engineering Practice. Available online: https://www.wiley.com/en-us/Soil+Mechanics+in+Engineering+Practice%2C+3rd+Edition-p-9780471086581 (accessed on 8 June 2022).
- Carman, P.C. Permeability of Saturated Sands, Soils and Clays. J. Agric. Sci. 1939, 29, 262–273. [Google Scholar] [CrossRef]
- Hazen, A. Discussion of Dams on Sand Foundation by A.C. Transp. ASAE 1911, 73, 199–203. [Google Scholar]
- Safari, M.; Gholami, R.; Jami, M.; Ananthan, M.A.; Rahimi, A.; Khur, W.S. Developing a Porosity-Permeability Relationship for Ellipsoidal Grains: A Correction Shape Factor for Kozeny-Carman’s Equation. J. Pet. Sci. Eng. 2021, 205, 108896. [Google Scholar] [CrossRef]
- Chapuis, R.P.; Aubertin, M. On the Use of the Kozeny-Carman Equation to Predict the Hydraulic Conductivity of Soils. Can. Geotech. J. 2003, 40, 616–628. [Google Scholar] [CrossRef]
- Côté, J.; Fillion, M.-H.; Konrad, J.-M. Estimating Hydraulic and Thermal Conductivities of Crushed Granite Using Porosity and Equivalent Particle Size. J. Geotech. Geoenvironmental Eng. 2011, 137, 834–842. [Google Scholar] [CrossRef]
- Belkhatir, M.; Schanz, T.; Arab, A. Effect of Fines Content and Void Ratio on the Saturated Hydraulic Conductivity and Undrained Shear Strength of Sand-Silt Mixtures. Environ. Earth Sci. 2013, 70, 2469–2479. [Google Scholar] [CrossRef]
- Su, L.J.; Zhang, Y.J.; Wang, T.X. Investigation on Permeability of Sands with Different Particle Sizes. Available online: https://www.researchgate.net/publication/288721987_Investigation_on_permeability_of_sands_with_different_particle_sizes (accessed on 8 June 2022).
- Xu, S.; Zhu, Y.; Cai, Y.; Sun, H.; Cao, H.; Shi, J. Predicting the Permeability Coefficient of Polydispersed Sand via Coupled CFD–DEM Simulations. Comput. Geotech. 2022, 144, 104634. [Google Scholar] [CrossRef]
- Liu, Y.F.; Jeng, D.S. Pore Scale Study of the Influence of Particle Geometry on Soil Permeability. Adv. Water Resour. 2019, 129, 232–249. [Google Scholar] [CrossRef]
- Garcia, X.; Akanji, L.T.; Blunt, M.J.; Matthai, S.K.; Latham, J.P. Numerical Study of the Effects of Particle Shape and Polydispersity on Permeability. Phys. Rev. E Stat. Nonlin. Soft Matter. Phys. 2009, 80, 021304. [Google Scholar] [CrossRef] [Green Version]
- Regassa, B.; Xu, N.; Mei, G. An Equivalent Discontinuous Modeling Method of Jointed Rock Masses for DEM Simulation of Mining-Induced Rock Movements. Int. J. Rock Mech. Min. Sci. 2018, 108, 1–14. [Google Scholar] [CrossRef]
- Dai, H.; Wang, Z.; Zhao, J.; Jia, X.; Liu, L.; Wang, J.; Abbasi, H.N.; Guo, Z.; Chen, Y.; Geng, H.; et al. Modeling and Optimizing of an Actual Municipal Sewage Plant: A Comparison of Diverse Multi-Objective Optimization Methods. J. Environ. Manag. 2023, 328, 116924. [Google Scholar] [CrossRef]
- Dai, H.; Zhao, J.; Wang, Z.; Chen, C.; Liu, X.; Guo, Z.; Chen, Y.; Zhang, S.; Li, J.; Geng, H.; et al. Optimal Control of Sewage Treatment Process Using a Dynamic Multi-Objective Particle Swarm Optimization Based on Crowding Distance. J. Environ. Chem. Eng. 2023, 11, 109484. [Google Scholar] [CrossRef]
- Zhao, J.; Dai, H.; Wang, Z.; Chen, C.; Cai, X.; Song, M.; Guo, Z.; Zhang, S.; Wang, X.; Geng, H. Self-Organizing Modeling and Control of Activated Sludge Process Based on Fuzzy Neural Network. J. Water Process. Eng. 2023, 53, 103641. [Google Scholar] [CrossRef]













| Sample ID | S1 | S2 | S3 | S4 | S5 | S6 |
|---|---|---|---|---|---|---|
| Porosity | 40% | 30% | 40% | 40% | 38% | 35% |
| Sample ID | S7 | S8 | S9 | S10 | S11 | S12 |
| Porosity | 38% | 35% | 35% | 32% | 30% | 35% |
| Sample ID | S1 | S2 | S3 | S4 | S5 | S6 |
|---|---|---|---|---|---|---|
| Cu | 1.65 | 3.05 | 3.58 | 3.66 | 3.68 | 3.05 |
| Cc | 1.07 | 1.20 | 0.80 | 1.06 | 0.89 | 1.29 |
| Sample ID | S7 | S8 | S9 | S10 | S11 | S12 |
| Cu | 2.38 | 3.36 | 3.52 | 3.11 | 2.93 | 3.45 |
| Cc | 1.34 | 1.11 | 1.14 | 1.31 | 1.27 | 0.98 |
| Metric | Expression [43] | Range |
|---|---|---|
| IoU | Metric is between 0 and 1, and the closer it is to 1, the better the model performs. | |
| Precision | ||
| Recall | ||
| Accuracy | ||
| Specificity |
| Sample ID | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | S10 | S11 | S12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| deq20 (mm) | 6.26 | 2.71 | 1.72 | 2.21 | 2.01 | 2.46 | 3.29 | 1.19 | 1.24 | 2.30 | 2.90 | 2.30 |
| 2.31 | 1.93 | 2.03 | 1.95 | 2.04 | 1.86 | 1.99 | 1.98 | 2.03 | 1.93 | 1.92 | 2.00 | |
| d20 (mm) | 10.29 | 5.20 | 3.94 | 4.49 | 4.16 | 4.82 | 6.34 | 3.66 | 3.74 | 4.69 | 5.48 | 4.55 |
| Sample ID | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | S10 | S11 | S12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| K (cm/s) | 3.45 | 2.30 | 4.58 | 4.30 | 5.81 | 1.37 | 2.70 | 2.72 | 2.62 | 0.86 | 0.99 | 3.04 |
| α | 162.29 | 48.79 | 39.42 | 52.27 | 36.65 | 77.88 | 87.99 | 26.74 | 28.39 | 76.80 | 79.58 | 48.88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, J.; Shen, Z.; Zhang, W.; Song, W. Deep-Learning-Enhanced CT Image Analysis for Predicting Hydraulic Conductivity of Coarse-Grained Soils. Water 2023, 15, 2623. https://doi.org/10.3390/w15142623
Peng J, Shen Z, Zhang W, Song W. Deep-Learning-Enhanced CT Image Analysis for Predicting Hydraulic Conductivity of Coarse-Grained Soils. Water. 2023; 15(14):2623. https://doi.org/10.3390/w15142623
Chicago/Turabian StylePeng, Jiayi, Zhenzhong Shen, Wenbing Zhang, and Wen Song. 2023. "Deep-Learning-Enhanced CT Image Analysis for Predicting Hydraulic Conductivity of Coarse-Grained Soils" Water 15, no. 14: 2623. https://doi.org/10.3390/w15142623
APA StylePeng, J., Shen, Z., Zhang, W., & Song, W. (2023). Deep-Learning-Enhanced CT Image Analysis for Predicting Hydraulic Conductivity of Coarse-Grained Soils. Water, 15(14), 2623. https://doi.org/10.3390/w15142623











