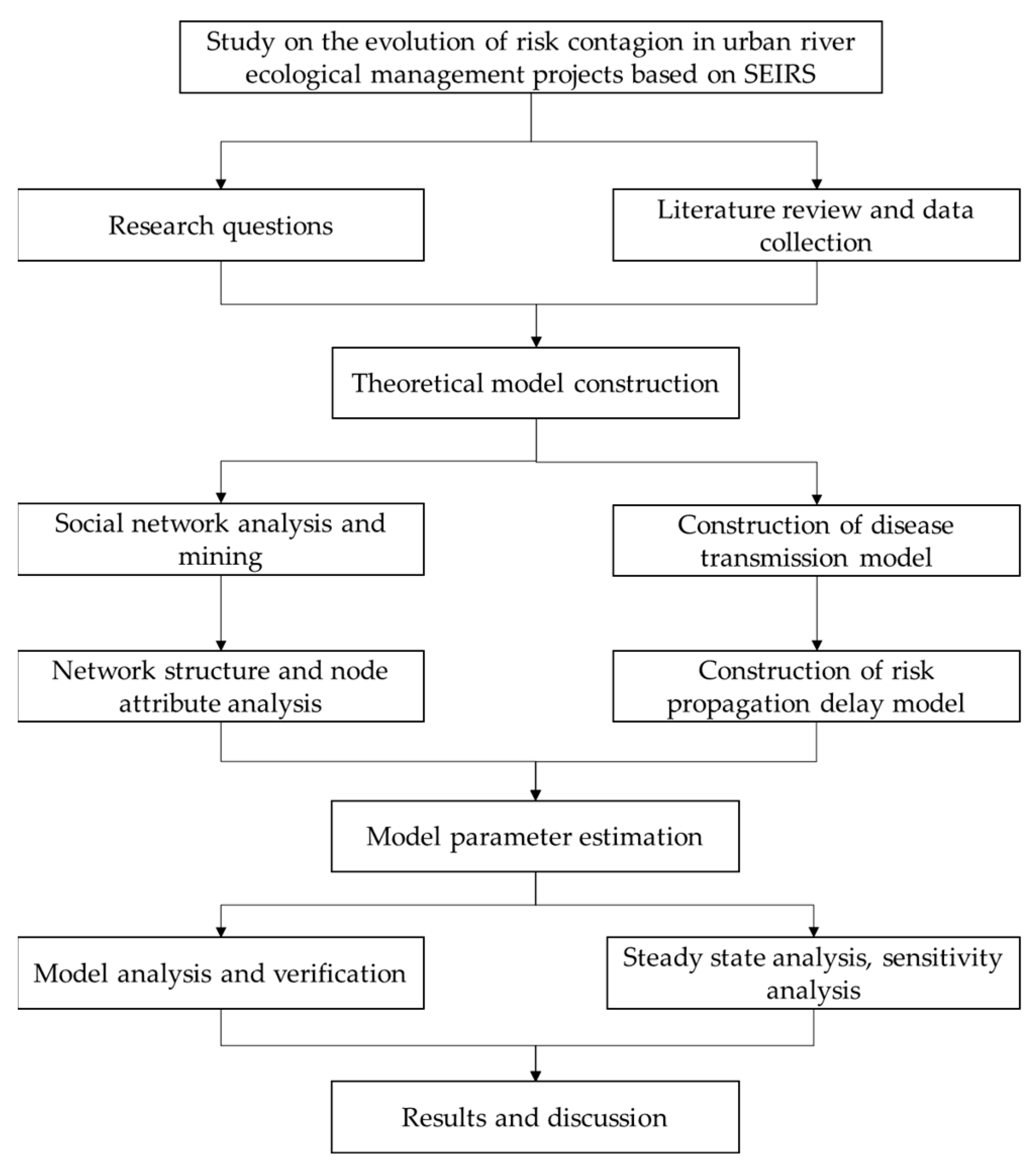
Study on the Evolution of Risk Contagion in Urban River Ecological Management Projects Based on SEIRS
Abstract
1. Introduction
2. Complex Network of Risks
2.1. Risk Identification
- (1)
- (2)
- The list of common problems in the inspection of water conservancy project construction management (2020, Ministry of Water Resources).
- (3)
- Accident investigation report of the safety production management platform of construction units.
2.2. Complex Network Construction and Characterization
2.2.1. Construction of Risk Networks
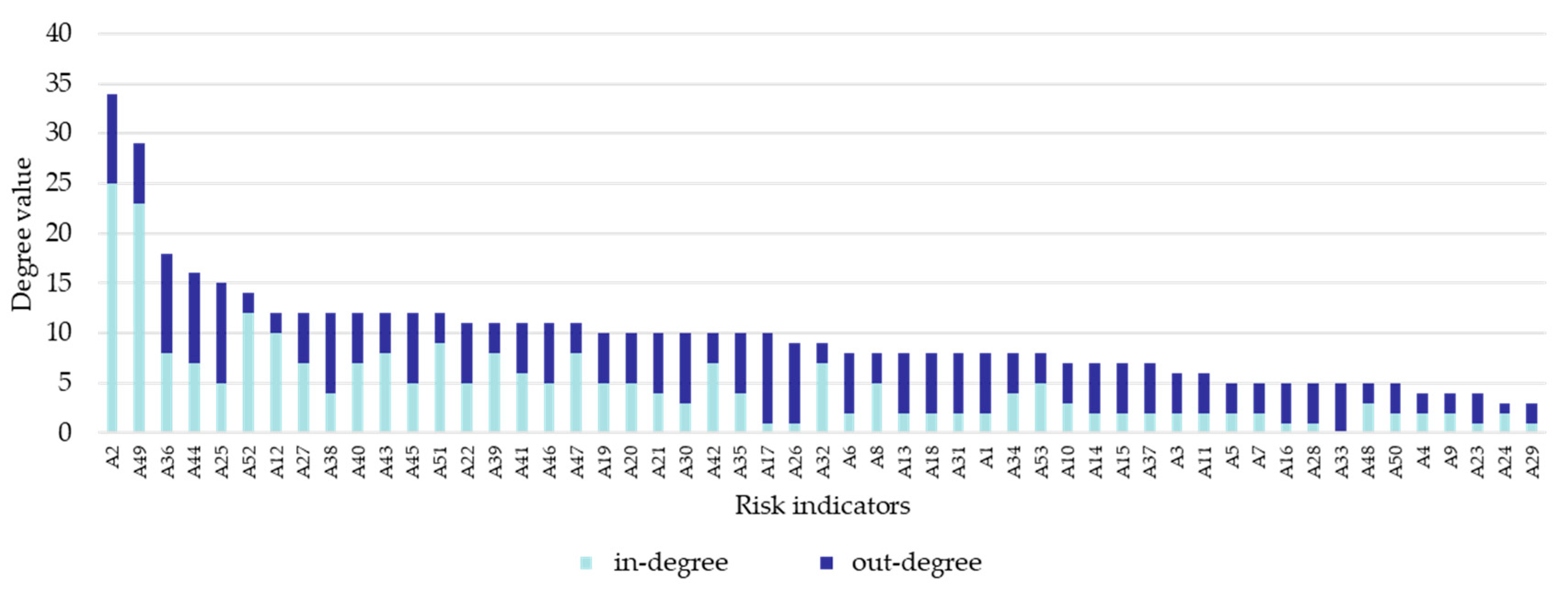
2.2.2. Network Characteristics and Network Visualization
2.3. Analysis of Risk Propagation and Delay Effects
2.3.1. Propagation Effects
2.3.2. Delay Effects
3. SEIRS-Based Risk Contagion Model for Urban River Ecological Management
3.1. Model Assumptions
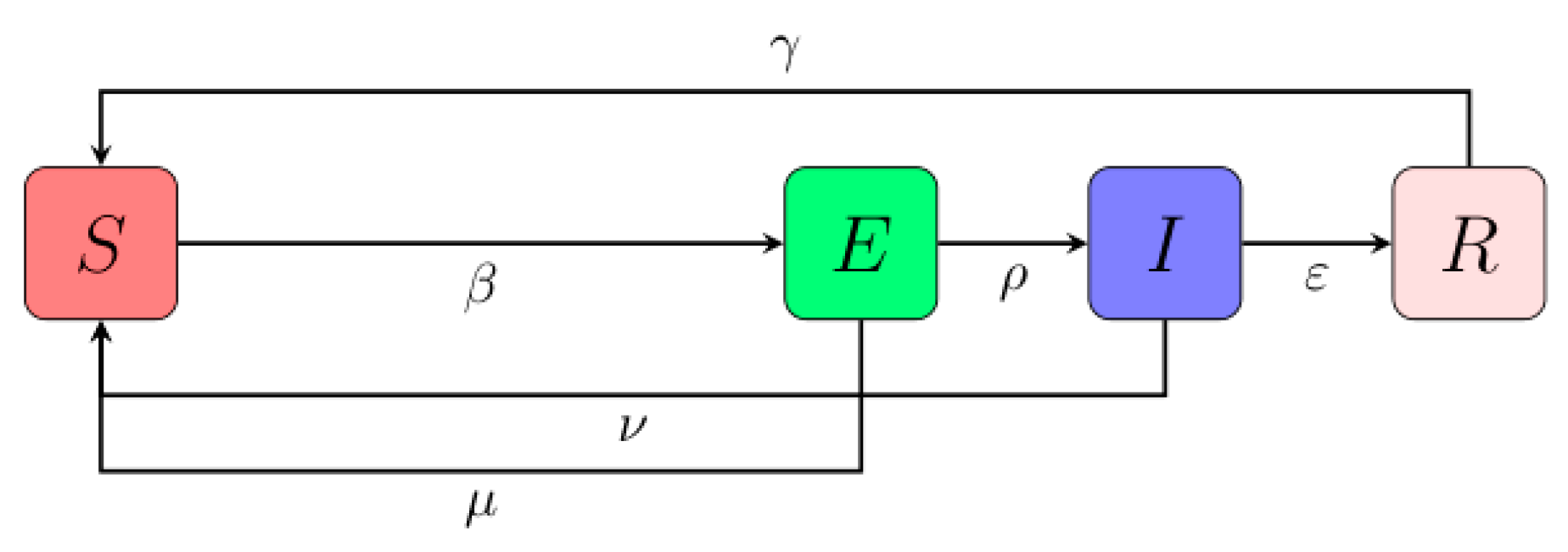
3.2. Construction Based on the SEIRS Model
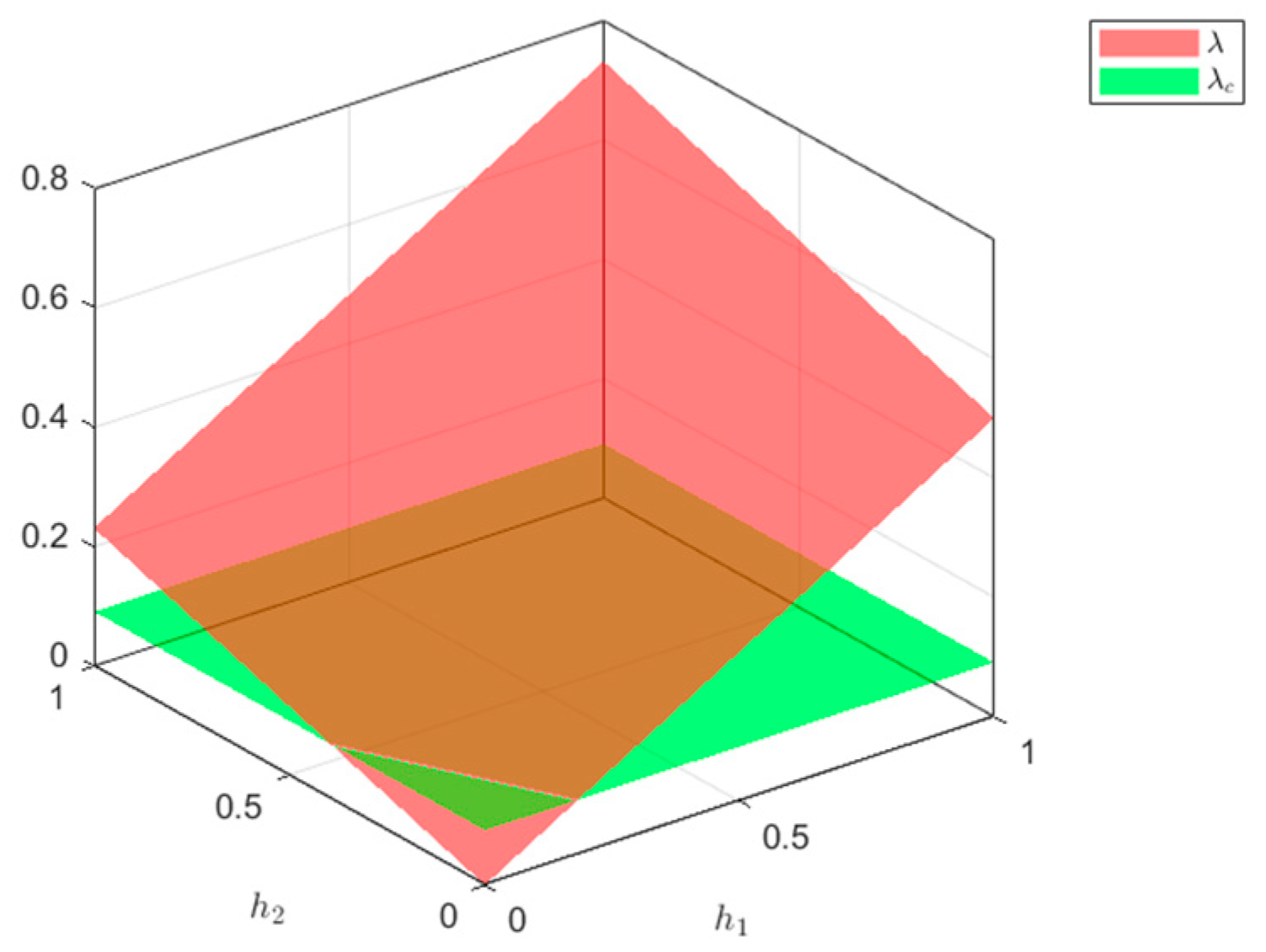
3.3. Immunization Strategy Construction
4. Numerical Simulation
4.1. Initial Model Parameter Setting
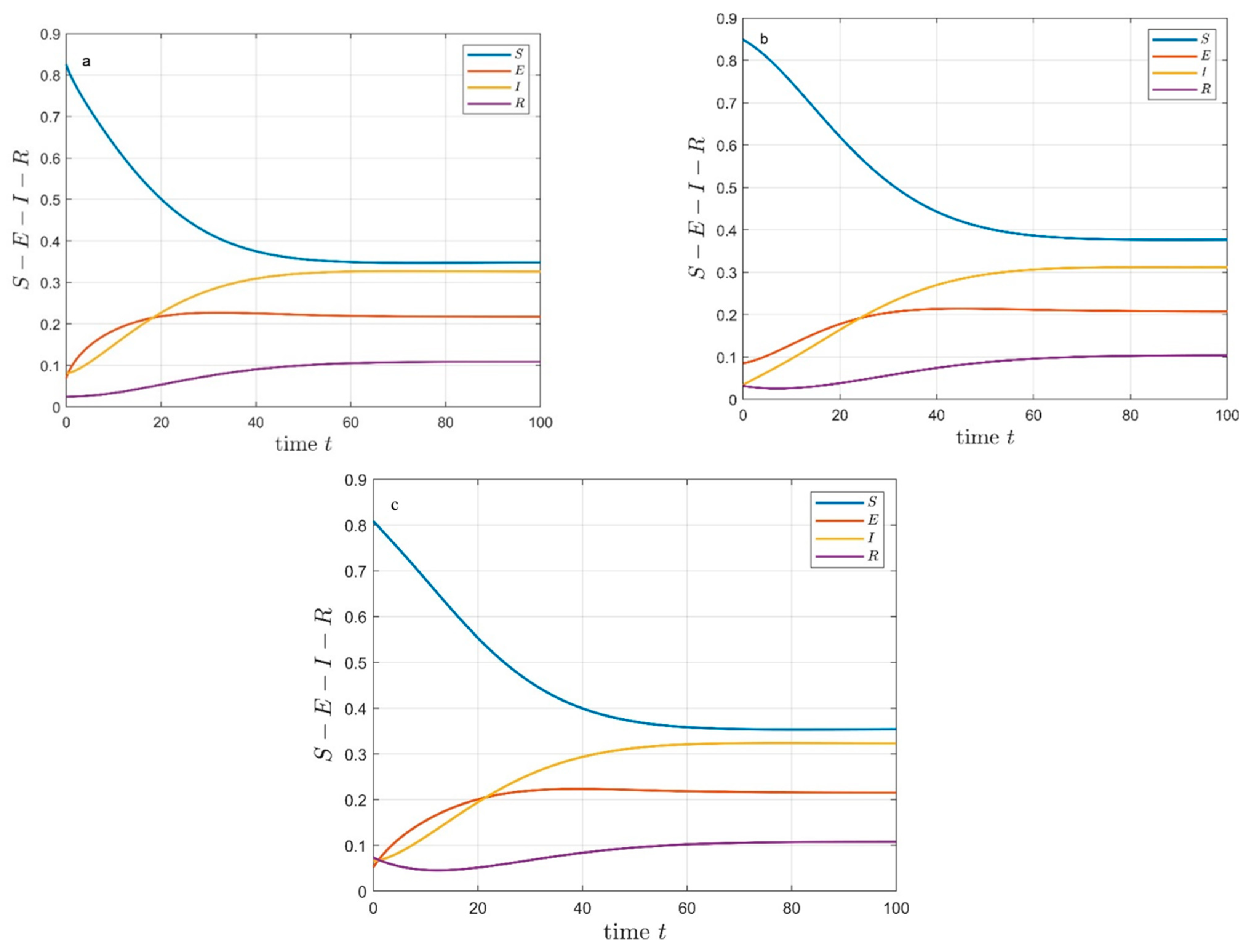
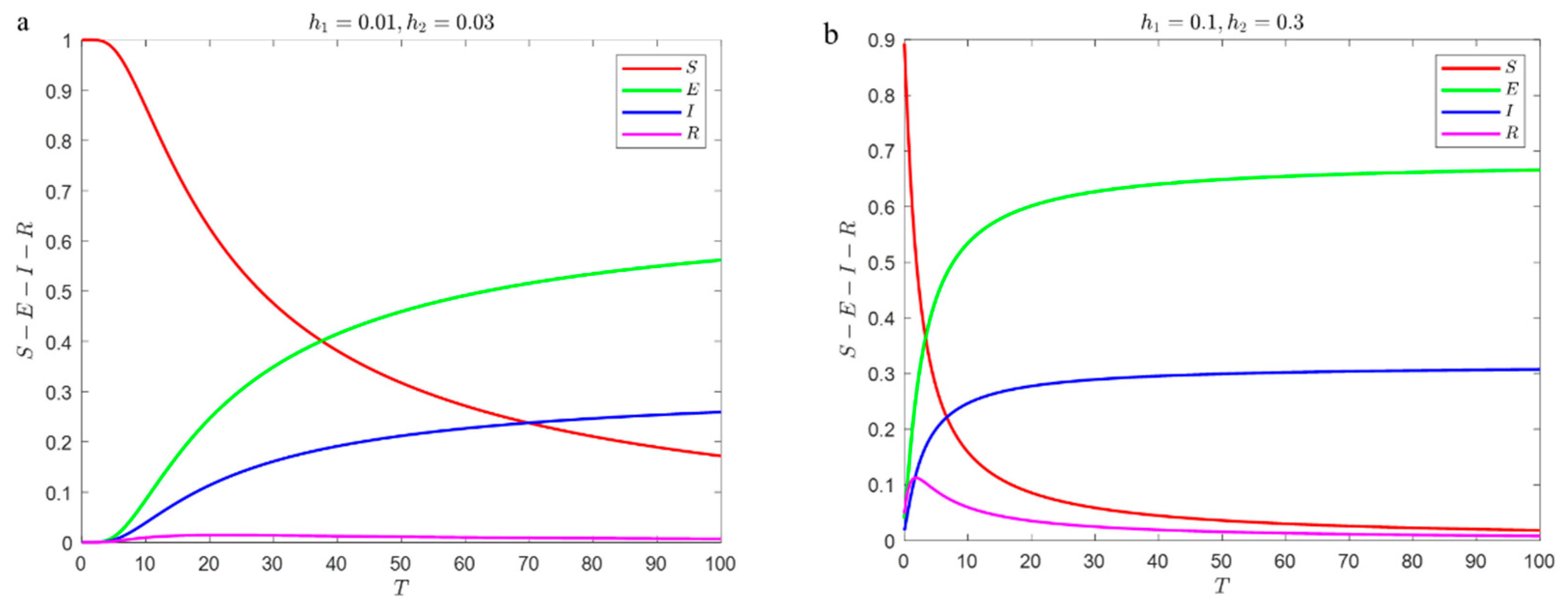
4.2. Model Dynamics Simulation
4.3. Dynamic Simulation Analysis of the SEIRS Model
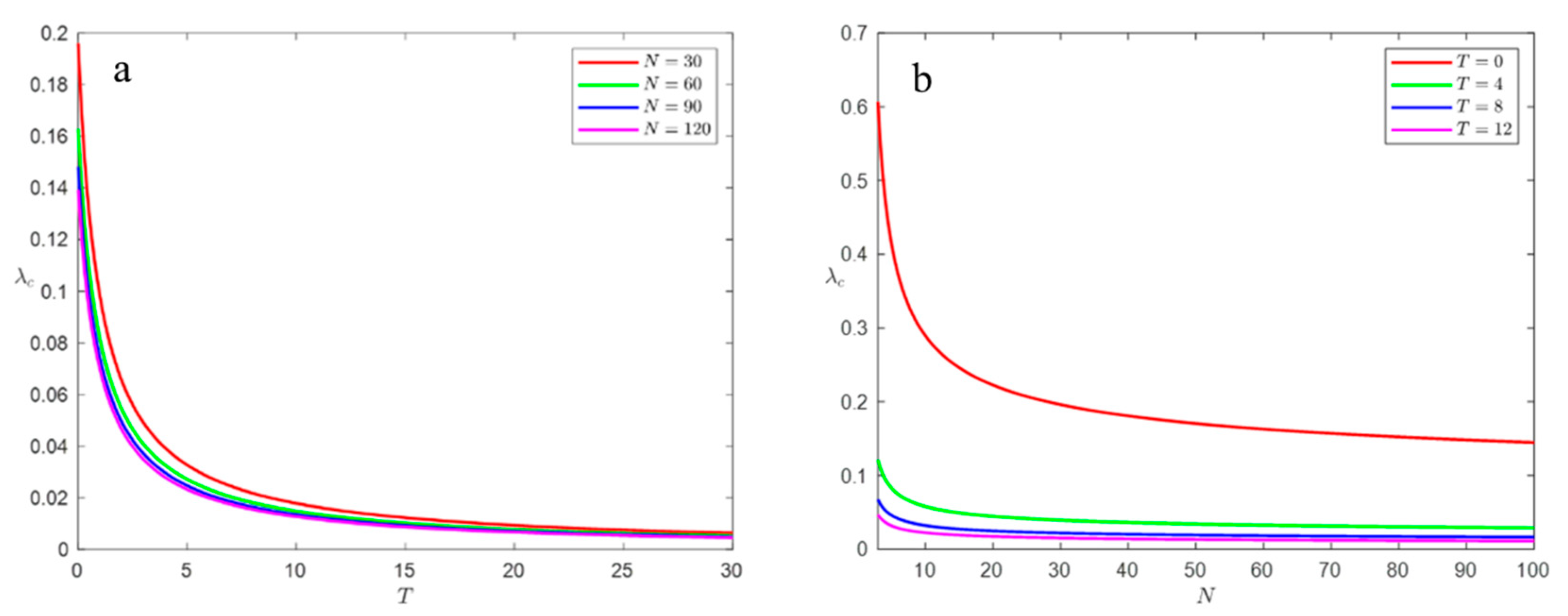
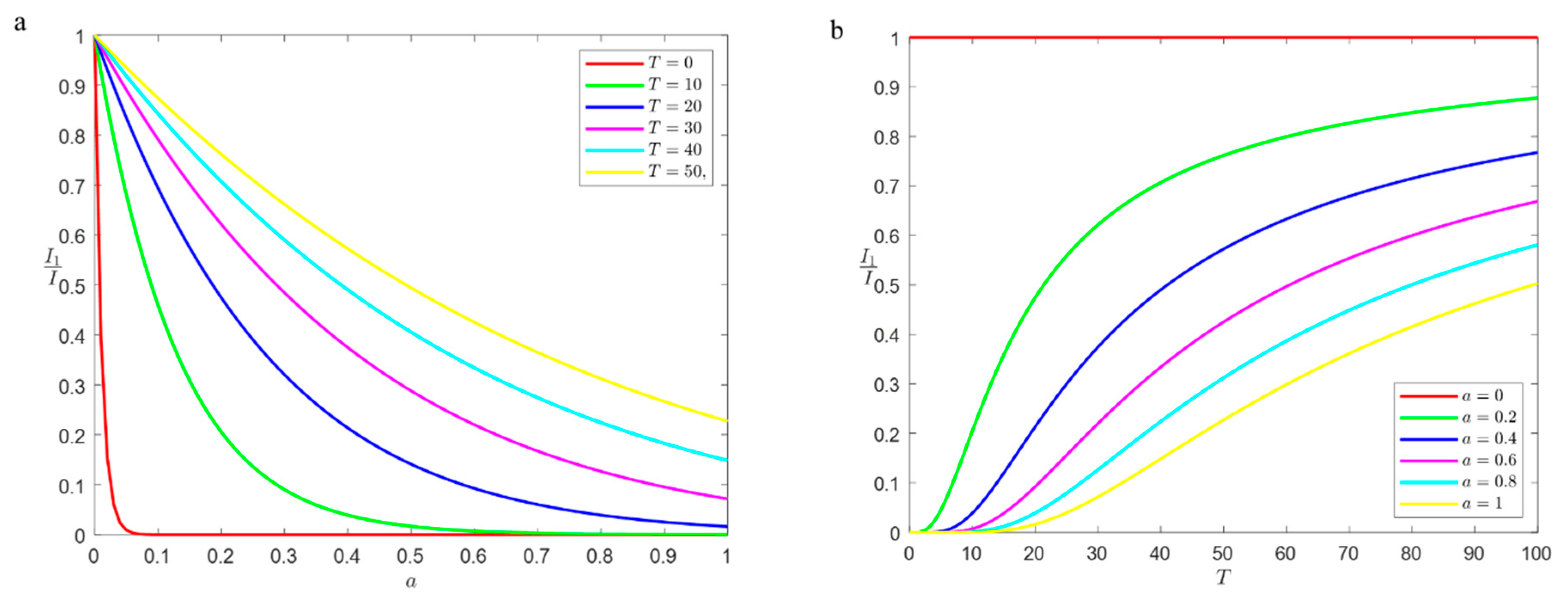
4.3.1. Effect of Delay Time and Network Size on Propagation Thresholds
4.3.2. Effect of Delay Time on Steady-State Density
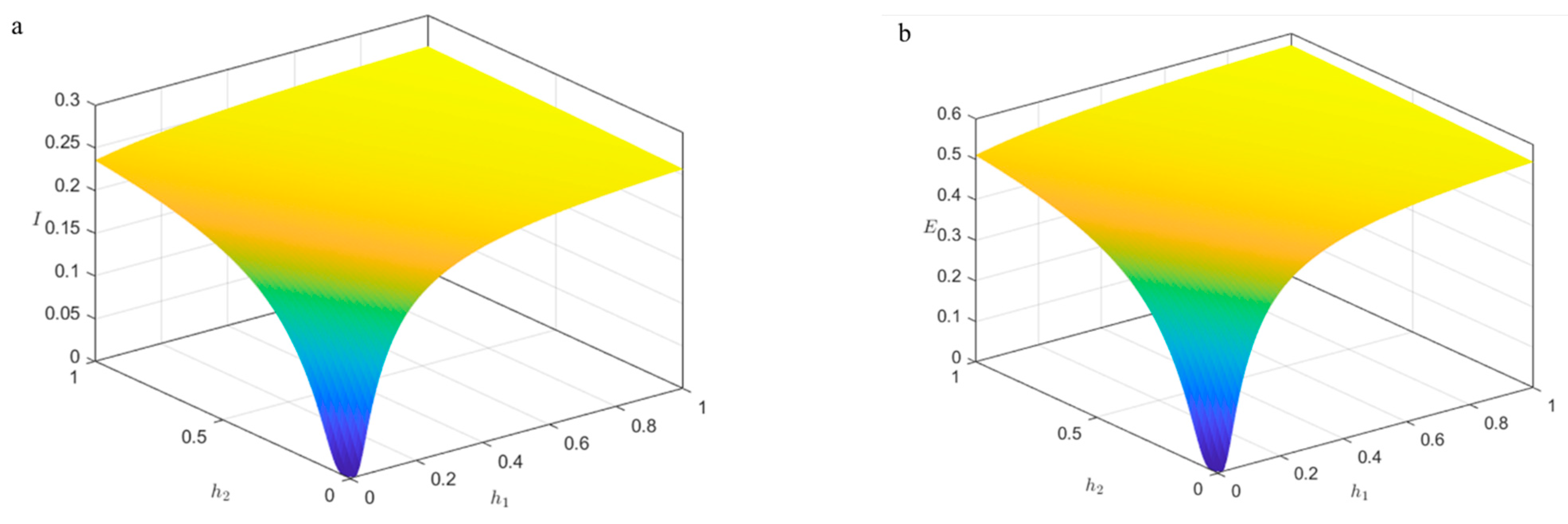
4.3.3. Infection Rate Effects on Steady-State Density
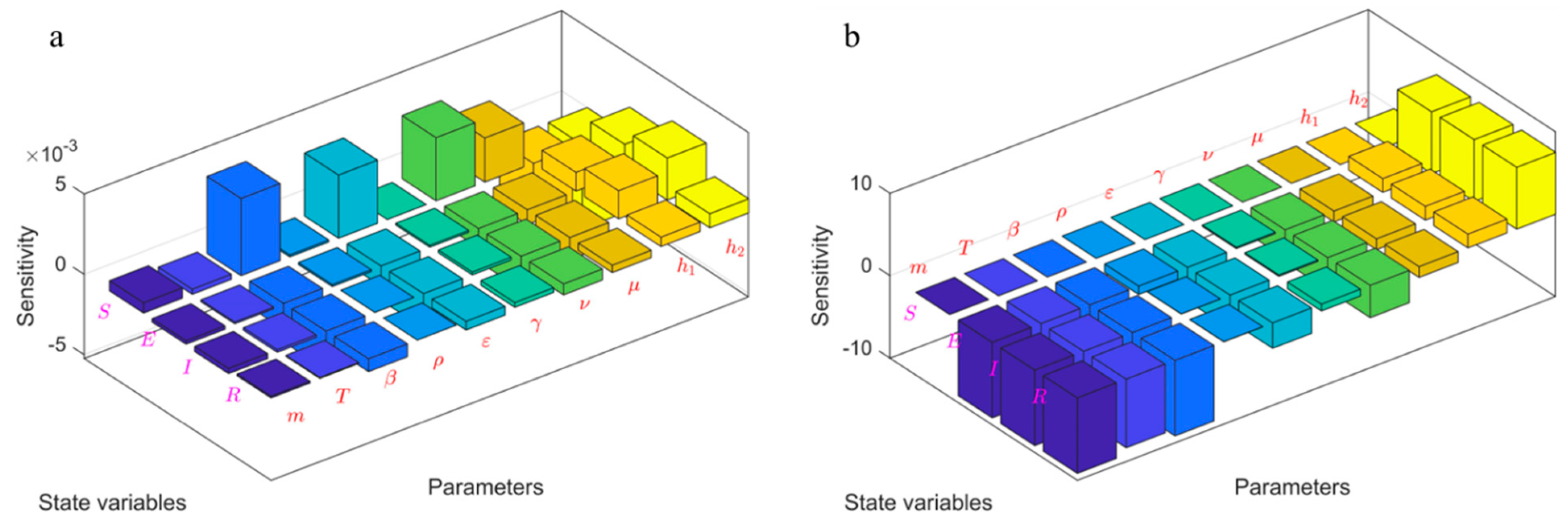
4.3.4. Sensitivity Analysis
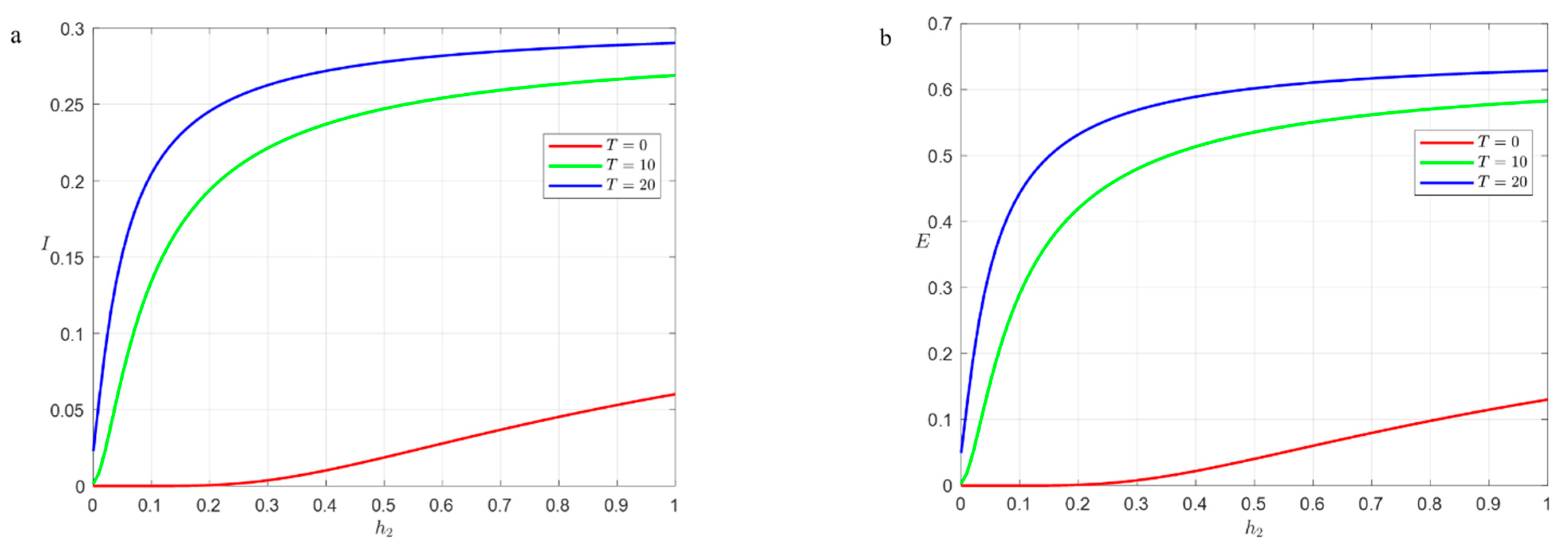
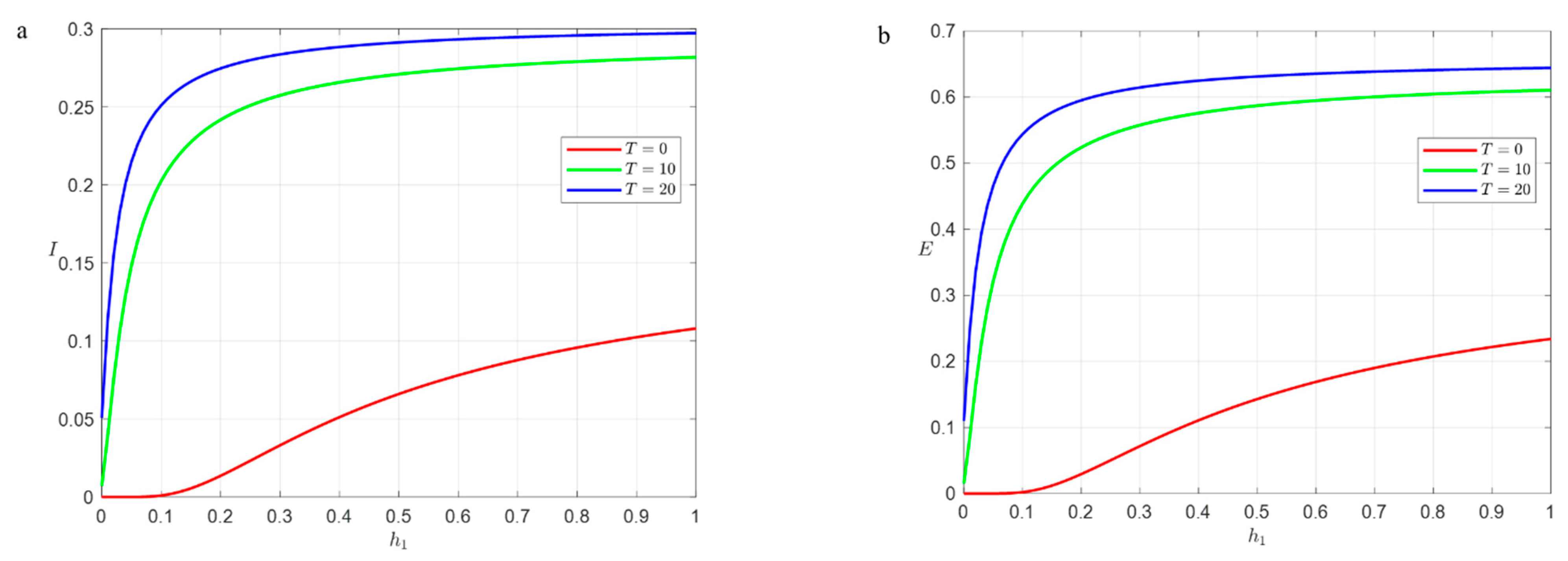
4.4. Immunization Strategy
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Equilibrium Point Stability and Steady-State Density Analysis
Appendix A.1.1. Equilibrium Point and Stability of the Model
Risk Aversion Balance Point and Stability
Risk Outbreak Equilibrium and Stability Analysis
Appendix A.2. Steady-State Density Analysis of the Model
References
- Xin, T.X.; Fan, L. Study on human-induced risk infection process in airport Flight area based on SEIRS model. Ind. Eng. 2016, 19, 56–63. [Google Scholar]
- Deng, G.; Lu, F.; Wu, L.; Xu, C. Social network analysis of virtual water trade among major countries in the world. Sci. Total Environ. 2021, 753, 142043. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhao, L.; Huang, R. SIRaRu rumor spreading model in complex networks. Phys. A Stat. Mech. Appl. 2014, 398, 43–55. [Google Scholar] [CrossRef]
- Tian, R.-Y.; Zhang, X.-F.; Liu, Y.-J. SSIC model: A multi-layer model for intervention of online rumors spreading. Phys. A Stat. Mech. Its Appl. 2015, 427, 181–191. [Google Scholar] [CrossRef]
- Jeon, B.N.; Olivero, M.P.; Wu, J. Multinational Banking and Financial Contagion: Evidence from Foreign Bank Subsidiaries; SSRN: Rochester, NY, USA, 2013. [Google Scholar]
- Mingyuan, Z.; Qin, X. Propagation model and intervention effect analysis of Unsafe Behavior of construction workers. China Saf. Sci. J. 2021, 31, 1–9. [Google Scholar] [CrossRef]
- Jianjia, H.; Jusheng, L.; Fuyuan, X. Dynamic Modeling and Simulation of time Encroachment Propagation based on SIR Model. Appl. Res. Comput. 2018, 35, 1360–1364. [Google Scholar]
- Zanette, D.H. Dynamics of rumor propagation on small-world networks. Phys. Rev. E 2002, 65, 041908. [Google Scholar] [CrossRef]
- Ikeda, K.; Okada, Y.; Toriumi, F.; Sakaki, T.; Kazama, K.; Noda, I.; Shinoda, K.; Suwa, H.; Kurihara, S. Multi-agent information diffusion model for twitter. In Proceedings of the 2014 IEEE/WIC/ACM International Joint Conferences on Web Intelligence (WI) and Intelligent Agent Technologies (IAT), Warsaw, Poland, 11–14 August 2014; pp. 21–26. [Google Scholar]
- Zhu, K.; Ying, L. Information Source Detection in the SIR Model: A Sample Path Based Approach. IEEE/ACM Trans. Netw. 2016, 24, 408–421. [Google Scholar] [CrossRef]
- Kermack, W.O.; McKendrick, A.G. Contributions to the mathematical theory of epidemics-II. The problem of endemicity. Bull. Math. Biol. 1991, 53, 57–87. [Google Scholar]
- Xue, M.; Xu, F.; Yang, Y.; Tao, Z.; Chen, Y.; Wang, S.; Yin, J.; Min, M.; Shi, D.; Yao, C. Diagnosis of sepsis with inflammatory biomarkers, cytokines, endothelial functional markers from SIRS patients. Medicine 2022, 101, e28681. [Google Scholar] [CrossRef]
- Chernov, A.A.; Shemendyuk, A.A.; Kelbert, M.Y. Fair insurance premium rate in connected SEIR model under epidemic outbreak. Math. Model. Nat. Phenom. 2021, 16, 34. [Google Scholar] [CrossRef]
- Lu, M.; Men, K.; Ma, Y.H. Evolution simulation of public opinion in group Social networks based on SIS model. J. Jilin Univ. (Inf. Sci. Ed.) 2023, 41, 106–111. [Google Scholar] [CrossRef]
- Jianquan, L.; Zhien, M. Analysis of two types of SEIS infectious disease models with definite incubation period. Syst. Sci. Math. 2006, 26, 9. [Google Scholar]
- Yu, Z.; Arif, R.; Fahmy, M.A.; Sohail, A. Self organizing maps for the parametric analysis of COVID-19 SEIRS delayed model. Chaos Solitons Fractals 2021, 150, 111202. [Google Scholar] [CrossRef]
- Khalkho, B.R.; Kurrey, R.; Deb, M.K.; Karbhal, I.; Sahu, B.; Sinha, S.; Sahu, Y.K.; Jain, V.K. A simple and convenient dry-state SEIRS method for glutathione detection based on citrate functionalized silver nanoparticles in human biological fluids. New J. Chem. 2021, 45, 1339–1354. [Google Scholar] [CrossRef]
- Chunlin, D.; Zhen, H.; Liu, Y. Research on the transmission and prevention of mass incidents based on SIS model. Chin. J. Inf. 2016, 35, 79–84+90. [Google Scholar]
- Hallam, T.G.; Zhien, M. Persistence in population models with demographic fluctuations. J. Math. Biol. 1986, 24, 327–339. [Google Scholar] [CrossRef]
- Qin, X.; Fan, L. Safety Risk communication mechanism of amphibious seaplanes. Traffic Inf. Saf. 2022, 40, 1–9. [Google Scholar]
- Zhang, H.Y.; Liu, Y.H. A Study on Risk System of Water Conservancy and Hydropower Engineering. Adv. Mater. Res. 2012, 459, 450–453. [Google Scholar] [CrossRef]
- He, Z.; Huang, D.; Zhang, C.; Fang, J. Toward a stakeholder perspective on social stability risk of large hydraulic engineering projects in China: A social network analysis. Sustainability 2018, 10, 1223. [Google Scholar] [CrossRef]
- Yang, Z.; Feng, L.J. Application of Improved LEC Method in the Construction of Water Conservancy Project Hazard Evaluation. Adv. Mater. Res. 2014, 1028, 297–299. [Google Scholar] [CrossRef]
- Meng, J.; Zhang, J. Study on risk assessment of EPC water conservancy project based on entropy weight set pair analysis. IOP Conf. Ser. Earth Environ. Sci. 2021, 804, 022045. [Google Scholar] [CrossRef]
- Xin, W.; Wang, Y. Research on influencing factors of reservoir construction risk based on interpretative structural modeling. World J. Eng. Technol. 2021, 9, 727–736. [Google Scholar] [CrossRef]
- Sun, X. Research on risk management of engineering project. In Proceedings of the 2016 International Conference on Logistics, Informatics and Service Sciences (LISS), Sydney, Australia, 24–27 July 2016; pp. 1–5. [Google Scholar]
- Chen, J. Risk management of large water conservancy projects. J. Yangtze River Sci. Res. Inst. 2012, 29, 15. [Google Scholar]
- Liu, X.; Xu, C.; Zhang, Z.; Zhang, Y.; Wu, S. Study on the role of eco-environmental impact assessment in performance management assessment of large water conservancy projects. Ekoloji 2019, 28, 1165–1172. [Google Scholar]
- Zeng, J.; An, M.; Smith, N.J. Application of a fuzzy based decision making methodology to construction project risk assessment. Int. J. Proj. Manag. 2007, 25, 589–600. [Google Scholar] [CrossRef]
- Arabi, S.; Eshtehardian, E.; Shafiei, I. Using Bayesian networks for selecting risk-response strategies in construction projects. J. Constr. Eng. Manag. 2022, 148, 04022067. [Google Scholar] [CrossRef]
- El-Sayegh, S.M.; Manjikian, S.; Ibrahim, A.; Abouelyousr, A.; Jabbour, R. Risk identification and assessment in sustainable construction projects in the UAE. Int. J. Constr. Manag. 2021, 21, 327–336. [Google Scholar] [CrossRef]
- Perry, J.G.; Hayes, R. Risk and its management in construction projects. Proc. Inst. Civ. Eng. 1985, 78, 499–521. [Google Scholar] [CrossRef]
- Heng, Y.; Wu, M.; Wen, X.; Bedon, C. Identifying Key Risk Factors in Air Traffic Controller Workload by SEIR Model. Math. Probl. Eng. 2022, 2022, 7600754. [Google Scholar] [CrossRef]
- Yuting, W.; Chun, F.; Ke, Z.; Ming, L.; Song, X. Research on SEIRS Based Quality Risk Transmission Model and Simulation of Construction Projects. Oper. Res. Manag. 2020, 29, 214–221. [Google Scholar]


| Stage | Risk 1 Level | Risk 2 Level |
|---|---|---|
| 1 Project concept stage | 1 Political Risk | A1 Policy risk |
| A2 Legal and regulatory risks | ||
| 2 Economic Risks | A3 Inflation risks | |
| A4 Risk of interest rate changes | ||
| A5 Financing risk | ||
| 3 Natural environmental risks | A6 Hydrological and geological risks | |
| A7 Risk of meteorological conditions | ||
| A8 Ecological environment risk | ||
| 4 Social Risks | A9 Sociocultural risk | |
| A10 Resident negotiated land acquisition risk | ||
| A11 Social security situation | ||
| A12 Public opinion | ||
| 2 Project decision stage | 5 Project decision risk | A13 Project approval risk |
| A14 Basic acceptance risk before implementation | ||
| A15 Risk of decision-making error | ||
| A16 Risk of land change | ||
| A17 Risk of incomplete collection of basic data | ||
| 3 Project preparation phase | 6 Bidding risks | A18 Risk of document loss |
| A19 Risk of improper competition | ||
| A20 Information leakage risk | ||
| A21 Bid evaluation risk | ||
| A22 Normative risk of bidding process | ||
| 7 Plan and design risks | A23 Risk of qualification of design unit | |
| A24 design schedule lag | ||
| A25 There are defects, errors, omissions, and frequent changes in the design plan | ||
| A26 Survey accuracy risk | ||
| 8 Prepare for risks before construction | A27 Construction site layout and technical preparation risk | |
| A28 Project contract risks | ||
| A29 Risk of insufficient supply of substances (materials) and materials | ||
| A30 Risk of illegal start | ||
| 4 Project implementation phase | 9 Construction personnel risk | A31 Technical water risk |
| A32 Weak security awareness | ||
| A33 Employee qualification risk | ||
| A34 Risk of construction personnel slowing down | ||
| 10 Construction technical risks | A35 (construction) drawings improper design risk | |
| A36 Engineering and technical risks | ||
| A37 Construction machinery and equipment condition risk | ||
| A38 Cross operation condition risk | ||
| A39 Risk of construction accidents | ||
| 11 Construction management risks | A40 Safety management risks | |
| A41 Coordination risks of participating parties (including technical disclosure) | ||
| A42 Rationality of construction organization design | ||
| A43 Plan Adjustment and engineering change risk | ||
| A44 Contract management and enforcement risks | ||
| A45 Risk of organizational structure setup confusion | ||
| A46 Manage permission risk | ||
| 12 Construction duration factor risk | A47 Certification period | |
| A48 Construction period | ||
| A49 Risk of construction delay | ||
| 13 Completion acceptance risk | A50 Risk of file transfer not in place | |
| A51 Quality assessment risk | ||
| A52 Audit risk | ||
| A53 Risk of cost overruns |
| A1 | A2 | A3 | A4 | A5 | A6 | A7 | … | A47 | A48 | A49 | A50 | A51 | A52 | A53 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | … | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| A2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | … | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| A3 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | … | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| A4 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | … | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| A5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | … | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| A6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | … | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| A7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | … | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ⁝ | ⁝ | ⁝ | ⁝ | ⁝ | ⁝ | ⁝ | ⁝ | 0 | ⁝ | ⁝ | ⁝ | ⁝ | ⁝ | ⁝ | ⁝ |
| A47 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | … | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| A48 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | … | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| A49 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | … | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| A50 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | … | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| A51 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | … | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| A52 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | … | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| A53 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | … | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Parameter Name | Overall Network | Parameter Names | Overall Network |
|---|---|---|---|
| Number of nodes | 53 | Network diameter | 7 |
| Number of network edges | 255 | Network average aggregation coefficient | 0.2977 |
| Network density | 0.0925 | Intermediation centrality | 0.0331 |
| Network average path | 2.5287 | Approach centrality | 0.3015 |
| Network average | 9.6226 | Global network efficiency | 0.5281 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Zhu, J.; Xie, J. Study on the Evolution of Risk Contagion in Urban River Ecological Management Projects Based on SEIRS. Water 2023, 15, 2622. https://doi.org/10.3390/w15142622
Xu J, Zhu J, Xie J. Study on the Evolution of Risk Contagion in Urban River Ecological Management Projects Based on SEIRS. Water. 2023; 15(14):2622. https://doi.org/10.3390/w15142622
Chicago/Turabian StyleXu, Junke, Jiwei Zhu, and Jiancang Xie. 2023. "Study on the Evolution of Risk Contagion in Urban River Ecological Management Projects Based on SEIRS" Water 15, no. 14: 2622. https://doi.org/10.3390/w15142622
APA StyleXu, J., Zhu, J., & Xie, J. (2023). Study on the Evolution of Risk Contagion in Urban River Ecological Management Projects Based on SEIRS. Water, 15(14), 2622. https://doi.org/10.3390/w15142622





