Numerical Simulation of a Three-Stage Electrical Submersible Pump under Stall Conditions
Abstract
:1. Introduction
2. Numerical Methods
2.1. Turbulence Model
2.2. Entropy Production
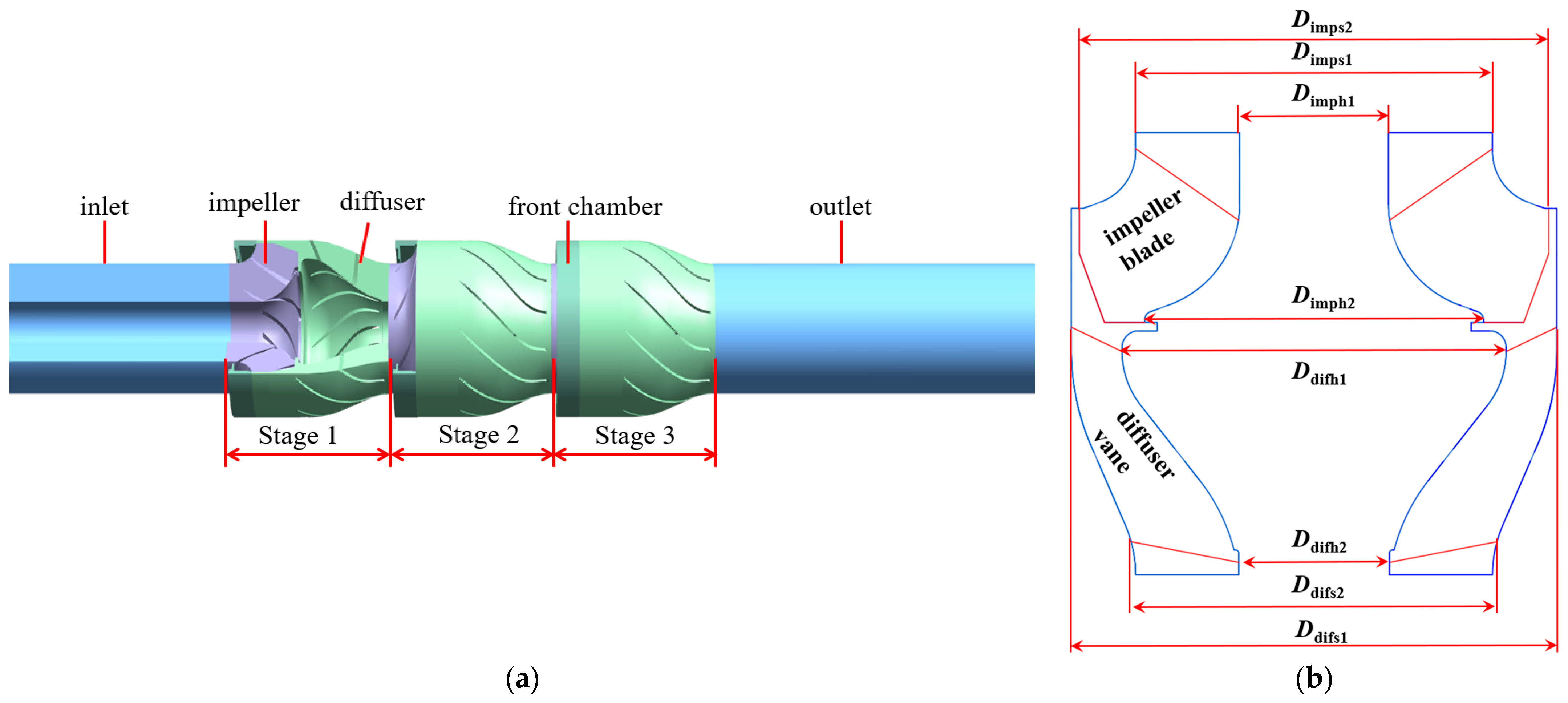
2.3. Computational Model
2.4. Mesh and Boundary Condition
3. Results and Discussions
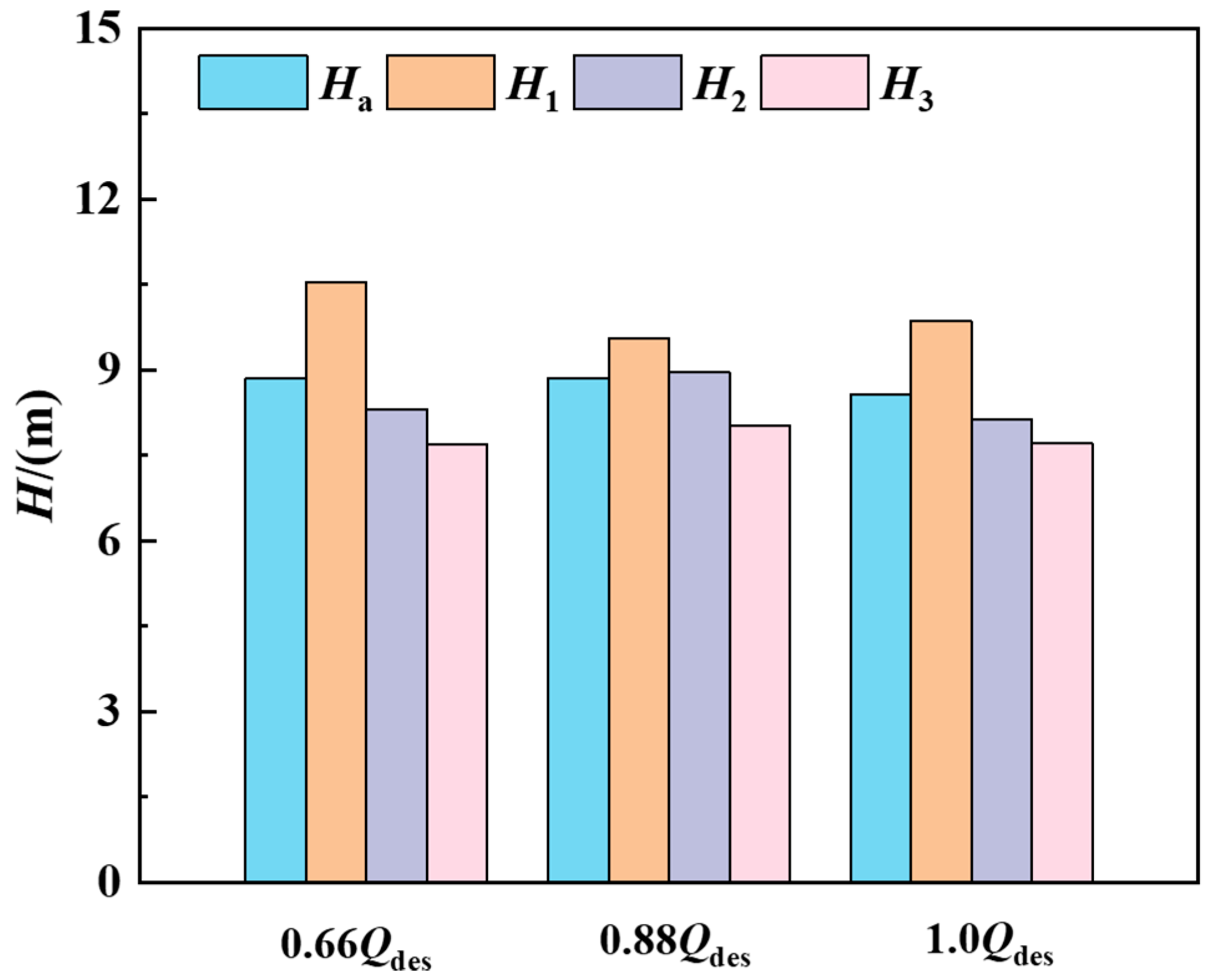
3.1. External Characteristics Comparison
3.2. Analysis of Flow Field under Design Conditions
3.3. Analysis of Flow Field under Critical Stall Conditions
3.4. Analysis of Flow Field under Deep Stall Conditions
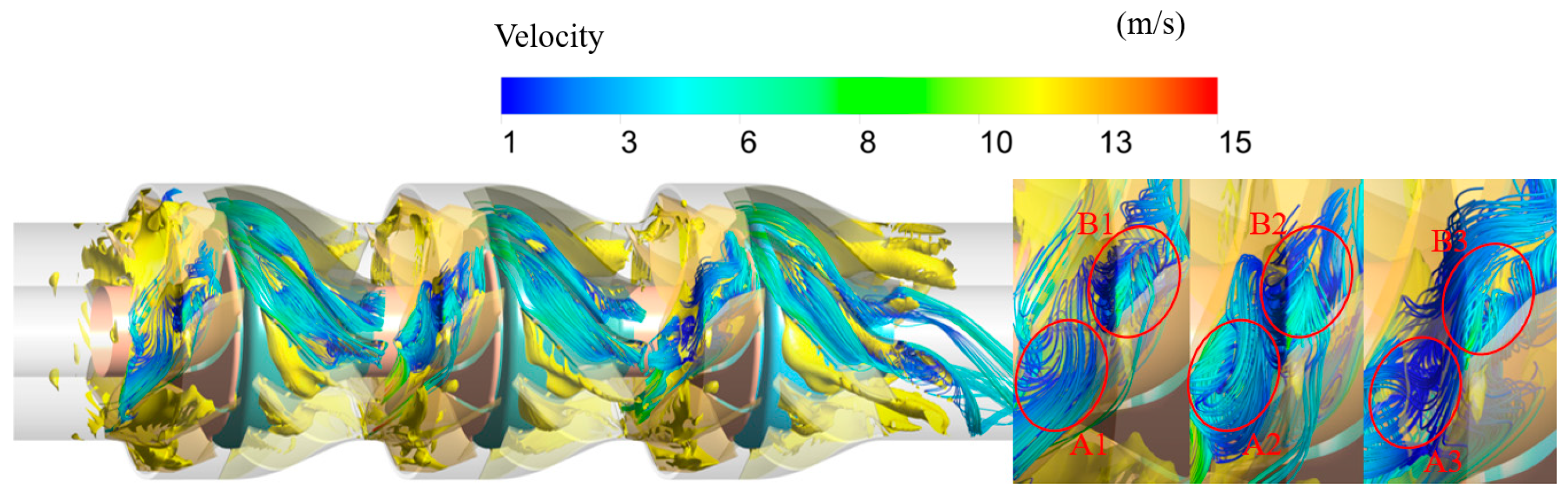
3.5. Vortex Evolution Process in the Impeller and Diffuser under Stall Conditions
3.6. Energy Loss Analysis
4. Conclusions
- (1)
- Under critical stall conditions, impeller 1 generates inlet and multiple channel vortices, which when combined with inherent secondary flow and wake, result in turbulence within the impeller’s flow field. The internal vortex evolution period of impeller 1 is approximately 0.75T; however, the scale of internal vortices in impellers 2 and 3 is small with no apparent evolution period.
- (2)
- Under deep stall conditions, large-scale vortex structures manifest within all stages of the impeller, resulting in severe channel blockage. Flow separation commences at the leading edge of the guide vanes in the diffuser, with vortices developing and expanding inside the channel to cause a significant impact on outlet performance. The scales and evolution patterns of these vortices vary across different channels within impeller 1.
- (3)
- The turbulent entropy production power within the impeller and diffuser constitutes the primary component of total entropy production power. The entropy production power loss inside the impeller increases with the increase in stages, and the power loss inside the diffuser is the same in each stage. Under deep stall conditions, frequent vortex shedding inside these components results in significant energy loss.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jese, U.; Fortes-Patella, R.; Antheaume, S. High head pump-turbine: Pumping mode numerical simulations with a cavitation model for off-design conditions. IOP Conf. Ser.-Earth Environ. Sci. 2014, 22, 032048. [Google Scholar] [CrossRef]
- Jese, U.; Fortes-Patella, R. Unsteady numerical analysis of the rotating stall in pump-turbine geometry. IOP Conf. Ser.-Earth Environ. Sci. 2016, 49, 042005. [Google Scholar] [CrossRef]
- Day, I. Stall, Surge, and 75 Years of Research. J. Turbomach. 2015, 138, 011001. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, Y.; Du, X. A review of rotating stall of pump turbines. J. Hydroelectr. Eng. 2015, 34, 16–24. [Google Scholar]
- Yang, J.; Yuan, S.; Pei, J.; Zhang, J. Overview of rotating stall in centrifugal pumps with vaned diffuser. J. Drain. Irrig. Mach. Eng. 2015, 33, 369–373. [Google Scholar]
- Zhang, N.; Yang, M.; Li, Z.; Sun, X. Pressure pulsation of centrifugal pump with tilt volute. J. Mech. Eng. 2012, 48, 164–168. [Google Scholar] [CrossRef]
- Ullum, U.; Wright, J.; Dayi, O.; Ecder, A.; Soulaimani, A.; Piché, R.; Kamath, H. Prediction of rotating stall within an impeller of a centrifugal pump based on spectral analysis of pressure and velocity data. J. Phys. Conf. Ser. 2006, 52, 36–45. [Google Scholar] [CrossRef]
- Li, W.; Ping, Y.; Shi, W. Research progress in rotating stall in mixed-flow pumps with guide vane. J. Drain. Irrig. Mach. Eng. 2019, 37, 737–745. [Google Scholar]
- Zhou, L.; Bai, L.; Li, W.; Shi, W.; Wang, C. PIV validation of different turbulence models used for numerical simulation of a centrifugal pump diffuser. Eng. Comput. 2018, 35, 2–17. [Google Scholar] [CrossRef]
- Yang, Y. Interstage difference of pressure pulsation in a three-stage electrical submersible pump. J. Pet. Sci. Eng. 2021, 196, 107653. [Google Scholar] [CrossRef]
- Goto, A. Study of internal flows in a mixed-flow pump impeller at various tip clearances using three-dimensional viscous flow computations. J. Turbomach. 1992, 114, 373–382. [Google Scholar] [CrossRef]
- Goto, A. The effect of tip leakage flow on part-load performance of a mixed-flow pump impeller. J. Turbomach. 1992, 114, 383–391. [Google Scholar] [CrossRef]
- Wang, F. Research progress of computational model for rotating turbulent flow in fluid machinery. Trans. Chin. Soc. Agric. Mach. 2016, 47, 1–14. [Google Scholar]
- El-Emam, M.A.; Zhou, L.; Yasser, E.; Bai, L.; Shi, W. Computational methods of erosion wear in centrifugal pump: A state-of-the-art review. Arch. Comput. Methods Eng. 2022, 29, 3789–3814. [Google Scholar] [CrossRef]
- Hang, J.; Bai, L.; Zhou, L.; Jiang, L.; Shi, W.; Agarwal, R. Inter-stage energy characteristics of electrical submersible pump under gassy conditions. J. Energy 2022, 256, 124624. [Google Scholar] [CrossRef]
- Hong, W.; Hiroshi, T. Experimental and numerical study of unsteady flow in a diffuser pump at off-design conditions. J. Fluids Eng. 2003, 125, 767–778. [Google Scholar]
- Pan, Z.; Li, J.; Li, X.; Yuan, S. Curve instability and rotating stall. Trans. Chin. Soc. Agric. Mach. 2012, 43, 64–68. [Google Scholar]
- Feng, J.; Wang, C.; Luo, X. Rotating stall in centrifugal pump impellers under part-load conditions. J. Hydroelectr. Eng. 2018, 37, 117–124. [Google Scholar]
- Li, X.; Yuan, S.; Pan, Z.; Li, Y.; Liu, W. Dynamic characteristics of rotating stall in mixed flow pump. J. Appl. Math. 2013, 2013, 4819–4828. [Google Scholar] [CrossRef] [Green Version]
- Hu, F.; Wu, P.; Wu, D.; Wang, L. Numerical study on the stall behavior of a water jet mixed-flow pump (Article). J. Mar. Sci. Technol. 2014, 19, 438–449. [Google Scholar]
- Fujisawa, N.; Inui, T.; Ohta, Y. Evolution process of diffuser stall in a centrifugal compressor with vaned diffuser. J. Turbomach. 2019, 141, 41009. [Google Scholar] [CrossRef]
- Jese, U.; Skotak, A.; Mikulasek, J. Cavitating vortices in the guide vanes region related to the pump-turbine pumping mode rotating stall. J. Phys. Conf. Ser. 2017, 813, 12043. [Google Scholar] [CrossRef]
- Hou-Lin, L.U.; Dong-Sheng, Y.A.N.G.; Ming-Gao, T.A.N.; Kai, W.A.N.G.; Su-Guo, Z.H.U.A.N.G.; Hui, D.U. 3D-PIV measurements of stall in double blade centrifugal pump. J. Shanghai Jiaotong Univ. 2012, 46, 734–739. [Google Scholar]
- Li, Y.; Li, R.; Wang, X.; Zhao, W.; Li, P. Numerical simulation of unstable characteristics in head curve of mixed-flow Pump. J. Drain. Irrig. Mach. Eng. 2013, 31, 6. [Google Scholar]
- Miyabe, M.; Maeda, H.; Umeki, I.; Jittani, Y. Unstable head-flow characteristic generation mechanism of a low specific speed mixed flow pump. J. Therm. Sci. 2006, 15, 115–120. [Google Scholar] [CrossRef]
- Ying, G. Numerical Analysis of Flow Field of Electrical Submersible Pump; Zhejiang University: Zhejiang, China, 2004. [Google Scholar]
- Stel, H.; Sirino, T.; Ponce, F.J.; Chiva, S.; Morales, R.E.M. Numerical investigation of the flow in a multi-stage electric submersible pump (Article). J. Pet. Sci. Eng. 2015, 136, 41–54. [Google Scholar] [CrossRef]
- Li, W.; Zhou, L.; Shi, W.D.; Ji, L.; Yang, Y.; Zhao, X. PIV experiment of the unsteady flow field in mixed-flow pump under part loading condition. Exp. Therm. Fluid Sci. 2017, 83, 191–199. [Google Scholar] [CrossRef]
- Tuzson, J. Centrifugal Pump Design; John Wiley and Sons: New York, NY, USA, 2000. [Google Scholar]
- Chen, Q. Predictive Performance of Several Turbulence Models in Turbomachinery Related Flows; Tsinghua University: Beijing, China, 2007. [Google Scholar]
- Bai, L.; Yang, Y.; Zhou, L.; Li, Y.; Xiao, Y.; Shi, W. Optimal design and performance improvement of an electric submersible pump impeller based on Taguchi approach. Energy 2022, 252, 124032. [Google Scholar] [CrossRef]
- Han, Y.; Zhou, L.; Bai, L.; Shi, W.; Agarwal, R. Comparison and validation of various turbulence models for U-bend flow with a magnetic resonance velocimetry experiment. Phys. Fluids 2021, 33, 125117. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. Turbul. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Sun, L.; Pan, Q.; Zhang, D.; Zhao, R.; van Esch, B.B. Numerical study of the energy loss in the bulb tubular pump system focusing on the off-design conditions based on combined energy analysis methods. Energy. 2022, 258, 124794. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Y.; Liu, H.; Xiao, Y.; Jiang, L.; Li, M. A numerical investigation on energy characteristics of centrifugal pump for cavitation flow using entropy production theory. Int. J. Heat Mass Transfer. 2023, 201, 123591. [Google Scholar] [CrossRef]
- Kock, F.; Herwig, H. Entropy production calculation for turbulent shear flows and their implementation in cfd codes. Int. J. Heat Fluid Flow 2005, 26, 672–680. [Google Scholar] [CrossRef]
- Zhou, L.; Hang, J.; Bai, L.; Krzemianowski, Z.; El-Emam, M.A.; Yasser, E.; Agarwal, R. Application of entropy production theory for energy losses and other investigation in pumps and turbines: A review. Appl. Energy 2022, 318, 119211. [Google Scholar] [CrossRef]
- Tao, R.; Xiao, R.; Wang, F.; Liu, W. Improving the cavitation inception performance of a reversible pumpturbine in pump mode by blade profile redesign: Design concept, method and applications. Renew. Energy 2019, 133, 325–342. [Google Scholar] [CrossRef]
- Cai, Z.; Luo, S. Secondary flow and wake development in fluid machinery impeller. J. Huazhong Univ. Sci. Technol Nat. Sci. Ed. 2001, 29, 4. [Google Scholar]
- Wang, C.; Wang, F.; An, D.; Yao, Z.; Xiao, R.; Lu, L.; He, C.; Zou, Z. A general alternate loading technique and its applications in the inverse designs of centrifugal and mixed-flow pump impellers. Sci. China (Technol. Sci.) 2021, 64, 898–918. [Google Scholar] [CrossRef]












| Constants | Value |
|---|---|
| 0.31 | |
| 5/9 | |
| 0.44 | |
| 3/40 | |
| 0.0828 | |
| 9/100 | |
| 0.85 | |
| 1 | |
| 0.5 | |
| 0.856 |
| Impeller Hydraulic Geometry Parameters | Hydraulic Geometry Parameters of Diffuser | ||
|---|---|---|---|
| Inlet inner diameter Dimph1/mm | 36 | Inlet inner diameter Ddifh1/mm | 76 |
| Inlet outer diameter Dimps1/mm | 86.5 | Inlet outer diameter Ddifs1/mm | 117.5 |
| Outlet inner diameter Dimph2/mm | 82 | Outlet inner diameter Ddifh2/mm | 36.5 |
| Outlet outer diameter Dimps2/mm | 113.5 | Outlet outer diameter Ddifs2/mm | 86.5 |
| Number of blades Zimp/vanes | 7 | Number of blades Zdif/ vanes | 11 |
| Inlet blade angle βimp1/° | 25 | Inlet blade angle βdif1/° | 55 |
| Outlet blade angle βimp2/° | 36 | Outlet blade angle βdif2/° | 87 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wang, Z.; Song, X.; Bai, L.; El-Emam, M.A.; Zhou, L. Numerical Simulation of a Three-Stage Electrical Submersible Pump under Stall Conditions. Water 2023, 15, 2619. https://doi.org/10.3390/w15142619
Wang Y, Wang Z, Song X, Bai L, El-Emam MA, Zhou L. Numerical Simulation of a Three-Stage Electrical Submersible Pump under Stall Conditions. Water. 2023; 15(14):2619. https://doi.org/10.3390/w15142619
Chicago/Turabian StyleWang, Yuqiang, Zhe Wang, Xiangyu Song, Ling Bai, Mahmoud A. El-Emam, and Ling Zhou. 2023. "Numerical Simulation of a Three-Stage Electrical Submersible Pump under Stall Conditions" Water 15, no. 14: 2619. https://doi.org/10.3390/w15142619






