Abstract
The increasingly stringent requirements in terms of flexibility and efficiency for hydraulic turbines pose new challenges for designers. Although computational fluid dynamics has offered new opportunities to significantly improve the performance in the preliminary design phase, the design of a hydraulic turbine still represents a challenging task requiring considerable engineering input and know-how. In such a scenario, the inverse three-dimensional design strategy has recently demonstrated its effectiveness in improving the machine performance, and interesting applications have been proposed for Francis turbines and reversible pump turbines. This paper presents and discusses the most interesting design solutions so far documented. The influence of blade staking and load distribution on the hydrodynamic performance is discussed. Finally, optimized blade load distributions are reported to provide useful design guidelines for the development of the new generation of hydraulic turbines.
1. Introduction
Hydropower represents the largest and historically most developed renewable energy source and is expected to play a key role in the ongoing energy transition [1]. With a share between 16 and 17% of the entire world’s energy production [2] and 53% of the whole renewable electricity generation [3], hydropower will support the energy transition by providing both low-cost renewable electricity and large-scale energy storage to support grid stability, which is threatened by increasing electricity generation from intermittent and unpredictable energy sources such as wind and solar.
Despite the variety of hydraulic turbines that can be fitted in modern hydropower plants, the Francis type represents the most spread configuration due to its wide operating range in terms of both water discharge and head. Moreover, reversible pump turbines (RPTs) today are generally preferred over other solutions in the new generation of storage hydropower plants [4] due to their compactness and cost efficiency. However, hydropower and pumped hydropower plants are required to operate over wider operating ranges and with frequent start and stops, forcing the machines to operate far from their design conditions. Taking these considerations into account, it is easy to understand the new challenges faced in the design of Francis turbines and pump turbines.
The hydraulic design of Francis runners is typically represented by an iterative approach requiring considerable engineering input. Indeed, despite the rise in modern optimization techniques, mainly based on computational fluid dynamics (CFD), know-how still plays a fundamental role in the design process. The traditional design methodologies adopted in industry relies on the definition of the runner blade geometry in terms of the blade angle distributions both in the streamwise and spanwise directions, so as to meet the performance requirements. The process continues by iterating the runner geometry until a satisfactory compromise between the design objectives is achieved, after which expensive experimental verifications are undertaken [5]. In this scenario, it is clear that even a modest improvement in the design methodology can result in greater competitiveness and faster project development.
In the inverse design method (IDM) for hydraulic machinery, a series of system parameters are set to achieve the desired system behavior, e.g., secondary flow suppression or runner efficiency. In contrast to the traditional design approach, where geometrical parameters are treated as design variables, the IDM focuses on hydrodynamic parameters, guaranteeing more direct control over the machine hydrodynamics. Instead of defining a blade angle distribution, the designer specifies the runner blade loading distribution, hence indirectly defining the pressure distribution on the blades. This relationship between blade loading and pressure distribution represents the strength of the IDM method, since it results in a more physically intuitive method for reaching the desired flow field rather than defining the blade angles. Once the loading distribution is defined, the angle distribution of the runner blade is evaluated in order to define the runner geometry. Consequently, the numerical effort necessary to reach a satisfactory result via CFD analyses may be drastically reduced.
However, despite the successful application of this method in the hydraulic pump field, the interest in its adoption for hydraulic turbines has grown in recent years. As a result of this, the main aim of this paper is to illustrate the results achieved so far in the field of hydraulic turbines to identify the most promising developments to be adopted in modern design strategies of hydraulic turbines.
The remaining paper is structured as follows: Section 2 presents an account of the development and implementation of the IDM method; in Section 3, the basic theory of the IDM is presented and analyzed by describing both the governing equations and the numerical implementation approach; in Section 4, the most interesting design solutions recently adopted in the field of Francis turbines and pump turbines are presented and analyzed; and finally, in Section 5, the most promising strategies for developing the new generation of hydraulic turbines are identified and discussed.
2. Literature Overview of the Inverse Design Method
The turbomachinery field is dominated by viscous, turbulent, three-dimensional, unsteady flow. Recent developments, both in experimental and computational techniques, have provided a better understanding of the three-dimensional flow fields in many types of turbomachinery. However, using these results to optimize the blade geometry still represents a challenge for turbomachinery designers. In fact, the current design practice consists of incremental changes to existing geometries, the impact of which on the flow field is evaluated using analysis methods, without the possibility of controlling—even in an approximate way—the machine fluid dynamics in the design phase. It is hence difficult for a designer to incorporate their knowledge of fluid dynamics directly into the optimization process, since there are no clear correlations between the blade shape and the fluid flow field.
As the name implies, the direct design approach involves the direct control of the geometric parameters defining the three-dimensional geometry of the blades. However, even a slight change in one parameter at one location can greatly affect the flow field upstream and/or downstream. This difficulty is further amplified by the large number of geometric variables defining the three-dimensional blade geometry, whose simultaneous impact on the flow field cannot be controlled during the design phase. Therefore, the direct design approach represents a time-consuming method mainly based on designer experience, due to the lack of a direct relationship between the geometric control parameters and the internal flow characteristics.
In contrast, the inverse design method (IDM) uses the fluid dynamic parameters of the blade load distribution as input data. Furthermore, the influence of other geometric design parameters such as the meridional shape and number of blades can be analyzed more independently for the same blade loading pattern.
The advantages of such an approach are evident. The IDM has several important features compared to conventional design methods [6,7], such as being controlled by hydrodynamic parameters. Moreover, the IDM can handle 3D flow effects, allowing the designers to gain a good understanding of the secondary flow development. Thanks to such an approach, the costs associated with optimization processes can be reduced.
Although traditional and inverse design approaches generally share the same goals, such as increasing hydraulic efficiency, there are clear differences in the final blade geometries. The blade angle distribution of a conventionally designed impeller is generally quite uniform, whereas blades designed using the IDM generally exhibit greater complexity, with significant blade angle variations in both the flow and span directions. However, before entering into the theoretical aspects of the method, it is interesting to briefly present an account of its development and implementation in the fluid machine field.
Originally developed for the hydraulic design of hydrofoils, the first computational implementations of the IDM for hydraulic pumps are dated between the 1980s and 1990s. These first codes used IDMs in a general design method developed for two-dimensional incompressible potential flows.
However, the first appearance of IDMs for impeller design dates back to World War II, when the group of scientists led by Werner von Braun used a similar approach for the design of the V-1 and V-2 rockets [8]. Since the 1950s, several two-dimensional and later quasi-three-dimensional inverse design methods have been developed thanks to various researchers [9,10]. They were able to further improve this method and significantly increase the design quality using the approach established by Wu [11] in 1952 to calculate the flows combination on relative stream surfaces upstream or midway in blade rows.
The application of the IDM for turbomachinery design was first studied in 1984 by Hawthorne et al. [12] and Tan et al. [13]. These researchers initially based their studies on two-dimensional flow calculations assuming a non-viscous and incompressible flow. However, because of the strong simplifications introduced into the fluid flow evaluation, the contribution of these first applications in the blade design was limited: the blade geometry was determined imposing the flow conditions at the machine walls without considering the influence of the boundary layer or the blade thickness [13].
Thanks to the contribution of several researchers, such as Borges [14,15] and Zangeneh et al. [16,17,18], the IDM then evolved into a three-dimensional method based on the potential flow theory.
In particular, in 1990, Borges [14] proposed a design strategy based on setting the distribution of the mean swirl over the runner meridional section. This approach was applied in the design of a slow-speed radial turbine and validated in an experimental campaign [15]. The IDM approach allowed to increase the hydraulic efficiency by about 1.4% in comparison with the conventional design strategy. Starting from these promising results, in 1991, Borges [19] presented a through-flow (hub-to-shroud) inverse method for the design of a rotor of a mixed flow pump. The fluid was considered inviscid, incompressible, and irrotational at the inlet and the blade thickness was neglected. Borges was able to obtain reasonable pressure distributions on the blade surfaces with a small amount of CPU time.
In 1996, Zangeneh et al. [16] adopted a new implementation of the three-dimensional compressible inverse design method to study the design of a radial and mixed flow turbomachine. Their method considered as input the distribution of the circumferentially averaged swirl velocity on the meridional geometry of the impeller, while the corresponding blade geometry was then interactively calculated. Here, two different approaches were proposed for the solution of the flow field: In the first approach, named approximate, the variation in the density in the pitch was neglected, thus resulting in a simplified and time-saving algorithm. In the second approach, named exact, the velocities and densities in the entire three-dimensional flow field were evaluated using a fast Fourier transform over the tangential direction. These two approaches were applied on the case of a high-speed radial turbine (subsonic), resulting in two blade geometries with almost negligible differences. The flows resulting from the two geometries were computed using a three-dimensional inviscid Euler model. Both showed a good correlation between the estimated and resulting distributions of and a negligible fluid field variation, confirming the effectiveness of the method, which was applied in several application cases ranging from the field of compressible and non-compressible fluid turbomachines (operating machines and prime movers).
Zangeneh et al. successfully applied a derivative of the mean swirl distribution to suppress secondary flows in a mixing pump impeller [20] and a compressor diffuser [21]. In addition, Goto et al. [22] investigated a different approach to redesign pump diffuser vanes with the aim of suppressing flow separation. Based on this last model, Zangeneh et al. [23] attempted to design a centrifugal compressor with diffuser blades.
In 1998, Demeulenaere et al. [24] developed an IDM that incorporated the specified pressure distribution instead of an average vortex distribution to design compressor and turbine blades using the Euler model for three-dimensional inviscid flows. De Vito et al. [25] combined the method in [24] with a direct two-dimensional Navier–Stokes method in an iterative scheme to redesign a turbine blade.
Dang et al. developed a particular IDM by using the Euler model for two-dimensional cascades [26] and then for fully three-dimensional geometries [27] by employing a specified pressure distribution and thickness distribution.
The IDM was then extended for other different blade types by several researchers such as Jiang et al. [28]. Damle et al. [29] used the same approach to increase the efficiency of a first stage rotor of a centrifugal compressor. Then, Daneshkhah et al. [30] developed a two-dimensional inverse Navier–Stokes method using a given pressure and thickness distribution to redesign a subsonic turbine and a transonic compressor. In addition, Wang et al. [31] presented a 3D inverse method based on the Navier–Stokes equations using a prescribed pressure distribution for three-dimensional cascades.
The benefits derived by the direct imposition of the blade load and/or of the static pressure distribution have been repeatedly proven over the years.
As an example, in the optimization proposed by Tiow et al. [32] for the high-speed NASA rotos 67, the blade load distribution was found to be strictly related to both the location and intensity of the shock, hence demonstrating its effectiveness as a design parameter. Other interesting applications can be found for several specific applications such as pumps [33,34,35], turbines, pump turbines, compressors [21,23,36], diffusers [22,37,38], and inducers [39,40].
Despite the fact that in such examples the flow evaluation was based on potential flow theory without viscosity, the fluid viscous effect can be introduced by considering further parameters related to the viscosity of the fluid, such as the clogging distribution, the vorticity, or the entropy gradient [41].
However, it is important to emphasize how the IDM is based on different approaches to the flow field calculation. Specifically, the IDM can be classified into four different categories: the “inviscid” category, as described in the references by Pàscoa et al. [42] and also by Zangeneh et al. [43]; the “viscous” category [30,44,45]; the “compressible” category, analyzed in particular by Zangeneh et al. [16]; and the “incompressible” category, studied in the initial phase by researchers such as Hawthorne et al., Tan et al., and Borges [12,13,14,15,19].
Despite the intense evolution witnessed here from the first two-dimensional implementations with incompressible flows to the most recent three-dimensional applications with viscous and/or compressible flows, the concept behind the IDM remains the same. Furthermore, all applications currently do not take into account the unsteady behavior of the flow and thus do not directly address the important aspect of the instability of turbomachinery.
Finally, in 2020, Leguizamón and Avellan [5] proposed an open-source implementation of the IDM method specifically developed for Francis hydraulic turbines, representing the first non-proprietary software available to the public.
Nowadays, the notable development of computational fluid dynamics (CFD) has made it possible to evaluate the fluid dynamics in turbomachinery in ever greater detail at an ever lower computational cost. In this scenario, the combination of the IDM and CFD would represent a powerful tool for turbomachinery development and optimization. However, since a fully three-dimensional turbulence flow calculation approach cannot be easily directly introduced into the IDM, the trial-and-error design process of turbomachinery still represents the only one viable solution. Nevertheless, the IDM can still play a crucial role during the design phase by significantly reducing the number of iterative steps to be performed during the performance evaluation of the design outcomes.
3. IDM and Suppression of Secondary Flows
3.1. Secondary Flows: The Example of the “Jet–Wake” Phenomenon
The performance of hydraulic machines is affected by the development of secondary flows, the causes of which vary depending on the type of machine and on the flow direction. One of the simplest is certainly represented by the so-called “jet–wake” flow [46] developed in radial pumps and compressors and characterized by a low velocity wake region near to the blade suction side combined with a jet region close to the pressure side.
As reported by Zangeneh et al. [18], the onset of this structure is mainly due to secondary flows, causing the transport of low momentum fluid regions in the impeller. According to Balje [47], the development of secondary flows in the channels of turbomachinery is controlled by two parameters:
the Richardson number, connected to the rotational velocity ω of the impeller:
the Richardson number due to the curvature of the duct faces:
where W represents the fluid speed in the relative frame, y is the distance in the normal direction to the flow trajectories, and R is the radius of curvature of the relative fluid trajectories, i.e., the curvature of the interblade channel. The Richardson numbers govern the flow within the boundary layer near the surfaces of the blade-to-blade and meridian channels. While the Richardson number represents the local ratio between the mean value of the Coriolis forces and the inertial force of the relative flow, the Richardson number represents the local ratio between the centrifugal force induced by the channel curvature radius R and the inertial force of the relative flow. The parameters and , defined by Bajle, allow the quantification of the stability of the flow, i.e., the possible onset of secondary flows under the influence of the impeller angular velocity ω and the channel curvature radius R. Specifically, the fluid flow will manifest a stable behavior for values of and above 0.
Figure 1 shows a schematization of the distribution of the Richardson parameters in a pump runner. According to the Richardson stability criteria, due to the channel curvature R, the fluid flow shows a stable behavior close to the blade pressure side (PS) where > 0. Indeed, the curvature of the flow relative trajectories induces a static pressure gradient in the angular coordinate (Figure 1), with a greater pressure corresponding to the blade suction side. On the contrary, due to the Coriolis forces, i.e., the effect of the angular velocity ω, the flow is stable on the blade suction side SS ( > 0), while it is unstable on the PS (Figure 1), resulting in conflicting effects.
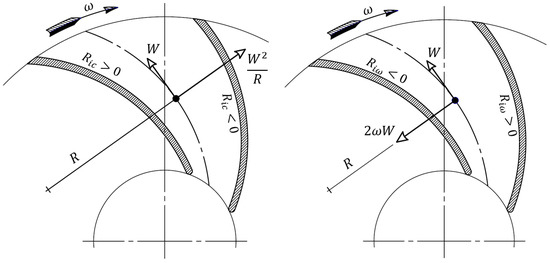
Figure 1.
The parameters and , studied along the blade-to-blade duct of a pump impeller.
In turbomachines with a predominantly radial geometry, the most important effect is associated with the angular velocity ω and hence the flow unsteadiness is located mainly on the blade PS. Here, the production of turbulent kinetic energy increases in the orthogonal direction to the relative flow trajectories. In this scenario, the turbulent vortex cores produce flow stratification with high-energy particles mixed with low-energy particles (Figure 2).
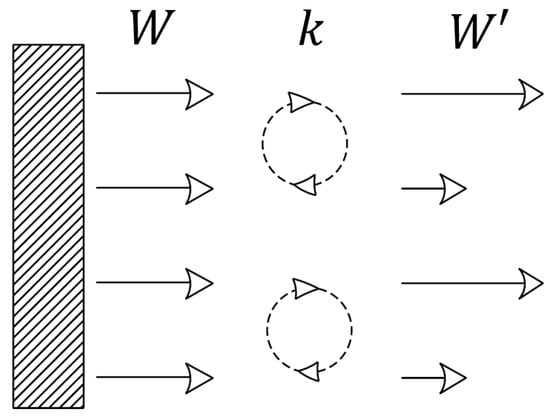
Figure 2.
Mixing of the relative velocity magnitude W due to the production of turbulent kinetic energy k.
It is precisely because of this stratification that a differentiation occurs between the trajectories of particles characterized by high and low energy densities. In particular, it can be demonstrated that the generally greater influence of the Coriolis force in comparison to the centrifugal force drives the fluid particles with a higher relative speed W towards the blade PS. On the contrary, particles with a lower velocity W tend to flow towards the blade suction side, driven by the pressure gradient. Similarly, in the meridional section, fluid particles with a low kinetic energy density tend to flow toward the low-pressure region, i.e., toward the runner shroud surface, where > 0. This leads to the development of two separate flow regions: the wake region, characterized by a low energy density, and the jet region, characterized by a high energy density (Figure 3). The volume fraction between the wake and jet regions is defined by the balance between the centrifugal and Coriolis forces and hence by the runner geometry.
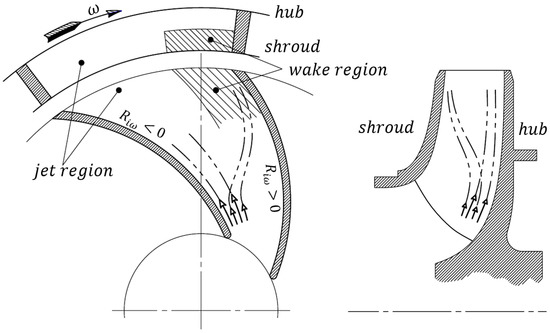
Figure 3.
Representation of the jet region and the wake region in the interblade channel.
Despite the formulation of the secondary flow theory, bringing a simple example related to the pump and compressor field, the above discussion can be extended to the case of hydraulic turbines also affected by secondary flows with different characteristics but with similar driving factors (pressure gradients, velocity gradients, etc.).
3.2. The IDM and the Suppression of Secondary Flows
The development of secondary flows is a non-negligible source of hydraulic losses in both pumps and turbines. In this scenario, the 3D inverse design method represents the most efficient approach to understand and control the three-dimensional effect of the flow field occurring in turbomachinery.
By introducing the momentum equation in the non-viscous flow [48], it is possible to relate the static pressure gradient to the effect of the centrifugal and Coriolis forces on the flow:
where the term in brackets on the right-hand side stands for the so-called “reduced static pressure”, which is also denoted by . According to Equation (3), in a rotating system, the gradients of the reduced pressure are generated as a result of the streamline curvature and of the Coriolis acceleration. Secondary flows are generated whenever there is a gradient of reduced static pressure in the flow field in the vorticity direction. Thus, by controlling the gradients of reduced static pressure at certain points in the impeller, it should be possible to minimize the secondary flows and reduce the non-uniformity of the flow field.
As reported by Zangeneh et al. [49], to suppress these secondary flows, it is important to optimize the distribution of the predicted pressure coefficient, , on the suction surface of the impeller, defined as [50]:
The most effective way to independently control the distribution of the blade load on the hub and the surface of the impeller is represented by IDMs 3D formulation. Detailed information on the theory, governing equations, and numerical implementation of the inverse design method can be found in references [16,41,51].
To summarize, following Hawthorne et al. [12] and Tan et al. [13], in the IDM, the blades are represented by sheets of vorticity whose strength is directly related to the specified bound circulation, , defined as:
For incompressible flows, the pressure loading is directly related to the meridional derivative of , or blade loading, namely:
where the term stands for the pressure difference across the blade, is the meridional velocity at the blades, and is the meridional distance in the streamwise direction. In this scenario, the development and intensity of the secondary flows can be controlled by controlling the distribution.
Another complementary solution to suppress secondary flows in radial and mixed flow turbomachinery is to assume suitable stacking conditions. In pumps, a linear lean of the blade trailing edge against the direction of rotation is usually adopted. With this approach, close to the impeller outlet section, the load decreases at the shroud and increases at the hub. However, there are limits to the inclination of the blade trailing edge due to structural and manufacturing constraints.
In recent years, several studies have been performed on the influence of the blade load distribution on the hydrodynamic behavior of both hydraulic pumps [52,53] and compressors [23,36].
Zangeneh et al. [16,20,50] suggested a flexible distribution of the meridional derivative , which is generally specified along the hub and shroud streamlines (Figure 4). For each streamline, the distribution is represented by three segments and four parameters: the connection point locations NC and ND, the slope of the linear line SLOPE, and the loading at the leading edge DRVT. These are used to control the distribution curve.
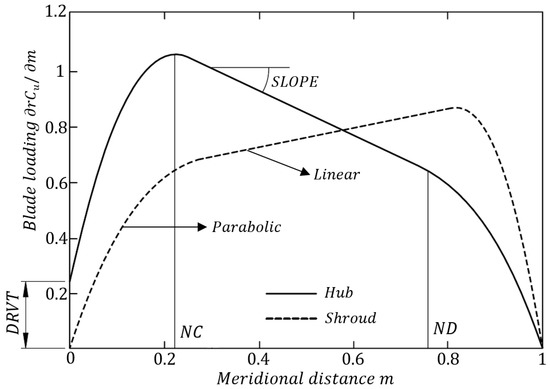
Figure 4.
Blade loading distribution and its parameters for impellers.
The blade loading inside the blade channel is determined by a linear interpolation between the hub and shroud. For pump applications, good results were obtained with SLOPE = 30°, NC = 0.2–0.3, and ND = 0.7–0.8.
In summary, the 3D inverse design method uses the blade loading distribution combined with the stacking conditions at the trailing edge as input parameters. This approach enables directly controlling the blade pressure loading. In this way, the designer can control the development of secondary flows, hence reducing the jet–wake structure.
As anticipated above, the jet–wake phenomenon is just an example to show the correlation between IDMs and secondary flows related to the pump/compressor fields. However, this method is also applicable to hydraulic turbines, whose flow field is also characterized by secondary flows, such as interblade vortexes, with different characteristics but with a correlation with the blade loading. Since this paper does not focus on secondary flows, a detailed description of all the possible secondary flows is avoided. Detailed information on secondary flows occurring in Francis turbines and in reversible pump turbines operating at off-design conditions can be found in references [54,55,56,57]
In this scenario, IDM adoption could limit the development of the interblade vortexes by modifying the flow incidence condition. Moreover, the control of the static pressure distribution represents an effective method for the suppression of cavitation phenomena without compromising the hydraulic efficiency.
In the next section, different applications for turbines and pump turbines and the corresponding results of the inverse 3D design method are presented in order highlight efficient guidelines for the design of the new generation of hydraulic turbines. For a better understanding, a flow chart for the basic calculation process of the inverse design method is reported below (Figure 5).
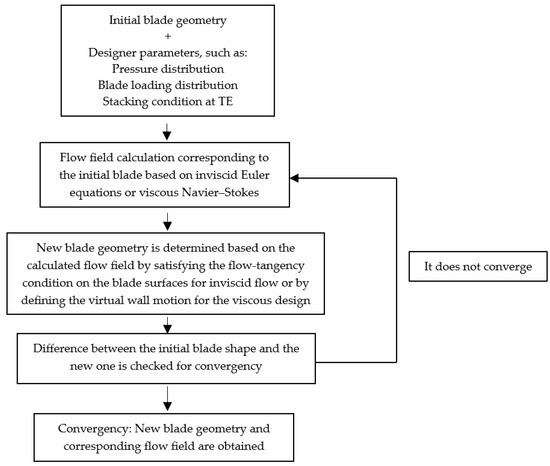
Figure 5.
Flow chart of the inverse design method.
4. IDM Applications in Hydraulic Turbines
Three-dimensional inverse design methods are traditionally applied to pumps due to the higher risk of flow separation phenomena. Many researchers have obtained successful results in terms of the efficiency and performance of hydraulic pumps [20,33,34,35], as previously reported.
Only recently have analyses and applications of the inverse design method also started to be used for pump turbines and Francis turbines. This section contains all the results of the applications to hydraulic turbines so far documented with a discussion about the most interesting results in terms of design guidelines.
4.1. Application in Pump Turbines
Thanks to their high efficiency range and competitive costs, pumped hydro today represents the most diffused and mature solution for energy storage with an approximate installed worldwide capacity of 130 GW [58]. It also provides ancillary services (e.g., grid frequency and voltage control) to support grid stability.
Representing the core mechanical equipment adopted in the new generation of pumped hydro facilities, pump turbines are usually required to operate with high hydraulic efficiency both in the pumping and turbine mode, also rapidly switching from one operating condition to the other. However, the development of a unique design procedure for the pump turbine impeller to optimize both the pump and turbine efficiency is still a challenge. Just to mention one aspect, for the same nominal head and revolution speed, the pump diameter suggested by the design theory and experience is larger than the turbine one.
Thus, the traditional pump turbine design process is pump orientated, and the behavior in the turbine mode is verified in a second phase. This is due to the fact that the demands in pump mode are more challenging (e.g., cavitation and flow stability), whereas in turbine mode, it is easier to meet the turbine requirements because the impeller is larger than needed.
It is also important to maintain good performance in the whole operating range of a pump turbine and to guarantee flexible operation in both modes. This is still a big challenge since in pump operation, instabilities and cavitation occurrences limit the normal operating range, and in turbine operation, draft tube vortices with pressure fluctuations and instabilities mainly determine smooth operation and limit the operating range.
To solve this challenge, some authors have tried to apply the IDM method in order to better control the flow stability. Kerschberger and Gehrer [59] developed an important study on a runner blade profile for a low-head pump turbine in order to increase the stable operating range in pumping mode. For the blade design, they applied Zangeneh’s model of a 3D inverse design method [16]. The input parameters were the meridional shape of the impeller, the design operating point, the blade number, the blade loading distribution in the meridional direction, and the blade thickness. As a result of the optimization process, the final runner showed a steeper slope of the head–capacity curve and moved the instability onset to higher head values compared to the reference model. Moreover, the cavitation free zone was widened by shifting the onset of suction side cavitation to lower flow rates and the overall efficiency level was significantly improved.
Combining the 3D inverse design method with CFD analyses, design of experiment (DoE), response surface methodology (RSM), and multi-objective genetic algorithms (MOGA), Yang and Xiao [60] presented a multi-objective optimization strategy for pump turbine design, aimed at controlling the onset and development of secondary flows. As introduced in the first part of this section, the design initially started from the pump mode. While the meridional geometry was fixed, the design focused on the blade loading distributions and the blade trailing edge lean angle. Linear stacking was imposed on the high-pressure edge of the blades, corresponding to the trailing edge in pump mode. The slope of the lean angle was varied from −10 to +10 degrees with positive stacking in the case of the hub preceding the shroud in the rotational direction. To better control the secondary flows, the optimized blade loading distributions were aft loaded on both the hub and shroud and the maximum loading difference between the hub and the shroud was located on the fore part of the impeller. Regarding stacking conditions, the average blade angle at the leading edge increased by 2.38 degrees compared to the baseline impeller.
The pump turbine design was improved by IDM application. The efficiencies in both modes and in the whole operating range were improved, but the main enhancements were obtained for the pump mode with secondary flow near the shroud corner and the complete suppression of the crossflow from the suction to the pressure side in the optimized design.
Other studies have focused on the pump turbine stability problems near the no-load conditions in turbine mode. Yin et al. [61] analyzed the blade loading distributions in runners with and without an S-shaped curve near the no-load conditions. They demonstrated a correlation between the S-shaped curve and the hydraulic loss in the runner, which greatly increased with decreasing flow rate values. Moreover, through a direct analysis of the blade loading distribution, they identified a method for suppressing the S shape by broadening the meridional passage. This design method was also applied by Lu et al. [62], who confirmed that decreasing the meridional velocity by broadening the meridional section could effectively suppress the negative slope of the performance curve. However, the effects of this modification of the meridional passage in pump mode were not investigated.
The behavior in both modes was investigated in the same period by Chen et al. [63]. By means of the inverse IDM, they started applying a specific blade loading distribution in which the peaks of were located in the forepart of the shroud and in the hub aft part. Then, they modified the blade shape on the blade low pressure side and tested different blade stacking angles on the pressure side. Among all the combinations of blade shape, one resulted in an improvement in the performance, the internal flow, and the efficiency in pump mode but not in turbine mode. Benefits in terms of secondary flow removal and efficiency were also obtained by an appropriate choice of the stacking angle at the shroud in pump mode and at the hub in turbine mode.
Wang et al. [64] employed the same optimization process used by Yang and Xiao [60] to design a middle/high-head pump turbine runner, adopting a fore-loaded distribution at both the hub and shroud in order to improve the efficiency of the runner in turbine mode. They analyzed the influence of the different input parameters on the pump and turbine efficiencies, demonstrating adverse effects. As a result, the efficiency of the optimized runner was increased by about 2% in turbine mode with a negligible variation in the efficiency in pump mode. An optimization process based on the same fore-loaded blade loading distributions was applied by Xuhe et al. [65]. The final geometry was characterized by a big positive blade lean on the high pressure side and a fixed meridional shape, resulting in an improved runner performance in particular for turbine operation.
A similar strategy was also adopted by Zhu et al. [66] for a reversible middle-head pump turbine runner with a large negative blade lean angle, a fore-loaded distribution on the hub, and an aft loaded one on the shroud.
This runner geometry improved the efficiency at small flow rates in pumping mode with an enhancement in the performance in the hump region. With this combination of blade loading distributions and stacking conditions, the cavitation performance was also significantly improved, with lower pressure fluctuations in comparison with the solution characterized by a large positive blade lean angle and a fore-loaded distribution both at the hub and the shroud. Starting from these results, Zhu et al. stressed the positive impact of the large negative blade lean if combined with a proper meridional channel shape. In particular, they highlighted the possibility of also reducing the S-shaped region in turbine mode by properly broadening the meridional channel shape.
A more complex optimization strategy was proposed years later, in 2017, by Liu et al. [67], who combined the 3D inverse design method, CFD analysis, DoE, RSM, and a MOGA. With this optimization strategy, the researchers aimed to offer guidelines for the design of an ultrahigh-head turbine runner with high efficiency and stability, highlighting the influence of different design parameters on the runner performance. The blade loading distributions of the initial runner on the hub and shroud were both back-loaded, while the optimized blade loading distributions were middle-loaded on the hub and back-loaded on the shroud. The adopted runner had a negative blade lean angle and the blade cross-sections were distorted near the low-pressure side compared to the initial one, which had no lean on the high-pressure side. The runner efficiencies increased by about 0.6% and 0.7% in pump and turbine mode, respectively. The proposed blade loading distribution (middle-loaded on hub and back-loaded on shroud) was also tested on other runners, confirming its effectiveness in improving the efficiency in both turbine and pump mode and the cavitation behavior. By fixing this combination of blade loading, the effect of blade lean on the runner performance was also investigated. Runners with a large positive blade lean angle had an improved efficiency in both modes, while runners with a large negative blade lean angle had an increased efficiency in pump mode that decreased in turbine mode.
Besides the efficiency, the choice of the blade lean angle showed an impact on the discharge angle and the mass flow distribution along the span with possible consequences on pressure fluctuations and hence on the runner hydraulic stability, particularly at deep partial loads in turbine mode. To analyze this influence, Zhu et al. compared two reversible pump turbine runners, one with a big positive blade lean and the other with a big negative blade lean [68]. The analyzed runners had the same input parameters as Zhu’s previous work [66]. The runner with a negative blade lean angle and rake angle, whose load distribution was more uniform, showed a greater operational stability, confirming the effectiveness of the negative lean angle in limiting the low pressure separation region.
The following year, Wang et al. [69] optimized a pump turbine runner by trying to simultaneously minimize the secondary flow and profile loss factors while maintaining the same meridional profile, stacking characteristics, and load distribution in pump mode. As Zangeneh et al. [50] previously demonstrated, to suppress secondary flows and increase the efficiency in pump mode, a moderate aft-loaded hub loading distribution is suggested, whereas to minimize the profile loss and increase the efficiency in turbine mode, a very strong fore-loaded streamwise loading distribution on the hub was suggested. The optimization process resulted in three designs, characterized by the same fore-loaded loading on the shroud section. In the first one, aimed at minimizing the secondary flows, the area of low momentum flow towards the pressure side of the blade was reduced, contributing to a more uniform flow at the exit of the passage. In the same way, the design with a minimal profile loss presented a significantly smaller flow separation on the blade suction side than the others.
The trade-off design, which had a hub loading distribution between the two previous solutions, resulted in a compromise in terms of runner performance.
Another interesting application of the 3D inverse design method is the one reported by Hu et al. [70] focusing on a multi-objective optimization of an ultrahigh-head pump turbine runner with splitter blades. The optimization only focused on the blade loadings and on the splitter work ratio , defined as:
The total number of optimization variables was 17 (16 parameters for the blade loadings and 1 for the splitter work ratio ). The optimized blade loading distribution, improving the efficiency in turbine operation, resulted in the splitter blades being much more loaded and having a bigger wrap angle compared to the initial design. Moreover, the researchers demonstrated a positive influence of the splitter ratio ; a larger value of improved the flow pattern and the pressure distribution, increasing the pump efficiency by 0.34% and the turbine efficiency by 2.07% compared to the initial runner.
A similar approach, again based on the 3D inverse design method combined with CFD and a MOGA, was proposed by Hu et al. [71], whose study aimed at broadening the operating range of pump turbines to deep-part loads and considered the efficiency, anti-cavitation, and stability aspects. In this work, there were eight parameters for the blade loading pattern together with the blade lean angle. A positive lean angle was defined as the direction of rotation along the pump mode, while a negative angle was the opposite.
From the optimization results, different runner designs were analyzed in order to investigate the influence of the geometry on the efficiency and cavitation performance under pump mode, and on the rated efficiency and deep-load efficiency under turbine mode. Regarding the runner geometry features, the shape of the shroud section has a greater impact on the runner cavitation performance; the larger the wrap angle, the larger the improvement in runner cavitation performance, but the smaller the pump peak efficiency.
As regards the turbine efficiency, the blade shape plays a key role. In particular, runners with a lower arch and a smaller wrap angle have an effectively improved turbine-rated efficiency, while a higher arch and a larger wrap angle can improve the part-load efficiency. From all the analyses, runners with a fore-loaded shroud section and an aft-loaded hub section are optimal. This runner solution is the trade-off configuration of cavitation (NPSHr decreases by 0.36 m) and pump peak efficiency performance (increased by 0.45%). The turbine-rated efficiency increases by 0.12% and the efficiency at 40% output increases by 9.2%.
4.2. Applications in Francis Turbines
As previously reported, nowadays, only a few documented IDM applications in the field of Francis turbines are available. Indeed, hydraulic turbines tend to be less susceptible to flow detachment compared to pumps due to the deceleration of the flow speed in the relative frame. Nevertheless, in the hydraulic turbine field, the advantages provided by the application of the IDM are also undeniable. Beyond the suppression of secondary flows, necessary in order to increase the hydraulic efficiency, one of the most important flow features controlled during the design phase is represented by the machine cavitating behavior. The cavitation onset is indeed associated with a variety of phenomena detrimental for safe machine operating conditions, such as fast erosion, noise or vibrations, and a reduced stable operating range.
To the authors’ knowledge, one of the first IDM applications in the hydraulic turbine field was proposed in 2002 by Okamoto and Goto [72], who applied the 3D inverse method of Zangeneh [16] to suppress the cavitation phenomena without deteriorating the hydraulic efficiency of a Francis turbine runner. The original runner, designed according to the traditional approach with high blade loading in the inlet section, showed a strong vortex cavitation developing from the hub suction surface corner. Without modifying the meridional geometry, the modification of the blade loading close to the leading edge on the hub allowed to suppress the low static pressure region associated with the onset of the cavitation phenomenon. A better solution for blade loading distribution at the leading edge was aft-loaded at the hub surface to suppress pressure reduction, and fore-loaded at the shroud surface, while the opposite situation occurred in the outlet section. Benefits were also derived from the use of a positive stacking condition.
After a few years, in 2010, Daneshkah and Zangeneh [73] described the parametric design of a high specific speed Francis turbine runner. Similar to Okamoto’s research [72], the aim of this paper was to obtain a cavitation-free runner characterized by a high hydraulic efficiency. In fact, the original runner was affected by a low pressure region on the hub suction surfaces and by a strong cavitation on the shroud near the trailing edge region. The commercial 3D inverse design code TURBOdesign-1 [16], based on a three-dimensional inviscid inverse design method, was adopted for the runner hydraulic design. The distribution of the circumferentially averaged swirl velocity was arranged in the blade meridional channel and the corresponding blade shape was computed iteratively. Since the cavitation phenomenon occurred in the baseline in a region between the midspan and hub runner surfaces in proximity to the trailing edge, a fore-loaded distribution was specified corresponding to the hub, while the same loading distribution as the baseline runner was adopted for the shroud surface. Three different stacking configurations were investigated: −15, −30, and −45 degrees. The negative sign, according to the authors’ nomenclature, indicates the direction of stacking in such a way that the pressure loading on the hub suction is reduced and the pressure loading at the shroud is increased. According to the results obtained by Okamoto, the optimization of the runner via an IDM approach results in a sharp improvement in the machine cavitation behavior, also resulting in a rise in the hydraulic efficiency in almost the entire operating range.
In 2019, Ma et al. [74] performed a study related to a comprehensive hydraulic improvement of a traditional Francis turbine runner by adopting the 3D inverse design software TURBOdesign-5.2 combined with the ANSYS CFX software for the numerical solution of the RANS equations. The authors proposed a two-step multi-objective optimization of the hydrodynamic behavior of a high-specific-speed Francis turbine.
Using the three-segment blade load parametrization proposed by Zangeneh [16,20], in the first part of the optimization procedure, a series of seven control variables were adopted for the full parametrization of the blade geometry, while no modification was proposed for the runner hub and shroud surfaces. In the second part, the effect induced by the meridional projection of the blade’s leading and trailing edges was also evaluated while keeping constant the blade lean and load distribution. More details about the design variables and the optimization search domain can be found in study [74]. Three groups of runners were selected to explain and demonstrate the effects of the following design parameters: blade lean, blade loading, and meridional shape.
For runners characterized by a relatively short flow passage, the adoption of a high negative inlet lean angle impacted the pressure distribution in the runner outlet section. By increasing the blade lean, the low pressure region enlarges along the blade suction side near the outlet, likely reducing the cavitation characteristics. In terms of efficiency, the runners achieved an improvement from 0.37% up to 0.91%.
5. Conclusions
The effectiveness of the three-dimensional inverse design method in the optimization of hydraulic machines has been widely demonstrated with several applications in radial pumps and compressor fields. Nevertheless, despite the inherent potential of the method, few studies regarding the IDM application for the design of hydraulic turbines are available. As a result of this, the main aim of this research is to analyze the influence of the blade load distribution on the hydrodynamic of Francis turbines and reversible pump turbines operating in turbine mode.
In this paper, the most interesting design solutions so far documented regarding the application of the 3D inverse design method are presented and discussed in order to provide useful design guidelines to be implemented in the design strategies of the new generation hydraulic turbines.
For pump turbine applications, the performance requirements in pump mode are prioritized in the design phase. In fact, RPTs are usually first designed in pump mode and then verified in turbine mode. In this case, designers should keep in mind a high efficiency, no cavitation, and a good stability in order to optimize the pump turbine design. Nevertheless, it is important to underline how the blade load optimization also influences the machine hydrodynamics in turbine mode. A summary of the most effective design strategies aimed at improving turbine mode without deteriorating the pump mode performance is reported in the following:
- ▪ To improve the efficiency under the two operating modes, a middle-loaded blade loading distribution in the hub and a back-loaded distribution on the shroud can be adopted. If designers want to concentrate on the turbine mode in order to increase its efficiency, a large positive blade lean angle on the high-pressure side is suggested, which means blades are leaning linearly against the direction of rotation in pump mode.
- ▪ Large blade lean angles may also induce a drop in the lowest pressure, negatively affecting the cavitation characteristics. To avoid this, the blade loading on the shroud should be reduced near the low-pressure side.
- ▪ Adopting a fore-loaded distribution at the shroud and an aft-loaded one at the hub and broadening the meridional section could effectively suppress the negative slope of the characteristic curve. Consequently, the runner may have a stable performance curve and hence may satisfy the requirements for safe operation in pumped storage plants.
In order to satisfy the balance of cavitation, efficiency, and also stability, designers can apply a combination of the hub aft-loaded and shroud fore-loaded loading patterns with a positive blade lean angle for the runners targeting a wide output range. Additionally, geometric characteristics have to be considered. For example, it is recommended to maximize the pump peak efficiency and the turbine-rated efficiency for runners with a small wrap angle and low arch blades, whereas it is recommended to maximize the cavitation performance and part-load efficiency for runners with a large wrap angle and high arch blades.
For Francis turbine application, the low susceptibility to flow detachment reduces the potential benefits of IDM application in the design phase. Nevertheless, the IDM still represents a powerful tool to optimize the machine's hydrodynamics by improving the efficiency and cavitation behavior:
- ▪ To guarantee a high hydraulic efficiency, it is recommended to load the hub forward and the shroud downward. Moreover, a high negative inlet lean angle is recommended for runners with a relatively short flow passage.
- ▪ The machine cavitation behavior can be improved by adopting an aft-loaded blade at the hub surface and a fore-loaded blade at the shroud surface at the leading edge to suppress pressure reductions, while the opposite situation occurs at the outlet section. Benefits are also derived from the use of positive stacking conditions.
- ▪ The adoption of a negative lean angle may also improve the machine cavitation behavior, resulting in a decrease in the pressure loading on the hub suction side and a pressure rise at the shroud surface. Furthermore, in the case of a limited flow passage length, the inlet blade lean also affects the pressure in the runner outlet section, with potential benefits in terms of pressure pulsation control.
In conclusion, the three-dimensional inverse design strategy has recently demonstrated its effectiveness in improving the performance both in pump and Francis turbines. Moreover, the IDM represents a powerful tool to control turbines’ hydrodynamics and its application could also be extended to off design operating conditions in order to extend the machines’ operative ranges.
Finally, the IDM applications so far proposed have not considered the typical transient phenomena characterizing the fluid flow in hydraulic turbines. In this scenario, more studies are needed in order to link the transient flow behavior to the adopted blade load distribution.
Author Contributions
Conceptualization, G.Z.; Methodology, G.Z. and M.S.; Writing—Original Draft Preparation, G.Z. and M.S.; Writing—Review and Editing, G.C. and A.S.; Supervision, G.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| absolute velocity | |
| pressure coefficient | |
| head | |
| non-dimensional meridional distance | |
| PS | pressure side |
| pressure | |
| radius | |
| radius of curvature of the relative fluid trajectories | |
| flow angular momentum | |
| rotational velocity Richardson number | |
| curvature Richardson number | |
| splitter ratio | |
| SS | suction side |
| peripheral velocity | |
| relative velocity | |
| y | coordinate perpendicular relative flow trajectories |
| blades number | |
| Greek symbols | |
| blade angle | |
| angular coordinate in meridional plan | |
| density | |
| angular velocity | |
| Subscripts | |
| meridional component | |
| tangential component | |
| Superscripts | |
| s | splitter |
| + | blade pressure side |
| – | blade suction side |
| * | static |
| Abbreviations | |
| CFD | computational fluid dynamics |
| DOE | design of experience |
| IDM | inverse design method |
| LPS | Latin hypercube sampling |
| MOGA | multi-objective genetic algorithm |
| PHES | pumped hydro energy storage |
| RBF | radial basis function |
| RES | renewable energy sources |
| RPT | reversible pump turbine |
| RSM | response surface method |
References
- Gaudard, L.; Romerio, F. The future of hydropower in Europe: Interconnecting climate, markets and policies. Environ. Sci Policy 2014, 37, 172–181. [Google Scholar] [CrossRef]
- Killingtveit, A. 8–Hydropower. In Managing Global Warming: An Interface of Technology and Human Issues; Academic Press: Cambridge, MA, USA, 2018. [Google Scholar] [CrossRef]
- REN21. Renewables 2022 Global Status Report; Technical Report; Secretariat: Paris, France, 2022. [Google Scholar]
- Baxter, R. Energy Storage: A Nontechnical Guide; PennWell: Tulsa, OK, USA, 2006. [Google Scholar]
- Leguizamón, S.; Avellan, F. Open-Source Implementation and Validation of a 3D Inverse Design Method for Francis Turbine Runners. Energies 2020, 13, 2020. [Google Scholar] [CrossRef]
- Wu, J.C.; Shimmei, K.; Tani, K.; Niikura, K.; Sato, J. CFD-based design optimization for hydro turbines. J. Fluids Eng.-Trans. ASME 2007, 129, 159–168. [Google Scholar] [CrossRef]
- Koini, G.N.; Sarakinos, S.S.; Nikolos, I.K. A software tool for parametric design of turbomachinery blades. Adv. Eng. Softw. 2009, 40, 41–51. [Google Scholar] [CrossRef]
- Westra, R.W. Inverse-Design and Optimization Methods for Centrifugal Pump Impellers; University of Twente: Enschede, The Netherlands, 2008. [Google Scholar]
- Peng, G.; Cao, S.; Ishizuka, M.; Hayama, S. Design optimization of axial flow hydraulic turbine runner: Part I—An improved Q3D inverse method. Int. J. Numer. Methods Fluids 2002, 39, 517–531. [Google Scholar] [CrossRef]
- Cao, S.L.; Peng, G.; Yu, Z. Hydrodynamic Design of Rotodynamic Pump Impeller for Multiphase Pumping by Combined Approach of Inverse Design and CFD Analysis. J. Fluids Eng. 2005, 127, 330–338. [Google Scholar] [CrossRef]
- Wu, C.H. A General Theory of Three-Dimensional Flow in Subsonic and Supersonic Turbomachines of Axial-, Radial-, and Mixed-Flow Types; NASA Technical Reports Server NACA-TN-2604; Lewis Flight Propulsion Laboratory: Cleveland, OH, USA, 1952. [Google Scholar]
- Hawthorne, W.R.; Wang, C.; McCune, J.E.; Tan, C.S. Theory of Blade Design for Large Deflections: Part I—Two-Dimensional Cascade. J. Eng. Gas Turbines Power 1984, 106, 346–353. [Google Scholar] [CrossRef]
- Hawthorne, W.R.; McCune, J.E.; Wang, C.; Tan, C.S. Theory of Blade Design for Large Deflections: Part II—Annular Cascades. J. Eng. Gas Turbines Power 1984, 106, 354–365. [Google Scholar] [CrossRef]
- Borges, J.E. A Three-Dimensional Inverse Method for Turbomachinery: Part I—Theory. J. Turbomach. 1990, 112, 346–354. [Google Scholar] [CrossRef]
- Borges, J.E. A Three-Dimensional Inverse Method for Turbomachinery: Part II—Experimental Verification. J. Turbomach. 1990, 112, 355–361. [Google Scholar] [CrossRef]
- Zangeneh, M. A compressible three-dimensional design method for radial and mixed flow turbomachinery blades. Int. J. Numer. Methods Fluids 1991, 13, 599–624. [Google Scholar] [CrossRef]
- Zangeneh, M. An Inverse Design Method for Radial Turbomachines; VKI: Sint-Genesius-Rode, Belgium, 1992. [Google Scholar]
- Zangeneh, M. Development of a 3D Inverse Design Code for Application to Different Turbo and Hydraulic Machinery Components. In Proceedings of the JSME Centennial Grand Congress, Tokyo, Japan, 13–16 July 1997; Volume I, pp. 195–200. [Google Scholar]
- Borges, J.E. A Proposed Through-Flow Inverse Method for the Design of Mixed-Flow Pumps. In Proceedings of the Third International Conference on Inverse Design Concepts and Optimization in Engineering Sciences (ICIDES-3), Washington, DC, USA, 23–25 October 1991. [Google Scholar]
- Zangeneh, M.; Goto, A.; Takemura, T. Suppression of secondary flows in a mixed-flow pump impeller by application of three-dimensional inverse design method: Part 1. design and numerical validation. J. Turbomach. 1996, 118, 536–543. [Google Scholar] [CrossRef]
- Zangeneh, M. Inverse design of centrifugal compressor vaned diffusers in inlet shear flows. J. Turbomach. 1996, 118, 385–393. [Google Scholar] [CrossRef]
- Goto, A.; Zangeneh, M. Hydrodynamic design of pump diffuser using inverse design method and CFD. J. Fluids Eng. 2002, 124, 319–328. [Google Scholar] [CrossRef]
- Zangeneh, M.; Schleer, M.; Ploger, F.; Hong, S.S.; Roduner, C.; Ribi, B.; Abhari, R.S. Investigation of an inversely designed centrifugal compressor stage—Part 1: Design and numerical verification. J. Turbomach. 2004, 126, 73–81. [Google Scholar] [CrossRef]
- Demeulenaere, A.; van den Braembussche, R.A. Three-dimensional inverse method for turbomachinery blading design. J. Turbomach. 1998, 120, 247–255. [Google Scholar] [CrossRef]
- De Vito, L.; van den Braembussche, R.A.; Deconinck, H. A novel two-dimensional viscous inverse design method for turbomachinery blading. J. Turbomach. 2003, 125, 310–316. [Google Scholar] [CrossRef]
- Dang, T.; Isgro, V. Euler-based inverse method for turbomachine blades, part 1: Two-dimensional cascade. AIAA J. 1995, 33, 2309–2315. [Google Scholar] [CrossRef]
- Dang, T.; Damle, S.; Qiu, X. Euler-based inverse method for turbomachine blades, part 2: Three-dimensional flows. AIAA J. 2000, 38, 2007–2013. [Google Scholar] [CrossRef]
- Jiang, J.; Dang, T. Design method for turbomachine blades with finite thickness by the circulation method. J. Turbomach. 1997, 119, 539–543. [Google Scholar] [CrossRef]
- Damle, S.; Dang, T.; Stringham, J.; Razinsky, E. Practical use of three-dimensional inverse method for compressor blade design. J. Turbomach. 1999, 121, 321–325. [Google Scholar] [CrossRef]
- Daneshkhah, K.; Ghaly, W. Aerodynamic inverse design for viscous flow in turbomachinery blading. J. Propuls. Power 2007, 23, 814–820. [Google Scholar] [CrossRef]
- Wang, Z.M.; Cai, R.X.; Chen, H.J.; Jia, X.C. A three-dimensional inverse method using Navier-stokes equations for turbomachinery blading. Inverse Probl. Eng. 2000, 8, 529–551. [Google Scholar] [CrossRef]
- Tiow, W.T.; Zangeneh, M. Application of a three-dimensional viscous transonic inverse method to NASA rotor 67. Proc. Inst. Mech. Eng. Part A J. Power Energy 2002, 216, 243–255. [Google Scholar] [CrossRef]
- Sakurai, T.; Saito, S.; Goto, A.; Ashihara, K. Pump Design System Based on Inverse Design Method and Its Application to Development of Diffuser Pump Series. In Proceedings of the 3rd ASME/JSME Joint Fluid Engineering Conference, San Francisco, CA, USA, 18–23 July 1999. [Google Scholar]
- Ashihara, K.; Goto, A. Study on Pump Impeller with Splitter Blades Designed by 3-D Inverse Design Method. In Proceedings of the ASME Fluids Engineering Division Summer Meeting, Boston, MA, USA, 11–15 June 2000. [Google Scholar]
- Sogawa, Y.; Nohmi, M.; Sakurai, T.; Goto, A. Hydrodynamic Design System for Pumps Based on 3-D CAD, CFD, and Inverse Design Method. J. Fluids Eng. 2002, 124, 329–335. [Google Scholar]
- Schleer, M.; Zangeneh, M.; Roduner, C.; Ribi, B.; Pløger, F.; Abhari, R.S.; Hong, S.S. Investigation of an Inversely Designed Centrifugal Compressor Stage—Part II: Experimental Investigations. J. Turbomach. 2004, 126, 82–90. [Google Scholar] [CrossRef]
- Goto, A.; Zangeneh, M. Compact Design of Diffuser Pumps Using Three-Dimensional Inverse Design Method. In Proceedings of the 3rd ASME/JSME Joint Fluids Engineering Conference, San Francisco, CA, USA, 18–23 July 1999. [Google Scholar]
- Vogt, D.; Roduner, C.; Zangeneh, M. Improving a Vaned Diffuser for a Given Centrifugal Impeller by 3D Inverse Design. In Proceedings of the ASME Turbo Expo 2002: Power for Land, Sea, and Air, Amsterdam, The Netherlands, 3–6 June 2002. [Google Scholar]
- Ashihara, K.; Goto, A.; Kamijo, K.; Yamada, H. Improvements of Inducer Inlet Backflow Characteristics Using 3-D Inverse Design Method. In Proceedings of the 38th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Indianapolis, IN, USA, 7–10 July 2002. [Google Scholar]
- Ashihara, K.; Goto, A. Effects of Blade Loading on Pump Inducer Performance and Flow Fields. In Proceedings of the ASME 2002 Joint, U.S.-European Fluids Engineering Division Conference, Montreal, QC, Canada, 14–18 July 2002. [Google Scholar]
- Zangeneh, M. Inviscid-Viscous Interaction Method for Three-Dimensional Inverse Design of Centrifugal Impellers. J. Turbomach. 1994, 116, 280–290. [Google Scholar] [CrossRef]
- Páscoa, J.; Mendes, A.; Gato, L.; Páscoa, J. A fast iterative inverse method for turbomachinery blade design. Mech. Res. Commun. 2009, 36, 630–637. [Google Scholar] [CrossRef]
- Choo, B.M.F.; Zangeneh, M. Development of an (Adaptive) Unstructured 2-D Inverse Design Method for Turbomachinery Blades. In Proceedings of the ASME Turbo Expo 2002: Power for Land, Sea, and Air, Amsterdam, The Netherlands, 3–6 June 2002. [Google Scholar]
- Daneshkhah, K.; Ghaly, W. An Inverse Blade Design Method for Subsonic and Transonic Viscous Flow in Compressors and Turbines. Inverse Probl. Sci. Eng. 2006, 14, 211–231. [Google Scholar] [CrossRef]
- Roidl, B.; Ghaly, W. Redesign of a Low Speed Turbine Stage Using a New Viscous Inverse Design Method. J. Turbomach. 2010, 133, 011009. [Google Scholar] [CrossRef]
- Dean, R.; Senoo, Y. Rotating Wakes in vaneless diffusers. Tran. ASME J. Basic Eng. 1961, 82, 563–574. [Google Scholar] [CrossRef]
- Balje, O.E. A model for centrifugal compressor rotors. Trans. ASME Power 1978, 100, 148–158. [Google Scholar] [CrossRef]
- Zangeneh, M.; Dawes, W.N.; Hawthorne, W.R. Three-Dimensional Flow in Radial-Inflow Turbines. ASME Paper 88-GT-103; American Society of Mechanical Engineers: New York, NY, USA, 1988. [Google Scholar]
- Zangeneh, M.; Goto, A.; Harada, H. On the design criteria for suppression of secondary flows in centrifugal and mixed-flow impellers. ASME J. Turbomach. 1998, 120, 723–735. [Google Scholar] [CrossRef]
- Zangeneh, M.; Goto, A.; Harada, H. On the Role of Three-Dimensional Inverse Design Methods in Turbomachinery Shape Optimization. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 1999, 213, 27–42. [Google Scholar] [CrossRef]
- Yang, W.; Liu, B.; Xiao, R. Three-dimensional inverse design method for hydraulic machinery. Energies 2019, 12, 3210. [Google Scholar] [CrossRef]
- Tuzson, J. Centrifugal Pump Design; John Wiley & Sons Inc.: New York, NY, USA, 2000. [Google Scholar]
- Cavazzini, G.; Pavesi, G.; Santolin, A.; Ardizzon, G.; Lorenzi, R. Using splitter blades to improve suction performance of centrifugal impeller pumps. Proc. Inst. Mech. Eng. Part A J. Power Energy 2015, 229, 309–323. [Google Scholar] [CrossRef]
- Doussot, F.; Balarac, G.; Brammer, J.; Métais, O.; Ségoufin, C. Numerical simulation and analysis at partial load in Francis turbines: Three-dimensional topology and frequency signature of inter-blade vortices. IOP Conf. Ser. Earth Environ. Sci. 2019, 240, 022045. [Google Scholar] [CrossRef]
- Zhou, L.; Liu, M.; Wang, Z.; Liu, D.; Zhao, Y. Numerical simulation of the blade channel vortices in a Francis turbine runner. Eng. Comput. 2017, 34, 364–376. [Google Scholar] [CrossRef]
- Cavazzini, G.; Houdeline, J.B.; Pavesi, G.; Teller, O.; Ardizzon, G. Unstable behaviour of pump-turbines and its effects on power regulation capacity of pumped-hydro energy storage plants. Renew. Sustain. Energy Rev. 2018, 94, 399–409. [Google Scholar] [CrossRef]
- Zanetti, G.; Cavazzini, G.; Santolin, A. Three-dimensional evolution of the flow unsteadiness in the S-shape of pump-turbines and its correlation with the runner geometry. J. Energy Storage 2022, 57, 106176. [Google Scholar] [CrossRef]
- Yang, C.-J.; Jackson, R.B. Opportunities and barriers to pumped-hydro energy storage in the United States. Renew. Sustain. Energy Rev. 2011, 15, 839–844. [Google Scholar] [CrossRef]
- Kerschberger, P.; Gehrer, A. Hydraulic Development of High Specific-speed Pump-turbines by Means of an Inverse Design Method, Numerical Flow-Simulation (CFD) and Model Testing. IOP Conf. Ser. Earth Environ. Sci. 2010, 12, 012039. [Google Scholar] [CrossRef]
- Yang, W.; Xiao, R. Multiobjective optimization design of a pump–turbine impeller based on an inverse design using a combination optimization strategy. J. Fluid Eng. 2014, 136, 014501. [Google Scholar] [CrossRef]
- Yin, J.; Wang, D.; Wei, X.; Wang, L. Hydraulic improvement to eliminate S-shaped curve in pump turbine. ASME J. Fluids Eng. 2013, 135, 071105. [Google Scholar] [CrossRef]
- Lu, J.; Xi, G.; Qi, D. Blade Optimization of Mixed-Flow Pump by Using Inverse Design Method and Neural Network. J. Xi’an Jiaotong Univ. 2004, 38, 308–312. [Google Scholar]
- Chen, C.; Zhu, B.; Singh, P.M.; Choi, Y.D. Design of a pump-turbine based on the 3D inverse design method. KSFM J. Fluid 2015, 18, 5–10. [Google Scholar] [CrossRef]
- Wang, X.H.; Zhu, B.S.; Cao, S.L.; Tan, L. Full 3-D viscous optimization design of a reversible pump turbine runner. IOP Conf. Ser. Mater. Sci. Eng. 2013, 52, 22014. [Google Scholar] [CrossRef]
- Xuhe, W.; Baoshan, Z.; Lei, T.; Jie, Z.; Shuliang, C. Development of a pump-turbine runner based on multiobjective optimization. IOP Conf. Ser. Earth Environ. Sci. 2014, 22, 012028. [Google Scholar] [CrossRef]
- Zhu, B.S.; Wang, X.H.; Tan, L.; Zhou, D.Y.; Zhao, Y.; Cao, S.L. Optimization design of a reversible pump-turbine runner with high efficiency and stability. Renew. Energy 2015, 81, 366e376. [Google Scholar] [CrossRef]
- Liu, L.; Zhu, B.; Bai, L.; Liu, X.; Zhao, Y. Parametric Design of an Ultrahigh-Head Pump-Turbine Runner Based on Multi Objective Optimization. Energies 2017, 10, 1169. [Google Scholar] [CrossRef]
- Zhu, B.; Tan, L.; Wang, X.; Ma, Z. Investigation on flow characteristics of pump-turbine runners with large blade lean. J. Fluid Eng.-T Asme 2018, 140, 031101. [Google Scholar] [CrossRef]
- Wang, P.; Vera-Morales, M.; Vollmer, M.; Zangeneh, M.; Zhu, B.S.; Ma, Z. Optimization of a Pump-as-turbine Runner Using a 3D Inverse Design Methodology. In Proceedings of the 29th IAHR Symposium on Hydraulic Machinery and Systems, Kyoto, Japan, 16–21 September 2018; Volume 240. [Google Scholar]
- Hu, Z.N.; Zhu, B.S.; Liu, X.B.; Ma, Z.; Xue, C. Multiobjective Optimization Design of Ultrahigh-head Pump Turbine Runners with Splitter Blades. In Proceedings of the 29th IAHR Symposium on Hydraulic Machinery and Systems, Kyoto, Japan, 16–21 September 2018; Volume 240. [Google Scholar]
- Hu, Z.; Cheng, Y.; Liu, D.; Chen, H.; Ji, B.; Ding, J. Broadening the operating range of pump-turbine to deep-part load by runner optimization. Renew. Energy 2023, 207, 73–88. [Google Scholar] [CrossRef]
- Okomoto, H.; Goto, A. Suppression of Cavitation in a Francis Turbine Runner by Application of 3D Inverse Design Method. In Proceedings of the ASME 2002 Joint U.S.-European Fluids Engineering Division Conference, Montreal, QC, Canada, 14–18 July 2002. FEDSM2002-31192. [Google Scholar]
- Daneshkah, K.; Zangeneh, M. Parametric design of a Francis turbine runner by means of a three-dimensional inverse design method. IOP Conf. Ser. Earth Environ. Sci. 2010, 12, 012058. [Google Scholar] [CrossRef]
- Ma, Z.; Zhu, B.; Rao, C.; Shangguan, Y. Comprehensive Hydraulic Improvement and Parametric Analysis of a Francis Turbine Runner. Energies 2019, 12, 307. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).