Surface Water Quality Assessment through Remote Sensing Based on the Box–Cox Transformation and Linear Regression
Abstract
:1. Introduction
2. Materials and Methods
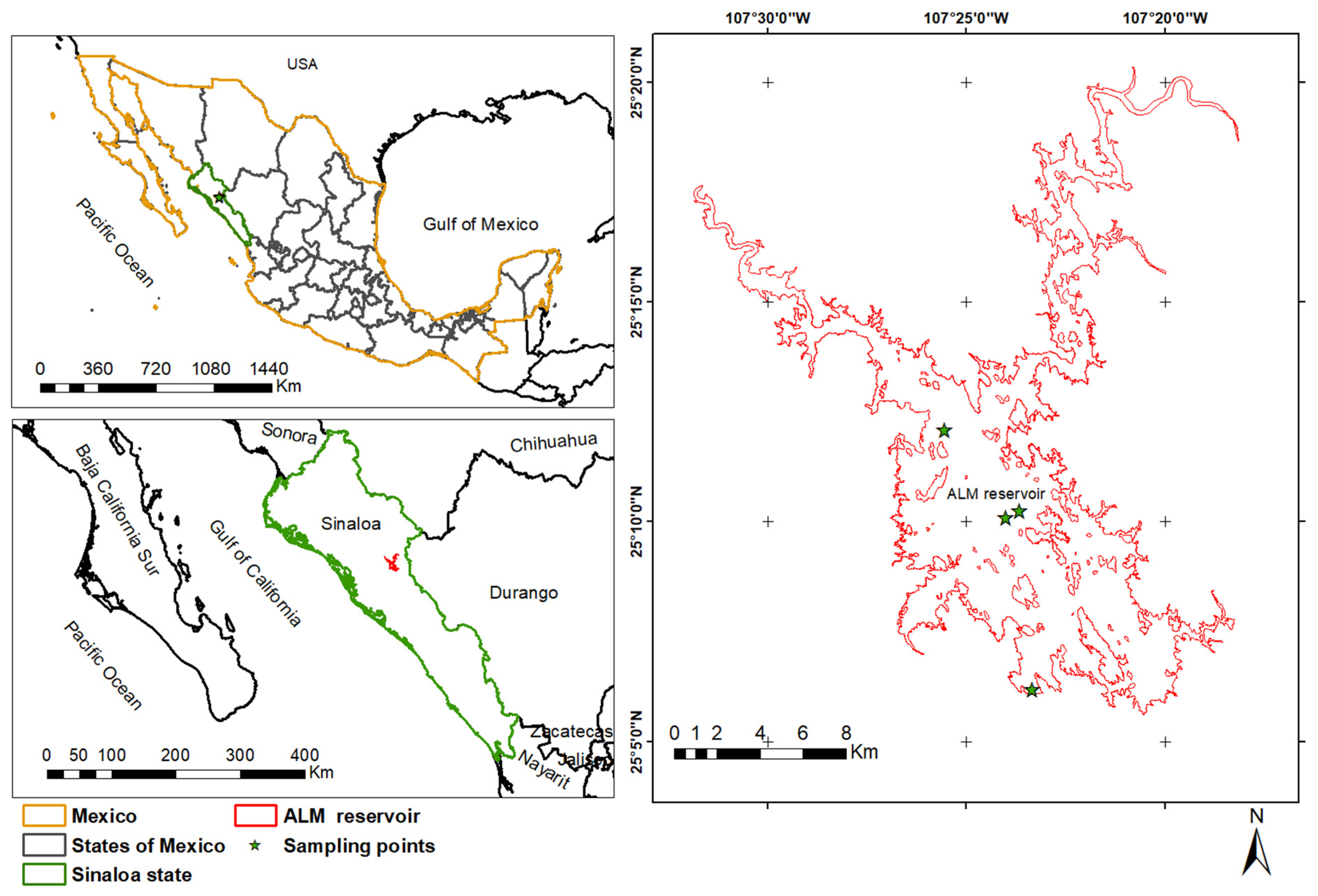
2.1. Study Area
2.2. Methodology
2.2.1. Satellite Imagery Acquisition
2.2.2. Imagery Pre-Processing
2.2.3. Reflectance Data Extraction
2.2.4. Water Quality Monitoring
2.2.5. Box–Cox Transformation of Water Quality Parameters
2.2.6. Multiple Linear Regression
2.2.7. Model Performance Evaluation
2.2.8. Multiple Linear Regression Significance Testing
2.2.9. Water Quality Model Validation
2.2.10. Water Quality Mapping
3. Results and Discussion
3.1. Water Quality from Field Sampling
3.2. Box–Cox Transformation
3.3. Multiple Linear Regression Modeling and Discriminant Analysis
3.4. Model Validation
3.5. Spatial and Temporal Distribution of Water Quality Parameters from Optimized Models
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ziemińska-Stolarska, A.; Kempa, M. Modeling and Monitoring of Hydrodynamics and Surface Water Quality in the Sulejów Dam Reservoir, Poland. Water 2021, 13, 296. [Google Scholar] [CrossRef]
- Posthuma, L.; Zijp, M.C.; De Zwart, D.; Van de Meent, D.; Globevnik, L.; Koprivsek, M.; Birk, S. Chemical pollution imposes limitations to the ecological status of European surface waters. Sci. Rep. 2020, 10, 14825. [Google Scholar] [CrossRef]
- Ryu, J.H. UAS-based real-time water quality monitoring, sampling, and visualization platform (UASWQP). HardwareX 2022, 11, e00277. [Google Scholar] [CrossRef]
- Schaeffer, B.A.; Schaeffer, K.G.; Keith, D.; Lunetta, R.S.; Conmy, R.; Gould, R.W. Barriers to adopting satellite remote sensing for water quality management. Int. J. Remote Sens. 2013, 34, 7534–7544. [Google Scholar] [CrossRef]
- Sayers, M.J.; Bosse, K.R.; Shuchman, R.A.; Ruberg, S.A.; Fahnenstiel, G.L.; Leshkevich, G.A.; Stuart, D.G.; Johengen, T.H.; Burtner, A.M.; Palladino, D. Spatial and temporal variability of inherent and apparent optical properties in western Lake Erie: Implications for water quality remote sensing. J. Great Lakes Res. 2019, 45, 490–507. [Google Scholar] [CrossRef]
- Zhang, Y.; Kong, X.; Deng, L.; Liu, Y. Monitor water quality through retrieving water quality parameters from hyperspectral images using graph convolution network with superposition of multi-point effect: A case study in Maozhou River. J. Environ. Manag. 2023, 342, 118283. [Google Scholar] [CrossRef]
- Zhang, D.; Li, X.; Huang, Y.; Zhang, L.; Zhu, Z.; Sun, X.; Lan, Z.; Guo, W. Hyperspectral remote sensing technology for water quality monitoring: Knowledge graph analysis and frontier trend. Front. Environ. Sci. 2023, 11, 1133325. [Google Scholar]
- Dev, P.J.; Shanmugam, P. A new theory and its application to remove the effect of surface-reflected light in above-surface radiance data from clear and turbid waters. J. Quant. Spectrosc. Radiat. Transf. 2014, 142, 75–92. [Google Scholar] [CrossRef]
- Mascarenhas, V.; Keck, T. Marine Optics and Ocean Color Remote Sensing. In YOUMARES 8—Oceans across Boundaries: Learning from Each Other; Jungblut, S., Liebich, V., Bode, M., Eds.; Conference Paper; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Gholizadeh, M.H.; Melesse, A.M.; Reddi, L. A comprehensive review on water quality parameters estimation using remote sensing techniques. Sensors 2016, 16, 1298. [Google Scholar] [CrossRef] [Green Version]
- Chuvieco, E. Digital Image Processing (I): From Raw to Corrected Data. In Fundamentals of Satellite Remote Sensing; Chuvieco, E., Ed.; CRC Press: Boca Raton, FL, USA; London, UK, 2020; pp. 153–234. [Google Scholar]
- Markogianni, V.; Kalivas, D.; Petropoulos, G.; Dimitriou, E. Analysis on the feasibility of Landsat 8 imagery for water quality parameters assessment in an oligotrophic Mediterranean lake. J. Geotech. Eng. 2017, 11, 906–914. [Google Scholar]
- Ahmed, M.; Mumtaz, R.; Baig, S.; Zaidi, S.M.H. Assessment of correlation amongst physico-chemical, topographical, geological, lithological and soil type parameters for measuring water quality of Rawal watershed using remote sensing. Water Supply 2022, 22, 3645–3660. [Google Scholar] [CrossRef]
- Khalil, M.T.; Saad, A.; Ahmed, M.; El Kafrawy, S.B.; Emam, W.W. Integrated field study, remote sensing and GIS approach for assessing and monitoring some chemical water quality parameters in Bardawil lagoon, Egypt. Int. J. Innov. Res. Sci. Eng. Technol. 2016, 5, 10–15680. [Google Scholar]
- Theologou, I.; Patelaki, M.; Karantzalos, K. Can single empirical algorithms accurately predict inland shallow water quality status from high resolution, multi-sensor, multi-temporal satellite data? Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 40, 1511. [Google Scholar] [CrossRef] [Green Version]
- Bonansea, M.; Bazán, R.; Ledesma, C.; Rodriguez, C.; Pinotti, L. Monitoring of regional lake water clarity using Landsat imagery. Hydrol. Res. 2015, 46, 661–670. [Google Scholar] [CrossRef]
- Valentini, M.; dos Santos, G.B.; Muller, B. Multiple linear regression analysis (MLR) applied for modeling a new WQI equation for monitoring the water quality of Mirim Lagoon, in the state of Rio Grande do Sul—Brazil. SN Appl. Sci. 2021, 3, 70. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Homaei, F.; Farhadi, H. Reliability assessment of water quality index based on guidelines of national sanitation foundation in natural streams: Integration of remote sensing and data-driven models. Artif. Intell. Rev. 2021, 54, 4619–4651. [Google Scholar] [CrossRef]
- Kadam, A.K.; Wagh, V.M.; Muley, A.A.; Umrikar, B.N.; Sankhua, R.N. Prediction of water quality index using artificial neural network and multiple linear regression modelling approach in Shivganga River basin, India. Model. Earth Syst. Environ. 2019, 5, 951–962. [Google Scholar] [CrossRef]
- Ewaid, S.H.; Abed, S.A.; Kadhum, S.A. Predicting the Tigris River water quality within Baghdad, Iraq by using water quality index and regression analysis. Environ. Technol. Innov. 2018, 11, 390–398. [Google Scholar] [CrossRef]
- Wang, X.; Yang, W. Water quality monitoring and evaluation using remote sensing techniques in China: A systematic review. Ecosyst. Health Sust. 2019, 5, 47–56. [Google Scholar] [CrossRef] [Green Version]
- Sharaf El Din, E.; Zhang, Y. Estimation of both optical and nonoptical surface water quality parameters using Landsat 8 OLI imagery and statistical techniques. J. Appl. Remote Sens. 2017, 11, 046008. [Google Scholar] [CrossRef]
- Feng, L.; Hu, C.; Han, X.; Chen, X.; Qi, L. Long-term distribution patterns of chlorophyll-a concentration in China’s largest freshwater lake: MERIS full-resolution observations with a practical approach. Remote Sens. 2014, 7, 275–299. [Google Scholar] [CrossRef] [Green Version]
- Qi, L.; Hu, C.; Duan, H.; Barnes, B.B.; Ma, R. An EOF-based algorithm to estimate chlorophyll a concentrations in Taihu Lake from MODIS land-band measurements: Implications for near real-time applications and forecasting models. Remote Sens. 2014, 6, 10694–10715. [Google Scholar] [CrossRef] [Green Version]
- Asadollahfardi, G.; Heidarzadeh, N.; Mosalli, A.; Sekhavati, A. Optimization of water quality monitoring stations using genetic algorithm, a case study, Sefid-Rud River, Iran. Adv. Environ. Res. 2018, 7, 87–107. [Google Scholar]
- Quevedo-Castro, A.; Rangel-Peraza, J.G.; Bandala, E.; Amabilis-Sosa, L.; Rodríguez-Mata, A.; Bustos-Terrones, Y. Developing a water quality index in a tropical reservoir using a measure of multiparameters. J. Water Sanit. Hyg. Dev. 2018, 8, 752–766. [Google Scholar] [CrossRef]
- Quevedo-Castro, A.; Lopez, J.L.; Rangel-Peraza, J.G.; Bandala, E.; Bustos-Terrones, Y. Study of the water quality of a tropical reservoir. Environments 2019, 6, 7. [Google Scholar] [CrossRef] [Green Version]
- Quevedo-Castro, A.; Bandala, E.R.; Rangel-Peraza, J.G.; Amábilis-Sosa, L.E.; Sanhouse-García, A.; Bustos-Terrones, Y.A. Temporal and spatial study of water quality and trophic evaluation of a large tropical reservoir. Environments 2019, 6, 61. [Google Scholar] [CrossRef] [Green Version]
- CONAGUA. Subdirección General Técnica. Presas de México. Available online: http://sina.conagua.gob.mx/sina/tema.php?tema=presasPrincipalesandver=reporteando=2andn=nacional (accessed on 13 November 2022).
- Sanhouse-Garcia, A.J.; Bustos-Terrones, Y.; Rangel-Peraza, J.G.; Quevedo-Castro, A.; Pacheco, C. Multi-temporal analysis for land use and land cover changes in an agricultural region using open source tools. Remote Sens. Appl. Soc. Environ. 2017, 8, 278–290. [Google Scholar] [CrossRef]
- INEGI. Compendio de Información Geográfica Municipal 2010; Badiraguato; Instituto Nacional de Estadística y Geografía: Aguascalientes, Mexico, 2015; Available online: https://www.inegi.org.mx/contenidos/app/mexicocifras/datos_geograficos/25/25003.pdf (accessed on 26 February 2023).
- Monjardin-Armenta, S.A.; Plata-Rocha, W.; Pacheco-Angulo, C.E.; Franco-Ochoa, C.; Rangel-Peraza, J.G. Geospatial Simulation Model of Deforestation and Reforestation Using Multicriteria Evaluation. Sustainability 2020, 12, 10387. [Google Scholar] [CrossRef]
- USGS. United States Geological Survey. Earth Explorer. 2021. Available online: https://www.usgs.gov/landsat-missions/using-usgs-landsat-level-1-data-product (accessed on 2 July 2023).
- Congedo, L. Semi-automatic classification plugin documentation. Release 2016, 4, 29. [Google Scholar]
- Chavez, P.S. Image-based atmospheric corrections–revisited and improved. Photogramm. Eng. Remote Sens. 1996, 62, 1025–1036. [Google Scholar]
- Prieto-Amparan, J.A.; Villarreal-Guerrero, F.; Martinez-Salvador, M.; Manjarrez-Domínguez, C.; Santellano-Estrada, E.; Pinedo-Alvarez, A. Atmospheric and radiometric correction algorithms for the multitemporal assessment of grasslands productivity. Remote Sens. 2018, 10, 219. [Google Scholar] [CrossRef] [Green Version]
- Huguet, A.; Vacher, L.; Relexans, S.; Saubusse, S.; Froidefond, J.M.; Parlanti, E. Properties of fluorescent dissolved organic matter in the Gironde Estuary. Org. Geochem. 2009, 40, 706–719. [Google Scholar] [CrossRef]
- Hansen, C.H.; Williams, G.P.; Adjei, Z.; Barlow, A.; Nelson, E.J.; Miller, A.W. Reservoir water quality monitoring using remote sensing with seasonal models: Case study of five central-Utah reservoirs. Lake Reserv. Manag. 2015, 31, 225–240. [Google Scholar] [CrossRef]
- APHA. Standard Methods for the Examination of Water and Wastewater, 18th ed.; American Public Health Association: Washington, DC, USA, 1992. [Google Scholar]
- Loaiza, J.G.; Rangel-Peraza, J.G.; Sanhouse-García, A.J.; Monjardín-Armenta, S.A.; Mora-Félix, Z.D.; Bustos-Terrones, Y.A. Assessment of Water Quality in A Tropical Reservoir in Mexico: Seasonal, Spatial and Multivariable Analysis. Int. J. Environ. Res. Public Health 2021, 18, 7456. [Google Scholar] [CrossRef]
- Ritchie, J.C.; Zimba, P.V.; Everitt, J.H. Remote sensing techniques to assess water quality. Photogramm. Eng. Remote Sens. 2003, 69, 695–704. [Google Scholar] [CrossRef] [Green Version]
- Elkorashey, R.M. Utilizing chemometric techniques to evaluate water quality spatial and temporal variation. A case study: Bahr El-Baqar drain-Egypt. Environ. Technol. Innov. 2022, 26, 102332. [Google Scholar] [CrossRef]
- Vélez, J.I.; Correa, J.C.; Marmolejo-Ramos, F. A new approach to the Box–Cox transformation. Front. Appl. Math. Stat. 2015, 1, 12. [Google Scholar] [CrossRef] [Green Version]
- Peterson, R.A. Finding Optimal Normalizing Transformations via best Normalize. R J. 2021, 13, 3010–3329. [Google Scholar] [CrossRef]
- Etemadi, S.; Khashei, M. Etemadi multiple linear regression. Measurement 2021, 186, 110080. [Google Scholar] [CrossRef]
- Ouma, Y.O.; Okuku, C.O.; Njau, E.N. Use of artificial neural networks and multiple linear regression model for the prediction of dissolved oxygen in rivers: Case study of hydrographic basin of River Nyando, Kenya. Complexity 2020, 9570789, 23. [Google Scholar] [CrossRef]
- Abunama, T.; Othman, F.; Ansari, M.; El-Shafie, A. Leachate generation rate modeling using artificial intelligence algorithms aided by input optimization method for an MSW landfill. Environ. Sci. Pollut. Res. Int. 2019, 26, 3368–3381. [Google Scholar] [CrossRef] [PubMed]
- Jahani, A.; Rayegani, B. Forest landscape visual quality evaluation using artificial intelligence techniques as a decision support system. Stoch. Environ. Res. Risk Assess. 2020, 34, 1473–1486. [Google Scholar] [CrossRef]
- Zhou, Z.; Huang, T.; Ma, W.; Li, Y.; Zeng, K. Impacts of water quality variation and rainfall runoff on Jinpen Dam, in Northwest China. Water Sci. Eng. 2015, 8, 301–308. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez-Farias, F.A.; Hernandez-Garza, M.d.R.; Gonzalez, G.D. Organic carbon and pesticide pollution in a tropical coastal lagoon-estuarine system in Northwest Mexico. Int. J. Environ. Pollut. 2006, 26, 234. [Google Scholar] [CrossRef]
- Rodríguez, H.B.; González, L.C.; Trigueros, J.A.; Ávila, J.A.; Arciniega, M.A. Calidad del agua: Caracterización espacial en época de sequía en el río Fuerte, Sinaloa, México. Rev. Cienc. Desde Occident. 2016, 3, 35–47. [Google Scholar]
- Fregoso-López, M.G.; Armienta-Hernández, M.A.; Alarcón-Silvas, S.G.; Ramírez-Rochín, J.; Fierro-Sañudo, J.F.; Páez-Osuna, F. Assessment of nutrient contamination in the waters of the El Fuerte River, southern Gulf of California, Mexico. Environ. Monit. Assess. 2020, 192, 417. [Google Scholar] [CrossRef]
- Zhang, H.; Richardson, P.A.; Belayneh, B.E.; Ristvey, A.; Lea-Cox, J.; Copes, W.E.; Moorman, G.W.; Hong, C. Comparative Analysis of Water Quality between the Runoff Entrance and Middle of Recycling Irrigation Reservoirs. Water 2015, 7, 3861–3877. [Google Scholar] [CrossRef] [Green Version]
- Fang, J.; Wu, F.; Xiong, Y.; Wang, S. A comparison of the distribution and sources of organic matter in surface sediments collected from northwestern and southwestern plateau lakes in China. J. Limnol. 2017, 76, 571–580. [Google Scholar] [CrossRef] [Green Version]
- Markogianni, V.; Kalivas, D.; Petropoulos, G.P.; Dimitriou, E. Estimating chlorophyll-a of inland water bodies in Greece based on landsat data. Remote Sens. 2020, 12, 2087. [Google Scholar] [CrossRef]
- Abbas, M.M.; Melesse, A.M.; Scinto, L.J.; Rehage, J.S. Satellite estimation of chlorophyll-a using moderate resolution imaging spectroradiometer (MODIS) sensor in shallow coastal water bodies: Validation and improvement. Water 2019, 11, 1621. [Google Scholar] [CrossRef] [Green Version]
- Shinmura, S.; Shinmura, S. New Theory of Discriminant Analysis; Springer: Singapore, 2016; pp. 81–97. [Google Scholar]
- Batur, E.; Maktav, D. Assessment of Surface Water Quality by Using Satellite Images Fusion Based on PCA Method in the Lake Gala, Turkey. IEEE Trans. Geosci. Remote Sens. 2018, 57, 2983–2989. [Google Scholar] [CrossRef]
- Kumar, M.; Kumar, M.; Denis, D.M.; Verma, O.P.; Mahato, L.L.; Pandey, K. Investigating water quality of an urban water body using ground and space observations. Spat. Inf. Res. 2021, 29, 897–906. [Google Scholar] [CrossRef]
- Mejía Ávila, D.; Torres-Bejarano, F.; Martínez Lara, Z. Spectral indices for estimating total dissolved solids in freshwater wetlands using semi-empirical models. A case study of Guartinaja and Momil wetlands. Int. J. Remote Sens. 2022, 43, 2156–2184. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, F.; Chen, S.; Wang, C.; Chen, J.; Zhou, H.; Xue, Y. Remote Sensing Evaluation of Total Suspended Solids Dynamic with Markov Model: A Case Study of Inland Reservoir across Administrative Boundary in South China. Sensors 2020, 20, 6911. [Google Scholar] [CrossRef] [PubMed]
- Maliki, A.A.A.; Chabuk, A.; Sultan, M.A.; Hashim, B.M.; Hussain, H.M.; Al-Ansari, N. Estimation of Total Dissolved Solids in Water Bodies by Spectral Indices Case Study: Shatt al-Arab River. Water Air Soil Pollut. 2020, 231, 482. [Google Scholar] [CrossRef]
- Obaid, A.A.; Ali, K.A.; Abiye, T.A.; Adam, E.M. Assessing the utility of using current generation high-resolution satellites (Sentinel 2 and Landsat 8) to monitor large water supply dam in South Africa. Remote Sens. Appl. Soc. Environ. 2021, 22, 100521. [Google Scholar] [CrossRef]
- Lin, L.; Wang, F.; Chen, H.; Fang, H.; Zhang, T.; Cao, W. Ecological health assessments of rivers with multiple dams based on the biological integrity of phytoplankton: A case study of North Creek of Jiulong River. Ecol. Indic. 2021, 121, 106998. [Google Scholar] [CrossRef]
- Mohsen, A.; Elshemy, M.; Zeidan, B. Water quality monitoring of Lake Burullus (Egypt) using Landsat satellite imageries. Environ. Sci. Pollut. Res. 2020, 28, 15687–15700. [Google Scholar] [CrossRef]
- Bohn, V.Y.; Carmona, F.; Rivas, R.; Lagomarsino, L.; Diovisalvi, N.; Zagarese, H.E. Development of an empirical model for chlorophyll-a and Secchi Disk Depth estimation for a Pampean shallow lake (Argentina). Egypt. J. Remote Sens. Space Sci. 2018, 21, 183–191. [Google Scholar] [CrossRef]
- Tyler, A.N.; Svab, E.; Preston, T.; Présing, M.; Kovács, W.A. Remote sensing of the water quality of shallow lakes: A mixture modelling approach to quantifying phytoplankton in water characterized by high-suspended sediment. Int. J. Remote Sens. 2006, 27, 1521–1537. [Google Scholar] [CrossRef]
- Pahlevan, N.; Smith, B.; Schalles, J.; Binding, C.; Cao, Z.; Ma, R.; Alikas, K.; Kangro, K.; Gurlin, D.; Hà, N.; et al. Seamless retrievals of chlorophyll-a from Sentinel-2 (MSI) and Sentinel-3 (OLCI) in inland and coastal waters: A machine learning approach. Remote Sens. Environ. 2020, 240, 111604. [Google Scholar] [CrossRef]
- Vanhellemont, Q. Adaptation of the dark spectrum fitting atmospheric correction for aquatic applications of the Landsat and Sentinel-2 archives. Remote Sens. Environ. 2019, 225, 175–192. [Google Scholar] [CrossRef]
- Maciel, F.P.; Pedocchi, F. Evaluation of ACOLITE atmospheric correction methods for Landsat-8 and Sentinel-2 in the Río de la Plata turbid coastal waters. Int. J. Remote Sens. 2022, 43, 215–240. [Google Scholar] [CrossRef]
- Pahlevan, N.; Mangin, A.; Balasubramanian, S.; Smith, B.; Alikas, K.; Arai, K.; Barbosa, C.; Bélanger, S.; Binding, C.; Bresciani, M.; et al. ACIX-Aqua: A global assessment of atmospheric correction methods for Landsat-8 and Sentinel-2 over lakes, rivers, and coastal waters. Remote Sens. Environ. 2021, 258, 112366. [Google Scholar] [CrossRef]
- Zolfaghari, K.; Pahlevan, N.; Simis, S.G.; O’Shea, R.E.; Duguay, C.R. Sensitivity of remotely sensed pigment concentration via Mixture Density Networks (MDNs) to uncertainties from atmospheric correction. J. Great Lakes Res. 2022, 49, 341–356. [Google Scholar] [CrossRef]
- de Keukelaere, L.; Sterckx, S.; Adriaensen, S.; Knaeps, E.; Reusen, I.; Giardino, C.; Bresciani, M.; Hunter, P.; Neil, C.; van der Zande, D.; et al. Atmospheric correction of Landsat-8/OLI and Sentinel-2/MSI data using iCOR algorithm: Validation for coastal and inland waters. Eur. J. Remote Sens. 2018, 51, 525–542. [Google Scholar] [CrossRef] [Green Version]
- Warren, M.A.; Simis, S.G.H.; Selmes, N. Complementary water quality observations from high and medium resolution Sentinel sensors by aligning chlorophyll-a and turbidity algorithms. Remote Sens. Environ. 2021, 265, 112651. [Google Scholar] [CrossRef]
- Rangel-Peraza, J.G.; De Anda, J.; González-Farias, F.; Erickson, D. Statistical assessment of water quality seasonality in large tropical reservoirs. Lakes Reserv. Res. Manag. 2009, 14, 315–323. [Google Scholar] [CrossRef]






| Sensor | Year | Acquisition Date | Path/Row |
|---|---|---|---|
| Landsat 8 OLI | 2015 | May 4th | 32/43 |
| October 27th | |||
| 2016 | May 22nd | ||
| September 11th | |||
| 2017 | March 6th | ||
| September 30th | |||
| 2018 | February 2nd | ||
| October 2nd | |||
| 2019 | January 17th |
| Power | Transformation | Description |
|---|---|---|
| Square | ||
| Untransformed data | ||
| Square root | ||
| Cube root | ||
| Logarithm | ||
| Inverse square root | ||
| Reciprocal |
| Parameter | Box–Cox Optimized Mathematical Model | r2 |
|---|---|---|
| TOC | Box–Cox (TOC) = 1 + (TOC1.3294 − 1)/(1.3294 × 4.573790.329397) | 0.96 |
| TDS | Box–Cox (TDS) = 1 + (TDS4.16779 − 1)/(4.16779 × 97.64533.16779) | 0.88 |
| Chl-a | Box–Cox (Chl-a) = 1 + (Chl-a0.333508 − 1)/(0.333508 × 1.435840.666492) | 0.85 |
| Water Quality Normalized Parameter | Kolmogorov-Smirnov Test | |
|---|---|---|
| Dn Value | p-Value | |
| Chl-a | 0.2393 | 0.2544 |
| TDS | 0.1644 | 0.7149 |
| COT | 0.1554 | 0.7769 |
| Parameter | Multiple Linear Regression Model | r2 | RMSE |
|---|---|---|---|
| TOC | Box–Cox (TOC) = 9.61963 − 700.238 × B1 + 707.462 × B2 − 39.2047 × B3 − 25.1903 × B4 − 18.2743 × B5 + 216.704 × B6 − 243.629 × B7 | 0.95 | 0.165 |
| TDS | Box–Cox (TDS) = 34.849 − 3057.55 × B1 + 4137.63 × B2 − 2526.38 × B3 + 2696.15 × B4 + 1827.6 × B5 − 6080.39 × B6 + 2858.29 × B7 | 0.88 | 3.867 |
| Chl-a | Box–Cox (Chl-a) = −38.8501 + 212.068 × B1 + 1213.14 × B2 + 1207.01 × B3 − 2935.1 × B4 + 261.245 × B5 − 2468.64 × B6 + 3907.26 × B7 | 0.87 | 3.430 |
| Iteration | Model | Discriminated Bands | r2 | RMSE |
|---|---|---|---|---|
| 1 | Box–Cox (TOC) = 9.61963 − 700.238 × B1 + 707.462 × B2 − 39.2047 × B3 − 25.1903 × B4 − 18.2743 × B5 + 216.704 × B6 − 243.629 × B7 | 0 | 0.9608 | 0.1658 |
| 2 | Box–Cox (TOC) = 9.82457 − 711.379 × B1 + 705.351 × B2 − 48.6016 × B3 − 25.9899 × B5 + 245.128 × B6 − 273.573 × B7 | B4 | 0.9611 | 0.1676 |
| 3 | Box–Cox (TOC) = 9.03939 − 661.472 × B1 + 667.836 × B2 − 45.8407 × B3 + 147.039 × B6 − 191.869 × B7 | B4, B5 | 0.9423 | 0.1694 |
| 4 | Box–Cox (TOC) = 8.92542 − 682.488 × B1 + 677.616 × B2 − 38.4808 × B3 + 3.95873 × B6 | B4, B5, B7 | 0.9521 | 0.1829 |
| 5 | Box–Cox (TOC) = 8.87165 − 688.128 × B1 + 688.322 × B2 − 40.7919 × B3 | B4, B5, B7, B6 | 0.9520 | 0.1835 |
| 6 | Box–Cox (TOC) = 9.15197 − 620.429 × B1 + 587.138 × B2 | B4, B5, B7, B6, B3 | 0.9350 | 0.2024 |
| Iteration | Parameter | Estimate | Standard Error | t-Statistic | p-Value |
|---|---|---|---|---|---|
| TOC model with all bands | |||||
| 1 | Constant | 9.61963 | 2.15541 | 4.46302 | 0.0012 |
| B1 | −700.238 | 100.765 | −6.94922 | <0.0000 | |
| B2 | 707.462 | 109.424 | 6.4653 | 0.0001 | |
| B3 | −39.2047 | 53.3205 | −0.735266 | 0.4791 | |
| B4 | −25.1903 | 136.359 | −0.184735 | 0.8571 | |
| B5 | −18.2743 | 56.7695 | −0.321903 | 0.7542 | |
| B6 | 216.704 | 237.583 | 0.912119 | 0.3832 | |
| B7 | −243.629 | 244.321 | −0.997167 | 0.3422 | |
| TOC model after discriminating B4 | |||||
| 2 | Constant | 9.82457 | 1.46585 | 6.70228 | <0.0000 |
| B1 | −711.379 | 91.8242 | −7.74718 | <0.0000 | |
| B2 | 705.351 | 97.8209 | 7.21064 | <0.0000 | |
| B3 | −48.6016 | 23.9244 | −2.03147 | 0.0671 | |
| B5 | −25.9899 | 40.4164 | −0.643053 | 0.5334 | |
| B6 | 245.128 | 185.017 | 1.32489 | 0.2121 | |
| B7 | −273.573 | 187.063 | −1.46247 | 0.1716 | |
| TOC model after discriminating B4 and B5 | |||||
| 3 | Constant | 9.03939 | 0.526595 | 17.1657 | <0.0000 |
| B1 | −661.472 | 56.2812 | −11.753 | <0.0000 | |
| B2 | 667.836 | 80.4374 | 8.30256 | <0.0000 | |
| B3 | −45.8407 | 23.0887 | −1.98542 | 0.0704 | |
| B6 | 147.039 | 102.673 | 1.43211 | 0.1776 | |
| B7 | −191.869 | 134.751 | −1.42388 | 0.18 | |
| TOC model after discriminating B4, B5, and B7 | |||||
| 4 | Constant | 8.92542 | 0.531479 | 16.7936 | <0.0000 |
| B1 | −682.488 | 55.898 | −12.2095 | <0.0000 | |
| B2 | 677.616 | 83.0813 | 8.15606 | <0.0000 | |
| B3 | −38.4808 | 23.4277 | −1.64254 | 0.1244 | |
| B6 | 3.95873 | 21.4212 | 0.184804 | 0.8562 | |
| TOC model after discriminating B4, B5, B7, and B6 | |||||
| 5 | Constant | 8.87165 | 0.47848 | 18.5413 | <0.0000 |
| B1 | −688.128 | 47.2176 | −14.5735 | <0.0000 | |
| B2 | 688.322 | 60.099 | 11.4531 | <0.0000 | |
| B3 | −40.7919 | 19.3641 | −2.10657 | 0.0537 | |
| TOC model after discriminating B4, B5, B7, B6, and B3 | |||||
| 6 | Constant | 9.15197 | 0.510097 | 17.9416 | <0.0000 |
| B1 | −620.429 | 42.8204 | −14.4891 | <0.0000 | |
| B2 | 587.138 | 44.5094 | 13.1913 | <0.0000 | |
| Parameter | Final Model | Bands Used | r2 |
|---|---|---|---|
| TOC | Box–Cox (TOC) = 9.15197 − 620.429 × B1 + 587.138 × B2 | B1, B2 | 0.9263 |
| TDS | Box–Cox (TDS) = 55.7042 − 3387.46 × B1 + 4108.64 × B2 − 2874.84 × B3 + 3514.37 × B4 + 1386.56 × B5 − 3490.39 × B6 | B1, B2, B3, B4, B6 | 0.8753 |
| Chl-a | Box–Cox (Cha-a) = −24.4586 + 1204.69 × B2 + 956.358 × B3 − 2506.71 × B4 + 996.356 × B7 | B2, B3, B4, B7 | 0.8100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Loaiza, J.G.; Rangel-Peraza, J.G.; Monjardín-Armenta, S.A.; Bustos-Terrones, Y.A.; Bandala, E.R.; Sanhouse-García, A.J.; Rentería-Guevara, S.A. Surface Water Quality Assessment through Remote Sensing Based on the Box–Cox Transformation and Linear Regression. Water 2023, 15, 2606. https://doi.org/10.3390/w15142606
Loaiza JG, Rangel-Peraza JG, Monjardín-Armenta SA, Bustos-Terrones YA, Bandala ER, Sanhouse-García AJ, Rentería-Guevara SA. Surface Water Quality Assessment through Remote Sensing Based on the Box–Cox Transformation and Linear Regression. Water. 2023; 15(14):2606. https://doi.org/10.3390/w15142606
Chicago/Turabian StyleLoaiza, Juan G., Jesús Gabriel Rangel-Peraza, Sergio Alberto Monjardín-Armenta, Yaneth A. Bustos-Terrones, Erick R. Bandala, Antonio J. Sanhouse-García, and Sergio A. Rentería-Guevara. 2023. "Surface Water Quality Assessment through Remote Sensing Based on the Box–Cox Transformation and Linear Regression" Water 15, no. 14: 2606. https://doi.org/10.3390/w15142606
APA StyleLoaiza, J. G., Rangel-Peraza, J. G., Monjardín-Armenta, S. A., Bustos-Terrones, Y. A., Bandala, E. R., Sanhouse-García, A. J., & Rentería-Guevara, S. A. (2023). Surface Water Quality Assessment through Remote Sensing Based on the Box–Cox Transformation and Linear Regression. Water, 15(14), 2606. https://doi.org/10.3390/w15142606












