1. Introduction
In recent years, there has been an increase in the vulnerability of some areas to the changing climate [
1], with many aspects related to the hydrological cycle [
2]. Urban areas are a particularly vulnerable environment as a result of rapid urbanization, population growth, and increased demand for water [
3]. However, water shortages are not the only problem experienced by residents of rapidly growing cities [
4,
5]. The increase in surface runoff due to the increase in paved areas significantly reduces the infiltration of rainwater into the ground, intensifying the effects of droughts [
6]. This problem is particularly noticeable in countries with low water resources. One of them is Poland, whose renewable freshwater resources per capita are among the lowest in Europe [
7,
8]. Changes in hydrological conditions within the catchment can also reduce the habitat area for aquatic organisms [
9]. Furthermore, considering that the intensity of rainfall is increasing due to climate change [
10,
11], waterlogging [
12] and flooding [
13] are becoming increasing threats. These phenomena can have negative socioeconomic impacts and, in some cases, even lead to the death of residents [
14]. Therefore, it is not surprising that there is a growing interest in managing water in the circular economy model. In this case, the goal is no longer to use and remove resources but to preserve them in use and revive them [
15,
16]. Rainwater harvesting systems are becoming very popular [
17,
18]. The possibility of using rainwater as an energy source is also being analyzed [
19]. On the other hand, Deksissa et al. [
20] showed that green infrastructure (GI) activities, including most stormwater management facilities [
21], can be aligned with the principles of the circular economy. Therefore, the widest possible implementation of such solutions should be pursued.
This is confirmed by research by Song et al. [
22], who noted that the existing gray infrastructure requires nature-based restoration using GI. The need to use nature-based solutions that eliminate the negative effects of urbanization has also been highlighted by other authors [
23,
24]. These solutions can, for example, be based on the idea of reducing runoff from catchments using low-impact development (LID) facilities [
25,
26]. Moreover, stormwater infiltration facilities can also be integrated within drainage networks [
27]. On the other hand, when soil and water conditions do not allow stormwater to be discharged into the ground, systems can be made to reduce stormwater’s peak flow [
28,
29].
The implementation of devices such as rain gardens or drainage wells is generally considered the easiest way to manage stormwater [
30]. However, studies [
31] indicate that the best results are achieved by using LID facilities together with more classical solutions, such as stormwater retention. This was also confirmed by other studies carried out in Central Europe [
27,
32], according to which one of the most beneficial ways of managing stormwater is its surface infiltration with retention. Infiltration basins and tanks are most often used for this purpose. These are facilities in the form of a field depression, the surface of which should be sown with grass in order to stabilize the ground and improve the aesthetics of the stormwater infiltration system. In both cases, efforts should be made to integrate the facility into the surroundings and shape its scarp with a slope of no less than 1:2. Despite many similarities, infiltration basins and tanks differ in the maximum fill level, which is definitely higher in the case of the latter facilities. The application of infiltration basins and tanks can improve the functioning of drainage systems and help reduce the negative phenomena observed in stormwater receivers [
33]. It can also contribute to the supply of groundwater resources and the increase in biodiversity in urban areas while providing a striking landscape feature [
34]. However, it is important to remember that these facilities cannot be implemented indiscriminately. Measures aimed at improving the efficiency of stormwater management within urban catchments should assume the implementation of such solutions, whose application under the given conditions will be technically and financially justified. It is also important to correctly determine the dimensions of the facilities that will guarantee the safety of the system’s operation in the coming years. In the case of Poland, the required capacity of the infiltration basins and tanks is often determined on the basis of the total catchment area and the percentage of the impervious area. However, an earlier study by the authors [
35] showed that one of the key parameters in the process of dimensioning stormwater infiltration facilities is the type of soil within the catchment area, which is usually not taken into account. Furthermore, when designing infiltration basins and tanks, the moisture content of the soil within the facility should be considered, which is currently neglected.
One significant barrier that hinders the implementation of facilities dedicated to surface stormwater infiltration with retention is the scarcity of available space for their development. Considering that the commonly used calculation method overlooks many aspects of the design of stormwater infiltration facilities, a reliable sizing of such facilities requires the development of a comprehensive hydrodynamic model. This significantly extends the process of designing the drainage infrastructure and generates additional costs. If the implementation of the infiltration system turns out to be technically unjustified as a result of the required area of the infiltration basin or tank being too high in relation to the area available for its development, then these costs become unreasonable, and the implementation of the investment is unnecessarily delayed. Therefore, it seems essential to develop a new and simplified method, the use of which would allow a relatively quick initial assessment of the required area of a stormwater infiltration facility without incurring additional costs.
Comprehensive studies aimed at developing a new method for selecting the geometry of infiltration basins and tanks have not yet been conducted. There are also no data on the assessment of the impact of the stormwater infiltration facility parameters on the required area of its bottom. Although in the literature one can find a description of models that have been developed to support the design process of LID facilities [
36] or stormwater storage facilities [
37], they cannot be applied to other facilities due to their different nature.
The aim of this research was to develop a new method for selecting the geometry of the infiltration basins and tanks, the use of which in the preliminary design phase of the drainage infrastructure will allow assessing the appropriateness of using such facilities in a given location. The research also included an analysis of the impact of the parameters characterizing these facilities on their required area. The final stage of the research was to verify the correctness of the models with the example of a real urban catchment.
2. Materials and Methods
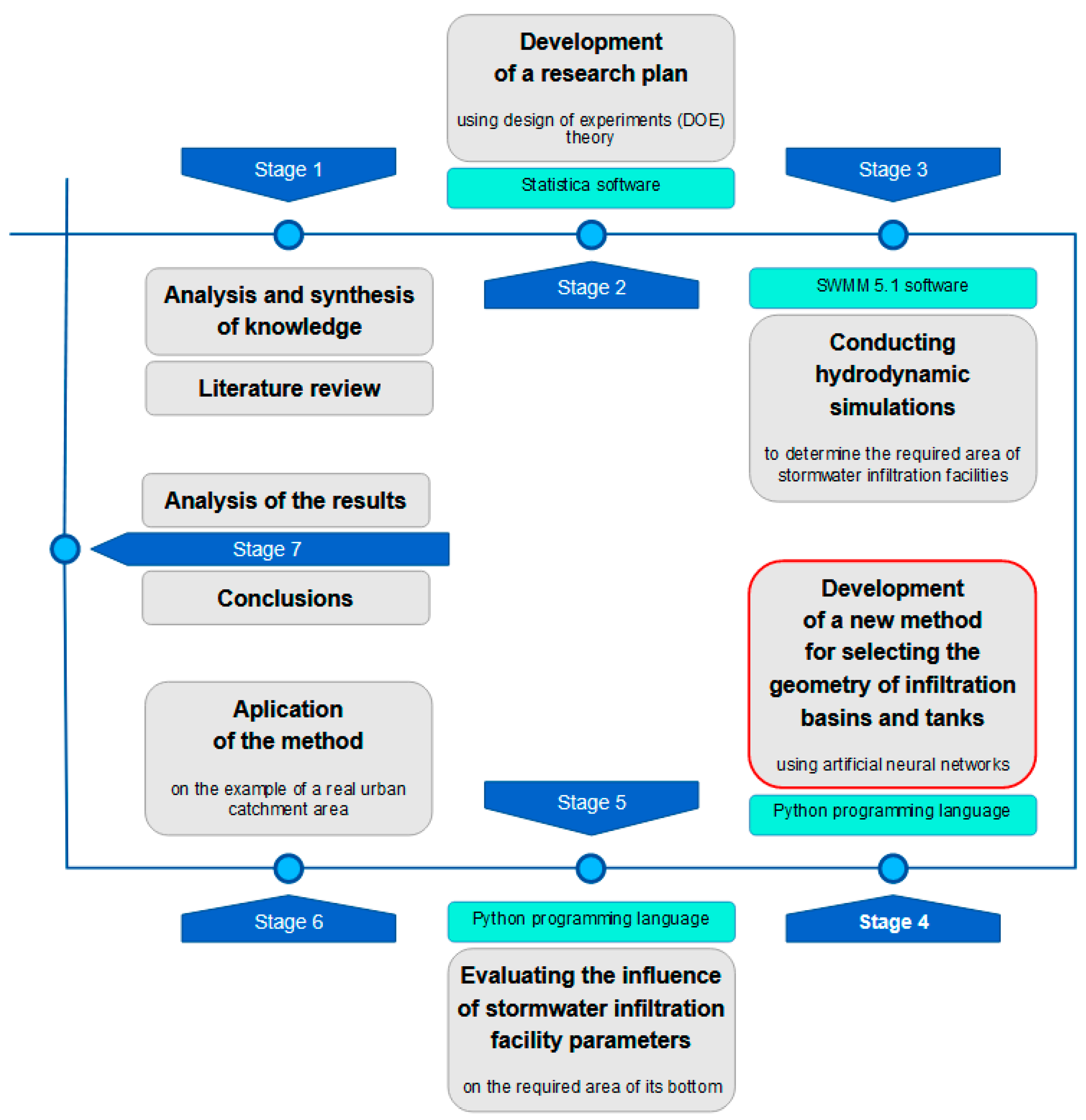
This study was conducted according to the procedure shown in
Figure 1. As in the previous stage of the analysis [
35], the required area of the stormwater infiltration facility was determined using SWMM 5.1 software (EPA SWMM, Cincinnati, Ohio, USA). The development of the research plan was made possible by using Statistica software (TIBCO Statistica, Palo Alto, CA, USA). The artificial neural networks were generated using the Python programming language.
2.1. Research Plan
Previous studies by the authors [
35] showed that the total catchment area (
Ac), the type of soil within it, and the percent of impervious area (
C) are of key importance in the design process of stormwater infiltration facilities. On the other hand, the importance of the other parameters considered in the analysis, such as the depth of depression storage (
hd), length of the system (
Ld), average slope of the catchment surface (
is), catchment load (
Lc), average slope of the conduits’ bottom (
ic), catchment roughness coefficient (
nc), or number of subcatchments (
ns), is significantly lower. Considering the above, as well as the limitations of the Statistica software [
38] regarding the number of parameters in the research plans, the next stage of the analysis considered only those catchment parameters whose influence on the obtained simulation results was the most significant. In addition to the total catchment area (
Ac) and the percentage of impervious area (
C), soil permeability was also taken into account. Considering the infiltration model, which was the Green–Ampt model [
39], the latter parameter was described by the permeability of saturated soil (
K) and the suction head (
Ψ). These parameters were directly derived from the type of soil [
40]. Furthermore, the value of the water deficit (Δ
θc) was taken into account, which was analyzed in the range from Δ
θc = 0% (for fully water-saturated soil) to Δ
θc = 100% (for completely drained soil).
As in the previous stage of the research [
35], the analysis was carried out while assuming a maximum fill level (
himax) of 0.30 m and 1.0 m for the infiltration basins and tanks [
41]. The sand parameters for the stormwater infiltration facilities were adopted based on the guidelines of the US Environmental Protection Agency [
40]. The value of the water deficit within the infiltration facility was analyzed in the range from Δ
θi = 0% to Δ
θi = 100%. Different lengths for the bottom sides of the infiltration facility and slopes of its scarp were also considered.
Due to the fact that the parameter having the least influence on the required infiltration area (
Si) turned out to be the number of subcatchments (
ns) [
35], the research was carried out while assuming no division of the drained area into subcatchments.
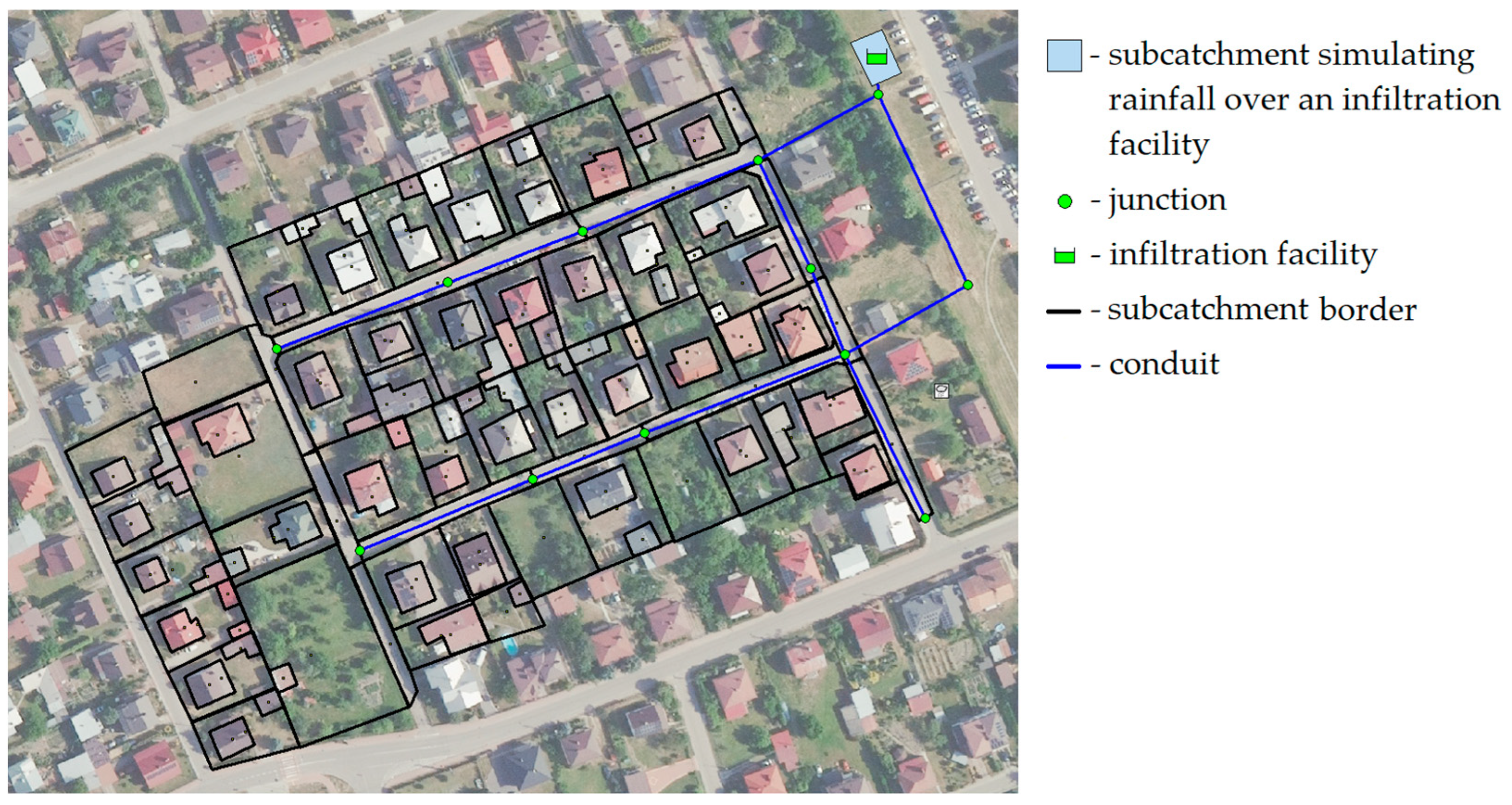
Figure 2 shows the layout of the considered system, which was analyzed in the SWMM software. The values of the other parameters characterizing the catchment were assumed to be equal to the average of the range considered in the previous stage of the analysis [
35].
Considering a large number of input variables and a wide range of their values, it was decided to use the design of experiments (DOE) theory. The five-factor research plan developed using Statistica software included parameters such as the percentage of impervious area (
C), the values of the water deficit within the catchment (Δ
θc) and the stormwater infiltration facilities (Δ
θi), the ratio of the bottom side lengths of the facilities (
a), and the slope of the scarp (1:
m). This resulted in 47 combinations of input parameters, 5 of which were the central point (
Appendix A).
The total catchment area (Ac) was not included in the research plan. This was due to the fact that this parameter is crucial for determining the required area of stormwater infiltration facilities (Si), and therefore, it was decided to extend the scope of the simulations. All combinations of input parameters were analyzed five times, assuming different total catchment areas (Ac) (i.e., 1.0 ha, 4.5 ha, 8.0 ha, 11.5 ha, and 15.0 ha). Since the results of hydrodynamic simulations of the central point would be the same in each case, this combination was analyzed for 25 different areas (Ac).
The type of soil within the catchment is also important for the process of stormwater infiltration. The presence of soils such as sand, loamy sand, sandy loam, silt loam, loam, clay loam, and clay was considered. These are soils characterized by hydraulic conductivities ranging from 0.25 mm/h for clay to more than 120 mm/h for sand [
40]. Due to the fact that the research plan was carried out for 5 different total catchment areas (
Ac), 7 types of soil, and 2 types of facilities, the implementation of this stage of research required the analysis of 3290 catchments. In each case, such an area of the bottom of the stormwater infiltration facility (
Si) was searched for so that at the rainfall generating the accumulation of the largest amount of stormwater, the fill level in the facility was equal to the allowed value (
himax). For this purpose, successive areas of the bottom of the facility (
Sij) were assumed, and its surface area was calculated at the maximum fill level (
Sijmax). The calculated area was also assigned to the catchment that simulated the rainfall over the facility. The defined model catchments were then loaded with rainfall of durations ranging from
t = 10 min to
t = 210 min, and the maximum fill levels in the infiltration basins and tanks (
hijmax) were determined. The simulations were run until the determined value of
hijmax reached the assumed value (
himax). All simulations were carried out using SWMM 5.1 software.
2.2. Rainfall Data
Rainfall is formed by the interaction of various weather factors in the atmosphere. It is a random phenomenon characterized by significant variability in time and space [
42]. Duka et al. [
43] indicated that there is no single best representation of a storm, with the result that a given distribution will be better in some cases and worse in others. The possibility of using different rainfall data was also noted by Fioramonte et al. [
44]. Considering this, this study was conducted using the same rainfall model as in the previous stage of the analysis [
35]. This model was developed by Bogdanowicz and Stachy [
45], and it is currently the most popular model used in Poland. Its use is recommended for various regions of the country (except mountainous areas) when the probability of rainfall is less than 100%. It is widely used in stormwater management analyses in Poland [
46] and is also recommended in design guidelines [
47]. All the equations, on the basis of which the depth of rainfall of a given duration were determined, can be found in the paper by Bogdanowicz and Stachy [
45].
The maximum depth of rainfall for the central region was determined for various rainfall durations in the range from
t = 10 min to
t = 210 min, assuming a probability of
p = 50%. The assumed value of
p is in line with the guidelines of the European Standard [
48] for residential areas. The range of rainfall durations was determined by the characteristics of the catchment area (mainly the type of soil within it), the drainage system, and the stormwater infiltration facilities. In each case, the critical duration of rainfall (
to), which caused the maximum filling in the facility, was within the considered range of rainfall durations (
t). The study yielded 201 rainfall characteristics, which were implemented in the SWMM 5.1 software after being converted to the appropriate form.
Figure 3 shows the values of the rainfall depth and intensity that were used in the analysis.
2.3. Green–Ampt Infiltration Model
The research was carried out with the assumption that both the infiltration within the catchment area and the infiltration through the bottom of the stormwater infiltration facility would be reflected using the modified Green–Ampt infiltration model [
39]. The Green–Ampt method was added to the SWMM in 1981 [
49]. It assumes that water infiltrates into the ground in a saturated soil layer vertically downward. Below the so-called wetting front, there is soil where the moisture content corresponds to some known initial value.
According to the described method [
50,
51], the cumulative depth of water which infiltrated into the soil at a given moment in time
F(
ti) can be determined from Equation (1), while the infiltration rate
f(
ti) is described by Equation (2). After transformation, these relationships take the form of Equations (3) and (4):
where
F(
ti) is the cumulative depth of the water which infiltrated into the soil at a given moment in time
ti;
f(
ti) is the infiltration rate at a given moment in time
ti;
K is the saturated hydraulic conductivity;
Ψ is the suction head along the wetting front;
Lga is the depth of the saturated layer below the surface;
hs is the depth of ponded water at the surface;
η is the soil porosity;
θin is the initial moisture content; and Δ
θ is the water deficit.
The modified Green–Ampt method, which was used in the research, additionally assumes that there is no reduction in the moisture deficit in the surface layer of the soil during rainfall, with an intensity lower than the hydraulic conductivity of saturated soil (
K) [
40].
2.4. Method for Selecting the Initial Geometry of the Infiltration Basins and Tanks
The considered combinations of input parameters, along with the values of the required bottom area of the stormwater infiltration facilities (Si) determined by the successive approximation method, were implemented in Python. The total catchment area (Ac), the percentage of impervious area (C), the values of the water deficit within the catchment (Δθc) and the stormwater infiltration facility (Δθi), the ratio of the bottom side lengths of the facility (a), and the slope of the facility scarp (1:m) were treated as quantitative input variables. The parameter values included in the simulations were considered. On the other hand, the type of soil was assumed to be a qualitative input variable, assigning it seven categories (sand, loamy sand, sandy loam, silt loam, loam, clay loam, and clay). The results of the hydrodynamic simulations (Si) were defined as a quantitative output variable. Artificial neural networks, specifically multilayer perception (MLP) networks, were used as a tool. This means that information flows through the network in only one direction: from the inputs to the outputs. The results obtained for particular combinations of input parameters were used to create two artificial neural networks separately for infiltration basins and tanks, the application of which would make it possible to quickly indicate the required bottom area of a stormwater infiltration facility (Si).
To develop ANN models, the dataset was divided into three sets: training (70% of the data), validation (15% of the data), and testing (15% of the data) [
52]. The individual activation functions could be described by any mathematical functions available in the TensorFlow library. Among the ANNs generated by the software, those with the lowest error values were selected. The generated ANNs were subjected to a performance evaluation using the mean squared error (
MSE) and the coefficient of determination (
R2). The mean squared error (
MSE) is a commonly used metric for evaluating the performance of regression models. The
MSE measures the mean square difference between the predicted and actual values in a dataset according to Equation (5). To determine the value of the coefficient of determination (
R2), the sum of the squares of the differences between the measured
yi values and the predicted
ŷi values divided by the sum of the squares of the differences between the observed
yᵢ values and their mean
ӯ was calculated. The coefficient of determination (
R2) is described by Equation (6) [
53]:
where
n is the amount of data in the set;
yi is the measured value;
ŷi is the predicted value; and
ӯ is the mean value of the dataset.
Using ANNs, the impact of the input parameters on the results of the hydrodynamic simulations was further evaluated. Sensitivity analysis was performed using SHapley Additive exPlanations (SHAP). SHAP is a tool used in the interpretation of prediction models. SHAP provides the global and local measures of significance of the model input parameters relative to the output variable, which are based on Shapley’s game theory [
54].
2.5. Case Study
The suitability of the ANNs was verified by using a real urban catchment as an example. The catchment is located in Kolbuszowa County, Podkarpackie Voivodeship, Poland (N: 50°14′40.93″, E: 21°45′51.15″) (
Figure 4). The catchment area is 3855 hectares, with a share of impervious surfaces of 50.17%. It is dominated by single-family buildings.
The slope of the catchment area is variable, ranging from 1.57% to 2.43%. The elevation and slope values of the catchment were determined using the digital elevation model (DEM) of the study area with a resolution of 1 m [
55].
A field survey was conducted within the catchment area to determine the soil types. Twelve boreholes were drilled, with three of them within the potential location of the infiltration facility. The thicknesses of the individual soil layers are presented in
Table 1.
Under the top layer of organic soil, there is a layer of loam with a thickness of 40–80 cm. Below this layer, more permeable soils have been found. At a depth of 170–400 cm, there is only sand. Due to the presence of soils with very good permeability at a depth of more than 170 cm, as well as the presence of a groundwater table at a level of 340 cm below the ground level, the catchment area has favorable conditions for the application of stormwater infiltration facilities.
To represent the hydrological and hydraulic conditions within the catchment area, a model of the catchment was developed in the SWMM software. One hundred twenty-seven subcatchments with a similar land use and slope were defined (
Figure 5). Although the number of subcatchments has a negligible effect on the required bottom area of stormwater infiltration facilities [
35], it was decided to reflect the drained catchment characteristics as accurately as possible. This allowed us to additionally verify the correctness of this assumption. The elevations and geometry of the drainage system conduits were determined based on Geoportal data [
55]. The drainage system consists of 13 conduits ranging from 15.44 to 74.49 m in length. The slope of the conduits in the drainage network varies from 0.62% to 2.77%.
3. Results
3.1. Results of the Hydrodynamic Simulations
Using SWMM 5.1 software, a dataset of the required bottom area of the infiltration basins and tanks (Si) was collected.
The research confirmed that both the total catchment area (
Ac) and the permeability of the soil within the catchment are of key importance to determining the value of
Si (
Figure 6 and
Figure 7). The simulation results obtained for sand and loamy sand were consistent, regardless of the water deficit values within the catchment (Δ
θc) and the facility (Δ
θi). This confirms that the intensity of rainfall, which is critical for the design of stormwater infiltration facilities, was lower than the water absorption capacities of soils characterized by significant permeability each time, even when Δ
θc = 0%. When using the Bogdanowicz–Stachy model [
45], the critical rainfall duration for which the maximum fill level in the infiltration basin was obtained exceeded 60 min and was extended with the increase in the total catchment area. However, sometimes the durations (
to) were considerably higher. In one of the cases considered (
Ac = 15 ha,
C = 10%), the duration of
to exceeded 110 min. In the case of the infiltration tanks, the durations of rainfall that caused the maximum fill level in the facility (
to) were even higher, with a minimum of 120 min.
The simulations performed for catchments with sandy loam showed that only with significant water saturation of the soil was the necessary bottom area of the stormwater infiltration facility (Si) greater than that determined for soils with higher hydraulic conductivity (K). In the case of the studied catchments, these were those fully saturated with water (Δθc). For the infiltration tanks, a similar trend was also observed for silt loam. On the other hand, studies carried out for facilities with a lower designed fill level (himax = 0.3 m) indicated differences in the values of Si obtained for sandy and silt loam. However, they were insignificant, and the number of cases for which their occurrence was observed decreased as the total catchment area (Ac) increased.
The analysis also showed that the absolute differences between the values of Si determined for different soils were greater for the infiltration basins than for the infiltration tanks, resulting from their low designed fill level (himax = 0.3 m). However, the percentage differences were definitely lower due to the high values of Si obtained on the basis of the hydrodynamic simulations. The required area of the bottom of the infiltration basin (Si), which was determined for a catchment characterized by a 10 percent share of the impervious area (C) and average values of the water deficit (Δθc, Δθi), was more than eight times higher when clay soils were present within the catchment than when they were sandy soils. At higher fractions of impervious surfaces in the total catchment area, these differences ranged from approximately 20% to almost 150%. In the case of the infiltration tanks, these differences sometimes exceeded 300%, and in the case of the catchment areas with the smallest degree of sealing (C = 10%), they were even 900% or more, with the differences increasing along with the reduction in the total catchment area (Ac).
The analysis of the results of the hydrodynamic simulations also confirmed that in the case of both considered types of facilities, an important role was played by the initial water deficit within the catchment (Δθc). The influence of this parameter was particularly important in the case of soils with low hydraulic conductivity (K).
Based on the results of the hydrodynamic simulations, it was also found that for the infiltration basins, the slope of the scarp of the infiltration facility (1:m) did not significantly affect the required area of its bottom (Si). With regard to the infiltration tanks, some differences were already noticeable, which was probably due to the higher designed fill levels of these facilities (himax), but they were not too large. In addition, it should be noted that the capacities of the facilities, which were determined at different values of m, with comparable values of the other input parameters almost did not differ at all. This allows us to conclude that the capacities of both considered facilities are only slightly determined by the slope of the scarp (1:m).
The results for the systems cooperating with facilities characterized by a different ratio for the bottom side lengths (a) indicated that this parameter also had little influence on the final results. However, confirmation of the thesis regarding the slight influence of the considered parameters on the required infiltration area (Si) requires further research.
3.2. The New Method of Selecting the Geometry of Infiltration Basins and Tanks
The results of the hydrodynamic simulations, carried out using SWMM 5.1 software, were implemented in Python. According to the adopted research methodology, two artificial neural networks from the generated ANNs were selected for the infiltration basins and tanks. These ANNs described the relationships between the individual parameters of the drainage systems.
Both the artificial neural network for predicting the bottom area of the infiltration basins and the ANN for predicting the bottom area of the infiltration tanks were characterized by an analogous architecture. Both ANNs had 13 neurons in the input layer. Six of them were quantitative variables, while the remaining seven neurons resulted from the determination of one qualitative variable with seven categories. The first hidden layer had 11 neurons and used the logarithmic activation function. The second hidden layer consisted of seven neurons, and the activation function was exponential. The output layer had one neuron and also used the exponential activation function. All layers were densely connected layers. This means that each neuron in each layer is connected to all neurons in the previous layer. The conceptual diagram of the architecture of the developed ANNs is shown in
Figure 8.
Table 2 presents the calculated values of the mean squared error (
MSE) and the coefficient of determination (
R2) for the developed ANNs.
Developing ANNs using Python software has many advantages. One of them is the ability to create a web application, for which web frameworks in Python such as Flask or Django are used. In the case of an application based on generated ANNs, the user is able to quickly check the approximate bottom area of the infiltration facilities for defined input data. The simple interface of the application is shown in
Figure 9.
The user’s task is to define all the values of the input parameters (i.e., the total catchment area (Ac), the percentage of impervious area (C), the values of the water deficit within the catchment (Δθc) and the stormwater infiltration facility (Δθi), the ratio of the bottom side lengths of the facilities (a), and the slope of the scarp (1:m)) and to select one of the seven soil categories (sand, loamy sand, sandy loam, loam, silt loam, clay loam, and clay). After entering the design data and pressing the “Calculate” button, the required bottom areas of the infiltration facilities appear in the browser window. Determining the subsequent values of the Si parameter requires redefining the values of the input variables.
The user of the application does not have to define the rainfall data for which the required bottom areas of the stormwater infiltration facilities are to be determined. The simulations, which were carried out on model catchments, made it possible to determine the Si values for over 200 rainfall characteristics and to select those resulting in the highest fill level in the facility in a given case. As a result, the Si values generated using ANNs correspond to the values determined for rainfall, which is critical under the given conditions.
3.3. Application of Artificial Neural Networks to Evaluate the Effect of the Input Parameters on the Required Bottom Area of Stormwater Infiltration Facilities
The study showed that the bottom area of the stormwater infiltration facility can be determined with high accuracy using a machine learning model. Evaluation of the influence of the input parameters on the required
Si area was performed using the SHapley Additive exPlanations (SHAP) method. The results of the analysis are presented in
Figure 10.
The global importance factors for the input parameters are shown in
Figure 10a,c. It should be noted that the SHAP values assigned to the individual input variables represent the mean absolute value of the impact. The SHAP value gives information on the overall importance or contribution of the parameters to the predictions of the model. When analyzing the SHAP values (
Figure 10a,c), it was observed that in the case of both the infiltration basins and tanks, the total catchment area (
Ac), the percentage of impervious area (
C), and the type of soil within the catchment had a decisive impact on the required bottom area (
Si). The other input variables showed a significantly lower degree of influence on the value of
Si. The lowest impact was recorded for the ratio of the bottom side lengths of the facilities (
a).
Whether the input variable had a positive or negative impact on the value of the output variable in a given case is shown in
Figure 10b,d. The SHAP value for a single calculation case was determined on the basis of the difference between the predicted value considering all input parameters and the predicted result without a given input parameter. To take into account the dependencies between the input parameters of the model, this difference was calculated for all possible combinations of these parameters. Then, this difference was averaged, with the weighting being proportional to the number of combinations containing a given feature.
The research shows that high values for the total catchment area (
Ac) and the percentage of impervious area (
C) led to an increase in the expected bottom area of the infiltration facility (
Si). For the infiltration tank, the maximum difference between the predicted value of
Si considering all input parameters and the predicted result without the total catchment area (
Ac) was 789.72 m
2. For the infiltration basin, this difference was 1972.02 m
2. In the case of the percentage of impervious area (
C), these differences were equal to a maximum of 499.86 m
2 for the infiltration tank and 1529.64 m
2 for the infiltration basin. When analyzing the SHAP values for the type of soil, it was noticed that the SHAP value increased with the decrease in the hydraulic conductivity (
K) of the soil. Therefore, the highest SHAP values were recorded for cases where clay was present within the catchment. In all such cases, the SHAP values were positive. On the other hand, for soils such as sand, loamy sand, sandy loam, and silt loam, the SHAP values were negative in all cases. When analyzing the data presented in
Figure 10b,d, it can also be seen that the SHAP values were similar for these soils. This was probably due to the fact that with rainfall with a probability of
p = 50%, all or at least a major part of it that falls within impermeable surfaces is subject to surface retention and infiltration into the ground. However, it should be assumed that an increase in rainfall intensity would result in an increase in the differences observed between these types of soil due to an increase in the share of surface runoff in the hydrological balance of the catchment.
3.4. Application of the Method to the Example of a Real Urban Catchment
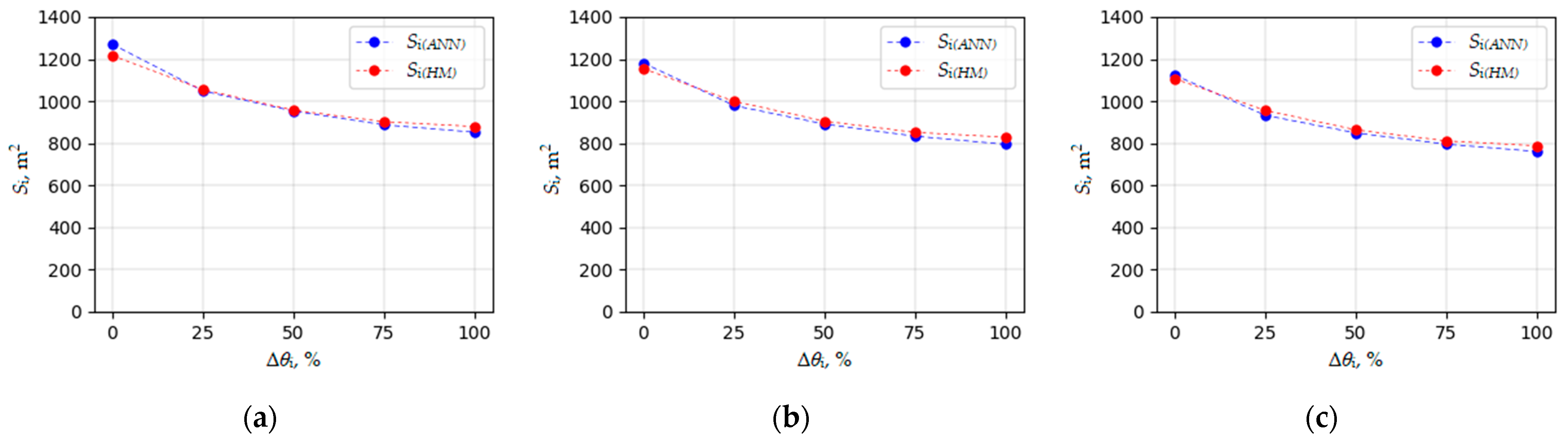
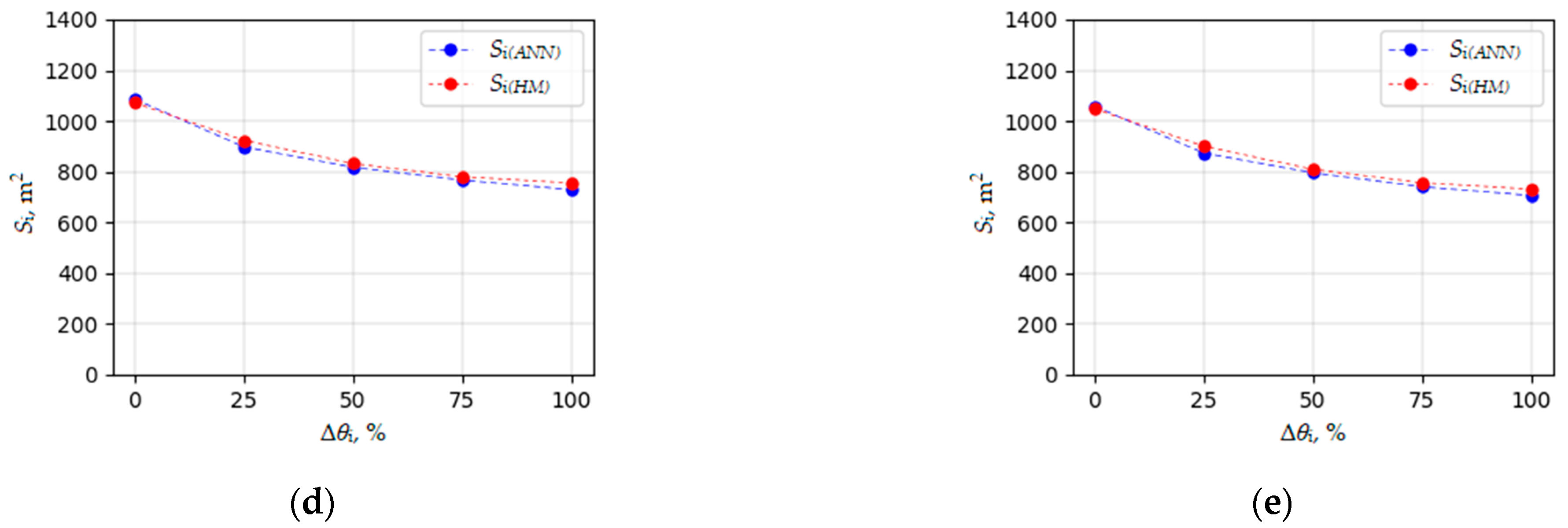
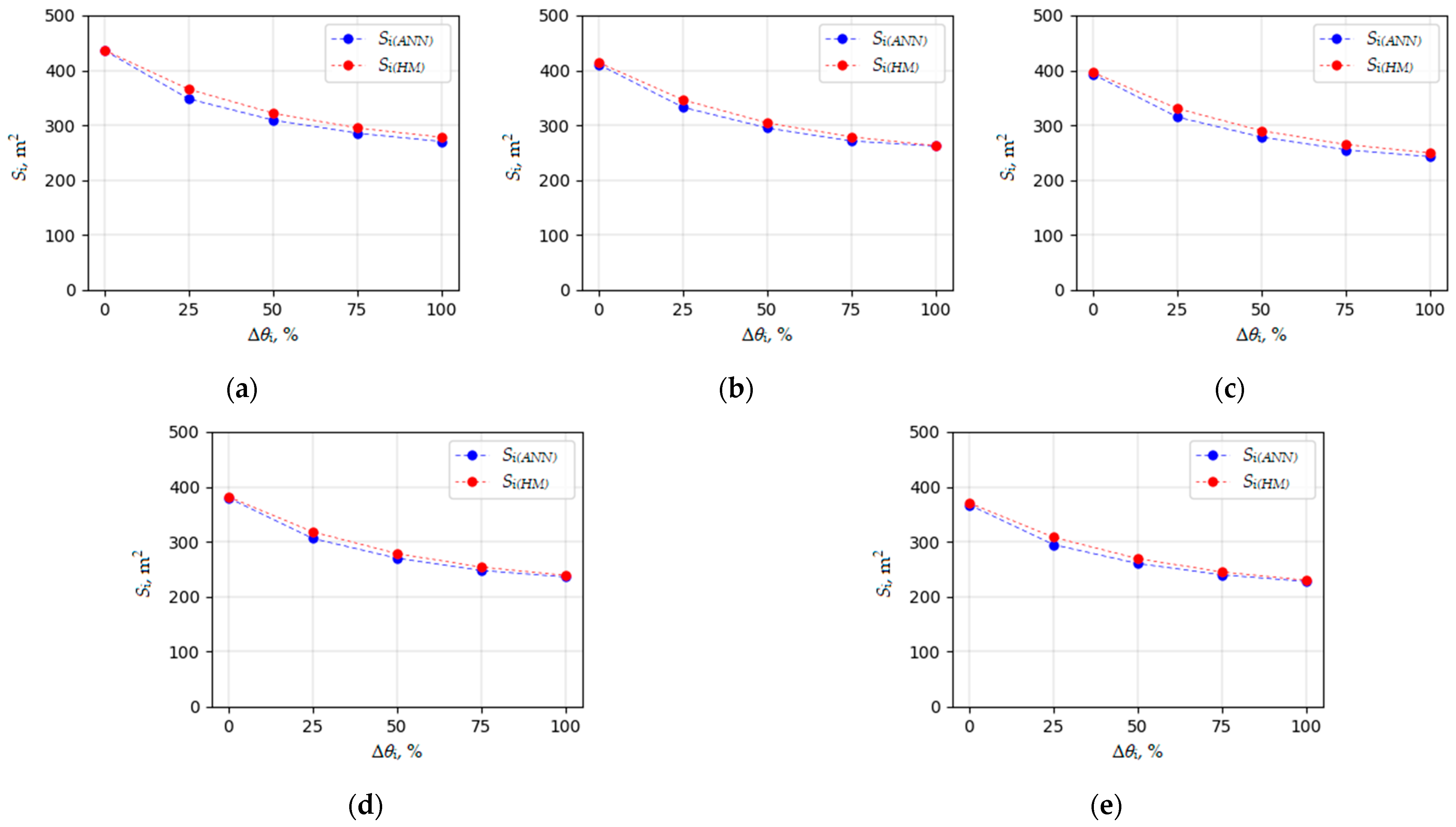
In order to confirm the applicability of the ANN models developed with Python for determining the required stormwater infiltration area, they were applied to a real urban catchment described in
Section 2.4. The results from the ANNs were compared with the results from the hydrodynamic simulations. This research was carried out for different values of the water deficit within the catchment (Δ
θc) and the stormwater infiltration facility (Δ
θi) (
Table 3 and
Appendix B).
The analysis of the data from
Table 3 allowed us to conclude that both generated artificial neural networks can be used as a valuable tool for quickly determining the initial required bottom area of stormwater infiltration facilities. The maximum percentage error between the values obtained from hydrodynamic modeling and those generated by artificial neural networks was 5.09%. The median percentage error was 2.17%. This suggests a tendency for the developed ANNs to slightly overestimate the output values in a situation where loam is present within the catchment area. The reported errors probably resulted from the omission of certain hydraulic and hydrological parameters that describe the functioning of the analyzed real drainage system and the urban catchment (e.g., average surface slope and channel roughness coefficient).
4. Discussion
The discharge of excess surface water into infiltration basins or infiltration tanks is often considered one of the most beneficial ways to manage stormwater [
32]. The application of these green infrastructure facilities within urban catchments can bring significant benefits to both people and the surrounding environment. However, in high-density areas, the lack of space available for the development of such facilities can be a problem. The soil and water conditions in the area should also be considered. In some cases, it may be difficult and sometimes even impossible to use infiltration basins or tanks. In such conditions, it may be helpful to use the method described in the paper for selecting the geometry of these facilities. Thanks to this, it will be possible to quickly but accurately estimate the size of the area required for the installation of a specific type of facility. Knowing the approximate area of stormwater infiltration facilities, both the designer and investor will be able to assess whether their application within the catchment area is feasible as well as indicate which facility will be a more favorable option under the given conditions.
The methodology used in Poland for designing stormwater infiltration facilities is based solely on the total catchment area (
Ac) and the degree of its sealing (
C), while the type of soil present is mostly ignored. However, research confirmed the relationships from the previous stage of the analysis [
35], according to which this parameter significantly affects the required area of the stormwater infiltration facility (
Si). With a significant water deficit within the catchment (Δ
θc), differences in the
Si values were noticeable only for soils with low hydraulic conductivity (
K). However, it should be noted that the critical rainfall durations for the design of the infiltration basins and tanks were found to be significantly longer than those applicable to the dimensioning of pipes. Long-lasting rainfalls often occur immediately after each other, with the risk that the soil will not be able to dry completely before critical rainfall occurs. On the other hand, for the catchments characterized by significant water saturation at the beginning of rain, clear differences between the results obtained for different types of soil were observed, reaching from tens to even hundreds of percent. This demonstrates the need to take this parameter into account at the design stage of the infiltration facilities, for which the computational model that was developed as part of the research can be used.
The importance of soil type has already been emphasized by other authors. For example, Basri et al. [
56] noticed that the soil type affects the formation of the peak discharge in the watershed and, consequently, also the susceptibility to a river flood. On the other hand, Mind’je et al. [
57] noted that physiographic data, which include the soil type, are important inputs in rainfall-discharged flow modeling. However, some researchers have pointed out that maximum and minimum infiltration rates are not key determinants of the total runoff volume and peak discharge [
58]. However, it should be noted that this study [
58] considered a very narrow range of infiltration intensities from 1 to 5 mm/h, which certainly influenced the results of the sensitivity analysis. These values correspond to moist clay and loamy soils. In the case of permeable soils, the maximum infiltration rate can significantly exceed 100 mm/h [
59]. Therefore, considering the type of soil within the catchment seems to be a necessity when designing stormwater management systems. Despite this, descriptions of hydrodynamic simulations carried out without taking into account the type of soil can be found in the literature [
34,
37]. Such an approach increases the risk of an undersized drainage infrastructure and, consequently, its overloading and increased flood risk. Otherwise, the stormwater management system could be oversized, resulting in an increase in the required investment outlays.
The choice of the design values of the initial deficit within the catchment (Δθc) and the stormwater infiltration facility (Δθi) is up to the investor and should be preceded by a detailed risk analysis taking into account the location of the facility. When designing infiltration basins or tanks in the immediate vicinity of buildings, the aim should be to ensure the highest possible level of protection for residents. Under such conditions, it will be reasonable to assume the most unfavorable design conditions (i.e., complete saturation of the soil with water). However, if the facility is to be located in a green area outside the catchment, and the possible increase in filling above the designed fill level will not cause significant damage, then the assumed water deficit values can be higher. This will reduce the area of the facility and, as a result, also the amount of investment outlays for its implementation.
This study also showed that the geometry of the infiltration facility does not significantly affect the final results. Therefore, it can be assumed that the developed computational model can also be applied to irregularly shaped facilities. Thus, it will be possible to test the applicability of infiltration basins and tanks in natural depressions and the possibility of their integration into the surroundings, especially in the absence of other available areas. This is particularly important because urban areas currently suffer from a lack of green spaces [
60], and such spaces can significantly affect the lifestyle and health of residents [
61]. In the case of Poland, as well as other European countries, this problem is further exacerbated by the difficulties in interpreting existing law and the lack of legal definitions of basic solutions in the field of water law [
62]. Under such conditions, the investor’s reluctance to invest in an expensive hydrodynamic model should not come as a surprise, especially with a limited budget and uncertainty about the availability of space for the development of a given facility and the feasibility of its construction.
The research confirmed the legitimacy of using machine learning methods to support the drainage infrastructure design process. Considering that designing a climate-resilient urban infrastructure requires constant updating of urban design criteria [
10], a change in approach to this issue is inevitable. The use of the computational model described in this paper provides an opportunity to quickly interpret the data characterizing the catchment and the stormwater infiltration facility, which facilitates decision making and improves work efficiency. The validity of the model application was confirmed in the example of a real urban catchment. The differences between the values of the required bottom area of infiltration facilities, obtained using artificial neural networks, and the values determined by hydrodynamic modeling oscillated between −4.23% and 5.09%. This result can be considered satisfactory.
Artificial neural networks that have been developed using the Python programming language can easily be used to build web applications dedicated to the design of a drainage infrastructure. The use of such an application can significantly reduce the time involved in the design process as well as facilitate the selection of the most suitable infiltration facility. Due to this technique, designers can save time by avoiding the need to create a complex hydrodynamic model of an urban catchment in situations where the use of infiltration facilities is not reasonable, for example, due to the lack of sufficient space for development. When the application is used, the results for the geometry of infiltration facilities are available immediately. This makes it possible to quickly analyze multivariant design concepts and carefully examine only those variants that yield the most favorable results.
The limitation of this study is the use of a rainfall model that is dedicated to the territory of Poland. As a result, the new model for sizing infiltration basins and tanks, developed with the Python programming language, cannot be applied to other countries. Due to the limitations of the Bogdanowicz–Stachy model, its use is also impossible for mountainous areas, which have different climatic conditions compared with the rest of the country, as well as more varied relief. However, similar computational models can be developed by considering different rainfall data, which should be the subject of future research. The development of such a tool for other regions of the world will require a series of hydrodynamic simulations for model catchments that will be loaded with rainfalls of different characteristics. Based on the results of these simulations, it will be possible to generate ANN models. Future studies should also take into account the need to continuously update the developed models and adapt them to climate change. The response to climate change is essential due to the potential threats it poses. These threats include an increase in the frequency and magnitude of natural disasters, including floods and droughts, which can affect human life and health.
Future studies should also consider rainfalls with a lower probability of occurrence (
p). The authors focused on rainfall with a probability of
p = 50%, as this value is recommended for residential areas in Europe [
48]. However, these types of facilities can also be used in areas with higher flood protection requirements. It should be expected that rainfall of higher intensity will generate more runoff from green areas, especially in the case of soils with low hydraulic conductivity. This, in turn, will certainly affect the nature of the runoff and the functioning of infiltration facilities.
It should also be noted that the studies used only designed rainfall events, which may not fully reflect the complexity of real weather phenomena. However, the use of such rainfall data is a more universal approach, ensuring the possibility of applying the method over a larger area of the country [
35]. The use of continuous rainfall data characteristic of one specific area unfortunately excludes such a possibility. It is also important that continuous simulation requires long-term rainfall data, which in many locations in Poland is still not available. It also happens that even in places covered by weather monitoring, these data are incomplete and difficult to access. If data availability improves in the coming years, then future research will certainly benefit from comparing the results obtained based on both methods.
In addition to expanding the range of analyzed rainfall data, an important aspect of future research should also be the development of new methods for sizing other facilities for application within drainage networks. The research results prove that the use of SWMM software and artificial neural networks allows both the development of a method for sizing a given type of facility and an indication of the significance of the parameters considered during hydrodynamic modeling. In addition, attention should be paid to heterogeneous catchments characterized by a significant diversification of topographic and soil parameters. This research assumed homogeneity of the catchment as the basis for the hydrodynamic simulations. Extending the research toward heterogeneous catchments will certainly make a significant contribution to the current state of knowledge.
It should also be borne in mind that the designed infiltration facilities were verified only on the basis of hydrodynamic simulations. For this reason, the next stage of research should be verification of the method based on long-term observations of the infiltration systems that will be designed using this method.
Regardless of conducting research on the design of stormwater management facilities, attention should be paid to promoting the idea of sustainable stormwater management and raising the environmental awareness of the public. In the case of Poland, as well as many other countries, there is still a widespread belief that stormwater is waste that should be disposed of as soon as possible. Changing this attitude, combined with a common understanding of stormwater runoff as a resource, should be the first step in transforming cities into water-sensitive cities [
63]. This is particularly important in light of recent experiences from various countries showing the urgent need for sustainable stormwater management in residential areas [
64].