Optimal Exploitation of Urban Water Supply Networks Based on Pressure Management with the Nondominated Sorting Differential Evolution (NSDE) Algorithm
Abstract
1. Introduction
2. Materials and Methods
2.1. The Optimization Algorithm
- NSDE exhibits a good balance between convergence (finding solutions close to the true Pareto front) and diversity (exploring different regions of the Pareto front). It has been observed to maintain a diverse set of high-quality solutions throughout the optimization process.
- NSDE is known for its efficiency in terms of computational time and resource utilization. It can effectively handle large-scale optimization problems and converge to near-optimal solutions within a reasonable number of iterations.
- NSDE is robust against noisy or uncertain objective functions. It can handle objective functions with stochastic variations or noise, making it suitable for real-world optimization scenarios where objective values might be subject to variability.
- NSDE tends to produce a well-distributed set of solutions that cover different regions of the Pareto front. This feature allows decision-makers to gain insights into the trade-offs between conflicting objectives and make informed decisions based on their preferences.
- NSDE can be easily adapted and applied to various domains, including water supply network optimization. It can handle different types of decision variables, constraints, and objective functions commonly encountered in such applications.
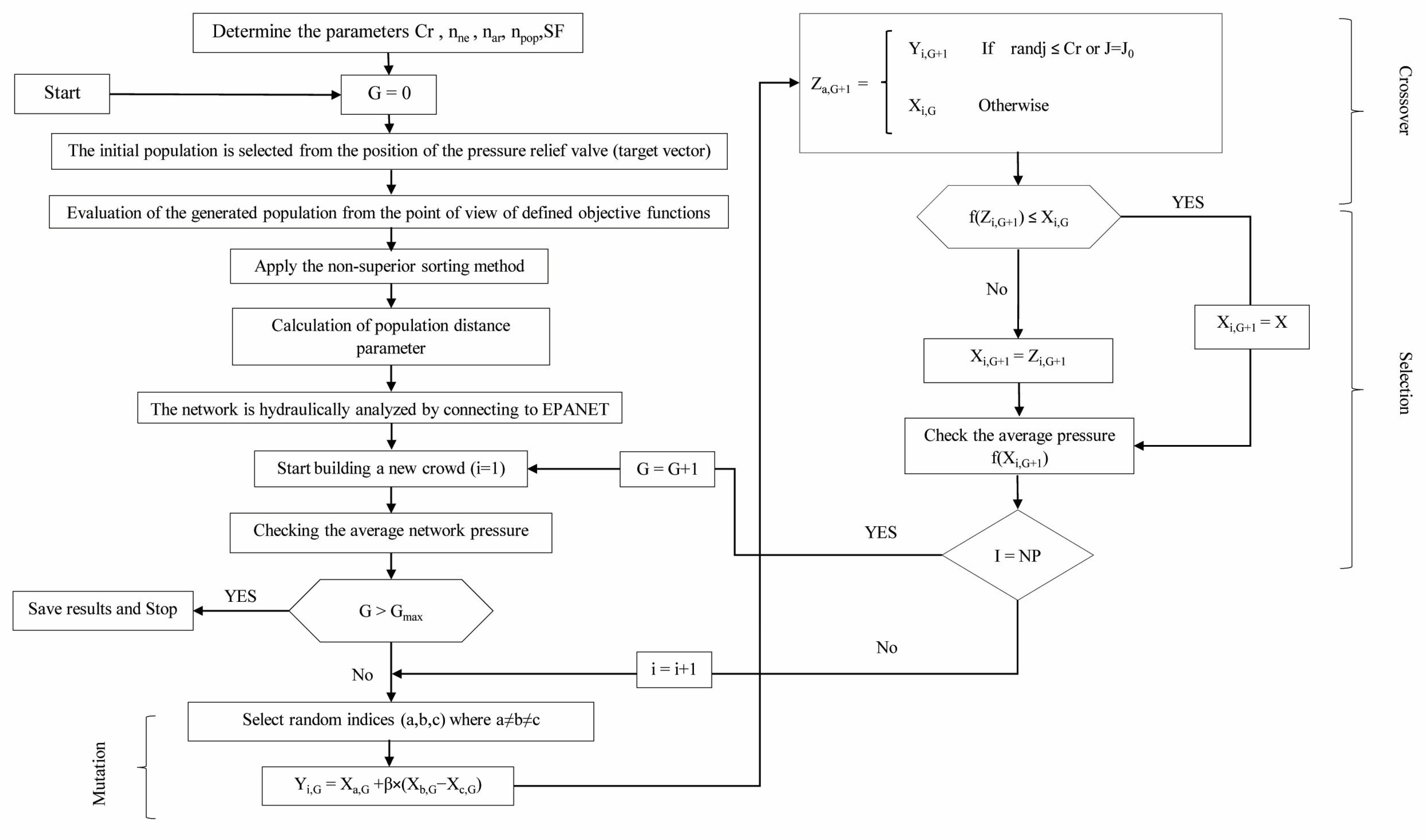
- Generate the initial population based on constraints and scale of the problem,
- Evaluate the population based on the defined objective functions,
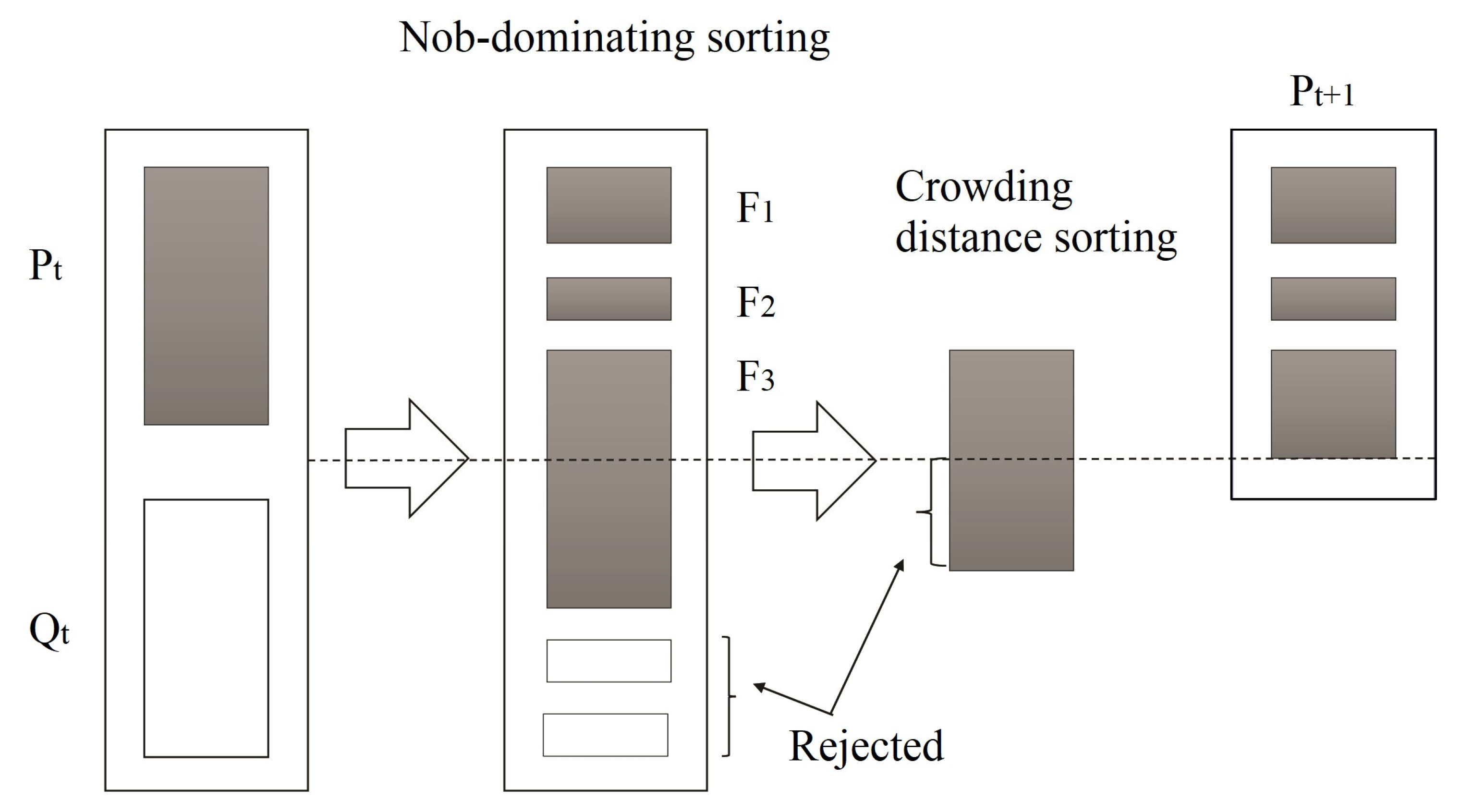
- Apply the non-superior sorting method to categorize the population based on their performance,
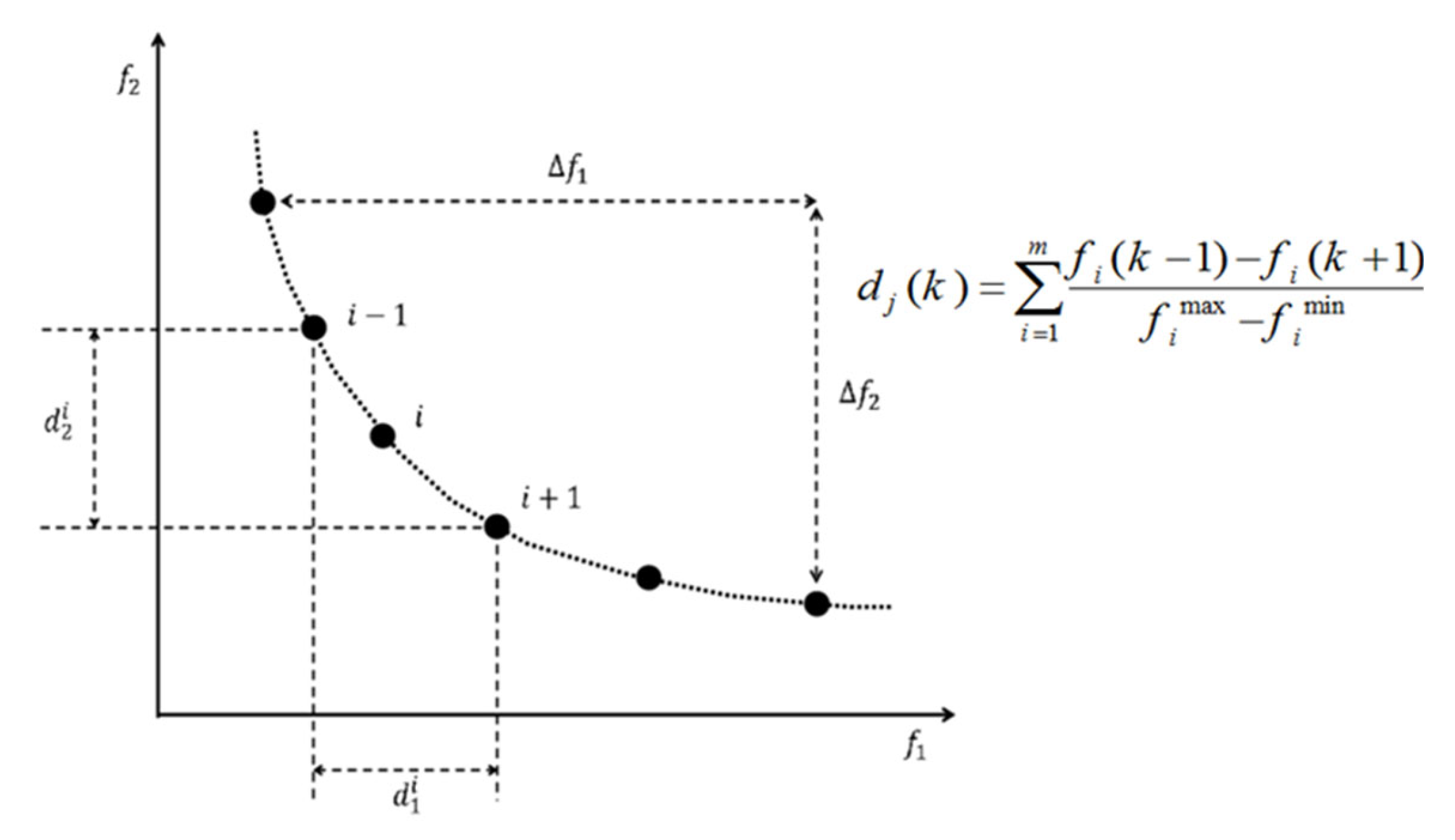
- Calculate the control parameter called Crowding Distance for each member in each group, which represents the closeness of the target sample to other members of the population in that group (target group),
- Select the parent population for reproduction,
- Perform jump and intersection.
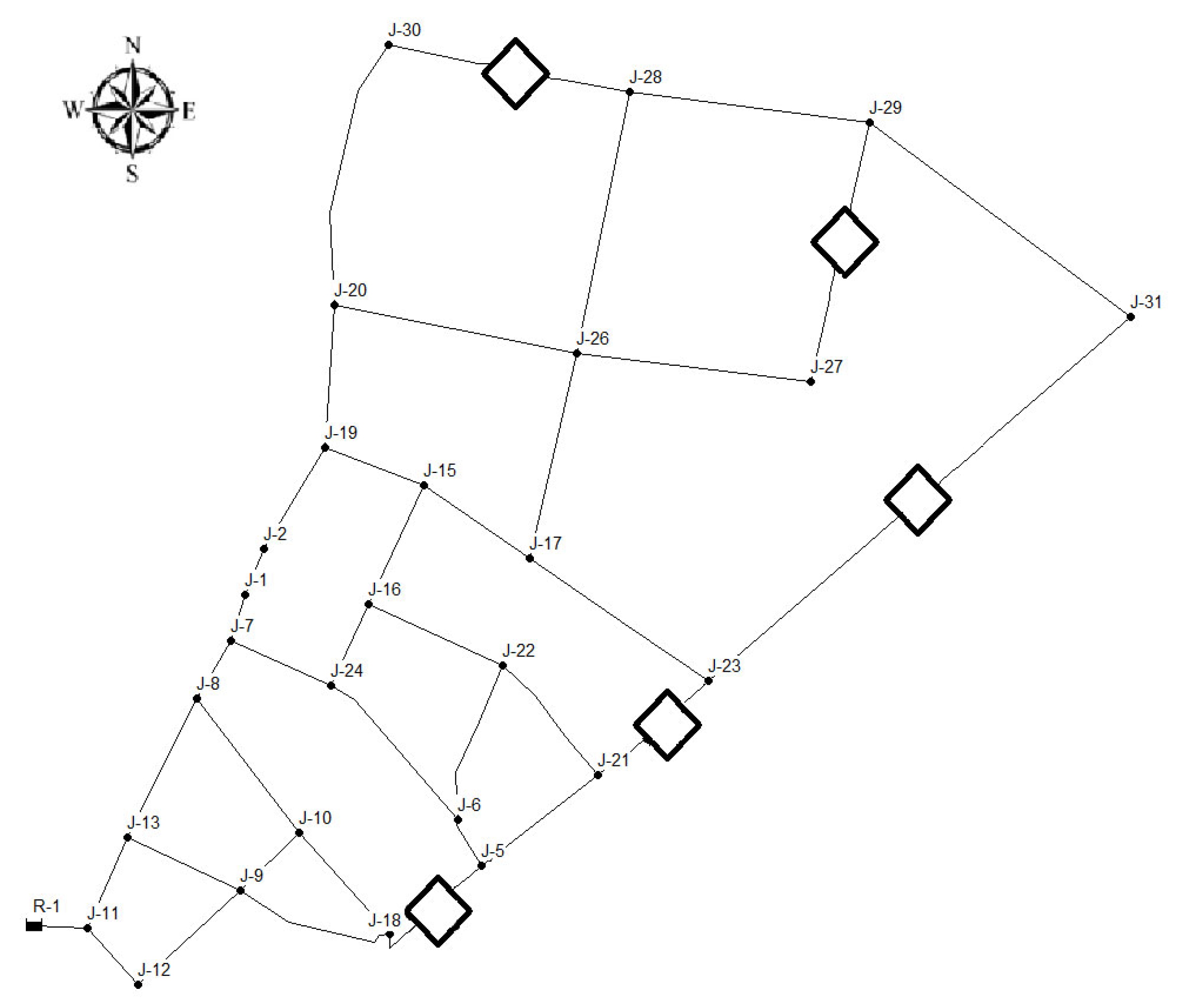
2.2. The EPANET Model
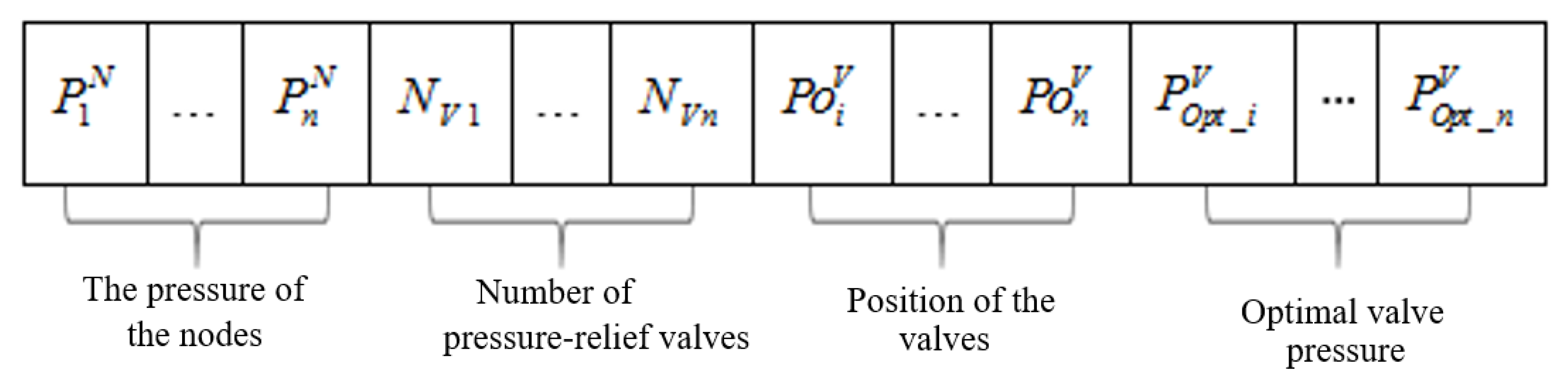
2.3. Algorithm Implementation and Coding
2.4. Equations and Laws in Water Distribution Networks
- Losses due to friction along the walls of the pipes;
- Losses due to disturbances in the flow caused by equipment and other factors that alter the flow conditions (known as local losses).
2.5. Formulation of the Optimization
2.6. Alternative Techniques
- Alternative optimization techniques offer different search strategies and exploration-exploitation balances. By considering multiple approaches, you can explore different regions of the search space and potentially discover better solutions that may have been missed by a single technique. Each technique has its strengths and weaknesses, so combining them can provide a more comprehensive search.
- Different optimization techniques may have specific adaptations or variations designed for particular problem characteristics. By exploring alternative techniques, you may find an approach that is better suited for the specific problem at hand. For example, some techniques may excel in handling discrete variables or constraints, while others may be more efficient for continuous optimization or multi-objective problems.
- Comparing the performance of different optimization techniques can provide valuable insights into their strengths and limitations. It allows you to assess factors such as convergence speed, solution quality, robustness, and scalability. Comparative analysis helps in selecting the most suitable optimization technique for a given problem and understanding the trade-offs involved.
- By using alternative optimization techniques, you can benchmark and verify the results obtained using NSDE. This process ensures the reliability and accuracy of the optimization outcomes. Verification through different techniques provides confidence that the solutions achieved are robust and not biased due to a particular algorithm’s limitations.
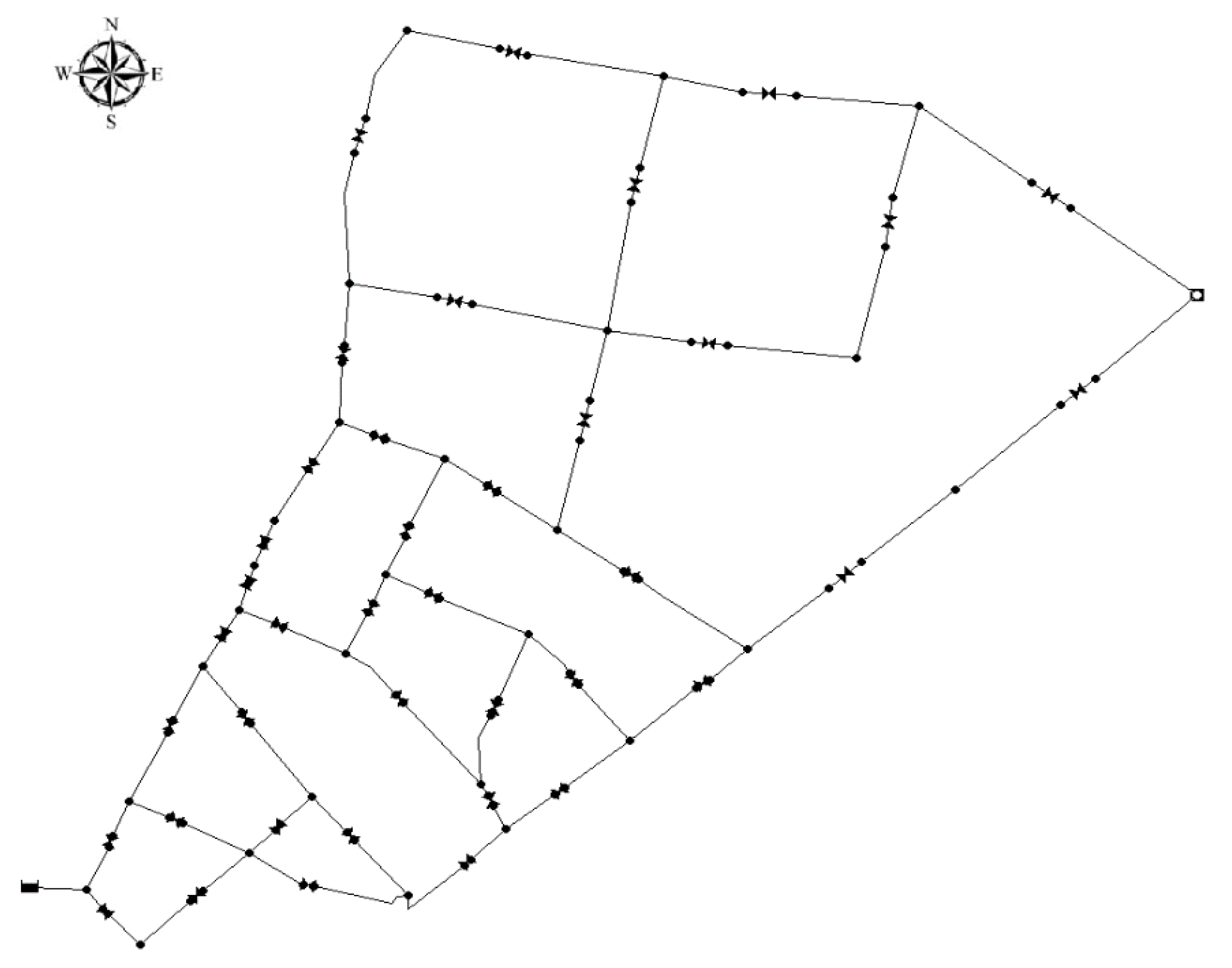
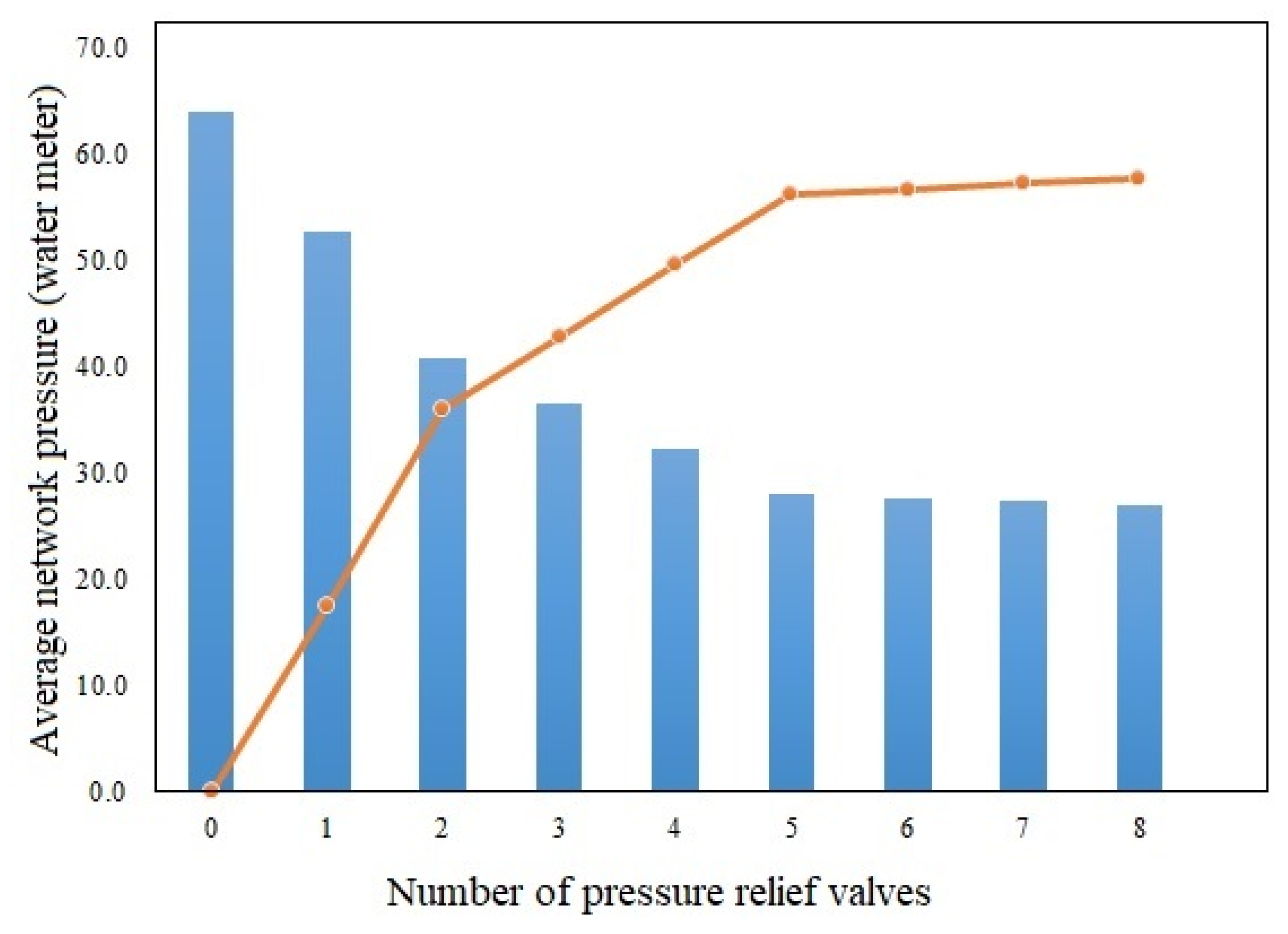
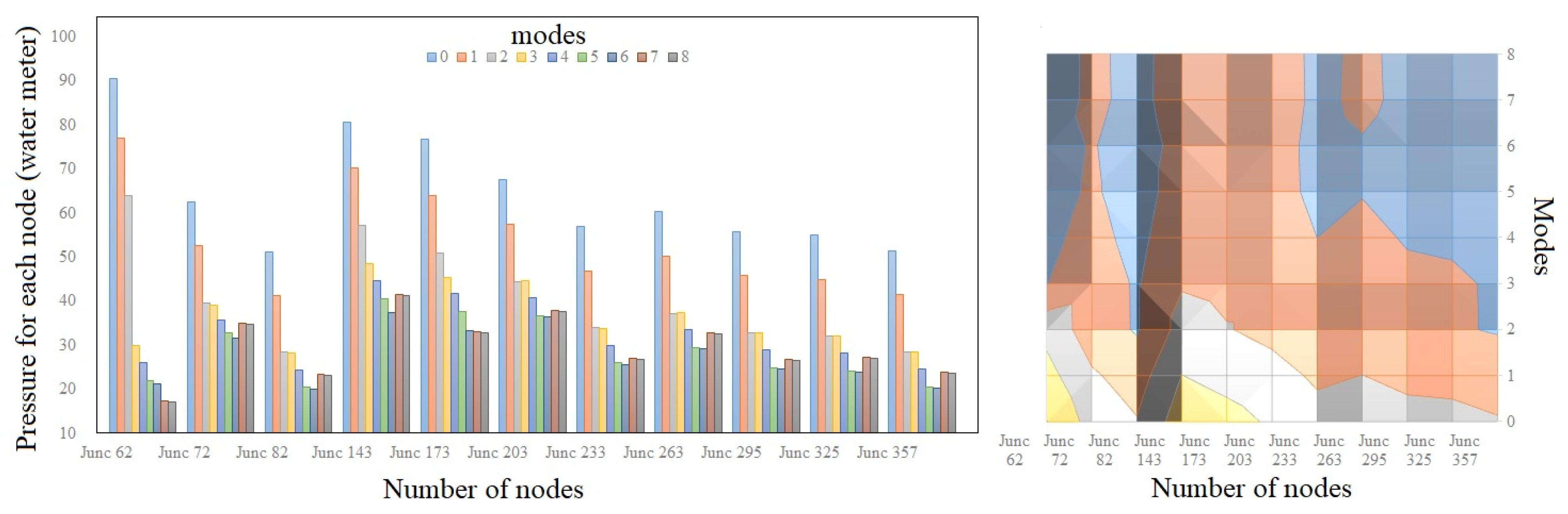
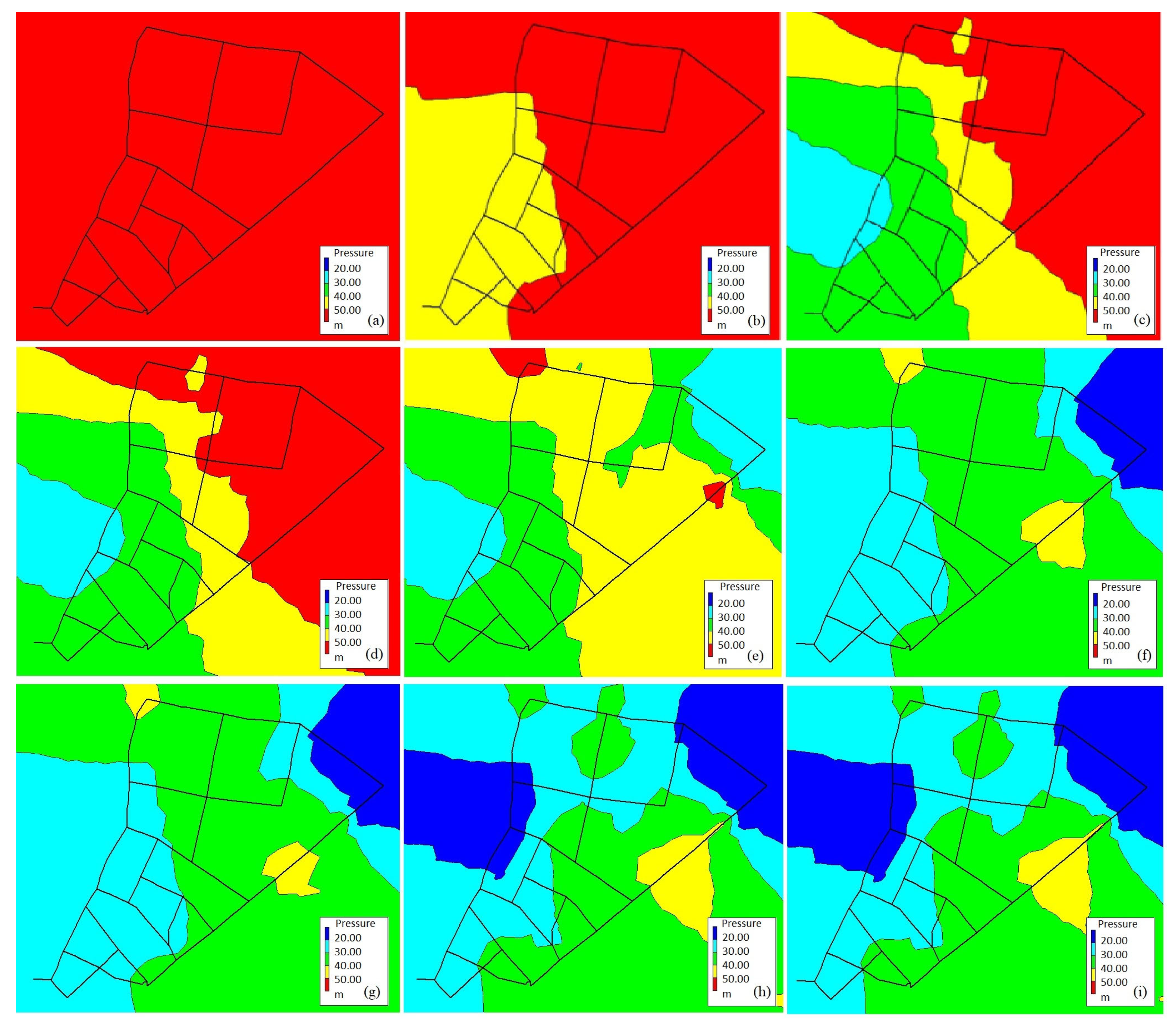
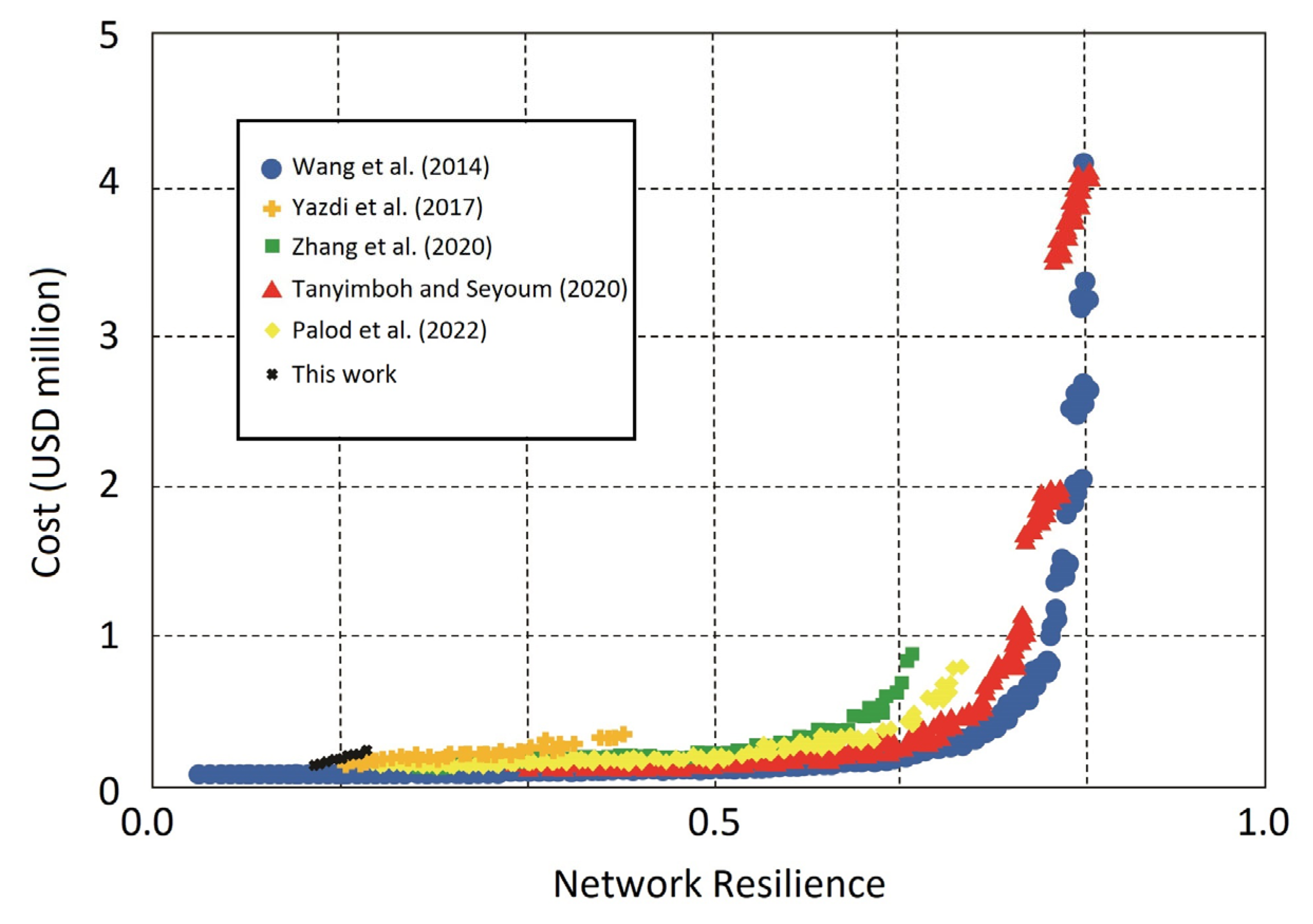
3. Results and Discussion
- The final point can be determined based on a fixed and predetermined number of pressure-relief valves in the system,
- The minimum required pressure reduction in the desired network can be used to determine the final point (in general, the minimum required improvement in the objective function),
- The final point can be determined based on the location on the curve where increasing the number of pressure-relief valves does not significantly decrease the pressure and leakage of the entire system network,
- The maximum approved budget for the pressure management plan can be used to determine the end point.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| NSDE | Nondominated Sorting Differential Evolution |
| PSO | Particle swarm optimization |
| EPANET | US Environmental Protection Agency’s hydraulic design software |
| GA | Genetic algorithm |
| NSGA-II | Non-Dominated Sorting Genetic Algorithm II |
| CP | Crossover probability |
References
- Elsherif, S.M.; Wang, S.; Taha, A.F.; Sela, L.; Giacomoni, M.H.; Abokifa, A.A. Control-theoretic modeling of multi-species water quality dynamics in drinking water networks: Survey, methods, and test cases. An. Rev. Control 2022, 55, 466–485. [Google Scholar] [CrossRef]
- Nasir, M.; Sadollah, A.; Yoon, J.H.; Geem, Z.W. Comparative study of harmony search algorithm and its applications in China, Japan and Korea. Appl. Sci. 2020, 10, 3970. [Google Scholar] [CrossRef]
- Kumar, V.; Yadav, S.M. A state-of-the-Art review of heuristic and metaheuristic optimization techniques for the management of water resources. Water Supply 2022, 22, 3702–3728. [Google Scholar] [CrossRef]
- Yousefi, H.; Moridi, A. Multiobjective optimization of agricultural planning considering climate change impacts: Minab reservoir upstream watershed in Iran. J. Irrig. Drain. Eng. 2022, 148, 04022007. [Google Scholar] [CrossRef]
- Heydari Mofrad, H.; Yazdi, J. An enhanced multi-objective evolutionary algorithm for the rehabilitation of urban drainage systems. Eng. Optimiz. 2022, 54, 349–367. [Google Scholar] [CrossRef]
- Araujo, L.S.; Ramos, H.; Coelho, S.T. Pressure control for leakage minimization in water distribution systems management. Water Resour. Manag. 2006, 20, 133–149. [Google Scholar] [CrossRef]
- Creaco, E.; Pezzinga, G. Multiobjective optimization of pipe replacements and control valve installations for leakage attenuation in water distribution networks. J. Water Resour. Plan. Manag. 2014, 141, 04014059. [Google Scholar] [CrossRef]
- Saldarriagaa, J.; Salcedo, C.A. Determination of optimal location and settings of pressure reducing valves in water distribution networks for minimizing water losses. Eng. Proc. 2015, 119, 973–983. [Google Scholar] [CrossRef]
- Gupta, A.; Bokde, N.; Marathe, D.; Kulat, K. Leakage Reduction in Water Distribution Systems with Efficient Placement and Control of Pressure Reducing Valves Using Soft Computing Techniques. Eng. Technol. Appl. Sci. Res. 2017, 7, 1528. [Google Scholar] [CrossRef]
- Dini, M.; Asadi, A. Optimal operational scheduling of available partially closed valves for pressure management in water distribution networks. Water Resour. Manag. 2020, 34, 2571–2583. [Google Scholar] [CrossRef]
- Jafari-Asl, J.; Kashkooli, B.S.; Bahrami, M. Using particle swarm optimization algorithm to optimally locate and control pressure reducing valves for leakage minimization in water distribution systems. Sustain. Water Resour. Manag. 2020, 6, 64. [Google Scholar] [CrossRef]
- Ortega-Ballesteros, A.; Iturriaga-Bustos, F.; Perea-Moreno, A.J.; Muñoz-Rodríguez, D. Advanced Pressure Management for Sustainable Leakage Reduction and Service Optimization: A Case Study in Central Chile. Sustainability 2022, 14, 12463. [Google Scholar] [CrossRef]
- Montalvo, I.; Izquierdo, J.; Schwarze, S.; Pérez-García, R. Multi-objective particle swarm optimization applied to water distribution systems design: An approach with human interaction. Math. Comput. Model. 2010, 52, 1219–1227. [Google Scholar] [CrossRef]
- Sayyed, M.A.; Gupta, R.; Tanyimboh, T.T. Modelling pressure deficient water distribution networks in EPANET. Proc. Eng. 2014, 89, 626–631. [Google Scholar] [CrossRef]
- Cheung, P.B.; Van Zyl, J.E.; Reis, L.F.R. Extension of EPANET for pressure driven demand modeling in water distribution system. Comput. Control Water Indust. 2005, 1, 311–316. [Google Scholar]
- De Paola, F.; Fontana, N.; Galdiero, E.; Giugni, M.; Savic, D.; Degli Uberti, G.S. Automatic multi-objective sectorization of a water distribution network. Proc. Eng. 2014, 89, 1200–1207. [Google Scholar] [CrossRef]
- Farmani, R.; Savic, D.A.; Walters, G.A. Evolutionary multi-objective optimization in water distribution network design. Eng. Optimiz. 2005, 37, 167–183. [Google Scholar] [CrossRef]
- Zhang, K.; Yan, H.; Zeng, H.; Xin, K.; Tao, T. A practical multi-objective optimization sectorization method for water distribution network. Sci. Total Environ. 2019, 656, 1401–1412. [Google Scholar] [CrossRef]
- Siew, C.; Tanyimboh, T.T. Penalty-free feasibility boundary convergent multi-objective evolutionary algorithm for the optimization of water distribution systems. Water Resour. Manag. 2012, 26, 4485–4507. [Google Scholar] [CrossRef]
- Yazdi, J.; Choi, Y.H.; Kim, J.H. Non-dominated sorting harmony search differential evolution (NS-HS-DE): A hybrid algorithm for multi-objective design of water distribution networks. Water 2017, 9, 587. [Google Scholar] [CrossRef]
- Ramesh, H.; Santhosh, L.; Jagadeesh, C.J. Simulation of hydraulic parameters in water distribution network using EPANET and GIS. In Proceedings of the International Conference on Ecological, Environmental and Biological Sciences, Dubai, United Arab Emirates, 7–8 January 2012; pp. 350–353. [Google Scholar]
- Ahmadullah, R.; Dongshik, K. Designing of hydraulically balanced water distribution network based on GIS and EPANET. Int. J. Adv. Comput. Sci. Appl. 2016, 7, 118–125. [Google Scholar] [CrossRef]
- Sonaje, N.P.; Joshi, M.G. A review of modeling and application of water distribution networks (WDN) softwares. Int. J. Technol. Res. Appl. 2015, 3, 174–178. [Google Scholar]
- Gheibi, M.; Emrani, N.; Eftekhari, M.; Behzadian, K.; Mohtasham, M.; Abdollahi, J. Assessing the failures in water distribution networks using a combination of geographic information system, EPANET 2, and descriptive statistical analysis: A case study. Sustain. Water Resour. Manag. 2022, 8, 47. [Google Scholar] [CrossRef]
- Zarei, N.; Azari, A.; Heidari, M.M. Improvement of the performance of NSGA-II and MOPSO algorithms in multi-objective optimization of urban water distribution networks based on modification of decision space. Appl. Water Sci. 2022, 12, 133. [Google Scholar] [CrossRef]
- Sivakumar, P.; Gorev, N.B.; Tanyimboh, T.T.; Kodzhespirova, I.F.; Suribabu, C.R.; Neelakantan, T.R. Dynamic pressure-dependent simulation of water distribution networks considering volume-driven demands based on noniterative application of EPANET 2. J. Water Resour. Plan. Manag. 2020, 146, 06020005. [Google Scholar] [CrossRef]
- Hassanvand, M.R.; Salimi, A.H.; Kisi, O.; Mohammadi, H.O.; Abouzari, N. Investigating application of adaptive neuro fuzzy inference systems method and Epanet software for modeling green space water distribution network. Iran. J. Sci. Technol. Trans. Civil Eng. 2021, 45, 2765–2777. [Google Scholar] [CrossRef]
- Tahani, M.; Kandi, A.; Moghimi, M.; Houreh, S.D. Rotational speed variation assessment of centrifugal pump-as-turbine as an energy utilization device under water distribution network condition. Energy 2020, 213, 118502. [Google Scholar] [CrossRef]
- Navin, U.; Dohare, D. A Critical Review on Design and Analysis of Water Distribution Network Using WaterGEMS and EPANET Softwares. SAMRIDDHI A J. Phys. Sci. Eng. Technol. 2022, 14, 381–385. [Google Scholar] [CrossRef]
- Ball, J.W.; Tullis, J.P. Application of Butterfly Valves for Free Discharge, Minimum Pressure Drop, and for Choking Cavitation. Div; ASCE: Reston, VA, USA, 1973. [Google Scholar]
- Wang, Q.; Guidolin, M.; Savic, D.; Kapelan, Z. Two-objective Design of Benchmark Problems of a Water Distribution System via MOEAs: Towards the Best-known Approximation of the True Pareto Front. J. Water Resour. Plan. Manag. 2014, 141, 04014060. [Google Scholar] [CrossRef]
- Zhang, T.; Xu, X.; Li, Z.; Abu-Siada, A.; Guo, Y. Optimum location and parameter setting of STATCOM based on improved differential evolution harmony search algorithm. IEEE Access 2020, 8, 87810–87819. [Google Scholar] [CrossRef]
- Tanyimboh, T.T.; Seyoum, A.G. Design optimization of water distribution networks: Real-world case study with penalty-free multi-objective genetic algorithm using pressure-driven simulation. Water SA 2020, 46, 465–475. [Google Scholar] [CrossRef]
- Palod, N.; Prasad, V.; Khare, R. A new multi-objective evolutionary algorithm for the optimization of water distribution networks. Water Supply 2022, 22, 8972. [Google Scholar] [CrossRef]
| Parameter | Population Size | Max Iteration | Crossover Pop. | Scaling Factor |
|---|---|---|---|---|
| Value | 150 | 100 | 0.70 | 0.50 |
| No. | Active Valve Number | Ave. Network Pressure (Water Meters) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Active valve number | 63.96 | ||||||||
| 1 | Active valve number | 1 | 52.71 | |||||||
| 2 | Active valve number | 1 | 25 | 40.86 | ||||||
| 3 | Active valve number | 1 | 4 | 13 | 36.55 | |||||
| 4 | Active valve number | 1 | 4 | 6 | 15 | 32.25 | ||||
| 5 | Active valve number | 1 | 4 | 11 | 13 | 26 | 28.06 | |||
| 6 | Active valve number | 1 | 4 | 11 | 13 | 26 | 38 | 27.71 | ||
| 7 | Active valve number | 1 | 4 | 13 | 14 | 26 | 33 | 20 | 27.36 | |
| 8 | Active valve number | 1 | 4 | 6 | 15 | 26 | 33 | 20 | 13 | 27.05 |
| No. | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| Percentage reduction | 0 | 17.589 | 36.116 | 42.855 | 49.578 | 56.129 | 56.676 | 57.223 | 57.708 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cemiloglu, A.; Licai, Z.; Ugurenver, A.; Nanehkaran, Y.A. Optimal Exploitation of Urban Water Supply Networks Based on Pressure Management with the Nondominated Sorting Differential Evolution (NSDE) Algorithm. Water 2023, 15, 2583. https://doi.org/10.3390/w15142583
Cemiloglu A, Licai Z, Ugurenver A, Nanehkaran YA. Optimal Exploitation of Urban Water Supply Networks Based on Pressure Management with the Nondominated Sorting Differential Evolution (NSDE) Algorithm. Water. 2023; 15(14):2583. https://doi.org/10.3390/w15142583
Chicago/Turabian StyleCemiloglu, Ahmed, Zhu Licai, Abbas Ugurenver, and Yaser A. Nanehkaran. 2023. "Optimal Exploitation of Urban Water Supply Networks Based on Pressure Management with the Nondominated Sorting Differential Evolution (NSDE) Algorithm" Water 15, no. 14: 2583. https://doi.org/10.3390/w15142583
APA StyleCemiloglu, A., Licai, Z., Ugurenver, A., & Nanehkaran, Y. A. (2023). Optimal Exploitation of Urban Water Supply Networks Based on Pressure Management with the Nondominated Sorting Differential Evolution (NSDE) Algorithm. Water, 15(14), 2583. https://doi.org/10.3390/w15142583








