Analysis and Exploration of the Impact of Average Sea Level Change on Navigational Safety in Ports
Abstract
1. Introduction
2. Sea-Level-Rise Analysis
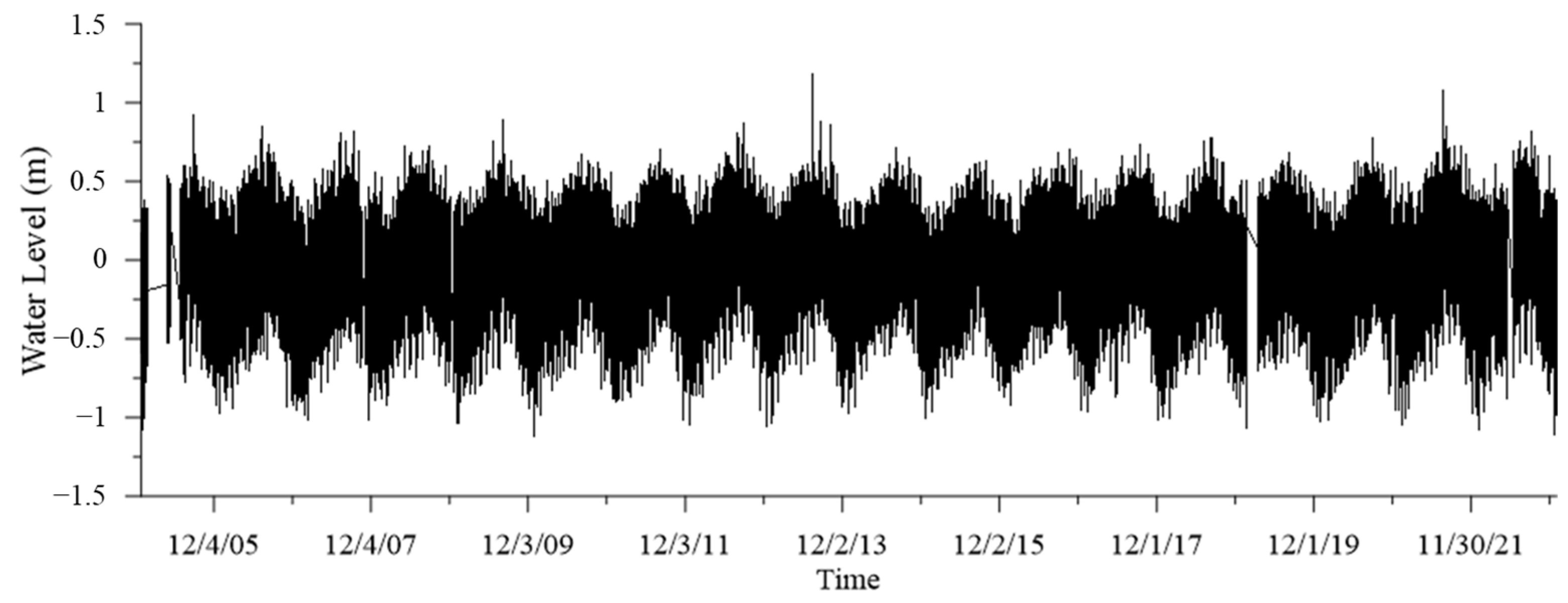
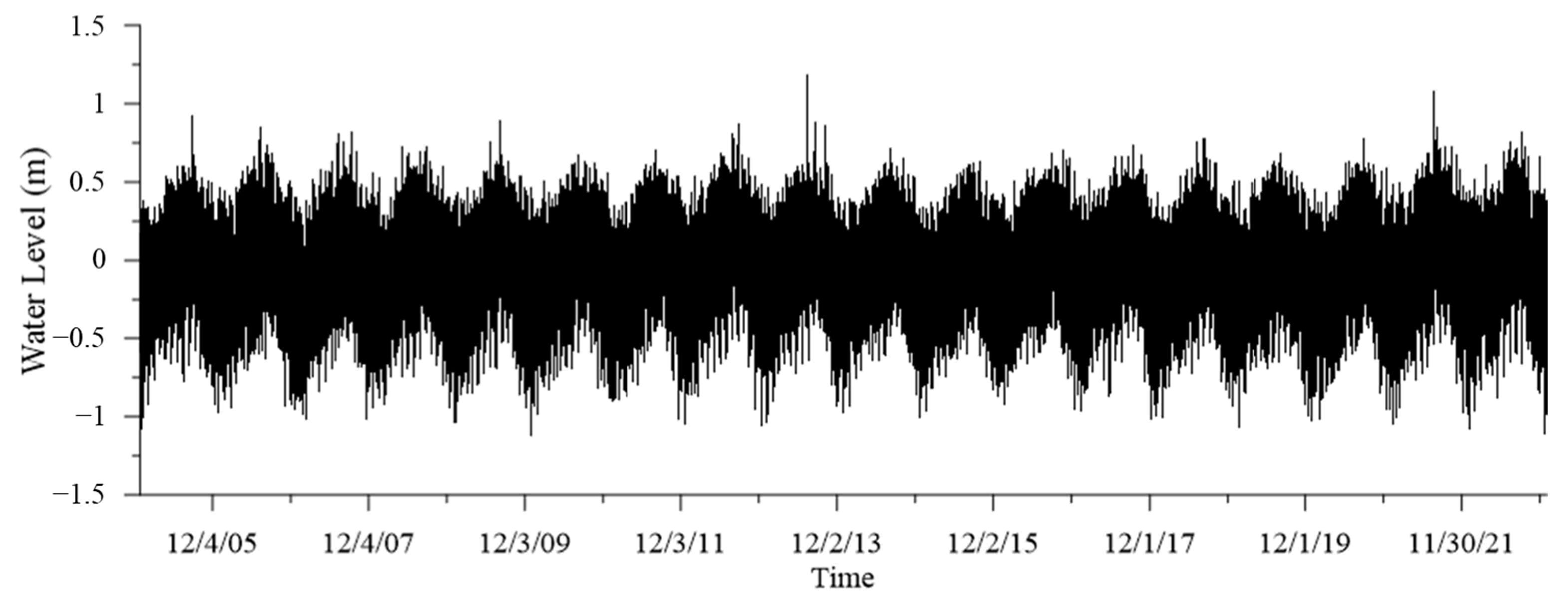
2.1. Analysis of Water Level Data
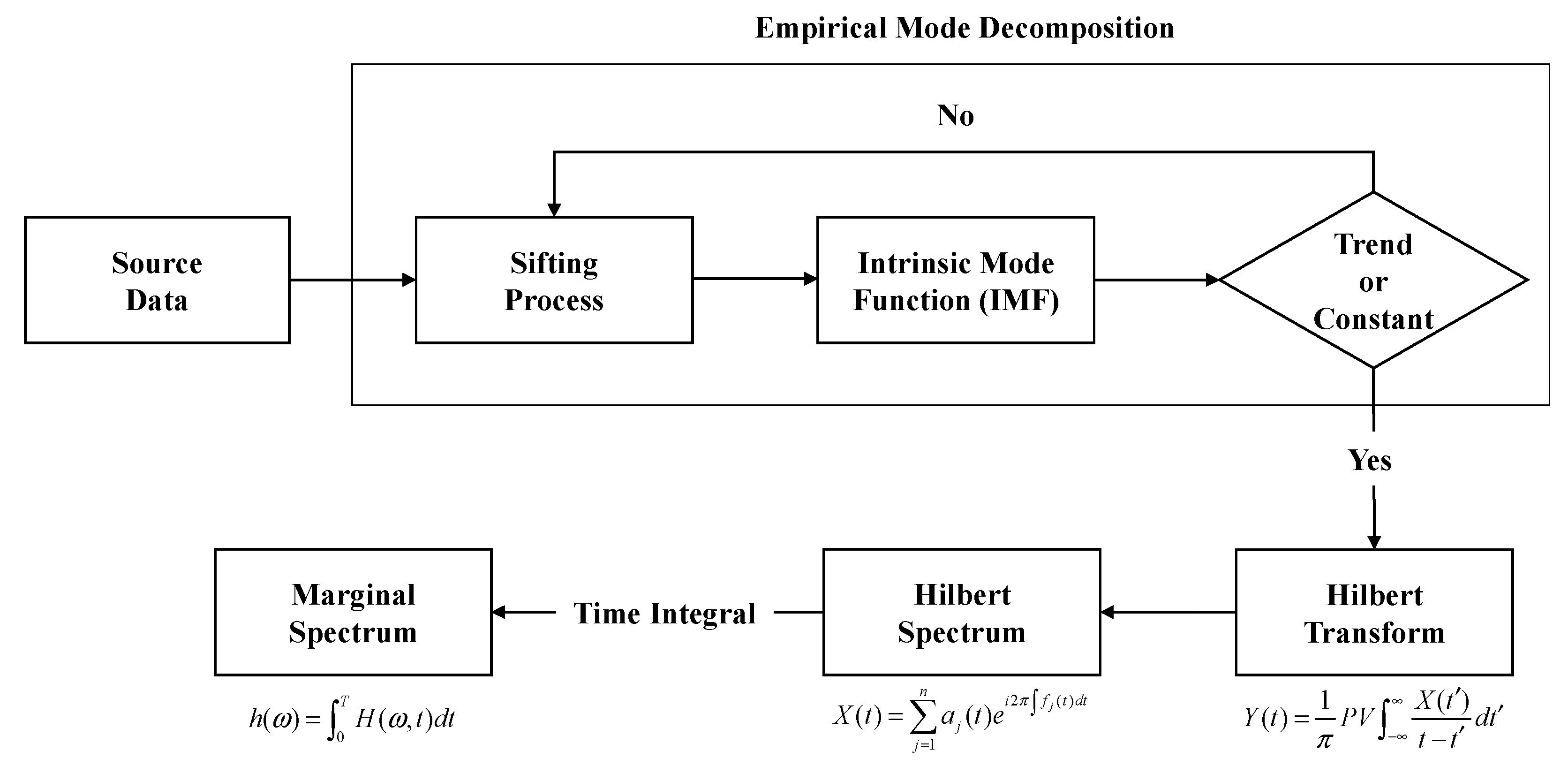
2.2. Methods for Analyzing Sea Level
3. Hydrodynamic Characteristic Analysis
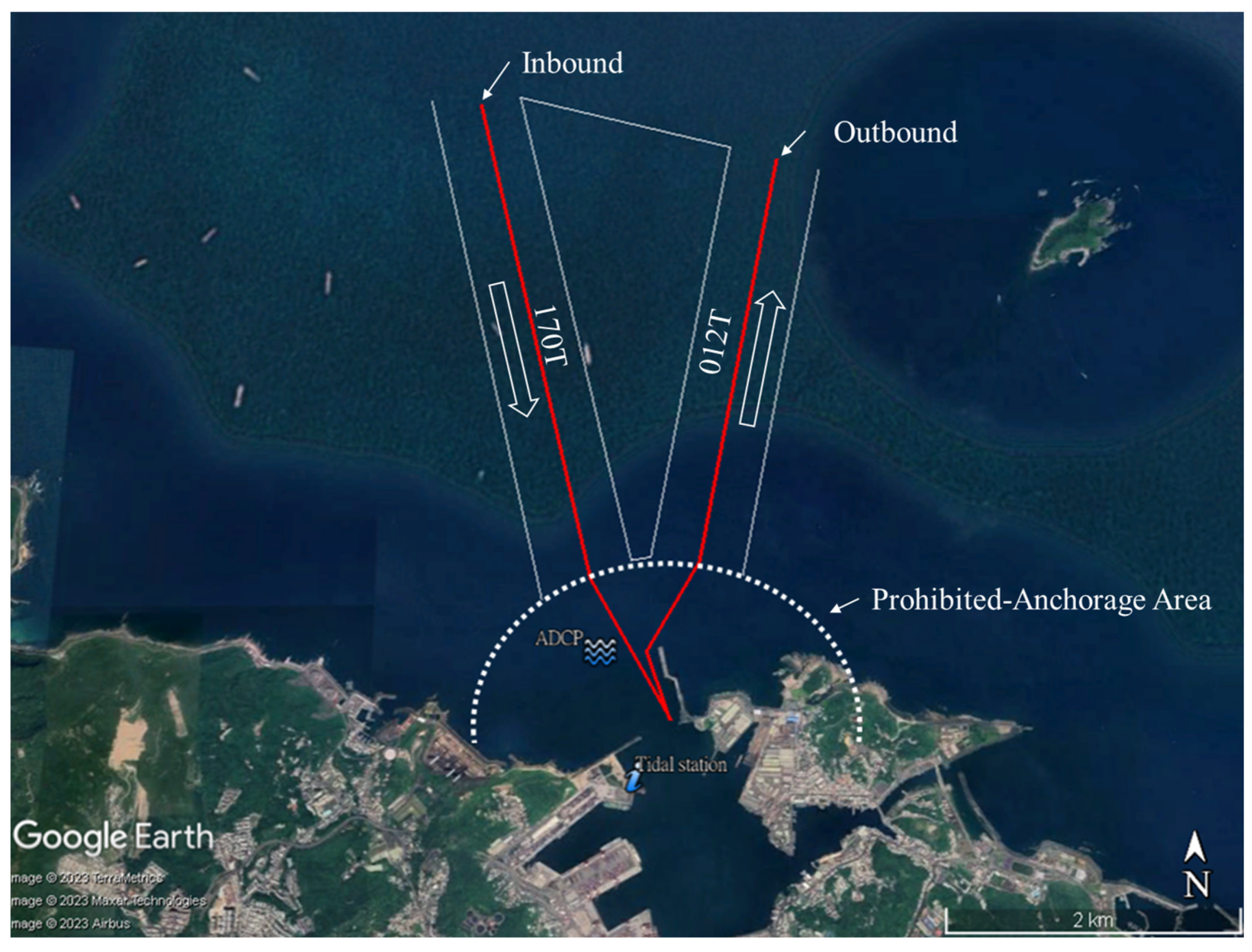
3.1. Model Setup
3.2. Model Calculation Range and Settings
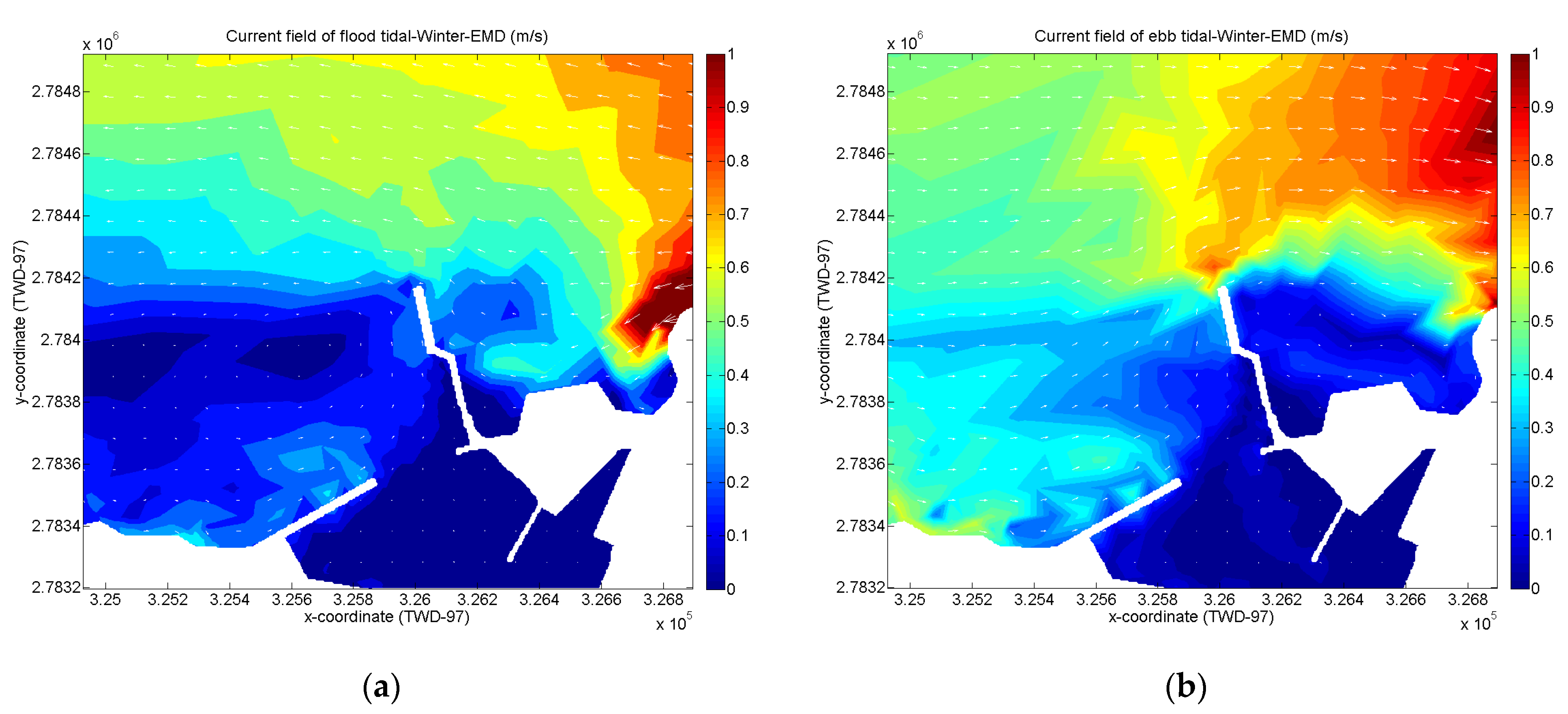
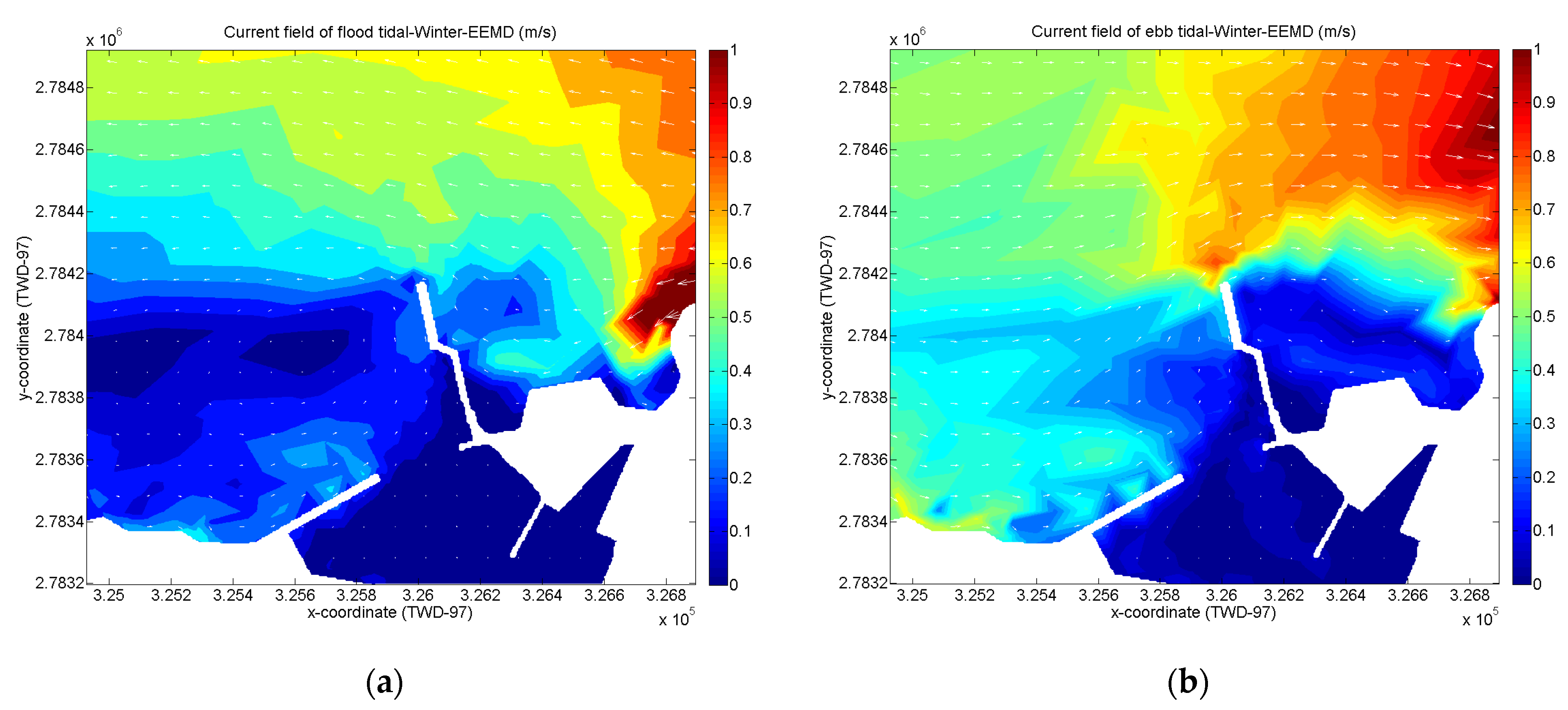
3.3. Hydraulic Simulation Results Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Douglas, B.C. Chapter 3 Sea level change in the era of the recording tide gauge. In International Geophysics; Elsevier: Amsterdam, The Netherlands, 2001; Volume 75, pp. 37–64. [Google Scholar]
- Mitrovica, J.X.; Tsimplis, M.E.; Davis, J.L.; Milne, G.A. Recent mass balance of polar ice sheets inferred from patterns of global sea-level change. Nature 2001, 409, 1026–1029. [Google Scholar] [CrossRef] [PubMed]
- Church, J.A.; White, N.J.; Coleman, R.; Lambeck, K.; Mitrovica, J.X. Estimates of regional distribution of sea level rise over the 1950–2000 period. J. Clim. 2004, 17, 2609–2625. [Google Scholar] [CrossRef]
- Church, J.; White, N.J. Sea-level rise from the late 19th to the Early 21st Century. Surv. Geophys. 2011, 32, 585–602. [Google Scholar] [CrossRef]
- Shum, C.K.; Kuo, C.Y. Observation and geophysical causes of present-day sea level rise. In Climate Change and Food Security in South Asia; Springer: Dordrecht, The Netherlands, 2011; pp. 85–104. [Google Scholar]
- Merrifield, M.A.; Merrifield, S.T.; Mitchum, G.T. An Anomalous Recent Acceleration of Global Sea Level Rise. J. Clim. 2009, 22, 5772–5781. [Google Scholar] [CrossRef]
- Allan, R.P.; Hawkins, E.; Bellouin, N.; Collins, B. IPCC, 2021: Summary for Policymakers. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK, 2023; in press. [Google Scholar]
- Rahmstorf, S. A semi-empirical approach to projecting future sea level rise. Science 2007, 315, 368–370. [Google Scholar] [CrossRef]
- Rahmstorf, S. Response to comment on “A semi-empirical approach to projecting future sea level rise”. Science 2007, 317, 1866. [Google Scholar] [CrossRef]
- Horton, R.; Herweijer, C.; Rosenzweig, C.; Liu, J.; Gornitz, V.; Ruane, A.C. Sea level rise projections for current generation CGCMs based on the semi-empirical method. Geophys. Res. Lett. 2008, 35, L02715. [Google Scholar] [CrossRef]
- Zhan, J.G.; Wang, Y.; Cheng, Y.S. The analysis of China sea level change. Chin. J. Geophys. 2009, 52, 1725–1733. (In Chinese) [Google Scholar]
- Wisha, U.J.; Wijaya, Y.J.; Hisaki, Y. Sea Level Variability in the Equatorial Malacca Strait: The Influence of Climatic–Oceanographic Factors and Its Implications for Tidal Properties in the Estuarine Zone. Climate 2023, 11, 70. [Google Scholar] [CrossRef]
- Iglesias, I.; Bio, A.; Melo, W.; Avilez-Valente, P.; Pinho, J.; Cruz, M.; Gomes, A.; Vieira, J.; Bastos, L.; Veloso-Gomes, F. Hydrodynamic Model Ensembles for Climate Change Projections in Estuarine Regions. Water 2022, 14, 1966. [Google Scholar] [CrossRef]
- Aguilera-Vidal, M.; Muñoz-Perez, J.J.; Contreras, A.; Contreras, F.; Lopez-Garcia, P.; Jigena, B. Increase in the Erosion Rate Due to the Impact of Climate Change on Sea Level Rise: Victoria Beach, a Case Study. J. Mar. Sci. Eng. 2022, 10, 1912. [Google Scholar] [CrossRef]
- KobaYashi, H.; Endo, M. The Ship Maneuverability Effect on the Safety Assessment of Navigation. Jpn. Inst. Navig. 1994, 120, 8–14. (In Japanese) [Google Scholar]
- Arai, Y.; Fukuto, J. Natural environmental conditions in safety evaluation of navigation environment. Jpn. Inst. Navig. 1994, 120, 15–20. (In Japanese) [Google Scholar]
- Goossens, L.H.J.; Glansdorp, C.C. Operational benefits and risk reduction of marine accidents. J. Navig. 1998, 51, 369–381. [Google Scholar] [CrossRef]
- Gucma, L. Navigation risk assessment for vessels manoeuvring in various conditions. WIT Trans. Model. Simul. 2002, 31, 149–158. [Google Scholar]
- Akten, N. Analysis of shipping casualties in the Bosporus. J. Navig. 2004, 57, 345–356. [Google Scholar] [CrossRef]
- Gucma, L. The risk assessment of ships manoeuvring on the waterways based on generalized simulation data. WIT Trans. Built Environ. 2007, 94, 411–418. [Google Scholar]
- Yip, T.L. Port traffic risks—A study of accidents in Hong Kong waters. Transp. Res. Part E Logist. Transp. Rev. 2008, 44, 921–931. [Google Scholar] [CrossRef]
- Szelangiewicz, T.; Wiśniewski, B.; Żelazny, K. The influence of wind, wave and loading condition on total resistance and speed of the vessel. Pol. Marit. Res. 2014, 21, 61–67. [Google Scholar] [CrossRef]
- Chen, C.; Shiotani, S.; Sasa, K. Effect of ocean currents on ship navigation in the East China Sea. Ocean. Eng. 2015, 104, 283–293. [Google Scholar] [CrossRef]
- Toffoli, A.; Lefèvre, J.M.; Bitner-Gregersen, E.; Monbaliu, J. Towards the identification of warning criteria: Analysis of a ship accident database. Appl. Ocean. Res. 2005, 27, 281–291. [Google Scholar] [CrossRef]
- Rusu, E. Modelling of wave-current interactions at the mouths of the Danube. J. Mar. Sci. Technol. 2010, 15, 143–159. [Google Scholar] [CrossRef]
- Arslan, O.; Turan, O. Analytical investigation of marine casualties at the Strait of Istanbul with SWOT-AHP method. Marit. Policy Manag. 2011, 36, 131–145. [Google Scholar] [CrossRef]
- Chen, C. Case Study on Wave-Current Interaction and its Effects on Ship Navigation. J. Hydrodyn. 2018, 30, 411–419. [Google Scholar] [CrossRef]
- Lee, C.C. Safety Manoeuvring Tendency for Ship in/out-port of Taichung. J. Taiwan Marit. Saf. Secur. Stud. 2013, 4, 1–18. (In Chinese) [Google Scholar]
- Chou, C.C.; Chen, C.Y.; Chang, P.C.; Chang, T.M.; Hsu, H.Z.; Chang, K.E. Use the grid to analyze the influential factors on marine accidents. Lect. Notes Electr. Eng. 2014, 293, 867–874. [Google Scholar]
- Chou, C.C.; Su, Y.L.; Li, R.F.; Tsai, C.L.; Ding, J.F. Key navigation safety factors in Taiwanese harbours and surrounding waters. J. Mar. Sci. Technol. 2015, 23, 685–693. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.L.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R. A new view of nonlinear water waves: The Hilbert spectrum. Annu. Rev. Fluid Mech. 1999, 31, 417–457. [Google Scholar] [CrossRef]
- Chen, Y.W. A Study on the Relationship between Climatic Factors and Sea Level Height Fluctuation of Keelung and Kaohsiung Ports. Master’s Thesis, National Taiwan Ocean University, Keelung, Taiwan, 2003. (In Chinese). [Google Scholar]
- Doong, D.J.; Tzeng, K.T.; Yang, I.S. Sea Level Fluctuation at Keelung and Kaohsiung. In Proceedings of the 30th Ocean Engineering Conference in Taiwan, Hsinchu, Taiwan, 13–14 November 2008; pp. 625–630. (In Chinese). [Google Scholar]
- Sung, Y.P. Prediction of Sea-Level Change around Taiwan by Using Tides and Satellite Data. Master’s Thesis, National Cheng Kung University, Tainan, Taiwan, 2012. (In Chinese). [Google Scholar]
- Lan, W.H. Assessment of Seasonal-to-Decadal Variability and Trends of Regional Sea Level in the North Pacific Ocean Using Satellite Altimetry and Tide Gauges. Ph.D. Thesis, National Cheng Kung University, Tainan, Taiwan, 2018. (In Chinese). [Google Scholar]
- Lan, W.H.; Kuo, C.Y.; Lin, S.F. Impact of sea level variations on hydrographic survey. Taiwan J. Geoinformatics 2022, 10, 99–120. (In Chinese) [Google Scholar]
- Chiang, Y.C.; Hsiao, S.S.; Lin, M.C. A Quasi-3D Sediment Transport Modeling for Coastal Morphodynamics. In Proceedings of the 21st International Offshore and Polar Engineering Conference, Maui, HI, USA, 19–24 June 2011; pp. 1053–1058. (In Chinese). [Google Scholar]
- Chiang, Y.C.; Hsiao, S.S. Coastal Morphological Modeling. In Sediment Transport in Aquatic Environments; InTech: Rijeka, Croatia, 2011; Chapter 10; pp. 203–230. [Google Scholar]
- Wang, H.Y.; Fang, H.M.; Hsiao, S.S. Morphological Characteristics of Tidal Inlets Subject to a Short Term Typhoon Event: A Case Study in Lanyan River Estuary. J. Mar. Sci. Technol. 2018, 26, 552–561. [Google Scholar]
- Kirby, J.T. A parabolic equation for the combined refraction-diffraction of Stokes waves by mildly varying topography. J. Fluid Mech. 1983, 136, 453–466. [Google Scholar] [CrossRef]
- Mizuguchi, M. An heuristic model of wave height distribution in surf zone. In Coastal Engineering 1980; American Society of Civil Engineers: Reston, VA, USA, 1980; pp. 278–289. [Google Scholar]
- Falconer, R.A. Numerical modeling of tidal circulation in harbors. J. Waterw. Port Coast. Ocean. Div. 1980, 106, 31–48. [Google Scholar] [CrossRef]
- Dean, R.G.; Dalrymple, R.A. Water Wave Mechanics for Engineers and Scientists; World Scientific Publishing Company: Singapore, 1984; Volume 2. [Google Scholar]
- Ponce, V.M.; Yabusaki, S.B. Modeling circulation in depth-averaged flow. J. Hydraul. Div. 1981, 107, 1501–1518. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S.; Stewart, R.W. Radiation stresses in water waves; a physical discussion, with applications. Deep. Sea Res. Oceanogr. Abstr. 1964, 11, 529–562. [Google Scholar] [CrossRef]
- Matushevskiy, T.V. Method of separation of wave induced and turbulent motions in the near-surface layer of the ocean. In On Problems of Ocean Dynamics; Gidrometeoizdat: Leningrad, Russia, 1975; pp. 124–151. (In Russian) [Google Scholar]

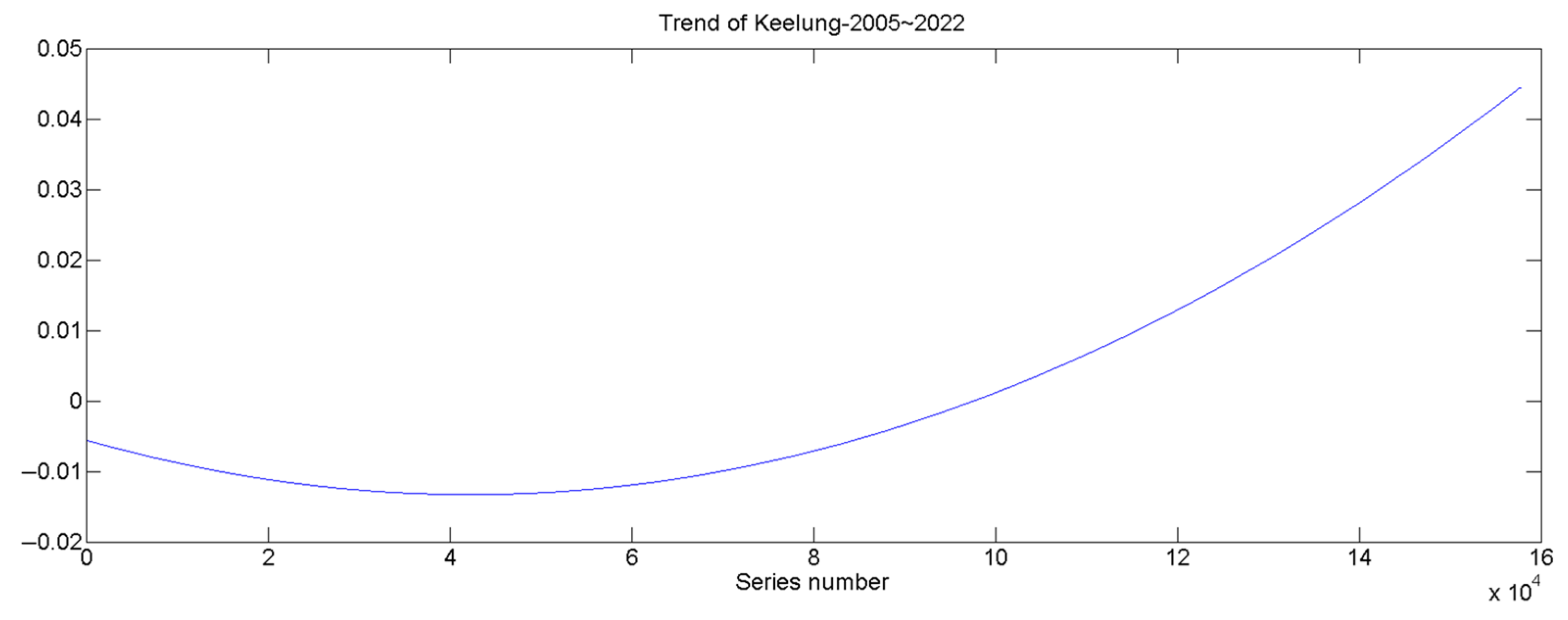
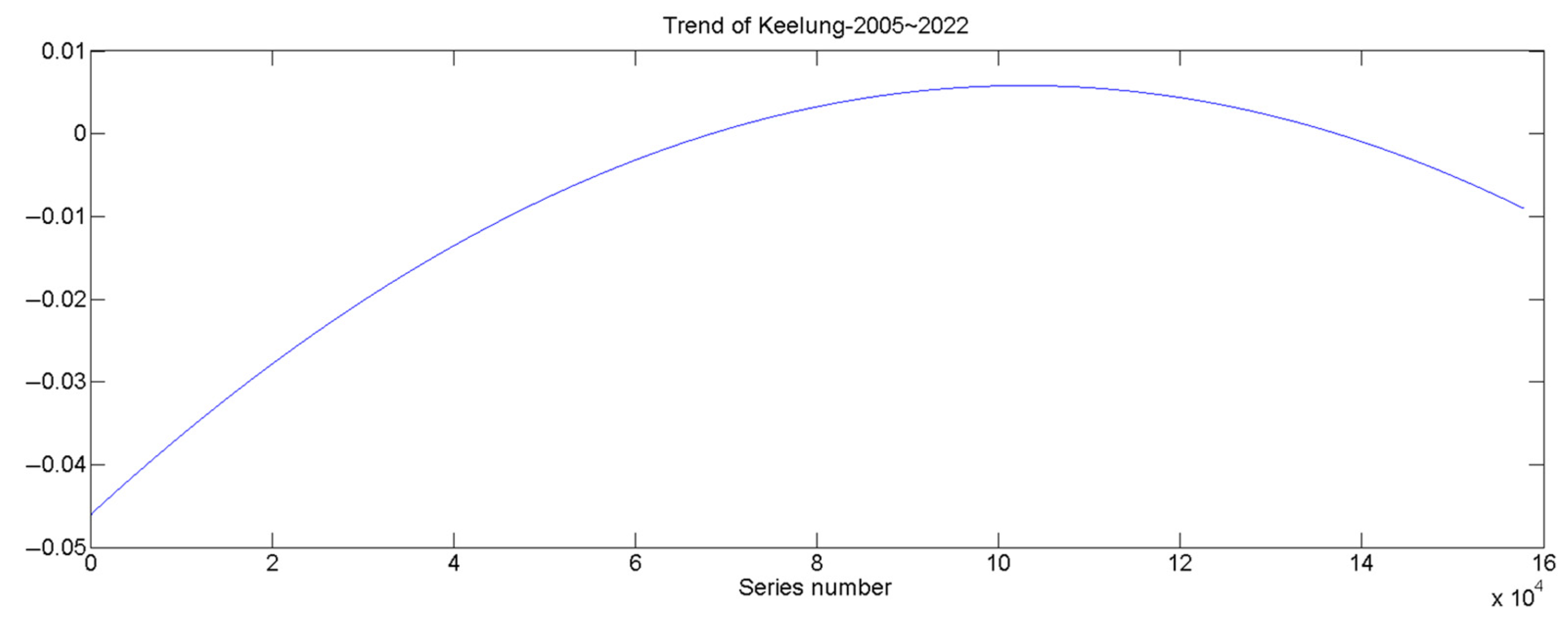



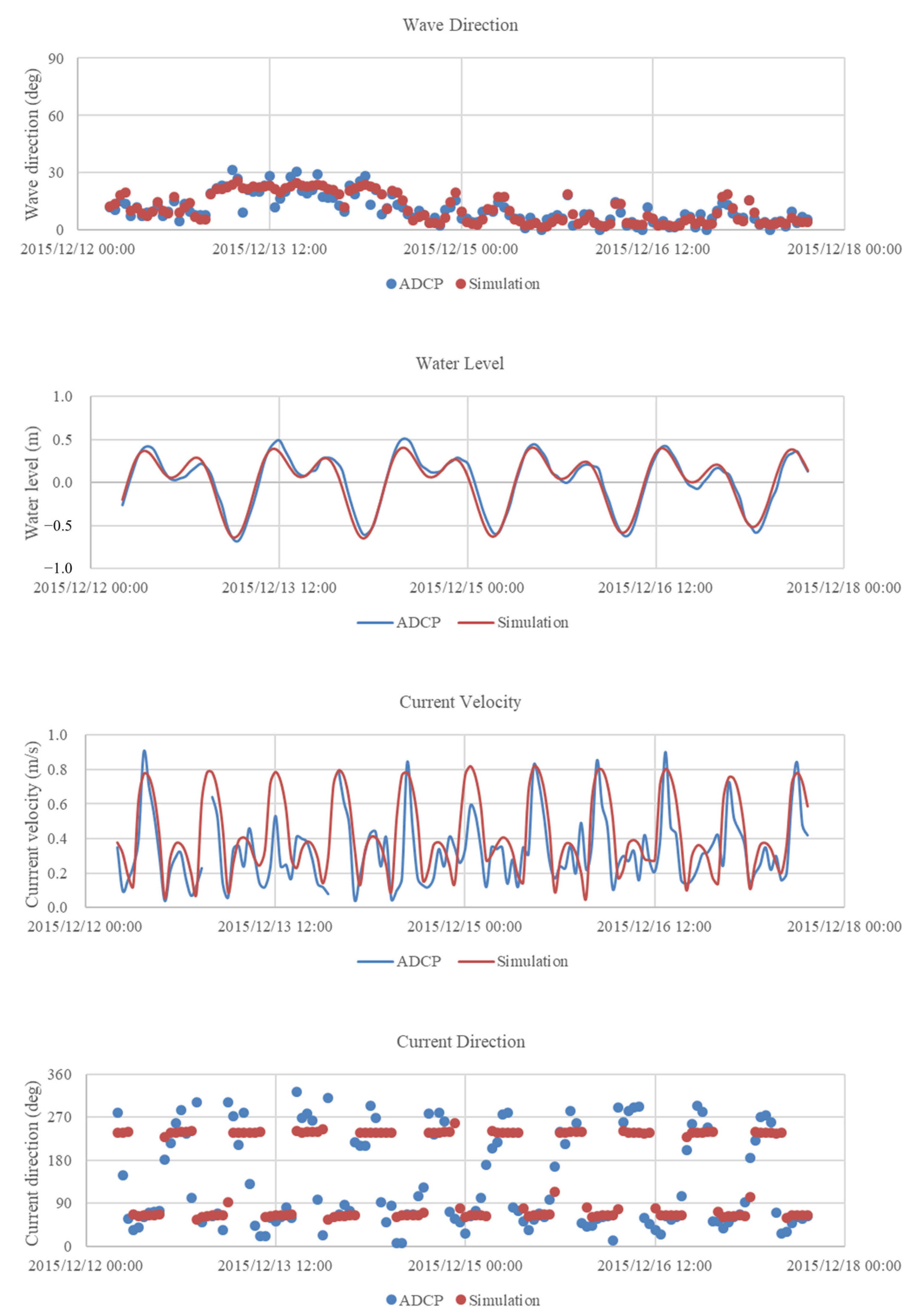
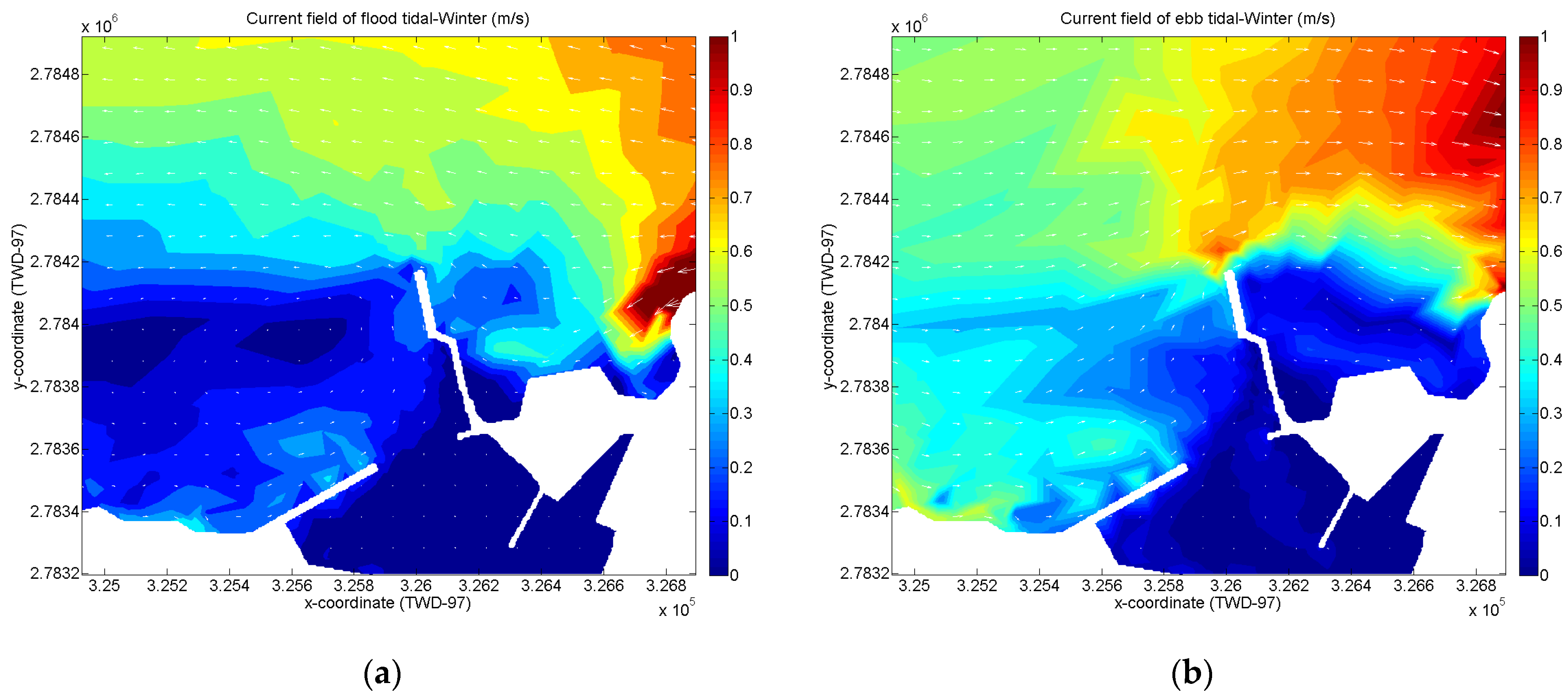


| Analysis Method | Avg. SLR | Avg. SLR Rate |
|---|---|---|
| SMA | 17.68 mm | 0.98 mm/yr |
| EMD | 51.20 mm | 2.84 mm/yr |
| EEMD | 57.73 mm | 3.21 mm/yr |
| Item | Model Setup |
|---|---|
| Area | 5 km × 6 km |
| Grid size | 25 m |
| Number of grid points | 200 × 240 |
| Time step | |
| Time scale | 1.0 |
| Wave condition | 2.5 m; 8.0 s; NNE |
| Original | SMA | EMD | EEMD | |||||
|---|---|---|---|---|---|---|---|---|
| V (m/s) | Dir. | V (m/s) | Dir. | V (m/s) | Dir. | V (m/s) | Dir. | |
| a | 0.6943 | 272.72 | 0.6945 | 272.72 | 0.6946 | 272.73 | 0.6947 | 272.73 |
| b | 0.6706 | 271.07 | 0.6707 | 271.08 | 0.6709 | 271.08 | 0.6709 | 271.08 |
| c | 0.6033 | 269.17 | 0.6034 | 269.18 | 0.6035 | 269.20 | 0.6036 | 269.20 |
| d | 0.4952 | 268.05 | 0.4953 | 268.08 | 0.4953 | 268.13 | 0.4954 | 268.13 |
| e | 0.3925 | 266.77 | 0.3926 | 266.82 | 0.3926 | 266.90 | 0.3927 | 266.90 |
| f | 0.2400 | 293.97 | 0.2401 | 294.03 | 0.2402 | 294.12 | 0.2402 | 294.11 |
| g | 0.1623 | 351.56 | 0.1624 | 351.59 | 0.1626 | 351.63 | 0.1626 | 351.62 |
| h | 0.1975 | 27.90 | 0.1976 | 27.87 | 0.1977 | 27.80 | 0.1977 | 27.80 |
| i | 0.1209 | 31.43 | 0.1210 | 31.33 | 0.1210 | 31.12 | 0.1211 | 31.13 |
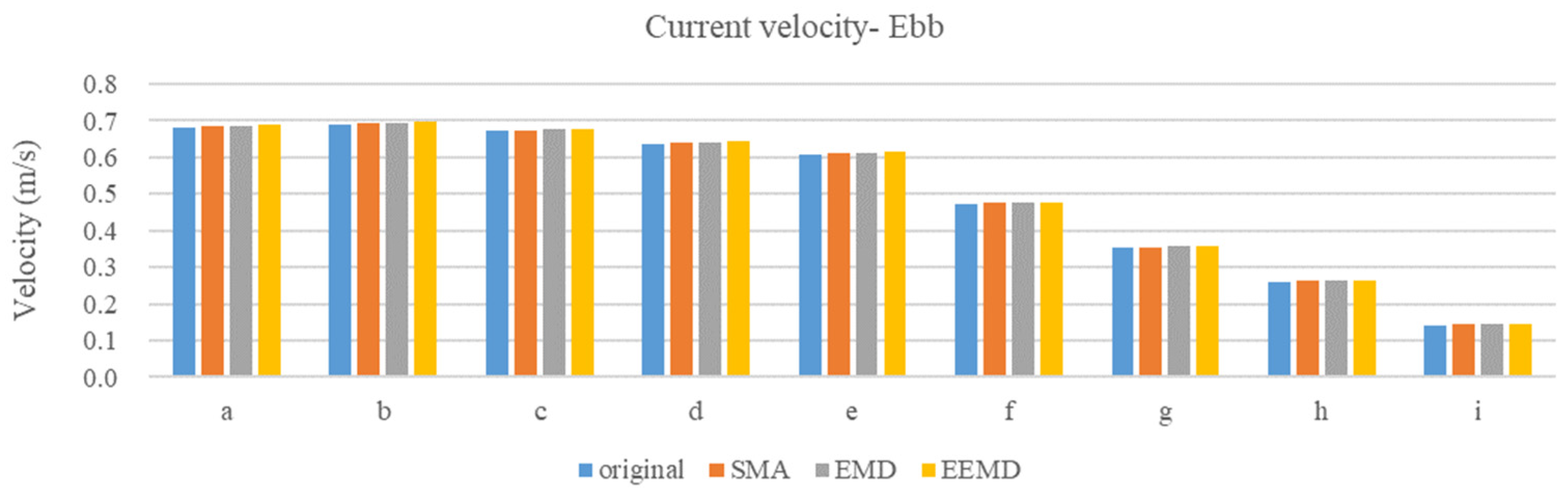
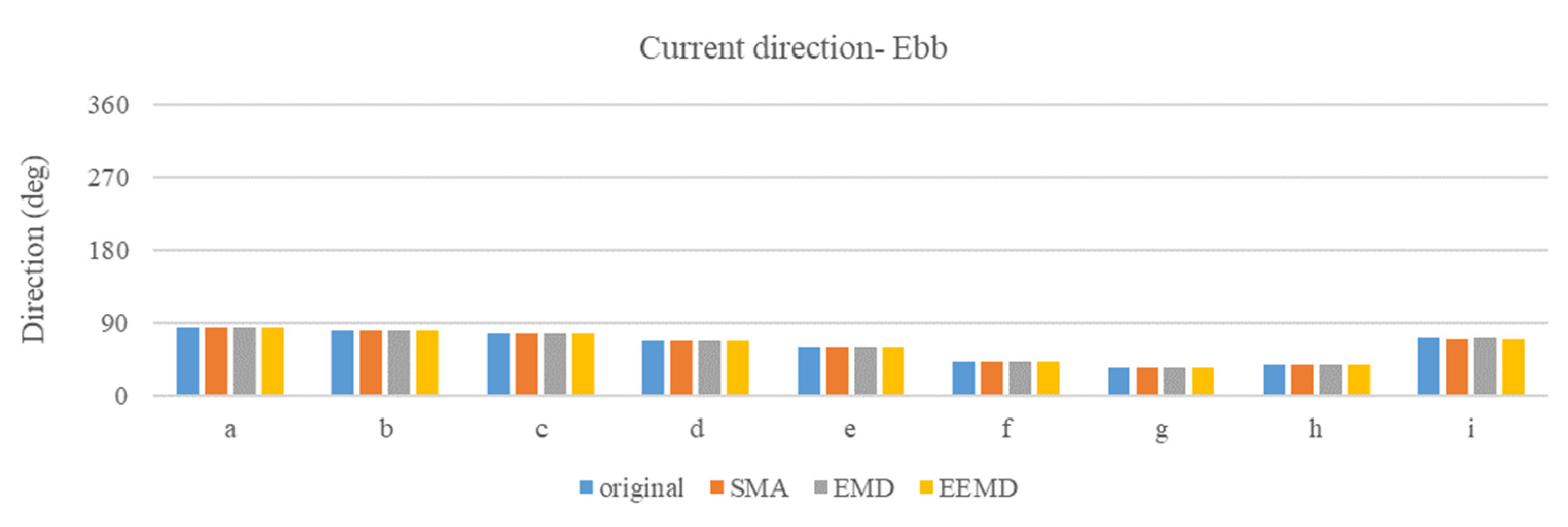
| Original | SMA | EMD | EEMD | |||||
|---|---|---|---|---|---|---|---|---|
| V (m/s) | Dir. | V (m/s) | Dir. | V (m/s) | Dir. | V (m/s) | Dir. | |
| a | 0.6834 | 84.04 | 0.6866 | 83.98 | 0.6871 | 83.97 | 0.6901 | 83.91 |
| b | 0.6906 | 80.70 | 0.6940 | 80.65 | 0.6945 | 80.64 | 0.6977 | 80.58 |
| c | 0.6714 | 75.96 | 0.6749 | 75.90 | 0.6754 | 75.89 | 0.6786 | 75.84 |
| d | 0.6370 | 67.68 | 0.6405 | 67.63 | 0.6410 | 67.62 | 0.6441 | 67.57 |
| e | 0.6094 | 59.68 | 0.6129 | 59.64 | 0.6135 | 59.63 | 0.6166 | 59.59 |
| f | 0.4722 | 42.57 | 0.4752 | 42.54 | 0.4757 | 42.53 | 0.4783 | 42.51 |
| g | 0.3531 | 33.85 | 0.3555 | 33.83 | 0.3561 | 33.83 | 0.3580 | 33.80 |
| h | 0.2614 | 38.18 | 0.2634 | 38.11 | 0.2638 | 38.15 | 0.2654 | 38.07 |
| i | 0.1421 | 70.36 | 0.1429 | 70.21 | 0.1435 | 70.25 | 0.1440 | 70.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, T.-H.; Wang, H.-Y. Analysis and Exploration of the Impact of Average Sea Level Change on Navigational Safety in Ports. Water 2023, 15, 2570. https://doi.org/10.3390/w15142570
Chang T-H, Wang H-Y. Analysis and Exploration of the Impact of Average Sea Level Change on Navigational Safety in Ports. Water. 2023; 15(14):2570. https://doi.org/10.3390/w15142570
Chicago/Turabian StyleChang, Tsai-Hsin, and Hsing-Yu Wang. 2023. "Analysis and Exploration of the Impact of Average Sea Level Change on Navigational Safety in Ports" Water 15, no. 14: 2570. https://doi.org/10.3390/w15142570
APA StyleChang, T.-H., & Wang, H.-Y. (2023). Analysis and Exploration of the Impact of Average Sea Level Change on Navigational Safety in Ports. Water, 15(14), 2570. https://doi.org/10.3390/w15142570






