An Application of Inverse Problem and Universal Solutions for Pumping Wells in Unconfined Aquifers
Abstract
:1. Introduction
2. Materials and Methods
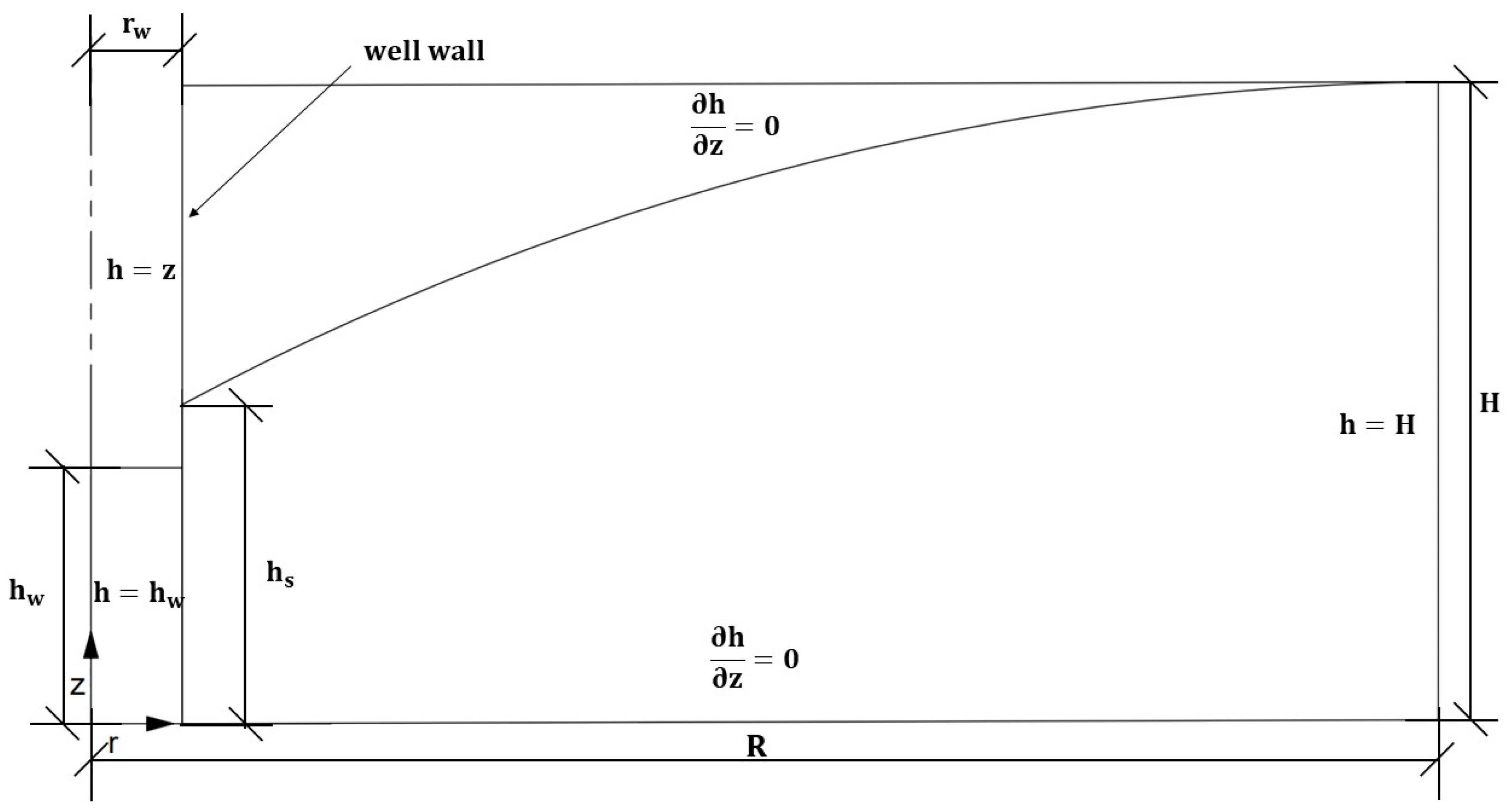
2.1. Mathematical Model
2.2. Discriminated Nondimensionalization Technique for Flow towards Pumping Wells
2.2.1. Discriminated Nondimensionalization Procedure
- New groups that remove classical ones appear. This occurs as a consequence of including spatial and general discrimination.
- Correct references for the problem variables are chosen, since ratios of lengths must include parameters in the same spatial direction, and aspect ratios can only appear modified by the ratio of other parameters.
- Universal solutions can be presented as universal type-curves in which the relationship between unknowns and data is depicted.
- Inverse problem methodologies can be developed using the universal solutions.
2.2.2. Discriminated Dimensionless Groups Achievement
2.2.3. Verification of the Dimensionless Groups
3. Results and Discussion
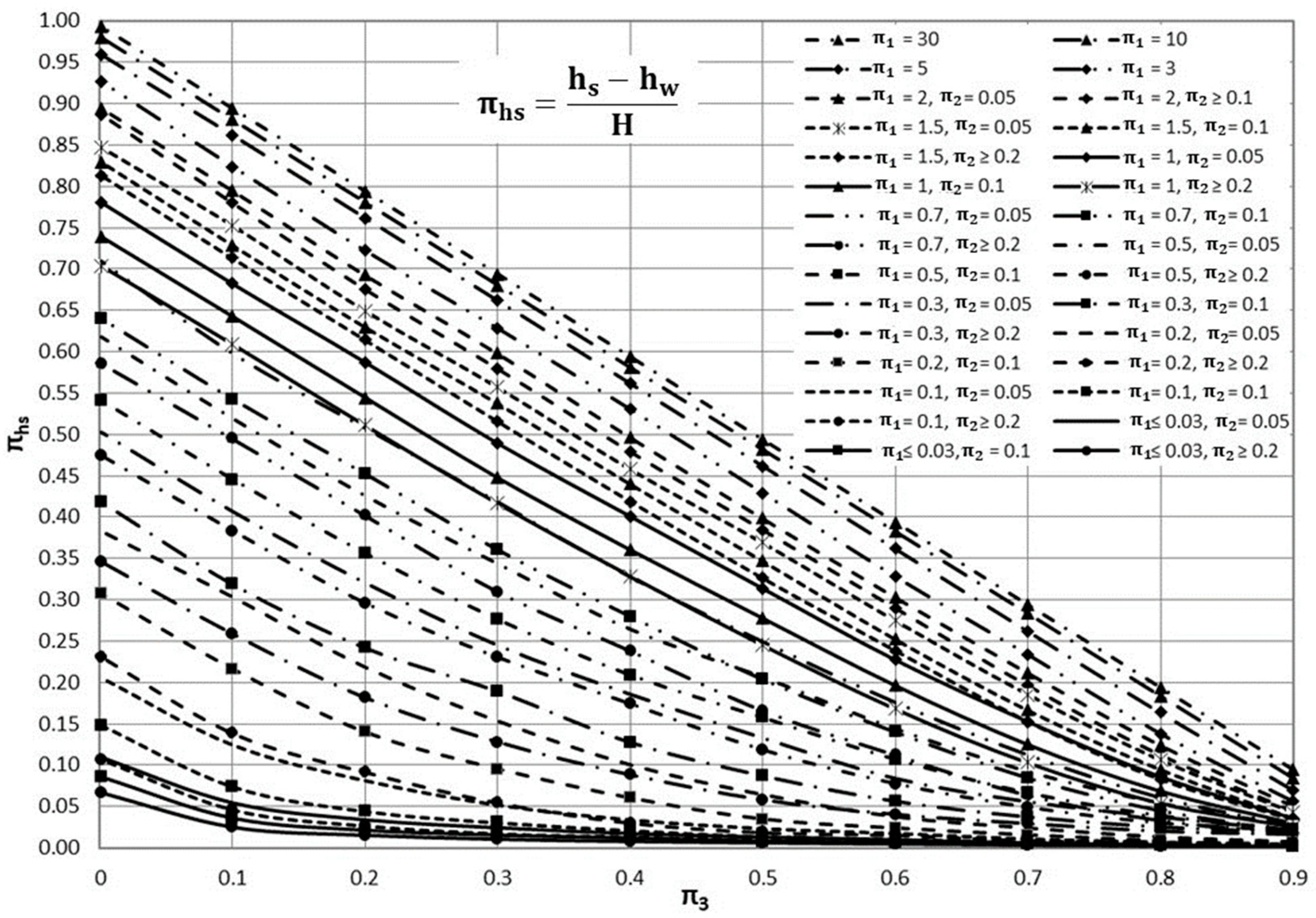
3.1. Universal Curves
3.2. Illustrative Example—Influence of Measure Deviations in the Calculation of Conductivity Values
- H = 10 m
- hw = 5 m
- R = 10 m
- rw = 1 m
- Q = 0.002308 m3/s
- hs = 8.471 m
- Kr = 0.0000225 m/s (named Kr,real, as it is the real value of the parameter in the example).
- Kz = 0.00001 m/s (named Kz,real, as it is the real value of the parameter in the example).
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| c1 | constant in Dupuit deduction (m) |
| H | aquifer thickness (m) |
| h | hydraulic potential (m) |
| h′ | dimensionless hydraulic potential |
| hs,real | real value of seepage surface (m) |
| hs | seepage surface (m) |
| hw | water height in the well (m) |
| K | hydraulic conductivity (m/s) |
| Kr,real | real value of radial hydraulic conductivity (m/s) |
| Kr | radial hydraulic conductivity (m/s) |
| Kz,real | real value of vertical hydraulic conductivity (m/s) |
| Kz | vertical hydraulic conductivity (m/s) |
| Lr | radial length quantity (m) |
| Lwc | water column quantity (m) |
| Lz | vertical length quantity (m) |
| Lα | angular length quantity (m) |
| Q | pumping flow (m3/s) |
| Qreal | real value of pumping flow (m3/s) |
| Qref | reference pumping flow (m3/s) |
| R | aquifer radius (m) |
| r | radial coordinate (m) |
| r′ | dimensionless radial coordinate |
| rw | well radius (m) |
| Sref | reference surface (m2) |
| T | time quantity (s) |
| vr | radial velocity (m/s) |
| vref | reference velocity (m/s) |
| vz | vertical velocity (m/s) |
| z | vertical coordinate (m) |
| z′ | dimensionless vertical coordinate |
| Δh | potential variation (m) |
| ξ | statistic error (%) |
| π1, π2, π3, πQ, πhs | discriminated dimensionless monomials |
| ∂ | partial derivative |
References
- Barlow, P.M.; Leake, S.A. Streamflow Depletion by Wells—Understanding and Managing the Effects of Groundwater Pumping on Streamflow. U.S. Geol. Surv. Circ. 2012, 1376, 84. [Google Scholar]
- Ayvaz, M.T.; Karahan, H. A Simulation/Optimization Model for the Identification of Unknown Groundwater Well Locations and Pumping Rates. J. Hydrol. 2008, 357, 76–92. [Google Scholar] [CrossRef]
- Massuel, S.; Amichi, F.; Ameur, F.; Calvez, R.; Jenhaoui, Z.; Bouarfa, S.; Kuper, M.; Habaieb, H.; Hartani, T.; Hammani, A. Considering Groundwater Use to Improve the Assessment of Groundwater Pumping for Irrigation in North Africa. Hydrogeol. J. 2017, 25, 1565–1577. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez-Estrella, T.; Pulido-Bosch, A. Methodologies for abstraction from coastal aquifers for supplying desalination plants in the south-east of Spain. Desalination 2009, 249, 1088–1098. [Google Scholar] [CrossRef]
- Ozelim, L.C.D.S.; Cavalcante, A.L. Combining Microtomography, 3D Printing, and Numerical Simulations to Study Scale Effects on the Permeability of Porous Media. Int. J. Geomech. 2019, 19, 04018194. [Google Scholar] [CrossRef]
- Custodio, E.; Llamas, M.R. Hidrología Subterránea; Omega: Barcelona, Spain, 1976; Volume 1. [Google Scholar]
- Dupuit, J.É.J. Études Théoriques et Pratiques sur le Mouvement des Eaux dans les Canaux Découverts et a Travers les Terrains Perméables: Avec des Considérations Relatives au Régime des Grandes Eaux, au Débouché a leur Donner, et a la Marche des Alluvions dans les Rivières a Fond Mobile; Dunod: Malakoff, France, 1863. [Google Scholar]
- Poeter, E.; Hsieh, P. Graphical Construction of Groundwater Flow Nets; The Groundwater Project: Guelph, ON, Canada, 2020. [Google Scholar]
- Boulton, N.S. The Flow Pattern Near a Gravity Well in a Uniform Water-Bearing Medium. J. Inst. Civ. Eng. 1951, 36, 534–550. [Google Scholar] [CrossRef]
- Bejan, A. Convection Heat Transfer; John Wiley & Sons: New York, NY, USA, 2013. [Google Scholar]
- Alhama, F.; Madrid-García, N. Análisis Dimensional Discriminado en Mecánica de Fluidos y Transferencia de Calor; Reverté: Barcelona, Spain, 2012. [Google Scholar]
- Buckingham, E. On Physically Similar Systems; Illustrations of the Use of Dimensional Equations. Phys. Rev. 1914, 4, 345. [Google Scholar] [CrossRef]
- Martínez-Moreno, E.; García-Ros, G.; Alhama, I.; Alhama, F. Characterization of Flow under Impervious Dams: Dimensionless Groups and Universal Solutions. Mathematics 2023, 11, 540. [Google Scholar] [CrossRef]
- Cánovas, M.; Alhama, I.; Alhama, F. Mathematical Characterization of Bènard-Type Geothermal Scenarios Using Discriminated Non-Dimensionalization of the Governing Equations. Int. J. Nonlinear Sci. Numer. Simul. 2015, 16, 23–34. [Google Scholar] [CrossRef]
- Manteca, I.A.; García-Ros, G.; López, F.A. Universal Solution for the Characteristic Time and the Degree of Settlement in Nonlinear Soil Consolidation Scenarios. A Deduction Based on Nondimensionalization. Commun. Nonlinear Sci. Numer. Simul. 2018, 57, 186–201. [Google Scholar] [CrossRef]
- García-Ros, G.; Alhama, I. Method to Determine the Constitutive Permeability Parameters of Non-Linear Consolidation Models by Means of the Oedometer Test. Mathematics 2020, 8, 2237. [Google Scholar] [CrossRef]
- Hall, H.P. An Investigation of Steady Flow toward a Gravity Well. La Houille Blanche 1955, 1, 8–35. [Google Scholar] [CrossRef] [Green Version]
- Ngspice. Open Source Mixed Mode, Mixed Level Circuit Simulator (Based on Bekeley’s Spice3f5). 2016. Available online: http://ngspice.sourceforge.net/ (accessed on 1 June 2021).
- Martínez-Moreno, E.; Garcia-Ros, G.; Alhama, I. A Different Approach to the Network Method: Continuity Equation in Flow Through Porous Media under Retaining Structures. Eng. Comput. 2020, 37, 3269–3291. [Google Scholar] [CrossRef]
- Sánchez-Pérez, J.F.; Alhama, I. Simultaneous Determination of Initial Porosity and Diffusivity of Water-Saturated Reinforced Concrete Subject to Chloride Penetration by Inverse Problem. Constr. Build. Mater. 2020, 25, 120412. [Google Scholar] [CrossRef]


| Case | Kr (m/s) | Kz (m/s) | R (m) | rw (m) | H (m) | hw (m) | Q (m3/s) | hs (m) |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.0001 | 0.0001 | 10 | 1 | 10 | 5 | 0.0103 | 7.736 |
| 2 | 0.000225 | 0.0001 | 15 | 1.5 | 10 | 5 | 0.0231 | 7.736 |
| 3 | 0.0001 | 0.0001 | 50 | 5 | 10 | 5 | 0.0104 | 5.343 |
| 4 | 0.0001 | 0.000025 | 50 | 5 | 5 | 2.5 | 0.0260 | 2.672 |
| 5 | 0.0001 | 0.0001 | 10 | 2.5 | 10 | 5 | 0.0171 | 7.349 |
| 6 | 0.0005 | 0.0001 | 22.36 | 5.59 | 10 | 5 | 0.0854 | 7.349 |
| 7 | 0.0001 | 0.0001 | 10 | 1 | 10 | 7 | 0.0070 | 8.240 |
| 8 | 0.0003 | 0.0001 | 10 | 1 | 5.77 | 4.07 | 0.0070 | 4.753 |
| Case | π1 | π2 | π3 | πQ | πhs |
|---|---|---|---|---|---|
| 1 | 1 | 0.1 | 0.5 | 0.295 | 0.274 |
| 2 | 1 | 0.1 | 0.5 | 0.295 | 0.274 |
| 3 | 0.2 | 0.1 | 0.5 | 0.297 | 0.034 |
| 4 | 0.2 | 0.1 | 0.5 | 0.297 | 0.034 |
| 5 | 1 | 0.25 | 0.5 | 0.408 | 0.235 |
| 6 | 1 | 0.25 | 0.5 | 0.408 | 0.235 |
| 7 | 1 | 0.1 | 0.7 | 0.334 | 0.124 |
| 8 | 1 | 0.1 | 0.7 | 0.334 | 0.123 |
| Deviations ξ (%) | Kr × 10−5 (m/s) | Max Deviations Kr (%) | Kz × 10−5 (m/s) | Max Deviations Kz (%) |
|---|---|---|---|---|
| 0 | 2.24 | 0.44 | 0.996 | 0.40 |
| 0.5 | 2.23/2.25 | 0.89 | 1.07/0.99 | 7.02 |
| 1 | 2.22/2.26 | 1.33 | 1.12/0.89 | 11.92 |
| 1.5 | 2.21/2.28 | 1.78 | 1.19/0.84 | 18.69 |
| 2 | 2.20/2.29 | 2.22 | 1.24/0.78 | 24.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez-Moreno, E.; Alhama, F.; Alhama, I.; García-Ros, G. An Application of Inverse Problem and Universal Solutions for Pumping Wells in Unconfined Aquifers. Water 2023, 15, 2524. https://doi.org/10.3390/w15142524
Martínez-Moreno E, Alhama F, Alhama I, García-Ros G. An Application of Inverse Problem and Universal Solutions for Pumping Wells in Unconfined Aquifers. Water. 2023; 15(14):2524. https://doi.org/10.3390/w15142524
Chicago/Turabian StyleMartínez-Moreno, Encarnación, Francisco Alhama, Iván Alhama, and Gonzalo García-Ros. 2023. "An Application of Inverse Problem and Universal Solutions for Pumping Wells in Unconfined Aquifers" Water 15, no. 14: 2524. https://doi.org/10.3390/w15142524






