Monitoring of Groundwater in a Limestone Island Aquifer Using Ambient Seismic Noise
Abstract
1. Introduction
1.1. Ambient Seismic Noise Correlations
1.2. The Geological and Hydrogeological Setting of the Maltese Islands

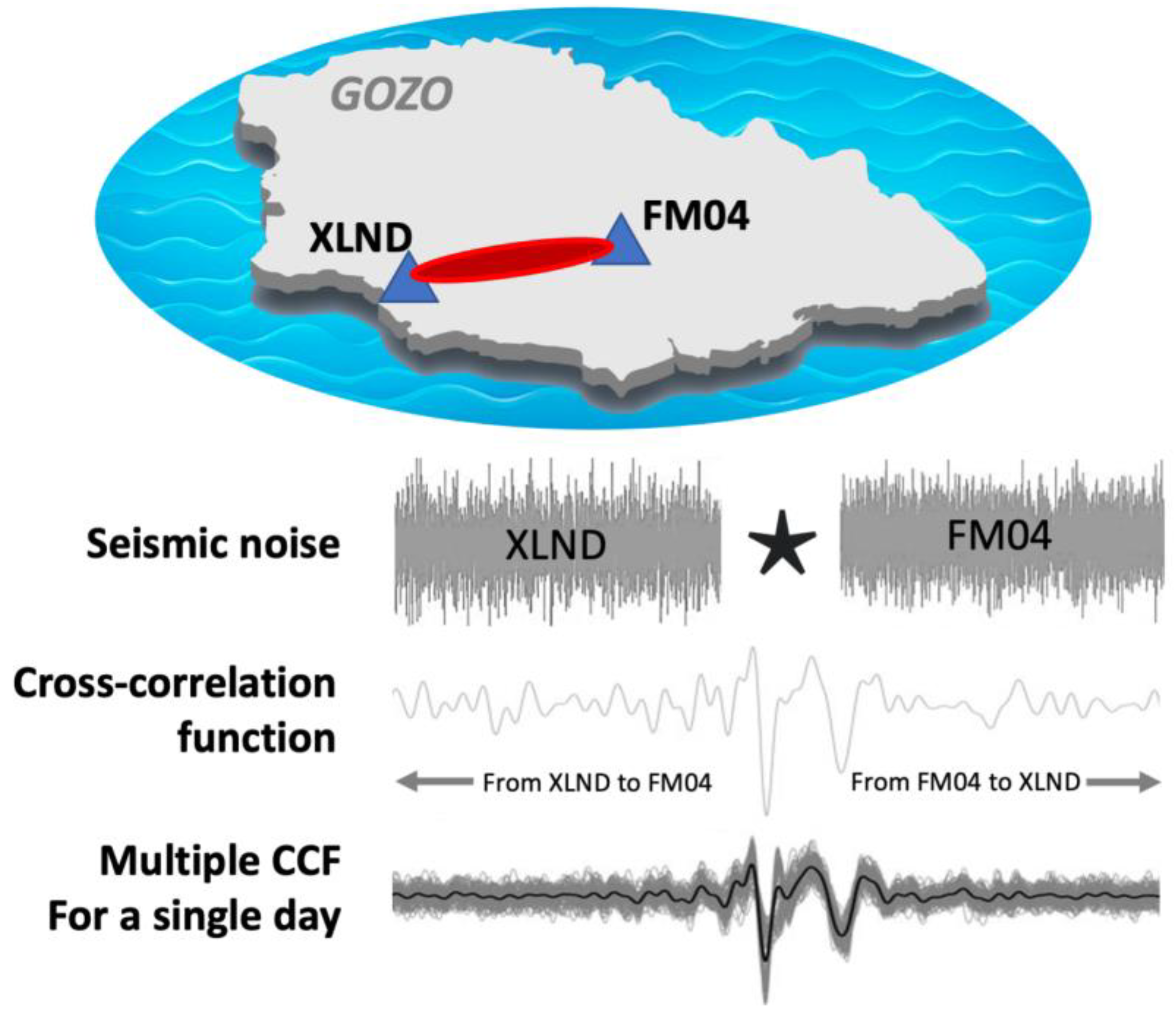
2. Materials and Methods
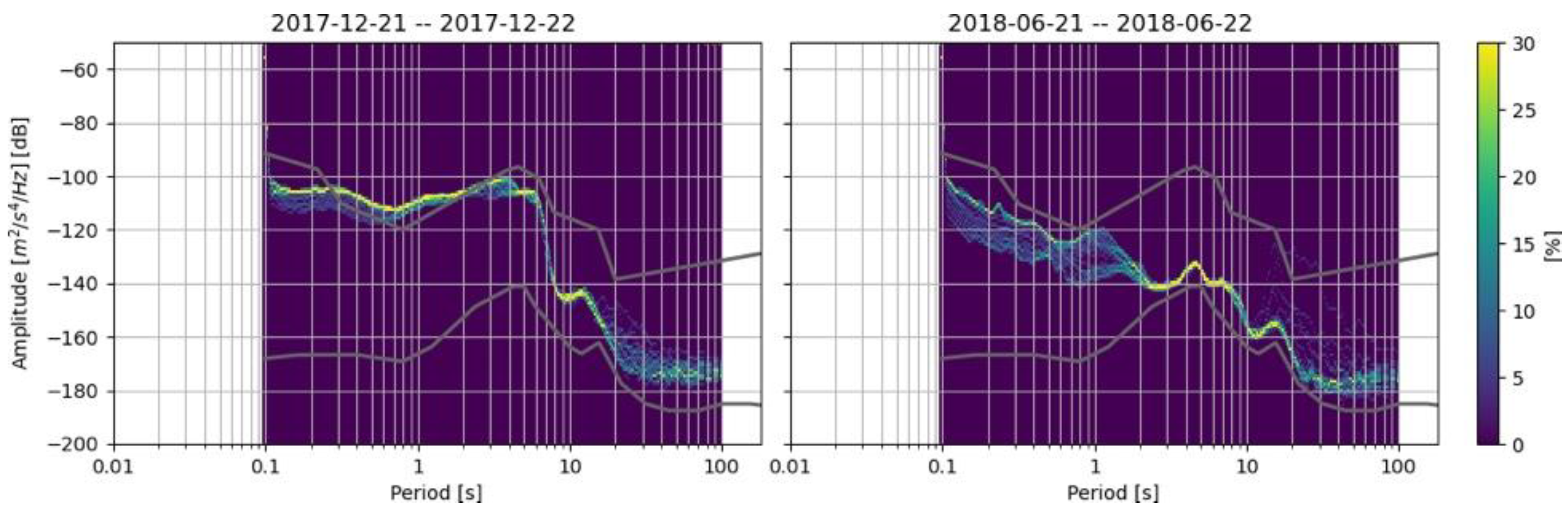
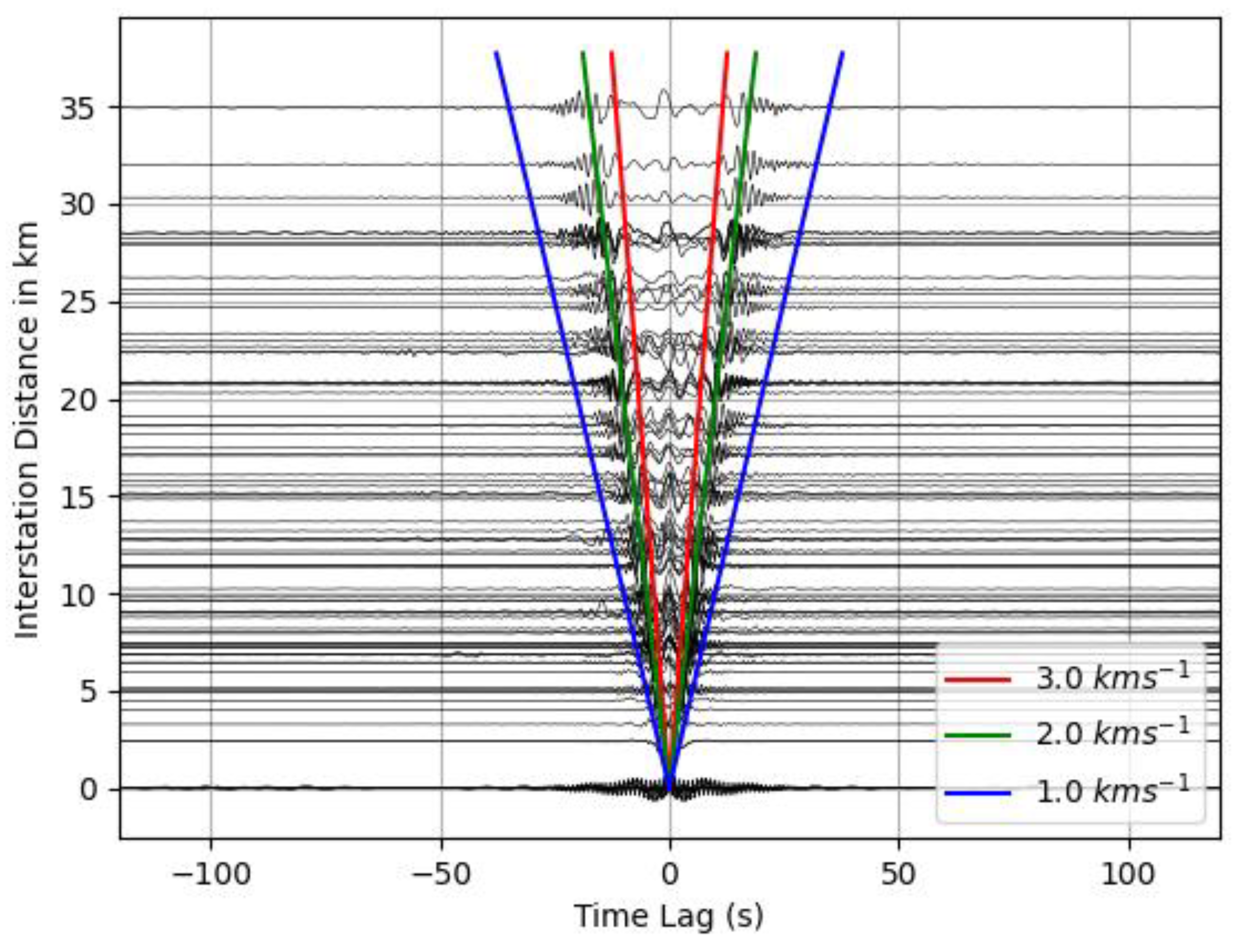
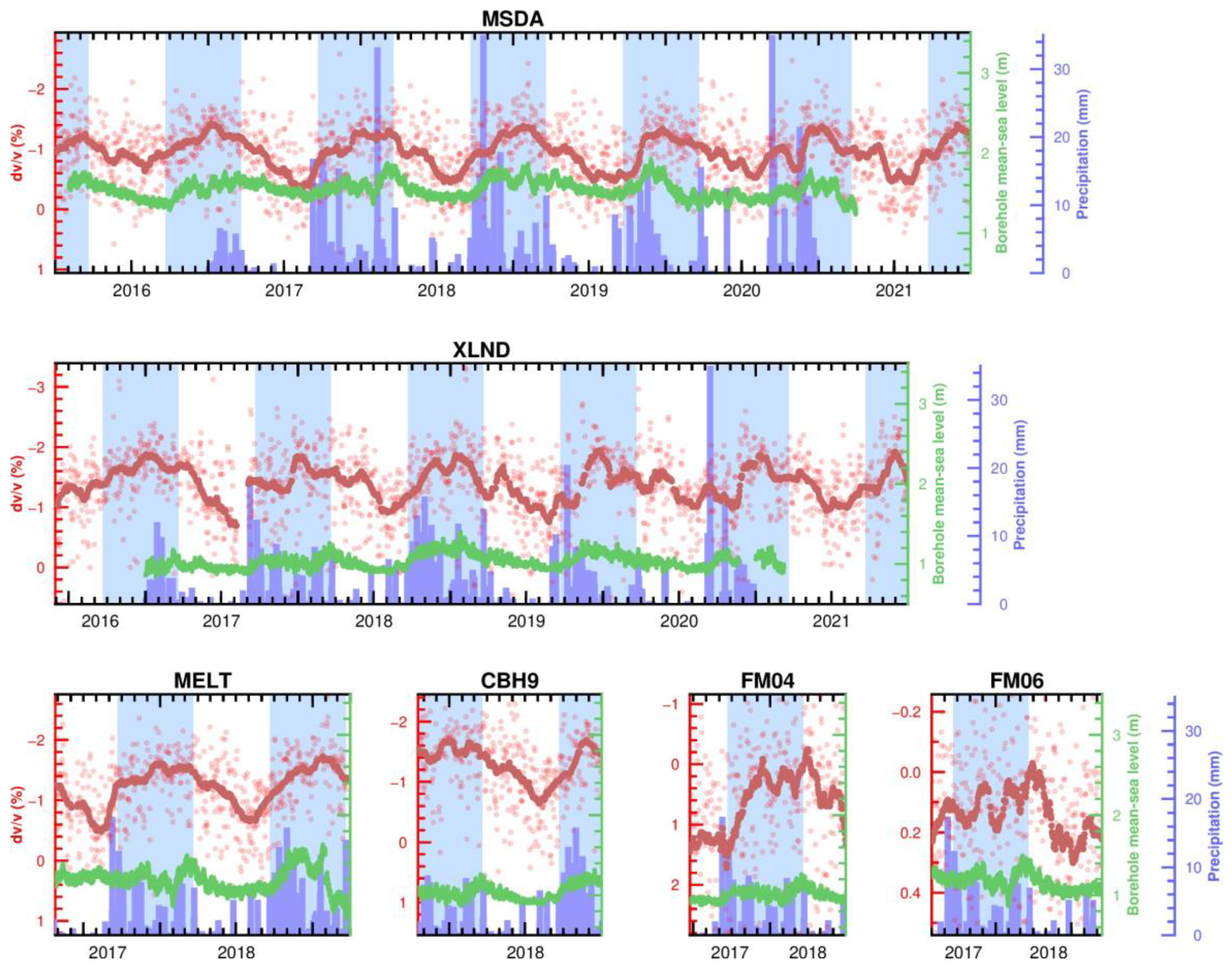
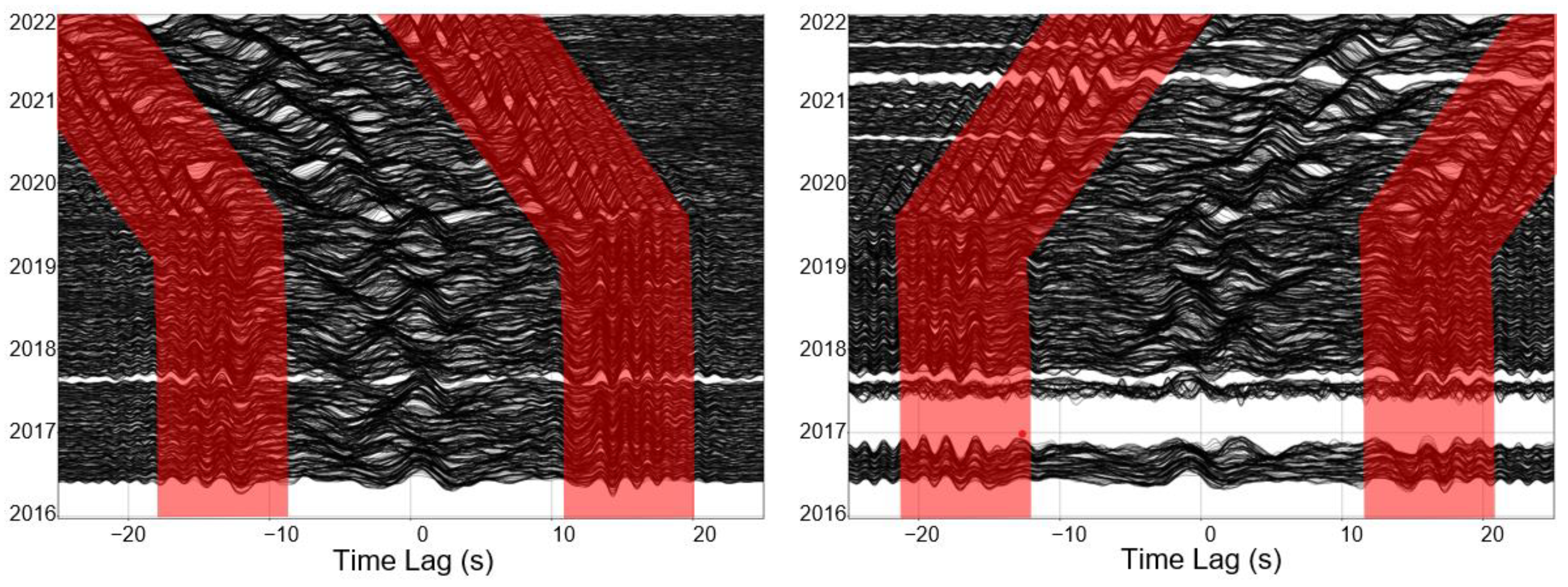
3. Results
4. Discussion
4.1. Station Problems: Power Outage and Timing Issues
4.2. Geological and Hydrogeological Considerations
4.3. Meteorological Considerations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kavusi, M.; Khashei Siuki, A.; Dastourani, M. Optimal design of groundwater monitoring network using the combined Election-Kriging method. Water Resour. Manag. 2020, 34, 2503–2516. [Google Scholar] [CrossRef]
- Zhou, Y.; Dong, D.; Liu, J.; Li, W. Upgrading a regional groundwater level monitoring network for Beijing Plain, China. Geosci. Front. 2013, 4, 127–138. [Google Scholar] [CrossRef]
- Healy, R.W.; Cook, P.G. Using groundwater levels to estimate recharge. Hydrogeol. J. 2002, 10, 91–109. [Google Scholar] [CrossRef]
- Gemitzi, A.; Lakshmi, V. Estimating groundwater abstractions at the aquifer scale using GRACE observations. Geosciences 2018, 8, 419. [Google Scholar] [CrossRef]
- United Nations. The United Nations World Water Development Report 2022: Groundwater Making the Invisible Visible: Facts and Figures; Technical Report; United Nations: Perugia, Italy, 2022. [Google Scholar]
- Bawden, G.W.; Thatcher, W.; Stein, R.S.; Hudnut, K.W.; Peltzer, G. Tectonic contraction across Los Angeles after removal of groundwater pumping effects. Nature 2001, 412, 812–815. [Google Scholar] [CrossRef] [PubMed]
- Ji, K.H.; Herring, T.A. Correlation between changes in groundwater levels and surface deformation from GPS measurements in the San Gabriel Valley, California. Geophys. Res. Lett. 2012, 39, L01301. [Google Scholar] [CrossRef]
- King, N.; Argus, D.; Langbein, J.; Agnew, D.; Bawden, G.; Dollar, R.; Liu, Z.; Galloway, D.; Reichard, E.; Yong, A.; et al. Space geodetic observation of expansion of the San Gabriel Valley, California, aquifer system, during heavy rainfall in winter 2004–2005. J. Geophys. Res. Solid Earth 2007, 112, B03409. [Google Scholar] [CrossRef]
- Chaussard, E.; Milillo, P.; Bürgmann, R.; Perissin, D.; Fielding, E.J.; Baker, B. Remote sensing of ground deformation for monitoring groundwater management practices: Application to the Santa Clara Valley during the 2012–2015 California drought. J. Geophys. Res. Solid Earth 2017, 122, 8566–8582. [Google Scholar] [CrossRef]
- Galloway, D.L.; Hoffmann, J. The application of satellite differential SAR interferometry-derived ground displacements in hydrogeology. Hydrogeol. J. 2007, 15, 133–154. [Google Scholar] [CrossRef]
- Ramillien, G.; Famiglietti, J.S.; Wahr, J. Detection of continental hydrology and glaciology signals from GRACE: A review. Surv. Geophys. 2008, 29, 361–374. [Google Scholar] [CrossRef]
- Rodell, M.; Velicogna, I.; Famiglietti, J.S. Satellite-based estimates of groundwater depletion in India. Nature 2009, 460, 999–1002. [Google Scholar] [CrossRef] [PubMed]
- Xanke, J.; Liesch, T. Quantification and possible causes of declining groundwater resources in the Euro-Mediterranean region from 2003 to 2020. Hydrogeol. J. 2022, 30, 379–400. [Google Scholar] [CrossRef]
- Xiao, M.; Koppa, A.; Mekonnen, Z.; Pagán, B.R.; Zhan, S.; Cao, Q.; Aierken, A.; Lee, H.; Lettenmaier, D.P. How much groundwater did California’s Central Valley lose during the 2012–2016 drought? Geophys. Res. Lett. 2017, 44, 4872–4879. [Google Scholar] [CrossRef]
- Kirsch, R. Groundwater Geophysics: A Tool for Hydrogeology; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Clements, T.; Denolle, M.A. Tracking groundwater levels using the ambient seismic field. Geophys. Res. Lett. 2018, 45, 6459–6465. [Google Scholar] [CrossRef]
- Christensen, N.; Wang, H. The influence of pore pressure and confining pressure on dynamic elastic properties of Berea sandstone. Geophysics 1985, 50, 207–213. [Google Scholar] [CrossRef]
- Sens-Schönfelder, C.; Wegler, U. Passive image interferometry and seasonal variations of seismic velocities at Merapi Volcano, Indonesia. Geophys. Res. Lett. 2006, 33, L21302. [Google Scholar] [CrossRef]
- Meier, U.; Shapiro, N.M.; Brenguier, F. Detecting seasonal variations in seismic velocities within Los Angeles basin from correlations of ambient seismic noise. Geophys. J. Int. 2010, 181, 985–996. [Google Scholar] [CrossRef]
- Illien, L.; Andermann, C.; Sens-Schönfelder, C.; Cook, K.; Baidya, K.; Adhikari, L.; Hovius, N. Subsurface moisture regulates Himalayan groundwater storage and discharge. AGU Adv. 2021, 2, e2021AV000398. [Google Scholar] [CrossRef]
- Lecocq, T.; Longuevergne, L.; Pedersen, H.A.; Brenguier, F.; Stammler, K. Monitoring ground water storage at mesoscale using seismic noise: 30 years of continuous observation and thermo-elastic and hydrological modeling. Sci. Rep. 2017, 7, 14241. [Google Scholar] [CrossRef]
- Mainsant, G.; Larose, E.; Brönnimann, C.; Jongmans, D.; Michoud, C.; Jaboyedoff, M. Ambient seismic noise monitoring of a clay landslide: Toward failure prediction. J. Geophys. Res. Earth Surf. 2012, 117, F01030. [Google Scholar] [CrossRef]
- Mao, S.; Lecointre, A.; van der Hilst, R.D.; Campillo, M. Space-time monitoring of groundwater fluctuations with passive seismic interferometry. Nat. Commun. 2022, 13, 4643. [Google Scholar] [CrossRef]
- Kim, D.; Lekic, V. Groundwater variations from autocorrelation and receiver functions. Geophys. Res. Lett. 2019, 46, 13722–13729. [Google Scholar] [CrossRef]
- Garambois, S.; Voisin, C.; Romero Guzman, M.; Brito, D.; Guillier, B.; Réfloch, A. Analysis of ballistic waves in seismic noise monitoring of water table variations in a water field site: Added value from numerical modelling to data understanding. Geophys. J. Int. 2019, 219, 1636–1647. [Google Scholar] [CrossRef]
- Voisin, C.; Guzmán, M.A.R.; Refloch, A.; Taruselli, M.; Garambois, S. Groundwater monitoring with passive seismic interferometry. J. Water Resour. Prot. 2017, 9, 1414–1427. [Google Scholar] [CrossRef]
- Sánchez-Pastor, P.; Obermann, A.; Schimmel, M.; Weemstra, C.; Verdel, A.; Jousset, P. Short-and long-term variations in the Reykjanes geothermal reservoir from seismic noise interferometry. Geophys. Res. Lett. 2019, 46, 5788–5798. [Google Scholar] [CrossRef]
- Sens-Schönfelder, C.; Wegler, U. Passive image interferometry for monitoring crustal changes with ambient seismic noise. Comptes Rendus Geosci. 2011, 343, 639–651. [Google Scholar] [CrossRef]
- Wang, Q.-Y.; Brenguier, F.; Campillo, M.; Lecointre, A.; Takeda, T.; Aoki, Y. Seasonal crustal seismic velocity changes throughout Japan. J. Geophys. Res. Solid Earth 2017, 122, 7987–8002. [Google Scholar] [CrossRef]
- Hallett, S.; Sakrabani, R.; Thompson, A.; Deeks, L.; Knox, J. Improving soil and water management for agriculture: Insights and innovation from Malta. J. Appl. Res. Pract. 2017, 1, 40–59. [Google Scholar] [CrossRef]
- Hartfiel, L.; Soupir, M.; Kanwar, R.S. Malta’s Water Scarcity Challenges: Past, Present, and Future Mitigation Strategies for Sustainable Water Supplies. Sustainability 2020, 12, 9835. [Google Scholar] [CrossRef]
- National Statistics Office. Key Figures for Malta 2019 Edition: Visuals and Words. 2019. Available online: https://nso.gov.mt/en/nso/Media/Salient-Points-of-Publications/Document/Key%20Figures%20for%20Malta%20-%202019%20Edition/Malta%20In%20Figures%20-%202019.pdf. (accessed on 15 December 2022).
- National Statistics Office. Regional Tourism: 2016–2018. 2019. Available online: https://nso.gov.mt/en/News_Releases/View_by_Unit/Unit_C3/Tourism_Statistics/Documents/2019/News2019_106.pdf (accessed on 15 December 2022).
- Sapiano, M. Integrated Water Resources Management in the Maltese Islands. Acque Sotter.-Ital. J. Groundw. 2020, 9, 25–32. [Google Scholar] [CrossRef]
- Fenech, S.; Knox, J.; Borg, M.; Camilleri, C.; Rizzo, A. Estimating impacts of land use change on evapotranspiration for three agricultural crops in Malta—A preliminary assessment. J. Agric. Sci. 2019, 11, 67–74. [Google Scholar] [CrossRef]
- Bonnefoy-Claudet, S.; Cotton, F.; Bard, P.-Y. The nature of noise wavefield and its applications for site effects studies: A literature review. Earth-Sci. Rev. 2006, 79, 205–227. [Google Scholar] [CrossRef]
- Groos, J. Broadband Seismic Noise: Classification and Green’s Function Estimation. Ph.D. Thesis, Karlsruher Institute für Technologie, Karlsruhe, Germany, 2010. [Google Scholar]
- Yang, Y.; Ritzwoller, M.H. Characteristics of ambient seismic noise as a source for surface wave tomography. Geochem. Geophys. Geosystems 2008, 9, Q02008. [Google Scholar] [CrossRef]
- Asten, M.W. Geological control on the three-component spectra of Rayleigh-wave microseisms. Bull. Seismol. Soc. Am. 1978, 68, 1623–1636. [Google Scholar]
- Gutenberg, B. Microseisms. Adv. Geophys. 1958, 5, 53–92. [Google Scholar]
- Ardhuin, F.; Stutzmann, E.; Schimmel, M.; Mangeney, A. Ocean wave sources of seismic noise. J. Geophys. Res. Ocean. 2011, 116, C09004. [Google Scholar] [CrossRef]
- Campillo, M.; Paul, A. Long-range correlations in the diffuse seismic coda. Science 2003, 299, 547–549. [Google Scholar] [CrossRef]
- Clarke, D.; Zaccarelli, L.; Shapiro, N.; Brenguier, F. Assessment of resolution and accuracy of the Moving Window Cross Spectral technique for monitoring crustal temporal variations using ambient seismic noise. Geophys. J. Int. 2011, 186, 867–882. [Google Scholar] [CrossRef]
- Lobkis, O.I.; Weaver, R.L. On the emergence of the Green’s function in the correlations of a diffuse field. J. Acoust. Soc. Am. 2001, 110, 3011–3017. [Google Scholar] [CrossRef]
- Sabra, K.G.; Gerstoft, P.; Roux, P.; Kuperman, W.; Fehler, M.C. Extracting time-domain Green’s function estimates from ambient seismic noise. Geophys. Res. Lett. 2005, 32, L03310. [Google Scholar] [CrossRef]
- Shapiro, N.M.; Campillo, M.; Stehly, L.; Ritzwoller, M.H. High-resolution surface-wave tomography from ambient seismic noise. Science 2005, 307, 1615–1618. [Google Scholar] [CrossRef] [PubMed]
- Wapenaar, K.; Fokkema, J. Green’s function representations for seismic interferometry. Geophysics 2006, 71, SI33–SI46. [Google Scholar] [CrossRef]
- Weaver, R.L.; Lobkis, O.I. Diffuse fields in open systems and the emergence of the Green’s function (L). J. Acoust. Soc. Am. 2004, 116, 2731–2734. [Google Scholar] [CrossRef]
- Grobbe, N.; Mordret, A.; Barde-Cabusson, S.; Ellison, L.; Lach, M.; Seo, Y.-H.; Viti, T.; Ward, L.; Zhang, H. A Multi-Hydrogeophysical Study of a Watershed at Kaiwi Coast (O’ahu, Hawai’i), using Seismic Ambient Noise Surface Wave Tomography and Self-Potential Data. Water Resour. Res. 2021, 57, 1–21. [Google Scholar] [CrossRef]
- Agius, M.; Magrini, F.; Diaferia, G.; Kästle, E.; Cammarano, F.; Faccenna, C.; Funiciello, F.; van der Meijde, M. Shear-velocity structure and dynamics beneath the Sicily Channel and surrounding regions of the Central Mediterranean inferred from seismic surface waves. Geochem. Geophys. Geosyst. 2022, 23, e2022GC010394. [Google Scholar] [CrossRef]
- Bensen, G.; Ritzwoller, M.; Barmin, M.; Levshin, A.L.; Lin, F.; Moschetti, M.; Shapiro, N.; Yang, Y. Processing seismic ambient noise data to obtain reliable broad-band surface wave dispersion measurements. Geophys. J. Int. 2007, 169, 1239–1260. [Google Scholar] [CrossRef]
- Lin, F.-C.; Moschetti, M.P.; Ritzwoller, M.H. Surface wave tomography of the western United States from ambient seismic noise: Rayleigh and Love wave phase velocity maps. Geophys. J. Int. 2008, 173, 281–298. [Google Scholar] [CrossRef]
- Lin, F.-C.; Ritzwoller, M.H.; Townend, J.; Bannister, S.; Savage, M.K. Ambient noise Rayleigh wave tomography of New Zealand. Geophys. J. Int. 2007, 170, 649–666. [Google Scholar] [CrossRef]
- Moschetti, M.; Ritzwoller, M.; Shapiro, N. Surface wave tomography of the western United States from ambient seismic noise: Rayleigh wave group velocity maps. Geochem. Geophys. Geosyst. 2007, 8, Q08010. [Google Scholar] [CrossRef]
- Sabra, K.G.; Gerstoft, P.; Roux, P.; Kuperman, W.; Fehler, M.C. Surface wave tomography from microseisms in Southern California. Geophys. Res. Lett. 2005, 32, L14311. [Google Scholar] [CrossRef]
- Yang, Y.; Ritzwoller, M.H.; Levshin, A.L.; Shapiro, N.M. Ambient noise Rayleigh wave tomography across Europe. Geophys. J. Int. 2007, 168, 259–274. [Google Scholar] [CrossRef]
- Yao, H.; van Der Hilst, R.D.; De Hoop, M.V. Surface-wave array tomography in SE Tibet from ambient seismic noise and two-station analysis—I. Phase velocity maps. Geophys. J. Int. 2006, 166, 732–744. [Google Scholar] [CrossRef]
- Lecocq, T.; Caudron, C.; Brenguier, F. MSNoise, a Python Package for Monitoring Seismic Velocity Changes Using Ambient Seismic Noise. Seismol. Res. Lett. 2014, 85, 715–726. [Google Scholar] [CrossRef]
- Duputel, Z.; Ferrazzini, V.; Brenguier, F.; Shapiro, N.; Campillo, M.; Nercessian, A. Real time monitoring of relative velocity changes using ambient seismic noise at the Piton de la Fournaise volcano (La Réunion) from January 2006 to June 2007. J. Volcanol. Geotherm. Res. 2009, 184, 164–173. [Google Scholar] [CrossRef]
- Brenguier, F.; Campillo, M.; Takeda, T.; Aoki, Y.; Shapiro, N.; Briand, X.; Emoto, K.; Miyake, H. Mapping pressurized volcanic fluids from induced crustal seismic velocity drops. Science 2014, 345, 80–82. [Google Scholar] [CrossRef]
- Brenguier, F.; Rivet, D.; Obermann, A.; Nakata, N.; Boué, P.; Lecocq, T.; Campillo, M.; Shapiro, N. 4-d noise-based seismology at volcanoes: Ongoing efforts and perspectives. J. Volcanol. Geotherm. Res. 2016, 321, 182–195. [Google Scholar] [CrossRef]
- Brenguier, F.; Shapiro, N.M.; Campillo, M.; Ferrazzini, V.; Duputel, Z.; Coutant, O.; Nercessian, A. Towards forecasting volcanic eruptions using seismic noise. Nat. Geosci. 2008, 1, 126–130. [Google Scholar] [CrossRef]
- Rivet, D.; Brenguier, F.; Cappa, F. Improved detection of preeruptive seismic velocity drops at the Piton de La Fournaise volcano. Geophys. Res. Lett. 2015, 42, 6332–6339. [Google Scholar] [CrossRef]
- Brenguier, F.; Campillo, M.; Hadziioannou, C.; Shapiro, N.M.; Nadeau, R.M.; Larose, É. Postseismic relaxation along the San Andreas fault at Parkfield from continuous seismological observations. Science 2008, 321, 1478–1481. [Google Scholar] [CrossRef]
- Taira, T.; Brenguier, F.; Kong, Q. Ambient noise-based monitoring of seismic velocity changes associated with the 2014 Mw 6.0 South Napa earthquake. Geophys. Res. Lett. 2015, 42, 6997–7004. [Google Scholar] [CrossRef]
- Wegler, U.; Nakahara, H.; Sens-Schönfelder, C.; Korn, M.; Shiomi, K. Sudden drop of seismic velocity after the 2004 Mw 6.6 mid-Niigata earthquake, Japan, observed with Passive Image Interferometry. J. Geophys. Res. Solid Earth 2009, 114, B06305. [Google Scholar] [CrossRef]
- Wegler, U.; Sens-Schönfelder, C. Fault zone monitoring with passive image interferometry. Geophys. J. Int. 2007, 168, 1029–1033. [Google Scholar] [CrossRef]
- Mordret, A.; Mikesell, T.D.; Harig, C.; Lipovsky, B.P.; Prieto, G.A. Monitoring southwest Greenland’s ice sheet melt with ambient seismic noise. Sci. Adv. 2016, 2, e1501538. [Google Scholar] [CrossRef] [PubMed]
- Larose, E.; Carrière, S.; Voisin, C.; Bottelin, P.; Baillet, L.; Guéguen, P.; Walter, F.; Jongmans, D.; Guillier, B.; Garambois, S.; et al. Environmental seismology: What can we learn on earth surface processes with ambient noise? J. Appl. Geophys. 2015, 116, 62–74. [Google Scholar] [CrossRef]
- Yang, Z.; Yuan, C.; Denolle, M.A. Detecting Elevated Pore Pressure due to Wastewater Injection Using Ambient Noise Monitoring. Seism. Rec. 2022, 2, 38–49. [Google Scholar] [CrossRef]
- Hillers, G.; Ben-Zion, Y.; Campillo, M.; Zigone, D. Seasonal variations of seismic velocities in the San Jacinto fault area observed with ambient seismic noise. Geophys. J. Int. 2015, 202, 920–932. [Google Scholar] [CrossRef]
- Mao, S.; Campillo, M.; van der Hilst, R.D.; Brenguier, F.; Stehly, L.; Hillers, G. High temporal resolution monitoring of small variations in crustal strain by dense seismic arrays. Geophys. Res. Lett. 2019, 46, 128–137. [Google Scholar] [CrossRef]
- Tsai, V.C. A model for seasonal changes in GPS positions and seismic wave speeds due to thermoelastic and hydrologic variations. J. Geophys. Res. Solid Earth 2011, 116, B04404. [Google Scholar] [CrossRef]
- Obermann, A.; Froment, B.; Campillo, M.; Larose, E.; Planès, T.; Valette, B.; Chen, J.; Liu, Q. Seismic noise correlations to image structural and mechanical changes associated with the Mw 7.9 2008 Wenchuan earthquake. J. Geophys. Res. Solid Earth 2014, 119, 3155–3168. [Google Scholar] [CrossRef]
- Sharo, A.A.; Taamneh, M.O.; Alawneh, A.S.; Nuseir, O.K.; Rababeh, S.R. P Wave Velocity of Limestone Influenced by Saturation: Experimental Study. Int. Rev. Civ. Eng. 2022, 13, 108–117. [Google Scholar] [CrossRef]
- Claerbout, J.F. Synthesis of a layered medium from its acoustic transmission response. Geophysics 1968, 33, 264–269. [Google Scholar] [CrossRef]
- Wapenaar, K. Retrieving the elastodynamic Green’s function of an arbitrary inhomogeneous medium by cross correlation. Phys. Rev. Lett. 2004, 93, 254301. [Google Scholar] [CrossRef]
- House, M. Geology and Structure of the Maltese Islands; Research Paper Series; Durham University, Department of Geography: Durham, UK, 1961; Volume 5, pp. 23–31. [Google Scholar]
- Felix, R. Oligo-Miocene stratigraphy of Malta and Gozo. Meded. Land 1973, 73–20, 1–103. [Google Scholar]
- Pedley, H.M. A new lithostratigraphical and palaeoenvironmental interpretation for the coralline limestone formations (Miocene) of the Maltese Islands. Overseas Geol. Miner. Resour. 1978, 54, 17. [Google Scholar]
- Pedley, H.M.; House, M.R.; Waugh, B. The geology of the Pelagian block: The Maltese Islands. In The Ocean Basins and Margins; Springer: New York, NY, USA, 1978; pp. 417–433. [Google Scholar]
- Pedley, H. Controls on Cenozoic carbonate deposition in the Maltese islands: Review and reinterpretation. Mem. Della Soc. Geol. Ital. 1987, 38, 81–94. [Google Scholar]
- Alexander, D. A review of the physical geography of Malta and its significance for tectonic geomorphology. Quat. Sci. Rev. 1988, 7, 41–53. [Google Scholar] [CrossRef]
- Pedley, H. Syndepositional tectonics affecting Cenozoic and Mesozoic deposition in the Malta and SE Sicily areas (Central Mediterranean) and their bearing on Mesozoic reservoir development in the N Malta offshore region. Mar. Pet. Geol. 1990, 7, 171–180. [Google Scholar] [CrossRef]
- Rehfeld, U.; Janssen, A.W. Development of phosphatized hardgrounds in the miocene Globigerina Limestone of the Maltese archipelago, including a description of Gamopleura melitensis sp. nov. (Gastropoda, Euthecosomata). Facies 1995, 33, 91–106. [Google Scholar] [CrossRef]
- Magri, O. A geological and geomorphological review of the Maltese Islands with special reference to the coastal zone. Territoris 2006, 6, 7–26. [Google Scholar]
- Baldassini, N.; Di Stefano, A. Stratigraphic features of the Maltese Archipelago: A synthesis. Nat. Hazards 2017, 86, 203–231. [Google Scholar] [CrossRef]
- Prampolini, M.; Gauci, C.; Micallef, A.S.; Selmi, L.; Vandelli, V.; Soldati, M. Geomorphology of the north-eastern coast of Gozo (Malta, Mediterranean Sea). J. Maps 2018, 14, 402–410. [Google Scholar] [CrossRef]
- Continental Shelf Department. Geological Map of the Maltese Islands. 2022. Available online: https://continentalshelf.gov.mt/en/Pages/Geological-Map-of-the-Maltese-Islands.aspx (accessed on 15 December 2022).
- Newbery, J. The perched water table in the upper limestone aquifer of Malta. J. Inst. Water Eng. 1968, 22, 551–570. [Google Scholar]
- Food and Agricultural Organisation. Malta Water Resources Review; Technical Report; FAO: Rome, Italy, 2006. [Google Scholar]
- Buhagiar, K. Water management strategies and the cave-dwelling phenomenon in late-medieval Malta. Mediev. Archaeol. 2007, 51, 103–131. [Google Scholar] [CrossRef]
- Sapiano, M.; Micallef, P.; Attard, G.; Zammit, M.-L. The evolution of water culture in Malta: An analysis of the changing perceptions towards water throughout the ages. Options Mediterranéennes Ser. A Semin. Mediterr. 2008, 83, 97–109. [Google Scholar]
- National Audit Office. Performance Audit: Safeguarding Malta’s Groundwater; Technical Report; NAO: Floriana, Malta, 2012. [Google Scholar]
- Galea, P.; Agius, M.R.; Bozionelos, G.; D’Amico, S.; Farrugia, D. A first national seismic network for the Maltese islands–The Malta seismic network. Seismol. Soc. Am. 2021, 92, 1817–1831. [Google Scholar] [CrossRef]
- Bozionelos, G.; Galea, P.; D’Amico, S.; Plasencia Linares, M.; Romanelli, M.; Rossi, G.; Vuan, A.; Sugan, M.; Agius, M. An augmented seismic network to study off-shore seismicity around the Maltese Islands: The FASTMIT experiment. Xjenza 2019, 7, 104–121. [Google Scholar]
- McNamara, D.E.; Buland, R.P. Ambient noise levels in the continental United States. Bull. Seismol. Soc. Am. 2004, 94, 1517–1527. [Google Scholar] [CrossRef]
- Gubbins, D. Time Series Analysis and Inverse Theory for Geophysicists; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Ratdomopurbo, A.; Poupinet, G. Monitoring a temporal change of seismic velocity in a volcano: Application to the 1992 eruption of Mt. Merapi (Indonesia). Geophys. Res. Lett. 1995, 22, 775–778. [Google Scholar] [CrossRef]
- Laudi, L. A Novel Approach to Groundwater Monitoring in the Maltese Islands: Analysis of Auto- and Cross-Correlation Functions of Ambient Seismic Noise. Master’s Thesis, University of Malta, Msida, Malta, 2023. [Google Scholar]
- OTT. Thalimedes. Available online: https://www.ott.com/download/leaflet-shaft-encoder-for-depth-and-water-level-measurement-ott-thalimedes-1/ (accessed on 23 June 2023).
- Barbagli, A.; Guastaldi, E.; Conti, P.; Giannuzzi, M.; Borsi, I.; Lotti, F.; Basile, P.; Favaro, L.; Mallia, A.; Xuereb, R.; et al. Geological and hydrogeological reconstruction of the main aquifers of the Maltese islands. Hydrogeol. J. 2021, 29, 2685–2703. [Google Scholar] [CrossRef]
- Farrugia, D.; Paolucci, E.; D’Amico, S.; Galea, P. Inversion of surface wave data for subsurface shear wave velocity profiles characterized by a thick buried low-velocity layer. Geophys. J. Int. 2016, 206, 1221–1231. [Google Scholar] [CrossRef]
- Pischiutta, M.; Villani, F.; D’Amico, S.; Vassallo, M.; Cara, F.; Di Naccio, D.; Farrugia, D.; Di Giulio, G.; Amoroso, S.; Cantore, L.; et al. Results from shallow geophysical investigations in the northwestern sector of the island of Malta. Phys. Chem. Earth Parts A/B/C 2017, 98, 41–48. [Google Scholar] [CrossRef]
- Hillers, G.; Campillo, M.; Ma, K.-F. Seismic velocity variations at TCDP are controlled by MJO driven precipitation pattern and high fluid discharge properties. Earth Planet. Sci. Lett. 2014, 391, 121–127. [Google Scholar] [CrossRef]
- Niemczynowicz, J. Urban hydrology and water management–present and future challenges. Urban Water 1999, 1, 1–14. [Google Scholar] [CrossRef]
- Owuor, S.O.; Butterbach-Bahl, K.; Guzha, A.C.; Rufino, M.C.; Pelster, D.E.; Díaz-Pinés, E.; Breuer, L. Groundwater recharge rates and surface runoff response to land use and land cover changes in semi-arid environments. Ecol. Process. 2016, 5, 1–21. [Google Scholar] [CrossRef]
- Beyreuther, M.; Barsch, R.; Krischer, L.; Megies, T.; Behr, Y.; Wassermann, J. ObsPy: A Python toolbox for seismology. Seismol. Res. Lett. 2010, 81, 530–533. [Google Scholar] [CrossRef]
- Wessel, P.; Smith, W.H.F.; Scharroo, R.; Luis, J.; Wobbe, F. Generic mapping tools: Improved version released. Trans. Am. Geophys. Union 2013, 94, 409–410. [Google Scholar] [CrossRef]
- Agius, M.R. Getting started with GMT: An introduction for seismologists. In Moment Tensor Solutions; D’Amico, S., Ed.; Springer: Cham, Switzerland, 2018; Available online: https://link.springer.com/chapter/10.1007/978-3-319-77359-9_31 (accessed on 2 July 2023).





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laudi, L.; Agius, M.R.; Galea, P.; D’Amico, S.; Schimmel, M. Monitoring of Groundwater in a Limestone Island Aquifer Using Ambient Seismic Noise. Water 2023, 15, 2523. https://doi.org/10.3390/w15142523
Laudi L, Agius MR, Galea P, D’Amico S, Schimmel M. Monitoring of Groundwater in a Limestone Island Aquifer Using Ambient Seismic Noise. Water. 2023; 15(14):2523. https://doi.org/10.3390/w15142523
Chicago/Turabian StyleLaudi, Luca, Matthew R. Agius, Pauline Galea, Sebastiano D’Amico, and Martin Schimmel. 2023. "Monitoring of Groundwater in a Limestone Island Aquifer Using Ambient Seismic Noise" Water 15, no. 14: 2523. https://doi.org/10.3390/w15142523
APA StyleLaudi, L., Agius, M. R., Galea, P., D’Amico, S., & Schimmel, M. (2023). Monitoring of Groundwater in a Limestone Island Aquifer Using Ambient Seismic Noise. Water, 15(14), 2523. https://doi.org/10.3390/w15142523






