Modeling of Distributed Control System for Network of Mineral Water Wells
Abstract
1. Introduction
- determination of the optimal number of production wells;
- monitoring the current state of the hydrogeological system;
- forecasting processes in the hydrogeological system for short-term (up to 10 years) and long-term (up to 100 years) perspectives.
2. Materials and Methods
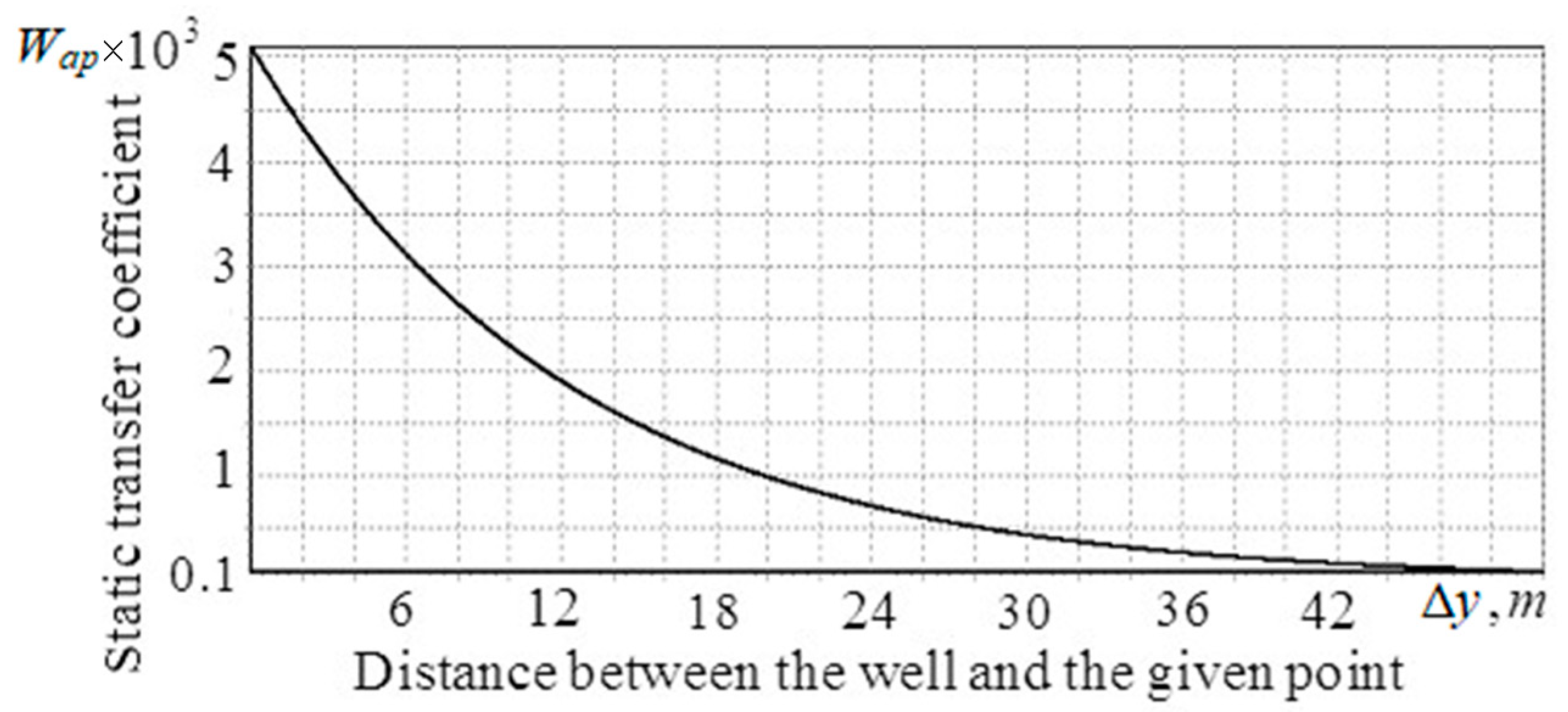
3. Results
3.1. Study of the Characteristics of the Hydrogeological Process
3.2. Determination of the Optimal Number of Production Wells
3.3. Synthesis of a Distributed Controller
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Malkov, A.V.; Pershin, I.M.; Pomelyayko, I.S.; Utkin, V.A.; Korolev, B.I.; Dubogrey, V.F.; Khmel, V.V.; Pershin, M.I. Kislovodsk Carbon Dioxide Mineral Water Field: System Analysis, Diagnostics, Forecast, Control; Nauka: Moscow, Russia, 2015; ISBN 978-5-02-039162-8. (In Russian) [Google Scholar]
- Pomelyaiko, I.S.; Malkov, A.V. Quality Problems of Surface Water and Groundwater at the Health Resorts in the Regions of Caucasian Mineral Waters and Ways to Their Solution. Water Resour. 2019, 46, 214–225. [Google Scholar] [CrossRef]
- Drovosekova, T.I.; Rusak, S.N.; Harish, N.P. Issues of and outlook for using geothermal water. In Proceedings of the 2019 International Science and Technology Conference “EastConf”, Vladivostok, Russia, 1–2 March 2019; p. 8725307. [Google Scholar] [CrossRef]
- Karlović, I.; Marković, T.; Smith, A.C.; Maldini, K. Impact of Gravel Pits on Water Quality in Alluvial Aquifers. Hydrology 2023, 10, 99. [Google Scholar] [CrossRef]
- Semyachkov, A.I.; Pochechun, V.A.; Semyachkov, K.A. Hydrogeoecological conditions of technogenic groundwater in waste disposal sites. J. Min. Inst. 2023, 260, 168–179. [Google Scholar] [CrossRef]
- Wang, J.; Xu, J. Spatial Distribution and Controlling Factors of Groundwater Quality Parameters in Yancheng Area on the Lower Reaches of the Huaihe River, Central East China. Sustainability 2023, 15, 6882. [Google Scholar] [CrossRef]
- Ostad, H.; Mohammadi, Z.; Fiorillo, F. Assessing the Effect of Conduit Pattern and Type of Recharge on the Karst Spring Hydrograph: A Synthetic Modeling Approach. Water 2023, 15, 1594. [Google Scholar] [CrossRef]
- Ahamed, A.; Knight, R.; Alam, S.; Morphew, M.; Susskind, T. Remote Sensing-Based Estimates of Changes in Stored Groundwater at Local Scales: Case Study for Two Groundwater Subbasins in California’s Central Valley. Remote Sens. 2023, 15, 2100. [Google Scholar] [CrossRef]
- Ramos, E.; Bux, R.K.; Medina, D.I.; Barrios-Piña, H.; Mahlknecht, J. Spatial and Multivariate Statistical Analyses of Human Health Risk Associated with the Consumption of Heavy Metals in Groundwater of Monterrey Metropolitan Area, Mexico. Water 2023, 15, 1243. [Google Scholar] [CrossRef]
- Gad, M.; Gaagai, A.; Eid, M.H.; Szűcs, P.; Hussein, H.; Elsherbiny, O.; Elsayed, S.; Khalifa, M.M.; Moghanm, F.S.; Moustapha, M.E.; et al. Groundwater Quality and Health Risk Assessment Using Indexing Approaches, Multivariate Statistical Analysis, Artificial Neural Networks, and GIS Techniques in El Kharga Oasis, Egypt. Water 2023, 15, 1216. [Google Scholar] [CrossRef]
- Golovina, E.; Shchelkonogova, O. Possibilities of Using the Unitization Model in the Development of Transboundary Groundwater Deposits. Water 2023, 15, 298. [Google Scholar] [CrossRef]
- Golovina, E.; Pasternak, S.; Tsiglianu, P.; Tselischev, N. Sustainable Management of Transboundary Groundwater Resources: Past and Future. Sustainability 2021, 13, 12102. [Google Scholar] [CrossRef]
- Shestopalov, M.Y.; Pershin, I.M.; Tsapleva, V.V. Distributed Control Systems Designing. In Proceedings of the 2019 III International Conference on Control in Technical Systems (CTS), St. Petersburg, Russia, 30 October–1 November 2019; pp. 85–88. [Google Scholar] [CrossRef]
- Pershin, I.M.; Papush, E.G.; Malkov, A.V.; Kukharova, T.V.; Spivak, A.O. Operational Control of Underground Water Exploitation Regimes. In Proceedings of the 2019 III International Conference on Control in Technical Systems (CTS), St. Petersburg, Russia, 30 October–1 November 2019; pp. 77–80. [Google Scholar] [CrossRef]
- Grigorev, G.S.; Salishchev, M.V.; Senchina, N.P. On the applicability of electromagnetic monitoring of hydraulic fracturing. J. Min. Inst. 2021, 250, 492–500. [Google Scholar] [CrossRef]
- Zhukovskiy, Y.L.; Korolev, N.A.; Malkova, Y.M. Monitoring of grinding condition in drum mills based on resulting shaft torque. J. Min. Inst. 2022, 256, 686–700. [Google Scholar] [CrossRef]
- Martirosyan, A.V.; Ilyushin, Y.V. The Development of the Toxic and Flammable Gases Concentration Monitoring System for Coalmines. Energies 2022, 15, 8917. [Google Scholar] [CrossRef]
- Zakharov, L.A.; Martyushev, D.A.; Ponomareva, I.N. Predicting dynamic formation pressure using artificial intelligence methods. J. Min. Inst. 2022, 253, 23–32. [Google Scholar] [CrossRef]
- Arefiev, I.B.; Afanaseva, O.V. Implementation of Control and Forecasting Problems of Human-Machine Complexes on the Basis of Logic-Reflexive Modeling. Lect. Notes Netw. Syst. 2022, 442, 187–197. [Google Scholar] [CrossRef]
- Kovalev, D.A.; Rusinov, L. Increase in environmental safety of recovery boiler. IOP Conf. Ser. Earth Environ. Sci. 2022, 990, 012068. [Google Scholar] [CrossRef]
- Veselov, G.E.; Sinicyn, A. Synthesis of sliding control system for automotive suspension under kinematic constraints. J. Vibroengineering 2021, 23, 1446–1455. [Google Scholar] [CrossRef]
- Pershin, I.M.; Liashenko, A.L.; Papush, E.G. General Principles for Designing Distributed Control Systems. In Proceedings of the 2020 Wave Electronics and its Application in Information and Telecommunication Systems (WECONF), St. Petersburg, Russia, 1–5 June 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Makarova, A.A.; Kaliberda, I.V.; Kovalev, D.A.; Pershin, I.M. Modeling a Production Well Flow Control System Using the Example of the Verkhneberezovskaya Area. In Proceedings of the 2022 Conference of Russian Young Researchers in Electrical and Electronic Engineering, St. Petersburg, Russia, 25–28 January 2022; pp. 760–764. [Google Scholar] [CrossRef]
- Sizov, S.; Drovosekova, T.; Pershin, I. Application of Machine Learning Methods in Modeling Hydrolithospheric Processes. Commun. Comput. Inf. Sci. 2021, 1395, 422–431. [Google Scholar] [CrossRef]
- Tsapleva, V.V.; Masyutina, G.V.; Danchenko, I.V. Construction of a mathematical model for the extraction of mineral raw materials. IOP Conf. Ser. Earth Environ. Sci. 2020, 613, 012154. [Google Scholar] [CrossRef]
- Pershin, I.; Sidyakin, P.; Belaya, E.; Shchitov, D. Modeling the formation of acoustic resonant waves in a closed space. IOP Conf. Ser. Mater. Sci. Eng. 2019, 698, 077054. [Google Scholar] [CrossRef]
- Martirosyan, A.V.; Martirosyan, K.V.; Mir-Amal, A.M.; Chernyshev, A.B. Assessment of a Hydrogeological Object’s Distributed Control System Stability. In Proceedings of the 2022 Conference of Russian Young Researchers in Electrical and Electronic Engineering, St. Petersburg, Russia, 25–28 January 2022; pp. 768–771. [Google Scholar] [CrossRef]
- Grigoriev, V.V.; Bystrov, S.V.; Mansurova, O.K.; Pershin, I.M.; Bushuev, A.B.; Petrov, V.A. Exponential stability regions estimation of nonlinear dynamical systems. Mekhatronika Avtom. Upr. 2020, 21, 131–135. [Google Scholar] [CrossRef]
- Dagaev, A.; Pham, V.D.; Kirichek, R.; Afanaseva, O.; Yakovleva, E. Method of Analyzing the Availability Factor in a Mesh Network. Commun. Comput. Inf. Sci. 2022, 1552, 346–358. [Google Scholar] [CrossRef]
- Liashenko, A.L.; Pershin, I.M.; Moreva, S.L. Development of a Distributed System of Control of the Supply of the Coolant in Steam Generator Installations. In Proceedings of the 2020 Wave Electronics and its Application in Information and Telecommunication Systems (WECONF), St. Petersburg, Russia, 1–5 June 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Fetisov, V.; Ilyushin, Y.V.; Vasiliev, G.G.; Leonovich, I.A.; Müller, J.; Riazi, M.; Mohammadi, A.H. Development of the automated temperature control system of the main gas pipeline. Sci. Rep. 2023, 13, 3092. [Google Scholar] [CrossRef] [PubMed]
- Martirosyan, A.V.; Ilyushin, Y.V.; Afanaseva, O.V. Development of a Distributed Mathematical Model and Control System for Reducing Pollution Risk in Mineral Water Aquifer Systems. Water 2022, 14, 151. [Google Scholar] [CrossRef]
- Pershin, I.M.; Malkov, A.V.; Pomelyayko, I.S. Design of a Distributed Debit Management Network of Operating Wells of Deposits of the CMW Region. Commun. Comput. Inf. Sci. 2021, 1396, 317–328. [Google Scholar] [CrossRef]
- Satsuk, T.P.; Sharyakov, V.A.; Sharyakova, O.L.; Kovalev, D.A.; Vorob’ev, A.A.; Makarova, E.I. Erratum to: Automatic Voltage Stabilization of an Electric Rolling Stock Catenary System. Russ. Electr. Eng. 2021, 92, 349. [Google Scholar] [CrossRef]
- Tsiglianu, P.; Romasheva, N.; Nenko, A. Conceptual Management Framework for Oil and Gas Engineering Project Implementation. Resources 2023, 12, 64. [Google Scholar] [CrossRef]
- González de Vallejo, L.I.; Ferrer, M.; Ortuño, L.; Oteo, C. Ingeniería Geológica; Prentice Hall-Pearson Educación: Madrid, Spain, 2002; p. 750. [Google Scholar]
- Ayvaz, M.T.; Karahan, H. A Simulation/Optimization Model for the Identification of Unknown Groundwater Well Locations and Pumping Rates. J. Hydrol. 2008, 357, 76–92. [Google Scholar] [CrossRef]
- Ilyushin, Y.V.; Afanaseva, O.V. Development of scada-model for trunk gas pipeline’s compressor station. J. Min. Inst. 2019, 240, 686–693. [Google Scholar] [CrossRef]
- Ilyushin, Y.V.; Asadulagi, M.-A.M. Development of a Distributed Control System for the Hydrodynamic Processes of Aquifers, Taking into Account Stochastic Disturbing Factors. Water 2023, 15, 770. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, Z.; Zhuang, C.; Dou, Z. Estimating Hydraulic Parameters of Aquifers Using Type Curve Analysis of Pumping Tests with Piecewise-Constant Rates. Water 2023, 15, 1661. [Google Scholar] [CrossRef]
- Angelaki, A.; Bota, V.; Chalkidis, I. Estimation of Hydraulic Parameters from the Soil Water Characteristic Curve. Sustainability 2023, 15, 6714. [Google Scholar] [CrossRef]
- Pershin, M.I.; Papush, E.G.; Spivak, A.O. Approximation Models for the Hydrolitospheric Processes. In Proceedings of the 2018 International Multi-Conference on Industrial Engineering and Modern Technologies (FarEastCon 2018), Vladivostok, Russia, 2–4 October 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Nosova, V.A.; Pershin, I.M. Determining the optimal number of wells during field development. In Proceedings of the 2021 4th International Conference on Control in Technical Systems (CTS 2021), St. Petersburg, Russia, 21–23 September 2021; pp. 42–44. [Google Scholar] [CrossRef]
- Ilyushin, Y.V.; Afanasieva, O.V. Synthesis of a distributed control system. Int. J. Control Theory Appl. 2016, 9, 41–60. [Google Scholar]
- Asadulagi, M.M.; Ioskov, G.V. Simulation of the control system for hydrodynamic process with random disturbances. Topical Issues of Rational Use of Natural Resources. In Proceedings of the International Forum-Contest of Young Researchers, St. Petersburg, Russia, 18–20 April 2018; pp. 399–405. [Google Scholar]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pershin, I.M.; Papush, E.G.; Kukharova, T.V.; Utkin, V.A. Modeling of Distributed Control System for Network of Mineral Water Wells. Water 2023, 15, 2289. https://doi.org/10.3390/w15122289
Pershin IM, Papush EG, Kukharova TV, Utkin VA. Modeling of Distributed Control System for Network of Mineral Water Wells. Water. 2023; 15(12):2289. https://doi.org/10.3390/w15122289
Chicago/Turabian StylePershin, Ivan M., Elena G. Papush, Tatyana V. Kukharova, and Vladimir A. Utkin. 2023. "Modeling of Distributed Control System for Network of Mineral Water Wells" Water 15, no. 12: 2289. https://doi.org/10.3390/w15122289
APA StylePershin, I. M., Papush, E. G., Kukharova, T. V., & Utkin, V. A. (2023). Modeling of Distributed Control System for Network of Mineral Water Wells. Water, 15(12), 2289. https://doi.org/10.3390/w15122289







