Ranking Sub-Watersheds for Flood Hazard Mapping: A Multi-Criteria Decision-Making Approach
Abstract
1. Introduction
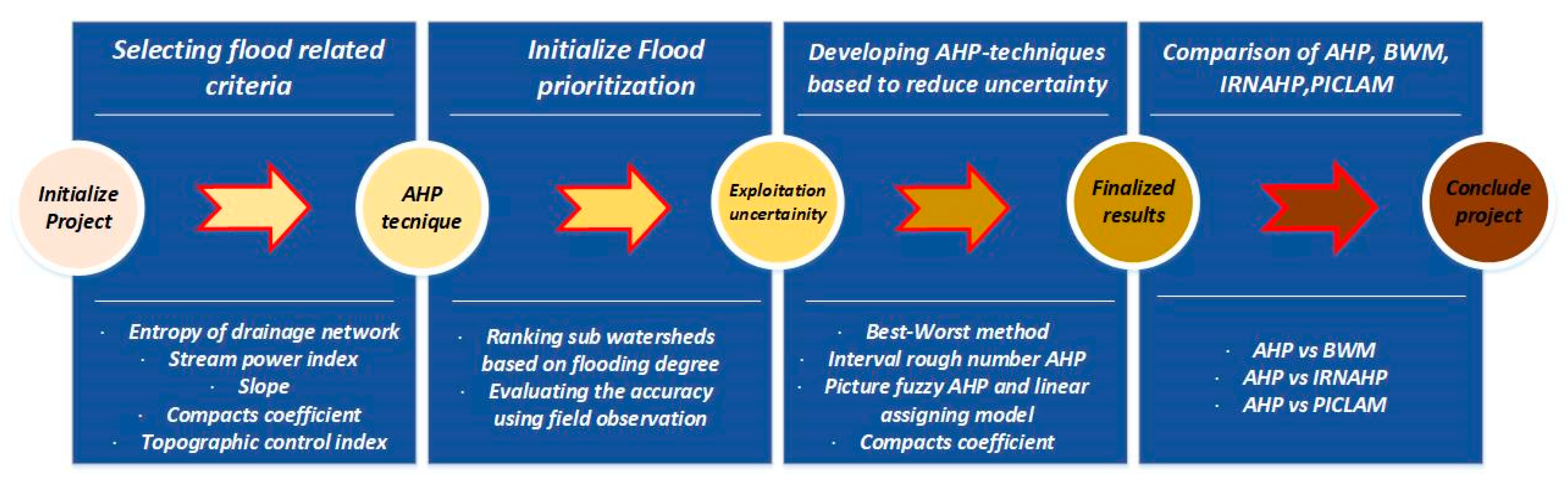
2. Materials and Methods
2.1. Study Area
2.2. Data and Methodology
2.3. Theoretical Backgrounds of Proposed Methods
2.3.1. Analytic Hierarchy Process (AHP)
2.3.2. IRNAHP
- IRN Mathematical Model
2.3.3. Best–Worst Method (BWM)
2.3.4. Picture Fuzzy Analytic Hierarchy Process and Picture Fuzzy Linear Assignment (PICALAM)
- Addition
- Multiplication
- Multiplication by a scalar; λ > 0
3. Analysis and Results
3.1. Morphometric Parameters
3.2. Ranking of Sub-Watersheds Using the AHP Technique
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ramkar, P.; Yadav, S.M. Flood risk index in data-scarce river basins using the AHP and GIS approach. Nat. Hazards 2021, 109, 1119–1140. [Google Scholar] [CrossRef]
- Papilloud, T.; Röthlisberger, V.; Loreti, S.; Keiler, M. Flood exposure analysis of road infrastructure—Comparison of different methods at national level. Int. J. Disaster Risk Reduct. 2020, 47, 101548. [Google Scholar] [CrossRef]
- Guha-Sapir, D.; Vos, F.; Below, R.; Ponserre, S. Annual Disaster Statistical Review 2011: The Numbers and Trends; Institute of Health and Society (IRSS): Brussels, Belgium, 2012. [Google Scholar]
- Mohleji, S.; Pielke, R., Jr. Reconciliation of trends in global and regional economic losses from weather events: 1980–2008. Nat. Hazards Rev. 2014, 15, 04014009. [Google Scholar] [CrossRef]
- Shabanikiya, H.; Seyedin, H.; Haghani, H.; Ebrahimian, A. Behavior of crossing flood on foot, associated risk factors and estimating a predictive model. Nat. Hazards 2014, 73, 1119–1126. [Google Scholar] [CrossRef]
- Yari, A.; Ardalan, A.; Ostadtaghizadeh, A.; Zarezadeh, Y.; Boubakran, M.S.; Bidarpoor, F.; Rahimiforoushani, A. Underlying factors affecting death due to flood in Iran: A qualitative content analysis. Int. J. Disaster Risk Reduct. 2019, 40, 101258. [Google Scholar] [CrossRef]
- Sepehri, M.; Malekinezhad, H.; Ilderomi, A.R.; Talebi, A.; Hosseini, S.Z. Studying the effect of rain water harvesting from roof surfaces on runoff and household consumption reduction. Sustain. Cities Soc. 2018, 43, 317–324. [Google Scholar] [CrossRef]
- Pham, B.T.; Luu, C.; Van Dao, D.; Van Phong, T.; Nguyen, H.D.; Van Le, H.; von Meding, J.; Prakash, I. Flood risk assessment using deep learning integrated with multi-criteria decision analysis. Knowl. Based Syst. 2021, 219, 106899. [Google Scholar] [CrossRef]
- Tang, Z.; Zhang, H.; Yi, S.; Xiao, Y. Assessment of flood susceptible areas using spatially explicit, probabilistic multi-criteria decision analysis. J. Hydrol. 2018, 558, 144–158. [Google Scholar] [CrossRef]
- Abdullah, M.F.; Siraj, S.; Hodgett, R.E. An Overview of Multi-Criteria Decision Analysis (MCDA) Application in Managing Water-Related Disaster Events: Analyzing 20 Years of Literature for Flood and Drought Events. Water 2021, 13, 1358. [Google Scholar] [CrossRef]
- Fernández, D.; Lutz, M. Urban flood hazard zoning in Tucumán Province, Argentina, using GIS and multicriteria decision analysis. Eng. Geol. 2010, 111, 90–98. [Google Scholar] [CrossRef]
- Vojtek, M.; Vojteková, J. Flood susceptibility mapping on a national scale in Slovakia using the analytical hierarchy process. Water 2019, 11, 364. [Google Scholar] [CrossRef]
- Sepehri, M.; Malekinezhad, H.; Hosseini, S.Z.; Ildoromi, A.R. Assessment of flood hazard mapping in urban areas using entropy weighting method: A case study in Hamadan city, Iran. Acta Geophys. 2019, 67, 1435–1449. [Google Scholar] [CrossRef]
- Schanze, J. Flood Risk Management: Hazards, Vulnerability and Mitigation Measures; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1–20. [Google Scholar]
- Tsakiris, G. Flood risk assessment: Concepts, modelling, applications. Nat. Hazards Earth Syst. Sci. 2014, 14, 1361–1369. [Google Scholar] [CrossRef]
- Das, S. Geographic information system and AHP-based flood hazard zonation of Vaitarna basin, Maharashtra, India. Arab. J. Geosci. 2018, 11, 576. [Google Scholar] [CrossRef]
- El-Magd, S.A.A.; Amer, R.A.; Embaby, A. Multi-criteria decision-making for the analysis of flash floods: A case study of Awlad Toq-Sherq, Southeast Sohag, Egypt. J. Afr. Earth Sci. 2020, 162, 103709. [Google Scholar] [CrossRef]
- Khosravi, K.; Shahabi, H.; Pham, B.T.; Adamowski, J.; Shirzadi, A.; Pradhan, B.; Dou, J.; Ly, H.-B.; Gróf, G.; Ho, H.L. A comparative assessment of flood susceptibility modeling using multi-criteria decision-making analysis and machine learning methods. J. Hydrol. 2019, 573, 311–323. [Google Scholar] [CrossRef]
- Sepehri, M.; Ildoromi, A.R.; Malekinezhad, H.; Hosseini, S.Z.; Talebi, A.; Goodarzi, S. Flood hazard mapping for the gonbad chi region, Iran. J. Environ. Eng. Sci. 2017, 12, 16–24. [Google Scholar] [CrossRef]
- Mahmoud, S.H.; Gan, T.Y. Multi-criteria approach to develop flood susceptibility maps in arid regions of Middle East. J. Clean. Prod. 2018, 196, 216–229. [Google Scholar] [CrossRef]
- Malekinezhad, H.; Sepehri, M.; Pham, Q.B.; Hosseini, S.Z.; Meshram, S.G.; Vojtek, M.; Vojteková, J. Application of entropy weighting method for urban flood hazard mapping. Acta Geophys. 2021, 69, 841–854. [Google Scholar] [CrossRef]
- Chen, Y.; Yu, J.; Khan, S. The spatial framework for weight sensitivity analysis in AHP-based multi-criteria decision making. Environ. Model. Softw. 2013, 48, 129–140. [Google Scholar] [CrossRef]
- Ahmadisharaf, E.; Kalyanapu, A.J.; Chung, E.-S. Spatial probabilistic multi-criteria decision making for assessment of flood management alternatives. J. Hydrol. 2016, 533, 365–378. [Google Scholar] [CrossRef]
- Ligmann-Zielinska, A.; Jankowski, P. Spatially-explicit integrated uncertainty and sensitivity analysis of criteria weights in multicriteria land suitability evaluation. Environ. Model. Softw. 2014, 57, 235–247. [Google Scholar] [CrossRef]
- Akbari, M.; Meshram, S.G.; Krishna, R.; Pradhan, B.; Shadeed, S.; Khedher, K.M.; Sepheri, M.; Ildoromi, A.R.; Alimerzaei, F.; Darabi, F. Identification of the Groundwater Potential Recharge Zones Using MCDM Models: Full Consistency Method (FUCOM), Best Worst Method (BWM) and Analytic Hierarchy Process (AHP). Water Resour. Manag. 2021, 35, 4727–4745. [Google Scholar] [CrossRef]
- Pamučar, D.; Stević, Ž.; Sremac, S. A new model for determining weight coefficients of criteria in mcdm models: Full consistency method (fucom). Symmetry 2018, 10, 393. [Google Scholar] [CrossRef]
- Gündoğdu, F.K.; Duleba, S.; Moslem, S.; Aydın, S. Evaluating public transport service quality using picture fuzzy analytic hierarchy process and linear assignment model. Appl. Soft Comput. 2021, 100, 106920. [Google Scholar] [CrossRef]
- Sepehri, M.; Ghahramani, A.; Kiani-Harchegani, M.; Ildoromi, A.R.; Talebi, A.; Rodrigo-Comino, J. Assessment of drainage network analysis methods to rank sediment yield hotspots. Hydrol. Sci. J. 2021, 66, 904–918. [Google Scholar] [CrossRef]
- Pham, B.T.; Luu, C.; Van Phong, T.; Trinh, P.T.; Shirzadi, A.; Renoud, S.; Asadi, S.; Van Le, H.; von Meding, J.; Clague, J.J. Can deep learning algorithms outperform benchmark machine learning algorithms in flood susceptibility modeling? J. Hydrol. 2021, 592, 125615. [Google Scholar] [CrossRef]
- Umer, Y.; Jetten, V.; Ettema, J. Sensitivity of flood dynamics to different soil information sources in urbanized areas. J. Hydrol. 2019, 577, 123945. [Google Scholar] [CrossRef]
- Huang, H.; Chen, X.; Wang, X.; Wang, X.; Liu, L. A depression-based index to represent topographic control in urban pluvial flooding. Water 2019, 11, 2115. [Google Scholar] [CrossRef]
- Meshram, S.G.; Singh, V.P.; Kahya, E.; Sepehri, M.; Meshram, C.; Hasan, M.A.; Islam, S.; Duc, P.A. Assessing erosion prone areas in a watershed using interval rough-analytical hierarchy process (IR-AHP) and fuzzy logic (FL). Stoch. Environ. Res. Risk Assess. 2021, 36, 297–312. [Google Scholar] [CrossRef]
- Olabode, O.F.; Oluwaniyi, O.E.; Adebayo, Q.A.; Asiwaju-Bello, Y.A. Morpho-lithostructural analysis of Ala River basin for flood risk assessment: Geospatial techniques intervention. Earth Sci. Inform. 2020, 13, 773–794. [Google Scholar] [CrossRef]
- Mohseni, N.; Salar, Y.S. Terrain indices control the quality of soil total carbon stock within water erosion-prone environments. Ecohydrol. Hydrobiol. 2021, 21, 46–54. [Google Scholar] [CrossRef]
- Ahmad, I.; Dar, M.A.; Teka, A.H.; Gebre, T.; Gadissa, E.; Tolosa, A.T. Application of hydrological indices for erosion hazard mapping using Spatial Analyst tool. Environ. Monit. Assess. 2019, 191, 482. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.; Zhu, D.; Deng, Y.; Sun, Q.; Ma, J.; Liu, F. Evaluation and empirical study of Happy River on the basis of AHP: A case study of Shaoxing City (Zhejiang, China). Mar. Freshw. Res. 2023. [Google Scholar] [CrossRef]
- López-Vicente, M.; Kramer, H.; Keesstra, S. Effectiveness of soil erosion barriers to reduce sediment connectivity at small basin scale in a fire-affected forest. J. Environ. Manag. 2021, 278, 111510. [Google Scholar] [CrossRef] [PubMed]
- Saaty, T.L. The Analytic Hierarchy Process; Mc Graw Hill Company: New York, NY, USA, 1980. [Google Scholar]
- Rezaei, J. Best-worst multi-criteria decision-making method. Omega 2015, 53, 49–57. [Google Scholar] [CrossRef]
- Bhat, M.S.; Alam, A.; Ahmad, S.; Farooq, H.; Ahmad, B. Flood hazard assessment of upper Jhelum basin using morphometric parameters. Environ. Earth Sci. 2019, 78, 54. [Google Scholar] [CrossRef]
- Bashir, B. Morphometric Parameters and Geospatial Analysis for Flash Flood Susceptibility Assessment: A Case Study of Jeddah City along the Red Sea Coast, Saudi Arabia. Water 2023, 15, 870. [Google Scholar] [CrossRef]
- Keesstra, S.; Nunes, J.P.; Saco, P.; Parsons, T.; Poeppl, R.; Masselink, R.; Cerdà, A. The way forward: Can connectivity be useful to design better measuring and modelling schemes for water and sediment dynamics? Sci. Total Environ. 2018, 644, 1557–1572. [Google Scholar] [CrossRef]
- Rodrigo Comino, J.; Keesstra, S.D.; Cerdà, A. Connectivity assessment in Mediterranean vineyards using improved stock unearthing method, LiDAR and soil erosion field surveys. Earth Surf. Process. Landf. 2018, 43, 2193–2206. [Google Scholar] [CrossRef]
- Zhang, S.; Guo, Y.; Wang, Z. Correlation between flood frequency and geomorphologic complexity of rivers network–a case study of Hangzhou China. J. Hydrol. 2015, 527, 113–118. [Google Scholar] [CrossRef]
- Gigović, L.; Pamučar, D.; Bajić, Z.; Drobnjak, S. Application of GIS-interval rough AHP methodology for flood hazard mapping in urban areas. Water 2017, 9, 360. [Google Scholar] [CrossRef]
- Cuong, B.C.; Kreinovich, V. Picture fuzzy sets-a new concept for computational intelligence problems. In Proceedings of the 2013 Third World Congress on Information and Communication Technologies (WICT 2013), Hanoi, Vietnam, 15–18 December 2013. [Google Scholar]
| Preference Factor | Degree of Preference | Explanation |
|---|---|---|
| 1 | Equally | Two factors contribute equally to the objective |
| 3 | Moderately | Experience and judgment slightly to moderately favor one factor over another |
| 5 | Strongly | Experience and judgment strongly or essentially favor one factor over another |
| 7 | Very strongly | A factor is strongly favored over another and its dominance is showed in practice |
| 9 | Extremely | The evidence of favoring one factor over another is of the highest degree possible of an affirmation |
| 2, 4, 6, 8 | Intermediate | Used to represent compromises between the preferences in weights1, 3, 5, 7 and 9 |
| Reciprocals | Opposites | Used for inverse comparison |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.44 | 1.00 | 1.63 | 2.30 | 3.00 | 3.73 | 4.47 | 5.23 |
| Linguistic Terms | Saaty’s Scale | Picture Fuzzy Numbers (PFNs) |
|---|---|---|
| Very High Importance | 7 | (0.9, 0.0, 0.05) |
| High Importance | 5 | (0.75, 0.05, 0.1) |
| Slightly More Importance | 3 | (0.6, 0.0, 0.3) |
| Equally Importance | 1 | (0.5, 0.1, 0.4) |
| Slightly Low Importance | 1/3 | (0.3, 0.0, 0.6) |
| Low Importance | 1/5 | (0.25, 0.05, 0.6) |
| Very Low Importance | 1/7 | (0.1, 0.0, 0.85) |
| Criteria | ||||
|---|---|---|---|---|
| Alternative | C1 | C2 | … | Cn |
| A1 | … | |||
| A2 | … | |||
| … | … | … | … | … |
| Am | … | |||
| Criteria | ||||
|---|---|---|---|---|
| Alternative | C1 | C2 | … | Cn |
| A1 | … | |||
| A2 | … | |||
| … | … | … | … | … |
| Am | … | |||
| Rank | ||||
| Alternative | 1st | 2st | … | mth |
| A1 | … | |||
| A2 | … | |||
| … | … | … | … | … |
| Am | … | |||
| Rank | ||||
|---|---|---|---|---|
| Alternative | 1st | 2st | … | mth |
| A1 | … | |||
| A2 | … | |||
| … | … | … | … | … |
| Am | … | |||
| Flood-Related Criteria | Flood-Related Criteria | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sub-Watershed | Slope | TCI | Entropy | Cc | SPI | Sub-Watershed | Slope | TCI | Entropy | Cc | SPI |
| 1 | 19.72 | −1.05 | 0.08 | 1.82 | −2.73 | 14 | 15.69 | −1.10 | 0.14 | 2.11 | −3.47 |
| 2 | 21.31 | −1.18 | 0.13 | 1.80 | −2.97 | 15 | 40.65 | −1.29 | 0.14 | 1.88 | −1.47 |
| 3 | 12.22 | −0.89 | 0.14 | 2.11 | −3.64 | 16 | 17.24 | −0.98 | 0.08 | 2.50 | −3.12 |
| 4 | 12.53 | −0.97 | 0.14 | 1.93 | −3.73 | 17 | 24.01 | −1.18 | 0.11 | 1.72 | −2.66 |
| 5 | 23.98 | −1.20 | 0.09 | 2.78 | −2.80 | 18 | 25.45 | −1.08 | 0.09 | 1.58 | −2.22 |
| 6 | 21.26 | −1.06 | 0.03 | 2.19 | −2.78 | 19 | 21.30 | −1.10 | 0.14 | 2.30 | −2.76 |
| 7 | 15.63 | −0.82 | 0.13 | 2.13 | −3.04 | 20 | 20.52 | −1.18 | 0.13 | 2.42 | −3.16 |
| 8 | 14.28 | −0.86 | 0.12 | 1.93 | −3.26 | 21 | 28.34 | −1.14 | 0.12 | 2.24 | −2.10 |
| 9 | 26.78 | −1.26 | 0.12 | 2.31 | −2.49 | 22 | 24.50 | −1.12 | 0.03 | 1.75 | −2.62 |
| 10 | 16.21 | −1.14 | 0.11 | 2.34 | −3.45 | 23 | 20.14 | −1.16 | 0.14 | 1.84 | −3.03 |
| 11 | 26.36 | −1.11 | 0.14 | 2.41 | −2.81 | 24 | 28.25 | −1.22 | 0.12 | 2.11 | −2.38 |
| 12 | 13.05 | −0.81 | 0.14 | 2.00 | −3.29 | 25 | 20.66 | −1.02 | 0.14 | 2.14 | −2.80 |
| 13 | 13.54 | −0.90 | 0.14 | 2.07 | −3.59 | ||||||
| AHP Method | BWM Method | IRN AHP Method | |||||
|---|---|---|---|---|---|---|---|
| Criteria | Wi (Expert #1) | Wi (Expert #2) | Wi (Expert #3) | Wi (Expert #1) | Wi (Expert #2) | Wi (Expert #3) | |
| Entropy | 0.488 | 0.593 | 0.391 | 0.487 (Best) | 0.475 (Best) | 0.423 (Best) | [0.46, 0.48], [0.5, 0.52] |
| SPI | 0.228 | 0.244 | 0.215 | 0.189 | 0.188 | 0.231 | [0.21, 0.22], [0.22, 0.23] |
| TCI | 0.142 | 0.150 | 0.163 | 0.142 | 0.141 | 0.115 | [0.15, 0.15], [0.15, 0.16] |
| Slope | 0.087 | 0.084 | 0.099 | 0.114 | 0.141 | 0.154 | [0.06, 0.07], [0.09, 0.09] |
| Cc | 0.056 | 0.044 | 0.053 | 0.068 (worst) | 0.055 (worst) | 0.077 (worst) | [0.03, 0.03], [0.05, 0.05] |
| Consistently | 0.02 | 0.07 | 0.05 | 0.081 | 0.088 | 0.038 | (expert #1) 0.06 (expert #2) 0.079 (expert #3) 0.1 |
| Criteria | Local Weight | Global Weight | Final Weight | Deffuzification (Score) | |
|---|---|---|---|---|---|
| Expert #1 | En | (0.76, 0.24, 0.14) | (0.85, 0.4, 0.08) | (0.73, 0.05, 0.12) | 1.31 |
| Expert #2 | (0.86, 0.14, 0.005) | ||||
| Expert #3 | (0.7, 0.3, 0.2) | ||||
| Expert #1 | SPI | (0.7, 0.3, 0.2) | (0.81, 0.48, 0.12) | (0.64, 0.09, 0.21) | 1.03 |
| Expert #2 | (0.76, 0.24, 0.14) | ||||
| Expert #3 | (0.65, 0.35, 0.24) | ||||
| Expert #1 | TCI | (0.65, 0.34, 0.24) | (0.77, 0.53, 0.16) | (0.5, 0.18, 0.36) | 0.55 |
| Expert #2 | (0.7, 0.3, 0.2) | ||||
| Expert #3 | (0.6, 0.4, 0.3) | ||||
| Expert #1 | Slope | (0.6, 0.4, 0.3) | (0.74, 0.56, 0.19) | (0.51, 0.16, 0.35) | 0.59 |
| Expert #2 | (0.65, 0.34, 0.24) | ||||
| Expert #3 | (0.55, 0.45, 0.35) | ||||
| Expert #1 | Cc | (0.5, 0.4, 0.6) | (0.67, 0.58, 0.25) | (0.4, 0.23, 0.47) | 0.21 |
| Expert #2 | (0.55, 0.4, 0.35) | ||||
| Expert #3 | (0.5, 0.4, 0.6) |
| Sub-Watershed | Entropy | SPI | TCI | Slope | Cc |
|---|---|---|---|---|---|
| 0 | (0.95, 0.52, 0.02) | (0.94, 0.64, 0.03) | (0.9, 0.69, 0.07) | (0.91, 0.48, 0.04) | (0.84, 0.56, 0.1) |
| 1 | (0.99, 0.89, 0.002) | (0.95, 0.71, 0.02) | (0.95, 0.84, 0.029) | (0.86, 0.6, 0.08) | (0.78, 0.64, 0.15) |
| 2 | (0.99, 0.94, 0.001) | (0.99, 0.95, 0.002) | (0.83, 0.54, 0.1) | (0.8, 0.47, 0.12) | (0.84, 0.73, 0.11) |
| 3 | (0.99, 0.99, 0.00) | (1, 1, 0.00) | (0.83, 0.64, 0.11) | (0.82, 0.47, 0.12) | (0.80, 0.67, 0.14) |
| 4 | (0.95, 0.6, 0.01) | (0.94, 0.66, 0.02) | (0.96, 0.86, 0.002) | (0.88, 0.65, 0.07) | (0.99, 0.99, 0.00) |
| . | … | … | … | … | … |
| . | … | … | … | … | … |
| . | … | … | … | … | … |
| 26 | (0.97, 0.75, 0.007) | (0.90, 0.48, 0.04) | (0.95, 0.72, 0.2) | (0.92, 0.69, 0.04) | (0.89, 0.75, 0.07) |
| 27 | (0.9, 0.3, 0.03) | (0.93, 0.61, 0.029) | (0.92, 0.76, 0.04) | (0.92, 0.56, 0.03) | (0.83, 0.53, 0.1) |
| 28 | (0.99, 0.99, 0.00) | (0.95, 0.73, 0.019) | (0.93, 0.84, 0.04) | (0.85, 0.58, 0.09) | (0.82, 0.6, 0.12) |
| 29 | (0.97, 0.77, 0.00) | (0.92, 0.55, 0.03) | (0.95, 0.90, 0.02) | (0.91, 0.7, 0.05) | (0.85, 0.71, 0.09) |
| 30 | (0.97, 0.77, 0.00) | (0.92, 0.55, 0.03) | (0.96, 0.89, 0.02) | (0.91, 0.7, 0.05) | (0.84, 0.73, 0.1) |
| Sub-Watersheds | 1th | 2th | 3th | 4th | 5th | 6th | 7th | 17th | 18th | 19th | 20th | 21th | 22th | 23th | 24th | 25th | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.00 | 0.59 | 2.34 | 0.00 | 0.00 | 0.00 | 0.00 | … | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 1 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | … | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.22 | 0.00 | 0.00 |
| 2 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | … | 1.53 | 0.00 | 0.55 | 0.00 | 0.00 | 0.00 | 0.00 | 1.03 | 0.59 |
| 3 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | … | 0.00 | 0.59 | 0.00 | 0.00 | 0.77 | 0.00 | 1.31 | 0.00 | 1.03 |
| 4 | 0.22 | 0.00 | 0.00 | 0.00 | 0.00 | 1.31 | 1.03 | … | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 5 | 1.31 | 0.00 | 0.00 | 0.81 | 0.00 | 1.03 | 0.00 | … | 0.00 | 0.55 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 25 | 0.00 | 0.00 | 0.77 | 0.00 | 0.00 | 0.00 | 0.00 | … | 1.03 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 26 | 0.55 | 0.00 | 0.00 | 0.00 | 0.00 | 0.59 | 0.22 | … | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 27 | 1.63 | 1.31 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | … | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 28 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | … | 0.59 | 0.00 | 0.00 | 0.00 | 0.00 | 1.31 | 0.00 | 0.00 | 0.00 |
| 29 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | … | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 30 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | … | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Sub-Watersheds | 1th | 2th | 3th | 4th | 5th | 6th | 7th | 17th | 18th | 19th | 20th | 21th | 22th | 23th | 24th | 25th | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | … | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | … | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | … | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | … | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 4 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | … | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | … | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 25 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | … | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 26 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | … | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 27 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | … | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 28 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | … | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 29 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | … | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 30 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | … | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, N.-M.; Bahramloo, R.; Sadeghian, J.; Sepehri, M.; Nazaripouya, H.; Nguyen Dinh, V.; Ghahramani, A.; Talebi, A.; Elkhrachy, I.; Pande, C.B.; et al. Ranking Sub-Watersheds for Flood Hazard Mapping: A Multi-Criteria Decision-Making Approach. Water 2023, 15, 2128. https://doi.org/10.3390/w15112128
Nguyen N-M, Bahramloo R, Sadeghian J, Sepehri M, Nazaripouya H, Nguyen Dinh V, Ghahramani A, Talebi A, Elkhrachy I, Pande CB, et al. Ranking Sub-Watersheds for Flood Hazard Mapping: A Multi-Criteria Decision-Making Approach. Water. 2023; 15(11):2128. https://doi.org/10.3390/w15112128
Chicago/Turabian StyleNguyen, Nguyet-Minh, Reza Bahramloo, Jalal Sadeghian, Mehdi Sepehri, Hadi Nazaripouya, Vuong Nguyen Dinh, Afshin Ghahramani, Ali Talebi, Ismail Elkhrachy, Chaitanya B. Pande, and et al. 2023. "Ranking Sub-Watersheds for Flood Hazard Mapping: A Multi-Criteria Decision-Making Approach" Water 15, no. 11: 2128. https://doi.org/10.3390/w15112128
APA StyleNguyen, N.-M., Bahramloo, R., Sadeghian, J., Sepehri, M., Nazaripouya, H., Nguyen Dinh, V., Ghahramani, A., Talebi, A., Elkhrachy, I., Pande, C. B., & Meshram, S. G. (2023). Ranking Sub-Watersheds for Flood Hazard Mapping: A Multi-Criteria Decision-Making Approach. Water, 15(11), 2128. https://doi.org/10.3390/w15112128







