Simulation and Dynamic Properties Analysis of the Anaerobic–Anoxic–Oxic Process in a Wastewater Treatment PLANT Based on Koopman Operator and Deep Learning
Abstract
:1. Introduction
2. Materials and Methods
2.1. Case Study and Data
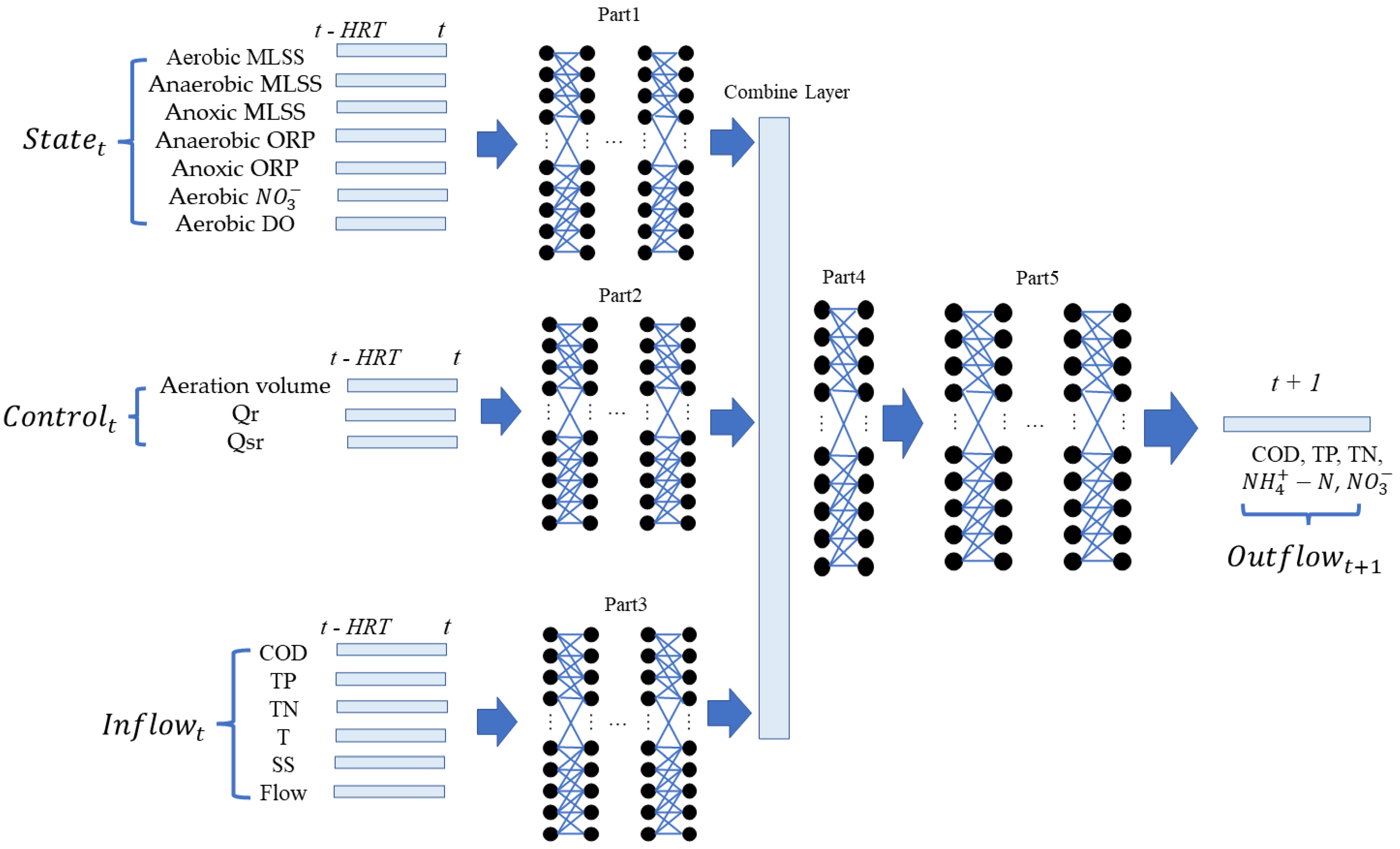
2.2. Deep Learning for A2O Process Simulation and Prediction
2.3. Koopman Operator and Deep Learning for A2O Process Simulation and Prediction
2.3.1. Dynamic System and the Koopman Operator
2.3.2. Dictionary Learning-Based Extended Dynamic Mode Decomposition
2.4. Dynamic Properties Analysis Based on Koopman Operator
3. Results and Discussion
3.1. Training Process of DNN and DLEDMD
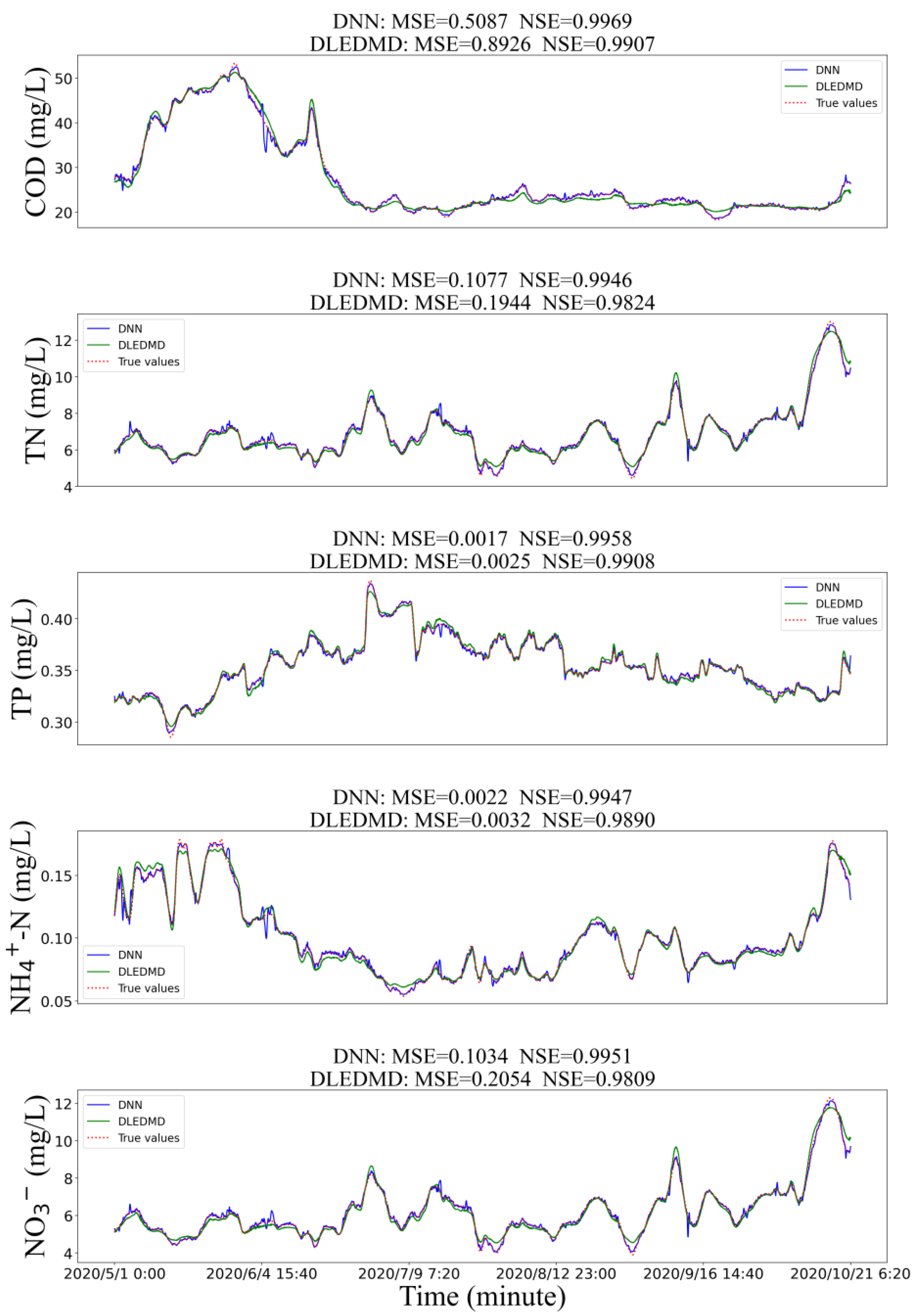
3.2. Simulation Performance
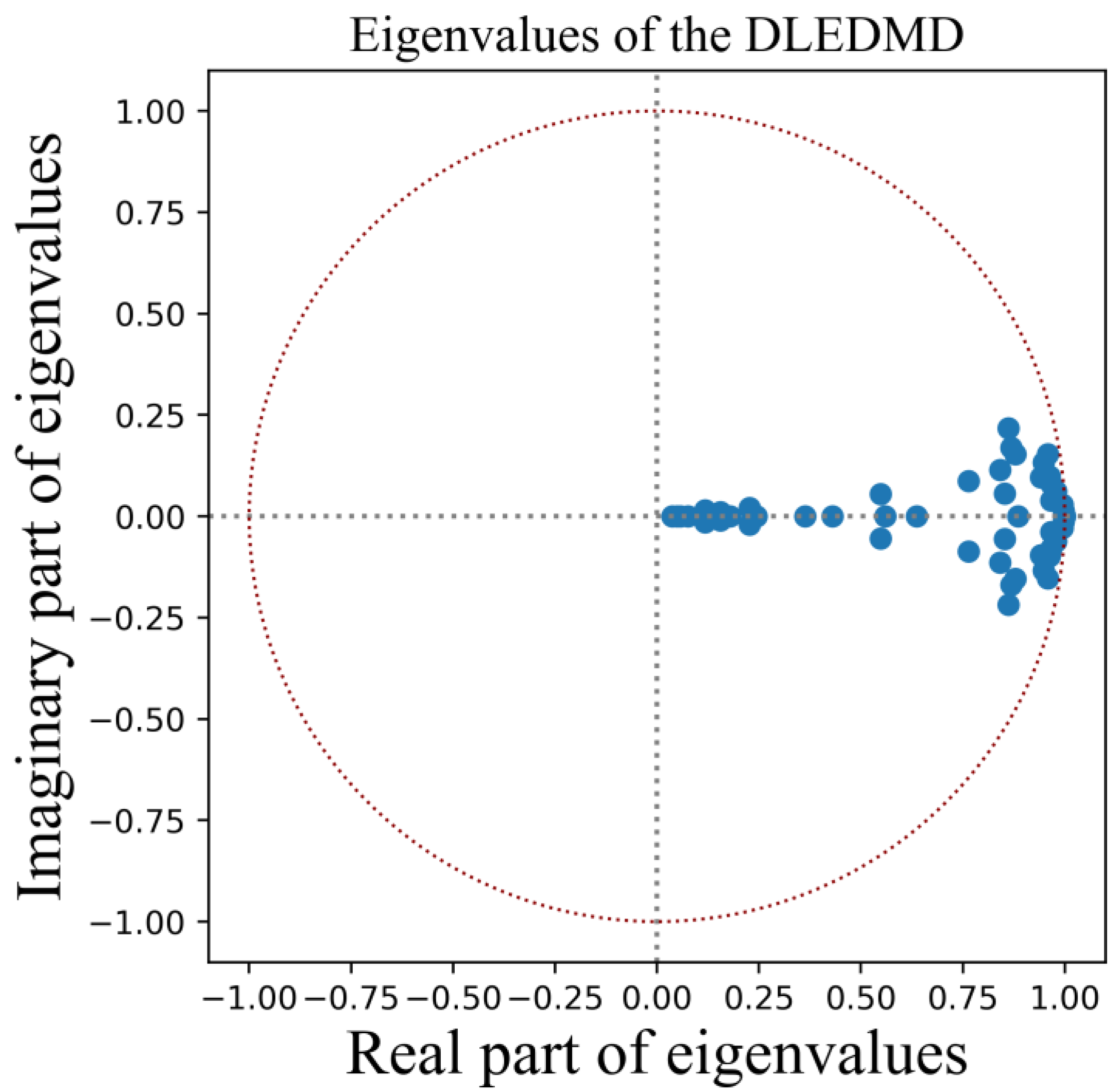
3.3. Eigenvalues of Koopman Matrix and Asymptotically Stablility of A2O Dynamic
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, K.; Wang, H.; Valverde-Pérez, B.; Zhai, S.; Vezzaro, L.; Wang, A. Optimal control towards sustainable wastewater treatment plants based on multi-agent reinforcement learning. Chemosphere 2021, 279, 130498. [Google Scholar] [CrossRef] [PubMed]
- Holenda, B.; Domokos, E.; Rédey, A.; Fazakas, J. Dissolved oxygen control of the activated sludge wastewater treatment process using model predictive control. Comput. Chem. Eng. 2008, 32, 1270–1278. [Google Scholar] [CrossRef]
- Liu, X.; Jing, Y.; Xu, J.; Zhang, S. Ammonia Control of a Wastewater Treatment Process Using Model Predictive Control. In Proceedings of the 26th Chinese Control and Decision Conference (2014 CCDC), Changsha, China, 31 May–2 June 2014; pp. 494–498. [Google Scholar]
- Elawwad, A.; Zaghloul, M.; Abdel-Halim, H. Simulation of municipal-industrial full scale WWTP in an arid climate by application of ASM3. J. Water Reuse Desalin. 2016, 7, 37–44. [Google Scholar] [CrossRef]
- Henze, M.; Gujer, W.; Mino, T.; van Loosdrecht, M. Activated Sludge Models ASM1, ASM2, ASM2d and ASM3; IWA Publishing: London, UK, 2000. [Google Scholar]
- Mulas, M.; Tronci, S.; Corona, F.; Haimi, H.; Lindell, P.; Heinonen, M.; Vahala, R.; Baratti, R. Predictive control of an activated sludge process: An application to the Viikinmäki wastewater treatment plant. J. Process. Control. 2015, 35, 89–100. [Google Scholar] [CrossRef]
- Guo, H.; Jeong, K.; Lim, J.; Jo, J.; Kim, Y.M.; Park, J.-P.; Kim, J.H.; Cho, K.H. Prediction of effluent concentration in a wastewater treatment plant using machine learning models. J. Environ. Sci. 2015, 32, 90–101. [Google Scholar] [CrossRef] [PubMed]
- Antwi, P.; Zhang, D.; Xiao, L.; Kabutey, F.T.; Quashie, F.K.; Luo, W.; Meng, J.; Li, J. Modeling the performance of Single-stage Nitrogen removal using Anammox and Partial nitritation (SNAP) process with backpropagation neural network and response surface methodology. Sci. Total. Environ. 2019, 690, 108–120. [Google Scholar] [CrossRef]
- Khatri, N.; Khatri, K.K.; Sharma, A. Prediction of effluent quality in ICEAS-sequential batch reactor using feedforward artificial neural network. Water Sci. Technol. 2019, 80, 213–222. [Google Scholar] [CrossRef]
- Hansen, L.D.; Stokholm-Bjerregaard, M.; Durdevic, P. Modeling phosphorous dynamics in a wastewater treatment process using Bayesian optimized LSTM. Comput. Chem. Eng. 2022, 160, 107738. [Google Scholar] [CrossRef]
- Liu, H.; Wang, Y.; Fan, W.; Liu, X.; Li, Y.; Jain, S.; Liu, Y.; Jain, A.K.; Tang, J. Trustworthy AI: A Computational Perspective. ACM Trans. Intell. Syst. Technol. 2022, 14, 4. [Google Scholar] [CrossRef]
- Samek, W.; Montavon, G.; Lapuschkin, S.; Anders, C.J.; Muller, K.-R. Explaining Deep Neural Networks and Beyond: A Review of Methods and Applications. Proc. IEEE 2021, 109, 247–278. [Google Scholar] [CrossRef]
- Anders, C.J.; Weber, L.; Neumann, D.; Samek, W.; Müller, K.-R.; Lapuschkin, S. Finding and removing Clever Hans: Using explanation methods to debug and improve deep models. Inf. Fusion 2022, 77, 261–295. [Google Scholar] [CrossRef]
- Fu, G.; Jin, Y.; Sun, S.; Yuan, Z.; Butler, D. The role of deep learning in urban water management: A critical review. Water Res. 2022, 223, 118973. [Google Scholar] [CrossRef]
- Kozlov, V.; Furta, S. Lyapunov’s first method for strongly non-linear systems. J. Appl. Math. Mech. 1996, 60, 7–18. [Google Scholar] [CrossRef]
- Datta, B.N. Chapter 7—Stability, inertia, and robust stability. In Numerical Methods for Linear Control Systems; Datta, B.N., Ed.; Academic Press: Cambridge, MA, USA, 2004; pp. 201–243. [Google Scholar]
- De Santis, E.; Di Benedetto, M.; Pola, G. Stabilizability of linear switching systems. Nonlinear Anal. Hybrid Syst. 2008, 2, 750–764. [Google Scholar] [CrossRef]
- Tu, J.H.; Rowley, C.W.; Luchtenburg, D.M.; Brunton, S.L.; Kutz, J.N. On dynamic mode decomposition: Theory and applications. J. Comput. Dyn. 2014, 1, 391–421. [Google Scholar] [CrossRef]
- Mardt, A.; Pasquali, L.; Wu, H.; Noé, F. VAMPnets for deep learning of molecular kinetics. Nat. Commun. 2018, 9, 5. [Google Scholar] [CrossRef] [PubMed]
- Montavon, G.; Lapuschkin, S.; Binder, A.; Samek, W.; Müller, K.-R. Explaining nonlinear classification decisions with deep Taylor decomposition. Pattern Recognit. 2017, 65, 211–222. [Google Scholar] [CrossRef]
- Zhang, Y.; Tino, P.; Leonardis, A.; Tang, K. A Survey on Neural Network Interpretability. IEEE Trans. Emerg. Top. Comput. Intell. 2021, 5, 726–742. [Google Scholar] [CrossRef]
- Budišić, M.; Mohr, R.M.; Mezić, I. Applied Koopmanism. Chaos Interdiscip. J. Nonlinear Sci. 2012, 22, 047510. [Google Scholar] [CrossRef]
- Williams, M.O.; Rowley, C.W.; Mezić, I.; Kevrekidis, I.G. Data fusion via intrinsic dynamic variables: An application of data-driven Koopman spectral analysis. Europhys. Lett. 2015, 109, 40007. [Google Scholar] [CrossRef]
- Bistrian, D.A.; Navon, I.M. An improved algorithm for the shallow water equations model reduction: Dynamic Mode Decomposition vs Pod: An Improved Algorithm for Dynamic Mode Decomposition vs Pod. Int. J. Numer. Methods Fluids 2015, 78, 552–580. [Google Scholar] [CrossRef]
- Bistrian, D.A.; Navon, I.M. The method of dynamic mode decomposition in shallow water and a swirling flow problem: The Dmd Method in Shallow Water and a Swirling Flow Problem. Int. J. Numer. Methods Fluids 2017, 83, 73–89. [Google Scholar] [CrossRef]
- Korda, M.; Mezić, I. Linear predictors for nonlinear dynamical systems: Koopman operator meets model predictive control. Automatica 2018, 93, 149–160. [Google Scholar] [CrossRef]
- Han, Y.; Hao, W.; Vaidya, U. Deep Learning of Koopman Representation for Control. In Proceedings of the 2020 59th IEEE Conference on Decision and Control (CDC), Jeju Island, Republic of Korea, 14–18 December 2020; pp. 1890–1895. [Google Scholar]
- Son, S.H.; Choi, H.-K.; Moon, J.; Kwon, J.S.-I. Hybrid Koopman model predictive control of nonlinear systems using multiple EDMD models: An application to a batch pulp digester with feed fluctuation. Control. Eng. Pract. 2021, 118, 104956. [Google Scholar] [CrossRef]
- Page, J.; Kerswell, R.R. Koopman analysis of Burgers equation. Phys. Rev. Fluids 2018, 3, 071901. [Google Scholar] [CrossRef]
- Klus, S.; Nüske, F.; Koltai, P.; Wu, H.; Kevrekidis, I.; Schütte, C.; Noé, F. Data-Driven Model Reduction and Transfer Operator Approximation. J. Nonlinear Sci. 2018, 28, 985–1010. [Google Scholar] [CrossRef]
- Tian, W.; Wu, H. Kernel Embedding Based Variational Approach for Low-Dimensional Approximation of Dynamical Systems. Comput. Methods Appl. Math. 2021, 21, 635–659. [Google Scholar] [CrossRef]
- Williams, M.O.; Kevrekidis, I.G.; Rowley, C.W. A Data-Driven Approximation of the Koopman Operator: Extending Dynamic Mode Decomposition. J. Nonlinear Sci. 2015, 25, 1307–1346. [Google Scholar] [CrossRef]
- Felix, D.; Dietrich, F.; Bollt, E.M.; Kevrekidis, I.G. Extended dynamic mode decomposition with dictionary learning: A data-driven adaptive spectral decomposition of the Koopman operator. Chaos Interdiscip. J. Nonlinear Sci. 2017, 27, 103111. [Google Scholar]
- Tian, W.; Liao, Z.; Zhang, Z.; Wu, H.; Xin, K. Flooding and Overflow Mitigation Using Deep Reinforcement Learning Based on Koopman Operator of Urban Drainage Systems. Water Resour. Res. 2022, 58, e2021WR030939. [Google Scholar] [CrossRef]
- Sengupta, S.; Nawaz, T.; Beaudry, J. Nitrogen and Phosphorus Recovery from Wastewater. Curr. Pollut. Rep. 2015, 1, 155–166. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Peitz, S.; Klus, S. Koopman operator-based model reduction for switched-system control of PDEs. Automatica 2019, 106, 184–191. [Google Scholar] [CrossRef]
- Junge, O.; Koltai, P. Discretization of the Frobenius–Perron Operator Using a Sparse Haar Tensor Basis: The Sparse Ulam Method. SIAM J. Numer. Anal. 2009, 47, 3464–3485. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Wu, H.; Noé, F. Variational Approach for Learning Markov Processes from Time Series Data. J. Nonlinear Sci. 2019, 30, 23–66. [Google Scholar] [CrossRef]


| Data Name and Unit | Type | Maximum | Minimum | Average | Median |
|---|---|---|---|---|---|
| Aerobic MLSS (g/L) | State | 5.733 | 2.515 | 3.878 | 3.975 |
| Anaerobic MLSS (g/L) | 6.111 | 0.774 | 3.455 | 3.505 | |
| Anoxic MLSS (g/L) | 6.405 | 2.861 | 3.966 | 3.873 | |
| Anaerobic ORP | −226.223 | −480.649 | −421.539 | −447.093 | |
| Anoxic ORP | −20.668 | −244.451 | −98.212 | −93.690 | |
| Aerobic (mg/L) | 32.873 | 1.546 | 9.287 | 3.348 | |
| Aerobic DO (mg/L) | 7.150 | 0.803 | 3.109 | 3.015 | |
| Aeration volume (m3/min) | Control | 29.755 | 18.277 | 23.892 | 23.961 |
| Qr (m3/s) | 2.332 | 0.906 | 1.915 | 1.962 | |
| Qsr (m3/s) | 5.534 | 4.399 | 4.834 | 4.815 | |
| COD (mg/L) | Influent/ Inflow | 650.329 | 49.315 | 270.051 | 229.321 |
| TN (mg/L) | 44.354 | 3.579 | 26.233 | 26.345 | |
| TP (mg/L) | 7.950 | 0.185 | 3.514 | 3.448 | |
| T (°C) | 30.922 | 21.351 | 26.054 | 26.386 | |
| SS (mg/L) | 67.341 | 0.000 | 7.506 | 3.789 | |
| Flow (m3/s) | 3.203 | 1.144 | 2.587 | 2.628 | |
| COD (mg/L) | Effluent/ Outflow | 53.355 | 18.252 | 27.431 | 22.983 |
| TN (mg/L) | 13.011 | 4.428 | 6.909 | 6.594 | |
| TP (mg/L) | 0.437 | 0.285 | 0.354 | 0.353 | |
| (mg/L) | 0.179 | 0.054 | 0.100 | 0.091 | |
| (mg/L) | 12.286 | 3.898 | 6.232 | 5.904 |
| Architecture | Activation Function | |
|---|---|---|
| Part1 (State) | -50-50-50 | |
| Part2 (Control) | -50-50-50 | |
| Part3 (Inflow) | -50-50-50 | |
| Part4 (Encoding) | 50-50-50-50 | |
| Part5 (Outflow) | 50-50-5 |
| Architecture | Activation Function | |
|---|---|---|
| Part1 (State) | -50-50-50 | |
| Part2 (Control) | -50-50-50 | |
| Part3 (Inflow) | -50-50-50 | |
| Part4 (Encoding) | 50-50-50-50 | |
| Part5 (Outflow) | 50-50-5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, W.; Liu, Y.; Xie, J.; Huang, W.; Chen, W.; Tao, T.; Xin, K. Simulation and Dynamic Properties Analysis of the Anaerobic–Anoxic–Oxic Process in a Wastewater Treatment PLANT Based on Koopman Operator and Deep Learning. Water 2023, 15, 1960. https://doi.org/10.3390/w15101960
Tian W, Liu Y, Xie J, Huang W, Chen W, Tao T, Xin K. Simulation and Dynamic Properties Analysis of the Anaerobic–Anoxic–Oxic Process in a Wastewater Treatment PLANT Based on Koopman Operator and Deep Learning. Water. 2023; 15(10):1960. https://doi.org/10.3390/w15101960
Chicago/Turabian StyleTian, Wenchong, Yuting Liu, Jun Xie, Weizhong Huang, Weihao Chen, Tao Tao, and Kunlun Xin. 2023. "Simulation and Dynamic Properties Analysis of the Anaerobic–Anoxic–Oxic Process in a Wastewater Treatment PLANT Based on Koopman Operator and Deep Learning" Water 15, no. 10: 1960. https://doi.org/10.3390/w15101960




