Flood-Triggering Rainfall and Potential Losses—The Copula-Based Approach on the Example of the Upper Nysa Kłodzka River
Abstract
1. Introduction
2. Study Area, Materials and Methods
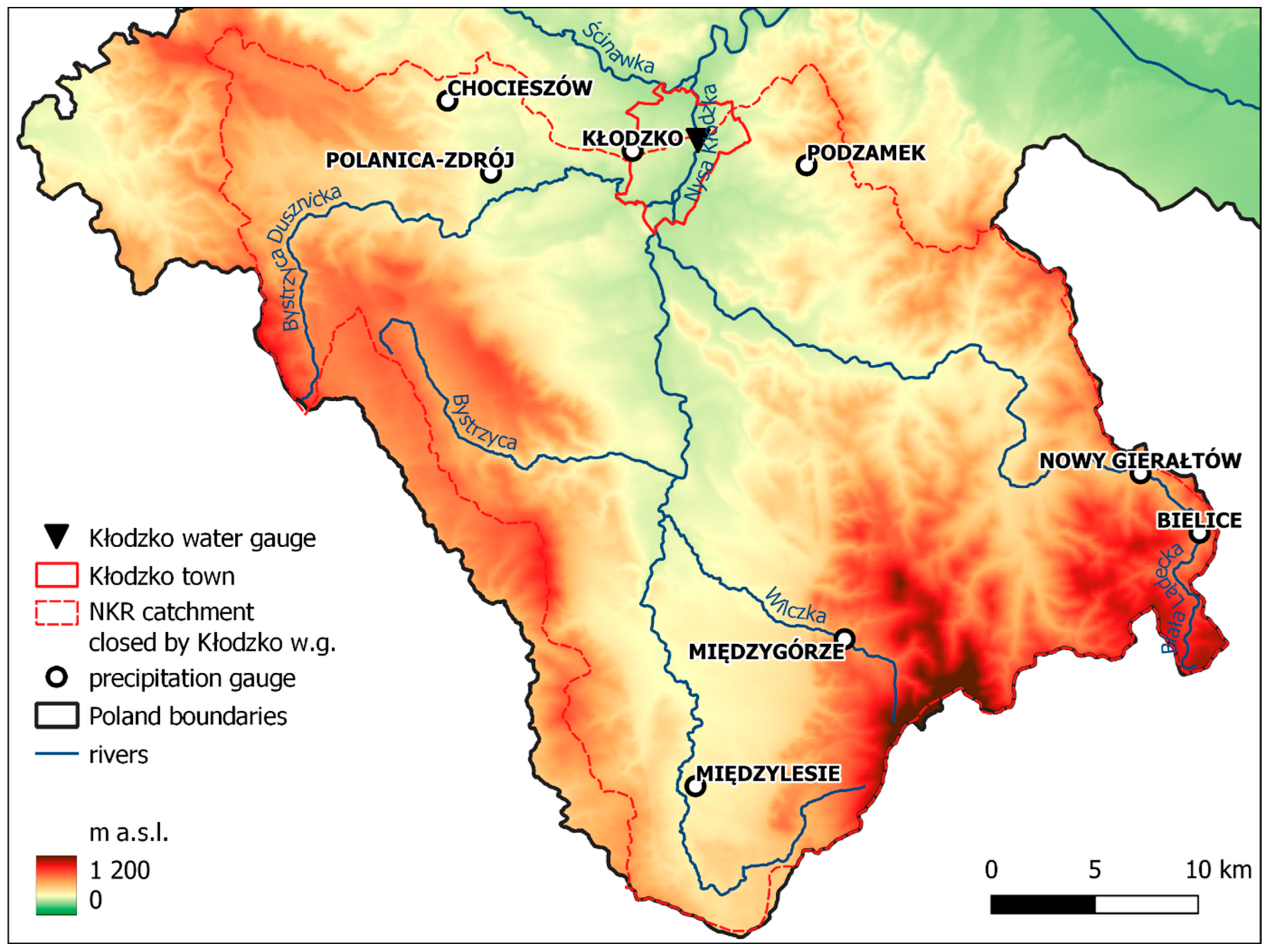
2.1. Study Area
2.2. Data
2.3. Methods
2.3.1. Selection of Significant Floods and Rainfall Data Preparation
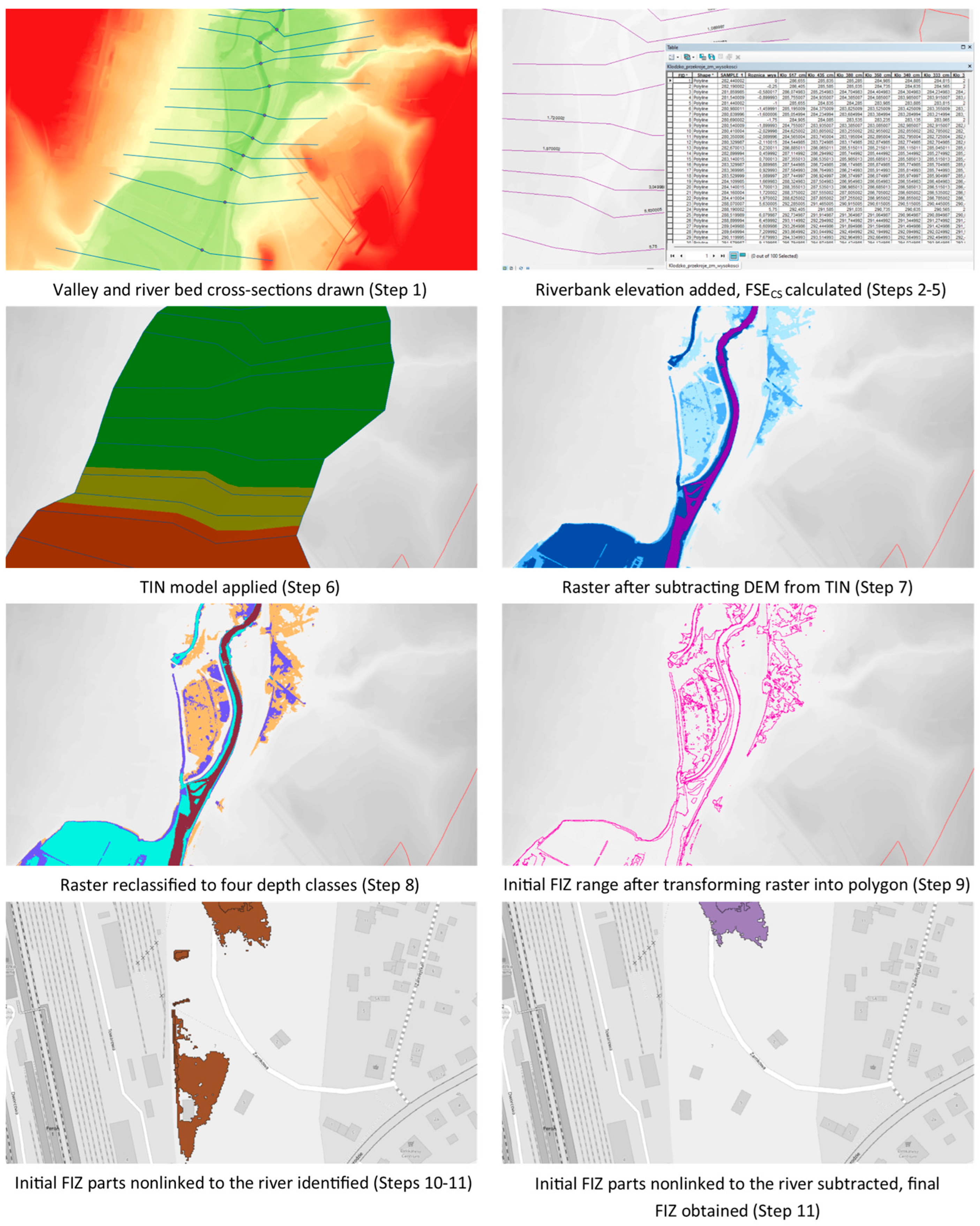
2.3.2. Estimation of FIZ Range
- The river-valley and river-bed cross-sections were drawn (for NKR and its tributaries within the Kłodzko town boundaries).
- For each cross-section, elevation of the riverbank from DEM was added.
- For Kłodzko water-gauge cross-section, values of H were added.
- The differences between Kłodzko water-gauge elevation and elevations of other cross-sections were calculated.
- FSE in each cross-section (FSECS) was calculated with the use of formula (Equation (1)):where d—difference between elevation of the water-gauge cross-section and the given cross-section (“+” for cross-sections upstream, “−“ for cross-sections downstream).FSECS = H + d
- To obtain FIZ, the triangulated irregular network (TIN) model was applied to interpolate floodwater surface for each H.
- TIN was transformed into raster, and DEM was subtracted from it.
- The obtained raster was reclassified according to four depth classes (see Section 2.3.3 for details).
- The reclassified raster was transformed into polygon layer presenting initial FIZ range and FWD.
- The range of initial FIZ was limited to the administrative boundaries of the Kłodzko town.
- The final FIZ was obtained by subtracting the FIZ parts not linked to the river (e.g., behind dikes or naturally lower than the river) and riverbeds area from the polygon layer.
2.3.3. Estimation of PFL
2.3.4. Estimation of Distribution Parameters
2.3.5. Application of Copulas
- Moderate asynchronicity representing “low–medium”, “medium–low”, “medium–high” and “high–medium” relation types (sectors Nos. 2, 4, 6, 8).
- High asynchronicity, representing “high–low” and “low–high” relation types (sectors No. 3 and 7).
- LoR/LoPFL describing the probable values with a probability of exceedance >62.5%;
- MeR/MePFL describing the probable values with a probability of exceedance in a range <62.5% and >37.5%;
- HiR/HiPFL describing the probable values with a probability of exceedance <37.5%.
3. Results
3.1. Selected Flood Events
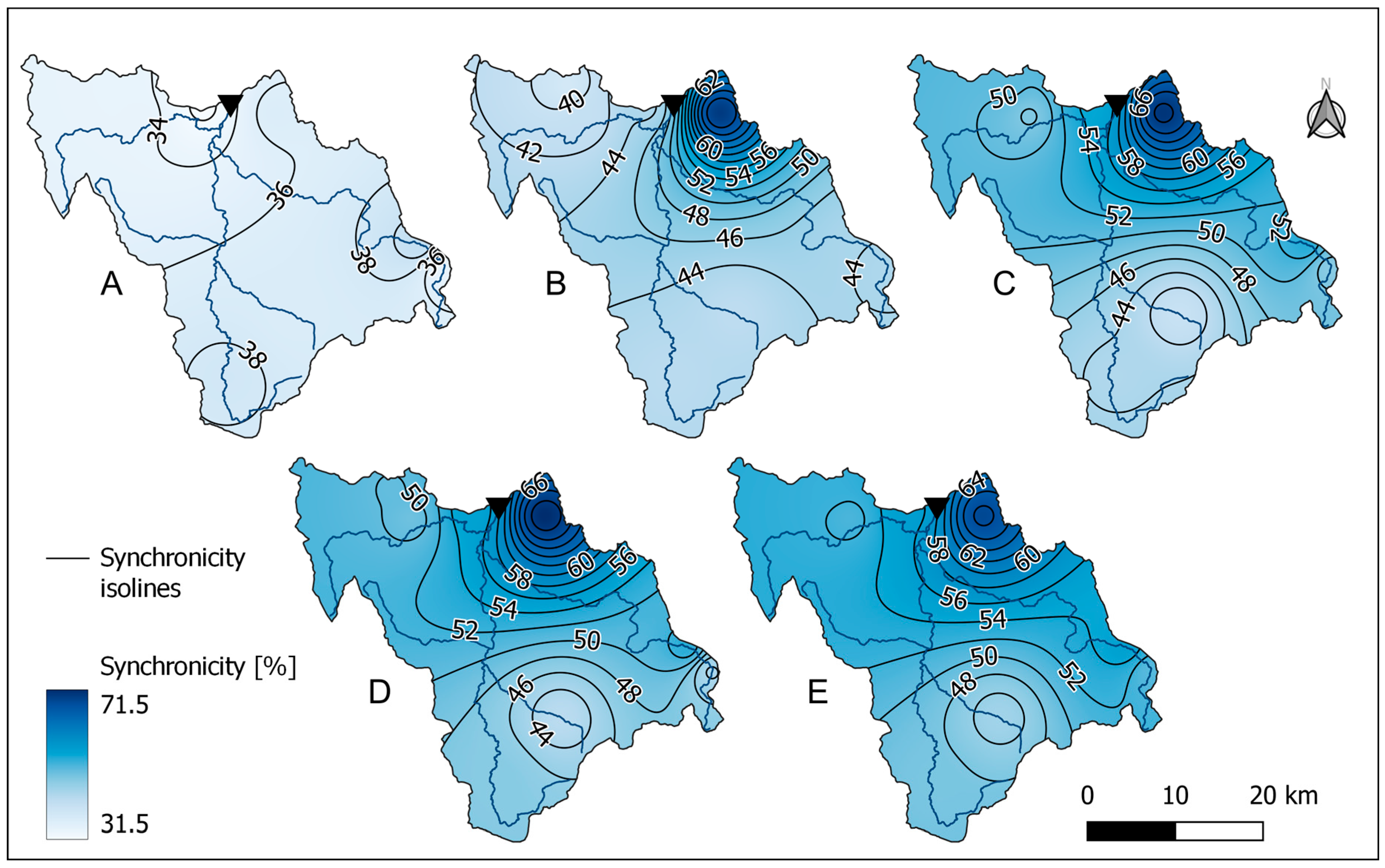
3.2. Synchronicity of Rainfall and PFL
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- European Parliament. FD 2007/60/EC, Directive of the European Parliament and Council of 23 October, 2007 on the Assessment and Management of Flood Risks, Official Journal L 288, 6 November 2007. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:32019L1937 (accessed on 10 February 2023).
- Graf, R. Flood risk management system in Poland. In Management of Water Resources in Poland; Zeleňáková, M., Kubiak-Wójcicka, K., Negm, A.M., Eds.; Springer Water: Cham, Switzerland, 2021; pp. 281–304. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Hegger, D.L.T.; Matczak, P.; Driessen, P.P.J. Flood-Risk Reduction: Structural Measures and Diverse Strategies. Proc. Natl. Acad. Sci. USA 2018, 115, 12321–12325. [Google Scholar] [CrossRef] [PubMed]
- Matczak, P.; Hegger, D. Improving Flood Resilience through Governance Strategies: Gauging the State of the Art. Wiley Interdiscip. Rev. Water 2021, 8, e1532. [Google Scholar] [CrossRef]
- Driessen, P.P.J.; Hegger, D.L.T.; Kundzewicz, Z.W.; van Rijswick, H.F.M.W.; Crabbé, A.; Larrue, C.; Matczak, P.; Pettersson, M.; Priest, S.; Suykens, C.; et al. Governance Strategies for Improving Flood Resilience in the Face of Climate Change. Water 2018, 10, 1595. [Google Scholar] [CrossRef]
- Blöschl, G.; Kiss, A.; Viglione, A.; Barriendos, M.; Böhm, O.; Brázdil, R.; Coeur, D.; Demarée, G.; Llasat, M.C.; Macdonald, N.; et al. Current European Flood-Rich Period Exceptional Compared with Past 500 Years. Nature 2020, 583, 560–566. [Google Scholar] [CrossRef]
- Fang, G.; Yang, J.; Li, Z.; Chen, Y.; Duan, W.; Amory, C.; Maeyer, P.D. Shifting in the Global Flood Timing. Sci. Rep. 2022, 12, 18853. [Google Scholar] [CrossRef]
- Paprotny, D.; Sebastian, A.; Morales-Nápoles, O.; Jonkman, S.N. Trends in Flood Losses in Europe over the Past 150 Years. Nat. Commun. 2018, 9, 1985. [Google Scholar] [CrossRef]
- Lehner, B.; Döll, P.; Alcamo, J.; Henrichs, T.; Kaspar, F. Estimating the Impact of Global Change on Flood and Drought Risks in Europe: A Continental, Integrated Analysis. Clim. Chang. 2006, 75, 273–299. [Google Scholar] [CrossRef]
- Dankers, R.; Feyen, L. Climate Change Impact on Flood Hazard in Europe: An Assessment Based on High-resolution Climate Simulations. J. Geophys. Res. Atmos. 2008, 113, D19105. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Pińskwar, I.; Brakenridge, G.R. Large Floods in Europe, 1985–2009. Hydrol. Sci. J. 2013, 58, 1–7. [Google Scholar] [CrossRef]
- Alfieri, L.; Burek, P.; Feyen, L.; Forzieri, G. Global Warming Increases the Frequency of River Floods in Europe. Hydrol. Earth Syst. Sci. 2015, 19, 2247–2260. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Pińskwar, I.; Brakenridge, G.R. Changes in River Flood Hazard in Europe: A Review. Hydrol. Res. 2018, 49, 294–302. [Google Scholar] [CrossRef]
- IPCC. Synthesis Report of the IPCC Sixth Assessment Report (AR6) Summary for Policymakers; IPCC: Geneva, Switzerland, 2023. [Google Scholar]
- Paprotny, D.; Morales-Nápoles, O. Estimating Extreme River Discharges in Europe through a Bayesian Network. Hydrol. Earth Syst. Sci. 2017, 21, 2615–2636. [Google Scholar] [CrossRef]
- Blöschl, G.; Hall, J.; Viglione, A.; Perdigão, R.A.P.; Parajka, J.; Merz, B.; Lun, D.; Arheimer, B.; Aronica, G.T.; Bilibashi, A.; et al. Changing Climate Both Increases and Decreases European River Floods. Nature 2019, 573, 108–111. [Google Scholar] [CrossRef]
- Bertola, M.; Viglione, A.; Lun, D.; Hall, J.; Blöschl, G. Flood Trends in Europe: Are Changes in Small and Big Floods Different? Hydrol. Earth Syst. Sci. 2020, 24, 1805–1822. [Google Scholar] [CrossRef]
- Rutgersson, A.; Kjellström, E.; Haapala, J.; Stendel, M.; Danilovich, I.; Drews, M.; Jylhä, K.; Kujala, P.; Larsén, X.G.; Halsnæs, K.; et al. Natural Hazards and Extreme Events in the Baltic Sea Region. Earth Syst. Dyn. 2021, 13, 251–301. [Google Scholar] [CrossRef]
- Venegas-Cordero, N.; Kundzewicz, Z.W.; Jamro, S.; Piniewski, M. Detection of Trends in Observed River Floods in Poland. J. Hydrol. Reg. Stud. 2022, 41, 101098. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Pińskwar, I. Are Pluvial and Fluvial Floods on the Rise? Water 2022, 14, 2612. [Google Scholar] [CrossRef]
- Alifu, H.; Hirabayashi, Y.; Imada, Y.; Shiogama, H. Enhancement of River Flooding Due to Global Warming. Sci. Rep. 2022, 12, 20687. [Google Scholar] [CrossRef]
- Tarasova, L.; Lun, D.; Merz, R.; Blöschl, G.; Basso, S.; Bertola, M.; Miniussi, A.; Rakovec, O.; Samaniego, L.; Thober, S.; et al. Shifts in Flood Generation Processes Exacerbate Regional Flood Anomalies in Europe. Commun. Earth Environ. 2023, 4, 49. [Google Scholar] [CrossRef]
- Dottori, F.; Szewczyk, W.; Ciscar, J.-C.; Zhao, F.; Alfieri, L.; Hirabayashi, Y.; Bianchi, A.; Mongelli, I.; Frieler, K.; Betts, R.A.; et al. Increased Human and Economic Losses from River Flooding with Anthropogenic Warming. Nat. Clim. Chang. 2018, 8, 781–786. [Google Scholar] [CrossRef]
- Jongman, B.; Hochrainer-Stigler, S.; Feyen, L.; Aerts, J.C.J.H.; Mechler, R.; Botzen, W.J.W.; Bouwer, L.M.; Pflug, G.; Rojas, R.; Ward, P.J. Increasing Stress on Disaster-Risk Finance Due to Large Floods. Nat. Clim. Chang. 2014, 4, 264–268. [Google Scholar] [CrossRef]
- Koks, E.E.; Thissen, M.; Alfieri, L.; Moel, H.D.; Feyen, L.; Jongman, B.; Aerts, J.C.J.H. The Macroeconomic Impacts of Future River Flooding in Europe. Environ. Res. Lett. 2019, 14, 084042. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Kanae, S.; Seneviratne, S.I.; Handmer, J.; Nicholls, N.; Peduzzi, P.; Mechler, R.; Bouwer, L.M.; Arnell, N.; Mach, K.; et al. Flood Risk and Climate Change: Global and Regional Perspectives. Hydrol. Sci. J. 2014, 59, 1–28. [Google Scholar] [CrossRef]
- Dolejš, M.; Raška, P.; Kohnová, S.; Schinke, R.; Warachowska, W.; Thaler, T.; Kočický, D. On the Right Track of Flood Planning Policy? Land Uptake in Central-European Floodplains (1990–2018). Landsc. Urban Plan 2022, 228, 104560. [Google Scholar] [CrossRef]
- Merz, B.; Blöschl, G.; Vorogushyn, S.; Dottori, F.; Aerts, J.C.J.H.; Bates, P.; Bertola, M.; Kemter, M.; Kreibich, H.; Lall, U.; et al. Causes, Impacts and Patterns of Disastrous River Floods. Nat. Rev. Earth Environ. 2021, 2, 592–609. [Google Scholar] [CrossRef]
- Löschner, L.; Herrnegger, M.; Apperl, B.; Senoner, T.; Seher, W.; Nachtnebel, H.P. Flood Risk, Climate Change and Settlement Development: A Micro-Scale Assessment of Austrian Municipalities. Reg. Environ. Chang. 2017, 17, 311–322. [Google Scholar] [CrossRef]
- Serinaldi, F.; Kilsby, C.G. A Blueprint for Full Collective Flood Risk Estimation: Demonstration for European River Flooding. Risk Anal. 2016, 37, 1958–1976. [Google Scholar] [CrossRef]
- de Moel, H.; Aerts, J.C.J.H. Effect of Uncertainty in Land Use, Damage Models and Inundation Depth on Flood Damage Estimates. Nat. Hazards 2011, 58, 407–425. [Google Scholar] [CrossRef]
- Ozga-Zielinski, B.; Adamowski, J.; Ciupak, M. Applying the Theory of Reliability to the Assessment of Hazard, Risk and Safety in a Hydrologic System: A Case Study in the Upper Sola River Catchment, Poland. Water 2018, 10, 723. [Google Scholar] [CrossRef]
- Dottori, F.; Kalas, M.; Salamon, P.; Bianchi, A.; Alfieri, L.; Feyen, L. An Operational Procedure for Rapid Flood Risk Assessment in Europe. Nat. Hazard Earth Syst. Sci. 2017, 17, 1111–1126. [Google Scholar] [CrossRef]
- Albrecher, H.; Kortschak, D.; Prettenthaler, F. Spatial Dependence Modeling of Flood Risk Using Max-Stable Processes: The Example of Austria. Water 2020, 12, 1805. [Google Scholar] [CrossRef]
- Amadio, M.; Scorzini, A.R.; Carisi, F.; Essenfelder, A.H.; Domeneghetti, A.; Mysiak, J.; Castellarin, A. Testing Empirical and Synthetic Flood Damage Models: The Case of Italy. Nat. Hazard Earth Syst. Sci. 2019, 19, 661–678. [Google Scholar] [CrossRef]
- Ha, J.; Kang, J.E. Assessment of Flood-Risk Areas Using Random Forest Techniques: Busan Metropolitan City. Nat. Hazards 2022, 111, 2407–2429. [Google Scholar] [CrossRef]
- van der Pol, T.D.; van Ierland, E.C.; Gabbert, S. Economic Analysis of Adaptive Strategies for Flood Risk Management under Climate Change. Mitig. Adapt. Strat. Glob. Chang. 2017, 22, 267–285. [Google Scholar] [CrossRef]
- Hudson, P.; Botzen, W.J.W. Cost–Benefit Analysis of Flood-zoning Policies: A Review of Current Practice. Wiley Interdiscip. Rev. Water 2019, 6, e1387. [Google Scholar] [CrossRef]
- Ventimiglia, U.; Candela, A.; Aronica, G.T. A Cost Efficiency Analysis of Flood Proofing Measures for Hydraulic Risk Mitigation in an Urbanized Riverine Area. Water 2020, 12, 2395. [Google Scholar] [CrossRef]
- Jiang, X.; Yang, L.; Tatano, H. Assessing Spatial Flood Risk from Multiple Flood Sources in a Small River Basin: A Method Based on Multivariate Design Rainfall. Water 2019, 11, 1031. [Google Scholar] [CrossRef]
- Prabaswara, M.H.M.A.; Wickramaarachchi, T.N. Event-Based Rainfall-Runoff Simulation Using Different Precipitation Loss Methods: Case Study in Tropical Monsoon Catchment. Sustain. Water Resour. Manag. 2023, 9, 16. [Google Scholar] [CrossRef]
- Wei, H.; Yu, T.; Tu, J.; Ke, F. Detection and Evaluation of Flood Inundation Using CYGNSS Data during Extreme Precipitation in 2022 in Guangdong Province, China. Remote Sens. 2023, 15, 297. [Google Scholar] [CrossRef]
- Szewrański, S.; Chruściński, J.; Kazak, J.; Świąder, M.; Tokarczyk-Dorociak, K.; Żmuda, R. Pluvial Flood Risk Assessment Tool (PFRA) for Rainwater Management and Adaptation to Climate Change in Newly Urbanised Areas. Water 2018, 10, 386. [Google Scholar] [CrossRef]
- Szeląg, B.; Suligowski, R.; Łagód, G.; Łazuka, E.; Wlaź, P.; Stránský, D.; Paola, F.D.; Fatone, F. Flood Occurrence Analysis in Small Urban Catchments in the Context of Regional Variability. PLoS ONE 2022, 17, e0276312. [Google Scholar] [CrossRef] [PubMed]
- Essenfelder, A.H.; Bagli, S.; Mysiak, J.; Pal, J.S.; Mercogliano, P.; Reder, A.; Rianna, G.; Mazzoli, P.; Broccoli, D.; Luzzi, V. Probabilistic Assessment of Pluvial Flood Risk Across 20 European Cities: A Demonstrator of the Copernicus Disaster Risk Reduction Service for Pluvial Flood Risk in Urban Areas. Water Econ. Policy 2022, 8, 2240007. [Google Scholar] [CrossRef]
- Wei, L.; Hu, K.; Hu, X. Rainfall Occurrence and Its Relation to Flood Damage in China from 2000 to 2015. J. Mt. Sci. 2018, 15, 2492–2504. [Google Scholar] [CrossRef]
- Rashid, M.M.; Wahl, T.; Villarini, G.; Sharma, A. Fluvial Flood Losses in the Contiguous United States Under Climate Change. Earths Future 2023, 11, e2022EF003328. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, J.; Singh, V.P. Application of Archimedean Copulas in the Analysis of the Precipitation Extremes: Effects of Precipitation Changes. Theor. Appl. Climatol. 2012, 107, 255–264. [Google Scholar] [CrossRef]
- Guan, X.; Dong, Z.; Luo, Y.; Zhong, D. Multi-Objective Optimal Allocation of River Basin Water Resources under Full Probability Scenarios Considering Wet–Dry Encounters: A Case Study of Yellow River Basin. Int. J. Environ. Res. Public Health 2021, 18, 11652. [Google Scholar] [CrossRef]
- Qian, L.; Wang, X.; Hong, M.; Dang, S.; Wang, H. Encounter Risk Prediction of Rich-Poor Precipitation Using a Combined Copula. Theor. Appl. Climatol. 2022, 149, 1057–1067. [Google Scholar] [CrossRef]
- Zhang, J.; Ding, Z.; You, J. The Joint Probability Distribution of Runoff and Sediment and Its Change Characteristics with Multi-Time Scales. J. Hydrol. Hydromech. 2014, 62, 218–225. [Google Scholar] [CrossRef]
- You, Q.; Jiang, H.; Liu, Y.; Liu, Z.; Guan, Z. Probability Analysis and Control of River Runoff–Sediment Characteristics Based on Pair-Copula Functions: The Case of the Weihe River and Jinghe River. Water 2019, 11, 510. [Google Scholar] [CrossRef]
- Qian, L.; Dang, S.; Bai, C.; Wang, H. Variation in the Dependence Structure between Runoff and Sediment Discharge Using an Improved Copula. Theor. Appl. Climatol. 2021, 145, 285–293. [Google Scholar] [CrossRef]
- Plewa, K.; Perz, A.; Wrzesiński, D.; Sobkowiak, L. Probabilistic Assessment of Correlations of Water Levels in Polish Coastal Lakes with Sea Water Level with the Application of Archimedean Copulas. Water 2019, 11, 1292. [Google Scholar] [CrossRef]
- Gu, H.; Yu, Z.; Li, G.; Ju, Q. Nonstationary Multivariate Hydrological Frequency Analysis in the Upper Zhanghe River Basin, China. Water 2018, 10, 772. [Google Scholar] [CrossRef]
- Mitkova, V.B.; Halmova, D. Analysis of The Joint Impact of Synchronous Discharges in Estimating the Flood Risk: Case Study on Hron River. IOP Conf. Ser. Earth Environ. Sci. 2019, 221, 012034. [Google Scholar] [CrossRef]
- Perz, A.; Sobkowiak, L.; Wrzesiński, D. Spatial Differentiation of the Maximum River Runoff Synchronicity in the Warta River Catchment, Poland. Water 2020, 12, 1782. [Google Scholar] [CrossRef]
- Sobkowiak, L.; Perz, A.; Wrzesiński, D.; Faiz, M.A. Estimation of the River Flow Synchronicity in the Upper Indus River Basin Using Copula Functions. Sustainability 2020, 12, 5122. [Google Scholar] [CrossRef]
- Xu, Y.; Lu, F.; Zhou, Y.; Ruan, B.; Dai, Y.; Wang, K. Dryness–Wetness Encounter Probabilities’ Analysis for Lake Ecological Water Replenishment Considering Non-Stationarity Effects. Front. Environ. Sci. 2022, 10, 806794. [Google Scholar] [CrossRef]
- Perz, A.; Sobkowiak, L.; Wrzesiński, D. Probabilistic Approach to Precipitation-Runoff Relation in a Mountain Catchment: A Case Study of the Kłodzka Valley in Poland. Water 2021, 13, 1229. [Google Scholar] [CrossRef]
- Perz, A.; Sobkowiak, L.; Wrzesiński, D. Co-Occurrence Probability of Water Balance Elements in a Mountain Catchment on the Example of the Upper Nysa Kłodzka River. Acta Geophys. 2022, 70, 1301–1315. [Google Scholar] [CrossRef]
- Perz, A.; Wrzesiński, D.; Sobkowiak, L.; Stodolak, R. Copula-Based Geohazard Assessment—Case of Flood-Prone Area in Poland. J. Hydrol. Reg. Stud. 2022, 44, 101214. [Google Scholar] [CrossRef]
- Wang, S.; Zhong, P.-A.; Zhu, F.; Xu, C.; Wang, Y.; Liu, W. Analysis and Forecasting of Wetness-Dryness Encountering of a Multi-Water System Based on a Vine Copula Function-Bayesian Network. Water 2022, 14, 1701. [Google Scholar] [CrossRef]
- Bartnik, A.; Jokiel, P. Geografia Wezbrań i Powodzi Rzecznych; Wydawnictwo Uniwersytetu Łódzkiego: Łódź, Poland, 2012. [Google Scholar] [CrossRef]
- Jokiel, P.; Bartnik, A. Wezbrania i powodzie. In Hydrologia Polski; Jokiel, P., Marszelewski, W., Pociask-Karteczka, J., Eds.; Wydawnictwo Naukowe PWN: Warszawa, Poland, 2017; pp. 167–175. ISBN 978-83-01-19379-9. (In Polish) [Google Scholar]
- Magnuszewski, A. Flood potential of Polish rivers. In Management of Water Resources in Poland; Zeleňáková, M., Kubiak-Wójcicka, K., Negm, A.M., Eds.; Springer Water: Cham, Switzerland, 2021; pp. 269–280. [Google Scholar] [CrossRef]
- Wrzesiński, D. Uncertainty of Flow Regime Characteristics of Rivers in Europe. Quaest. Geogr. 2013, 32, 43–53. [Google Scholar] [CrossRef]
- Pociask-Karteczka, J.; Kundzewicz, Z.W.; Twardosz, R.; Rajwa-Kuligiewicz, A. Natural hazards in Poland. In Exploring Natural Hazards: A Case Study Approach; Bartlett, D., Singh, R.P., Eds.; Chapman and Hall/CRC: New York, NY, USA, 2018; pp. 317–345. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Szamałek, K.; Kowalczak, P. The Great Flood of 1997 in Poland. Hydrol. Sci. J. 2009, 44, 855–870. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W. (Ed.) Changes in Flood Risk in Europe—IAHS Special Publication 10; IAHS Press: Oxfordshire, UK, 2012. [Google Scholar] [CrossRef]
- Bednorz, E.; Wrzesiński, D.; Tomczyk, A.M.; Jasik, D. Classification of Synoptic Conditions of Summer Floods in Polish Sudeten Mountains. Water 2019, 11, 1450. [Google Scholar] [CrossRef]
- Dumieński, G.; Mruklik, A.; Tiukało, A.; Bedryj, M. The Comparative Analysis of the Adaptability Level of Municipalities in the Nysa Kłodzka Sub-Basin to Flood Hazard. Sustainability 2020, 12, 3003. [Google Scholar] [CrossRef]
- Głównu Urząd Statystyczny. Available online: https://demografia.stat.gov.pl/BazaDemografia/Tables.aspx (accessed on 2 April 2023).
- Richling, A.; Solon, J.; Macias, A.; Balon, J.; Borzyszkowski, J.; Kistowski, M. (Eds.) Regionalna Geografia Fizyczna Polski; Bogucki Wyd. Naukowe: Poznań, Poland, 2021; ISBN 978-83-7986-381-5. (In Polish) [Google Scholar]
- Perz, A. Characteristics of the Flow Regime of the Kłodzka Valley Rivers. Bad. Fizjogr. Ser. A Geogr. Fiz. 2019, 70, 65–83. (In Polish) [Google Scholar] [CrossRef]
- Czernecki, B.; Głogowski, A.; Nowosad, J. Climate: An R Package to Access Free In-Situ Meteorological and Hydrological Datasets For Environmental Assessment. Sustainability 2020, 12, 394. [Google Scholar] [CrossRef]
- ISOK. Raport z Wykonania Map Zagrożenia Powodziowego i Map Ryzyka Powodziowego. 2013. Available online: https://www.kzgw.gov.pl/files/mzp-mrp/zal1.pdf (accessed on 15 January 2023).
- State Water Holding Polish Waters. Metodyka Opracowania Map Zagrożenia Powodziowego i Map Ryzyka Powodziowego w II Cyklu Planistycznym. 2020. Available online: https://powodz.gov.pl/www/powodz/Mapy/raport%202022/aMZPiMRP%20Zal1%20Metodyka%20RZEKI%2020200617%20v7.00%20pub.pdf (accessed on 15 January 2023).
- Rozporządzenie Ministra Infrastruktury z Dnia 16 Listopada 2022 r. w Sprawie Planu Gospodarowania Wodami Na Obszarze Dorzecza Odry. Available online: https://isap.sejm.gov.pl/isap.nsf/DocDetails.xsp?id=WDU20230000335 (accessed on 15 January 2023).
- Godyń, I. A Revised Approach to Flood Damage Estimation in Flood Risk Maps and Flood Risk Management Plans, Poland. Water 2021, 13, 2713. [Google Scholar] [CrossRef]
- Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Nelsen, R.B. An Introduction to Copulas; Springer: New York, NY, USA, 1999. [Google Scholar]
- Chen, F.-W.; Liu, C.-W. Estimation of the Spatial Rainfall Distribution Using Inverse Distance Weighting (IDW) in the Middle of Taiwan. Paddy Water Environ. 2012, 10, 209–222. [Google Scholar] [CrossRef]
- Clavet-Gaumont, J.; Huard, D.; Frigon, A.; Koenig, K.; Slota, P.; Rousseau, A.; Klein, I.; Thiémonge, N.; Houdré, F.; Perdikaris, J.; et al. Probable Maximum Flood in a Changing Climate: An Overview for Canadian Basins. J. Hydrol. Reg. Stud. 2017, 13, 11–25. [Google Scholar] [CrossRef]
- Zhang, B.; Wang, S.; Wang, Y. Probabilistic Projections of Multidimensional Flood Risks at a Convection-Permitting Scale. Water Resour. Res. 2021, 57, e2020WR028582. [Google Scholar] [CrossRef]
- Fan, Y.R.; Yu, L.; Shi, X.; Duan, Q.Y. Tracing Uncertainty Contributors in the Multi-Hazard Risk Analysis for Compound Extremes. Earths Future 2021, 9, e2021EF002280. [Google Scholar] [CrossRef]
- Tootoonchi, F.; Sadegh, M.; Haerter, J.O.; Räty, O.; Grabs, T.; Teutschbein, C. Copulas for Hydroclimatic Analysis: A Practice-oriented Overview. Wiley Interdiscip. Rev. Water 2022, 9, e1579. [Google Scholar] [CrossRef]
- Maranzoni, A.; D’Oria, M.; Rizzo, C. Quantitative Flood Hazard Assessment Methods: A Review. J. Flood Risk Manag. 2022, 16, e12855. [Google Scholar] [CrossRef]
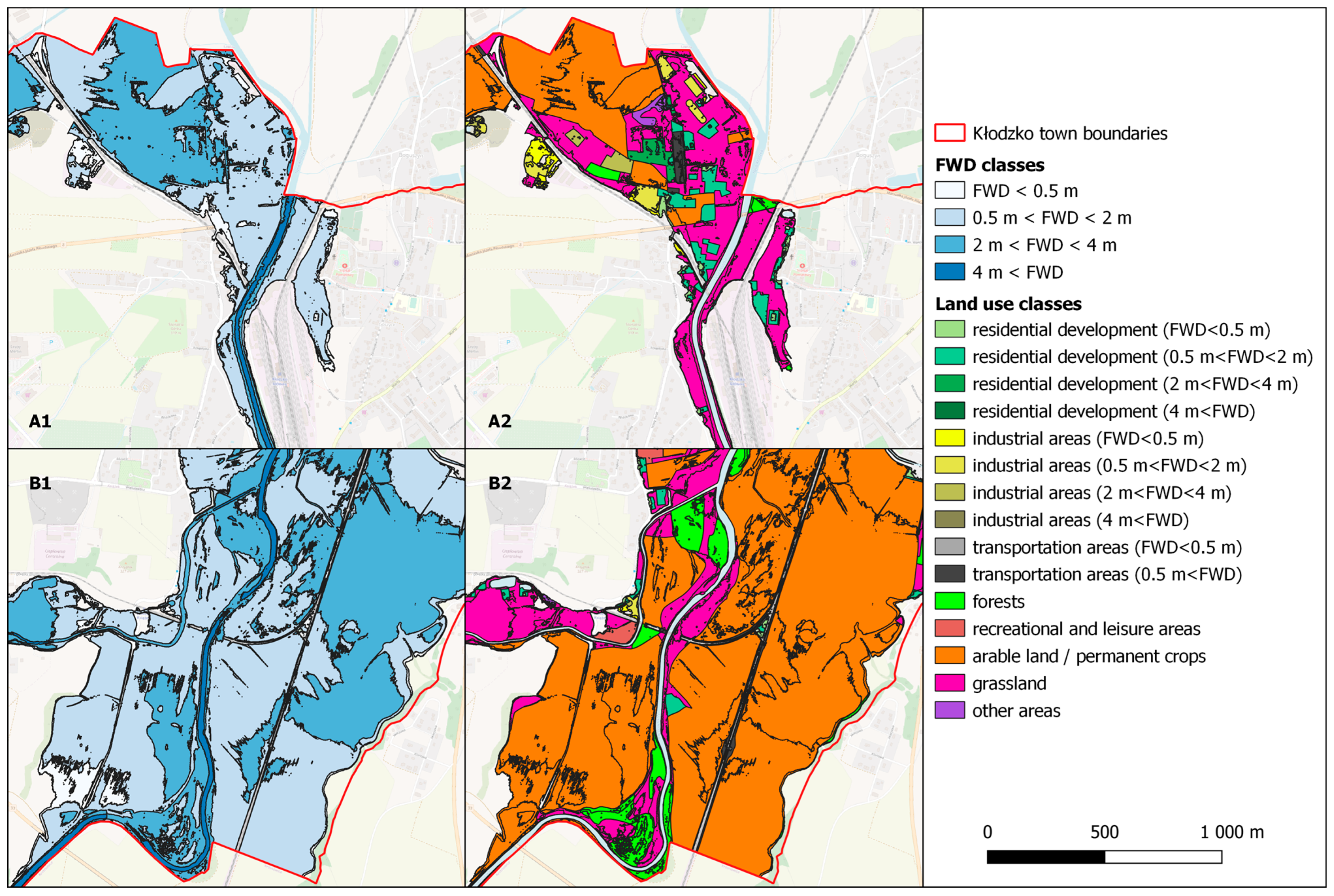
| Class No. | Class Name | FWD < 0.5 m | 0.5 m < FWD ≤ 2 m | 2 m < FWD ≤ 4 m | FWD > 4 m |
|---|---|---|---|---|---|
| 1 | Areas of residential development | 20% v | 35% v | 60% v | 95% v |
| 2 | Industrial areas | 20% v | 40% v | 60% v | 80% v |
| 3 | Transportation areas | 5% v | 10% v | 10% v | 10% v |
| 4 | Forests | 0.04 PLN/m2 (0.01 EUR/m2) | |||
| 5 | Recreational and leisure areas | 8.81 PLN/m2 (1.90 EUR/m2) | |||
| 6 | Arable land/permanent crops | 0.36 PLN/m2 (0.08 EUR/m2) | |||
| 7 | Grassland | 0.09 PLN/m2 (0.02 EUR/m2) | |||
| 8 | Other areas and surface waters | - | |||
| Copula Family | Kendall’s | |||
|---|---|---|---|---|
| Clayton | ||||
| Gumbel–Hougaard | ||||
| Frank |
| Sector | Relation Type | X | Y | |
|---|---|---|---|---|
| 1 | LoR–LoPFL | Synchronicity | X ≤ R62.5% | Y ≤ PFL62.5% |
| 2 | LoR–MePFL | Moderate asynchronicity | X ≤ R62.5% | PFL62.5% < Y ≤ PFL37.5% |
| 3 | LoR–HiPFL | High asynchronicity | X ≤ R62.5% | Y > PFL37.5% |
| 4 | MeR–LoPFL | Moderate asynchronicity | R62.5% < X ≤ R37.5% | Y ≤ PFL62.5% |
| 5 | MeR–MePFL | Synchronicity | R62.5% < X ≤ R37.5% | PFL62.5% < Y ≤ PFL37.5% |
| 6 | MeR–HiPFL | Moderate asynchronicity | R62.5% < X ≤ R37.5% | Y > PFL37.5% |
| 7 | HiR–LoPFL | High asynchronicity | X > R37.5% | Y ≤ PFL62.5% |
| 8 | HiR–MePFL | Moderate asynchronicity | X > R37.5% | PFL62.5% < Y ≤ PFL37.5% |
| 9 | HiR–HiPFL | Synchronicity | X > R37.5% | Y > PFL37.5% |
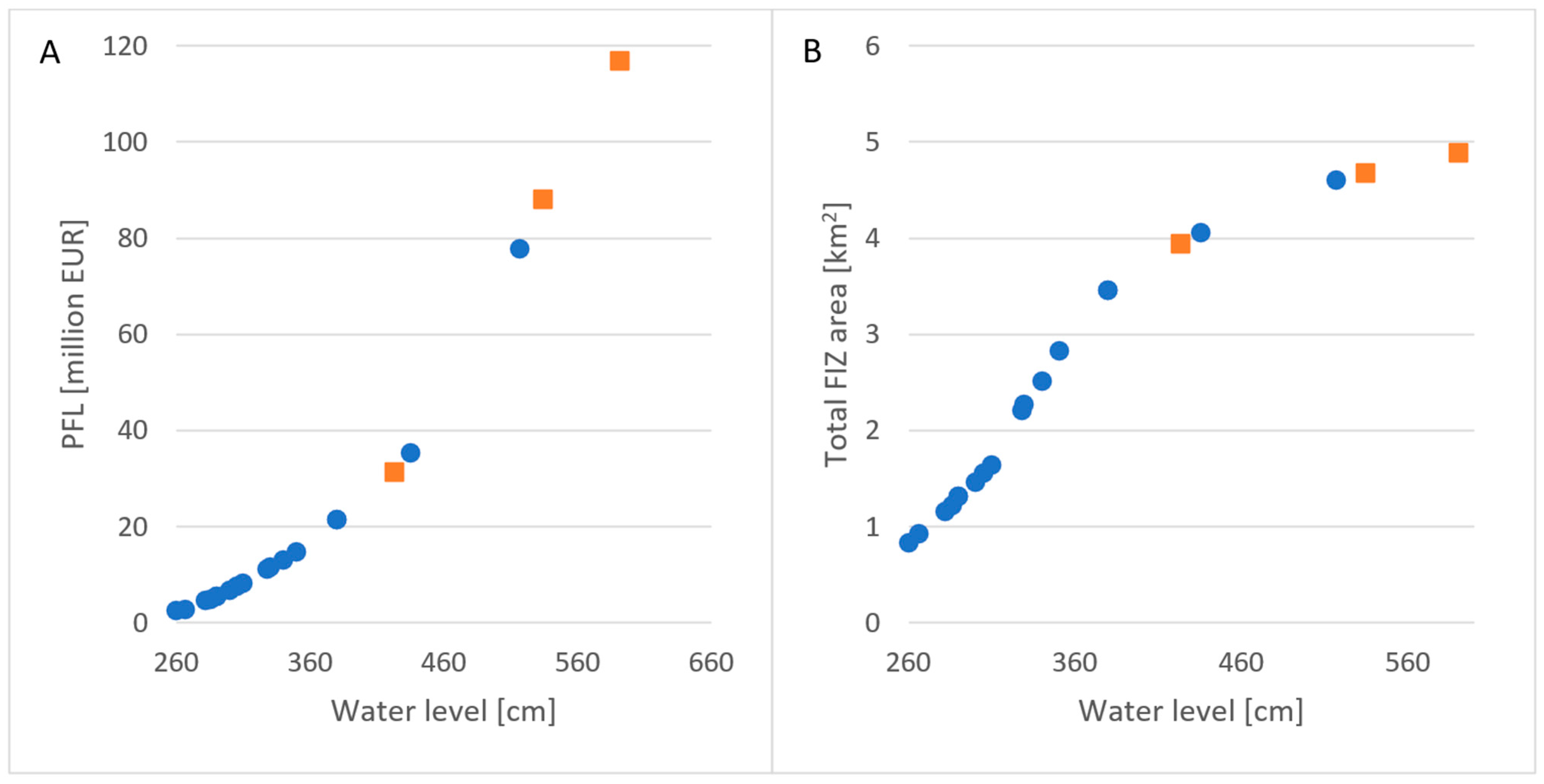
| No. | Date | H (cm) | Q (m3·s−1) | PFL (PLN Million (EUR Million)) 1 | Total FIZ Area (km2) |
|---|---|---|---|---|---|
| 1 | 30.05.1971 | 266 | 120 | 13.4 (2.89) | 0.9 |
| 2 | 02.07.1975 | 330 | 212 | 53.4 (11.51) | 2.3 |
| 3 | 03.08.1977 | 380 | 298 | 99.0 (21.34) | 3.5 |
| 4 | 23.08.1977 | 310 | 180 | 38.4 (8.28) | 1.6 |
| 5 | 10.07.1980 | 350 | 244 | 68.2 (14.7) | 2.8 |
| 6 | 21.07.1980 | 300 | 164 | 31.4 (6.77) | 1.5 |
| 7 | 23.10.1981 | 260 | 113 | 12.1 (2.61) | 0.8 |
| 8 | 09.08.1985 | 290 | 149 | 25.2 (5.43) | 1.3 |
| 9 | 06.09.1987 | 286 | 144 | 23.5 (5.06) | 1.2 |
| 10 | 14.05.1996 | 290 | 149 | 25.2 (5.43) | 1.3 |
| 11 | 08.07.1997 | 517 | 693 | 361.4 (77.89) | 4.6 |
| 12 | 20.07.1997 | 328 | 209 | 52.2 (11.25) | 2.2 |
| 13 | 23.07.1998 | 380 | 298 | 99.0 (21.34) | 3.5 |
| 14 | 21.07.2001 | 282 | 139 | 21.7 (4.68) | 1.2 |
| 15 | 08.08.2006 | 340 | 243 | 61.0 (13.15) | 2.5 |
| 16 | 27.06.2009 | 435 | 424 | 164.1 (35.37) | 4.1 |
| 17 | 22.07.2011 | 305 | 205 | 34.9 (7.52) | 1.6 |
| Probability | Return Period | H (cm) | Q (m3·s−1) | PFL (PLN Million (EUR Million)) 1 | Total FIZ Area (km2) |
|---|---|---|---|---|---|
| 10% | 10 years | 423 | 391 | 145.0 (31.25) | 3.9 |
| 1% | 100 years | 534 | 762 | 408.5 (88.04) | 4.7 |
| 0.2% | 500 years | 591 | 1025 | 542.6 (116.94) | 4.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perz, A.; Wrzesiński, D.; Budner, W.W.; Sobkowiak, L. Flood-Triggering Rainfall and Potential Losses—The Copula-Based Approach on the Example of the Upper Nysa Kłodzka River. Water 2023, 15, 1958. https://doi.org/10.3390/w15101958
Perz A, Wrzesiński D, Budner WW, Sobkowiak L. Flood-Triggering Rainfall and Potential Losses—The Copula-Based Approach on the Example of the Upper Nysa Kłodzka River. Water. 2023; 15(10):1958. https://doi.org/10.3390/w15101958
Chicago/Turabian StylePerz, Adam, Dariusz Wrzesiński, Waldemar W. Budner, and Leszek Sobkowiak. 2023. "Flood-Triggering Rainfall and Potential Losses—The Copula-Based Approach on the Example of the Upper Nysa Kłodzka River" Water 15, no. 10: 1958. https://doi.org/10.3390/w15101958
APA StylePerz, A., Wrzesiński, D., Budner, W. W., & Sobkowiak, L. (2023). Flood-Triggering Rainfall and Potential Losses—The Copula-Based Approach on the Example of the Upper Nysa Kłodzka River. Water, 15(10), 1958. https://doi.org/10.3390/w15101958






