Oil Discharge Trajectory Simulation at Selected Baltic Sea Waterway under Variability of Hydro-Meteorological Conditions
Abstract
:1. Introduction
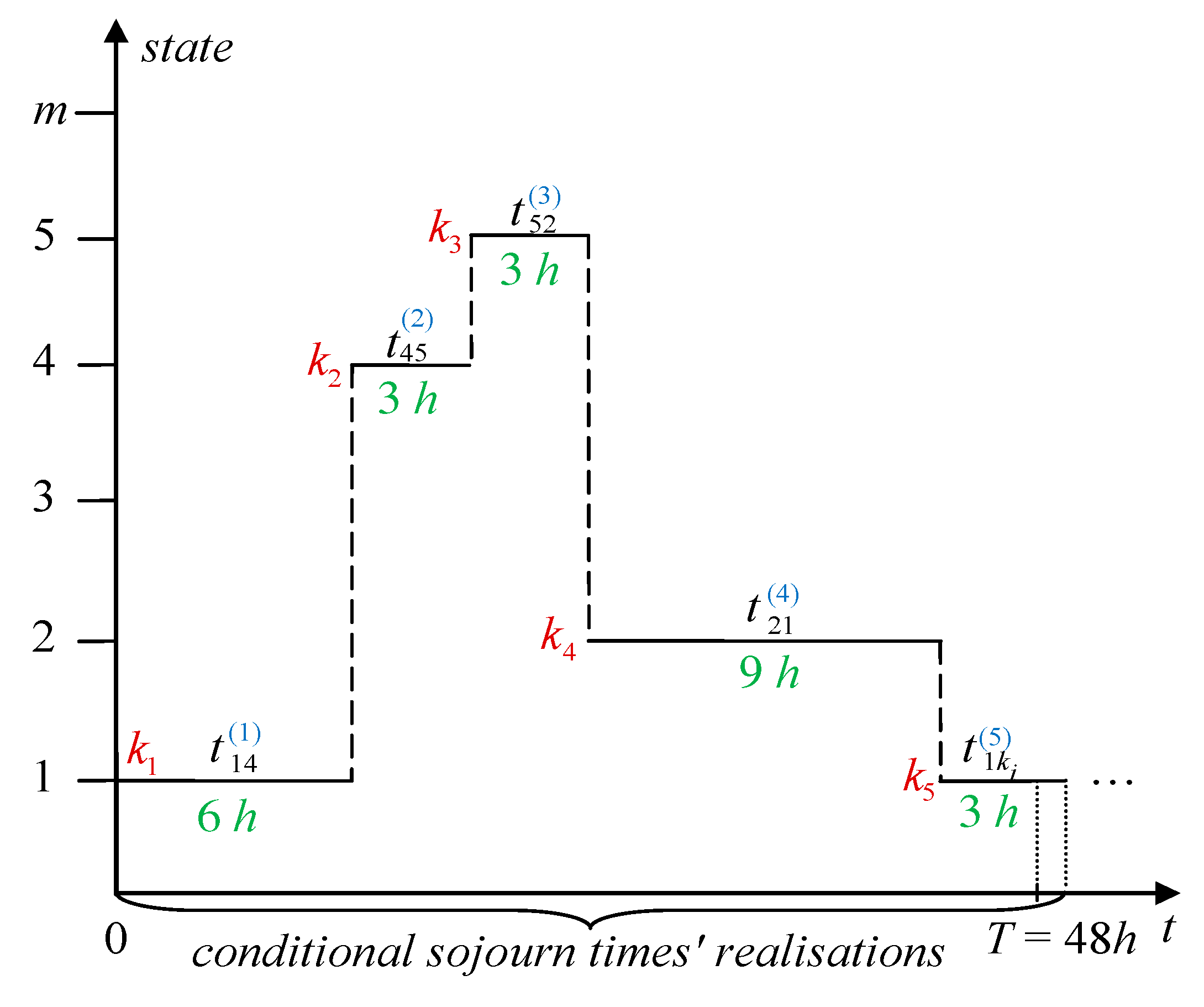
2. Process of Changing Hydro-Meteorological Conditions
2.1. Definition
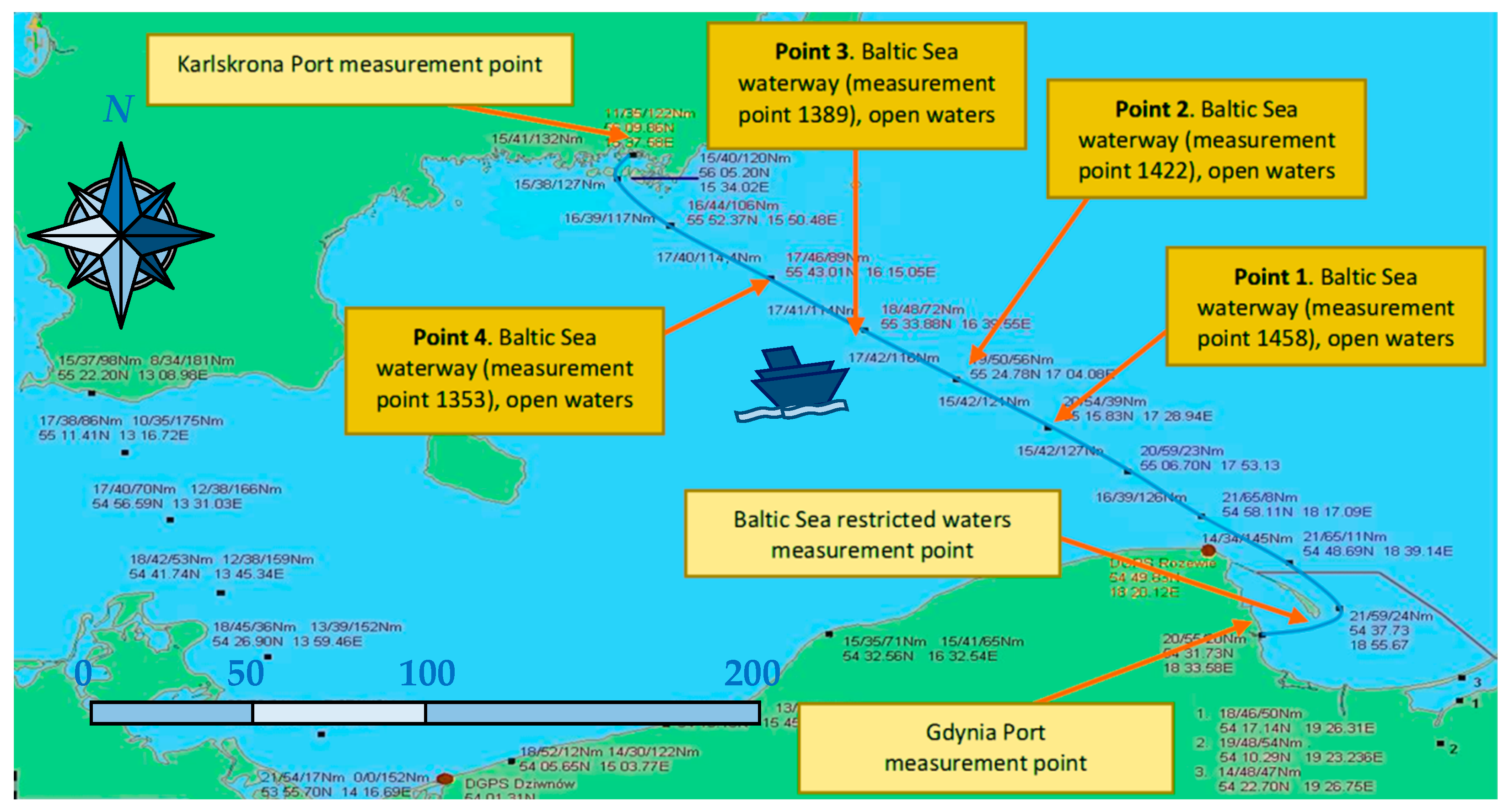
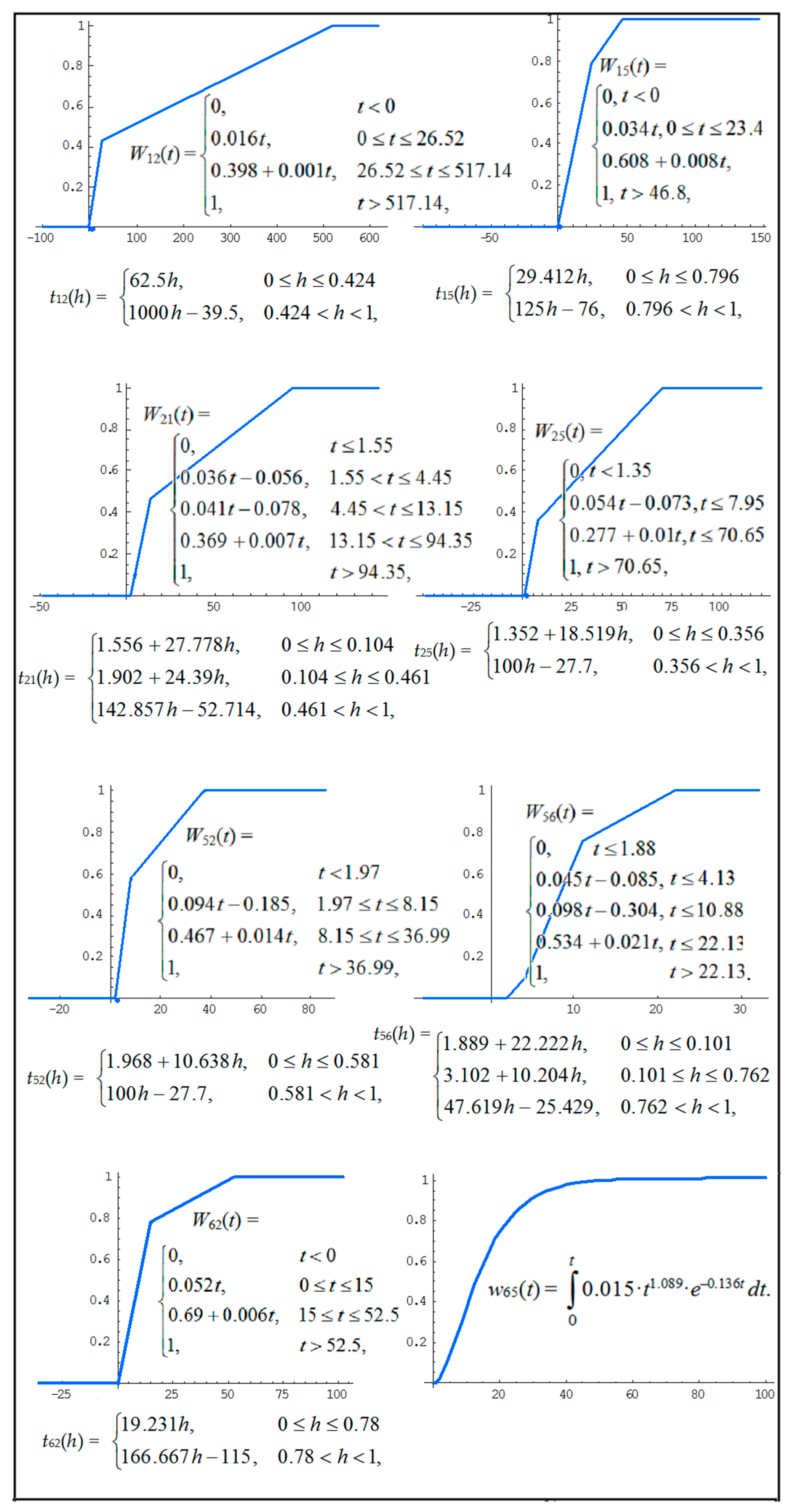
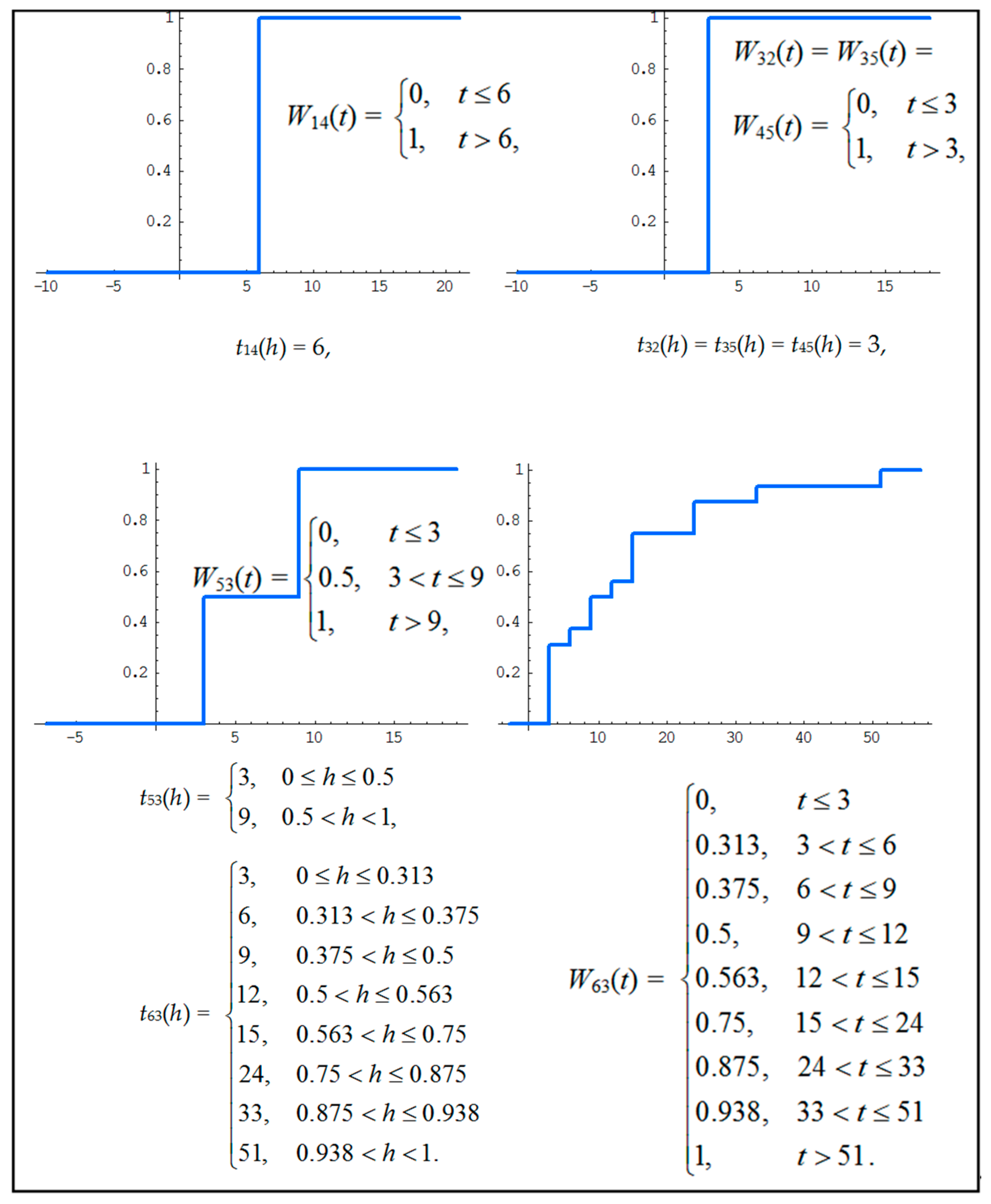
2.2. Parameters Identification for Selected Baltic Sea Waterway Area
- the velocity and direction of the wind;
- the height of the sea water level and waves;
- the direction of the currents;
- any obstacles to visibility such as fog or icing.
p52 = 0.76, p53 = 0.01, p56 = 0.23, p62 = 0.41, p63 = 0.15, p65 = 0.44.
2.3. Input Data for Simulation
- the experiment time T = 48 h;
- formula for generating the initial state coming from (1)
- formula for generating next states
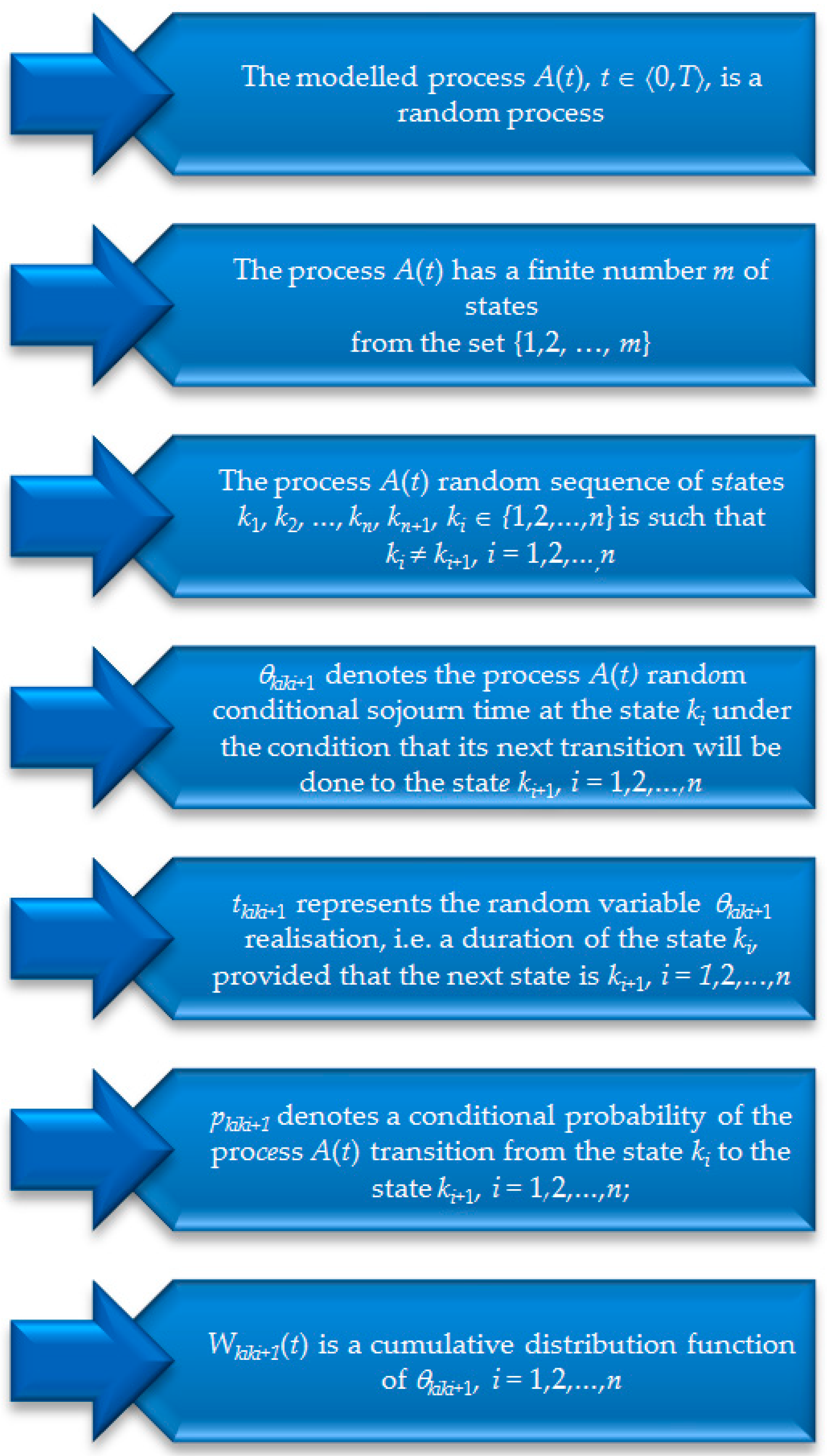
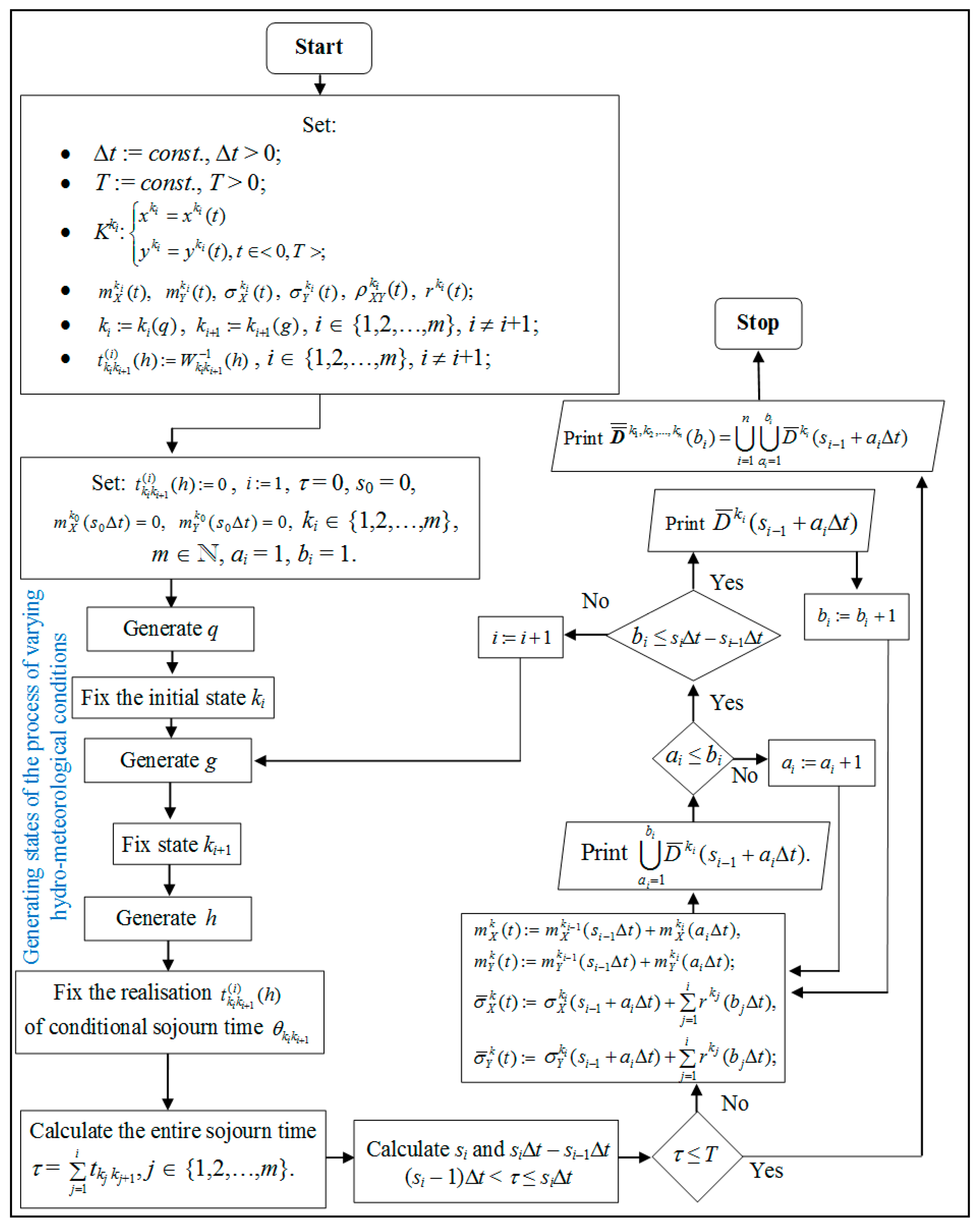
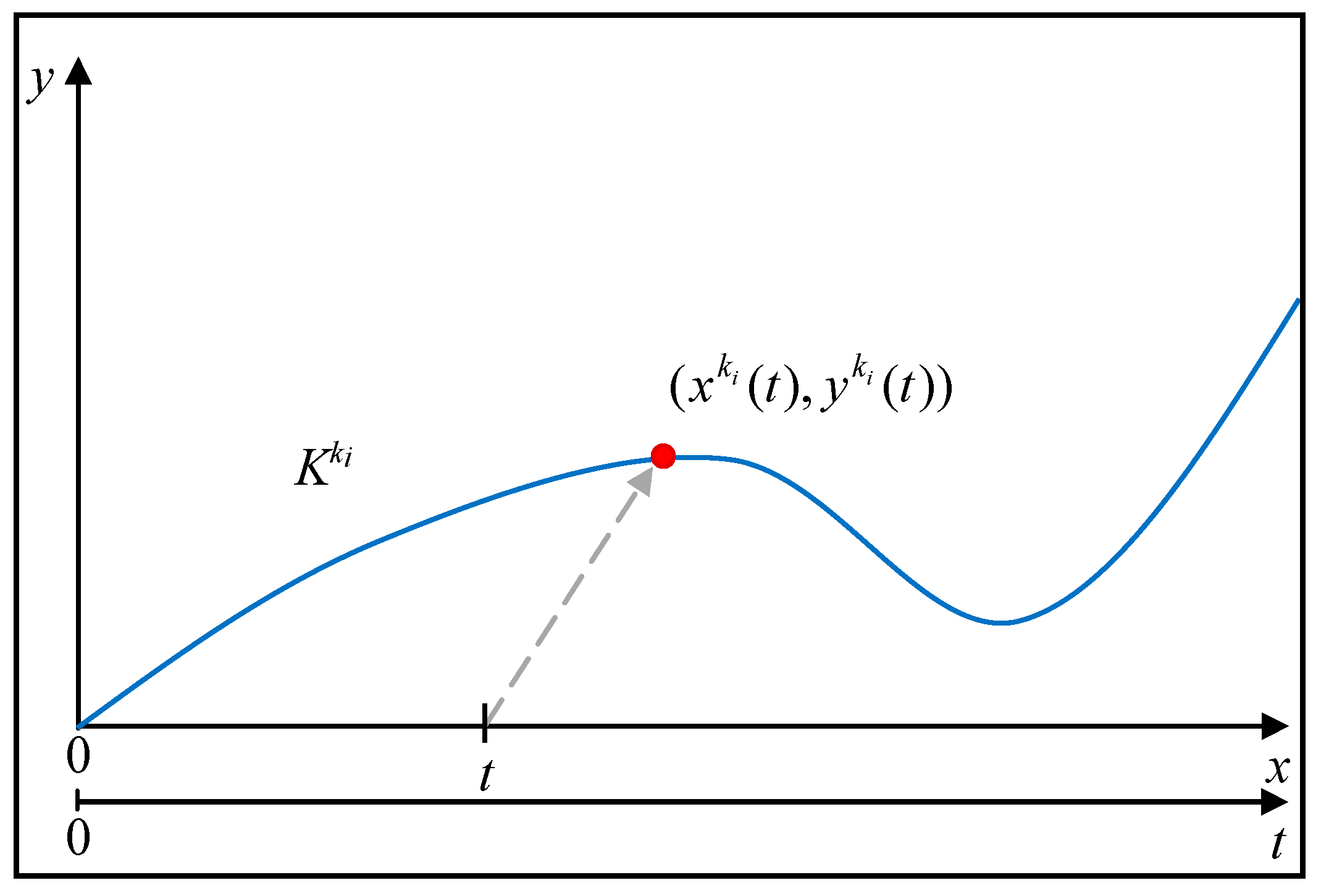
3. Algorithm
- expected values
- standard deviations , ;
- correlation coefficient .
- c2 = −2ln(1 − p);
- expected values
- standard deviations
- correlation coefficients ,
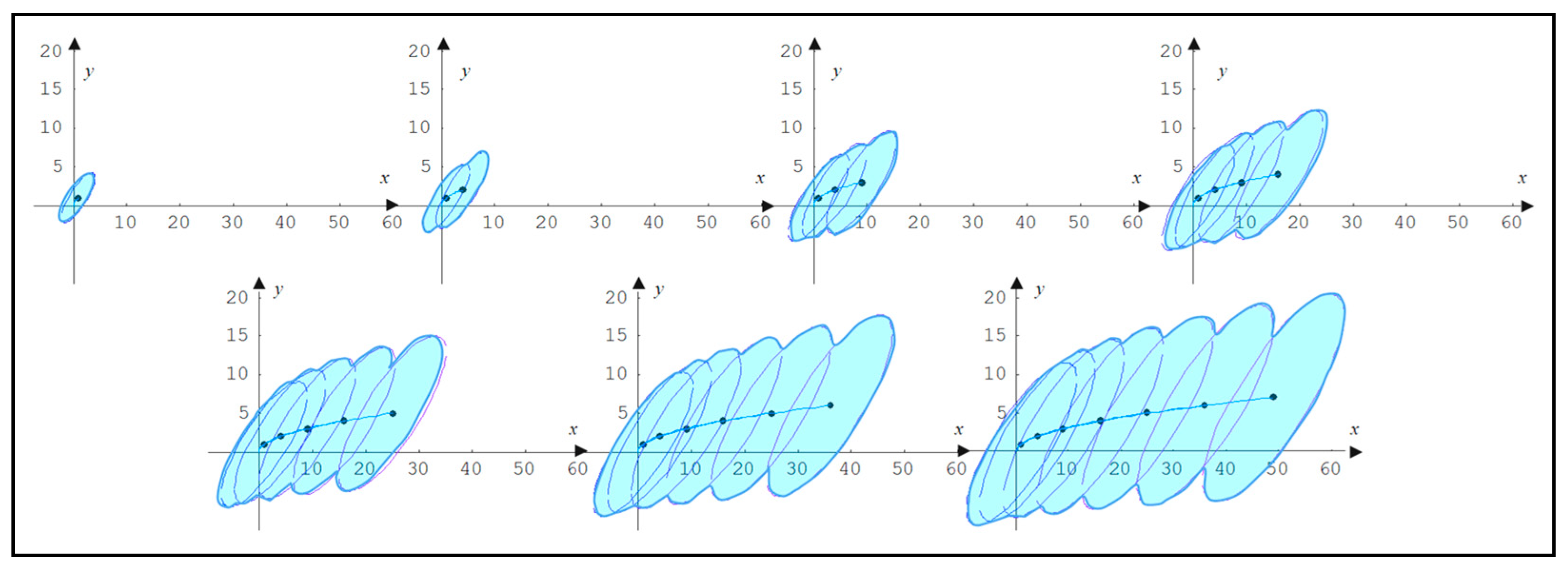
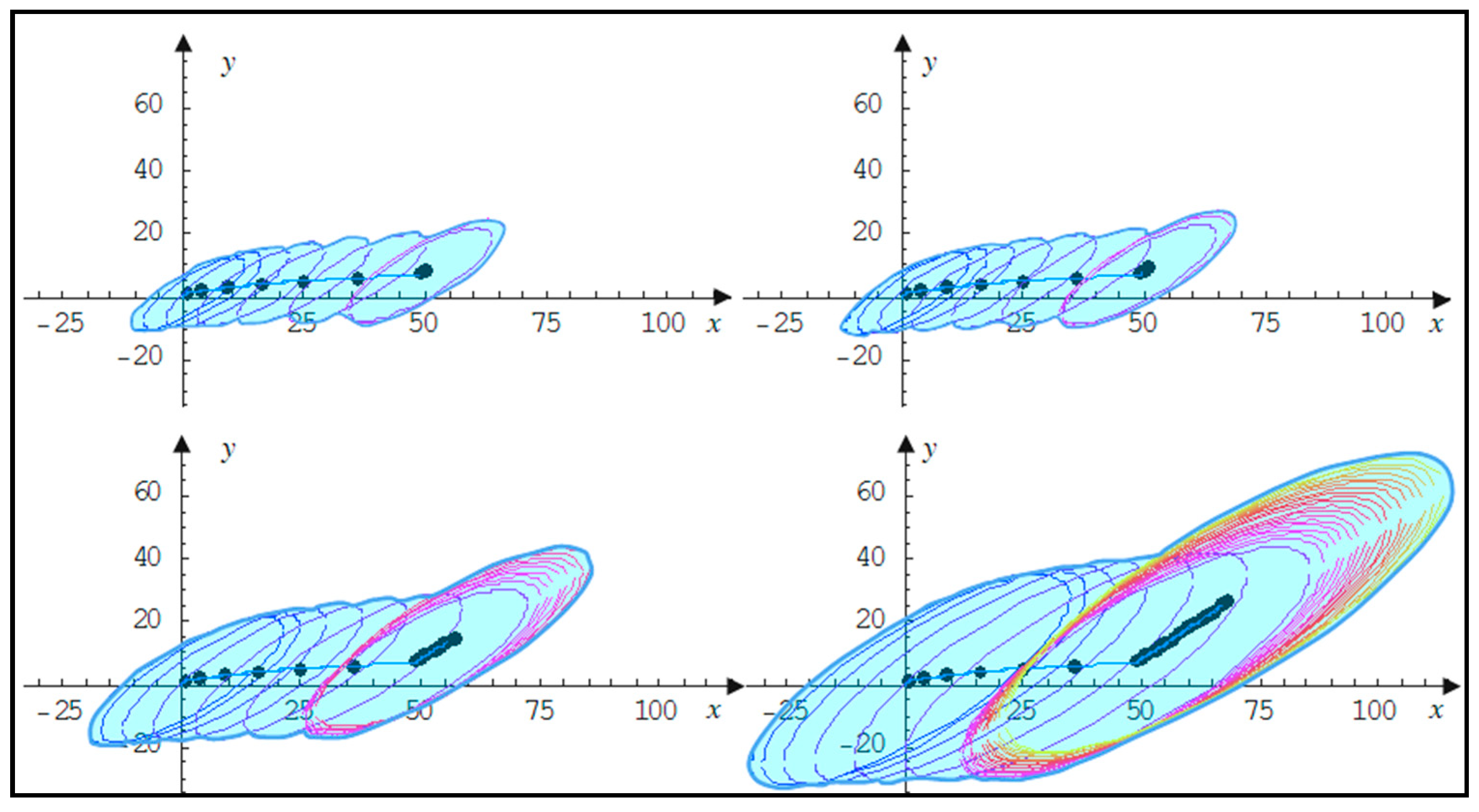
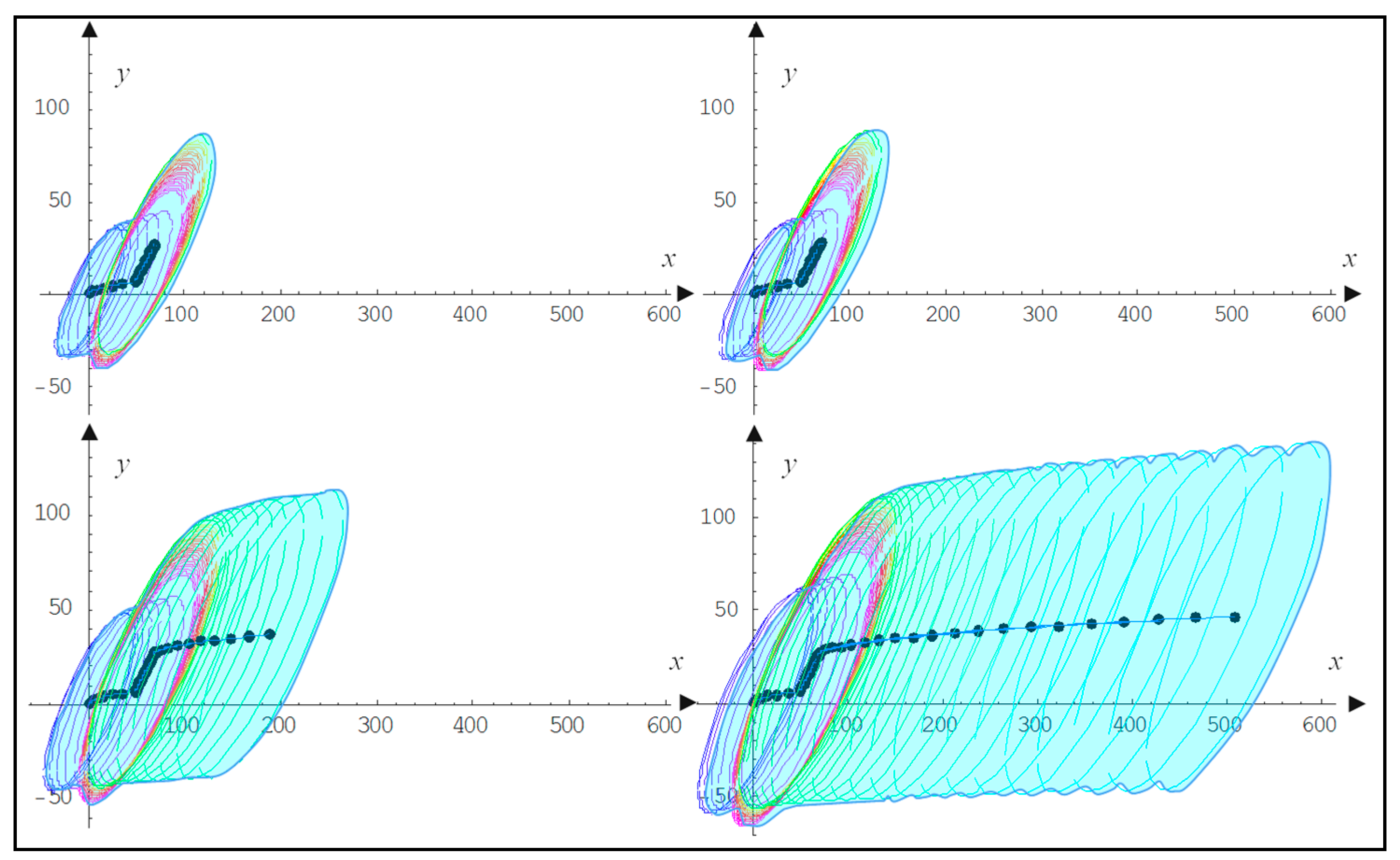
4. Application
4.1. Experiment
- = = = 0.1 + 0.2∙t;
- = 0.8;
- 0.5 + 0.5∙t,
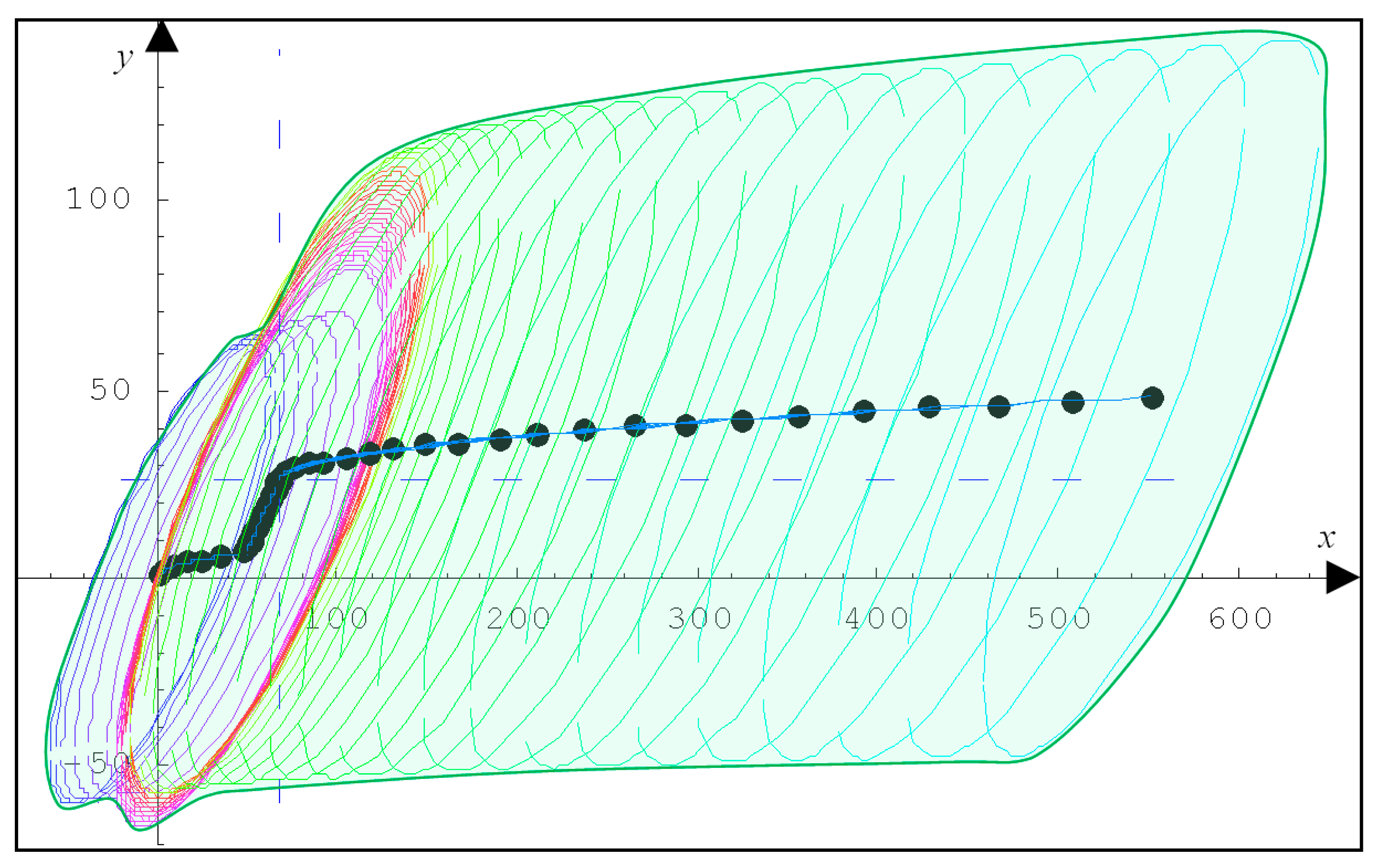
4.2. Discussion of Results and Further Developments
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fingas, M. Oil Spill Science and Technology, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Eckroth, J.R.; Madsen, M.M.; Hoell, E. Dynamic Modeling of Oil Spill Cleanup Operations. In Proceedings of the 38th AMOP Technical Seminar on Environmental Contamination and Response, Vancouver, BC, Canada, 2–4 June 2015; pp. 16–35. [Google Scholar]
- Federal Register. Rules and Regulations. § 254.6—Definitions. Federal Register, 18 October 2011, Volume 76.
- Cordes, E.E.; Jones, D.O.B.; Schlacher, T.A.; Amon, D.J.; Bernardino, A.F.; Brooke, S.; Carney, R.; DeLeo, D.M.; Dunlop, K.M.; Escobar-Briones, E.G.; et al. Environmental Impacts of the Deep-Water Oil and Gas Industry: A Review to Guide Management Strategies. Front. Environ. Sci. 2016, 4, 58. [Google Scholar] [CrossRef]
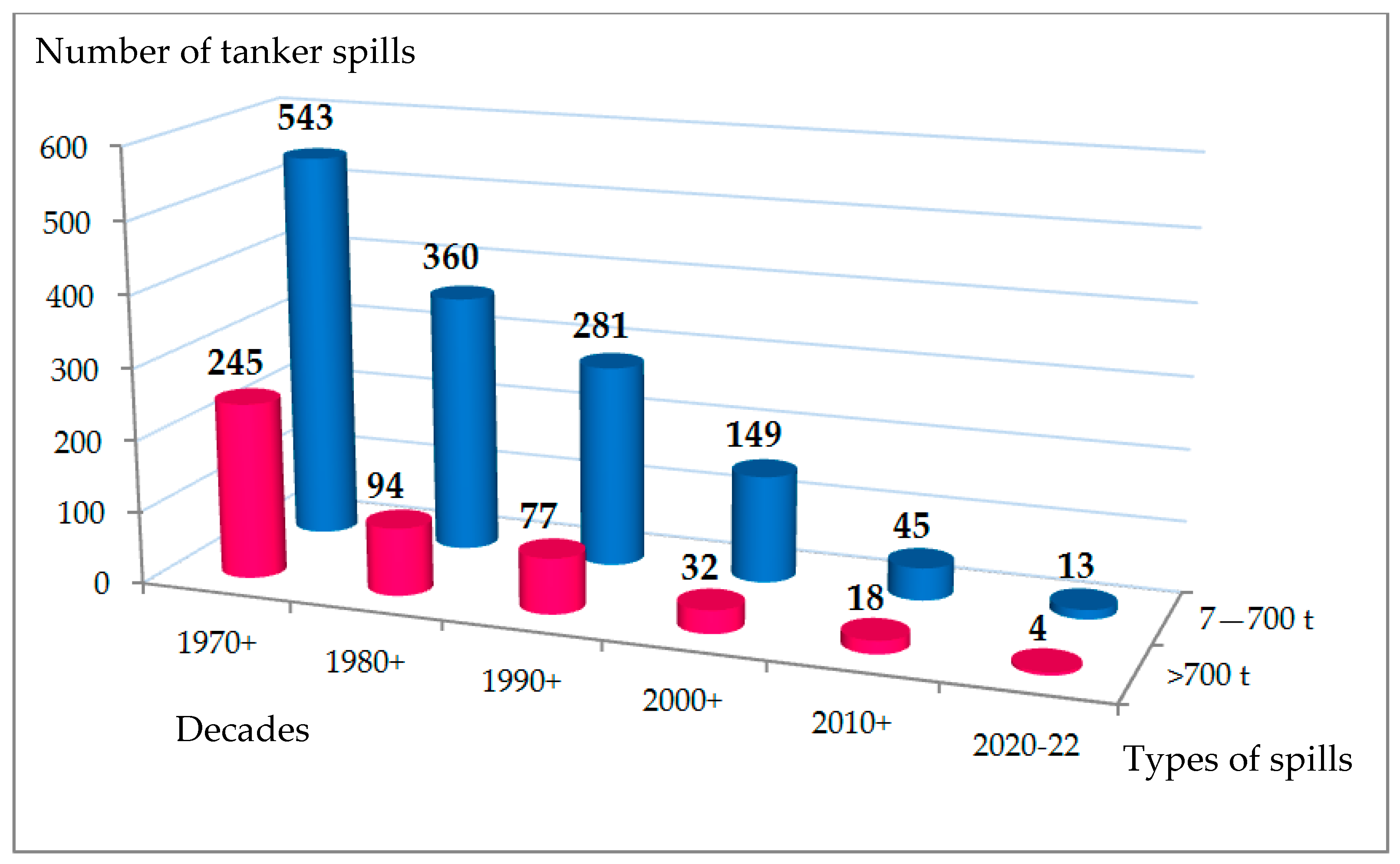
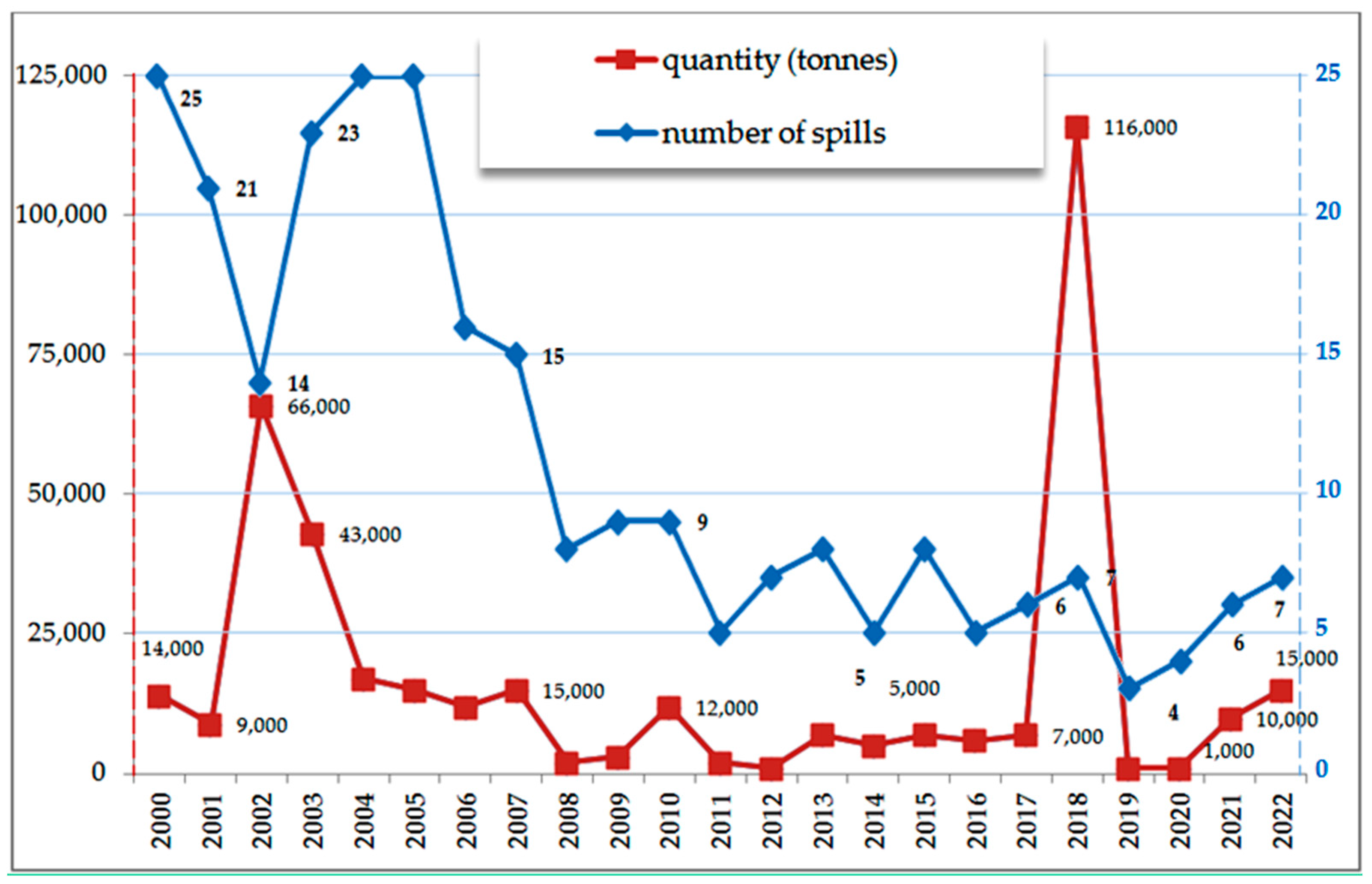
- The International Tanker Owners Pollution Federation Limited (ITOPF). Promoting Effective Spill Response, Oil Tanker Spill Statistics 2022; The International Tanker Owners Pollution Federation Limited (ITOPF): London, UK, 2023. [Google Scholar]
- Pocora, A.; Purcarea, A.A.; Nicolae, F.; Cotorcea, A. Modelling and simulation of oil spills in coastal waters. IOP Conf. Ser. Earth Environ. Sci. 2018, 172, 012012. [Google Scholar] [CrossRef]
- Dobrzycka-Krahel, A.; Bogalecka, M. The Baltic Sea under Anthropopressure—The Sea of Paradoxes. Water 2022, 14, 3772. [Google Scholar] [CrossRef]
- Nixon, Z.; Michel, J. Predictive Modeling of Subsurface Shoreline Oil Encounter Probability from the Exxon Valdez Oil Spill in Prince William Sound, Alaska. Environ. Sci. Technol. 2015, 49, 4354–4361. [Google Scholar] [CrossRef]
- Bogalecka, M. Consequences of maritime critical infrastructure accidents with chemical releases. Int. J. Mar. Navig. Saf. Sea Transp. 2019, 13, 771–779. [Google Scholar] [CrossRef]
- Bogalecka, M. Consequences of Maritime Critical Infrastructure Accidents. Environmental Impacts Modeling—Identification—Prediction—Optimization—Mitigation; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar] [CrossRef]
- Australian Maritime Safety Authority (AMSA). Oil Spill Monitoring Handbook; Wardrop Consulting and the Cawthron Institute for the Australian Maritime Safety Authority (AMSA); Marine Safety Authority of New Zealand (MSA): Canberra, Australia, 2003. [Google Scholar]
- Etkin, D.S. Estimating Cleanup Costs for Oil Spills. In Proceedings of the 1999 International Oil Spill Conference Proceedings, Seattle, WA, USA, 7–12 March 1999; p. 168. [Google Scholar]
- Kontovas, C.A.; Ventikos, N.P.; Psaraftis, H.N. Estimating the Consequences Costs of Oil Spills from Tankers. In Proceedings of the SNAME 2011 Annual Meeting, Houston, TX, USA, 16–18 November 2011. [Google Scholar]
- Nikula, P.; Tynkkynen, V.P. Oil Transportation and Maritime Safety. In Towards a Baltic Sea Region Strategy in Critical Infrastructure Protection; Pursiainen, C., Ed.; Nordregio: Stockholm, Sweden, 2007; Volume 5, pp. 141–164. [Google Scholar]
- Ornitz, B.; Champ, M. Oil Spills First Principles: Prevention and Best Response; Elsevier: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Armenio, E.; Ben Meftah, M.; De Padova, D.; De Serio, F.; Mossa, M. Monitoring Systems and Numerical Models to Study Coastal Sites. Sensors 2019, 19, 1552. [Google Scholar] [CrossRef] [PubMed]
- Bogalecka, M.; Dąbrowska, E. Monte Carlo Simulation Approach to Shipping Accidents Consequences Assessment. Water 2023, 15, 1824. [Google Scholar] [CrossRef]
- Dąbrowska, E.; Kołowrocki, K. Probabilistic Approach to Determination of Oil Spill Domains at Port and Sea Water Areas. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2020, 14, 51–58. [Google Scholar] [CrossRef]
- Kim, T.; Yang, C.-S.; Ouchi, K.; Oh, Y. Application of the method of moment and Monte-Carlo simulation to extract oil spill areas from synthetic aperture radar images. In Proceedings of the 2013 OCEANS—San Diego, San Diego, CA, USA, 23–27 September 2013; pp. 1–4. [Google Scholar]
- Jernelöv, A. The threats from oil spills: Now, then, and in the future. Ambio 2010, 39, 353–366. [Google Scholar] [CrossRef] [PubMed]
- Kulygin, V.V. A review of modern approaches of oil spill modelling. In Proceedings of the International Conference on Oil and Gas of Arctic Shelf, Murmansk, Russia, 2006. [Google Scholar]
- Zafirakou, A.; George, P.; Samaras, A.; Koutitas, C. Oil Spill Modeling Aiming at the Protection of Ports and Coastal Areas. Environ. Process. 2015, 2, 41–53. [Google Scholar] [CrossRef]
- Adofo, Y.K.; Nyankson, E.; Agyei-Tuffour, B. Dispersants as an oil spill clean-up technique in the marine environment: A review. Heliyon 2022, 8, e10153. [Google Scholar] [CrossRef] [PubMed]
- Oil Spill Prevention and Response Technical Advisory Committee (TAC). Minutes of the Meeting of 8 January 2016; California Department of Fish and Wildlife Office of Spill Prevention and Response: Sacramento, CA, USA, 2016. [Google Scholar]
- Fay, J.A. Physical Processes in the Spread of Oil on a Water Surface. In Proceedings of the Joint Conference on Prevention and Control of Oil Spills, sponsored by American Petroleum Industry, Environmental Protection Agency, and United States Coast Guard, Washington, DC, USA, 15–17 June 1971; pp. 463–468. [Google Scholar]
- Huang, J.C. A review of the state-of-the-art of oil spill fate/behavior models. In Proceedings of the International Oil Spill Conference Proceedings, San Antonio, TX, USA, 28 February–3 March 1983; Volume 1983, pp. 313–322. [Google Scholar]
- American Society of Civil Engineers (ASCE) Task Committee on Modeling of Oil Spills. State-of-the-art review of modelling transport and fate of oil spills. J. Hydraul. Eng. 1996, 122, 594–609. [Google Scholar] [CrossRef]
- Chen, C.S.; Huang, H.S.; Beardsley, R.C.; Liu, H.; Xu, Q. A finite volume numerical approach for coastal ocean circulation studies: Comparisons with finite difference models. J. Geophys. Res. 2007, 112, C3018. [Google Scholar] [CrossRef]
- De Dominicis, M.; Pinardi, N.; Zodiatis, G.; Lardner, R. MEDSLIK-II, a Lagrangian marine surface oil spill model for short-term forecasting—Part 1: Theory. Geosci. Model Dev. 2013, 6, 1851–1869. [Google Scholar] [CrossRef]
- Etkin, D.S.; Michel, J.; McCay, D.F.; Boufadel, M.; Li, H. Integrating state-of-the-art shoreline interaction knowledge into spill modeling. In Proceedings of the International Oil Spill Conference Proceedings, Savannah, GA, USA, 4–8 May 2008; pp. 915–922. [Google Scholar]
- Periáñez, R. Chemical and oil spill rapid response modelling in the Strait of Gibraltar-Alborán Sea. Ecol. Model. 2007, 207, 210–222. [Google Scholar] [CrossRef]
- Periáñez, R.; Pascual-Granged, A. Modelling surface radioactive, chemical and oil spills in the Strait of Gibraltar. Comput. Geosci. 2008, 34, 163–180. [Google Scholar] [CrossRef]
- Spaulding, M.L. A state-of-the-art review of oil spill trajectory and fate modeling. Oil Chem. Pollut. 1989, 4, 39–55. [Google Scholar] [CrossRef]
- Volckaert, F.; Tombroff, D. Progress Report to EEC Div. XI/B/l; IntechOpen Limited: London, UK, 1989. [Google Scholar]
- Wang, J.; Shen, Y. Development of an integrated model system to simulate transport and fate of oil spills in seas. Sci. China Technol. Sci. 2010, 53, 2423–2434. [Google Scholar] [CrossRef]
- Lehr, W.; Simecek-Beatty, D.; Aliseda, A.; Boufadel, M. Review of Recent Studies on Dispersed Oil Droplet Distribution. In Proceedings of the 37th AMOP Technical Seminar on Environmental Contamination and Response, Canmore, AB, Canada, 3–5 June 2014; pp. 1–8. [Google Scholar]
- McCay, D.F.; Reich, D.; Michel, J.; Etkin, D.; Symons, L.; Helton, D.; Wagner, J. Oil spill consequence analyses of potentially-polluting shipwrecks. In Proceedings of the 35th AMOP Technical Seminar on Environmental Contamination and Response, Vancouver, BC, Canada, 5–7 June 2012; pp. 751–774. [Google Scholar]
- Dąbrowska, E. Conception of Oil Spill Trajectory Modelling: Karlskrona Seaport Area as an Investigative Example. In Proceedings of the 2021 5th International Conference on System Reliability and Safety (ICSRS), Palermo, Italy, 24–26 November 2021; Piscataway: Institute of Electrical and Electronics Engineers (IEEE). pp. 307–311. [Google Scholar]
- Dąbrowska, E.; Kołowrocki, K. Monte Carlo Simulation Approach to Determination of Oil Spill Domains at Port and Sea Waters Areas. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2020, 14, 59–64. [Google Scholar] [CrossRef]
- Dąbrowska, E.; Kołowrocki, K. Modelling, Identification and Prediction of Oil Spill Domains at Port and Sea Water Areas. J. Pol. Saf. Reliab. Assoc. Summer Saf. Reliab. Semin. 2019, 10, 43–58. [Google Scholar]
- Grabski, F. Semi-Markov Processes: Application in System Reliability and Maintenance; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Kołowrocki, K.; Soszyńska-Budny, J. Reliability and Safety of Complex Technical Systems and Processes: Modeling—Identification—Prediction—Optimization, 1st ed.; Springer: London, UK, 2011. [Google Scholar]
- Dąbrowska, E. Monte Carlo Simulation Prediction of Oil Spill Domain Movement considering Oil Spill Layer Thickness and Changing Hydro-Meteorological Conditions Impacts. Waters, 2023; in press. [Google Scholar]
- Dąbrowska, E.; Soszyńska-Budny, J. Monte Carlo Simulation Forecasting of Maritime Ferry Safety and Resilience. In Proceedings of the 2018 IEEE International Conference on Industrial Engineering and Engineering Management—IEEM 2018, Bangkok, Thailand, 16–19 December 2018; ISBN 978-1-5386-6785-9. [Google Scholar]
- Kołowrocki, K.; Kuligowska, E. Operation and Climate-Weather Change Impact on Maritime Ferry Safety. In Safety and Reliability—Safe Societies in a Changing World; CRC Press: London, UK, 2018; pp. 849–858. ISBN 978-0-8153-8682-7. European Safety and Reliability Conference—ESREL 2018, Trondheim, Norway, 17–21 June 2018. [Google Scholar]
- Kołowrocki, K.; Kuligowska, E.; Soszyńska-Budny, J.; Torbicki, M. Safety and Risk Prediction of Port Oil Piping Transportation System Impacted by Climate-Weather Change Process. In Proceedings of the International Conference on Information and Digital Technologies 2017-IDT, Zilina, Slovakia, 5–7 July 2017; pp. 173–177, ISBN 978-1-5090-5688-0. [Google Scholar]
- Bogalecka, M.; Kołowrocki, K. Prediction of critical infrastructure accident losses of chemical releases impacted by climate-weather change. In Proceedings of the 2018 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Bangkok, Thailand, 16–19 December 2018; pp. 788–792. [Google Scholar] [CrossRef]
- Bogalecka, M.; Kołowrocki, K. Minimization of critical infrastructure accident losses of chemical releases impacted by climate-weather change. In Proceedings of the 2018 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Bangkok, Thailand, 16–19 December 2018; pp. 1657–1661. [Google Scholar] [CrossRef]
- Ellis, J. Analysis of accidents and incidents occurring during transport of packaged dangerous goods by sea. Saf. Sci. 2011, 49, 1231–1237. [Google Scholar] [CrossRef]
- Elliot, A.; Hurford, N.; Penn, C. Shear diffusion and the spreading of slicks. Mar. Pollut. Bull. 1986, 17, 308–313. [Google Scholar] [CrossRef]
- Bruno, M.F.; Molfetta, M.G.; Pratola, L.; Mossa, M.; Nutricato, R.; Morea, A.; Nitti, D.O.; Chiaradia, M.T. A Combined Approach of Field Data and Earth Observation for Coastal Risk Assessment. Sensors 2019, 19, 1399. [Google Scholar] [CrossRef] [PubMed]
- Farrington, J.W. Oil Pollution in the Marine Environment II: Fates and Effects of Oil Spills. Environ. Sci. Policy Sustain. Dev. 2014, 56, 16–31. [Google Scholar] [CrossRef]
- Hryniewicz, O.; Kaczmarek-Majer, K. Monitoring of Possibilisticaly Aggregated Complex Time Series. In Building Bridges Between Soft and Statistical Methodologies for Data Science. In Proceedings of 10th International Conference on Soft Methods in Probability and Statistics (SMPS), Valladolid, Spain, 14–16 September 2022; Advances in Intelligent Systems and Computing; Garcia-Escudero, L.A., Gordaliza, A., Mayo, A., Gomez, M.A.L., Gil, M.A., Grzegorzewski, P., Hryniewicz, O., Eds.; Springer Nature: Cham, Swizerland, 2023; pp. 208–215. [Google Scholar] [CrossRef]
- Van Belle, J.; van Barneveld-Biesma, J.; Bastiaanssen, V.; Buitenhuis, A.; Saes, L.; van Veen, G. ICOS Impact Assessment Report; Technopolis: Amsterdam, The Netherlands, 2018; pp. 48–51. [Google Scholar]
- EU-CIRCLE Report D2.3-GMU2. Identification Methods and Procedures of Climate-Weather Change Process Including Extreme Weather Hazards. 2016. Available online: http://jpsra.am.gdynia.pl/ (accessed on 16 May 2023).
- Gdynia Maritime University Safety Interactive Platform. Available online: http://gmu.safety.umg.edu.pl/ (accessed on 1 June 2022).
- Kołowrocki, K.; Kuligowska, E.; Soszyńska-Budny, J.; Torbicki, M. Simplified Impact Model of Critical Infrastructure Safety Related to Climate-Weather Change Process. In Proceedings of the International Conference on Information and Digital Technologies 2017-IDT, Zilina, Slovakia, 5–7 July 2017; pp. 187–190, ISBN 978-1-5090-5688-0. [Google Scholar]
- Kołowrocki, K.; Soszyńska-Budny, J.; Torbicki, M. Critical Infrastructure Impacted by Climate Change Safety and Resilience Indicators. In Proceedings of the 2018 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Bangkok, Thailand, 16–19 December 2018; pp. 986–990. [Google Scholar] [CrossRef]
- Kuligowska, E.; Torbicki, M. Climate-weather change process realizations uniformity testing for maritime ferry operating area. In Proceedings of the Applied Stochastic Models and Data Analysis International Conference with Demographics Workshop—ASMDA 2017, London, UK, 6–9 June 2017; pp. 605–618. [Google Scholar]
- Kuligowska, E.; Torbicki, M. Identification and prediction of climate-weather change processes for port oil piping transportation system and maritime ferry operation areas after their realisations successful uniformity testing. In Proceedings of the Applied Stochastic Models and Data Analysis International Conference with Demographics Workshop—ASMDA 2017, London, UK, 6–9 June 2017; pp. 621–630. [Google Scholar]
- Torbicki, M. Longtime Prediction of Climate-Weather Change Influence on Critical Infrastructure Safety and Resilience. In Proceedings of the 2018 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Bangkok, Thailand, 16–19 December 2018; pp. 996–1000. [Google Scholar] [CrossRef]
- Marseguerra, M.; Zio, E. Basics of the Monte Carlo Method with Application to System Reliability; LiLoLe: Hagen, Germany, 2002. [Google Scholar]
- Rao, M.S.; Naikan, V.N.A. Review of simulation approaches in reliability and availability modeling. Int. J. Perform. Eng. 2016, 12, 369–388. [Google Scholar]
- Law, A.M. Simulation Modelling and Analysis, 5th ed.; McGraw Hill Education: New York, NY, USA, 2000; ISBN 978-0-07-340132-4. [Google Scholar]
- National Oceanic and Atmospheric Administration (NOAA). Response Tools for Oil Spills. Available online: http://response.restoration.noaa.gov/oil-and-chemical-spills/oil-spills/response-tools/response-tools-oil-spills.html/ (accessed on 30 May 2022).
- National Oceanic and Atmospheric Administration (NOAA). Trajectory Analysis Handbook. NOAA Hazardous Material Response Division. Seattle: WA. Available online: http://www.response.restoration.noaa.gov/ (accessed on 30 May 2022).
- Horn, M.; French-McCay, D. Trajectory and fate modeling with acute effects assessment of hypothetical spills of diluted bitumen into rivers. In Proceedings of the 38th AMOP Technical Seminar on Environmental Contamination and Response, Vancouver, BC, Canada, 2–4 June 2015; pp. 549–581. [Google Scholar]
- Johansen, T.; Reed, M.; Boksburg, N.R. Natural dispersion revisited. Mar. Pollut. Bull. 2015, 93, 20–26. [Google Scholar] [CrossRef]
- Das, T.; Goerlandt, F. Bayesian inference modeling to rank response technologies in arctic marine oil spills. Available online: https://www.sciencedirect.com/science/article/abs/pii/S0025326X22008852 (accessed on 16 May 2023).
- Kut, P.; Pietrucha-Urbanik, K. Most Searched Topics in the Scientific Literature on Failures in Photovoltaic Installations. Energies 2022, 15, 8108. [Google Scholar] [CrossRef]
- Toruń, A.; Burniak, C.; Biały, J.; Tomaszewska, J.; Grzesik, N.; Hošková-Mayerová, Š.; Woch, M.; Zieja, M.; Rurak, A. Challenges for Air Transport Providers in Czech Republic and Poland. J. Adv. Transp. 2018, 6374592, 1–7. [Google Scholar] [CrossRef]
- Woch, M.; Zieja, M.; Tomaszewska, J. Analysis of the Time between Failures of Aircrafts. In Proceedings of the 2017 2th International Conference on System Reliability and Safety (ICSRS), Milan, Italy, 20–22 December 2017; pp. 112–118, ISBN 978-1-5386-3320-5. [Google Scholar]
- Eldeeb, H.M.; Ibrahim, A.; Mowafy, M.H.; Zeleňáková, M.; Abd-Elhamid, H.F.; Pietrucha-Urbanik, K.; Ghonim, M.T. Assessment of Dams’ Failure and Flood Wave Hazards on the Downstream Countries: A Case Study of the Grand Ethiopian Renaissance Dam (GERD). Water 2023, 15, 1609. [Google Scholar] [CrossRef]
| States | wh [m] | ws [m/s] |
|---|---|---|
| 1 | 0–2 | 0–17 |
| 2 | 2–5 | 0–17 |
| 3 | 5–14 | 0–17 |
| 4 | 0–2 | 17–33 |
| 5 | 2–5 | 17–33 |
| 6 | 5–14 | 17–33 |
| State | 1 | 2 | 3 | 4 | 5 | 6 | Total |
|---|---|---|---|---|---|---|---|
| ni | 405 | 237 | 0 | 0 | 27 | 11 | 680 |
| State | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1→ | – | 1516 | 0 | 1 | 31 | 0 |
| 2→ | 1001 | – | 0 | 0 | 435 | 0 |
| 3→ | 0 | 11 | – | 0 | 1 | 0 |
| 4→ | 0 | 0 | 0 | – | 1 | 0 |
| 5→ | 0 | 298 | 2 | 0 | – | 88 |
| 6→ | 0 | 45 | 16 | 0 | 48 | – |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dąbrowska, E. Oil Discharge Trajectory Simulation at Selected Baltic Sea Waterway under Variability of Hydro-Meteorological Conditions. Water 2023, 15, 1957. https://doi.org/10.3390/w15101957
Dąbrowska E. Oil Discharge Trajectory Simulation at Selected Baltic Sea Waterway under Variability of Hydro-Meteorological Conditions. Water. 2023; 15(10):1957. https://doi.org/10.3390/w15101957
Chicago/Turabian StyleDąbrowska, Ewa. 2023. "Oil Discharge Trajectory Simulation at Selected Baltic Sea Waterway under Variability of Hydro-Meteorological Conditions" Water 15, no. 10: 1957. https://doi.org/10.3390/w15101957





