Gas Release and Solution as Possible Mechanism of Oscillation Damping in Water Hammer Flow
Abstract
:1. Introduction
2. Mathematical Models
2.1. Continuity Equation
2.2. Gas Release and Solution Equation
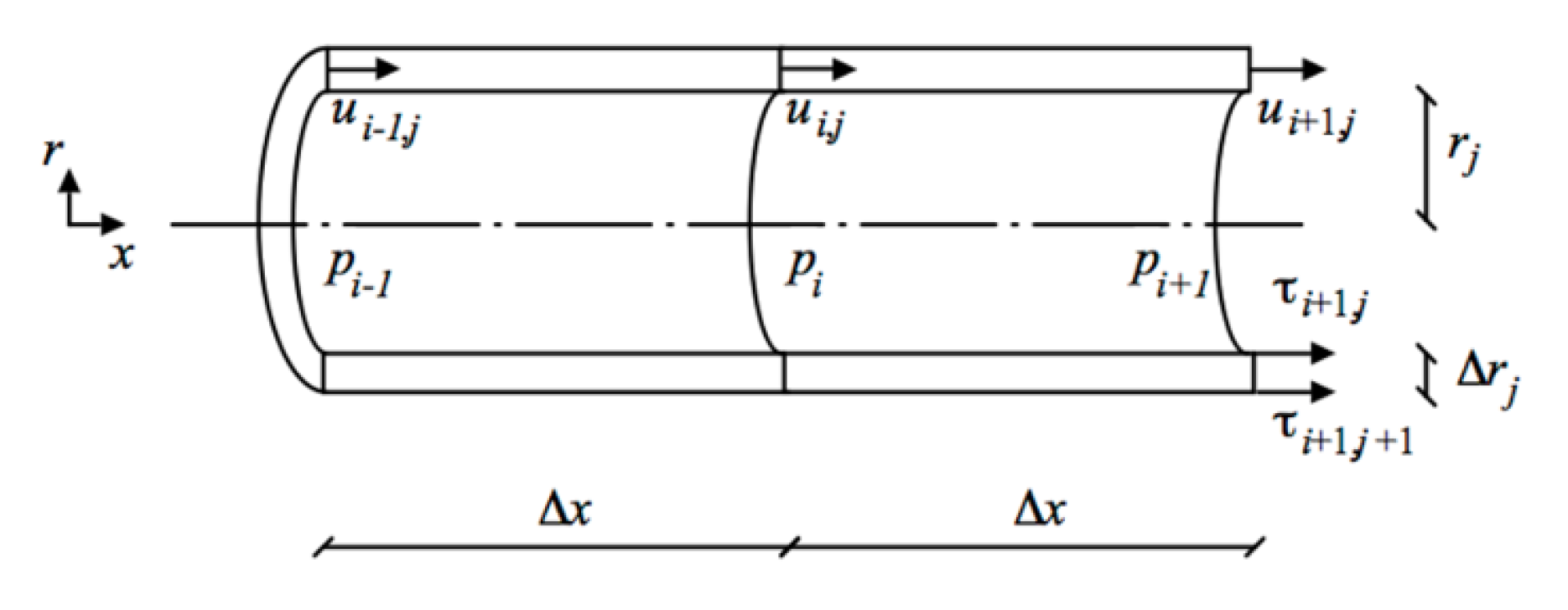
2.3. Momentum Equations
2.4. Boundary Conditions
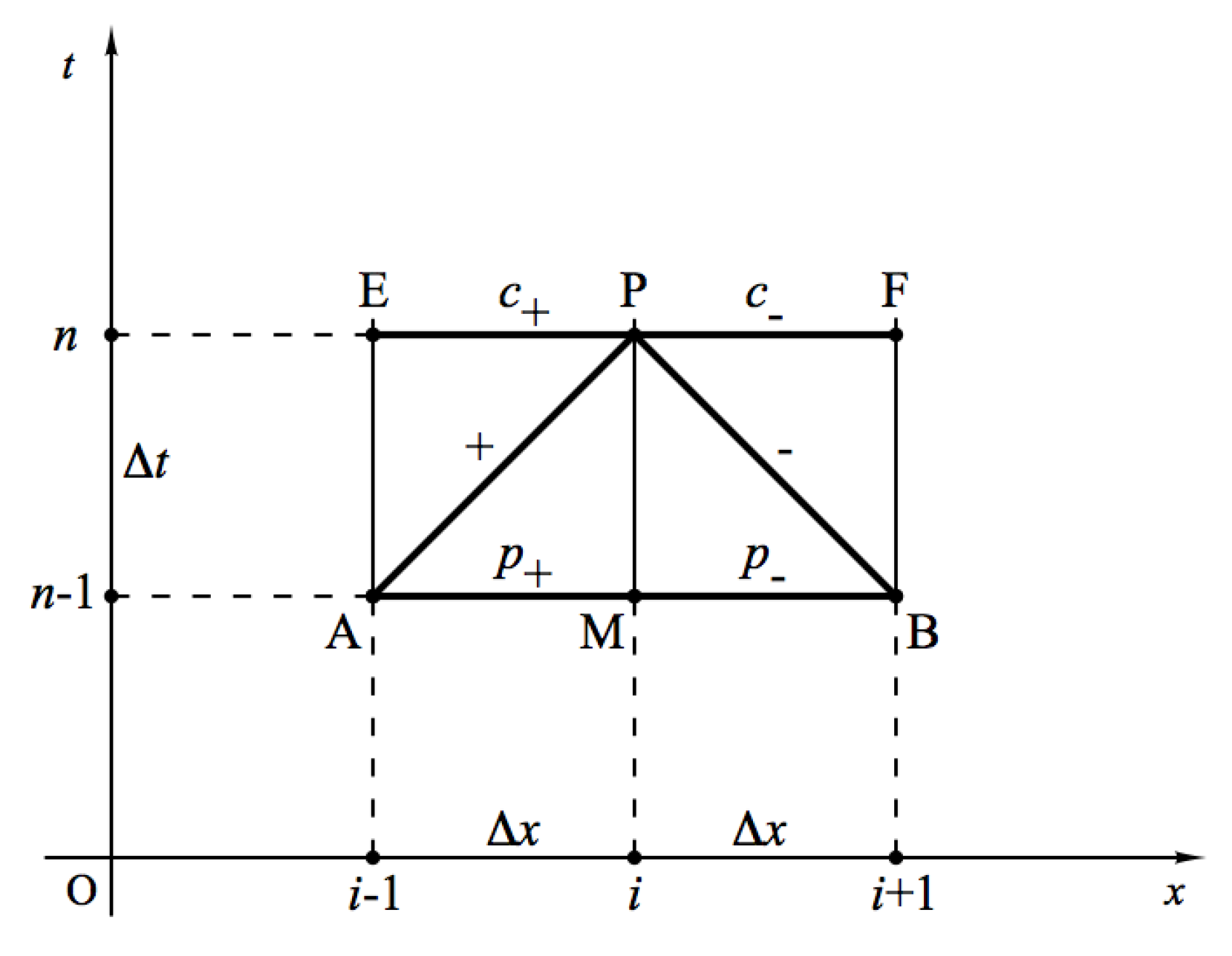
2.5. Method of Characteristics
2.6. Numerical Scheme
2.7. Micro-GA
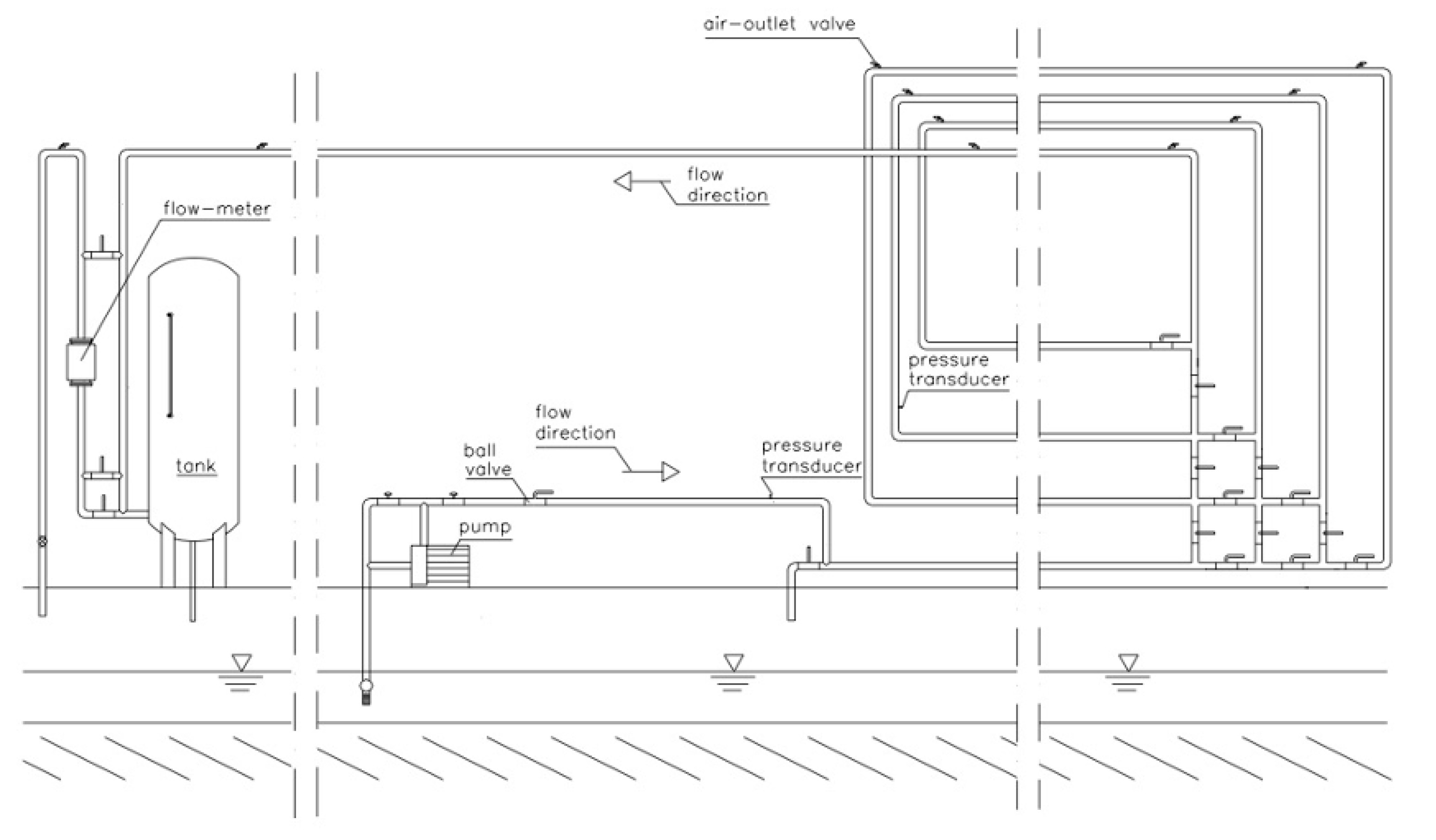
3. Experimental Installation
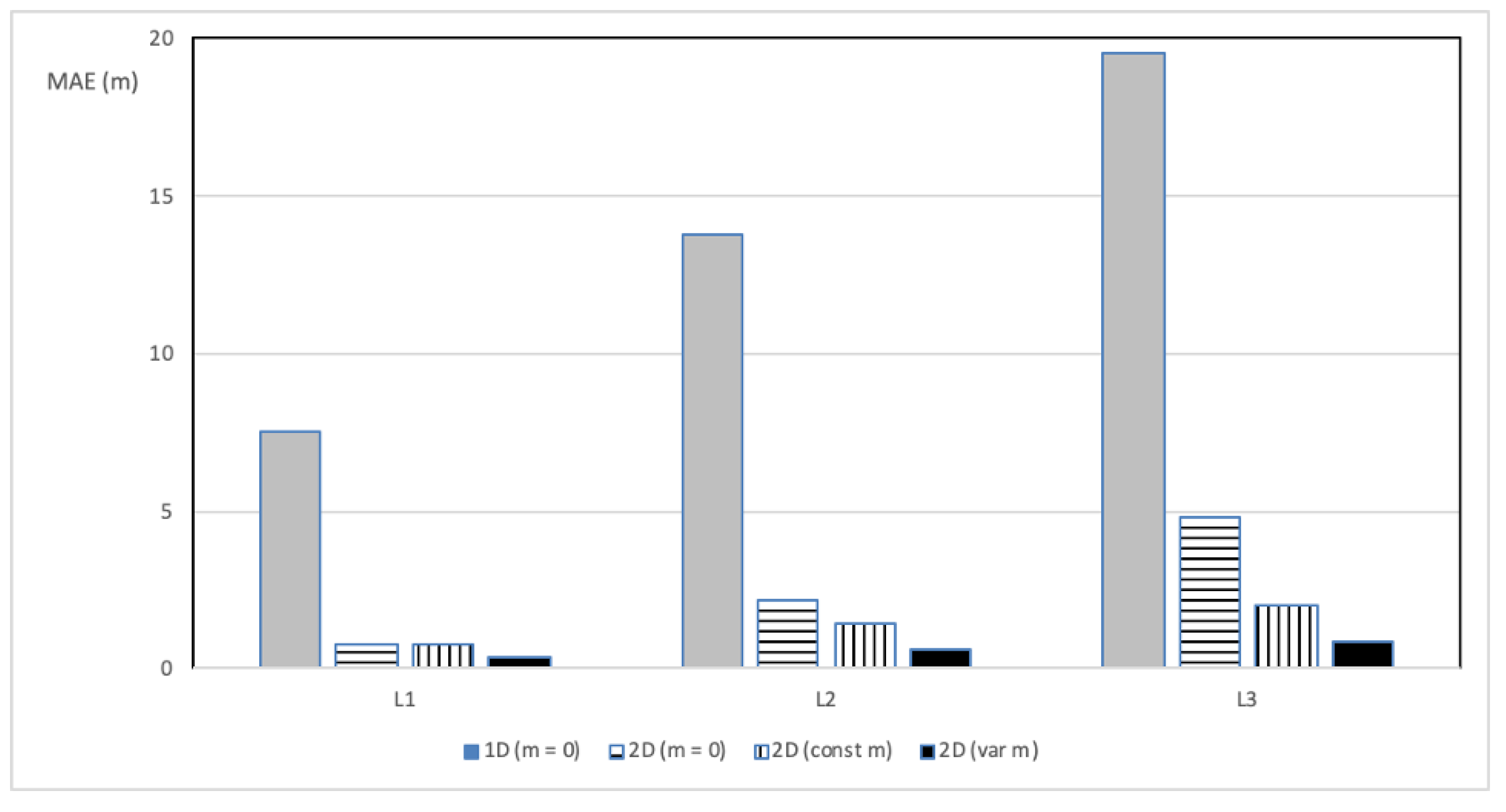
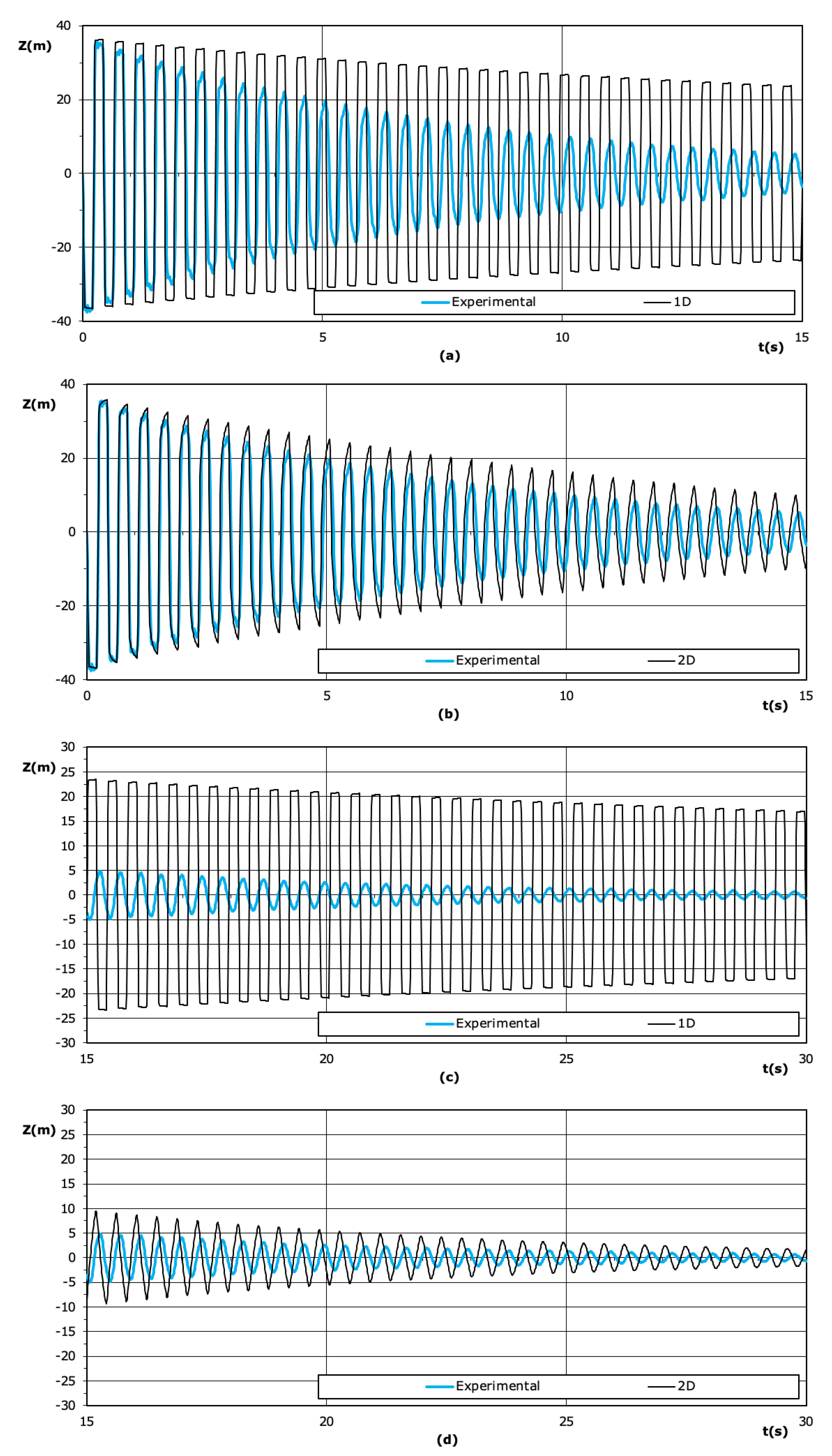
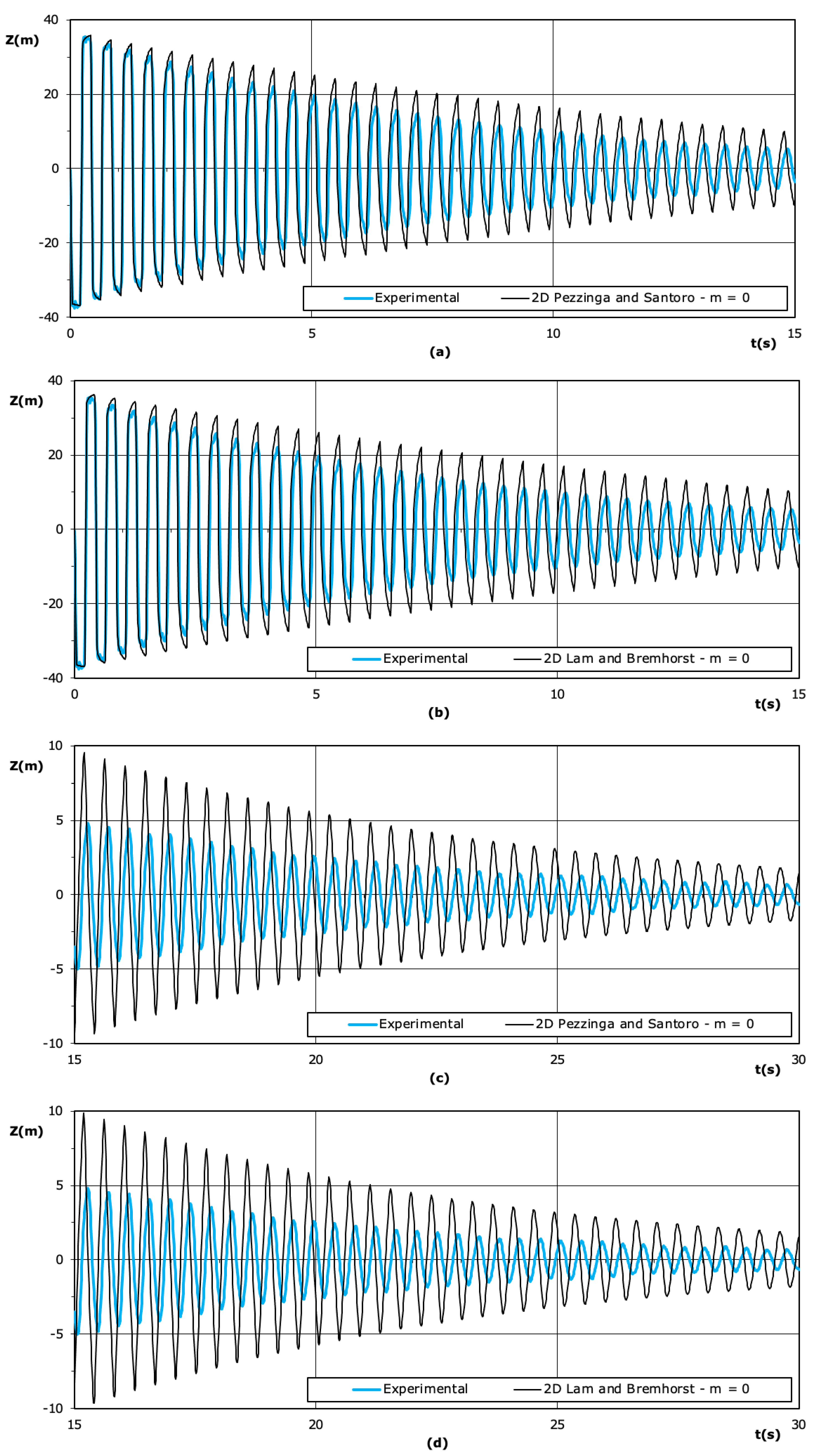
4. Analysis of Results
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ghidaoui, M.S.; Zhao, M.; McInnis, D.A.; Axworthy, D.H. A review of water hammer theory and practice. Appl. Mech. Rev. 2005, 58, 49–76. [Google Scholar] [CrossRef]
- Pezzinga, G. Evaluation of unsteady flow resistances by quasi-2D or 1D models. J. Hydraul. Eng. 2000, 126, 778–785. [Google Scholar] [CrossRef]
- Vardy, A.E.; Hwang, K.L. A characteristics model of transient friction in pipes. J. Hydraul. Res. 1991, 29, 669–684. [Google Scholar] [CrossRef]
- Eichinger, P.; Lein, G. The Influence of Friction on Unsteady Pipe Flow. In Proceedings of the International Conference on Unsteady Flow and Fluid Transients, Durham, UK, 29 September–1 October 1992; IAHR: Durham, UK, 1992; pp. 41–50. [Google Scholar]
- Silva-Araya, W.F.; Chaudhry, M.H. Computation of energy dissipation in transient flow. J. Hydraul. Eng. 1997, 123, 108–115. [Google Scholar] [CrossRef]
- Pezzinga, G. Quasi-2D Model for Unsteady Flow in Pipe Networks. J. Hydraul. Eng. 1999, 125, 676–685. [Google Scholar] [CrossRef]
- Pezzinga, G.; Brunone, B. Turbulence, friction and energy dissipation in transient pipe flow. In Vorticity and Turbulence Effects in Fluid Structures Interactions; Brocchini, M., Trivellato, F., Eds.; WIT Press: Southampton, UK, 2006; pp. 213–236. [Google Scholar]
- Vardy, A.E. On Sources of Damping in Water-Hammer. Water 2023, 15, 385. [Google Scholar] [CrossRef]
- Ferras, D.; Manso, P.A.; Schleiss, A.J.; Covas, D.I. Experimental distinction of damping mechanisms during hydraulic transients in pipe flow. J. Fluids Struct. 2016, 66, 424–446. [Google Scholar] [CrossRef]
- Kranenburg, C. Gas release during transient cavitation in pipes. J. Hydraul. Div. 1974, 100, 1383–1398. [Google Scholar] [CrossRef]
- Wiggert, D.C.; Sundquist, M.J. The Effect of Gaseous Cavitation on Fluid Transients. J. Fluids Eng. 1979, 101, 79–86. [Google Scholar] [CrossRef]
- Wylie, E.B. Low void fraction two-component two-phase flow. In Unsteady Flow and Fluid Transients; Bettess, R., Watts, J., Eds.; Balkema: Rotterdam, The Netherlands, 1992; pp. 3–9. [Google Scholar]
- Huygens, M.; Verhoeven, R.; Van Pocke, L. Air entrainment in water hammer phenomena. WIT Trans. Eng. Sci. 1998, 18, 10. [Google Scholar]
- Hadj-Taieb, E.; Lili, T. Transient flow of homogeneous gas-liquid mixtures in pipelines. Int. J. Numer. Methods Heat Fluid Flow 1998, 8, 350–368. [Google Scholar] [CrossRef]
- Lee, T.S.; Low, H.T.; Nguyen, D.T. Effects of air entrainment on fluid transients in pumping systems. J. Appl. Fluid Mech. 2007, 1, 55–61. [Google Scholar]
- Lee, T.S.; Low, H.T.; Huang, W.D. Numerical study of fluid transient in pipes with air entrainment. Int. J. Comput. Fluid Dyn. 2004, 18, 381–391. [Google Scholar] [CrossRef]
- Bergant, A.; Simpson, A.R.; Tijsseling, A.S. Water hammer with column separation: A historical review. J. Fluids Struct. 2006, 22, 135–171. [Google Scholar] [CrossRef]
- Fanelli, M. Hydraulic Transients with Water Column Separation; IAHR Working Group 1971–1991 Synthesis Report; IAHR: Delft, The Netherlands; ENEL-CRIS: Milan, Italy, 2000. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics: Course of Theoretical Physics; Pergamon Press: London, UK, 1959; Volume 6. [Google Scholar]
- Pezzinga, G. Second viscosity in transient cavitating pipe flows. J. Hydraul. Res. 2003, 41, 656–665. [Google Scholar] [CrossRef]
- Cannizzaro, D.; Pezzinga, G. Energy dissipation in transient gaseous cavitation. J. Hydraul. Eng. 2005, 131, 724–732. [Google Scholar] [CrossRef]
- Pezzinga, G.; Santoro, V.C. MOC-Z Models for Transient Gaseous Cavitation in Pipe Flow. J. Hydraul. Eng. 2020, 146, 04020076. [Google Scholar] [CrossRef]
- Lam, C.K.G.; Bremhorst, K.A. Modified Form of the k-ε Model for Predicting Wall Turbulence. J. Fluids Eng. 1981, 103, 456–460. [Google Scholar] [CrossRef]
- Wylie, E.B.; Streeter, V.L. Fluid Transients in Systems; Prentice-Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Zielke, W.; Perko, H.D.; Keller, A. Gas Release in Transient Pipe Flow. In Pressure Surges, Proceedings of the 6th International Conference, Cambridge, UK, 4–6 October 1989; BHRA: Cranfield, UK, 1990; pp. 3–13. [Google Scholar]
- Santoro, V.C.; Crimì, A.; Pezzinga, G. Developments and limits of discrete vapor cavity models of transient cavitating pipe flow: 1D and 2D flow numerical analysis. J. Hydraul. Eng. 2018, 144, 04018047. [Google Scholar] [CrossRef]
- Budny, D.D.; Wiggert, D.C.; Hatfield, F.J. The influence of structural damping on internal pressure during a transient pipe flow. J. Fluids Eng. 1991, 113, 424–429. [Google Scholar] [CrossRef]

| Test | (L/s) | (m/s) | (m) | |
|---|---|---|---|---|
| L1 | 0.207 | 0.091 | 68.12 | 5300 |
| L2 | 0.409 | 0.179 | 66.87 | 10,500 |
| L3 | 0.598 | 0.262 | 60.08 | 15,400 |
| Test | 2D—Constant Mass | 2D—Variable Mass | |
|---|---|---|---|
| (mg/m3) | (mg/m3) | (s) | |
| L1 | 1.96 | 0.00 | 753.2 |
| L2 | 17.30 | 6.16 | 754.2 |
| L3 | 28.64 | 14.96 | 815.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pezzinga, G. Gas Release and Solution as Possible Mechanism of Oscillation Damping in Water Hammer Flow. Water 2023, 15, 1942. https://doi.org/10.3390/w15101942
Pezzinga G. Gas Release and Solution as Possible Mechanism of Oscillation Damping in Water Hammer Flow. Water. 2023; 15(10):1942. https://doi.org/10.3390/w15101942
Chicago/Turabian StylePezzinga, Giuseppe. 2023. "Gas Release and Solution as Possible Mechanism of Oscillation Damping in Water Hammer Flow" Water 15, no. 10: 1942. https://doi.org/10.3390/w15101942






