Hybrid Optimization Algorithms of Firefly with GA and PSO for the Optimal Design of Water Distribution Networks
Abstract
:1. Introduction
2. Materials and Methods
2.1. Formulation of Pipe Networks Optimization
2.1.1. Total Pipe Cost
2.1.2. Objective Function
2.1.3. Hydraulic Constraints
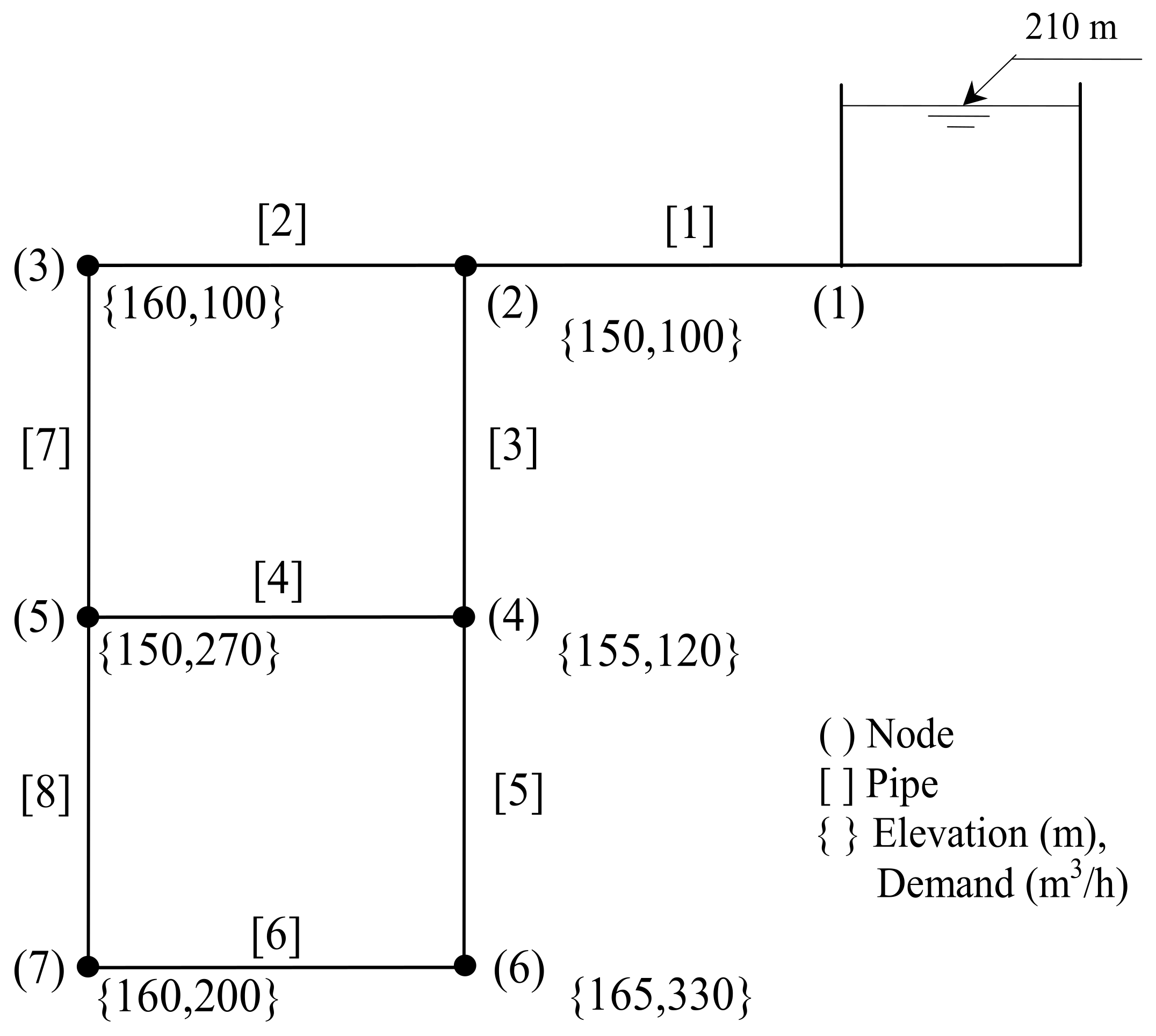
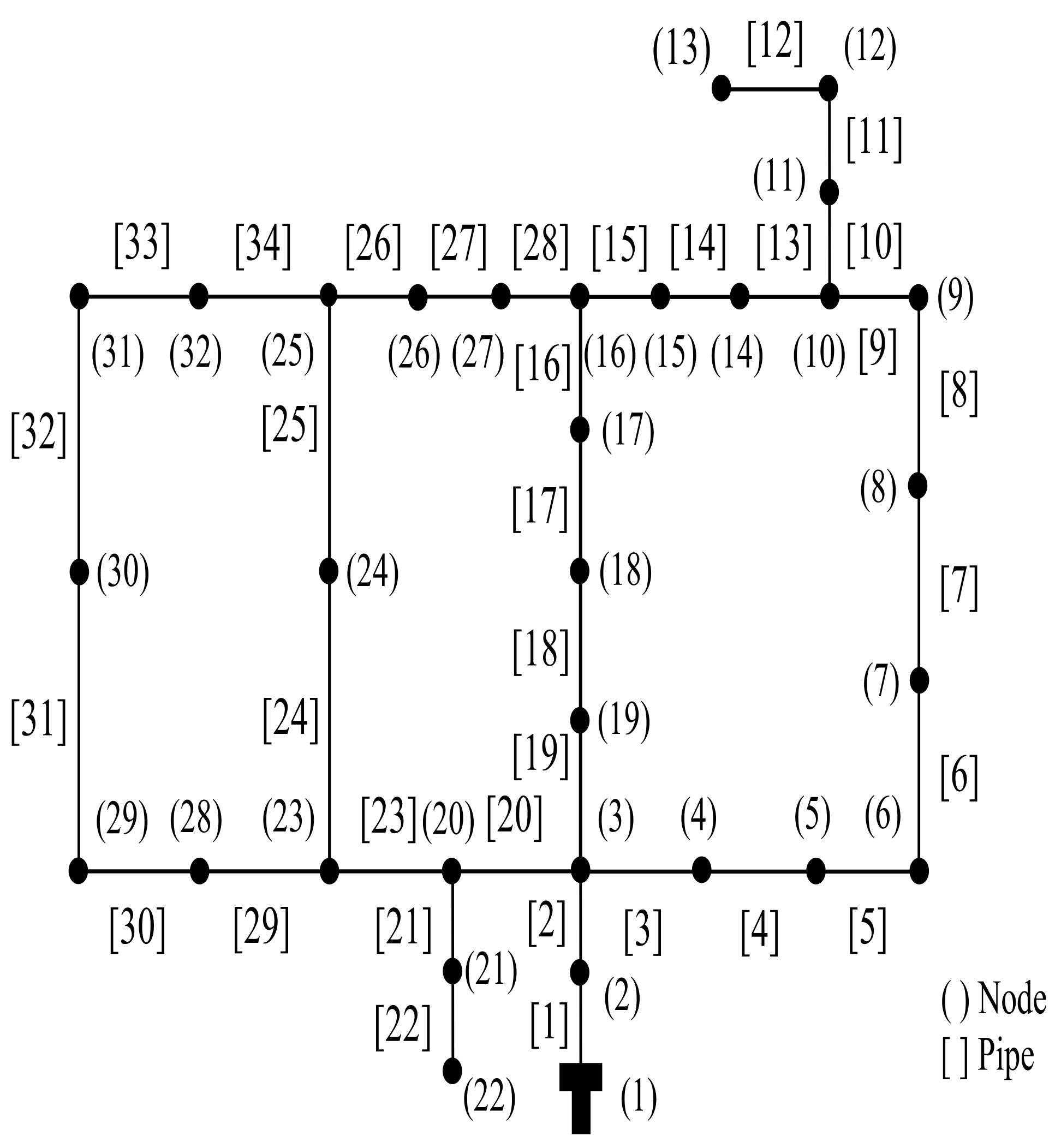
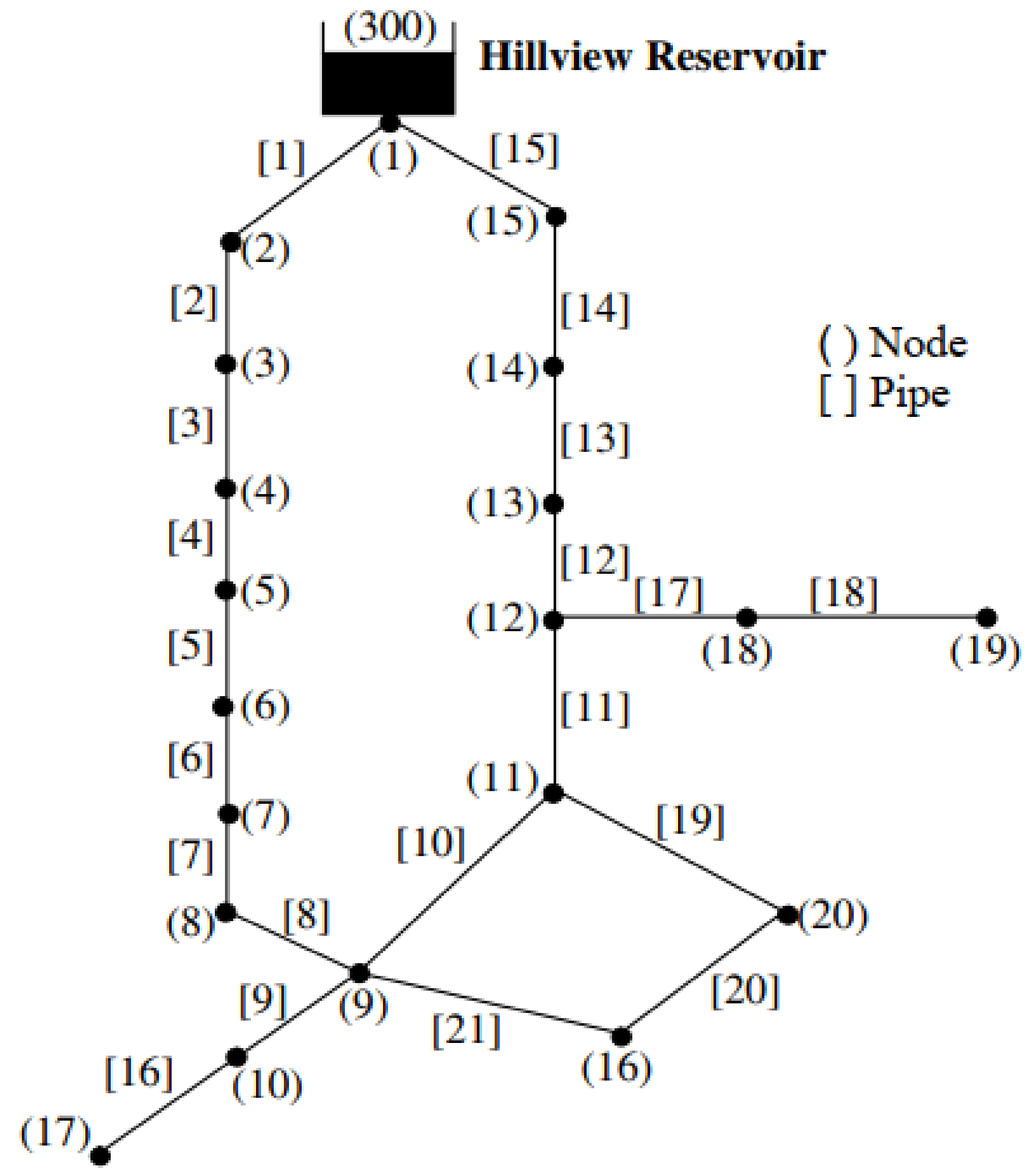
2.2. Benchmark Networks
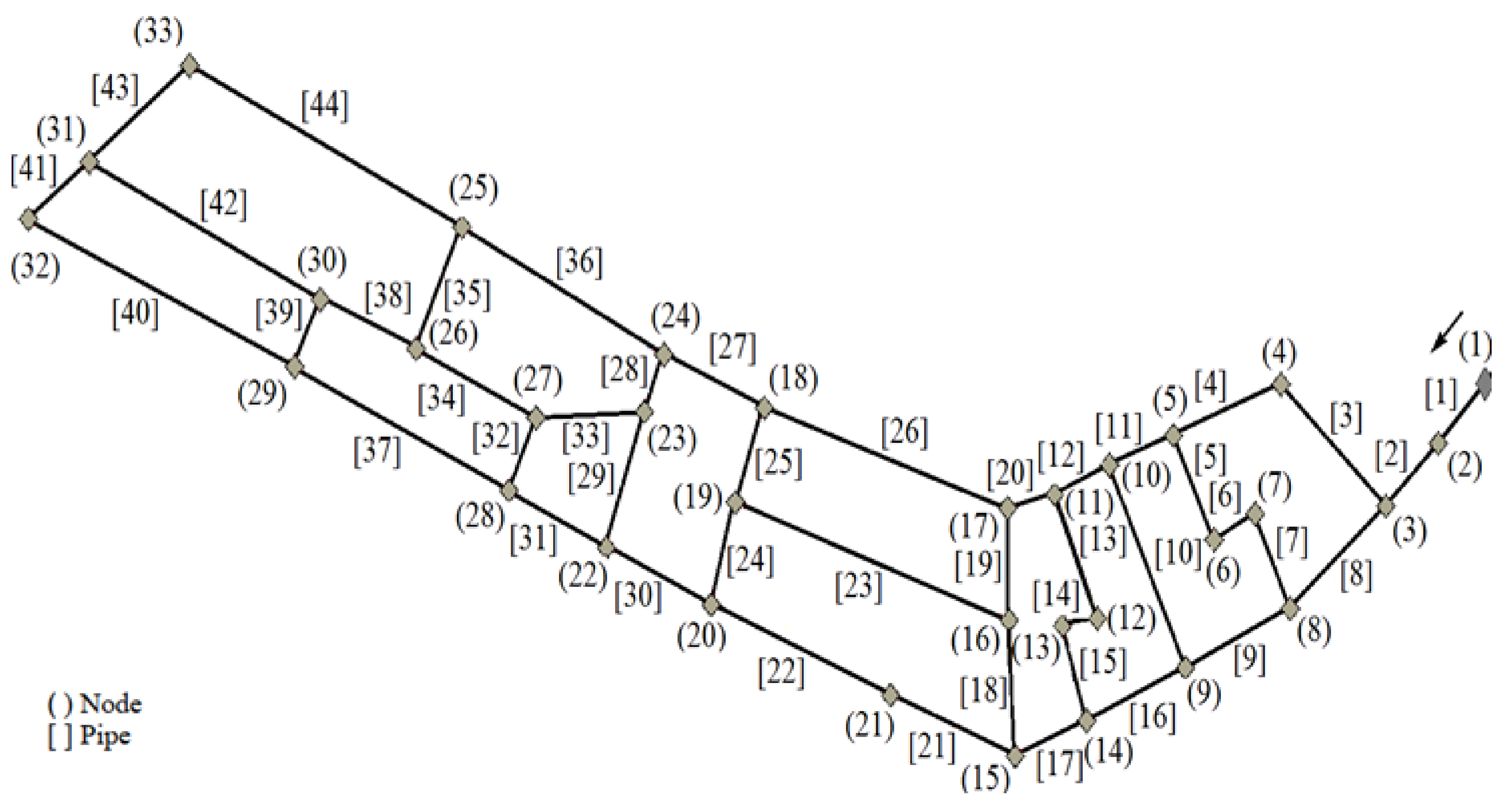
2.3. Real Case Study of El-Mostakbal City Network
3. Firefly Optimization Algorithm
3.1. Formulation of Firefly Algorithm (FA)
- Initialize the input parameters for FA.
- Generate an initial population of npop fireflies for the dimension of Npipes.
- The total construction cost of the network, CT and the corresponding constraint for each firefly is evaluated using the simulation model.
- The fitness of each firefly, fi, i = 1, 2, 3, …, npop (the summation of total construction cost and penalty due to the constraints violation [Equation (2)]) is computed.
- Compare the finesses fi and fj for each of the two fireflies i and j, respectively, (i and j = 1: npop and i ≠ j).
- If fi > fj, firefly i moves towards firefly j. Update the position of firefly i, Xi(t) according to Equation (7) and calculate its fitness f′i at the new position, Xi(t + 1).
- 7.
- If f′i < fi replace the position of the firefly i, Xi(t) with the updated one, Xi(t + 1) otherwise keep the old position of the firefly i.
- 8.
- Repeat Steps 5 to 7 until the maximum number of iterations, niter is reached.
- 9.
- Rank the fireflies and find the current best solution.
3.2. Hybrid Firefly-Particle Swarm Optimization (FAPSO) Model
- Initialize the input parameters of the FA and PSO algorithms.
- Generate an initial population of npop particles with random positions and velocity on Npipes dimensions in the solution space.
- Calculate the fitness, fi for each particle, i in the population (i =1, 2. 3. …, npop)
- Select the social global best, gbest and personal best, pbest particles.
- Compare each particle’s fitness fi value in the population with gbest in the last iteration (t − 2). If fi < or equal gbest(t − 2) (t > 2, t indicates the iteration number) start local search using FA as given in Equations (9) and (10)
- 6.
- Compare fitness, fi for each particle, i in the population with those of gbest and pbest particles. Update gbest for the population and pbest of every particle.
- 7.
- Repeat steps 5 to 6 until the maximum number of iterations, niter is reached.
3.3. Hybrid Firefly-Genetic Algorithm Model (FAGA)
- Generate a random initial population of npop fireflies.
- Calculate the fitness, fi for each firefly, i in the population (i =1, 2. 3. …, npop)
- Compare the fitness fi and fj for each of the two fireflies i, j, respectively, (i and j = 1: npop and i ≠ j).
- Apply genetic crossover for the two fireflies i and j for the case fj < f i according to Equations (13) and (14).
- 5.
- Replace the old solutions for the fireflies i and j with the new ones if they have better finesses.
- 6.
- Repeat steps 3 to 5 until reaching the maximum number of iterations, niter.
3.4. Models Parameters
4. Application and Results
Performance Evaluation
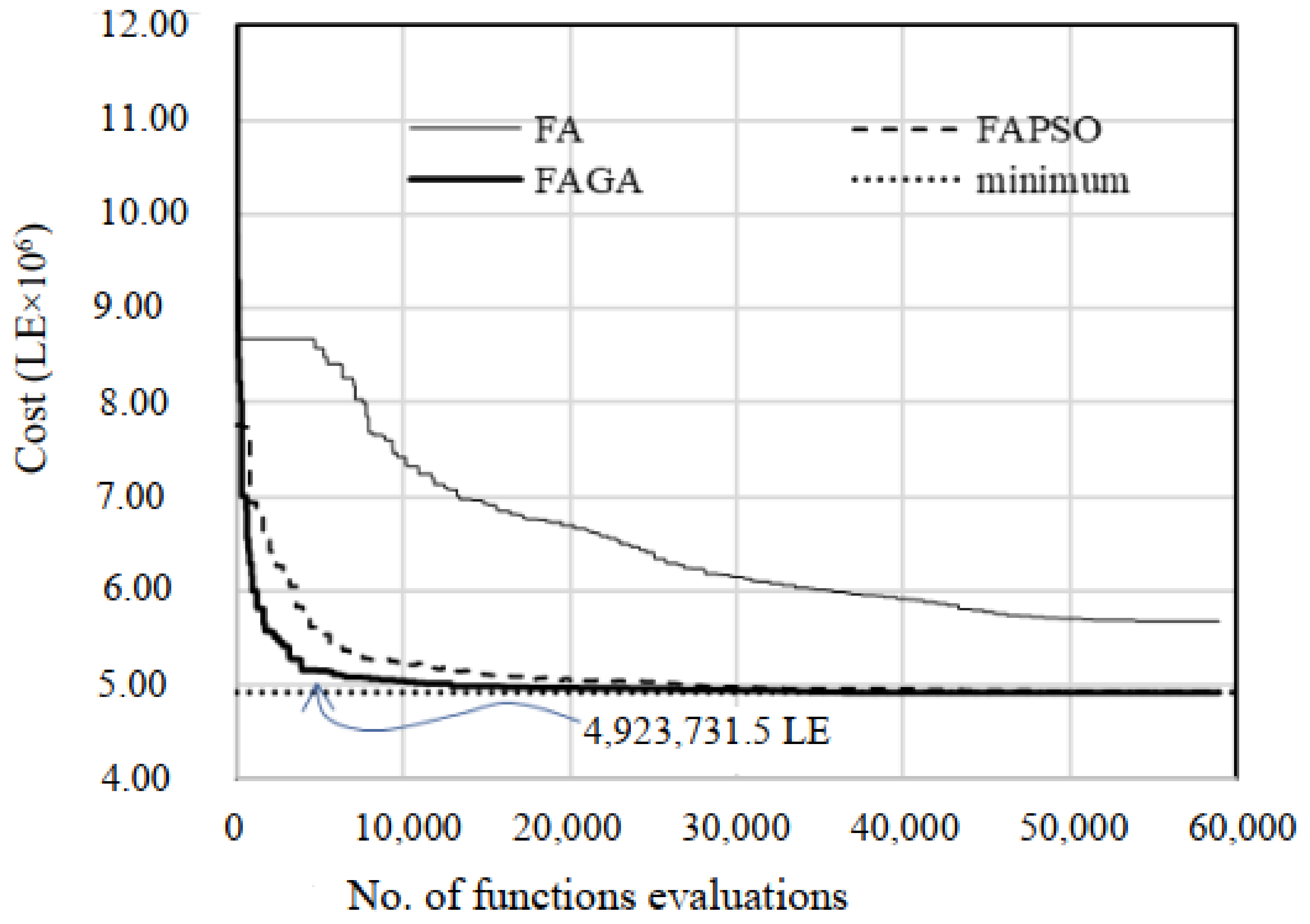
- Determine the known optimal solution f(x*) for the pipe networks (two-loop, 419,000, Hanoi, 6.081 × 106 and New York, 38,637,600). If the known optimal solution is not available, f(x*) is replaced with the best-known optimal solution (EL-Mostakbal, 4,923,731.5 obtained from the present study).
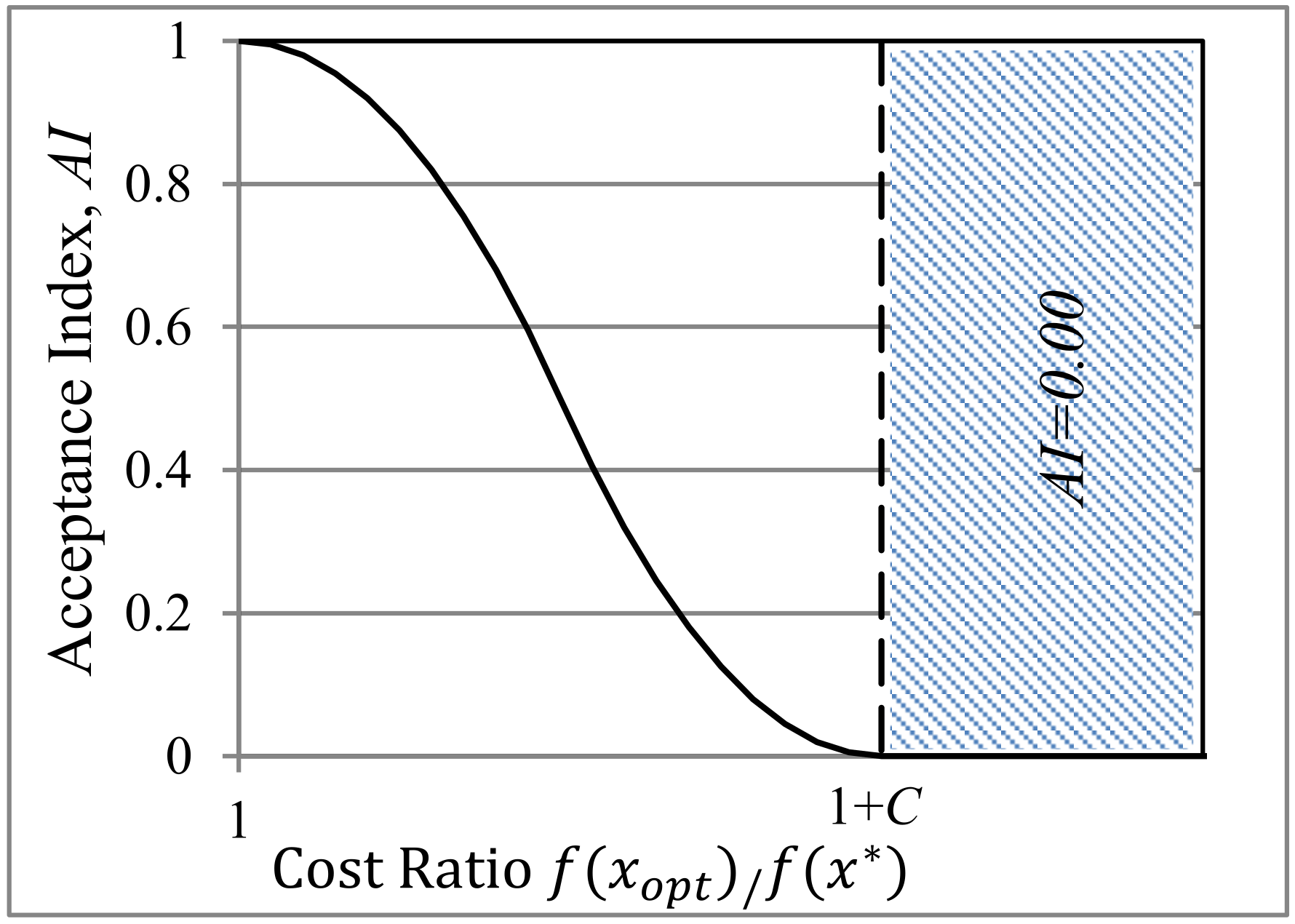
- The robustness of the optimization algorithm is measured by accepting optimal solutions slightly greater than the known optimal solution f(x*) such that where C = 0, 0.01 and 0.02.
- Run each of the three optimization algorithms considered in this study, FA, FAPSO and FAGA, 20 times for each of the four networks and denote the objective function at the termination point, , i = 1, 2, 3, …,20.
- Estimate the Acceptance Index AIi as given in Equation (17) using the principles of fuzzy logic [39]. Values of optimization error, C = 0, 0.01, and 0.02, are assumed to be acceptable. Zero value of C means a tenuous relationship between AIi and . At the same time, the second and third values of C denote continuous function (S-shape fuzzy membership function) to simulate the relationship between the Acceptance index, AIi and . As given in Equation (17), it is clear that AIi takes a value equal to 1 if and value between 1 and zero if while it takes value of zero if more than or equal .
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mala-Jetmarova, H.; Sultanova, N.; Savic, D. Lost in Optimization of Water Distribution Systems? A Literature Review of System Design. Water 2018, 10, 307. [Google Scholar] [CrossRef]
- Kumar, V.; Yadav, S.M. A state-of-the-Art review of heuristic and metaheuristic optimization techniques for the management of water resources. Water Supply 2022, 22, 3702–3728. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Reca, J.; Martinez, J.; Lopez, R. A hybrid water distribution networks design optimization method based on a search space reduction approach and a genetic algorithm. Water 2017, 9, 845. [Google Scholar] [CrossRef]
- Sangroula, U.; Han, K.-H.; Koo, K.-M.; Gnawali, K.; Yum, K.-T. Optimization of water distribution networks using genetic algorithm based SOP–WDN program. Water 2022, 14, 851. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A New Optimizer Using Particle Swarm Theory. In Proceedings of the 6th International Symposium on Micro Machine and Human Science; MHS’95, Nagoya, Japan, 4–6 October 1995. [Google Scholar]
- Sampathkumar, K.; Ramasamy, S.; Ramasubbu, B.; Karuppanan, S.; Lakshminarayanan, B. Hybrid optimization model for conjunctive use of surface and groundwater resources in water deficit irrigation system. Water Sci. Technol. 2021, 84, 3055–3071. [Google Scholar] [CrossRef]
- Si, B.; Tian, Z.; Chen, W.; Jin, X.; Zhou, X.; Shi, X. Performance assessment of algorithms for building energy optimization problems with different properties. Sustainability 2019, 11, 18. [Google Scholar] [CrossRef]
- Macedo, J.E.S.; Azevedo, J.R.G.; Bezzerra, S.T.M. Hybrid particle swarm optimization and tabu search for the design of large-scale water distribution networks. Braz. J. Water Resour. Porto Alegre 2021, 26, e11. [Google Scholar] [CrossRef]
- Gu, J.; Sun, Z.; Tang, H.; Jia, X.; Wang, S.; Yan, X.; Ye, G.; Wu, G. Hybrid optimization algorithm of particle swarm optimization and cuckoo search for preventive maintenance period optimization. Discret. Dyn. Nat. Soc. Hindawy 2016, 2016, 1–12. [Google Scholar] [CrossRef]
- El-Shorbagy, M.; Refaey, A. Hybridization of grasshopper optimization Algorithm with genetic algorithm for solving system of non-linear equation. IEEE Access 2020, 8, 220944–220961. [Google Scholar] [CrossRef]
- Zervoudakis, K.; Tsafarakis, S.; Paraskevi-Panagiota, S. A New Hybrid Firefly-Genetic Algorithm for the Optimal Product Line Design Problem; Springer Nature: Cham, Switzerland, 2020. [Google Scholar]
- Abdullah, A.; Deris, S.; Mohamed, M.; Hashim, S. A New Hybrid Firefly Algorithm for Complex and Nonlinear Problem. In Distributed Computing and Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Tahershamsi, A.; Kaveh, A.; Sheikholeslami, R.; Azad, S. An improved firefly with harmony search for optimization of water distribution systems. Sci. Iran. 2014, 21, 1591–1607. [Google Scholar]
- Gu, L.; Wang, G.; Wang, H.; Wang, D. An effective hybrid firefly algorithm with harmony search for global numerical optimization. Sci. World J. 2013, 2013, 125625. [Google Scholar] [CrossRef] [PubMed]
- Kora, P.; Krishna, K. Hybrid Firefly and Particle Swarm Optimization Algorithm for the Detection of Bundle Branch Block. Int. J. Cardiovasc. Acad. 2016, 2, 44–48. [Google Scholar] [CrossRef]
- Elkhechafi, M.; Hachemi, H.; Elkettani, Y. A new hybrid firefly with genetic algorithm for global optimization. Int. J. Manag. Appl. Sci. 2017, 3, 47–51. [Google Scholar]
- Aydilek, I.B. A hybrid firefly and particle swarm optimization algorithm for computationally expensive numerical problems. Appl. Soft Comput. 2018, 66, 232–249. [Google Scholar] [CrossRef]
- Nhu, V.; Ngo, P.; Pham, T.; Dou, J.; Song, X.; Hoang, N.; Tran, D.; Cao, D.; Aydilek, I.; Amiri, M.; et al. A new hybrid firefly–PSO optimized random subspace tree intelligence for torrential rainfall-induced flash flood susceptible mapping. Remote Sens. 2020, 12, 2688. [Google Scholar] [CrossRef]
- Khan, A.; Hizam, H.; Wahab, I.; Othman, M. Optimal power flow using hybrid firefly and particle swarm optimization algorithm. PLoS ONE 2020, 15, e0235668. [Google Scholar] [CrossRef]
- Yadav, H.; Chhikara, R.; Kumari, C. Hybrid model using firefly and BBO for feature selection in software production. Recent Adv. Comput. Sci. Commun. 2021, 14, 2754–2760. [Google Scholar] [CrossRef]
- Wahid, F.; Ghazali, R. A hybrid approach of firefly and genetic algorithm for solving optimisation problems. Int. J. Comput. Aided Eng. Technol. 2021, 14, 2754–2760. [Google Scholar] [CrossRef]
- Bilal; Pant, M. Parameter Optimization of Water distribution networks-A hybrid metaheuristic approach. Mater. Manuf. Process. 2020, 35, 737–749. [Google Scholar] [CrossRef]
- Ezzeldin, R.; Djebedjian, B. Optimal design of water distribution networks using whale optimization algorithm. Urban Water J. 2020, 17, 14–22. [Google Scholar] [CrossRef]
- Alperovits, E.; Shamir, U. Design of optimal water distribution systems. Water Resour. Res. 1997, 13, 885–900. [Google Scholar] [CrossRef]
- Fujiwara, O.; Khang, D.B. A two-phase decomposition method for optimal design of looped water distribution networks. Water Resour. Res. 1990, 26, 539–549. [Google Scholar] [CrossRef]
- Schaake, J.C.; Lai, D. Linear Programming and Dynamic Programming Applications to Water Distribution Network Design; Report 116; Hydrodynamics Laboratory, Department of Civil Engineering: Cambridge, MA, USA, 1969. [Google Scholar]
- Rayan, M.A.; Djebedjian, B.; Gad El-Hak, N.; Herric, A. Optimization of Potable Water Network (Case Study). In Proceedings of the 7th International Water Technology Conference (IWTC7), Alexandria, Egypt, 1–3 April 2003. [Google Scholar]
- Abdel-Gawad, H. Modified jaya algorithm for optimal design of water distribution networks. MEJ. Mansoura Eng. J. 2021, 46, 38–54. [Google Scholar] [CrossRef]
- El-Ghandour, H.; Elbeltagi, E. Comparison of five evolutionary algorithms for optimization of water distribution networks. J. Comput. Civ. Eng. ASCE 2018, 32, 04017066. [Google Scholar] [CrossRef]
- Yang, X.S. Firefly Algorithms for Multimodal Optimization; Watanabe, O., Zeugmann, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Li, Y.; Zhao, Y.; Shang, Y.; Liu, J. An improved firefly algorithm with dynamic self-adaptive adjustment. PLoS ONE 2021, 16, e0255951. [Google Scholar] [CrossRef] [PubMed]
- Kazemzadeh-Parsi, M.J.; Daneshmand, F.; Ahmadfard, M.A.; Adamowski, J. Optimal remediation design of unconfined contaminated aquifers based on the finite element method and a modified firefly algorithm. Water Resour. Manag. 2015, 29, 2895–2912. [Google Scholar] [CrossRef]
- Kazemzadeh-Parsi, M.J.; Daneshmand, F.; Ahmadfard, M.A.; Adamowski, J.; Martel, R. Optimal groundwater remediation design of pump and treat systems via a simulation-optimization approach and firefly algorithm. Eng. Optim. 2015, 47, 1–17. [Google Scholar] [CrossRef]
- Riza, L.S.; Munir, J.K.; Hays, R.N.; Sidarto, K.A. Determining the pressure distribution on water pipeline networks. In Proceedings of the 7th International Conference on Intelligent Systems, Modeling and Simulation, Bangkok, Thailand, 25–27 January 2016. [Google Scholar]
- Garousi-Nejad, I.; Bozorg-Haddad, O.; Loaiciga, H.A.; Marino, M.A. Application of the firefly algorithm to optimal operation of reservoirs with the purpose of irrigation supply and hydropower production. J. Irrig. Drain. Eng. 2016, 142, 04016041. [Google Scholar] [CrossRef]
- Yarpiz. Firefly Algorithm (FA), MATLAB Central File Exchange. Available online: https://www.mathworks.com/matlabcentral/fileexchange/52900-firefly-algorithm-fa (accessed on 14 October 2022).
- Mora-Melia, D.; Iglesias-Ray, P.L.; Martinez-Solano, F.J.; Ballesteros-Perez, P. Efficiency of evolutionary algorithms in water networks pipe sizing. Water Resour. Manag. 2015, 29, 4817–4831. [Google Scholar] [CrossRef]
- Cullinane, M.; Lancy, K.; Mays, L. Optimization-availability-based design of water-distribution networks. J. Hydraul. Eng. 1992, 118, 420–441. [Google Scholar] [CrossRef]
- El-Ghandour, H.; Elabd, S.; Elbeltagi, E. Assessment of optimal water distribution systems design under steady-state and transient conditions due to pipe roughness uncertainty. Ain Shams Eng. J. 2021, 12, 465–473. [Google Scholar] [CrossRef]
| Author’s | Hybrid Firefly Model | Case Study |
|---|---|---|
| Zervoudakis et al. (2020) [12] | Firefly and Genetic Algorithm | Product Line Design Problem |
| Abdullah et al. (2012) [13] | Firefly-Differential Evolution (HEFA) | Complex and Nonlinear Problems |
| Tahershamsi et al. (2014) [14] | Firefly-Harmoni Search | Optimization of Water Distribution Systems |
| Gu et al. (2013) [15] | Firefly and Harmony Search | Global Numerical Optimization |
| Kora and Krishna (2016) [16] | Firefly and Particle Swarm Optimization | Detection of Bundle Branch Block |
| Elkhechafi et al. (2017) [17] | Firefly- Genetic Algorithm | Global Optimization |
| Aydilek (2018) [18] | Firefly-Particle Swarm Optimization | Computationally Expensive Numerical Problems |
| Nhu et al. (2020) [19] | Firefly-Particle Swarm Optimization | Rainfall induced Flash Floods |
| Khan et al. (2020) [20] | Firefly-Particle Swarm Optimization | Standard IEEE 30-Bus Test System |
| Yadav et al. (2021) [21] | Firefly and Biogeography-Base Optimization | Software Production Line |
| Wahid and Ghazali (2021) [22] | Firefly and Genetic Algorithm | Minimization and Maximization Functions |
| Bilal and Millie Pant (2020) [23] | Firefly and Particle Swarm Optimization | Optimization of Water Distribution Systems |
| Model | Parameter | Pipe Network | |||
|---|---|---|---|---|---|
| Two-Loop | Hanoi | New York | El-Mostakbal | ||
| FA | niter | 1000 | 1000 | 1000 | 1000 |
| npop | 10 | 40 | 40 | 40 | |
| Γ | 1 | 1 | 1 | 1 | |
| β0 | 2 | 2 | 2 | 2 | |
| α0 | 0.2 | 0.2 | 0.2 | 0.2 | |
| FAPSO | niter | 130 | 150 | 200 | 150 |
| npop | 70 | 350 | 200 | 400 | |
| c1 | 1 | 1.49 | 1.49 | 1.49 | |
| c2 | 1.1 | 1.49 | 1.1 | 1.49 | |
| Γ | 1 | 1 | 1 | 1 | |
| β0 | 2 | 2 | 2 | 2 | |
| A | 0.2 | 0.2 | 0.2 | 0.2 | |
| FAGA | niter | 1000 | 1000 | 1000 | 1000 |
| npop | 10 | 40 | 40 | 40 | |
| Mu | 0.15 | 0.15 | 0.1 | 0.2 | |
| Author’s | Optimization Technique | Optimal Cost |
|---|---|---|
| Rayan et al. (2003) [28] | SUMT | 6,770,787 |
| El-Ghandour and El-Beltagi (2018) [30] | GA | 5,268,431 |
| PSO | 4,968,881.5 | |
| ACO | 5,484,596 | |
| MA | 5,055,519 | |
| SFLA | 5,181,846 | |
| Ezzeldin and Djebedjian (2020) [24] | WOA | 4,932,467.1 |
| Abdel-Gawad (2021) [29] | FSAJA | 4,926,560.7 |
| Present Study | FA | 5,676,331.79 |
| FAPSO | 4,932,901 | |
| FAGA | 4,923,731.5 |
| Pipe Number (Optimal Diameter, mm.) | |||||
|---|---|---|---|---|---|
| 1 (600) | 2 (500) | 3 (500) | 4 (500) | 5 (150) | 6 (150) |
| 7 (150) | 8 (150) | 9 (150) | 10 (150) | 11 (500) | 12 (500) |
| 13 (150) | 14 (150) | 15 (150) | 16 (150) | 17 (150) | 18 (150) |
| 19 (150) | 20 (500) | 21 (150) | 22 (150) | 23 (150) | 24 (150) |
| 25 (150) | 26 (400) | 27 (400) | 28 (250) | 29 (150) | 30 (150) |
| 31 (150) | 32 (150) | 33 (200) | 34 (150) | 35 (250) | 36 (300) |
| 37 (150) | 38 (250) | 39 (250) | 40 (200) | 41 (150) | 42 (150) |
| 43 (150) | 44 (200) | ||||
| Network | Optimization Algorithm | (1) | (2) | (3) | (4) | (5) | (6) |
|---|---|---|---|---|---|---|---|
| Min. Cost | Max. Cost | Mean | Standard. Deviation | F.E.N. | Sec Per 1000 Eval | ||
| Two-Loop | FA | 419,000 | 441,000 | 425,150 | 8317.86 | 6205 | 88.8 |
| FAPSO | 419,000 | 453,000 | 435,700 | 11,388.36 | 2596 | 85.3 | |
| FAGA | 419,000 | 420,000 | 419,160 | 370.33 | 2380 | 82 | |
| Hanoi | FA | 6,566,082.81 | 8,307,245.89 | 7,402,370.25 | 524,647.62 | 52,249 | 91.8 |
| FAPSO | 6,195,529.34 | 69,044,904.1 | 6,507,346.32 | 208,328.43 | 102,960 | 88.3 | |
| FAGA | 6,087,729.57 | 6,375,686.7 | 6,252,830.16 | 79,998.3 | 37,410 | 82 | |
| New York | FA | 38,637,600 | 62,390,579.7 | 44,093,383.99 | 5,396,845.17 | 22,335 | 91 |
| FAPSO | 38,637,600 | 61,551,400 | 40,393,718.25 | 5,139,391.02 | 13,916 | 89.2 | |
| FAGA | 38,637,600 | 38,796,300 | 38,662,992 | 58,771.06 | 9120 | 88.1 | |
| El-Mostakbal | FA | 5,676,331.79 | 6,263,583.1 | 5,913,233.06 | 170,902.64 | 55,216 | 94.3 |
| FAPSO | 4,932,901 | 5,214,838 | 5,046,771.6 | 92,426.21 | 58,842 | 90.5 | |
| FAGA | 4,923,731.5 | 5,025,247.3 | 4,949,974.37 | 35,382.66 | 37,440 | 88 |
| Network | Optimization Algorithm | Success Rate (Sr %) | ||
|---|---|---|---|---|
| C = 0 | C = 0.01 | C = 0.02 | ||
| Two-loop | FA | 25 | 56.01 | 60.65 |
| FAPSO | 15 | 15 | 16.69 | |
| FAGA | 84 | 98.18 | 99.54 | |
| Hanoi | FA | 0 | 0 | 0 |
| FAPSO | 0 | 0 | 0.1314 | |
| FAGA | 2 | 7.5 | 10.73 | |
| New York | FA | 5 | 8.31 | 13.03 |
| FAPSO | 5 | 5 | 5 | |
| FAGA | 84 | 94.6 | 98.65 | |
| El-Mostakbal | FA | 0 | 0 | 0 |
| FAPSO | 0 | 11.39 | 29.31 | |
| FAGA | 40 * | 66.89 | 77.1 | |
| Run No. | Acceptance Index (AI) | Run No. | Acceptance Index (AI) | ||||
|---|---|---|---|---|---|---|---|
| C = 0.00 | C = 0.01 | C = 0.02 | C = 0.00 | C = 0.01 | C = 0.02 | ||
| 1 | 1 | 1 | 1 | 11 | 0 | 0.687 | 0.922 |
| 2 | 1 | 1 | 1 | 12 | 0 | 0.687 | 0.922 |
| 3 | 1 | 1 | 1 | 13 | 0 | 0.687 | 0.922 |
| 4 | 1 | 1 | 1 | 14 | 0 | 0.687 | 0.922 |
| 5 | 1 | 1 | 1 | 15 | 0 | 0.687 | 0.922 |
| 6 | 1 | 1 | 1 | 16 | 0 | 0.247 | 0.790 |
| 7 | 1 | 1 | 1 | 17 | 0 | 0 | 0.091 |
| 8 | 1 | 1 | 1 | 18 | 0 | 0 | 0.004 |
| 9 | 0 | 0.879 | 0.970 | 19 | 0 | 0 | 0.002 |
| 10 | 0 | 0.819 | 0.955 | 20 | 0 | 0 | 0 |
| * Sr = (13.38/20) × 100 = 40%. | ∑ | 8.00 | 13.38 | 15.42 | |||
| Sr % | 40.0 * | 66.90 | 77.10 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ezzeldin, R.; Zelenakova, M.; Abd-Elhamid, H.F.; Pietrucha-Urbanik, K.; Elabd, S. Hybrid Optimization Algorithms of Firefly with GA and PSO for the Optimal Design of Water Distribution Networks. Water 2023, 15, 1906. https://doi.org/10.3390/w15101906
Ezzeldin R, Zelenakova M, Abd-Elhamid HF, Pietrucha-Urbanik K, Elabd S. Hybrid Optimization Algorithms of Firefly with GA and PSO for the Optimal Design of Water Distribution Networks. Water. 2023; 15(10):1906. https://doi.org/10.3390/w15101906
Chicago/Turabian StyleEzzeldin, Riham, Martina Zelenakova, Hany F. Abd-Elhamid, Katarzyna Pietrucha-Urbanik, and Samer Elabd. 2023. "Hybrid Optimization Algorithms of Firefly with GA and PSO for the Optimal Design of Water Distribution Networks" Water 15, no. 10: 1906. https://doi.org/10.3390/w15101906
APA StyleEzzeldin, R., Zelenakova, M., Abd-Elhamid, H. F., Pietrucha-Urbanik, K., & Elabd, S. (2023). Hybrid Optimization Algorithms of Firefly with GA and PSO for the Optimal Design of Water Distribution Networks. Water, 15(10), 1906. https://doi.org/10.3390/w15101906









