How to Minimize the Environmental Contamination Caused by Hydrocarbon Releases by Onshore Pipelines: The Key Role of a Three-Dimensional Three-Phase Fluid Flow Numerical Model
Abstract
:1. Introduction
2. Materials and Methods
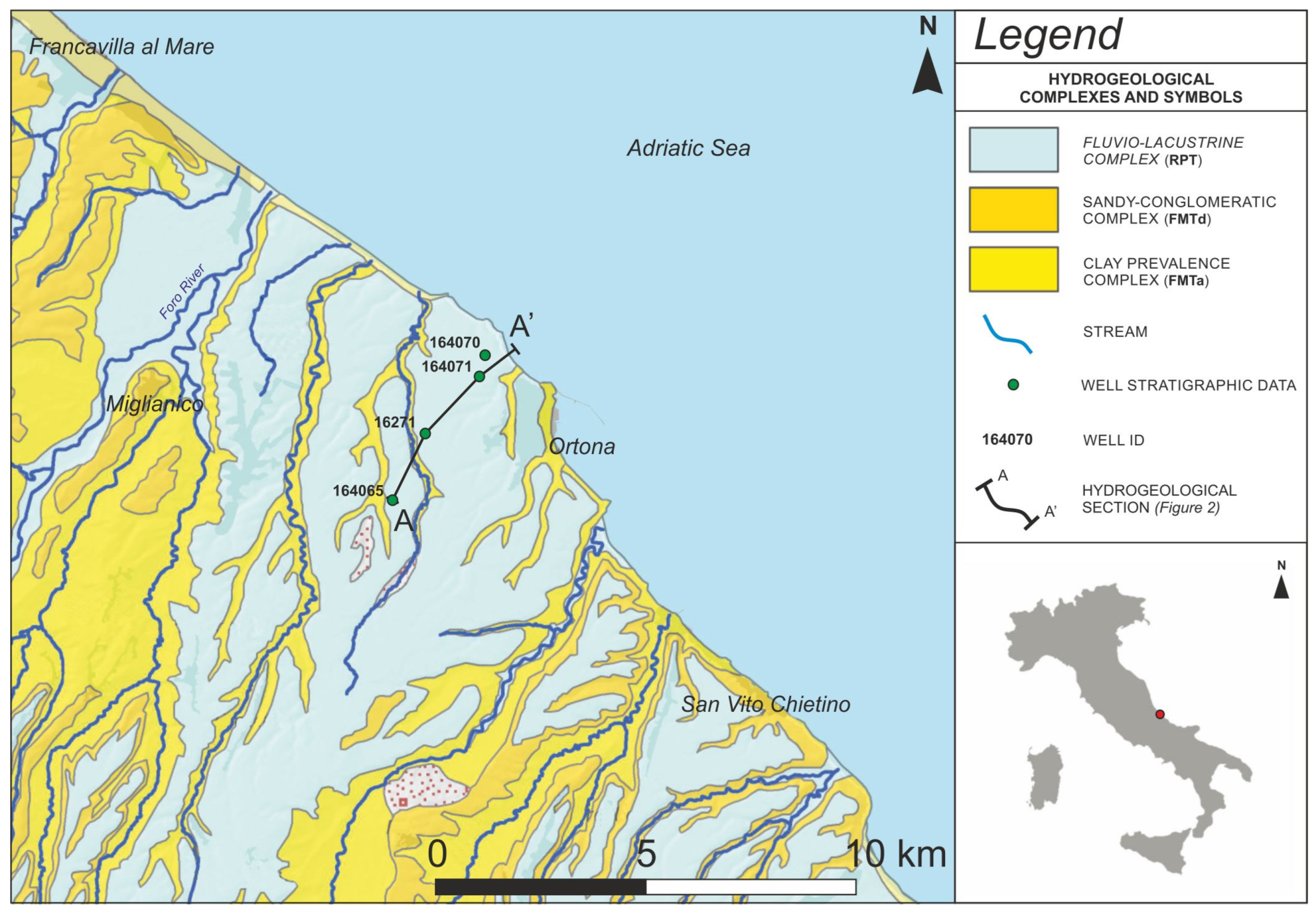
2.1. Study Area
2.2. Hydrogeological and Geological Data
2.3. Mathematical Model
2.4. Hydrogeological and Hydrocarbon Phase Parameters
3. Results
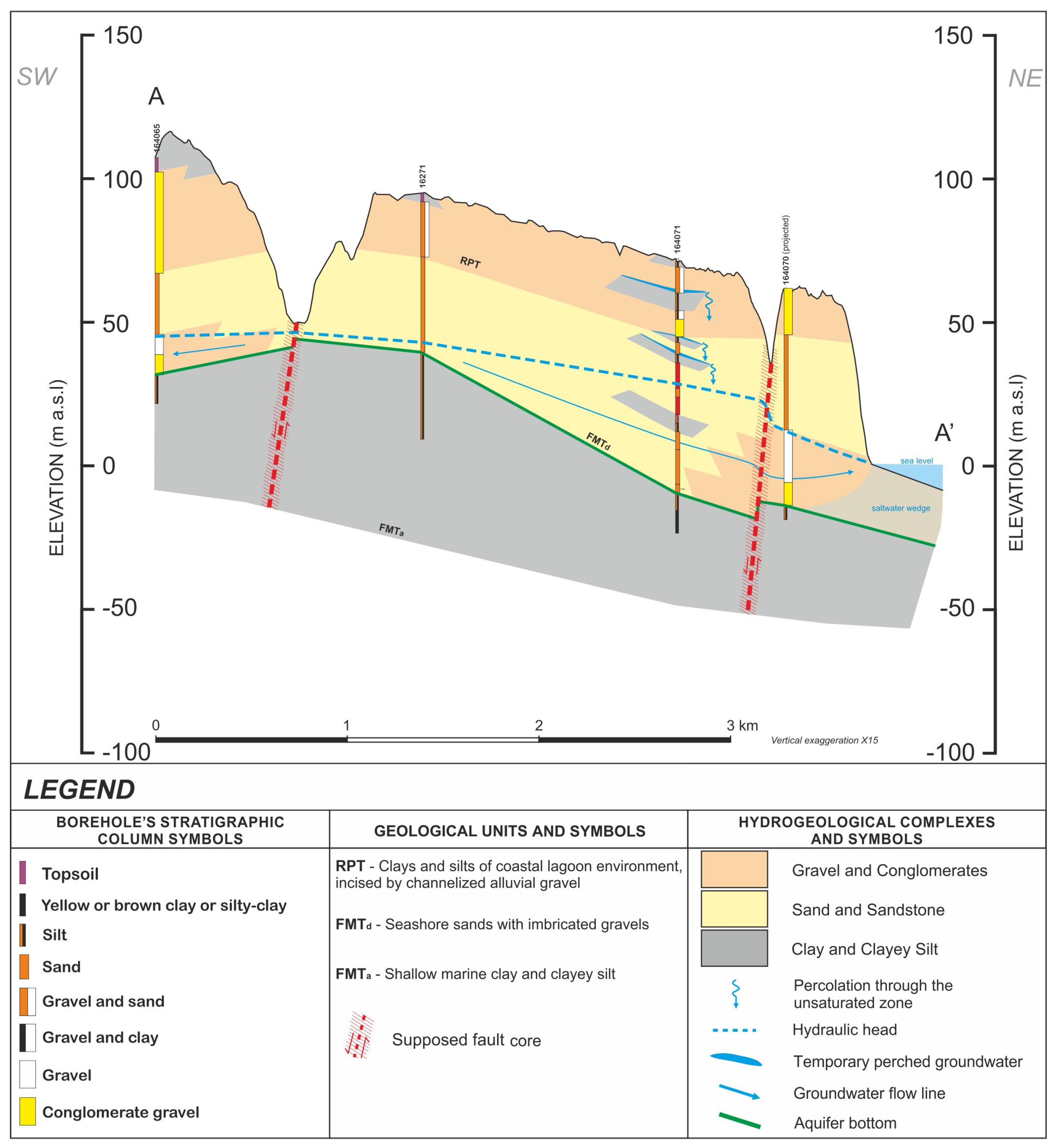
3.1. Hydrogeological Conceptual Model
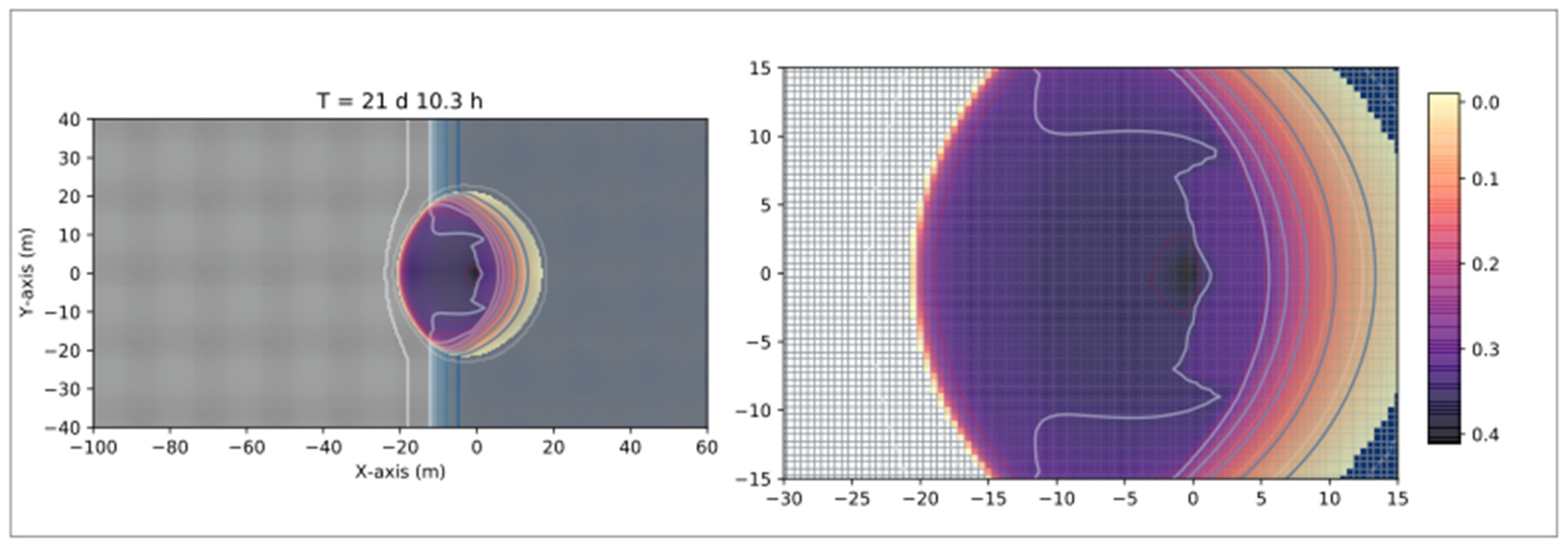
3.2. Three-Dimensional Numerical Simulations, Results, and Discussions
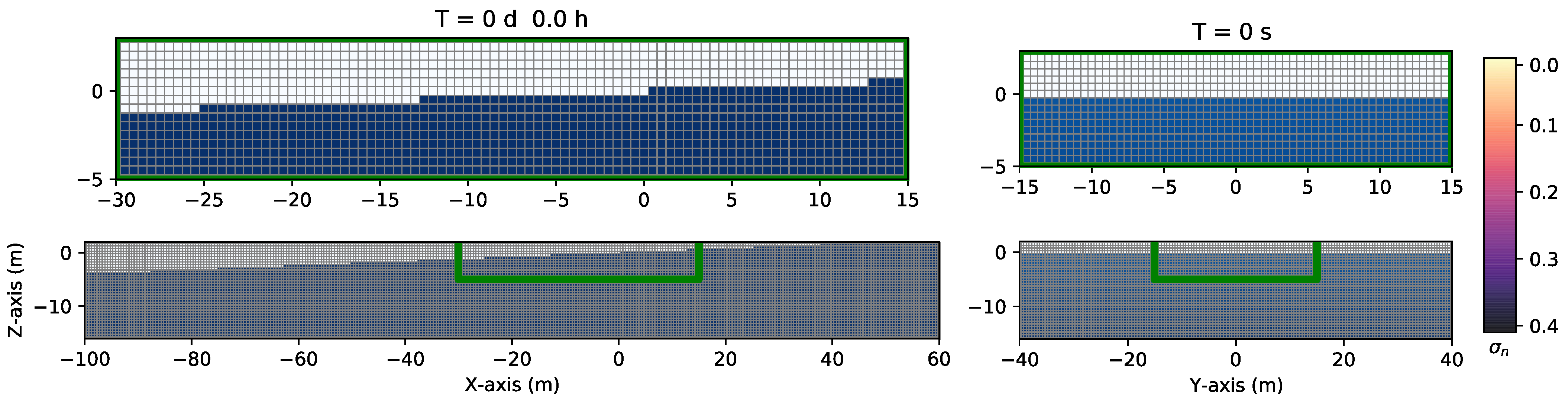
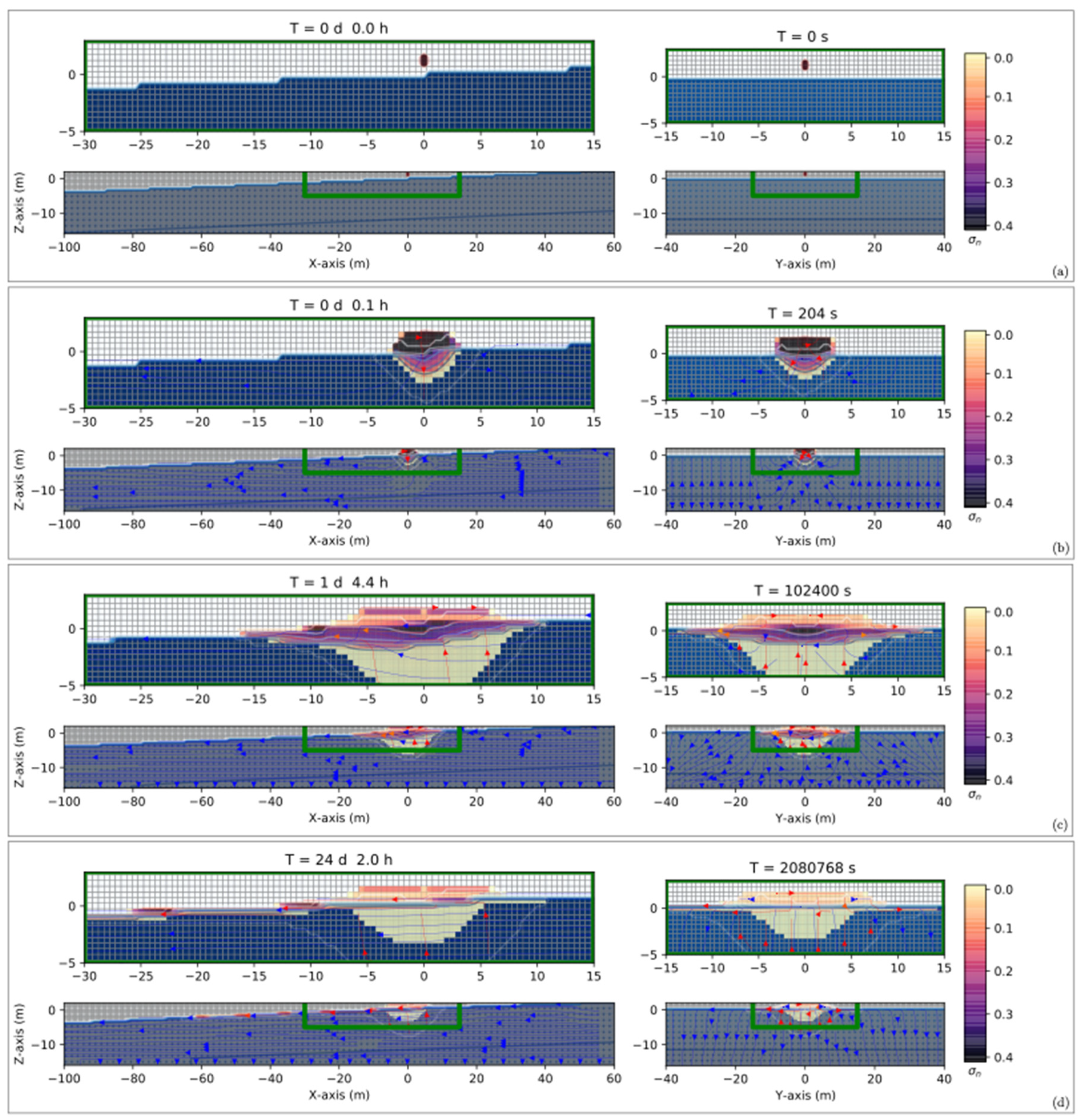
3.2.1. Numerical Simulations of a Gasoline Leak from an Oil Pipeline in a Dry Zone
3.2.2. Numerical Simulations of a Gasoline Leak from an Oil Pipeline in an Unsaturated Zone
3.2.3. Numerical Simulations of a Diesel Oil Leak from an Oil Pipeline in a Dry Zone
3.2.4. Numerical Simulations of a Diesel Oil Leak from an Oil Pipeline in an Unsaturated Zone
3.3. Effects on the Density of the Contaminant
3.4. Effects on the Water Saturation of the Unsaturated Zone
3.5. Effects on Pressure in the Oil Pipeline
3.6. Validation of the Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, X.; Chen, G.; Zhu, H. Quantitative risk analysis on leakage failure of submarine oil and gas pipelines using Bayesian network. Process Saf. Environ. Prot. 2016, 103, 163–173. [Google Scholar] [CrossRef]
- Xinhong, L.; Guoming, C.; Renren, Z.; Hongwei, Z.; Jianmin, F. Simulation and assessment of underwater gas release and dispersion from subsea gas pipelines leak. Process Saf. Environ. Prot. 2018, 119, 46–57. [Google Scholar] [CrossRef]
- Abbas, M.; Jardani, A.; Ahmed, A.S.; Revil, A.; Brigaud, L.; Bégassat, P.; Dupont, J.P. Redox potential distribution of an organic-rich contaminated site obtained by the inversion of self-potential data. J. Hydrol. 2017, 554, 111–127. [Google Scholar] [CrossRef]
- Gainer, A.; Cousins, M.; Hogan, N.; Siciliano, S.D. Petroleum hydrocarbon mixture toxicity and a trait-based approach to soil invertebrate species for site-specific risk assessments. Environ. Toxicol. Chem. 2018, 37, 2222–2234. [Google Scholar] [CrossRef]
- Yan, Y.; Xiong, G.; Zhou, J.; Wang, R.; Huang, W.; Yang, M.; Wang, R.; Geng, D. A whole process risk management system for the monitoring and early warning of slope hazards affecting gas and oil pipelines. Front. Earth Sci. 2022, 9, 812527. [Google Scholar] [CrossRef]
- Ning, P.; Jiang, Y.-J.; Tang, J.-J.; Xie, Q.-J. Research on the Early Warning Model for Pipelines Due to Landslide Geohazards under Multiple Influencing Factors. Water 2023, 15, 693. [Google Scholar] [CrossRef]
- Nesic, S. Key issues related to modelling of internal corrosion of oil and gas pipelines—A review. Corros. Sci. 2007, 49, 4308–4338. [Google Scholar] [CrossRef]
- Papavinasam, S. Corrosion Control in the Oil and Gas Industry; Elsevier: Amsterdam, The Netherlands, 2013; ISBN 97801239-73061. [Google Scholar]
- Farshad, M. Plastic Pipe Systems: Failure Investigation and Diagnosis; Elsevier: Oxford, UK, 2011. [Google Scholar]
- Liu, S.; Wang, Y.; Liang, Y. Environmental consequences analysis of oil spills from onshore pipelines with parametric uncertainty. Process Saf. Environ. Prot. 2020, 14, 123–134. [Google Scholar] [CrossRef]
- Murvay, P.S.; Silea, I. A survey on gas leak detection and localization techniques. J. Loss Prev. Process Ind. 2012, 25, 966–973. [Google Scholar] [CrossRef]
- Folga, S.M. Natural Gas Pipeline Technology Overview; Argonne National Lab.: Argonne, IL, USA, 2007. [Google Scholar]
- Batzias, F.; Siontorou, C.; Spanidis, P.M. Designing a reliable leak bio-detection system for natural gas pipelines. J. Hazard. Mater. 2011, 186, 35–58. [Google Scholar] [CrossRef]
- Qin, B.; Yunping, Z.; Min, F.; Xiaojian, S. Leakage detection technology of oil and gas transmission pipelines and its development trend. Petrol. Eng. Construct. 2007, 33, 19–23. [Google Scholar]
- Hayek, M. A model for Subsurface oil pollutant migration. Transp. Porous Med. 2017, 120, 373–393. [Google Scholar] [CrossRef]
- Hochmuth, D.P.; Sunada, D.K. Ground-Water Model of Two-Phase Immiscible Flow in Coarse Material. Groundwater 1985, 23, 617–626. [Google Scholar] [CrossRef]
- Pinder, G.F.; Abriola, L.M. On the simulation of nonaqueous phase organic compounds in the subsurface. Water Resour. Res. 1986, 22, 109S–119S. [Google Scholar] [CrossRef]
- Hossain, M.A.; Corapeilglu, M.Y. Modifying the USGS Solute Transport Computer Model to Predict High-Density Hydrocarbon Migration. Groundwater 1988, 6, 717–723. [Google Scholar] [CrossRef]
- Høst-Madsen, J.; Høgh-Jensen, K. Laboratory and numerical investigations of immiscible multiphase flow in soil. J. Hydrol. 1992, 135, 13–52. [Google Scholar] [CrossRef]
- Reeves, H.W.; Abriola, L.M. An iterative compositional model for subsurface multiphase flow. J. Contam. Hydrol. 1994, 15, 249–276. [Google Scholar] [CrossRef]
- Lagendijk, V.; Forkel, C.; Köngeter, J.; Braxein, A. Three-dimensional numerical modeling of multiphase flow and transport. J. Environ. Sci. Health Part A 2001, 36, 1473–1489. [Google Scholar] [CrossRef] [PubMed]
- Hoteit, H.; Firoozabadi, A. An efficient numerical model for incompressible two-phase flow in fractured media. Adv. Water Resour. 2008, 31, 891–905. [Google Scholar] [CrossRef]
- Ataie-Ashtiani, B.; Raeesi-Ardekani, D. Comparison of Numerical Formulations for Two-phase Flow in Porous Media. Geotech. Geol. Eng. 2010, 28, 373–389. [Google Scholar] [CrossRef]
- Park, C.-H.; Böttcher, N.; Wang, W.; Kolditz, O. Are upwind techniques in multi-phase flow models necessary? J. Comput. Phys. 2011, 230, 8304–8312. [Google Scholar] [CrossRef]
- Samimi, S.; Pak, A. A novel three-dimensional element free Galerkin (EFG) code for simulating two-phase fluid flow in porous materials. Eng. Anal. Bound. Elem. 2014, 39, 53–63. [Google Scholar] [CrossRef]
- Sun, Y.; Cao, X.; Liang, F. Investigation on underwater spreading characteristics and migration law of oil leakage from damaged submarine pipelines. Process Saf. Environ. Prot. 2019, 127, 329–347. [Google Scholar] [CrossRef]
- Sun, Y.; Cao, X.; Liang, F.; Bian, J. Investigation on underwater gas leakage and dispersion behaviors based on coupled Eulerian-Lagrangian CFD model. Process Saf. Environ. Prot. 2020, 136, 268–279. [Google Scholar] [CrossRef]
- Yang, M.; Khan, F.; Garaniya, V.; Chai, S. Multimedia fate modeling of oil spills in ice-infested waters: An exploration of the feasibility of fugacity-based approach. Process Saf. Environ. Prot. 2015, 93, 206–217. [Google Scholar] [CrossRef]
- Xu, Z.; Chai, J.; Wu, Y.; Qin, R. Transport and biodegradation modeling of gasoline spills in soil-aquifer system. Environ. Earth Sci. 2015, 74, 2871–2882. [Google Scholar] [CrossRef]
- Ahmed, M.; Saleem, M.R.; Zia, S.; Qamar, S. Central Upwind Scheme for a Compressible Two-Phase Flow Model. PLoS ONE 2015, 10, e0126273. [Google Scholar] [CrossRef]
- Zhang, J.; Liang, Z.; Han, C.J. Numerical Modeling of Mechanical Behavior for Buried Steel Pipelines Crossing Subsidence Strata. PLoS ONE 2015, 10, e0130459. [Google Scholar] [CrossRef]
- Feo, A.; Celico, F. High-resolution shock-capturing numerical simulations of three-phase immiscible fluids from the unsaturated to the saturated zone. Sci. Rep. 2021, 11, 5212. [Google Scholar] [CrossRef] [PubMed]
- Feo, A.; Celico, F. Investigating the migration of immiscible contaminant fluid flow in homogeneous and heterogeneous aquifers with high-precision numerical simulations. PLoS ONE 2022, 17, e0266486. [Google Scholar] [CrossRef]
- Pistiner, A. Oil plume distribution in an anisotropic porous medium. Transp. Porous Med. 2007, 70, 293–304. [Google Scholar] [CrossRef]
- Pistiner, A. Oil plume distribution in an aquifer near an impermeable barrier. Transp. Porous Med. 2009, 76, 67–75. [Google Scholar] [CrossRef]
- Pistiner, A.; Shapiro, M.; Rubin, H. Analysis of fuel pollutant migration in water flow through porous media. Int. J. Multiph. Flow 1989, 15, 135–154. [Google Scholar] [CrossRef]
- Pistiner, A.; Shapiro, M.; Rubin, H. Gravitational migration of fuel in porous media. Transp. Porous Med. 1992, 9, 187–205. [Google Scholar] [CrossRef]
- Chen, Z.X. Some invariant solutions to two-phase fluid displacement problem including capillary effect. SPE Reserv. Eng. 1988, 28, 691–700. [Google Scholar] [CrossRef]
- Weaver, J.W.; Charbeneau, R.J.; Tauxe, J.D.; Lien, B.K.; Provost, J.B. The Hydrocarbon Spill Screening Model (HSSM) Volume 1: User’s Guide; The United States Environmental Protection Agency: Washington, DC, USA, 1995.
- Charbeneau, R.J.; Weaver, J.W.; Lien, B.K. The Hydrocarbon Spill Screening Model (Hssm) Volume 2: Theoretical Background and Source Codes; The United States Environmental Protection Agency: Washington, DC, USA, 1995.
- Zheng, C.M. Recent developments and future directions for MT3DMS and related transport codes. Ground Water 2009, 47, 620–625. [Google Scholar] [CrossRef]
- Zheng, C.M. MT3DMS v53 Supplemental User’s Guide; Department of Geological, Sciences University of Alabama: Tuscaloosa, AL, USA, 2010. [Google Scholar]
- Ori, G.G.; Serafini, G.; Visentin, C.; Ricci Lucchi, F.; Casnedi, R.; Colalongo, M.; Mosna, S. The Pliocenee-Pleistocene foredeep (Marche and Abruzzo, Italy): An integrated approach to surface and subsurface geology. In Proceedings of the 3rd EAPG Conference, Adriatic Foredeep Fieldtrip Guidebook, Firenze, Italy, 26–30 May 1991; p. 85. [Google Scholar]
- Artoni, A.; Casero, P. Sequential balancing of growth structures, the late Tertiary example from the central Apennines. Bull. Société Géologique Fr. 1997, 168, 35–49. [Google Scholar]
- Carruba, S.; Casnedi, R.; Cesare, R.; Perotti, T.; Tornaghi, M.; Bolis, G. Tectonic and sedimentary evolution of the Lower Pliocene Periadriatic foredeep in Central Italy. Int. J. Earth Sci. 2006, 95, 665–683. [Google Scholar] [CrossRef]
- Centamore, E.; Nisio, S. Significative events in the Peryadriatic feredeeps evolution (Abruzzo e Italy). Studi Geol. Camerti 2003, 39–48. Available online: http://193.204.8.201:8080/jspui/handle/1336/862 (accessed on 1 January 2023).
- Di Celma, C.; Cantalamessa, G.; Didaskalou, P.; Lori, P. Sedimentology, architecture, and sequence stratigraphy of coarse-grained, submarine canyon fills from Pleistocene (Gelasiane-Calabrian) of the Peri-Adriatic basin, central Italy. Mar. Pet. Geol. 2010, 27, 1340–1365. [Google Scholar] [CrossRef]
- Ori, G.G.; Roveri, M.; Vannoni, F. Plio-Pleistocene Sedimentation in the Apenninic-Adriatic Foredeep (Central Adriatic Sea, Italy); Allen, P.A., Homewood, P., Eds.; IAS Special Publication: Gent, Belgium, 1986; Volume 8, pp. 183–198. [Google Scholar]
- Dattilo, P.; Pasi, R.; Bertozzi, G. Depositional and structural dynamics of the Pliocene peri-adriatic foredeep, NE Italy. J. Pet. Geol. 1999, 22, 19–36. [Google Scholar] [CrossRef]
- Tinterri, R.; Lipparini, L. Seismo-stratigraphic study of the Plio-Pleistocene foredeep deposits of the Central Adriatic Sea (Italy): Geometry and characteristics of deep-water channels and sediment waves. Mar. Pet. Geol. 2013, 42, 30–49. [Google Scholar] [CrossRef]
- Regione Abbruzzo. “Piano di Tutela delle Acque”. Relazione Generale e Allegati, Carta dei Complessi Idrogeologici. 2010. Available online: http://www.regione.abruzzo.it/pianoTutelaacque/docs/elaboratiPiano/CartografiaPiano/1_4.pdf (accessed on 1 January 2023).
- Kurganov, A.; Tadmor, E. New high-resolution central scheme for non-linear conservation laws and convection-diffusion equations. J. Comput. Phys. 2000, 160, 241–282. [Google Scholar] [CrossRef]
- Lax, P.; Wendroff, B. Systems of conservation laws. Commun. Pure Appl. Math. 1960, 3, 217–237. [Google Scholar] [CrossRef]
- Hou, T.Y.; LeFloch, P.G. Why nonconservative schemes converge to wrong solutions: Error analysis. Math. Comp. 1994, 62, 497–530. [Google Scholar] [CrossRef]
- Allen, G.; Goodale, T.; Lanfermann, G.; Radke, T.; Rideout, D.; Thornburg, J. Cactus Users’ Guide. 2011. Available online: http://www.cactuscode.org/documentation/UsersGuide.pdf (accessed on 1 January 2023).
- Cactus Developers. Cactus Computational Toolkit. Available online: http://www.cactuscode.org/ (accessed on 1 January 2023).
- Goodale, T.; Allen, G.; Lanfermann, G.; Massó, J.; Radke, T.; Seidel, E.; Shalf, J. The Cactus Framework and Toolkit: Design and Applications. In High Performance Computing for Computational Science—VECPAR 2002; Springer: Berlin, Germany, 2003. [Google Scholar]
- Schnetter, E.; Hawley, S.H.; Hawke, I. Evolutions in 3D numerical relativity using fixed mesh refinement. Class. Quantum Grav. 2004, 21, 1465–1488. [Google Scholar] [CrossRef]
- Schnetter, E.; Diener, P.; Dorband, E.N.; Tiglio, M. A multi-block infrastructure for three-dimensional time-dependent numerical relativity. Class. Quantum Grav. 2006, 23, S553. [Google Scholar] [CrossRef]
- Parker, J.C.; Lenhard, R.J.; Kuppusamy, T. A parametric model for constitutive properties governing multi-phase flow in porous media. Water Resour. Res. 1987, 23, 618–624. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A closed form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Freeze, R.A.; Cherry, J.A. Groundwater Book; Prentice-Hall Inc.: Englewood Cliffs, NJ, USA, 1979. [Google Scholar]
- Carsel, R.F.; Parrish, R.S. Developing joint probability distributions of soil water retention characteristics. Water Resour. Res. 1988, 24, 755–769. [Google Scholar] [CrossRef]
- Hamutoko, J.T.; Post, V.E.A.; Wanke, H.; Beyer, M.; Houben, G.; Mapani, B. The role of local perched aquifers in regional groundwater recharge in semi-arid environments: Evidence from the Cuvelai-Etosha Basin, Namibia. Hydrogeol. J. 2019, 27, 2399–2413. [Google Scholar] [CrossRef]
- Hernàndez-Diaz, R.; Petrella, E.; Bucci, A.; Naclerio, G.; Feo, A.; Sferra, G.; Chelli, A.; Zanini, A.; Gonzalez-Hernandez, P.; Celico, F. Integrating Hydrogeological and Microbiological Data and Modelling to Characterize the Hydraulic Features and Behaviour of Coastal Carbonate Aquifers: A Case in Western Cuba. Water 2019, 11, 1989. [Google Scholar] [CrossRef]
- Celico, F.; Petrella, E.; Celico, P. Hydrogeological behaviour of some fault zones in a carbonate aquifer of Southern Italy: An experimentally based model. Terra Nova 2006, 18, 308–313. [Google Scholar] [CrossRef]
- Andersson, J.E.; Ekman, L.; Nordqvist, R.; Winberg, A. Hydraulic testing and modeling of a low-angle fracture zone at Finnsjon, Sweden. J. Hydrol. 1991, 126, 45–77. [Google Scholar] [CrossRef]
- Antonellini, M.; Aydin, A. Effect of faulting on fluid flow in porous sandstones: Petrophysical properties. Am. Assoc. Petrol. Geol. Bull. 1994, 78, 355–377. [Google Scholar]
- Bense, V.F.; Van den Berg, E.H.; Van Balen, R.T. Deformation mechanisms and hydraulic properties of fault zones in unconsolidated sediments; the Roer Valley Rift System, The Netherlands. Hydrogeol. J. 2003, 11, 319–332. [Google Scholar] [CrossRef]
- Bense, V.F.; Gleeson, T.; Loveless, S.E.; Bour, O.; Scibek, J. Fault zone hydrogeology. Earth Sci. Rev. 2013, 127, 171–192. [Google Scholar] [CrossRef]
- Caine, J.S.; Evans, J.P.; Forster, C.B. Fault zone architecture and permeability structure. Geology 1996, 24, 1025–1028. [Google Scholar] [CrossRef]
- Chester, F.M.; Logan, J.M. Composite planar fabric of gouge from the Punchbowl fault, California. J. Struct. Geol. 1986, 9, 621–634. [Google Scholar] [CrossRef]
- Balsamo, F.; Storti, F. Grain size and permeability evolution of soft-sediment extensional sub-seismic and seismic fault zones in high-porosity sediments from the Crotone basin, southern Apennines, Italy. Mar. Pet. Geol. 2010, 27, 822–837. [Google Scholar] [CrossRef]
- Pizzati, M.; Balsamo, F.; Storti, F. Displacement-dependent microstructural and petrophysical properties of deformation bands and gouges in poorly lithified sandstone deformed at shallow burial depth (Crotone Basin, Italy). J. Struct. Geol. 2020, 137, 104069. [Google Scholar] [CrossRef]
- Acher, A.; Boiderie, P.; Yaron, B. Soil pollution by petroleum products. I. Multiphase migration of kerosene components in soil columns. J. Contam. Hydrol. 1989, 4, 333–345. [Google Scholar] [CrossRef]



| Parameter | Symbol | Value |
|---|---|---|
| Absolute permeability | ||
| Rock compressibility | ||
| Porosity | ||
| Water viscosity | ||
| Water density | ||
| Oil (gasoline) viscosity | ||
| Oil (gasoline) density | ||
| Air viscosity | ||
| Air density | ||
| Van Genuchten | ||
| Irreducible wetting phase saturation | ||
| Superficial tension air-water | ||
| Interfacial tension in nonaqueous water | ||
| Capillary pressure of air-water at zero saturation | ||
| Capillary pressure air-nonaqueous at zero saturation |
| Parameter | Symbol | Value |
|---|---|---|
| Absolute permeability | ||
| Rock compressibility | ||
| Porosity | ||
| Water viscosity | ||
| Water density | ||
| Oil (diesel oil) viscosity | ||
| Oil (diesel oil) density | ||
| Air viscosity | ||
| Air density | ||
| Van Genuchten | ||
| Irreducible wetting phase saturation | ||
| Superficial tension air-water | ||
| Interfacial tension in nonaqueous water | ||
| Capillary pressure of air-water at zero saturation | ||
| Capillary pressure air-nonaqueous at zero saturation |
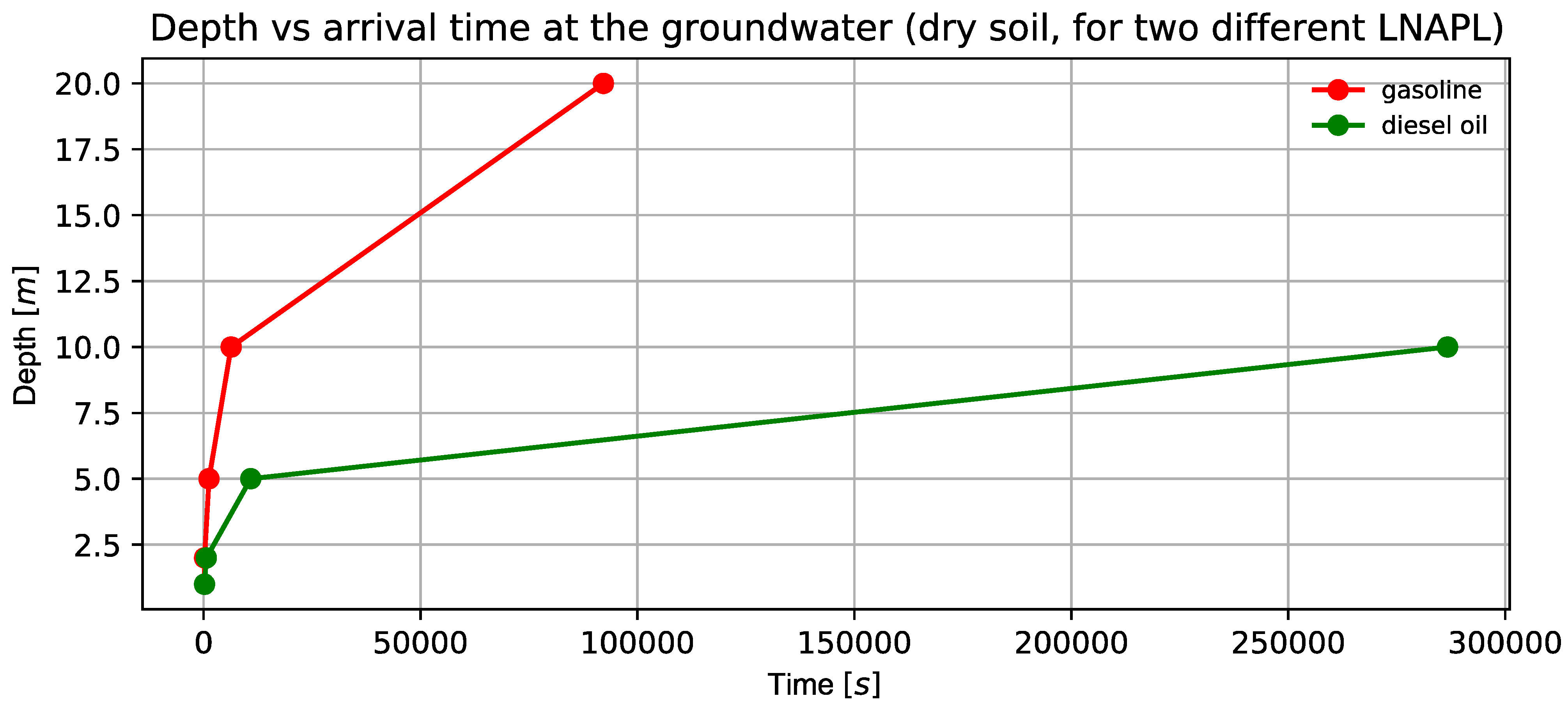
| Type (Density) | Thickness of the Unsaturated Zone (m) | Hydraulic Gradient | Arrival Time at the Groundwater Table (s) | Position in x after One Day and 4.4 h (m) |
|---|---|---|---|---|
| Gasoline | 1.0 | 0.04 | −16.0 | |
| 0.004 | −14.0 | |||
| Diesel oil | 1.0 | 0.04 | −6.0 | |
| 0.004 | −5.5 | |||
| Gasoline | 2.0 | 0.04 | −16.5 | |
| 0.004 | −15.0 | |||
| Diesel oil | 2.0 | 0.04 | 614.4 | −6.0 |
| 0.004 | 614.4 | −5.0 | ||
| Gasoline | 5.0 | 0.04 | 1228.8 | −16.5 |
| 0.004 | 1228.8 | −15.0 | ||
| Diesel oil | 5.0 | 0.04 | 10,854.4 | −3.5 |
| 0.004 | 12,288.0 | −3.5 | ||
| Gasoline | 10.0 | 0.04 | 6348.8 | −14.0 |
| 0.004 | 6348.8 | −12.5 | ||
| Diesel oil | 10.0 | 0.04 | 286,720.0 | - |
| 0.004 | 276,480.0 | - | ||
| Gasoline | 20.0 | 0.04 | 92,160.0 | −2.5 |
| 0.004 | 92,160.0 | −2.5 | ||
| Diesel oil | 20.0 | 0.04 | - | - |
| 0.004 | - | - |
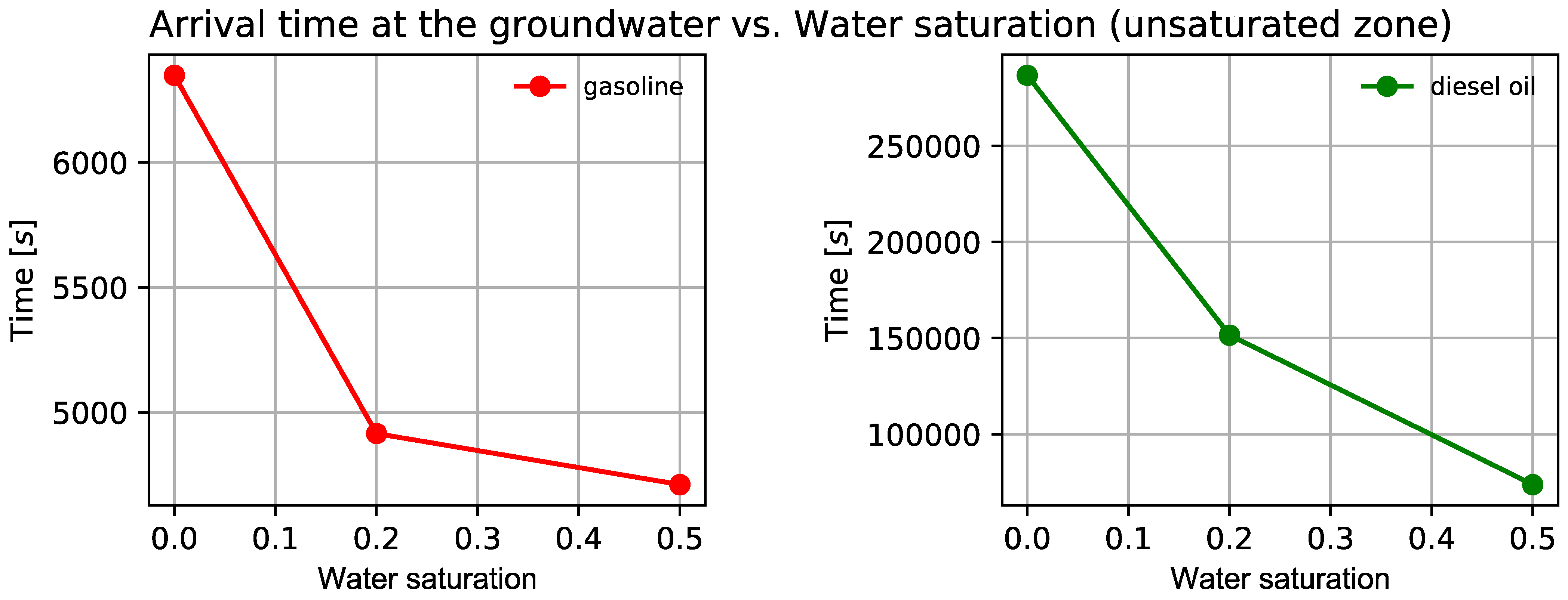
| Unsaturated Zone Depth (m) | Type of Contaminant | Water Saturation in the Unsaturated Zone | Arrival Time of to the Groundwater Table (s) | Position in x after 1 Day and 4.4 h (s) |
|---|---|---|---|---|
| 1.0 | Gasoline | 0.0 | −16.0 | |
| 0.2 | −16.0 | |||
| 0.5 | −16.0 | |||
| 1.0 | Diesel oil | 0.0 | −6.0 | |
| 0.2 | −6.0 | |||
| 0.5 | −6.0 | |||
| 10.0 | Gasoline | 0.0 | 6348.8 | −14.0 |
| 0.2 | 4915.0 | −16.0 | ||
| 0.5 | 4710.4 | −16.0 | ||
| 10.0 | Diesel oil | 0.0 | 286,720.0 | - |
| 0.2 | 151,552.0 | - | ||
| 0.5 | 73,720.0 | −1.5 |
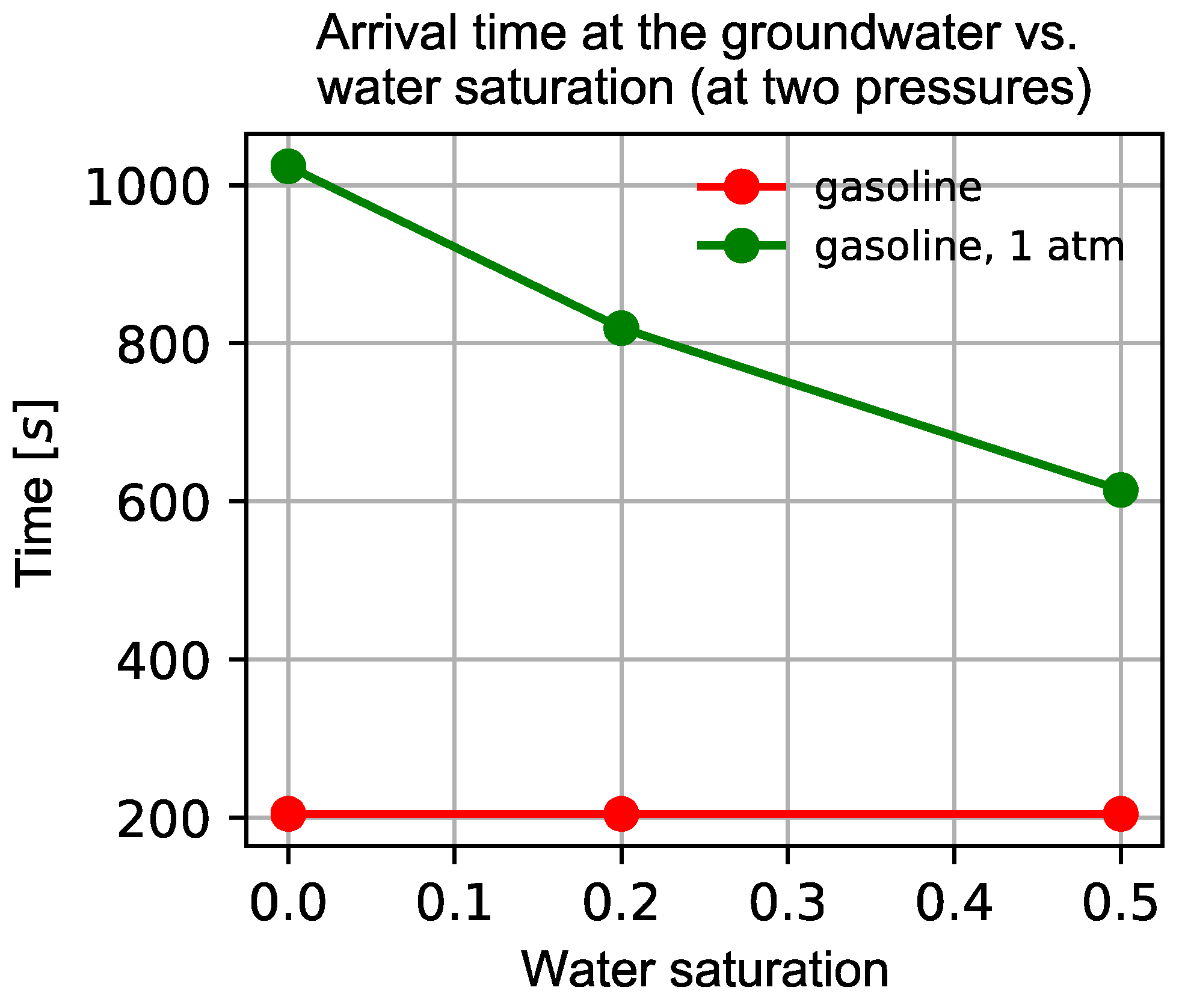
| Unsaturated Zone Depth (m) | Type of Contaminant | Water Saturation in the Unsaturated Zone | Arrival Time at the Groundwater Table (s) |
|---|---|---|---|
| 1.0 | Gasoline | 0.0 | 1024.0 |
| 1.0 | Gasoline | 0.20 | 819.2 |
| 1.0 | Gasoline | 0.50 | 614.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feo, A.; Pinardi, R.; Scanferla, E.; Celico, F. How to Minimize the Environmental Contamination Caused by Hydrocarbon Releases by Onshore Pipelines: The Key Role of a Three-Dimensional Three-Phase Fluid Flow Numerical Model. Water 2023, 15, 1900. https://doi.org/10.3390/w15101900
Feo A, Pinardi R, Scanferla E, Celico F. How to Minimize the Environmental Contamination Caused by Hydrocarbon Releases by Onshore Pipelines: The Key Role of a Three-Dimensional Three-Phase Fluid Flow Numerical Model. Water. 2023; 15(10):1900. https://doi.org/10.3390/w15101900
Chicago/Turabian StyleFeo, Alessandra, Riccardo Pinardi, Emanuele Scanferla, and Fulvio Celico. 2023. "How to Minimize the Environmental Contamination Caused by Hydrocarbon Releases by Onshore Pipelines: The Key Role of a Three-Dimensional Three-Phase Fluid Flow Numerical Model" Water 15, no. 10: 1900. https://doi.org/10.3390/w15101900
APA StyleFeo, A., Pinardi, R., Scanferla, E., & Celico, F. (2023). How to Minimize the Environmental Contamination Caused by Hydrocarbon Releases by Onshore Pipelines: The Key Role of a Three-Dimensional Three-Phase Fluid Flow Numerical Model. Water, 15(10), 1900. https://doi.org/10.3390/w15101900









