Application of Different Weighting Schemes and Stochastic Simulations to Parameterization Processes Considering Observation Error: Implications for Climate Change Impact Analysis of Integrated Watershed Models
Abstract
:1. Introduction
2. Materials and Methods
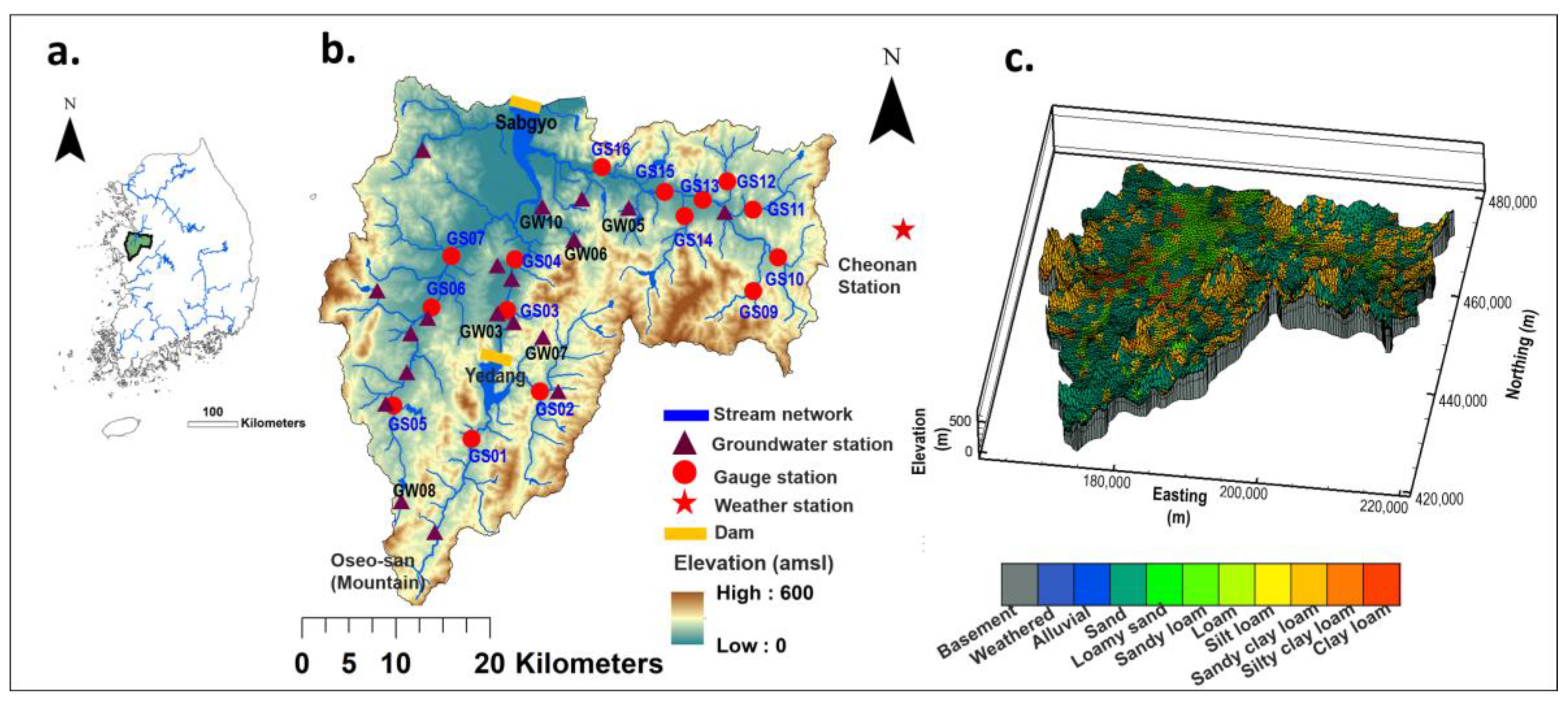
2.1. Study Site
2.2. Numerical Model
2.3. Model Calibration Process Considering Observation Errors
2.3.1. Estimation of Observation Error Weight Matrix for PEST
2.3.2. Stochastic Realization of Observation Sets Considering Measurement Uncertainty
2.4. Prediction of Future Variability of Watershed Processes with Different RCP Scenarios
3. Results
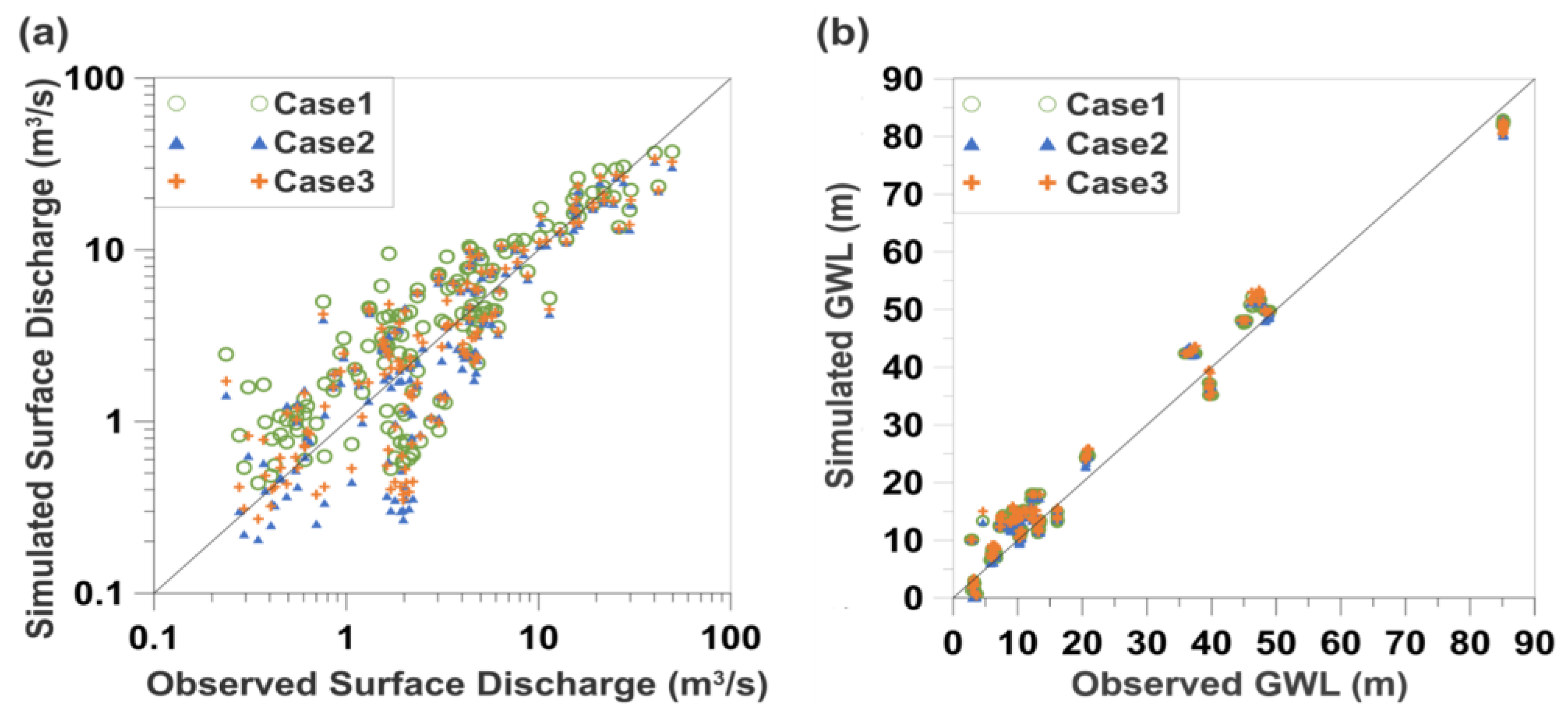
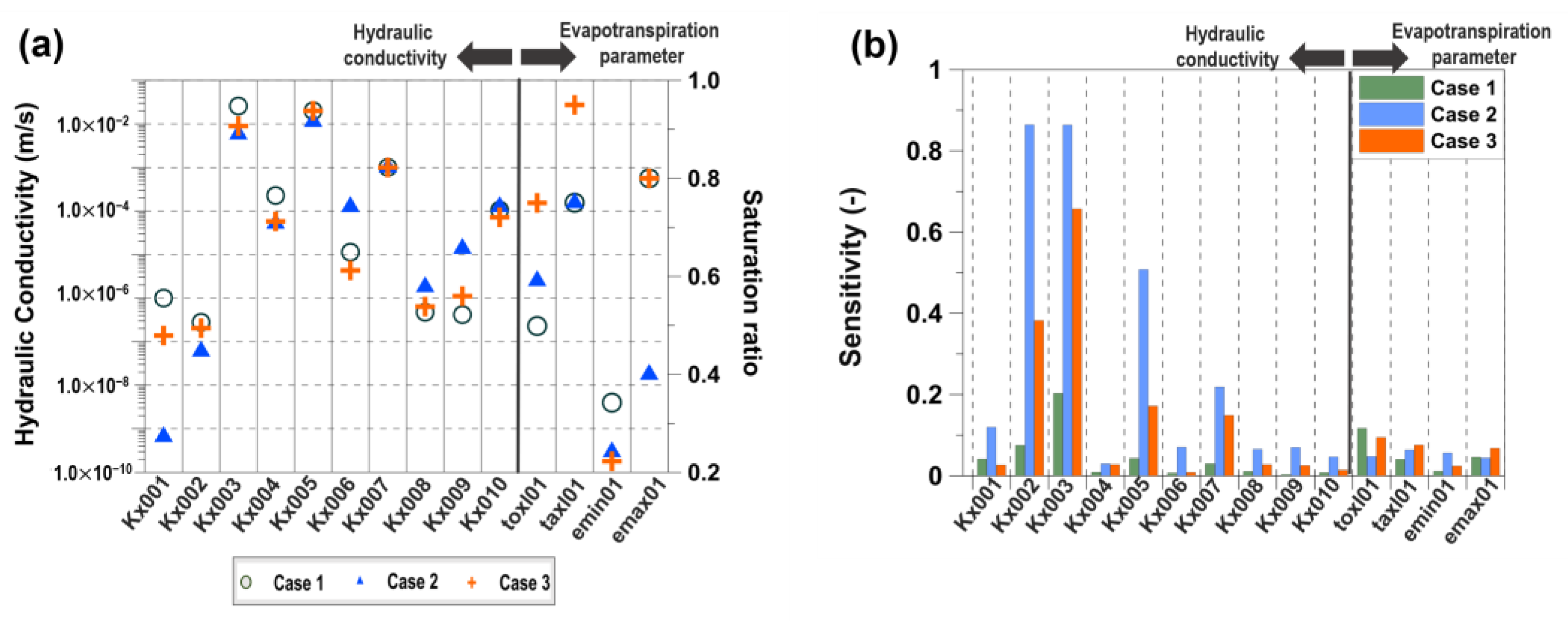
3.1. Comparisons of PEST Performance between Different Weighting Schemes
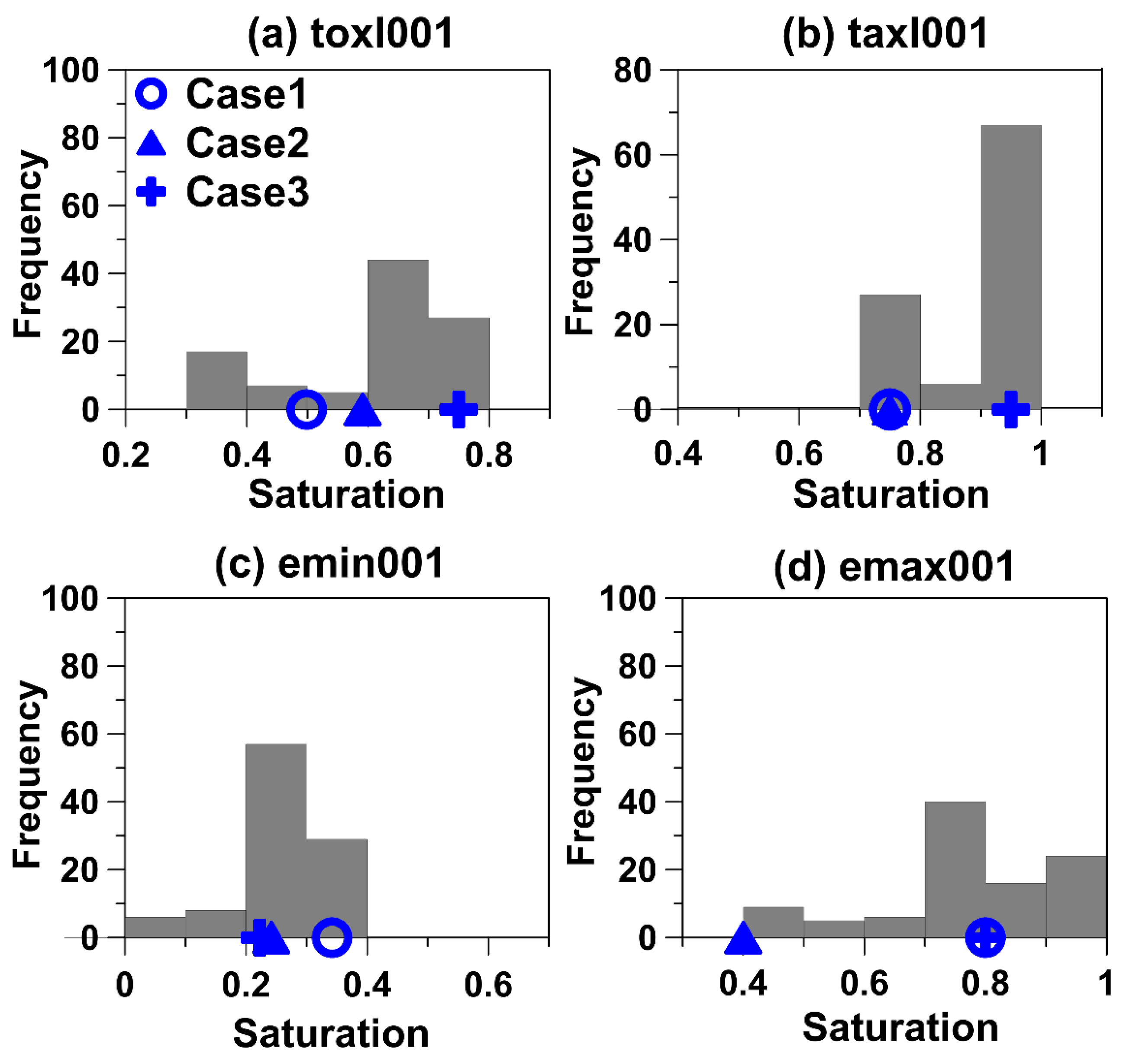
3.2. Results of Stochastic Simulations
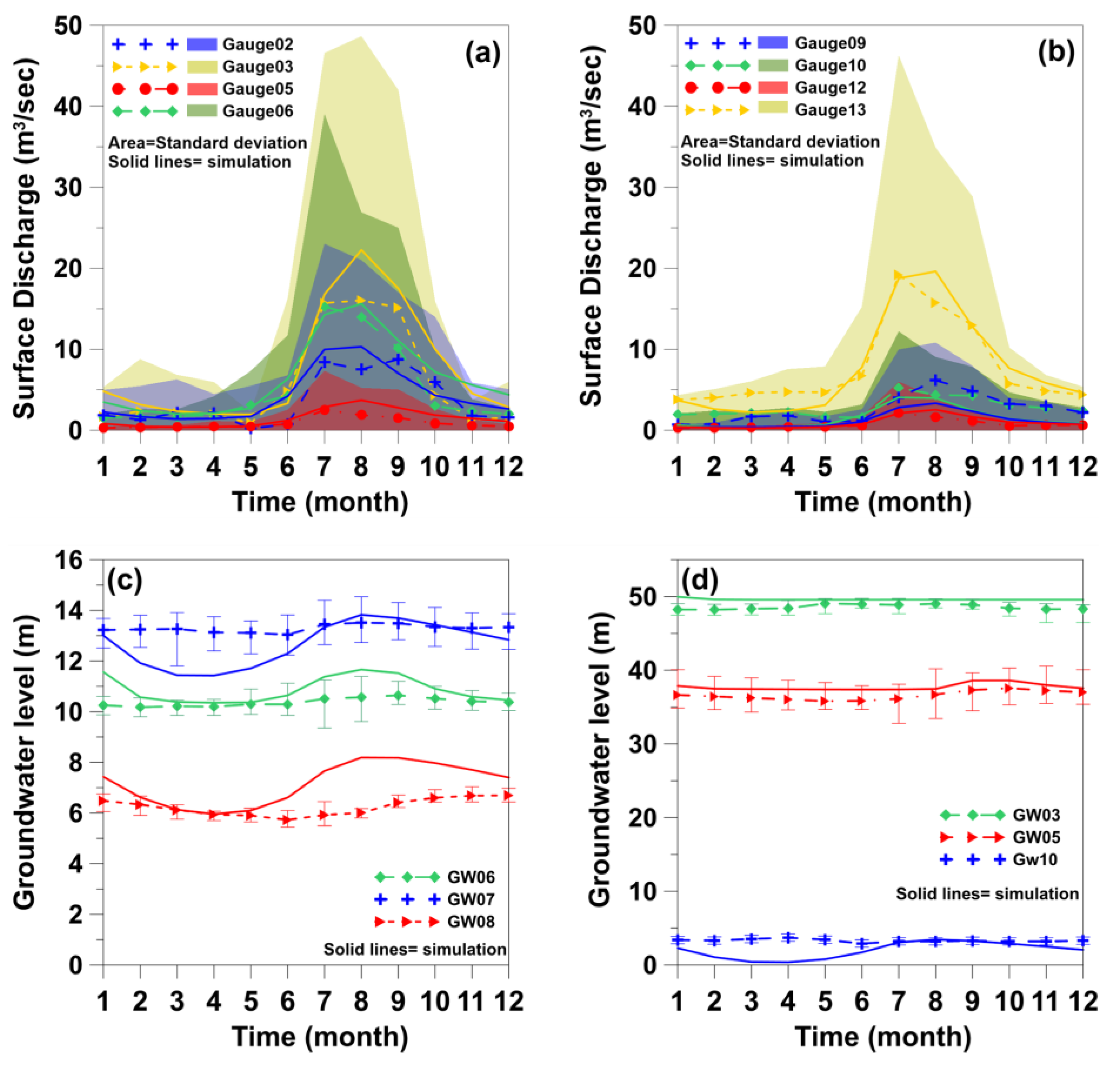
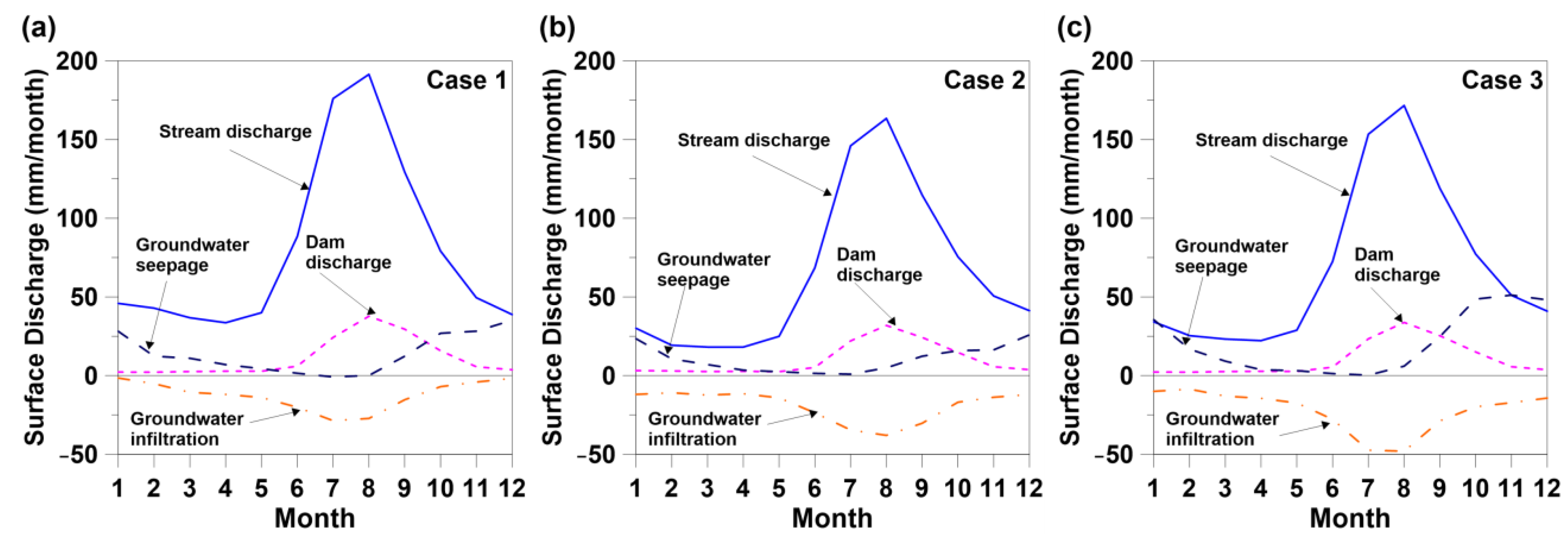
3.3. Analysis of Seasonal Hydrologic Variation in Groundwater-Surface Water Integrated System
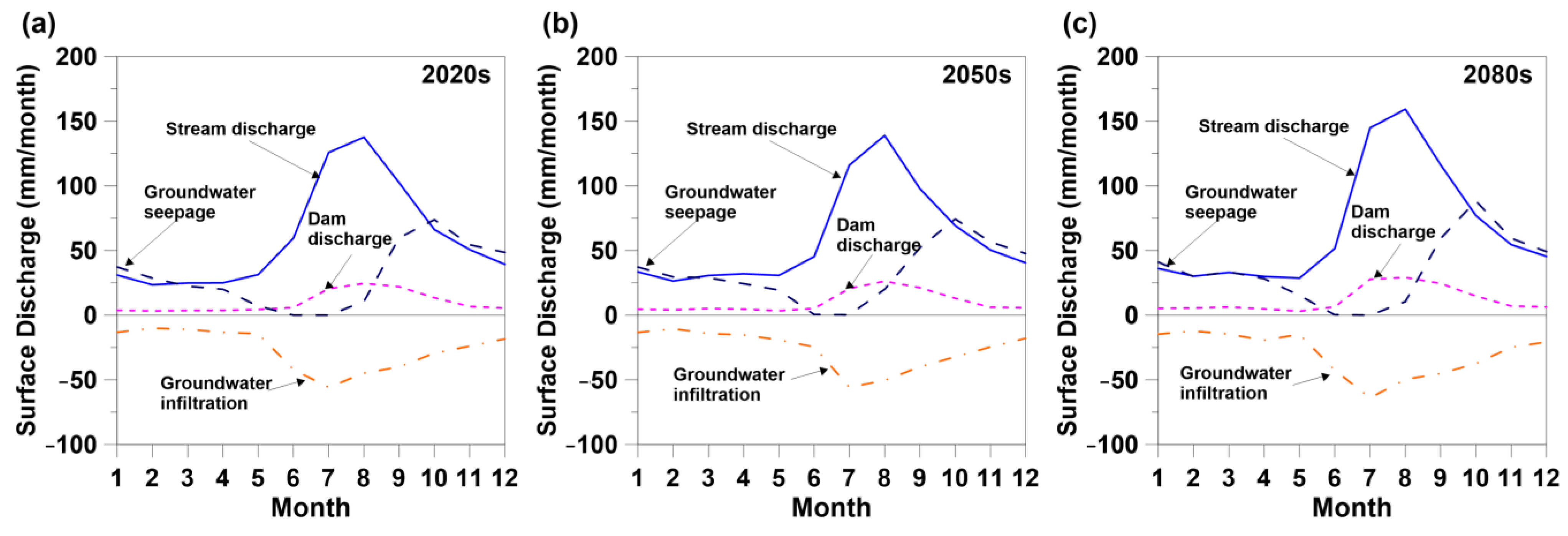
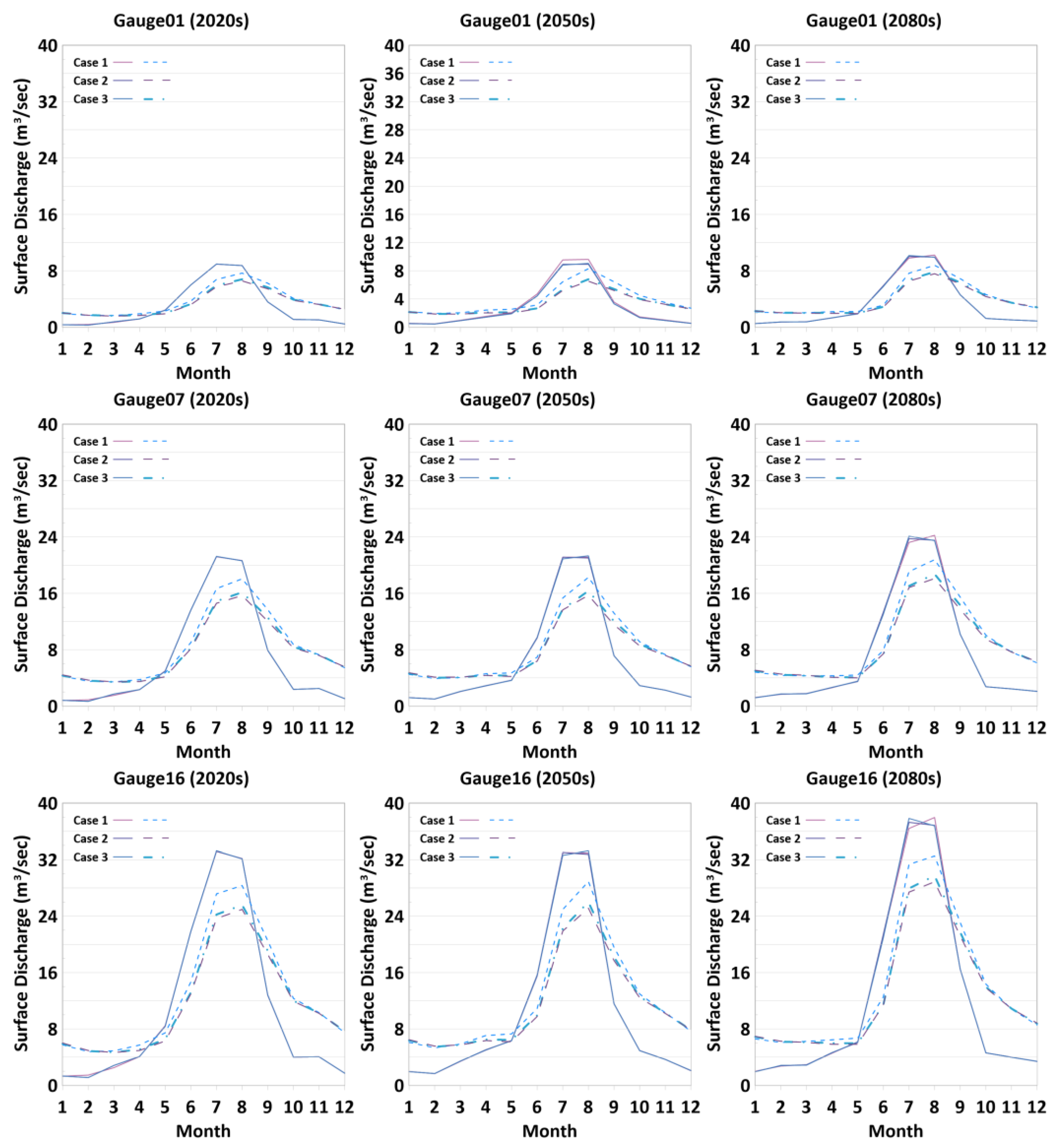
3.4. Predictions of Hydrological Responses and Groundwater–Surface Water Interactions under Different Climate Change Forcings
4. Discussions
4.1. Effect of the Different Observation-Error Weighting Schemes on the Parametrization of the Integrated Model
4.2. Potential Implication of Observation Error to the Model Parameterization and Performance
4.3. Effect of Groundwater–Surface Water Feedbacks on the Integrated Water System and Implications for Integrated Water System Management
5. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Taylor, R.G.; Scanlon, B.; Döll, P.; Rodell, M.; van Beek, R.; Wada, Y.; Longuevergne, L.; Leblanc, M.; Famiglietti, J.S.; Edmunds, M.; et al. Ground water and climate change. Nat. Clim. Chang. 2013, 3, 322–329. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2013: The Physical Science Basis; Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Van Vuuren, D.P.; Edmonds, J.; Kainuma, M.; Riahi, K.; Thomson, A.; Hibbard, K.; Hurtt, G.C.; Kram, T.; Krey, V.; Lamarque, J.-F.; et al. The representative concentration pathways: An overview. Clim. Chang. 2011, 109, 5–31. [Google Scholar] [CrossRef]
- Kløve, B.; Ala-Aho, P.; Bertrand, G.; Gurdak, J.J.; Kupfersberger, H.; Kværner, J.; Muotka, T.; Mykrä, H.; Preda, E.; Rossi, P.; et al. Climate change impacts on groundwater and dependent ecosystems. J. Hydrol. 2014, 518, 250–266. [Google Scholar] [CrossRef]
- Scibek, J.; Allen, D.M. Modeled impacts of predicted climate change on recharge and groundwater levels. Water Resour. Res. 2006, 42, W11405. [Google Scholar] [CrossRef]
- Ayugi, B.; Dike, V.; Ngoma, H.; Babaousmail, H.; Mumo, R.; Ongoma, V. Future Changes in Precipitation Extremes over East Africa Based on CMIP6 Models. Water 2021, 13, 2358. [Google Scholar] [CrossRef]
- Peters, D.L.; Dibike, Y.B.; Shudian, J.; Monk, W.A.; Baird, D.J. Effects of Climate Change on Navigability Indicators of the Lower Athabasca River, Canada. Water 2023, 15, 1373. [Google Scholar] [CrossRef]
- Majone, B.; Avesani, D.; Zulian, P.; Fiori, A.; Bellin, A. Analysis of high streamflow extremes in climate change studies: How do we calibrate hydrological models? Hydrol. Earth Syst. Sci. 2022, 26, 3863–3883. [Google Scholar] [CrossRef]
- Miguez-Macho, G.; Fan, Y. The role of groundwater in the Amazon water cycle: 1. Influence on seasonal streamflow, flooding and wetlands. J. Geophys. Res. Atmos. 2012, 117, D15113. [Google Scholar] [CrossRef]
- Pokhrel, Y.N.; Fan, Y.; Miguez-Macho, G. Potential hydrologic changes in the Amazon by the end of the 21st century and the groundwater buffer. Environ. Res. Lett. 2014, 9, 084004. [Google Scholar] [CrossRef]
- Stergiadi, M.; Di Marco, N.; Avesani, D.; Righetti, M.; Borga, M. Impact of Geology on Seasonal Hydrological Predictability in Alpine Regions by a Sensitivity Analysis Framework. Water 2020, 12, 2255. [Google Scholar] [CrossRef]
- Tian, Y.; Zheng, Y.; Wu, B.; Wu, X.; Liu, J.; Zheng, C. Modeling surface water-groundwater interaction in arid and semi-arid regions with intensive agriculture. Environ. Model. Softw. 2015, 63, 170–184. [Google Scholar] [CrossRef]
- Ala-Aho, P.; Rossi, P.M.; Isokangas, E.; Kløve, B. Fully integrated surface–subsurface flow modelling of groundwater–lake interaction in an esker aquifer: Model verification with stable isotopes and airborne thermal imaging. J. Hydrol. 2015, 522, 391–406. [Google Scholar] [CrossRef]
- Brannen, R.; Spence, C.; Ireson, A. Influence of shallow groundwater–surface water interactions on the hydrological connectivity and water budget of a wetland complex. Hydrol. Process. 2015, 29, 3862–3877. [Google Scholar] [CrossRef]
- Kalbus, E.; Reinstorf, F.; Schirmer, M. Measuring methods for groundwater—Surface water interactions: A review. Hydrol. Earth Syst. Sci. 2006, 10, 873–887. [Google Scholar] [CrossRef]
- Kiel, B.A.; Cardenas, M.B. Lateral hyporheic exchange throughout the Mississippi River network. Nat. Geosci. 2014, 7, 413–417. [Google Scholar] [CrossRef]
- Lautz, L.K.; Siegel, D.I. Modeling surface and ground water mixing in the hyporheic zone using MODFLOW and MT3D. Adv. Water Resour. 2006, 29, 1618–1633. [Google Scholar] [CrossRef]
- Erler, A.R.; Frey, S.K.; Khader, O.; d’Orgeville, M.; Park, Y.J.; Hwang, H.T.; Lapen, D.R.; Peltier, W.R.; Sudicky, E.A. Simulating climate change impacts on surface water resources within a lake-affected region using regional climate projections. Water Resour. Res. 2019, 55, 130–155. [Google Scholar] [CrossRef]
- Havril, T.; Tóth, Á.; Molson, J.W.; Galsa, A.; Mádl-Szőnyi, J. Impacts of predicted climate change on groundwater flow systems: Can wetlands disappear due to recharge reduction? J. Hydrol. 2018, 563, 1169–1180. [Google Scholar] [CrossRef]
- Persaud, E.; Levison, J.; MacRitchie, S.; Berg, S.J.; Erler, A.R.; Parker, B.; Sudicky, E. Integrated modelling to assess climate change impacts on groundwater and surface water in the Great Lakes Basin using diverse climate forcing. J. Hydrol. 2020, 584, 124682. [Google Scholar] [CrossRef]
- Schilling, O.S.; Cook, P.G.; Brunner, P. Beyond classical observations in hydrogeology: The advantages of including exchange flux, temperature, tracer concentration, residence time, and soil moisture observations in groundwater model calibration. Rev. Geophys. 2019, 57, 146–182. [Google Scholar] [CrossRef]
- Doherty, J. Calibration and Uncertainty Analysis for Complex Environmental Models, 1st ed.; Watermark Numerical Computing: Brisbane, QLD, Australia, 2015. [Google Scholar]
- Albers, B.M.C.; Molson, J.W.; Bense, V.F. Parameter sensitivity analysis of a two-dimensional cryo-hydrogeological numerical model of degrading permafrost near Umiujaq (Nunavik, Canada). Hydrogeol. J. 2020, 28, 905–919. [Google Scholar] [CrossRef]
- Christensen, S.; Doherty, J. Predictive error dependencies when using pilot points and singular value decomposition in groundwater model calibration. Adv. Water Resour. 2008, 31, 674–700. [Google Scholar] [CrossRef]
- Doherty, J.; Johnston, J.M. Methodologies for calibration and predictive analysis of a watershed model. J. Am. Water Resour. Assoc. 2003, 39, 251–265. [Google Scholar] [CrossRef]
- Moore, C.; Doherty, J. The role of the calibration process in reducing model predictive error. Water Resour. Res. 2005, 41, W05020. [Google Scholar] [CrossRef]
- Refsgaard, J.C.; van der Sluijs, J.P.; Brown, J.; van der Keur, P. A framework for dealing with uncertainty due to model structure error. Adv. Water Resour. 2006, 29, 1586–1597. [Google Scholar] [CrossRef]
- James, S.C.; Doherty, J.E.; Eddebbarh, A.A. Practical postcalibration uncertainty analysis: Yucca Mountain, Nevada. Ground Water 2009, 47, 851–869. [Google Scholar] [CrossRef]
- Liu, X.; Kitanidis, P.K. Large-scale inverse modeling with an application in hydraulic tomography. Water Resour. Res. 2011, 47, W02501. [Google Scholar] [CrossRef]
- Tiedeman, C.R.; Green, C.T. Effect of correlated observation error on parameters, predictions, and uncertainty. Water Resour. Res. 2013, 49, 6339–6355. [Google Scholar] [CrossRef]
- Hill, M.C.; Tiedeman, C.R. Effective Groundwater Model Calibration: With Analysis of Data, Sensitivities, Predictions, and Uncertainty; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- Gelhar, L.W. Stochastic Subsurface Hydrology; Prentice Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- McMillan, H.; Freer, J.; Pappenberger, F.; Krueger, T.; Clark, M. Impacts of uncertain river flow data on rainfall-runoff model calibration and discharge predictions. Hydrol. Process. 2010, 24, 1270–1284. [Google Scholar] [CrossRef]
- Korea Meteorological Administration. Available online: http://www.weather.go.kr/ (accessed on 3 April 2023).
- Geological Map of Korea. Available online: http://mgeo.kigam.re.kr (accessed on 3 April 2023).
- Korean Soil Information System. Available online: http://www.soil.rda.go.kr/ (accessed on 3 April 2023).
- Environmental Geographic Information Service. Available online: https://egis.me.go.kr/ (accessed on 3 April 2023).
- Groundwater Information Monitoring System. Available online: http://www.gims.go.kr/ (accessed on 3 April 2023).
- Aquanty. HydroGeoSphere User Manual; Aquanty Inc.: Waterloo, ON, Canada, 2015. [Google Scholar]
- Viessman, W.J.; Lewis, G.L. Introduction to Hydrology, 4th ed.; Harper Collins College Publisher: New York, NY, USA, 1996. [Google Scholar]
- HydroAlgorithmics Pty Ltd. AlgoMesh 2 User Guide; HydroAlgorithmics Inc.: Melbourne, VIC, Australia, 2020. [Google Scholar]
- Environmental Systems Research Institute. ArcGIS Desktop: Release 10.6.1; ESRI, Inc.: Redlands, CA, USA, 2018. [Google Scholar]
- Hwang, H.T.; Park, Y.J.; Frey, S.K.; Callaghan, M.V.; Berg, S.J.; Lapen, D.R.; Sudicky, E.A. Efficient numerical incorporation of water management operations in integrated hydrosystem models: Application to tile drainage and reservoir operating systems. J. Hydrol. 2019, 575, 1253–1266. [Google Scholar] [CrossRef]
- Kristensen, K.J.; Jensen, S.E. A model for estimating actual evapotranspiration from potential evapotranspiration. Hydrol. Res. 1975, 6, 170–188. [Google Scholar] [CrossRef]
- Wigmosta, M.S.; Vail, L.W.; Lettenmaier, D.P. A distributed hydrology-vegetation model for complex terrain. Water Resour. Res. 1994, 30, 1665–1679. [Google Scholar] [CrossRef]
- Valiantzas, J.D. Simplified versions for the Penman evaporation equation using routine weather data. J. Hydrol. 2006, 331, 690–702. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998. [Google Scholar]
- MCD15A3H MODIS/terra+aqua Leaf Area Index/FPAR 4-day L4 Global 500m SIN Grid V006 [Data Set]. NASA EOSDIS Land Processes DAAC. Available online: https://doi.org/10.5067/MODIS/MCD15A3H.006 (accessed on 3 April 2023).
- Water Resources Management Information System (WAMIS). Available online: http://www.wamis.go.kr (accessed on 3 April 2023).
- Rural Groundwater Net. Available online: http://www.groundwater.or.kr (accessed on 3 April 2023).
- Panday, S.; Huyakorn, P.S. A fully coupled physically-based spatially-distributed model for evaluating surface/subsurface flow. Adv. Water Resour. 2004, 27, 361–382. [Google Scholar] [CrossRef]
- Canadell, J.; Jackson, R.B.; Ehleringer, J.B.; Mooney, H.A.; Sala, O.E.; Schulze, E.D. Maximum rooting depth of vegetation types at the global scale. Oecologia 1996, 108, 583–595. [Google Scholar] [CrossRef]
- Ok, J.; Kim, D.J.; Han, K.; Jung, K.H.; Lee, K.D.; Zhang, Y.; Cho, H.-R.; Hwang, S.-A. Relationship between measured and predicted soil water content using soil moisture monitoring network (in Korean). Korean J. Agric. For. Meteorol. 2019, 21, 297–306. [Google Scholar]
- Chow, V.T. Open-Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Ebel, B.A.; Mirus, B.B.; Heppner, C.S.; VanderKwaak, J.E.; Loague, K. First-order exchange coefficient coupling for simulating surface water-groundwater interactions: Parameter sensitivity and consistency with a physics-based approach. Hydrol. Process. 2009, 23, 1949–1959. [Google Scholar] [CrossRef]
- Freeze, R.A.; Cherry, J.A. Groundwater; Prentice Hall: Englewood Cliffs, NJ, USA, 1979. [Google Scholar]
- Fetter, C.W.; Boving, T.; Kreamer, D. Contaminant Hydrogeology, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Namown Eng. Inc. Measurements and Computation of Streamflow of Sabgyo Watershed—Gangcheong, Wonypeong, Hannaedari; Geum River Flood Control Office: Gongju, Republic of Korea, 2005. (In Korean)
- Namown Eng. Inc.; Korea Institute of Construction Technology. Measurements and Computation of Streamflow of Sabgyo Watershed; Geum River Flood Control Office: Gongju, Republic of Korea, 2006. (In Korean)
- Perin, R.; Trigatti, M.; Nicolini, M.; Campolo, M.; Goi, D. Automated calibration of the EPA-SWMM model for a small suburban catchment using PEST: A case study. Environ. Model. Assess. 2020, 192, 374. [Google Scholar] [CrossRef]
- Kim, S.M.; Benham, B.L.; Brannan, K.M.; Zeckoski, R.W.; Doherty, J. Comparison of hydrologic calibration of HSPF using automatic and manual methods. Water Resour. Res. 2007, 43, W01402. [Google Scholar] [CrossRef]
- Linsley, R.K.; Kohler, M.A. Hydrology for Engineers; McGraw-Hill: London, UK, 1988. [Google Scholar]
- Thyer, M.; Renard, B.; Kavetski, D.; Kuczera, G.; Franks, S.W.; Srikanthan, S. Critical evaluation of parameter consistency and predictive uncertainty in hydrological modeling: A case study using Bayesian total error analysis. Water Resour. Res. 2009, 45, W00B14. [Google Scholar] [CrossRef]
- Park, E. A geostatistical evolution strategy for subsurface characterization: Theory and validation through hypothetical two-dimensional hydraulic conductivity fields. Water Resour. Res. 2020, 56, W026922. [Google Scholar] [CrossRef]
- Doherty, J.E.; Hunt, R.J. Approaches to Highly Parameterized Inversion: A Guide to Using PEST for Groundwater-Model Calibration; US Geological Survey Scientific Investigations Report 2010-5169; US Geological Survey: Reston, VA, USA, 2010.



| Parameter | Values | Sources/Notes | |
|---|---|---|---|
| Evaporation depth | 1(Urban)–3 m (Mixed trees) | Cubic decay with depth [51] | |
| Root depth | 0.1 (Urban)–3.5 (Mixed trees) | Cubic decay with depth [51,52] | |
| LAI | From 0.26–2.9 (Vegetation) to 0.45–4.1 (Deciduous) | Monthly averages used for simulation [48] | |
| Transpiration limiting saturation | Wilting point | 0.19 | [53] |
| Field capacity | 0.3 | [53] | |
| Oxic limit | Calibration target (toxl01) 1 | - | |
| Anoxic limit | Calibration target (taxl01) 1 | - | |
| Evaporation limiting saturation | Minimum | Calibration target (emin01) 1 | - |
| Maximum data | Calibration target (emax01) 1 | - | |
| Parameter | Values | Sources/Notes |
|---|---|---|
| Manning’s Roughness Coefficients | 0.0016 (Urban)–0.03 (Forest) | [54] |
| Rill Storage Height | 2.0 × 10−5 (urban)–5.0 × 10−3 (Wetland) | [38,51] |
| Obstruction Storage Height | 1.0 × 10−5 (Urban)–5.0 × 10−3 (Wetland) | [38,51] |
| Coupling Length | 0.01 m | [55] |
| Parameter | Values | Sources/Notes | |
|---|---|---|---|
| Hydraulic conductivity (m/s) | Basement rock | 1.0 × 10−10 | [56] |
| Weathered rock | Calibration target (kx001) 1 | ||
| Alluvial layer | Calibration target (kx002) 1 | ||
| Surface soil | Calibration target (kx003-kx010) 2 | ||
| Anisotropy (Kv/Kh) | Basement rock | 1 | [56] |
| Weathered rock | 1 | ||
| Alluvial layer | 1 | ||
| Surface soil | 0.1 | ||
| Specific Storage | Ss | 1 × 10−4–5.0 × 10−4 | [56] |
| Porosity | n | 0.05 (basement rock)–0.35 (Soil) | [56] |
| Van Genuchten parameters | α | 2.25 | [57] |
| β | 1.89 | ||
| Residual saturation | 0.18 | ||
| Model Performance Criteria | Components | Case 1 | Case 2 | Case 3 |
|---|---|---|---|---|
| RMSE * | Surface flow [m3/s] | 3.5 | 3.6 | 3.1 |
| GWL [m] | 3.9 | 3.8 | 4.0 | |
| Weighted RSS * | Surface flow [m3/s] | 12.2 | 0.5 | 1.4 |
| GWL [m] | 15.3 | 9.7 | 4.5 | |
| R2 * | Surface flow [m3/s] | 0.83 | 0.84 | 0.83 |
| NSE * | Surface flow [m3/s] | 0.83 | 0.82 | 0.83 |
| Parameter | PEST with Different Weights | Stochastic Model | ||||
|---|---|---|---|---|---|---|
| Case 1 (Difference Ratio) * | Case 2 (Difference Ratio) | Case 3 (Difference Ratio) | Mean | Standard Deviation | ||
| log(K) (m/s) | kx001 | 1.00 × 10−6 (4.43) | 6.60 × 10−10 (1.00) | 1.39 × 10−7 (0.24) | 1.84 × 10−7 | 2.86 × 10−7 |
| kx002 | 2.80 × 10−7 (0.33) | 6.04 × 10−8 (0.85) | 2.04 × 10−7 (0.51) | 4.16 × 10−7 | 8.61 × 10−8 | |
| kx003 | 2.59 × 10−2 (0.20) | 5.86 × 10−3 (0.82) | 8.97 × 10−3 (0.72) | 3.23 × 10−2 | 3.42 × 10−3 | |
| kx004 | 2.26 × 10−4 (4.50) | 5.17 × 10−5 (0.26) | 5.76 × 10−5 (0.40) | 4.11 × 10−5 | 2.74 × 10−5 | |
| kx005 | 2.00 × 10−2 (0.34) | 1.14 × 10−2 (0.23) | 2.00 × 10−2 (0.34) | 1.49 × 10−2 | 4.93 × 10−3 | |
| kx006 | 1.14 × 10−5 (1.79) | 1.27 × 10−4 (30.13) | 4.32 × 10−6 (0.06) | 4.08 × 10−6 | 2.88 × 10−6 | |
| kx007 | 1.00 × 10−3 (3.41) | 1.00 × 10−3 (3.41) | 1.00 × 10−3 (3.41) | 2.27 × 10−4 | 3.42 × 10−4 | |
| kx008 | 4.74 × 10−7 (0.72) | 1.82 × 10−6 (0.08) | 6.39 × 10−7 (0.62) | 1.69 × 10−6 | 1.79 × 10−6 | |
| kx009 | 4.19 × 10−7 (0.78) | 1.39 × 10−5 (6.20) | 1.11 × 10−6 (0.42) | 1.93 × 10−6 | 9.80 × 10−7 | |
| kx010 | 1.05 × 10−4 (0.77) | 1.26 × 10−4 (1.13) | 7.16 × 10−5 (0.21) | 5.92 × 10−5 | 4.02 × 10−5 | |
| ET Properties | toxl001 | 0.50 (0.18) | 0.59 (0.03) | 0.75 (0.23) | 0.61 | 0.14 |
| taxl001 | 0.75 (0.16) | 0.75 (0.16) | 0.95 (0.07) | 0.89 | 0.08 | |
| emin001 | 0.34 (0.21) | 0.24 (0.14) | 0.22 (0.21) | 0.28 | 0.09 | |
| emax001 | 0.80 (0.05) | 0.40 (0.47) | 0.80 (0.05) | 0.76 | 0.16 | |
| Hydrologic Component | Amount (mm/Month) | |||
|---|---|---|---|---|
| Case 1 | Case 2 | Case 3 | ||
| Rainy Season | Rain AET Surface Discharge | 203.4 25.3 146.3 | 203.4 31.5 123.2 | 203.4 31.1 129.1 |
| Groundwater Seepage 1 Stream Water Infiltration 1 Dam Discharge | 3.3 22.8 24.4 | 4.9 34.0 20.8 | 8.1 38.0 22.0 | |
| Dry Season | Rain AET Surface Discharge | 49.1 15.9 45.8 | 49.1 19.6 34.7 | 49.1 18.7 37.9 |
| Groundwater Seepage 1 Stream Water Infiltration 1 Dam Discharge | 19.1 7.0 4.7 | 17.1 11.9 4.8 | 27.0 14.3 4.6 | |
| Hydrologic Component | Amount (mm/Month) | |||
|---|---|---|---|---|
| 2020s (2011–2040) | 2050s (2041–2070) | 2080s (2071–2100) | ||
| Rainy Season | Rain AET Surface Discharge | 210.3 36.5 118.4 | 187.5 37.2 106.3 | 206.5 36.8 114.8 |
| Groundwater Seepage Stream Water Infiltration Dam Discharge | 34.3 62.3 20.4 | 38.3 57.8 18.5 | 38.3 59.7 19.6 | |
| Dry Season | Rain AET Surface Discharge | 70.4 21.3 42.9 | 73.5 21.6 42.9 | 68.0 21.7 39.5 |
| Groundwater Seepage Stream Water Infiltration Dam Discharge | 45.2 25.5 6.0 | 44.5 27.2 5.8 | 44.7 26.6 5.2 | |
| Hydrologic Component | Amount (mm/Month) | |||
|---|---|---|---|---|
| 2020s (2011–2040) | 2050s (2041–2070) | 2080s (2071–2100) | ||
| Rainy Season | Rain AET Surface Discharge | 211.3 36.7 106.2 | 206.8 38.2 106.3 | 249.9 39.9 126.3 |
| Groundwater Seepage Stream Water Infiltration Dam Discharge | 17.6 45.7 18.3 | 17.8 43.9 18.5 | 17.4 50.3 22.0 | |
| Dry Season | Rain AET Surface Discharge | 68.7 20.7 41.9 | 61.3 22.1 42.9 | 62.4 23.1 44.3 |
| Groundwater Seepage Stream Water Infiltration Dam Discharge | 36.5 16.7 5.6 | 39.8 18.4 5.8 | 43.1 19.3 6.7 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, E.; Lee, H.; Park, D.; Hwang, H.-T.; Park, C. Application of Different Weighting Schemes and Stochastic Simulations to Parameterization Processes Considering Observation Error: Implications for Climate Change Impact Analysis of Integrated Watershed Models. Water 2023, 15, 1880. https://doi.org/10.3390/w15101880
Lee E, Lee H, Park D, Hwang H-T, Park C. Application of Different Weighting Schemes and Stochastic Simulations to Parameterization Processes Considering Observation Error: Implications for Climate Change Impact Analysis of Integrated Watershed Models. Water. 2023; 15(10):1880. https://doi.org/10.3390/w15101880
Chicago/Turabian StyleLee, Eunhee, Hyeonju Lee, Dongkyu Park, Hyoun-Tae Hwang, and Changhui Park. 2023. "Application of Different Weighting Schemes and Stochastic Simulations to Parameterization Processes Considering Observation Error: Implications for Climate Change Impact Analysis of Integrated Watershed Models" Water 15, no. 10: 1880. https://doi.org/10.3390/w15101880
APA StyleLee, E., Lee, H., Park, D., Hwang, H.-T., & Park, C. (2023). Application of Different Weighting Schemes and Stochastic Simulations to Parameterization Processes Considering Observation Error: Implications for Climate Change Impact Analysis of Integrated Watershed Models. Water, 15(10), 1880. https://doi.org/10.3390/w15101880






