Intense Vortex Motion in a Two-Phase Bioreactor
Abstract
:1. Introduction
2. Materials and Methods
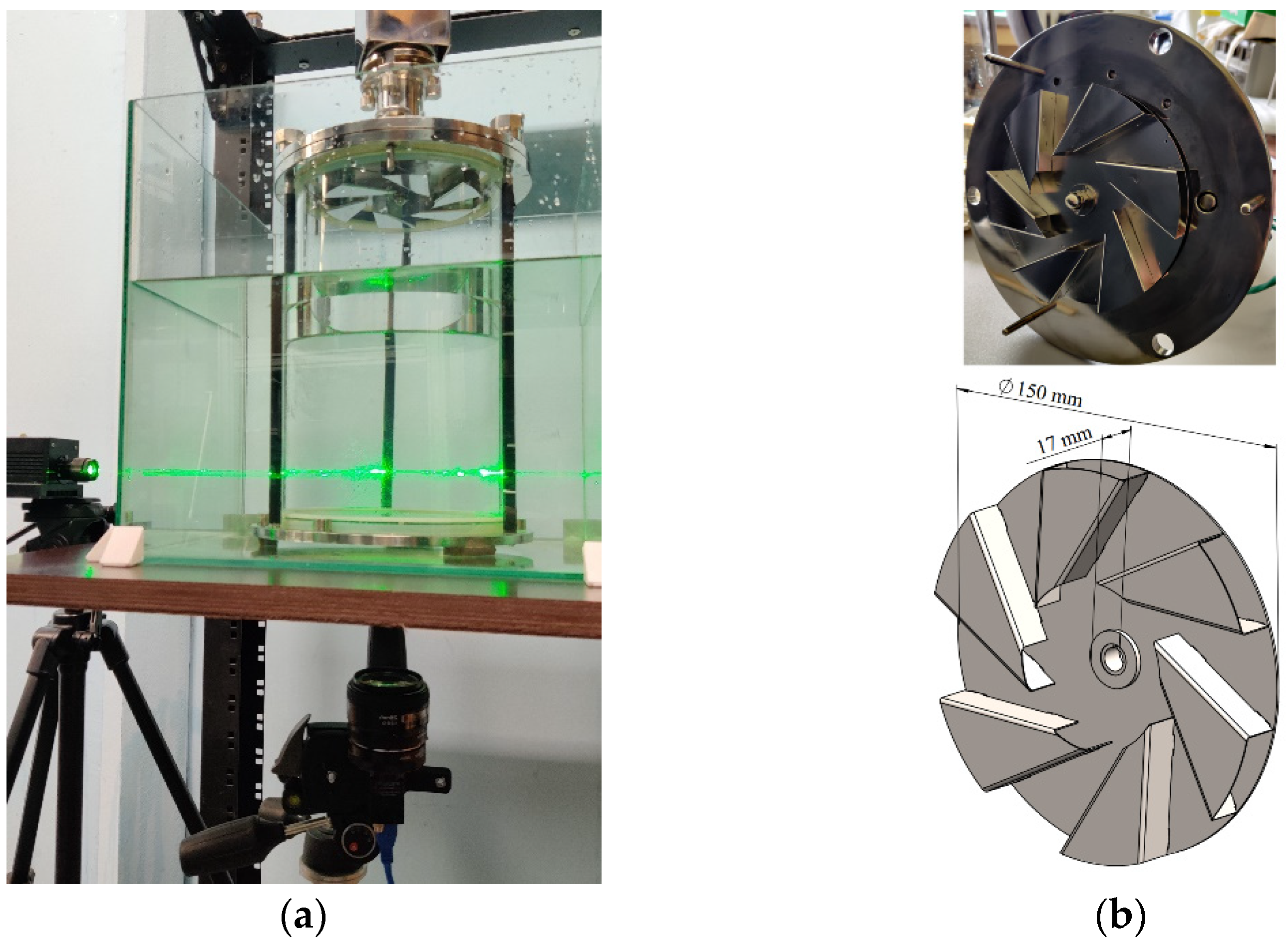
2.1. Experimental Setup
2.2. The CFD Approach
3. Results
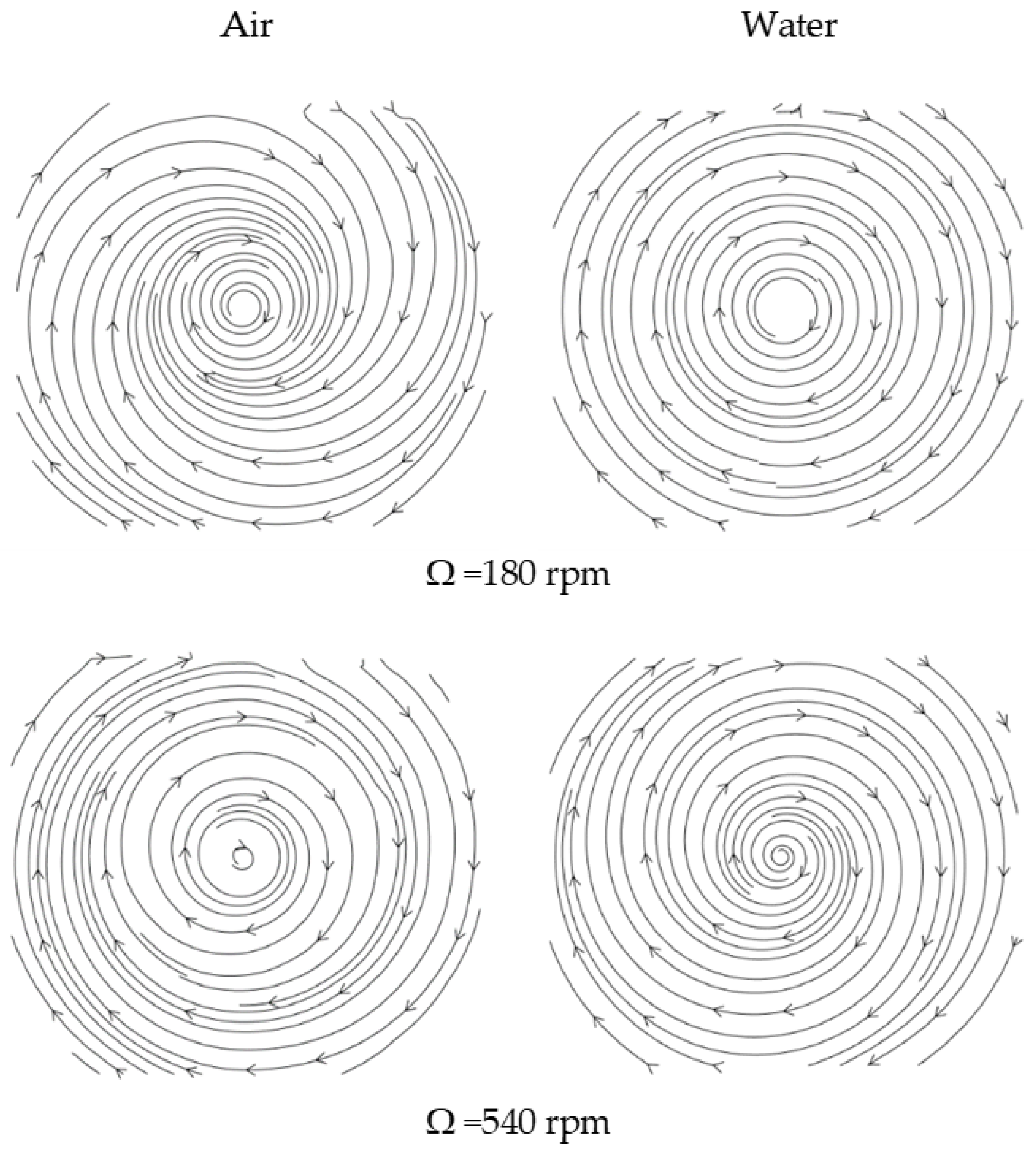
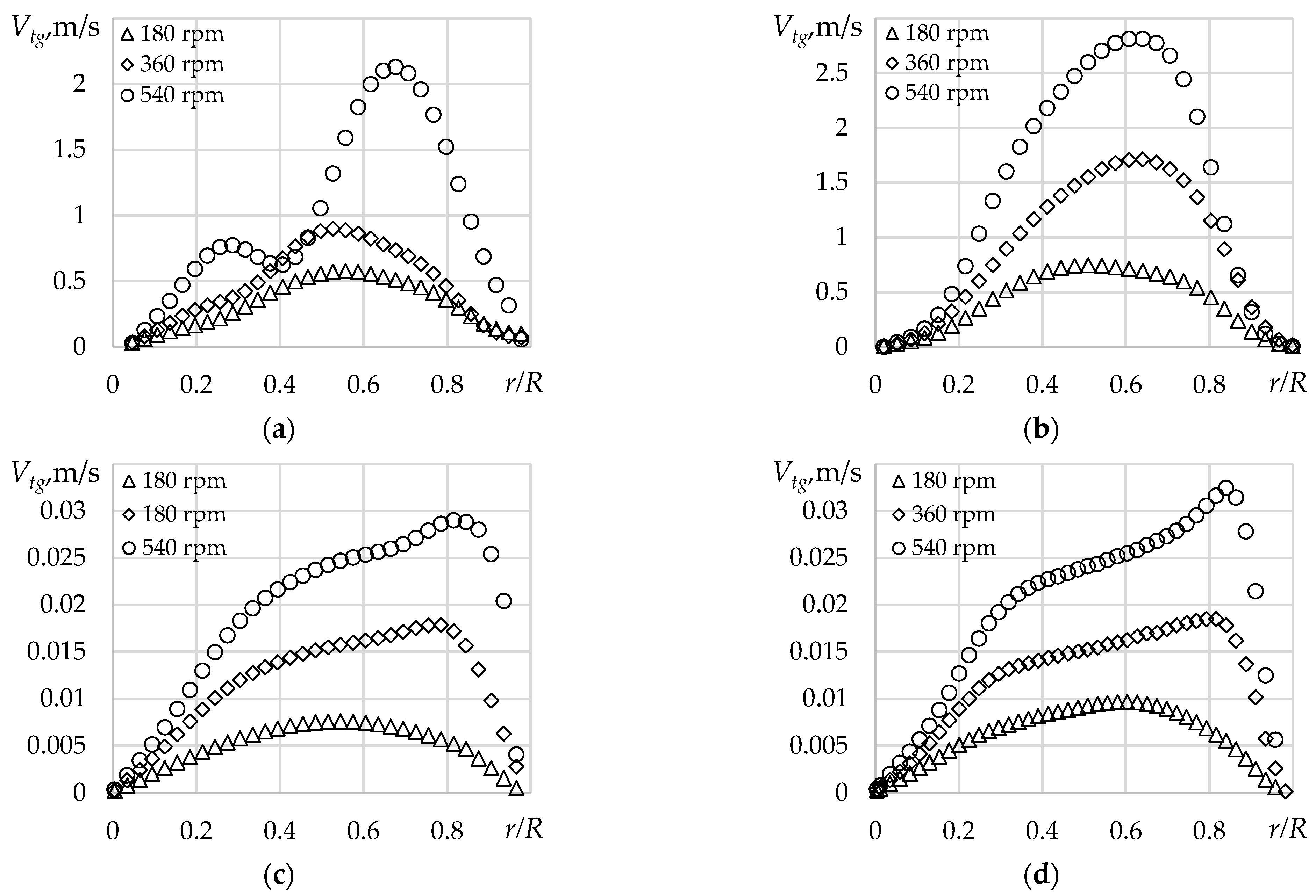
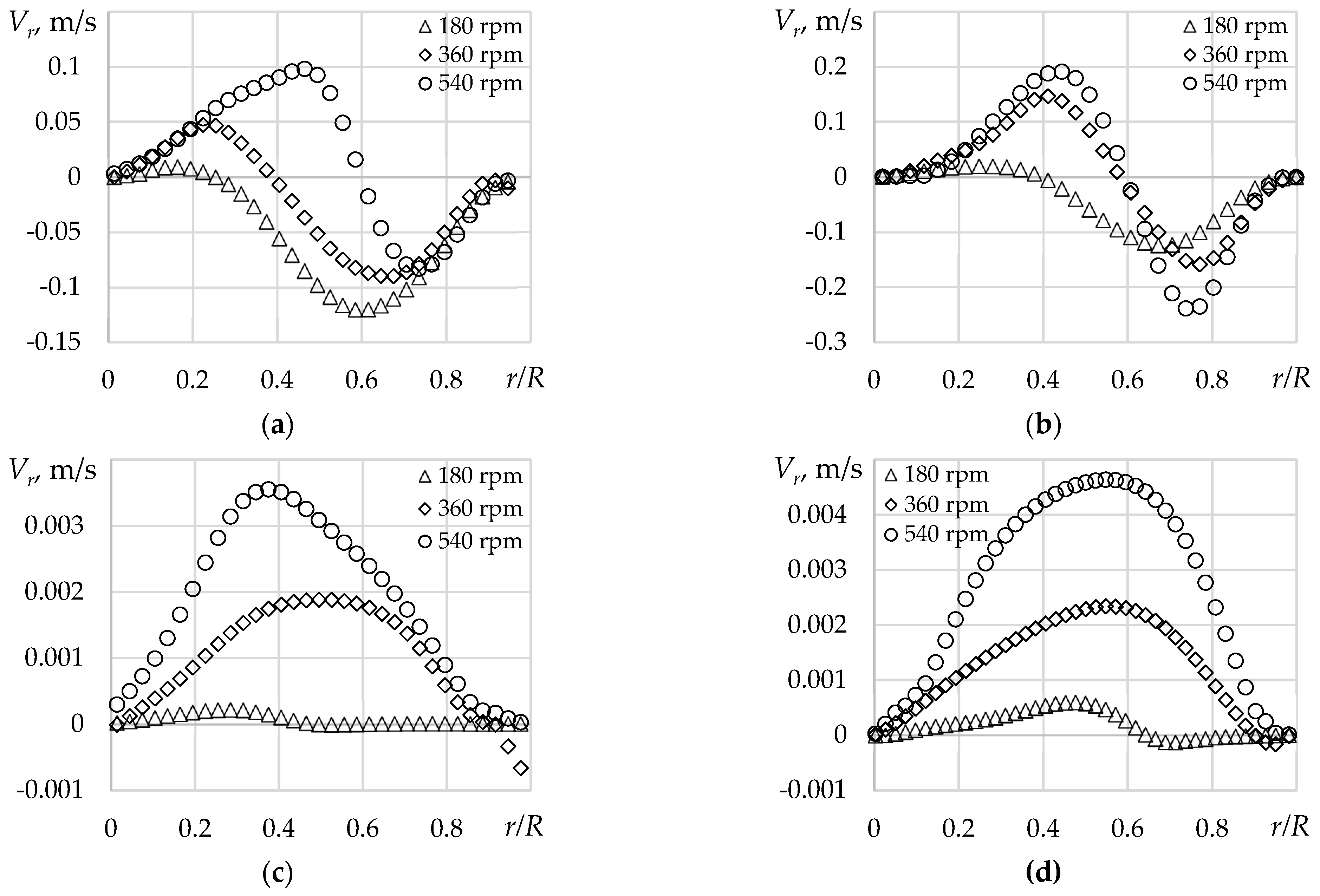
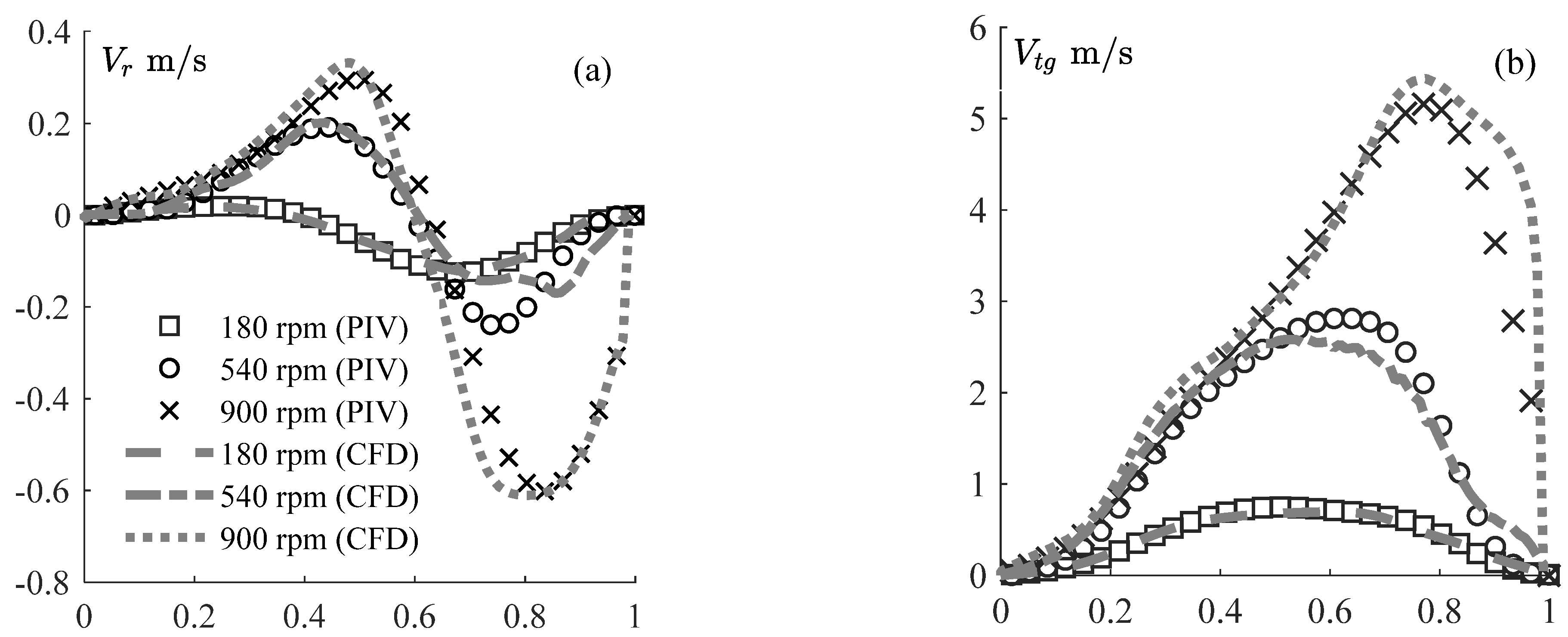
3.1. Experimental
3.2. Numerical Data
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| D | diameter of the reactor vessel |
| F | source term due to surface tension |
| g | gravitational acceleration |
| H | height of the reactor vessel |
| hg | height of model fluid |
| h= hg/H | dimensionless height of model fluid |
| I | identity tensor |
| p | pressure |
| p0 | initial pressure above the free surface |
| R | radius of the reactor vessel |
| Re = VtgmR/νg | the Reynolds number |
| s = μ(∇U + ∇UT − 2/3(∇∙U))I | viscous stress tensor |
| U | absolute velocity |
| Vax | axial component of velocity |
| Vr | radial component of velocity |
| Vtg | tangential component of velocity |
| Vtgm | the maximum value of the tangential component of velocity |
| Subscripts | |
| a | air |
| g | aqueous glycerol solution |
| l | liquid |
| r | radial component |
| R | rotary |
| S | stationary |
| tg | tangential component |
| m | maximum value |
| Greek | |
| μ = αμL + (1 − α)μa | dynamic viscosity |
| ρ = αρl + (1 − α)ρa | density |
| ρa | density of air |
| ρg | density of aqueous glycerol solution |
| νa | kinematic viscosity of air |
| νg | kinematic viscosity of aqueous glycerol solution |
| Ω | rotation speed of activator |
| σ | surface tension |
| Acronym | |
| CFD | Computational Fluid Dynamics modeling |
| CSF | Continuum Surface Force method |
| DNS | Direct Numerical Simulations |
| FVM | Finite Volume Method |
| MRF | Multiple Reference Frame method |
| NS | Navier–Stokes |
| PIV | Particle Image Velocimetry |
| VOF | Volume of Fluid method |
References
- Poincaré, H. Théories des Tourbillons; George Carre: Paris, France, 1893. [Google Scholar]
- Marusic, I.; Broomhall, S. Leonardo da Vinci and Fluid Mechanics. Annu. Rev. Fluid Mech. 2021, 53, 1–25. [Google Scholar] [CrossRef]
- Saffman, P.G. Vortex Dynamics; Cambridge University Press: New York, NY, USA, 1993. [Google Scholar]
- Shtern, V. Cellular Flows. In Topological Metamorphoses in Fluid Mechanics; Cambridge University Press: New York, NY, USA, 2018. [Google Scholar]
- Stepanova, E.V.; Chaplin, T.O.; Chashechkin, Y.D. Experimental investigation of oil transport in a compound vortex. J. Appl. Mech. Tech. Phy. 2013, 54, 79–86. [Google Scholar] [CrossRef]
- Shtern, V.N.; Naumov, I.V. Swirl-decay mechanism generating counterflows and cells in vortex motion. J. Eng. Thermophys. 2021, 30, 19–39. [Google Scholar] [CrossRef]
- Byalko, A.V. Underwater gas tornado. Phys. Scripta 2013, 155, 014030. [Google Scholar] [CrossRef]
- Faugaret, A.; Duguet, Y.; Fraigneau, Y.; Witkowsky, L. A simple model for arbitrary pollution effects on rotating free-surface flows. J. Fluid Mech. 2022, 932, A2. [Google Scholar] [CrossRef]
- Hejazi, H.A.; Khan, M.I.; Raza, A.; Smida, K.; Khan, S.U.; Tlili, I. Inclined surface slip flow of nanoparticles with subject to mixed convection phenomenon: Fractional calculus applications. J. Indian Chem. Soc. 2022, 99, 100564. [Google Scholar] [CrossRef]
- Naumov, I.V.; Sharifullin, B.R.; Kravtsova, A.Y.; Shtern, V.N. Velocity jumps and the Moffatt eddy in two-fluid swirling flows. Exp. Therm. Fluid. Sci. 2020, 116, 110116. [Google Scholar] [CrossRef]
- Naumov, I.V.; Chaplina, T.O.; Stepanova, E.V. Investigation of the influence of a vortex flow inductor on the shape of the interface between two immiscible liquids. Process. Geoenviron. 2020, 1, 599–610. (In Russian) [Google Scholar]
- Naumov, I.V.; Kashkarova, M.V.; Okulov, V.L.; Mikkelsen, R.F. The structure of the confined swirling flow under different phase boundary conditions at the fixed end of the cylinder. Thermophys. Aeromech. 2020, 27, 93–98. [Google Scholar] [CrossRef]
- Naumov, I.V.; Sharifullin, B.R.; Tsoy, M.A.; Shtern, V.N. Dual vortex breakdown in a two-fluid confined flow. Phys. Fluids 2020, 32, 061706. [Google Scholar] [CrossRef]
- Naumov, I.V.; Skripkin, S.G.; Shtern, V.N. Counter flow slip in a two-fluid whirlpool. Phys. Fluids 2021, 33, 061705. [Google Scholar] [CrossRef]
- Naumov, I.V.; Gevorgiz, R.G.; Skripkin, S.G.; Sharifullin, B.R. Experimental investigation of vortex structure formation in a gas-vortex bioreactor. Thermophys. Aeromech. 2022, 29, 719–724. [Google Scholar]
- Mertvetsov, N.P.; Ramazanov, Y.A.; Repkov, A.P.; Dudarev, A.N.; Kislykh, V.I. Gas-vortex bioreactors “BIOK”. In Use in Modern Biotechnology; Novosibirsk Branch of the Publishing House “Nauka”: Novosibirsk, Russia, 2002. (In Russian) [Google Scholar]
- Skripkin, S.G.; Tsoy, M.A.; Naumov, I.V. Visualization the different type of vortex breakdown in conical pipe flow with high cone angle. J. Flow Vis. Image Process. 2021, 28, 43–53. [Google Scholar] [CrossRef]
- Wu, S.; Li, B.; Zuo, Z.; Liu, S. Dynamics of a single free-settling spherical particle driven by a laser-induced bubble near a rigid boundary. Phys. Rev. Fluids 2021, 6, 093602. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, S.; Li, B.; Zuo, Z.; Pan, Z. Large cavitation bubbles in the tube with a conical-frustum shaped closed end during a transient process. Phys. Fluids 2022, 34, 063312. [Google Scholar] [CrossRef]
- Zeng, Q.; An, H.; Ohl, C.D. Wall shear stress from jetting cavitation bubbles: Influence of the stand-off distance and liquid viscosity. J. Fluid. Mech. 2022, 932, A14. [Google Scholar] [CrossRef]
- Siddiqui, M.S.; Rasheed, A.; Tabib, M.; Kvamsdal, T. Numerical investigation of modeling frameworks and geometric approximations on NREL 5MW wind turbine. Renew. Energ. 2019, 132, 1058–1075. [Google Scholar] [CrossRef]
- Mizzi, K.; Demirel, Y.K.; Banks, C.; Turan, O.; Kaklis, P.; Atlar, M. Design optimisation of Propeller Boss Cap Fins for enhanced propeller performance. Appl. Ocean Res. 2017, 62, 210–222. [Google Scholar] [CrossRef] [Green Version]
- Helal, M.M.; Ahmed, T.M.; Banawan, A.A.; Kotb, M.A. Numerical prediction of sheet cavitation on marine propellers using CFD simulation with transition-sensitive turbulence model. Alex. Eng. J. 2018, 57, 3805–3815. [Google Scholar] [CrossRef]
- Naumov, I.V.; Sharifullin, B.R.; Shtern, V.N. Vortex breakdown in the lower fluid of a two-fluid swirling flow. Phys. Fluids 2020, 32, 014101. [Google Scholar] [CrossRef]
- Sharifullin, B.R.; Naumov, I.V. Angular momentum transfer across the interface of two immiscible liquids. Thermophys. Aeromech. 2021, 28, 67–78. [Google Scholar] [CrossRef]
- Naumov, I.V.; Sharifullin, B.R.; Skripkin, S.G.; Tsoy, M.A.; Shtern, V.N. A Two-Story Tornado in a Lab. In Processes in GeoMedia—Volume V; Chaplina, T., Ed.; Springer: Cham, Germany, 2022; pp. 25–34. [Google Scholar]







| Ω, rpm | Vtgm, mm/s | Re | |
|---|---|---|---|
| h = 0.5 | 180 | 7.7 | 48.8 |
| 360 | 18.1 | 114.6 | |
| 540 | 29.2 | 184.9 | |
| 720 | 36 | 228 | |
| 900 | 46.8 | 296.5 | |
| h = 0.8 | 180 | 9.7 | 61.3 |
| 360 | 18.5 | 117.4 | |
| 540 | 32.4 | 205.5 | |
| 720 | 52.5 | 332.7 | |
| 900 | 77.1 | 488.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharifullin, B.R.; Skripkin, S.G.; Naumov, I.V.; Zuo, Z.; Li, B.; Shtern, V.N. Intense Vortex Motion in a Two-Phase Bioreactor. Water 2023, 15, 94. https://doi.org/10.3390/w15010094
Sharifullin BR, Skripkin SG, Naumov IV, Zuo Z, Li B, Shtern VN. Intense Vortex Motion in a Two-Phase Bioreactor. Water. 2023; 15(1):94. https://doi.org/10.3390/w15010094
Chicago/Turabian StyleSharifullin, Bulat R., Sergey G. Skripkin, Igor V. Naumov, Zhigang Zuo, Bo Li, and Vladimir N. Shtern. 2023. "Intense Vortex Motion in a Two-Phase Bioreactor" Water 15, no. 1: 94. https://doi.org/10.3390/w15010094
APA StyleSharifullin, B. R., Skripkin, S. G., Naumov, I. V., Zuo, Z., Li, B., & Shtern, V. N. (2023). Intense Vortex Motion in a Two-Phase Bioreactor. Water, 15(1), 94. https://doi.org/10.3390/w15010094








