Modeling Average Grain Velocity for Rectangular Channel Using Soft Computing Techniques
Abstract
:1. Introduction
2. Materials and Methods
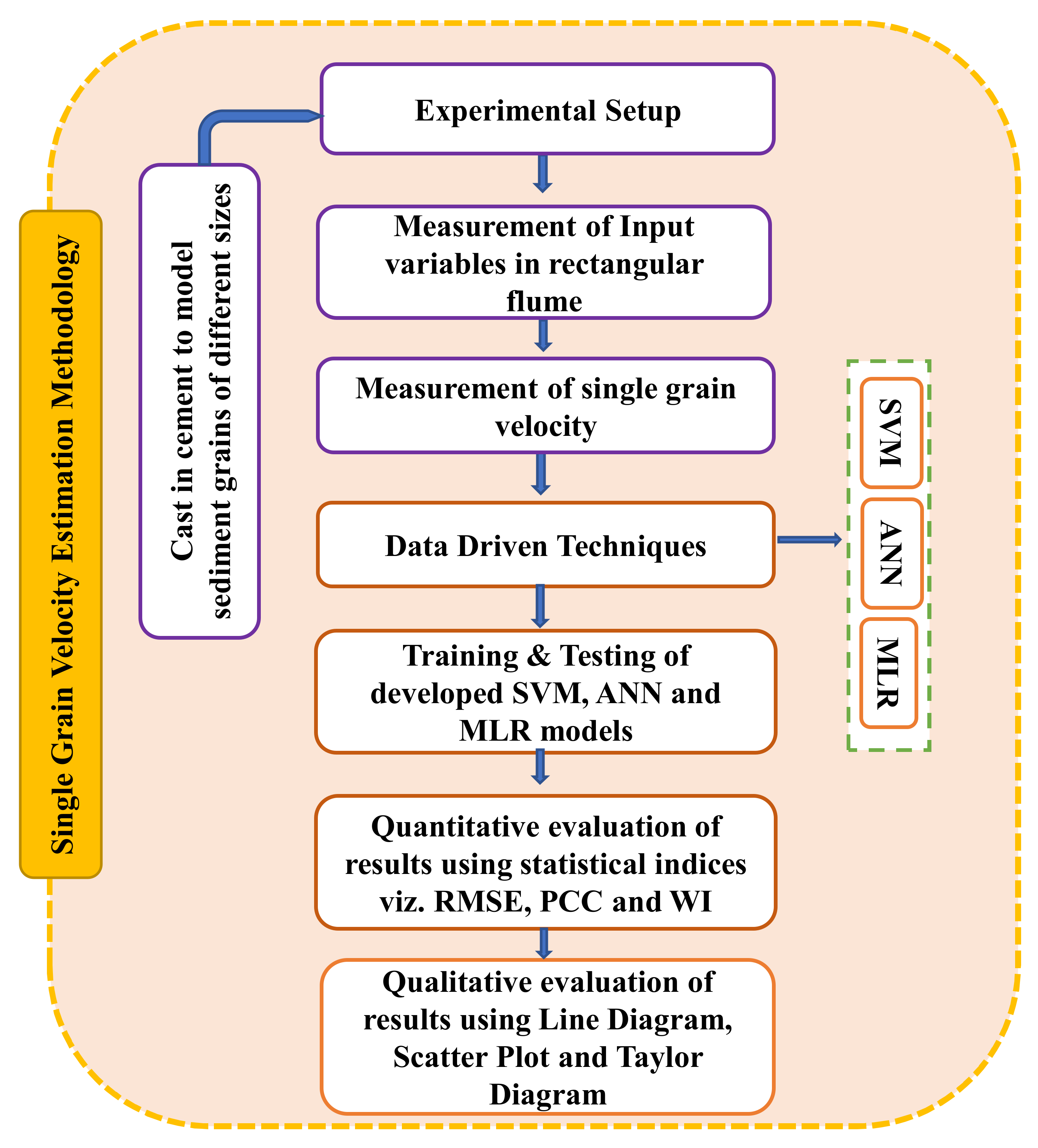
2.1. Experimental Setup and Data Observation
2.1.1. Methodology
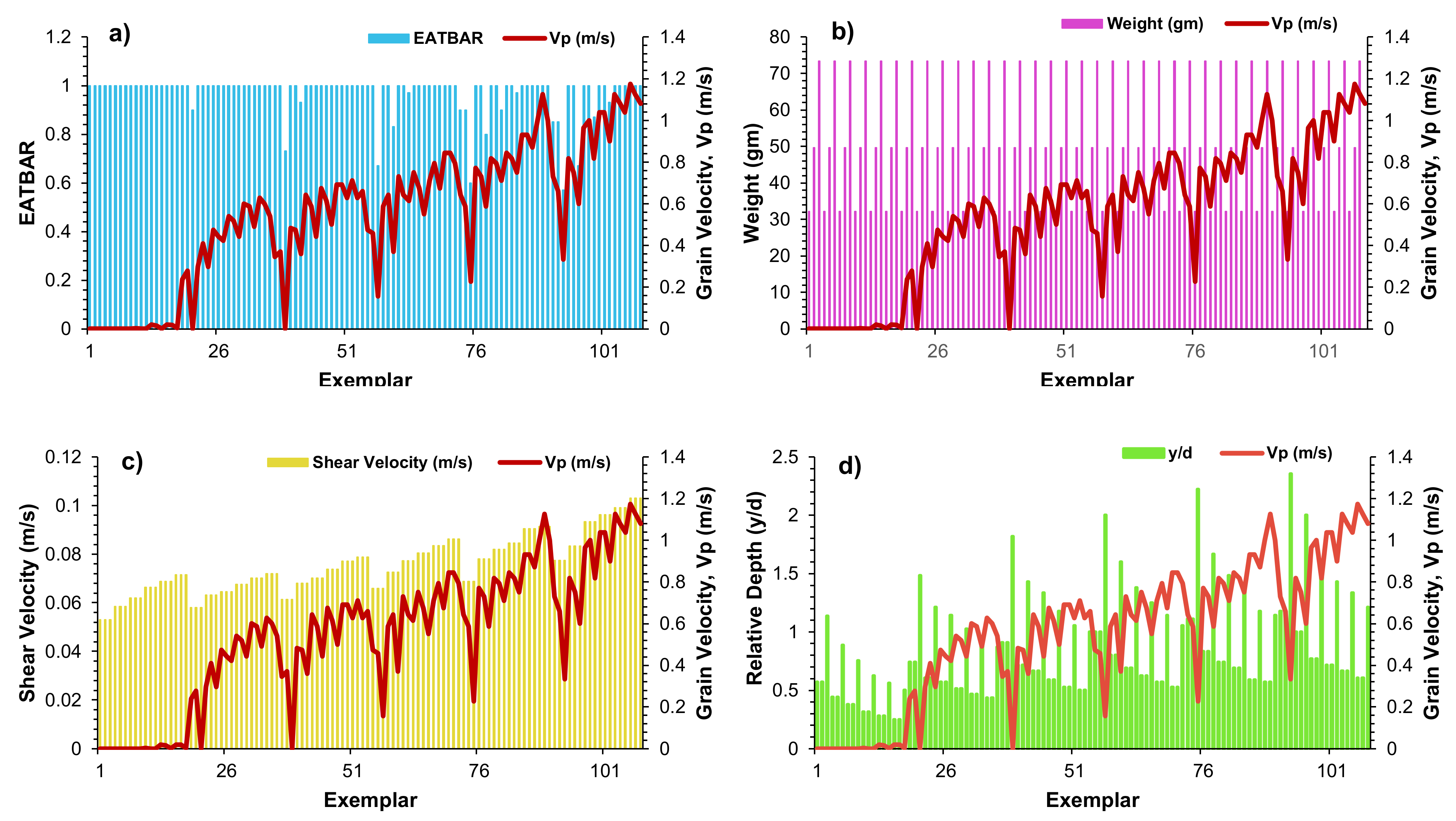
2.1.2. Input Parameters
2.2. Multiple Linear Regression—MLR
2.3. Artificial Neural Network—ANN
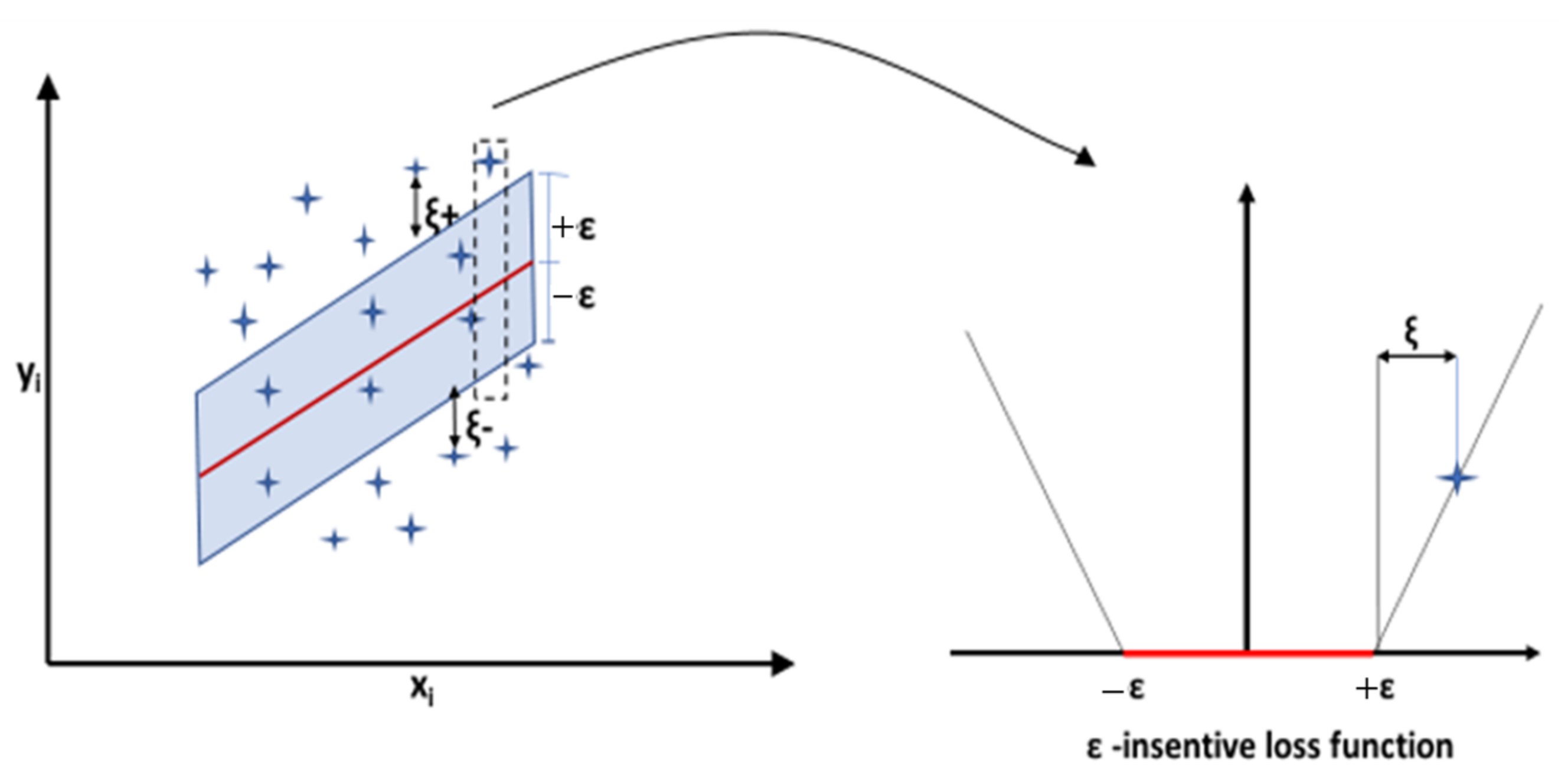
2.4. Support Vector Machine-SVM
2.5. Performance Evaluation
3. Results and Discussion
3.1. Statistical Parameters
3.2. Trial Selection
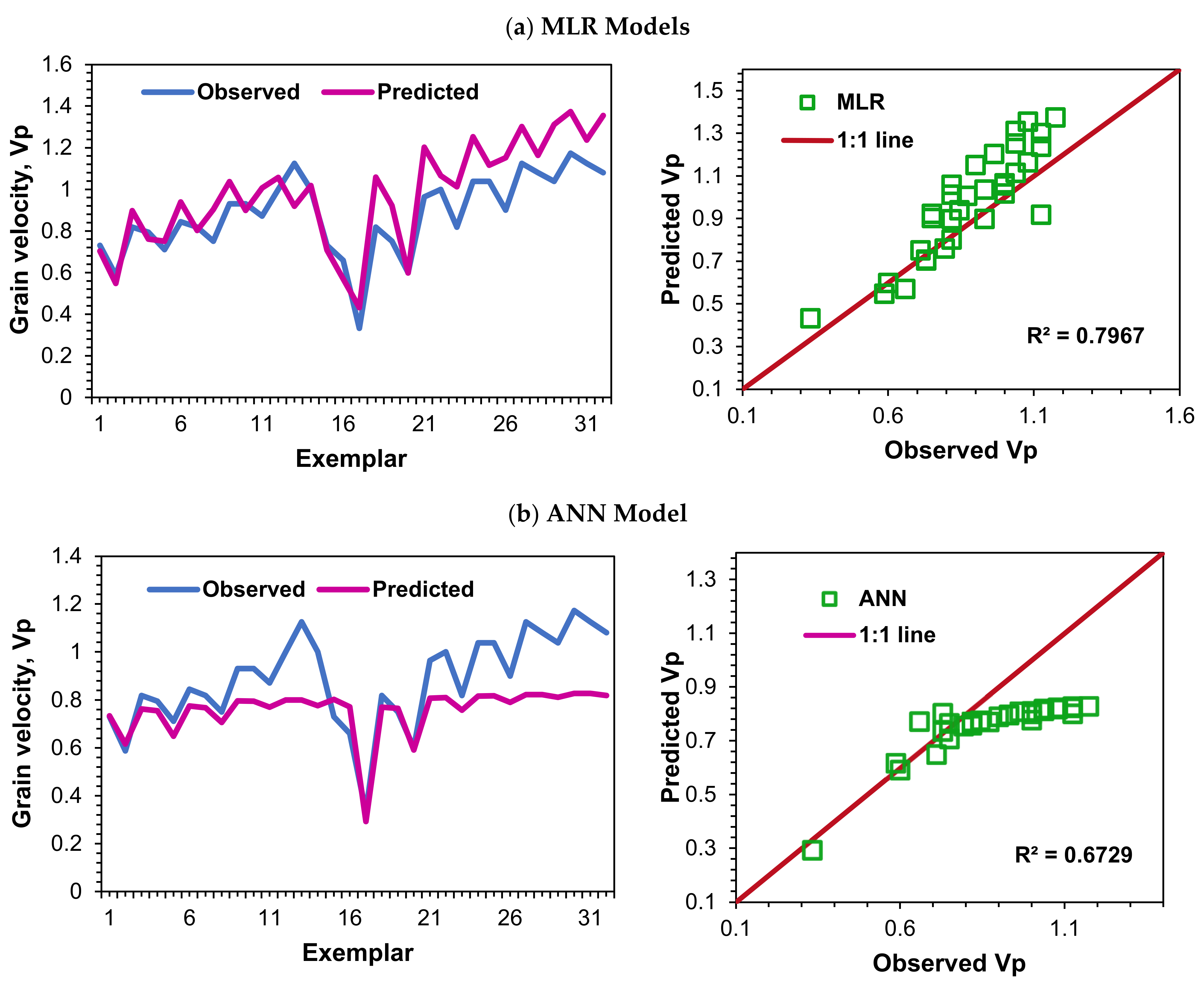
3.3. Quantitative Performance Evaluation
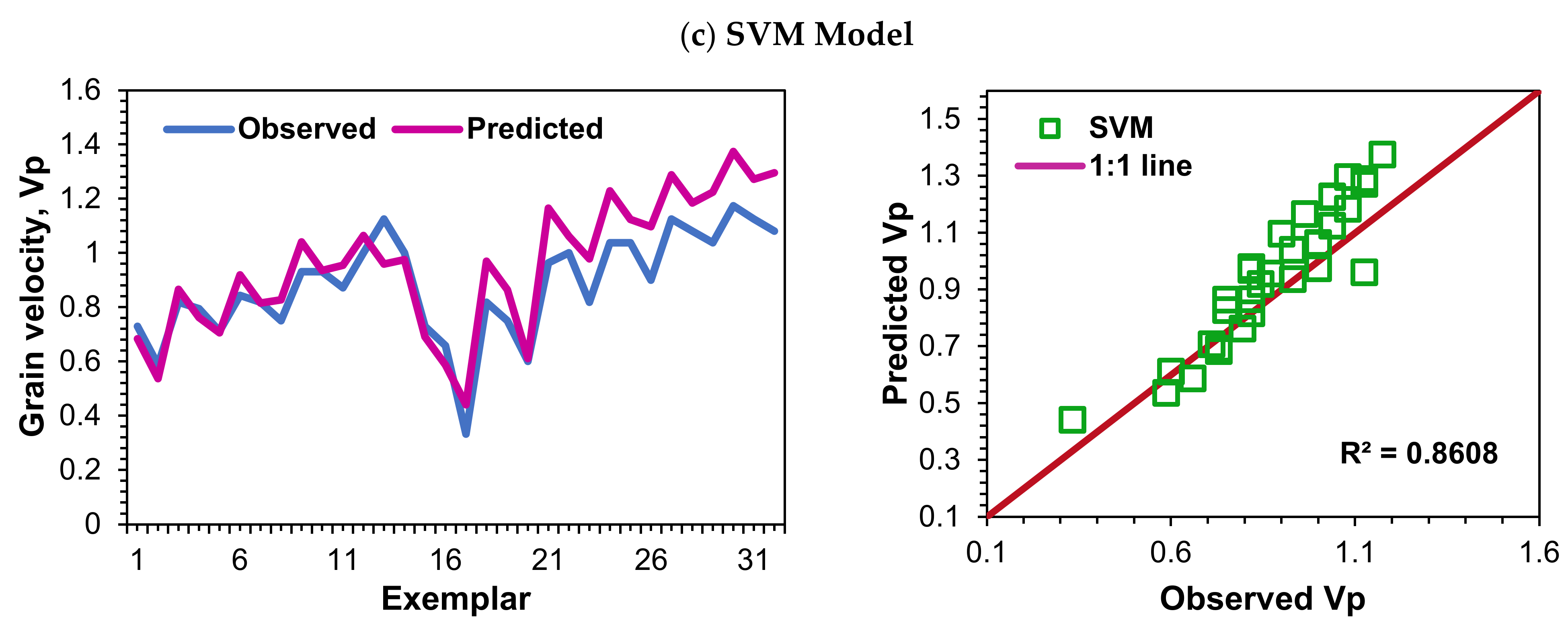
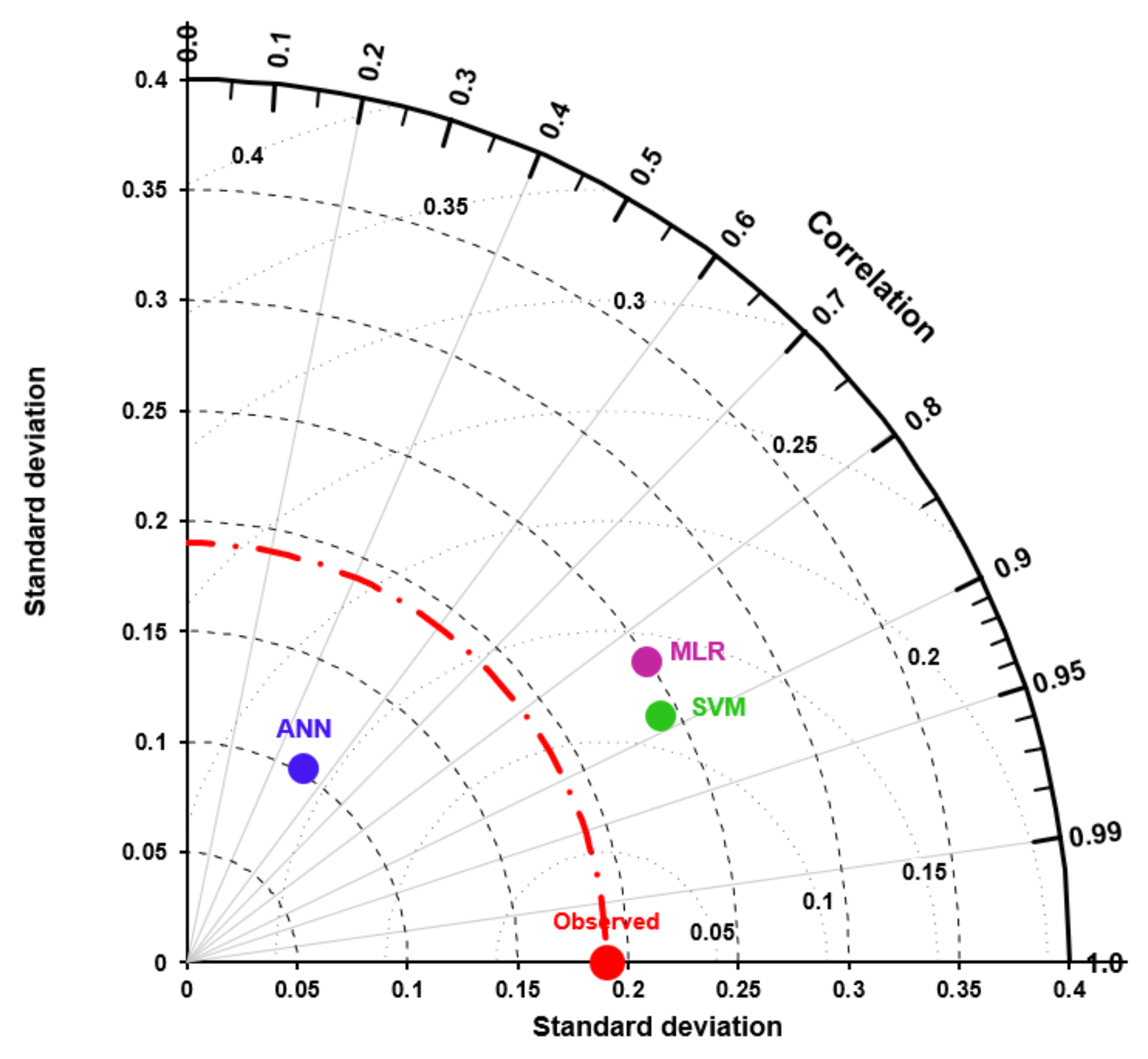
3.4. Qualitative Performance Evaluation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations and Nomenclature
References
- Chien, N.; Wan, Z. Mechanics of Sediment Transport; American Society of Civil Engineers (ASCE): Reston, VA, USA, 1999. [Google Scholar]
- Van Rijn, L.C. Sediment Transport, Part I: Bed Load Transport. J. Hydraul. Eng. 1984, 110, 1431–1456. [Google Scholar] [CrossRef] [Green Version]
- Van Rijn, L.C. Sediment Transport, Part II: Suspended Load Transport. J. Hydraul. Eng. 1984, 110, 1613–1641. [Google Scholar] [CrossRef]
- Gomez, B.; Church, M. An assessment of bed load sediment transport formulae for gravel bed rivers. Water Resour. Res. 1989, 25, 1161–1186. [Google Scholar] [CrossRef]
- Zhang, X.-D. Machine Learning. In A Matrix Algebra Approach to Artificial Intelligence; Zhang, X.-D., Ed.; Springer Singapore: Singapore, 2020; pp. 223–440. [Google Scholar]
- Safari, M.J.S.; Arashloo, S.R. Kernel ridge regression model for sediment transport in open channel flow. Neural Comput. Appl. 2021, 33, 11255–11271. [Google Scholar] [CrossRef]
- Novak, P.; Nalluri, C. Incipient Motion of Sediment Particles Over Fixed Beds. J. Hydraul. Res. 1984, 22, 181–197. [Google Scholar] [CrossRef]
- Tabarestani, M.K.; Zarrati, A.R. Sediment transport during flood event: A review. Int. J. Environ. Sci. Technol. 2015, 12, 775–788. [Google Scholar] [CrossRef] [Green Version]
- Papanicolaou, A.N.; Knapp, D.; Strom, K. Bedload Predictions by Using the Concept of Particle Velocity: Applications. In Hydraulic Measurements and Experimental Methods 2002; American Society of Civil Engineers: Reston, VA, USA, 2002; pp. 1–10. Available online: https://www.researchgate.net/publication/299813875_Bedload_Predictions_by_Using_the_Concept_of_Particle_Velocity_Applications (accessed on 12 March 2022).
- Julien, P.Y.; Bounvilay, B. Velocity of Rolling Bed Load Particles. J. Hydraul. Eng. 2013, 139, 177–186. [Google Scholar] [CrossRef]
- Cheng, N.-S.; Emadzadeh, A. Average Velocity of Solitary Coarse Grain in Flows over Smooth and Rough Beds. J. Hydraul. Eng. 2014, 140, 04014015. [Google Scholar] [CrossRef]
- Frey, P. Particle velocity and concentration profiles in bedload experiments on a steep slope. Earth Surf. Process. Landf. 2014, 39, 646–655. [Google Scholar] [CrossRef]
- Nourani, V.; Hosseini Baghanam, A.; Adamowski, J.; Kisi, O. Applications of hybrid wavelet–Artificial Intelligence models in hydrology: A review. J. Hydrol. 2014, 514, 358–377. [Google Scholar] [CrossRef]
- Demirci, M.; Baltaci, A. Prediction of suspended sediment in river using fuzzy logic and multilinear regression approaches. Neural Comput. Appl. 2013, 23, 145–151. [Google Scholar] [CrossRef]
- Misra, D.; Oommen, T.; Agarwal, A.; Mishra, S.K.; Thompson, A.M. Application and analysis of support vector machine based simulation for runoff and sediment yield. Biosyst. Eng. 2009, 103, 527–535. [Google Scholar] [CrossRef]
- Kakaei Lafdani, E.; Moghaddam Nia, A.; Ahmadi, A. Daily suspended sediment load prediction using artificial neural networks and support vector machines. J. Hydrol. 2013, 478, 50–62. [Google Scholar] [CrossRef]
- Meshram, S.G.; Singh, V.P.; Kisi, O.; Karimi, V.; Meshram, C. Application of Artificial Neural Networks, Support Vector Machine and Multiple Model-ANN to Sediment Yield Prediction. Water Resour. Manag. 2020, 34, 4561–4575. [Google Scholar] [CrossRef]
- Jain, S.K.; Chalisgaonkar, D. Setting Up Stage-Discharge Relations Using ANN. J. Hydrol. Eng. 2000, 5, 428–433. [Google Scholar] [CrossRef]
- Garbrecht, J.D. Comparison of Three Alternative ANN Designs for Monthly Rainfall-Runoff Simulation. J. Hydrol. Eng. 2006, 11, 502–505. [Google Scholar] [CrossRef] [Green Version]
- Mukerji, A.; Chatterjee, C.; Raghuwanshi, N.S. Flood Forecasting Using ANN, Neuro-Fuzzy, and Neuro-GA Models. J. Hydrol. Eng. 2009, 14, 647–652. [Google Scholar] [CrossRef]
- Rajaee, T.; Nourani, V.; Zounemat-Kermani, M.; Kisi, O. River Suspended Sediment Load Prediction: Application of ANN and Wavelet Conjunction Model. J. Hydrol. Eng. 2011, 16, 613–627. [Google Scholar] [CrossRef]
- Ab Ghani, A.; Azamathulla, H.M. Development of GEP-based functional relationship for sediment transport in tropical rivers. Neural Comput. Appl. 2014, 24, 271–276. [Google Scholar] [CrossRef]
- Bhattacharya, B.; Price, R.K.; Solomatine, D.P. Machine Learning Approach to Modeling Sediment Transport. J. Hydraul. Eng. 2007, 133, 440–450. [Google Scholar] [CrossRef]
- Sheikh Khozani, Z.; Safari, M.J.S.; Danandeh Mehr, A.; Wan Mohtar, W.H.M. An ensemble genetic programming approach to develop incipient sediment motion models in rectangular channels. J. Hydrol. 2020, 584, 124753. [Google Scholar] [CrossRef]
- Mehr, A.D.; Safari, M.J.S. Application of Soft Computing Techniques for Particle Froude Number Estimation in Sewer Pipes. J. Pipeline Syst. Eng. Pract. 2020, 11, 04020002. [Google Scholar] [CrossRef]
- Montes, C.; Berardi, L.; Kapelan, Z.; Saldarriaga, J. Predicting bedload sediment transport of non-cohesive material in sewer pipes using evolutionary polynomial regression–multi-objective genetic algorithm strategy. Urban Water J. 2020, 17, 154–162. [Google Scholar] [CrossRef] [Green Version]
- Wan Mohtar, W.H.M.; Afan, H.; El-Shafie, A.; Bong, C.H.J.; Ab Ghani, A. Influence of bed deposit in the prediction of incipient sediment motion in sewers using artificial neural networks. Urban Water J. 2018, 15, 296–302. [Google Scholar] [CrossRef]
- Vapnik, V.N. An overview of statistical learning theory. IEEE Trans. Neural Netw. 1999, 10, 988–999. [Google Scholar] [CrossRef] [Green Version]
- Ghorbani, M.A.; Khatibi, R.; Goel, A.; FazeliFard, M.H.; Azani, A. Modeling river discharge time series using support vector machine and artificial neural networks. Environ. Earth Sci. 2016, 75, 685. [Google Scholar] [CrossRef]
- Kumar, D.; Pandey, A.; Sharma, N.; Flügel, W.-A. Daily suspended sediment simulation using machine learning approach. Catena 2016, 138, 77–90. [Google Scholar] [CrossRef]
- Rahgoshay, M.; Feiznia, S.; Arian, M.; Hashemi, S.A.A. Modeling daily suspended sediment load using improved support vector machine model and genetic algorithm. Environ. Sci. Pollut. Res. 2018, 25, 35693–35706. [Google Scholar] [CrossRef] [PubMed]
- Einstein, H.A. The Bed-Load Function for Sediment Transportation in Open Channel Flows; US Government Printing Office: Washington, DC, USA, 1950; p. 71. [Google Scholar]
- Fernandez Luque, R.; Van Beek, R. Erosion And Transport Of Bed-Load Sediment. J. Hydraul. Res. 1976, 14, 127–144. [Google Scholar] [CrossRef] [Green Version]
- Abbott, J.E.; Francis, J.R.D.; Owen, P.R. Saltation and suspension trajectories of solid grains in a water stream. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1977, 284, 225–254. [Google Scholar] [CrossRef]
- Bridge, J.S.; Dominic, D.F. Bed Load Grain Velocities and Sediment Transport Rates. Water Resour. Res. 1984, 20, 476–490. [Google Scholar] [CrossRef]
- Kisi, Ö.; Çobaner, M. Modeling River Stage-Discharge Relationships Using Different Neural Network Computing Techniques. Clean Soil Air Water 2009, 37, 160–169. [Google Scholar] [CrossRef]
- Rajaee, T.; Mirbagheri, S.A.; Zounemat-Kermani, M.; Nourani, V. Daily suspended sediment concentration simulation using ANN and neuro-fuzzy models. Sci. Total Environ. 2009, 407, 4916–4927. [Google Scholar] [CrossRef]
- Hipni, A.; El-shafie, A.; Najah, A.; Karim, O.A.; Hussain, A.; Mukhlisin, M. Daily Forecasting of Dam Water Levels: Comparing a Support Vector Machine (SVM) Model With Adaptive Neuro Fuzzy Inference System (ANFIS). Water Resour. Manag. 2013, 27, 3803–3823. [Google Scholar] [CrossRef]
- Gholami, R.; Fakhari, N. Chapter 27-Support Vector Machine: Principles, Parameters, and Applications. In Handbook of Neural Computation; Samui, P., Sekhar, S., Balas, V.E., Eds.; Academic Press: Cambridge, MA, USA, 2017; pp. 515–535. [Google Scholar]
- Han, D.; Chan, L.; Zhu, N. Flood forecasting using support vector machines. J. Hydroinformatics 2007, 9, 267–276. [Google Scholar] [CrossRef]
- Lin, J.-Y.; Cheng, C.-T.; Chau, K.-W. Using support vector machines for long-term discharge prediction. Hydrol. Sci. J. 2006, 51, 599–612. [Google Scholar] [CrossRef]
- Cherkassky, V.; Ma, Y. Practical selection of SVM parameters and noise estimation for SVM regression. Neural Netw. 2004, 17, 113–126. [Google Scholar] [CrossRef] [Green Version]
- Sharafati, A.; Haghbin, M.; Haji Seyed Asadollah, S.B.; Tiwari, N.K.; Al-Ansari, N.; Yaseen, Z.M. Scouring Depth Assessment Downstream of Weirs Using Hybrid Intelligence Models. Appl. Sci. 2020, 10, 3714. [Google Scholar] [CrossRef]
- Kumari, A. Effect of Sediment Particle Orientation on its Movement under Varying Channel Slope and Discharge Conditions. Master’s Thesis, GB Pant University of Agriculture and Technology, Pantnagar, India, 2017. [Google Scholar]

| Variables | Mean | Median | Minimum | Maximum | Std. Dev. | C.V. | Skewness |
|---|---|---|---|---|---|---|---|
| All Data | |||||||
| λ | 0.9707 | 1.000 | 0.5700 | 1.000 | 0.0823 | 0.0848 | −3.283 |
| W | 51.733 | 49.60 | 32.200 | 73.40 | 16.966 | 0.32795 | 0.1874 |
| U* | 0.0754 | 0.0731 | 0.0529 | 0.1030 | 0.0120 | 0.1598 | 0.4072 |
| y/d | 0.8573 | 0.7142 | 0.2500 | 2.352 | 0.4281 | 0.4994 | 1.220 |
| Vp | 0.5473 | 0.600 | 0.0 | 1.174 | 0.3352 | 0.6124 | −0.2776 |
| Training Data | |||||||
| λ | 0.9793 | 1.0 | 0.6 | 1.0 | 0.0706 | 0.0721 | −3.964 |
| W | 51.476 | 49.6 | 32.2 | 73.4 | 17.035 | 0.3309 | 0.2091 |
| U* | 0.0696 | 0.0688 | 0.0529 | 0.0862 | 0.008 | 0.1150 | 0.0828 |
| y/d | 0.7894 | 0.6667 | 0.25 | 2.222 | 0.4031 | 0.5106 | 1.295 |
| Vp | 0.4070 | 0.474 | 0.0 | 0.8440 | 0.2793 | 0.6863 | −0.3741 |
| Testing Data | |||||||
| λ | 0.9503 | 1.0 | 0.57 | 1.0 | 0.1035 | 0.1089 | −2.368 |
| W | 52.344 | 49.6 | 32.2 | 73.4 | 17.05 | 0.3258 | 0.1369 |
| U* | 0.0892 | 0.0903 | 0.0774 | 0.103 | 0.0081 | 0.0914 | 0.1011 |
| y/d | 1.0185 | 0.8012 | 0.5714 | 2.352 | 0.4489 | 0.4407 | 1.1701 |
| Vp | 0.8806 | 0.8855 | 0.333 | 1.174 | 0.1901 | 0.2159 | −0.6570 |
| Model | Training | Testing | ||||
|---|---|---|---|---|---|---|
| RMSE (m/s) | PCC | WI | RMSE (m/s) | PCC | WI | |
| MLR | 0.1340 | 0.8756 | 0.7532 | 0.1459 | 0.8375 | 0.6789 |
| ANN | ||||||
| Trial-1 | 0.1266 | 0.8911 | 0.8106 | 0.3109 | 0.1509 | 0.3420 |
| Trial-2 | 0.0873 | 0.9502 | 0.8756 | 0.2154 | 0.3636 | 0.4579 |
| Trial-3 | 0.0689 | 0.9692 | 0.8799 | 0.1721 | 0.5176 | 0.5012 |
| Trial-4 | 0.0663 | 0.9728 | 0.8999 | 0.2302 | 0.1945 | 0.3666 |
| Trial-5 | 0.0699 | 0.9678 | 0.8916 | 0.1906 | 0.4365 | 0.4751 |
| Trial-6 | 0.0759 | 0.9625 | 0.9439 | 0.1821 | 0.4900 | 0.5058 |
| SVM | ||||||
| Trial-1 | 0.1423 | 0.8595 | 0.7475 | 0.1208 | 0.8852 | 0.7231 |
| Trial-2 | 0.1381 | 0.8675 | 0.7531 | 0.1341 | 0.8688 | 0.7022 |
| Trial-3 | 0.1431 | 0.8577 | 0.7479 | 0.1195 | 0.8877 | 0.7243 |
| Trial-4 | 0.1408 | 0.8622 | 0.7513 | 0.1247 | 0.8795 | 0.7150 |
| Model/Trial | Architecture |
|---|---|
| ANN | |
| Trial-1 | 4-1-1 |
| Trial-2 | 4-4-1 |
| Trial-3 | 4-5-1 |
| Trial-4 | 4-7-1 |
| Trial-5 | 4-5-5-1 |
| Trial-6 | 4-4-4-4-1 |
| SVM | |
| Trial-1 | C = 10, = 0.25, ε = 0.01 |
| Trial-2 | C = 10, = 0.25, ε = 0.1 |
| Trial-3 | C = 10, = 0.45, ε = 0.01 |
| Trial-4 | C = 10, = 0.45, ε = 0.05 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumari, A.; Kumar, A.; Kumar, M.; Kuriqi, A. Modeling Average Grain Velocity for Rectangular Channel Using Soft Computing Techniques. Water 2022, 14, 1325. https://doi.org/10.3390/w14091325
Kumari A, Kumar A, Kumar M, Kuriqi A. Modeling Average Grain Velocity for Rectangular Channel Using Soft Computing Techniques. Water. 2022; 14(9):1325. https://doi.org/10.3390/w14091325
Chicago/Turabian StyleKumari, Anuradha, Akhilesh Kumar, Manish Kumar, and Alban Kuriqi. 2022. "Modeling Average Grain Velocity for Rectangular Channel Using Soft Computing Techniques" Water 14, no. 9: 1325. https://doi.org/10.3390/w14091325
APA StyleKumari, A., Kumar, A., Kumar, M., & Kuriqi, A. (2022). Modeling Average Grain Velocity for Rectangular Channel Using Soft Computing Techniques. Water, 14(9), 1325. https://doi.org/10.3390/w14091325







