Multi-Objective-Based Tuning of Economic Model Predictive Control of Drinking Water Transport Networks
Abstract
:1. Introduction
- (i)
- by adding a steady-state target optimization layer between the RTO and the MPC [6],
- (ii)
- by considering the dynamics of the system in the real-time optimization stage by replacing the RTO by a Dynamic RTO (DRTO) [13], or
- (iii)
2. Problem Formulation
2.1. EMPC Applied to DWTN
2.2. Multi-Objective MPC of DWTN
- To provide a reliable water supply in the most economic way, minimizing water production and transport costs, written aswhere is the manipulated variables vector at time k, is a known vector related to economic costs of water treatment and is a known time-varying vector associated with the economic cost of water flow rates related to pumping stations (the time dependence is given by the electric pumping cost, which varies along the day).
- To guarantee the availability of enough water in each reservoir to satisfy its underlying demand, keeping a safety stock in order to face uncertainties and avoid stock-outs. This objective is reached by minimizingwhere is the amount of the soft constraint violation, which has been defined such that when there is no violation, then . When there is a violation, it is equal to the absolute amount of it in m, therefore, .
- To operate the DWTN under smooth control actions. This is reached by minimizingwhere is the vector of control signal variations, defined as .
3. Pareto Front Calculation of Multi-Objective Optimization Problems
3.1. Normalization
3.2. (Normalized) Weighted Sum (WS)
3.3. (Enhanced) Normalized Normal Constraint ((E)NNC)
4. Tuning Strategies for Multi-Objective EMPC
4.1. Decision-Making Strategy for Multi-Objective Optimization
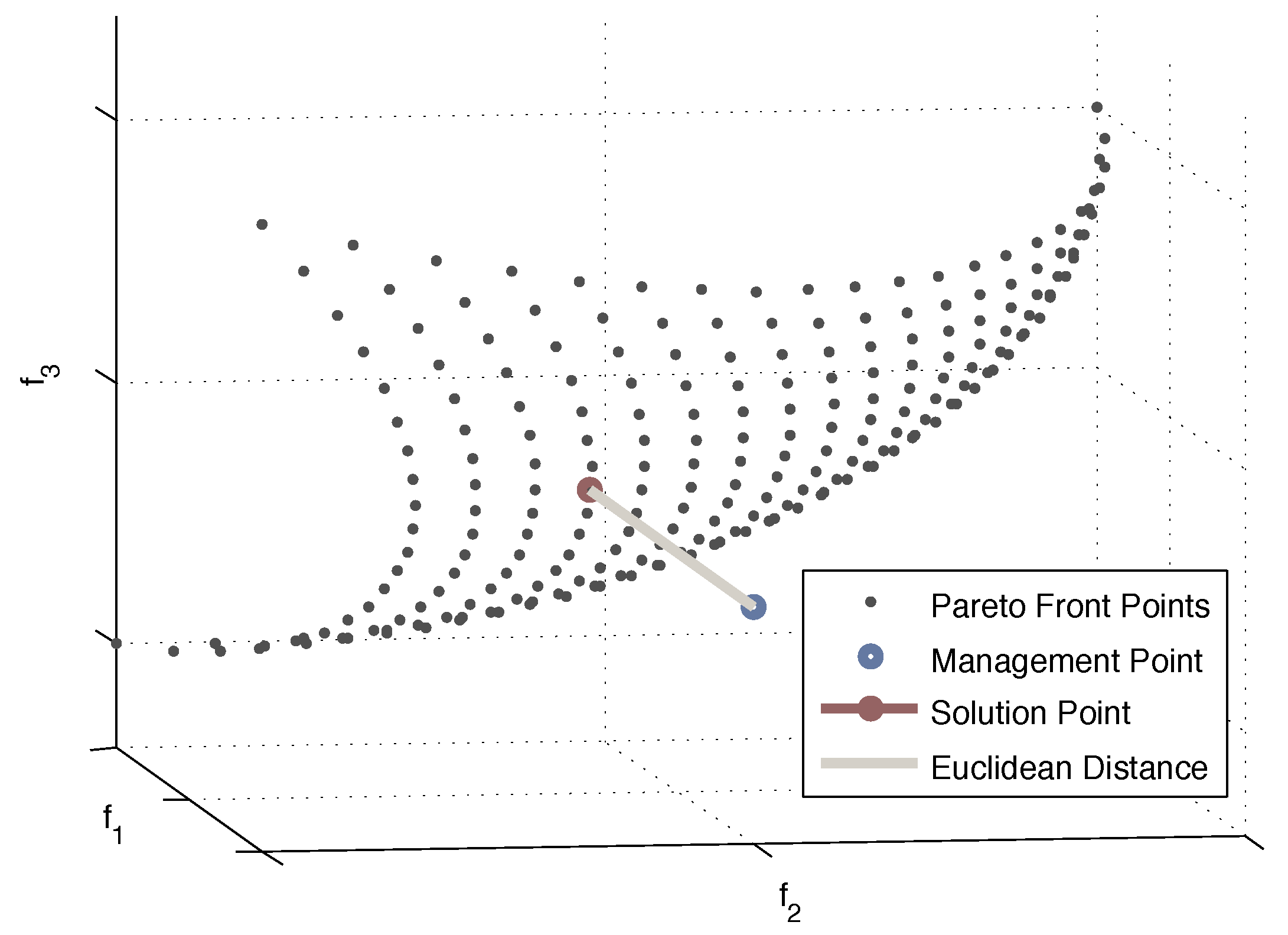
4.1.1. DM Based on a Management Point
4.1.2. DM Procedure and Prioritization
4.2. Tuning Strategy Proposals
4.2.1. Histogram-Based Weights Selection
- Step 1. Calculate the number of water-demand combinations for the Pareto front for the specified objective functions.
- Step 2. Select, for all Pareto fronts, the preferred solution according to the decision-making procedure described above.
- Step 3. Make a histogram of the occurrence of the different sets of selected weights for the Normalized Weighted Sum.
- Step 4. Select, in the histogram, the weights with the highest number of occurrences and use the weights for implementation in the MPC.
- Step 5. Evaluate the controller in an online setting (without computing the entire Pareto set in each iteration).
4.2.2. Model-Based Weights Selection
- Steps 1 to 3 are identical to the previous approach.
- Step 4. Calculate a regression model of the preferred set of weights as a function of the average of water demands.
- Step 5. Evaluate the controller in an online setting, i.e., in each MPC, use the regression model for the calculation of weights based on the water demand.
5. Application Example
5.1. Aggregate Model of the Barcelona DWTN
5.2. Pareto Front Generation for the DWTN Problem
5.3. Solver Errors
- Infeasibility problem errors;
- Resource limit errors, related to the maximum number of iterations; and
- Numerical errors, related to ill-conditioning issues.
5.4. Key Performance Indicators
5.5. DM Strategy Simulations
5.5.1. DM Exploiting ENNCP
5.5.2. DM Exploiting NWS
5.6. Weight Variations and Measured Disturbances
5.7. Tuning Strategy
5.8. Results Discussion
6. Conclusions and Further Work
Author Contributions
Funding
Conflicts of Interest
References
- Ellis, M.; Durand, H.; Christofides, P.D. A tutorial review of economic model predictive control methods. J. Process Control 2014, 24, 1156–1178. [Google Scholar] [CrossRef]
- Maciejowski, J.M. Predictive Control with Constraints; Prentice Hall: London, UK, 2002. [Google Scholar]
- Rawlings, J.; Mayne, D.; Diehl, M.M. Model Predictive Control: Theory, Computation, and Design, 2nd ed.; Nob Hill Publishing: Madison, WI, USA, 2020. [Google Scholar]
- Qin, J.; Badgwell, A. A survey of industrial model predictive control. Control Eng. Pract. 2003, 11, 733–764. [Google Scholar] [CrossRef]
- Limon, D.; Alamo, T. Tracking Model Predictive Control. In Encyclopedia of Systems and Control; Springer: London, UK, 2015; pp. 1475–1484. [Google Scholar] [CrossRef]
- Albalawi, F.; Alanqar, A.; Durand, H.; Christofides, P.D. A feedback control framework for safe and economically-optimal operation of nonlinear processes. AIChE J. 2016, 62, 2391–2409. [Google Scholar] [CrossRef]
- Ocampo-Martinez, C.; Puig, V.; Cembrano, G.; Quevedo, J. Application of Predictive Control Strategies to the Management of Complex Networks in the Urban Water Cycle [Applications of Control]. IEEE Control Syst. Mag. 2013, 33, 15–41. [Google Scholar]
- Tedesco, F.; Ocampo-Martinez, C.; Cassavola, A.; Puig, V. Centralised and Distributed Command Governor Approaches for the Operational Control of Drinking Water Networks. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 586–595. [Google Scholar] [CrossRef] [Green Version]
- Nassourou, M.; Blesa, J.; Puig, V. Robust Economic Model Predictive Control Based on a Zonotope and Local Feedback Controller for Energy Dispatch in Smart-Grids Considering Demand Uncertainty. Energies 2020, 13, 696. [Google Scholar] [CrossRef] [Green Version]
- Sebghati, A.; Shamaghdari, S. Tube-based robust economic model predictive control with practical and relaxed stability guarantees and its application to smart grid. Int. J. Robust Nonlinear Control 2020, 30, 7533–7559. [Google Scholar] [CrossRef]
- Angeli, D.; Müller, M.A. Economic Model Predictive Control: Some Design Tools and Analysis Techniques. In Handbook of Model Predictive Control; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 145–167. [Google Scholar]
- Maestre, J.; Lopez-Rodriguez, F.; Muros, F.; Ocampo-Martinez, C. A Modular Feedback for the Control of Networked Systems by Clustering: A Drinking Water Network Case Study. Processes 2021, 9, 389. [Google Scholar] [CrossRef]
- Kadam, J.V.; Marquardt, W. Integration of Economical Optimization and Control for Intentionally Transient Process Operation; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Souza, G.D.; Odloak, D.; Zanin, A.C. Real time optimization (RTO) with model predictive control (MPC). Comput. Chem. Eng. 2010, 34, 1999–2006. [Google Scholar] [CrossRef]
- Ferramosca, A.; Rawlings, J.; Limon, D.; Camacho, E. Economic MPC for a changing economic criterion. In Proceedings of the 49th IEEE Conference on Decision and Control, Atlanta, GA, USA, 15–17 December 2010. [Google Scholar]
- Garriga, J.L.; Soroush, M. Model predictive control tuning methods: A review. Ind. Eng. Chem. Res. 2010, 49, 3505–3515. [Google Scholar] [CrossRef]
- Vallerio, M.; Van Impe, J.; Logist, F. Tuning of NMPC controllers via multi-objective optimisation. Comput. Chem. Eng. 2014, 61, 38–50. [Google Scholar] [CrossRef] [Green Version]
- Wojszniz, W.; Mehta, A.; Wojszniz, P.; Thiele, D.; Blevins, T. Multi-objective optimization for model predictive control. ISA Trans. 2007, 46, 351–361. [Google Scholar] [CrossRef] [PubMed]
- Van der Lee, J.H.; Svrcek, W.; Young, B. A tuning algorithm for model predictive controllers based on genetic algorithms and fuzzy decision making. ISA Trans. 2008, 47, 53–59. [Google Scholar] [CrossRef] [PubMed]
- Alhajeri, M.; Soroush, M. Tuning Guidelines for Model-Predictive Control. Ind. Eng. Chem. Res. 2020, 59, 4177–4191. [Google Scholar] [CrossRef]
- Zavala, V.; Flores-Tlacuahuac, A. Stability of multi objective predictive control: A utopia-tracking approach. Automatica 2012, 48, 2627–2632. [Google Scholar] [CrossRef]
- Floures-Tlacuahuac, A.; Morales, P.; Rivera-Toledo, M. Multiobjective Non linear Model Preductive Ccontrol of a Class of Chemical Reactors. Ind. Eng. Chem. Res. 2012, 51, 5891–5899. [Google Scholar] [CrossRef]
- Barreiro-Gomez, J.; Ocampo-Martinez, C.; Quijano, N. Dynamical Tuning for Multi-objective Model Predictive Control based on Population Games. ISA Trans. 2017, 69, 175–186. [Google Scholar] [CrossRef] [Green Version]
- De Schutter, J.; Zanon, M.; Diehl, M. TuneMPC—A Tool for Economic Tuning of Tracking (N)MPC Problems. IEEE Control Syst. Lett. 2020, 4, 910–915. [Google Scholar] [CrossRef]
- Brdys, M.; Ulanicki, B. Operational Control of Water Systems: Structures, Algorithms and Applications. Automatica 1996, 32, 1619–1620. [Google Scholar]
- Puig, V.; Ocampo-Martinez, C.; Pérez, R.; Cembrano, G.; Quevedo, J.; Escobet, T. Real-Time Monitoring and Operational Control of Drinking-Water Systems; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Miettinen, K.M. Nonlinear multiobjective optimization. In International Series in Operations Research & Management Science; Kluwer Academic Publishers: Boston, MA, USA, 1999; Volume 12. [Google Scholar]
- Sanchis, J.; Martinez, M.; Blasco, X.; Salcedo, J.V. A new perspective on multiobjective optimization by enhanced normalized normal constraint method. Struct. Multidiscip. Optim. 2008, 36, 537–546. [Google Scholar] [CrossRef]
- Logist, F.; Van Impe, J. Novel insights for multi-objective optimisation in engineering using Normal Boundary Intersection and (Enhanced) Normalised Normal Constraint. Struct. Multidiscip. Optim. 2012, 45, 417–431. [Google Scholar] [CrossRef]
- Marler, R.T.; Arora, J.S. The weighted sum method for multi-objective optimization: New insights. Struct. Multidiscip. Optim. 2010, 41, 853–862. [Google Scholar] [CrossRef]
- Ocampo-Martinez, C.; Puig, V.; Cembrano, G.; Creus, R.; Minoves, M. Improving water management efficiency by using optimization-based control strategies: The Barcelona case study. Water Sci. Technol. Water Supply 2009, 9, 565–575. [Google Scholar] [CrossRef]
- Robles, D.; Puig, V.; Ocampo-Martinez, C.; Garza, L. Reliable Fault-Tolerant Model Predictive Control of Drinking Water Transport Networks. Control Eng. Pract. 2016, 55, 197–211. [Google Scholar] [CrossRef] [Green Version]
- Hosseini, S.; Barker, K.; Ramirez-Marquez, J.E. A review of definitions and measures of system resilience. Reliab. Eng. Syst. Saf. 2016, 145, 47–61. [Google Scholar] [CrossRef]
- Pietrucha-Urbanik, K.; Studziński, A. Qualitative analysis of the failure risk of water pipes in terms of water supply safety. Eng. Fail. Anal. 2019, 95, 371–378. [Google Scholar] [CrossRef]






| Type of Component | Quantity |
|---|---|
| Water storing tanks | 17 |
| Pumping stations | 26 |
| Valves | 35 |
| Nodes | 11 |
| Sectors of consume | 25 |
| Priority Percentages | Economic KPI | Safety KPI | Smoothness KPI | |||
|---|---|---|---|---|---|---|
| Day 2 | Day 3 | Day 2 | Day 3 | Day 2 | Day 3 | |
| [100 100 100] | 34.3553 | 33.7995 | 3873.5 | 3888.2 | 0.0040 | 0.0042 |
| [100 75 50] | 34.0348 | 33.5804 | 3900.5 | 3878.1 | 0.1699 | 0.1549 |
| [50 100 75] | 39.6096 | 38.9024 | 4195.9 | 3931.9 | 0.0495 | 0.0538 |
| [75 50 100] | 38.1425 | 36.4246 | 3716.1 | 3678.3 | 0.0019 | 0.0006 |
| Priority Percentages | Economic KPI | Safety KPI | Smoothness KPI | |||
|---|---|---|---|---|---|---|
| Day 2 | Day 3 | Day 2 | Day 3 | Day 2 | Day 3 | |
| [100 100 100] | 34.3553 | 33.7995 | 3873.5 | 3888.2 | 0.0040 | 0.0042 |
| [50 30 20] | 34.4205 | 33.7557 | 4853.6 | 4541.7 | 0.2184 | 0.2632 |
| [20 50 30] | 49.6496 | 48.7163 | 3360.7 | 3359.5 | 0.0186 | 0.0034 |
| [30 20 50] | 46.9891 | 43.6090 | 3658.0 | 2537.8 | 0.0003 | 0.0002 |
| Priority Percentages | Economic KPI | Safety KPI | Smoothness KPI | |||
|---|---|---|---|---|---|---|
| Day 2 | Day 3 | Day 2 | Day 3 | Day 2 | Day 3 | |
| [100 100 100] | 34.3305 | 33.6452 | 3809.5 | 3822.2 | 0.0039 | 0.0035 |
| [100 75 50] | 34.0022 | 33.4155 | 3501.8 | 3371.0 | 0.0086 | 0.0092 |
| [50 100 75] | 42.7737 | 42.1820 | 4068.1 | 4000.4 | 0.0024 | 0.0018 |
| [75 50 100] | 35.0110 | 34.2817 | 3578.0 | 3827.3 | 0.0028 | 0.0026 |
| Priority Percentages | Economic KPI | Safety KPI | Smoothness KPI | |||
|---|---|---|---|---|---|---|
| Day 2 | Day 3 | Day 2 | Day 3 | Day 2 | Day 3 | |
| [100 100 100] | 34.3305 | 33.6452 | 3809.5 | 3822.2 | 0.0039 | 0.0035 |
| [50 30 20] | 33.8902 | 33.1499 | 4704.4 | 4886.1 | 0.2069 | 0.2217 |
| [20 50 30] | 50.0738 | 48.7135 | 3309.9 | 3353.7 | 0.0032 | 0.0034 |
| [30 20 50] | 48.3035 | 49.6586 | 3402.5 | 2178.9 | 0.0002 | 0.0001 |
| Tuning Strategy | Economic KPI | Safety KPI | Smoothness KPI | |||
|---|---|---|---|---|---|---|
| Day 2 | Day 3 | Day 2 | Day 3 | Day 2 | Day 3 | |
| Original MPC | 34.4477 | 34.5007 | 3921.7 | 3912.3 | 0.0105 | 0.0103 |
| Normalised MPC | 34.5643 | 34.6338 | 3837.6 | 3838.3 | 0.0026 | 0.0025 |
| Histogram-Based Weighting | 34.1424 | 34.2004 | 3324.7 | 3337.2 | 0.0017 | 0.0017 |
| Adaptive Weighting | 33.4410 | 33.0017 | 3135.9 | 3023.0 | 0.0007 | 0.0006 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ocampo-Martinez, C.; Toro, R.; Puig, V.; Van Impe, J.; Logist, F. Multi-Objective-Based Tuning of Economic Model Predictive Control of Drinking Water Transport Networks. Water 2022, 14, 1222. https://doi.org/10.3390/w14081222
Ocampo-Martinez C, Toro R, Puig V, Van Impe J, Logist F. Multi-Objective-Based Tuning of Economic Model Predictive Control of Drinking Water Transport Networks. Water. 2022; 14(8):1222. https://doi.org/10.3390/w14081222
Chicago/Turabian StyleOcampo-Martinez, Carlos, Rodrigo Toro, Vicenç Puig, Jan Van Impe, and Filip Logist. 2022. "Multi-Objective-Based Tuning of Economic Model Predictive Control of Drinking Water Transport Networks" Water 14, no. 8: 1222. https://doi.org/10.3390/w14081222
APA StyleOcampo-Martinez, C., Toro, R., Puig, V., Van Impe, J., & Logist, F. (2022). Multi-Objective-Based Tuning of Economic Model Predictive Control of Drinking Water Transport Networks. Water, 14(8), 1222. https://doi.org/10.3390/w14081222








