Prediction of Flow Based on a CNN-LSTM Combined Deep Learning Approach
Abstract
:1. Introduction
2. Materials and Methods
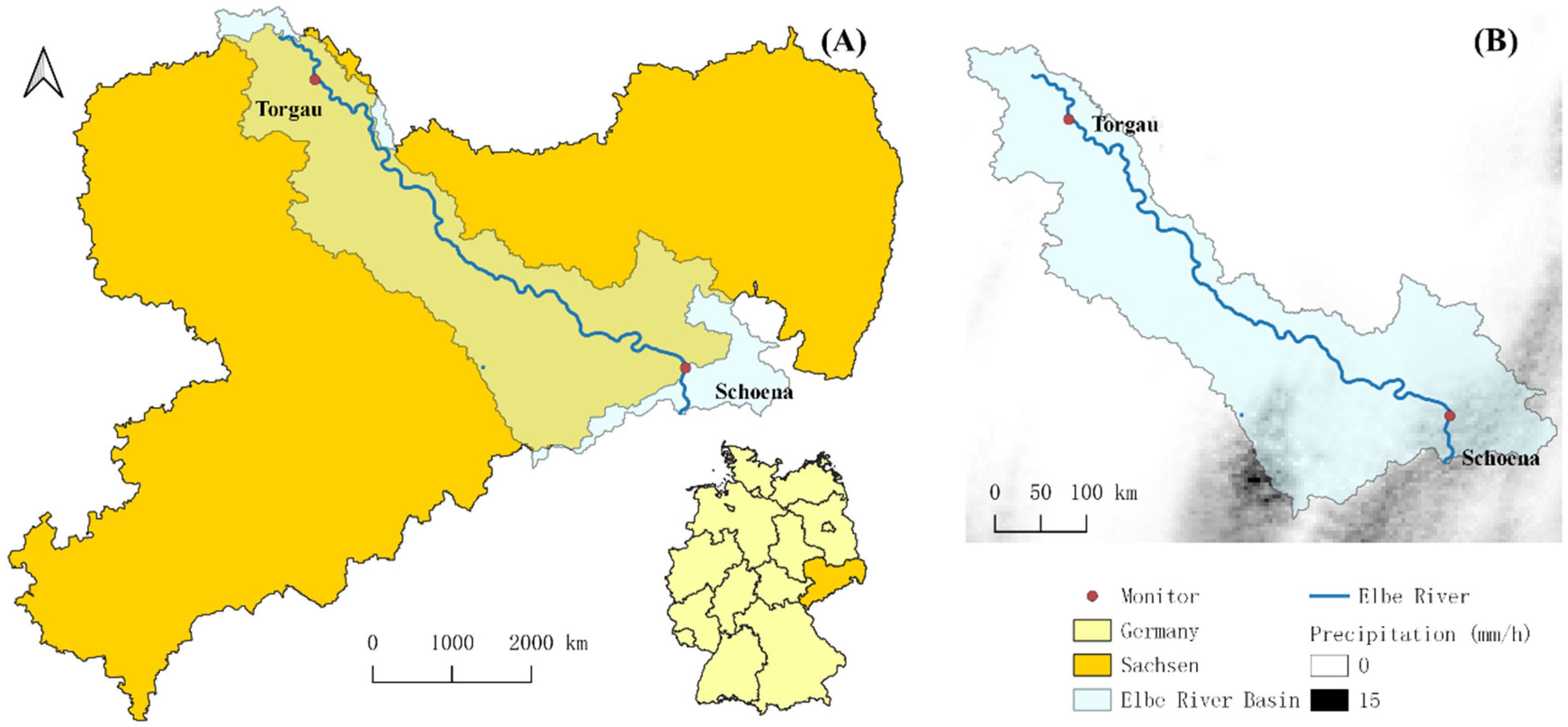
2.1. Study Area and Data Acquisition
2.2. Convolutional Neural Network (CNN)
2.3. Long Short-Term Memory (LSTM)
2.4. River Flow Simulation
2.5. Performance Evaluation
3. Results
3.1. Flow Time Series
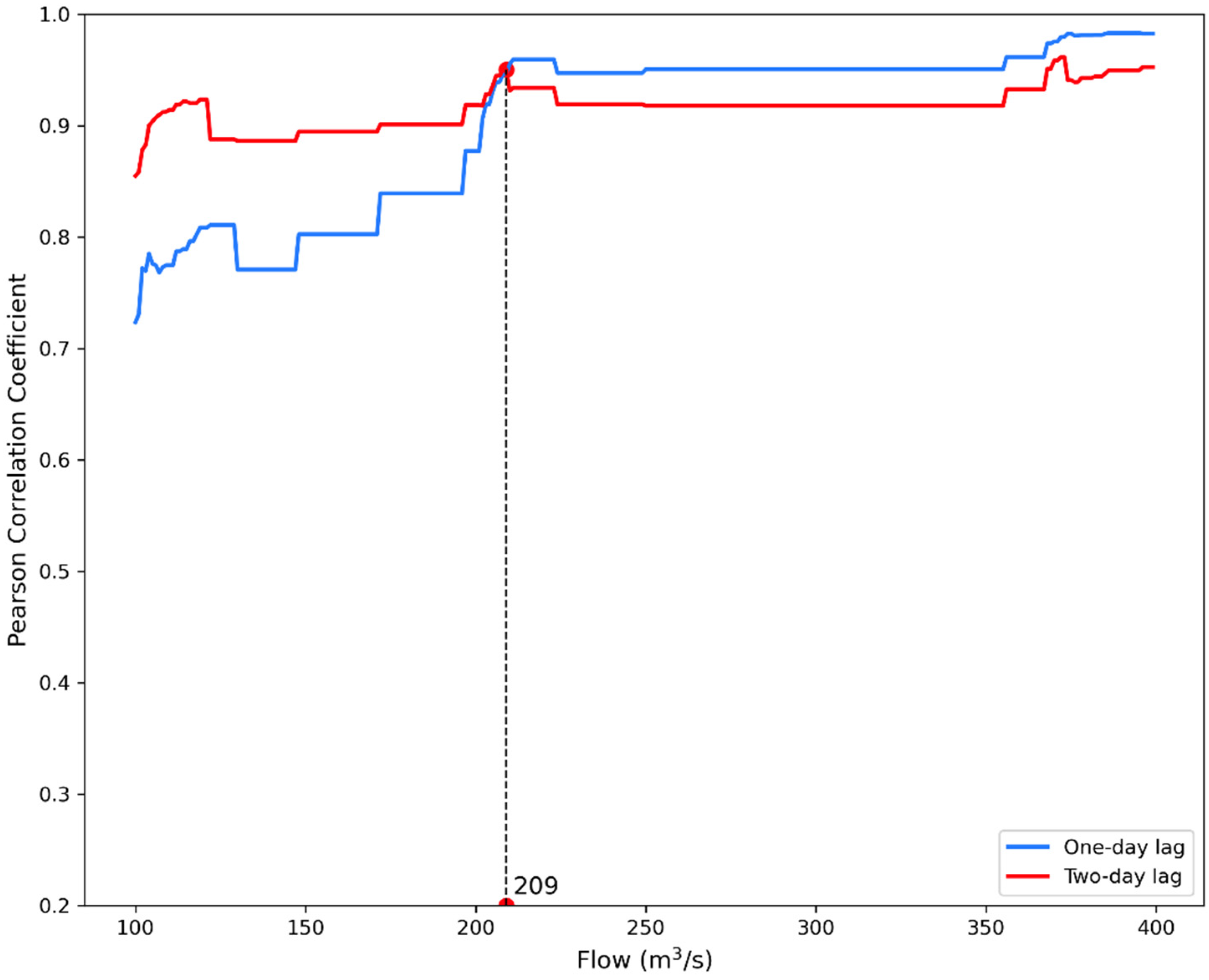
3.2. Input Selection
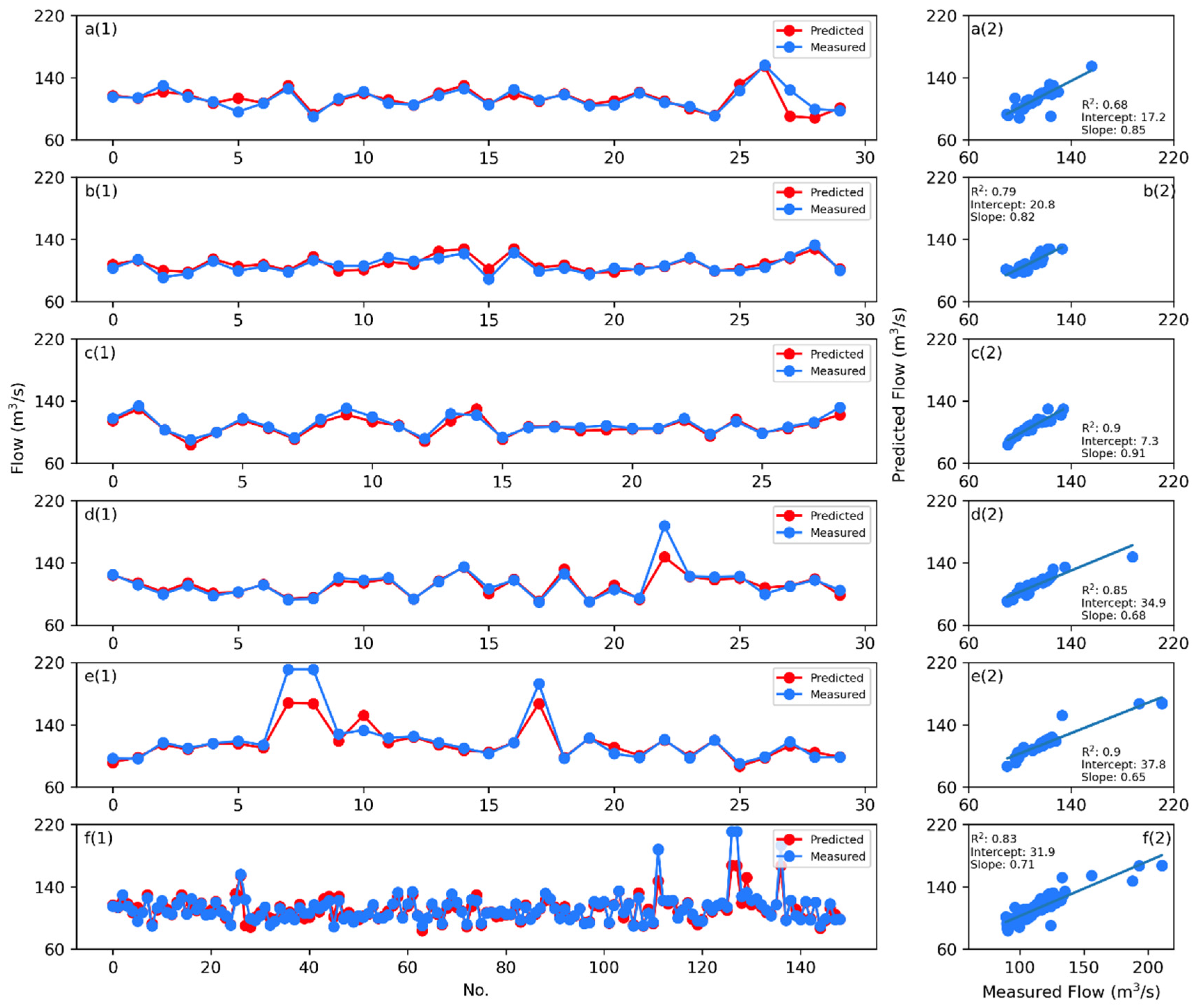
3.3. Flow Simulation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sitterson, J.; Knightes, C.; Parmar, R.; Wolfe, K.; Avant, B. An Overview of Rainfall-Runoff Model Types. 2018, p. 41. Available online: https://scholarsarchive.byu.edu/iemssconference/2018/Stream-C/41/ (accessed on 5 December 2021).
- Mulvaney, T.J. On the Use of Self-Registering Rain and Flood Gauges in Making Observations of the Relations of Rainfall and Flood Discharges in a given Catchment. Proc. Inst. Civ. Eng. Ireland. 1851, 4, 19–31. [Google Scholar]
- Freeze, R.A.; Harlan, R.L. Blueprint for a Physically-Based, Digitally-Simulated Hydrologic Response Model. J. Hydrol. 1969, 9, 237–258. [Google Scholar] [CrossRef]
- Dzubakova, K. Rainfall-Runoff Modelling: Its Development, Classification and Possible Applications. Acta Geogr. Univ. Comenianae. 2010, 54, 173–181. [Google Scholar]
- O’connell, P.E.; Nash, J.E.; Farrell, J.P. River Flow Forecasting through Conceptual Models Part II-The Brosna Catchment at Ferbane. J. Hydrol. 1970, 10, 317–329. [Google Scholar] [CrossRef]
- Porter, J.W.; McMahon, T.A. Application of a Catchment Model in Southeastern Australia. J. Hydrol. 1975, 24, 121–134. [Google Scholar] [CrossRef]
- Burnash, R.J.C.; Ferral, R.L.; McGuire, R.A. A Generalized Streamflow Simulation System: Conceptual Modeling for Digital Computers; US Department of Commerce: Washington, DC, USA; National Weather Service: Silver Spring, MD, USA; State of California, Department of Water Resources: Sacramento, CA, USA, 1973. [Google Scholar]
- Chiew, F.H.S.; McMahon, T.A. Improved modelling of the groundwater processes in MODHYDROLOG. In Proceedings of the Hydrology and Water Resources Symposium, Perth, Australia, 2–4 October 1991; pp. 492–497. [Google Scholar]
- Zhao, R.J.; Liu, X.R. The Xinanjiang Model. In Computer Models of Watershed Hydrology; Water Resources Publication: Littleton, CO, USA, 1995; pp. 215–232. [Google Scholar]
- Chiew, F.H.S.; Peel, M.C.; Western, A.W. Application and Testing of the Simple Rainfall-Runoff Model SIMHYD. In Mathematical Models of Small Watershed Hydrology and Applications; Water Resources Publication: Littleton, CO, USA, 2002; pp. 335–367. [Google Scholar]
- Refshaard, J.C.; Storm, B. MIKE SHE. In Computer Models of Watershed Hydrology; Water Resources Publication: Littleton, CO, USA, 1995; pp. 809–846. [Google Scholar]
- Donigian, A.S., Jr.; Bicknell, B.R.; Imhoff, J.C. Hydrological Simulation Program-Fortran (HSPF). Comput. Models Watershed Hydrol. 1995, 395–442. [Google Scholar]
- Brunner, G.W. HEC-RAS River Analysis System. Hydraulic Reference Manual. Version 1.0.; Hydrologic Engineering Center: Davis, CA, USA, 1995. [Google Scholar]
- Beven, K.; Lamb, R.; Quinn, P.; Romanowicz, R.; Freer, J. TOPMODEL. Computer Models of Watershed Hydrology; Singh, V.P., Ed.; Water Resources Publication: Littleton, CO, USA, 1995; pp. 627–668. [Google Scholar]
- Wood, E.F.; Roundy, J.K.; Troy, T.J.; van Beek, L.P.H.; Bierkens, M.F.P.; Blyth, E.; de Roo, A.; Döll, P.; Ek, M.; Famiglietti, J. Hyperresolution Global Land Surface Modeling: Meeting a Grand Challenge for Monitoring Earth’s Terrestrial Water. Water Resour. Research. 2011, 47, W05301. [Google Scholar] [CrossRef]
- Ahmed, A.N.; Othman, F.B.; Afan, H.A.; Ibrahim, R.K.; Fai, C.M.; Hossain, M.S.; Ehteram, M.; Elshafie, A. Machine Learning Methods for Better Water Quality Prediction. J. Hydrol. 2019, 578, 124084. [Google Scholar] [CrossRef]
- Clark, M.P.; Bierkens, M.F.P.; Samaniego, L.; Woods, R.A.; Uijlenhoet, R.; Bennett, K.E.; Pauwels, V.; Cai, X.; Wood, A.W.; Peters-Lidard, C.D. The Evolution of Process-Based Hydrologic Models: Historical Challenges and the Collective Quest for Physical Realism. Hydrol. Earth Syst. Sci. 2017, 21, 3427–3440. [Google Scholar] [CrossRef] [Green Version]
- Aziz, K.; Rahman, A.; Fang, G.; Shrestha, S. Application of Artificial Neural Networks in Regional Flood Frequency Analysis: A Case Study for Australia. Stoch. Environ. Res. Risk Assess. 2014, 28, 541–554. [Google Scholar] [CrossRef]
- Kişi, Ö. Streamflow Forecasting Using Different Artificial Neural Network Algorithms. J. Hydrol. Eng. 2007, 12, 532–539. [Google Scholar] [CrossRef]
- Sarle, W.S. Neural Networks and Statistical Models. In Proceedings of the Nineteenth Annual SAS Users Groups International Conference, Cary, NC, USA, 1994, 10–13 April 1994; SAS Institute: Cary, NC, USA; pp. 1538–1550. [Google Scholar]
- Shamseldin, A.Y. Application of a Neural Network Technique to Rainfall-Runoff Modelling. J. Hydrol. 1997, 199, 272–294. [Google Scholar] [CrossRef]
- Rosenblatt, F. The Perceptron: A Probabilistic Model for Information Storage and Organization in the Brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tu, J.V. Advantages and Disadvantages of Using Artificial Neural Networks versus Logistic Regression for Predicting Medical Outcomes. J. Clin. Epidemiol. 1996, 49, 1225–1231. [Google Scholar] [CrossRef]
- Bray, M.; Han, D. Identification of Support Vector Machines for Runoff Modelling. J. Hydroinformatics 2004, 6, 265–280. [Google Scholar] [CrossRef] [Green Version]
- Sivapragasam, C.; Liong, S.Y.; Pasha, M.F.K. Rainfall and Runoff Forecasting with SSA-SVM Approach. J. Hydroinformatics 2001, 3, 141–152. [Google Scholar] [CrossRef] [Green Version]
- Tehrany, M.S.; Pradhan, B.; Mansor, S.; Ahmad, N. Flood Susceptibility Assessment Using GIS-Based Support Vector Machine Model with Different Kernel Types. Catena 2015, 125, 91–101. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Mahjouri, N. Integrating Support Vector Regression and a Geomorphologic Artificial Neural Network for Daily Rainfall-Runoff Modeling. Appl. Soft Comput. 2016, 38, 329–345. [Google Scholar] [CrossRef]
- Behzad, M.; Asghari, K.; Eazi, M.; Palhang, M. Generalization Performance of Support Vector Machines and Neural Networks in Runoff Modeling. Expert Syst. Appl. 2009, 36, 7624–7629. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; de Brabanter, J.; Lukas, L.; Vandewalle, J. Weighted Least Squares Support Vector Machines: Robustness and Sparse Approximation. Neurocomputing 2002, 48, 85–105. [Google Scholar] [CrossRef]
- Schoppa, L.; Disse, M.; Bachmair, S. Evaluating the Performance of Random Forest for Large-Scale Flood Discharge Simulation. J. Hydrol. 2020, 590, 125531. [Google Scholar] [CrossRef]
- Wang, Z.; Lai, C.; Chen, X.; Yang, B.; Zhao, S.; Bai, X. Flood Hazard Risk Assessment Model Based on Random Forest. J. Hydrol. 2015, 527, 1130–1141. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.; Mendes, M.P.; Garcia-Soldado, M.J.; Chica-Olmo, M.; Ribeiro, L. Predictive Modeling of Groundwater Nitrate Pollution Using Random Forest and Multisource Variables Related to Intrinsic and Specific Vulnerability: A Case Study in an Agricultural Setting (Southern Spain). Sci. Total Environ. 2014, 476–477, 189–206. [Google Scholar] [CrossRef] [PubMed]
- Zakariah, M. Classification of Large Datasets Using Random Forest Algorithm in Various Applications: Survey. Int. J. Eng. Innov. Technol. 2014, 3, 189–198. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Representations by Back-Propagating Errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Lin Hsu, K.; Gupta, H.V.; Sorooshian, S. Application of a Recurrent Neural Network to Rainfall-Runoff Modeling. In Proceedings of the 1997 24th Annual Water Resources Planning and Management Conference; Houston, TX, USA, 6–9 April 1997. [Google Scholar]
- Kumar, D.N.; Raju, K.S.; Sathish, T. River Flow Forecasting Using Recurrent Neural Networks. Water Resour. Manag. 2004, 18, 143–161. [Google Scholar] [CrossRef]
- Han, H.; Choi, C.; Jung, J.; Kim, H.S. Deep Learning with Long Short Term Memory Based Sequence-to-Sequence Model for Rainfall-Runoff Simulation. Water 2021, 13, 437. [Google Scholar] [CrossRef]
- Adnan, R.M.; Zounemat-Kermani, M.; Kuriqi, A.; Kisi, O. Machine Learning Method in Prediction Streamflow Considering Periodicity Component; Springer: Singapore, 2021; pp. 383–403. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Dong, L.; Zhang, J. Predicting Polycyclic Aromatic Hydrocarbons in Surface Water by a Multiscale Feature Extraction-Based Deep Learning Approach. Sci. Total Environ. 2021, 799, 149509. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall-Runoff Modelling Using Long Short-Term Memory (LSTM) Networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef] [Green Version]
- Bai, Y.; Bezak, N.; Sapač, K.; Klun, M.; Zhang, J. Short-Term Streamflow Forecasting Using the Feature-Enhanced Regression Model. Water Resour. Manag. 2019, 33, 4783–4797. [Google Scholar] [CrossRef]
- Bai, Y.; Bezak, N.; Zeng, B.; Li, C.; Sapač, K.; Zhang, J. Daily Runoff Forecasting Using a Cascade Long Short-Term Memory Model That Considers Different Variables. Water Resour. Manag. 2021, 35, 1167–1181. [Google Scholar] [CrossRef]
- He, X.; Luo, J.; Zuo, G.; Xie, J. Daily Runoff Forecasting Using a Hybrid Model Based on Variational Mode Decomposition and Deep Neural Networks. Water Resour. Manag. 2019, 33, 1571–1590. [Google Scholar] [CrossRef]
- Barzegar, R.; Aalami, M.T.; Adamowski, J. Coupling a Hybrid CNN-LSTM Deep Learning Model with a Boundary Corrected Maximal Overlap Discrete Wavelet Transform for Multiscale Lake Water Level Forecasting. J. Hydrol. 2021, 598. [Google Scholar] [CrossRef]
- Deng, J.; Dong, W.; Socher, R.; Li, L.-J.; Li, K.; Fei-Fei, L. ImageNet: A Large-Scale Hierarchical Image Database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar] [CrossRef] [Green Version]
- Baek, S.-S.; Pyo, J.; Chun, J.A. Prediction of Water Level and Water Quality Using a CNN-LSTM Combined Deep Learning Approach. Water 2020, 12, 3399. [Google Scholar] [CrossRef]
- Hesse, C.; Martínková, M.; Möllenkamp, S.; Borowski, I. Baseline Assessment of the Elbe Basin. 2005. Available online: https://www.newater.uni-osnabrueck.de/deliverables/D331_Baseline_Assessment.pdf (accessed on 2 December 2021).
- Schwandt, D.; Hübner, G. Hydrologische Extreme Im Wandel Der Jahrhunderte-Auswahl Und Dokumentation Für Die Informationsplattform Undine. In Forum für Hydrologie und Wasserbewirtschaftung; Technischen Universität Braunschwei: Braunschweig, Germany, 2009; Volume 26, pp. 19–24. [Google Scholar]
- Lawrence, S.; Giles, C.L.; Tsoi, A.C.; Back, A.D. Face Recognition: A Convolutional Neural-Network Approach. IEEE Trans. Neural Netw. 1997, 8, 98–113. [Google Scholar] [CrossRef] [Green Version]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet Classification with Deep Convolutional Neural Networks. Adv. Neural Inf. Processing Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Nagi, J.; Ducatelle, F.; di Caro, G.A.; Cireşan, D.; Meier, U.; Giusti, A.; Nagi, F.; Schmidhuber, J.; Gambardella, L.M. Max-Pooling Convolutional Neural Networks for Vision-Based Hand Gesture Recognition. In Proceedings of the 2011 IEEE International Conference on Signal and Image Processing Applications, ICSIPA 2011, Kuala Lumpur, Malaysia, 16–18 November 2011; pp. 342–347. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.N. Compression of Fully-Connected Layer in Neural Network by Kronecker Product. In Proceedings of the 8th International Conference on Advanced Computational Intelligence, ICACI 2016, Chiang Mai, Thailand, 14–16 February 2016; pp. 173–179. [Google Scholar] [CrossRef] [Green Version]
- Salehinejad, H.; Sankar, S.; Barfett, J.; Colak, E.; Valaee, S. Recent Advances in Recurrent Neural Networks. arXiv 2017, arXiv:1801.01078. [Google Scholar]
- Graves, A. Long Short-Term Memory. In Supervised Sequence Labelling with Recurrent Neural Networks; Springer: Berlin/Heidelberg, Germany, 2012; pp. 37–45. [Google Scholar]
- Bastidas, L.A.; Hogue, T.S.; Sorooshian, S.; Gupta, H.V.; Shuttleworth, W.J. Parameter Sensitivity Analysis for Different Complexity Land Surface Models Using Multicriteria Methods. J. Geophys. Res. Atmos. 2006, 111, 20101. [Google Scholar] [CrossRef] [Green Version]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting through Conceptual Models Part I—A Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the Mean Squared Error and NSE Performance Criteria: Implications for Improving Hydrological Modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef] [Green Version]
- Bartl, S.; Schümberg, S.; Deutsch, M. Revising Time Series of the Elbe River Discharge for Flood Frequency Determination at Gauge Dresden. Nat. Hazards Earth Syst. Sci. 2009, 9, 1805–1814. [Google Scholar] [CrossRef] [Green Version]
- Moriasi, D.N.; Arnold, J.G.; Liew, M.W.; van Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Sahraei, S.; Asadzadeh, M.; Unduche, F. Signature-Based Multi-Modelling and Multi-Objective Calibration of Hydrologic Models: Application in Flood Forecasting for Canadian Prairies. J. Hydrol. 2020, 588, 125095. [Google Scholar] [CrossRef]
- Xu, W.; Jiang, Y.; Zhang, X.; Li, Y.; Zhang, R.; Fu, G. Using Long Short-Term Memory Networks for River Flow Prediction. Hydrol. Res. 2020, 51, 1358–1376. [Google Scholar] [CrossRef]
- Bhagwat, P.P.; Maity, R. Multistep-Ahead River Flow Prediction Using LS-SVR at Daily Scale. J. Water Resour. Prot. 2012, 4, 528–539. [Google Scholar] [CrossRef] [Green Version]
- Duda, P.B.; Hummel, P.R., Jr.; Imhoff, J.C. BASINS/HSPF: Model Use, Calibration, and Validation. Trans. ASABE 2012, 55, 1523–1547. [Google Scholar] [CrossRef]
- Daniell, T.M. Neural Networks. Applications in Hydrology and Water Resources Engineering. In Proceedings of the International Hydrology and Water Resource Symposium, Perth, Australia, 30 November–1 December 1991; Institution of Engineers: Perth, Australia, 1991; Volume 3, pp. 797–802. [Google Scholar]
- Peel, M.C.; McMahon, T.A. Historical Development of Rainfall-Runoff Modeling. Wiley Interdiscip. Rev. Water 2020, 7, e1471. [Google Scholar] [CrossRef]
- Imrie, C.E.; Durucan, S.; Korre, A. River Flow Prediction Using Artificial Neural Networks: Generalisation beyond the Calibration Range. J. Hydrol. 2000, 233, 138–153. [Google Scholar] [CrossRef]

| R2 | NSE | KGE | r | |||
|---|---|---|---|---|---|---|
| k1 | 0.96 | 0.96 | 0.87 | 0.99 | 0.87 | 1.01 |
| k2 | 0.46 | 0.46 | 0.47 | 0.75 | 0.58 | 0.80 |
| k3 | 0.92 | 0.92 | 0.92 | 0.97 | 0.95 | 1.05 |
| k4 | 0.97 | 0.97 | 0.92 | 0.99 | 0.96 | 1.06 |
| k5 | 0.90 | 0.90 | 0.75 | 0.97 | 0.76 | 1.05 |
| k6 | 0.78 | 0.78 | 0.75 | 0.89 | 0.78 | 0.98 |
| R2 | NSE | KGE | r | |||
|---|---|---|---|---|---|---|
| k1 | 0.63 | 0.63 | 0.82 | 0.82 | 1.03 | 1.00 |
| k2 | 0.76 | 0.76 | 0.86 | 0.89 | 0.93 | 1.02 |
| k3 | 0.86 | 0.86 | 0.93 | 0.95 | 0.96 | 0.98 |
| k4 | 0.81 | 0.81 | 0.73 | 0.92 | 0.74 | 0.99 |
| k5 | 0.82 | 0.82 | 0.68 | 0.95 | 0.69 | 0.97 |
| k6 | 0.81 | 0.81 | 0.76 | 0.91 | 0.77 | 0.99 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, P.; Zhang, J.; Krebs, P. Prediction of Flow Based on a CNN-LSTM Combined Deep Learning Approach. Water 2022, 14, 993. https://doi.org/10.3390/w14060993
Li P, Zhang J, Krebs P. Prediction of Flow Based on a CNN-LSTM Combined Deep Learning Approach. Water. 2022; 14(6):993. https://doi.org/10.3390/w14060993
Chicago/Turabian StyleLi, Peifeng, Jin Zhang, and Peter Krebs. 2022. "Prediction of Flow Based on a CNN-LSTM Combined Deep Learning Approach" Water 14, no. 6: 993. https://doi.org/10.3390/w14060993






