Effects of Orifice Sizes for Uncontrolled Filling Processes in Water Pipelines
Abstract
:1. Introduction
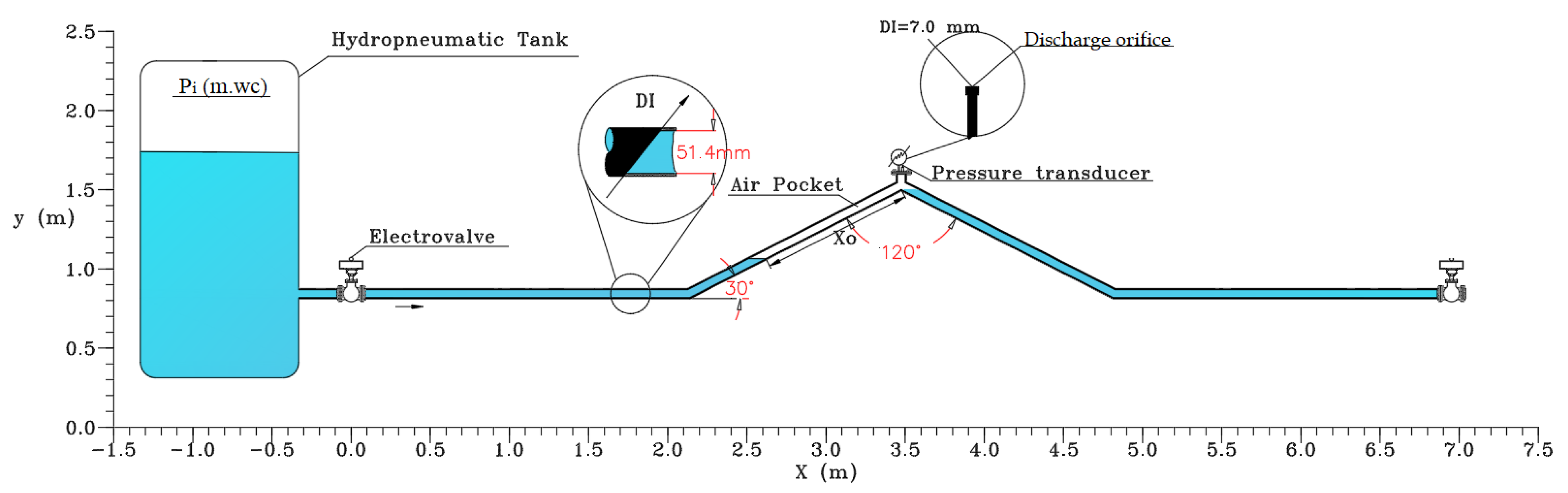
2. Experimental Model
3. Numerical CFD Model
3.1. Governing Equations
3.2. Turbulence Model
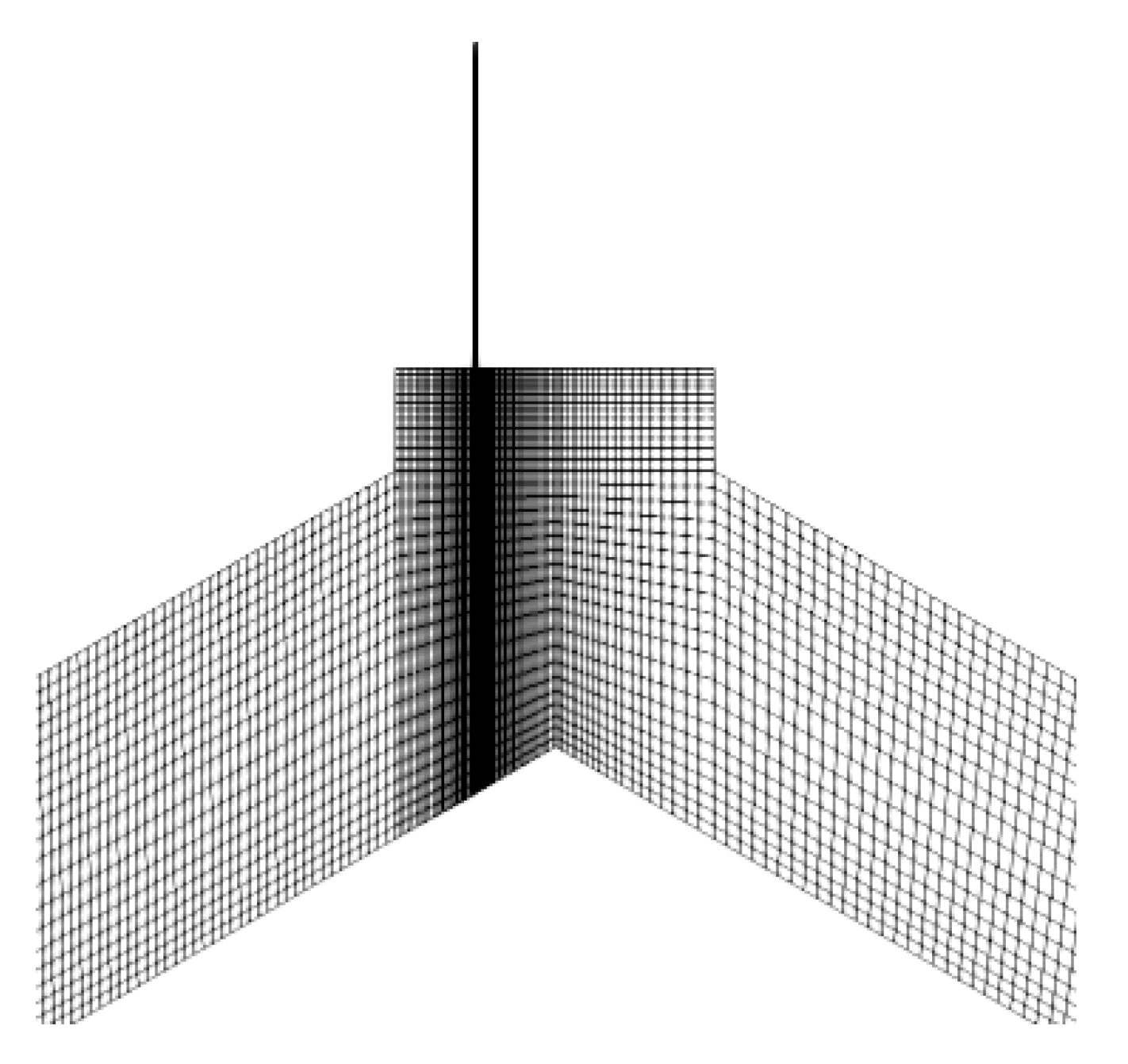
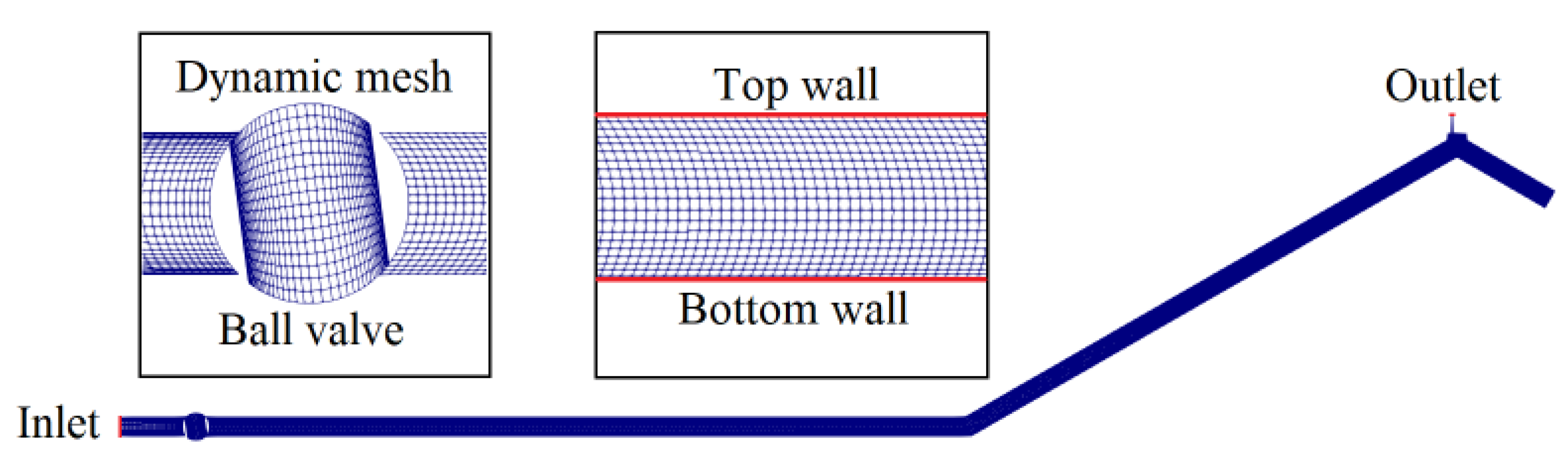
3.3. Assumptions, Boundary Conditions and Mesh Properties
- The air phase is simulated considering an ideal gas law.
- Fluids are considered compressible, non-isothermal, and immiscible.
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| inner diameter | |
| blending function (-) | |
| gravitational acceleration vector (m/s2) | |
| k | turbulence kinetic energy (m2/m2) |
| p | pressure (N/m2) |
| maximum pressure (N/m2) | |
| inlet pressure head (m.wc) | |
| shear stress in CFD model (N/m2) | |
| t | time (s) |
| u | velocity component (m/s) |
| velocity vector (m/s) | |
| initial air pocket length (m) | |
| air–water volume fraction (-) | |
| mixture kinematic viscosity (m2/s) | |
| mixture dynamic viscosity (kg/ms) | |
| mixture density (kg/m3) | |
| dissipation frequency (m2/s3) | |
| Subscripts | |
| a | refers to air phase (e.g., air density) |
| w | refers to water phase (e.g., water dynamic viscosity) |
| t | refers to turbulence conditions (turbulent kinematic viscosity) |
| Constants of the k-ω SST model | |
| 0.555 | |
| 0.09 | |
| 0.075 | |
| 0.85 | |
| 0.50 | |
| 0.44 | |
| 0.0828 | |
| 1.0 | |
| 0.856 | |
References
- AWWA. Air Release, Air/Vacuum Valves and Combination Air Valves (M51); American Water Works Association: Denver, CO, USA, 2016. [Google Scholar]
- Fuertes, V.S. Hydraulic Transients with Entrapped Air Pockets. Ph.D. Thesis, Department of Hydraulic Engineering, Polytechnic University of Valencia, Editorial Universitat Politècnica de València, Valencia, Spain, 2001. [Google Scholar]
- Ramezani, L.; Karney, B.; Malekpour, A. The challenge of air valves: A selective critical literature review. J. Water Resour. Plan. Manag. 2015, 141, 04015017. [Google Scholar] [CrossRef]
- McPherson, D.L.; Haeckler, C. Pipelines 2012: Innovations in Design, Construction, Operations, and Maintenance, Doing More with Less; American Society of Civil Engineers: Reston, VA, USA, 2012; pp. 983–989. [Google Scholar]
- Liou, C.P.; Hunt, W.A. Filling of pipelines with undulating elevation profiles. J. Hydraul. Eng. 1996, 122, 534–539. [Google Scholar] [CrossRef]
- Izquierdo, J.; Fuertes, V.S.; Cabrera, E.; Iglesias, P.L.; Garcia-Serra, J. Pipeline start-up with entrapped air. J. Hydraul. Res. 1999, 37, 579–590. [Google Scholar] [CrossRef]
- Liu, D.; Zhou, L.; Karney, B.; Zhang, Q.; Ou, C. Rigid-plug elastic-water model for transient pipe flow with entrapped air pocket. J. Hydraul. Res. 2011, 49, 799–803. [Google Scholar] [CrossRef]
- Zhou, L.; Liu, D.; Karney, B. Investigation of hydraulic transients of two entrapped air pockets in a water pipeline. J. Hydraul. Eng. 2013, 139, 949–959. [Google Scholar] [CrossRef]
- Zhou, L.; Pan, T.; Wang, H.; Liu, D.; Wang, P. Rapid air expulsion through an orifice in a vertical water pipe. J. Hydraul. Res. 2019, 57, 142–149. [Google Scholar] [CrossRef]
- Besharat, M.; Tarinejad, R.; Aalami, M.T.; Ramos, H.M. Study of a compressed air vessel for controlling the pressure surge in water networks: CFD and experimental analysis. Water Resour. Manag. 2016, 30, 2687–2702. [Google Scholar] [CrossRef]
- Hurtado-Misal, A.D.; Hernández-Sanjuan, D.; Coronado-Hernández, O.E.; Espinoza-Román, H.; Fuertes-Miquel, V.S. Analysis of Sub-Atmospheric Pressures during Emptying of an Irregular Pipeline without an Air Valve Using a 2D CFD Model. Water 2021, 13, 2526. [Google Scholar] [CrossRef]
- Zhou, L.; Liu, D.; Ou, C. Simulation of flow transients in a water filling pipe containing entrapped air pocket with VOF model. Eng. Appl. Comput. Fluid Mech. 2011, 5, 127–140. [Google Scholar] [CrossRef] [Green Version]
- Martins, N.M.C.; Delgado, J.N.; Ramos, H.M.; Covas, D.I.C. Maximum transient pressures in a rapidly filling pipeline with entrapped air using a CFD model. J. Hydraul. Res. 2017, 55, 506–519. [Google Scholar] [CrossRef]
- Fuertes-Miquel, V.S.; López-Jiménez, P.A.; Martínez-Solano, F.J.; López-Patiño, G. Numerical modelling of pipelines with air pockets and air valves. Can. J. Civ. Eng. 2016, 43, 1052–1061. [Google Scholar] [CrossRef] [Green Version]
- Coronado-Hernández, O.E.; Besharat, M.; Fuertes-Miquel, V.S.; Ramos, H.M. Effect of a commercial air valve on the rapid filling of a single pipeline: A numerical and experimental analysis. Water 2019, 11, 1814. [Google Scholar] [CrossRef] [Green Version]
- Besharat, M.; Coronado-Hernández, O.E.; Fuertes-Miquel, V.S.; Viseu, M.T.; Ramos, H.M. Backflow air and pressure analysis in emptying a pipeline containing an entrapped air pocket. Urban Water J. 2018, 15, 769–779. [Google Scholar] [CrossRef]
- Besharat, M.; Coronado-Hernández, O.E.; Fuertes-Miquel, V.S.; Viseu, M.T.; Ramos, H.M. Computational fluid dynamics for sub-atmospheric pressure analysis in pipe drainage. J. Hydraul. Res. 2019, 58, 553–565. [Google Scholar] [CrossRef]
- Coronado-Hernández, O.E.; Fuertes-Miquel, V.S.; Besharat, M.; Ramos, H.M. Subatmospheric pressure in a water draining pipeline with an air pocket. Urban Water J. 2018, 15, 346–352. [Google Scholar] [CrossRef]
- Aguirre-Mendoza, A.M.; Oyuela, S.; Espinoza-Román, H.G.; Coronado-Hernández, O.E. Fuertes-Miquel, V.S. Paternina-Verona, D.A. 2D CFD Modeling of Rapid Water Filling with Air Valves Using OpenFOAM. Water 2021, 13, 3104. [Google Scholar] [CrossRef]
- Fuertes-Miquel, V.S.; Coronado-Hernández, O.E.; Iglesias-Rey, P.L.; Mora-Meliá, D. Transient phenomena during the emptying process of a single pipe with water–air interaction. J. Hydraul. Eng. 2019, 57, 318–326. [Google Scholar] [CrossRef]
- Zhou, L.; Cao, Y.; Karney, B.; Bergant, A.; Tijsseling, A.S.; Liu, D.; Wang, P. Expulsion of Entrapped Air in a Rapidly Filling Horizontal Pipe. J. Hydraul. Eng. 2020, 146, 04020047. [Google Scholar] [CrossRef]
- Romero, G.; Fuertes-Miquel, V.S.; Coronado-Hernández, O.E.; Ponz-Carcelén, R.; Biel-Sanchis, F. Analysis of hydraulic transients during pipeline filling processes with air valves in large-scale installations. Urban Water J. 2020, 17, 568–575. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Wilcox, D.C. Reassessment of the scale-determining equation for advanced turbulence models. AIAA J. 1988, 26, 1299–1310. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. In Numerical Prediction of Flow, Heat Transfer, Turbulence and Combustion; 1983; pp. 96–116. [Google Scholar]
- Jasak, H. OpenFOAM: Open source CFD in research and industry. Int. J. Nav. Archit. Ocean. Eng. 2009, 1, 89–94. [Google Scholar]
- Jasak, H.; Jemcov, A.; Tukovic, Z. OpenFOAM: A C++ library for complex physics simulations. Int. Workshop Coupled Methods Numer. Dyn. 2007, 1000, 1–20. [Google Scholar]
- Coronado-Hernández, O.E.; Fuertes-Miquel, V.S.; Besharat, M.; Ramos, H.M. Experimental and numerical analysis of a water emptying pipeline using different air valves. Water 2017, 9, 98. [Google Scholar] [CrossRef]
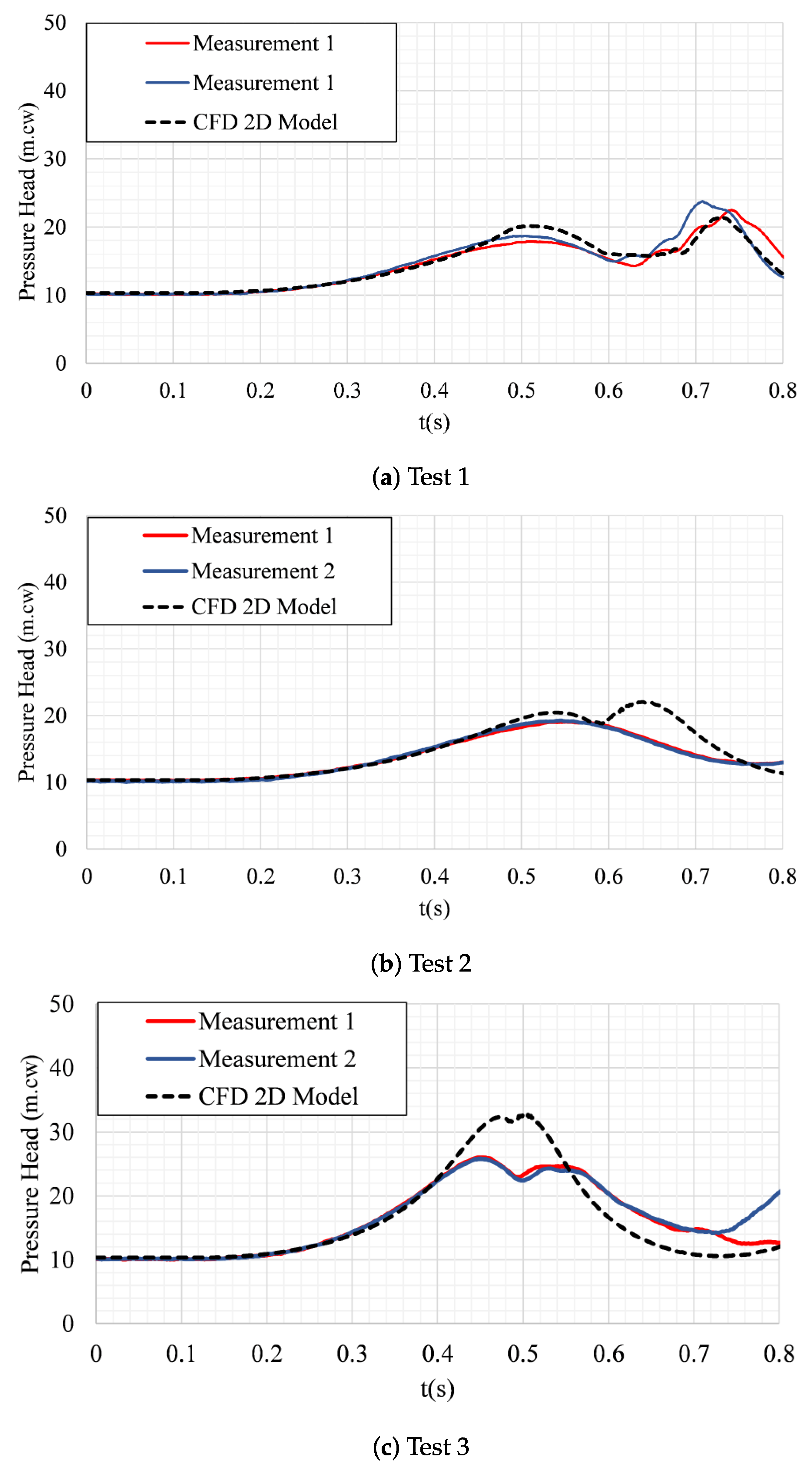
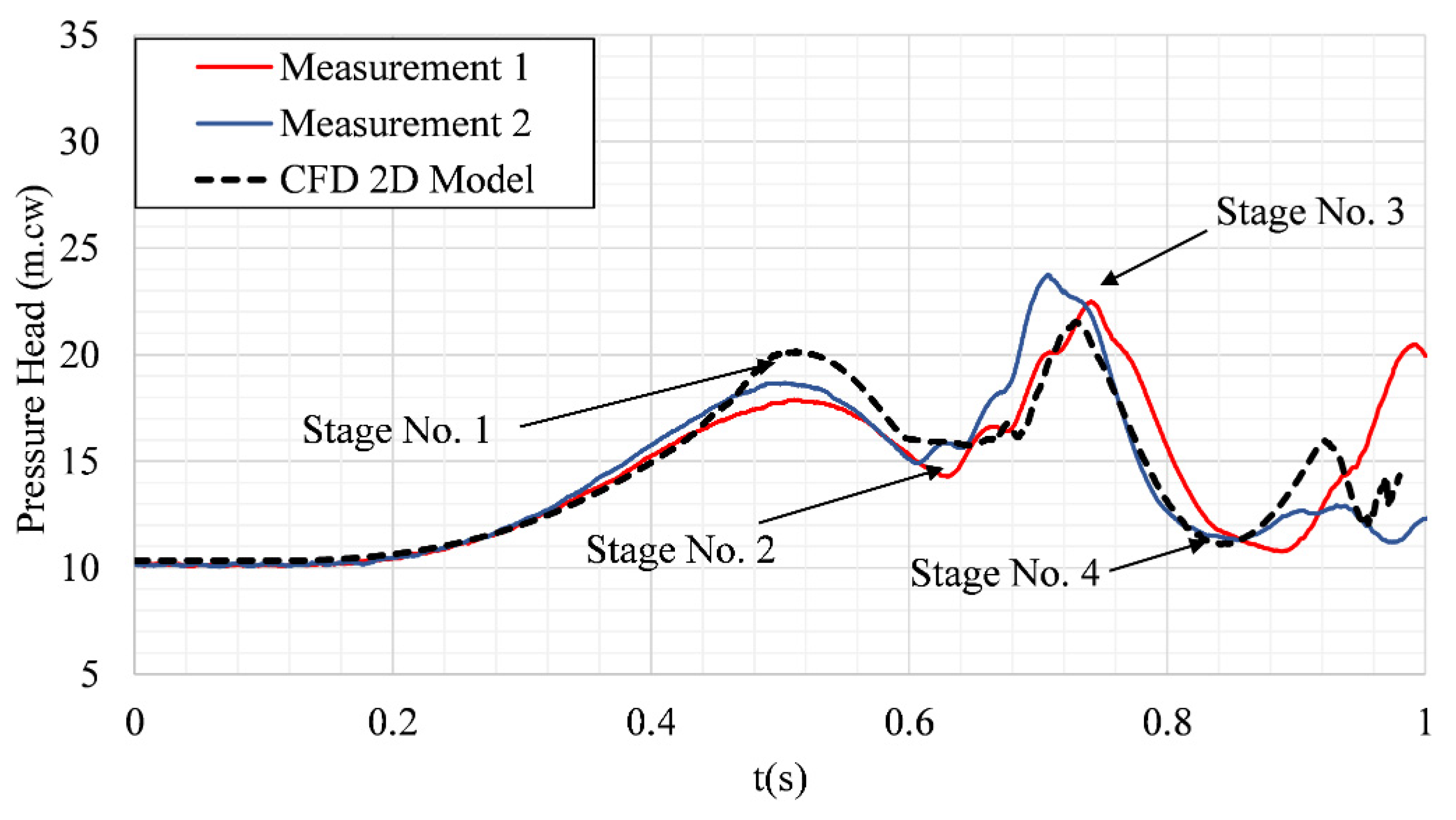
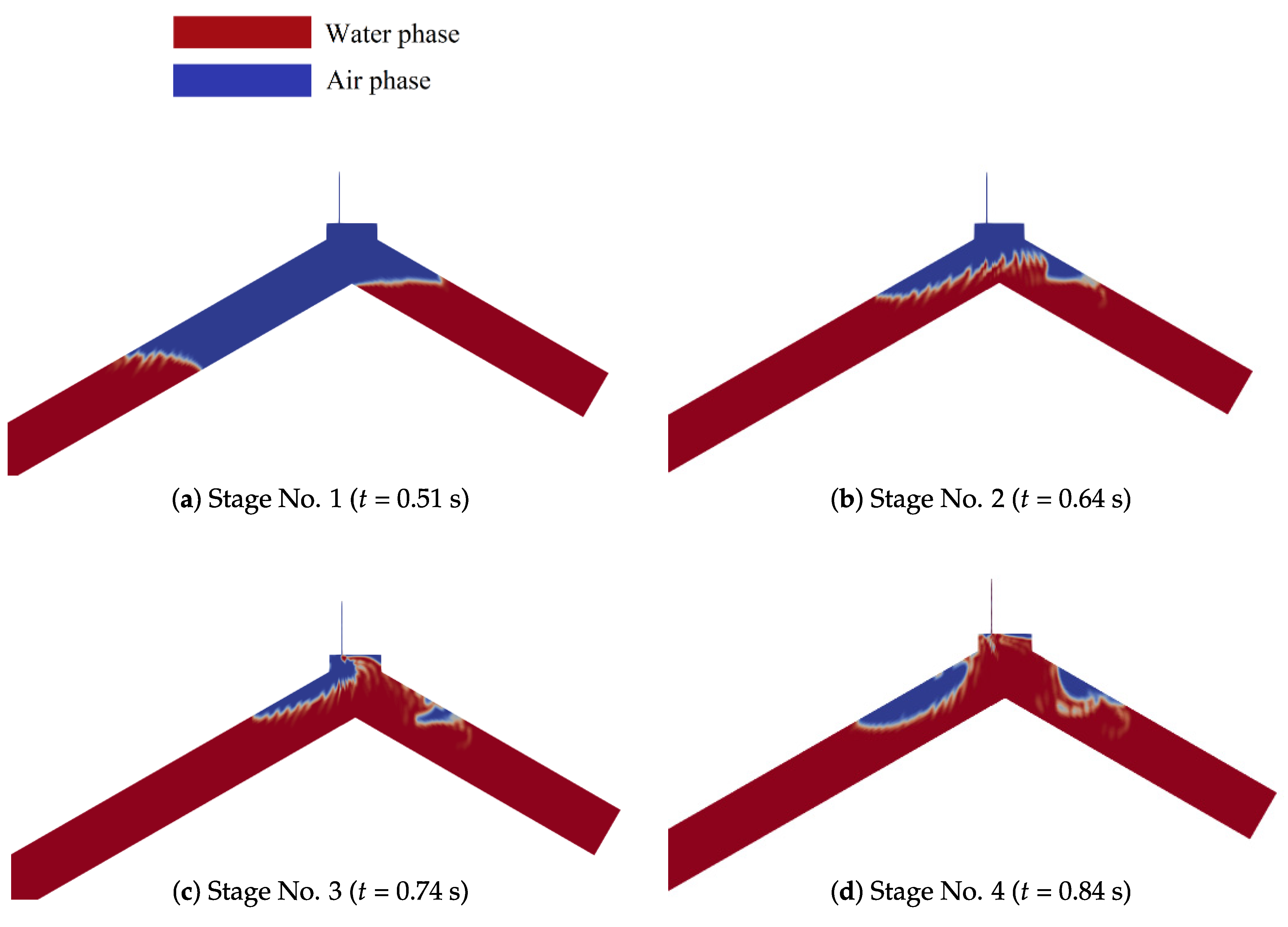
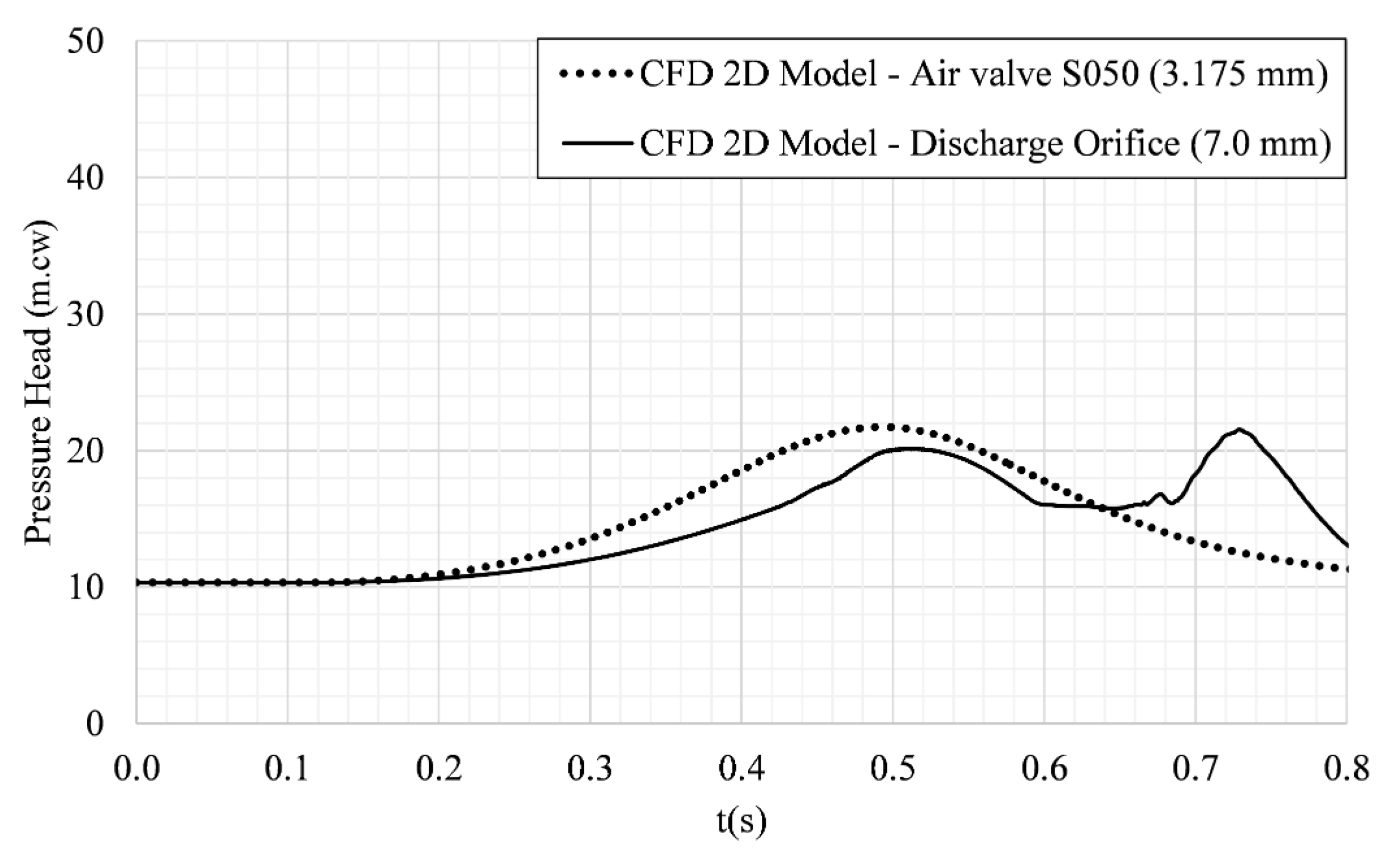
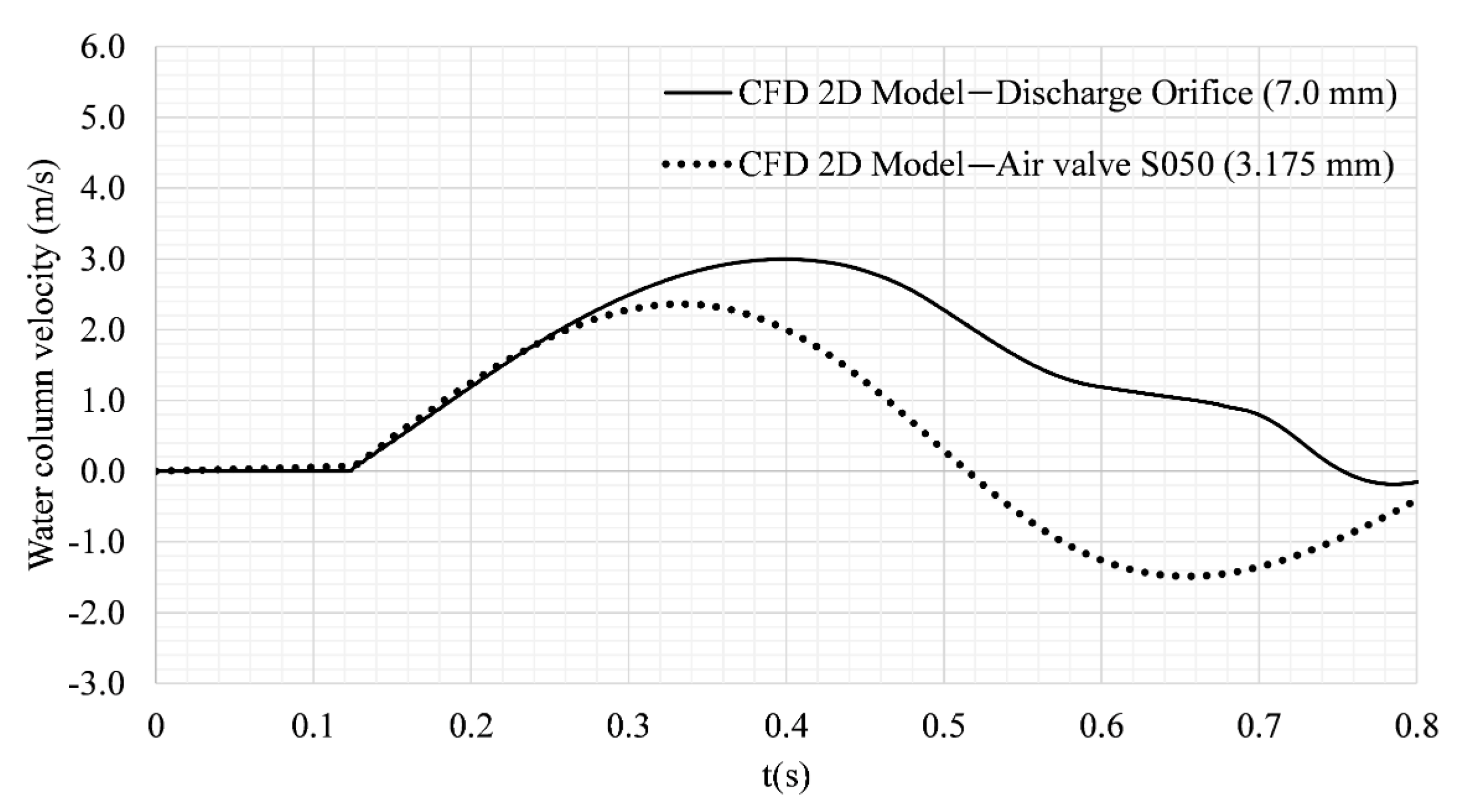
| Test | 1 | 2 | 3 |
|---|---|---|---|
| (m.wc) | 5.10 | 5.10 | 7.65 |
| (m) | 0.96 | 1.36 | 0.96 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aguirre-Mendoza, A.M.; Paternina-Verona, D.A.; Oyuela, S.; Coronado-Hernández, O.E.; Besharat, M.; Fuertes-Miquel, V.S.; Iglesias-Rey, P.L.; Ramos, H.M. Effects of Orifice Sizes for Uncontrolled Filling Processes in Water Pipelines. Water 2022, 14, 888. https://doi.org/10.3390/w14060888
Aguirre-Mendoza AM, Paternina-Verona DA, Oyuela S, Coronado-Hernández OE, Besharat M, Fuertes-Miquel VS, Iglesias-Rey PL, Ramos HM. Effects of Orifice Sizes for Uncontrolled Filling Processes in Water Pipelines. Water. 2022; 14(6):888. https://doi.org/10.3390/w14060888
Chicago/Turabian StyleAguirre-Mendoza, Andres M., Duban A. Paternina-Verona, Sebastian Oyuela, Oscar E. Coronado-Hernández, Mohsen Besharat, Vicente S. Fuertes-Miquel, Pedro L. Iglesias-Rey, and Helena M. Ramos. 2022. "Effects of Orifice Sizes for Uncontrolled Filling Processes in Water Pipelines" Water 14, no. 6: 888. https://doi.org/10.3390/w14060888







