Abstract
Groundwater is a crucial source of water supply in drought conditions, and an auxiliary water source in wet seasons. Due to its increasing importance in view of climate change, predicting groundwater level (GWL) needs to be improved to enhance management. We used adaptive neuro-fuzzy inference systems (ANFIS) to predict the GWL of the Urmia aquifer in northwestern Iran under various input scenarios using precipitation, temperature, groundwater withdrawal, GWL during the previous month, and river flow. In total, 11 input patterns from various combinations of variables were developed. About 70% of the data were used to train the models, while the rest were used for validation. In a second step, several metaheuristic algorithms, such as genetic algorithm (GA), particle swarm optimization (PSO), ant colony optimization for continuous domains (ACOR), and differential evolution (DE) were used to improve the model and, consequently, prediction performance. The results showed that (i) RMSE, MAPE, and NSE of 0.51 m, 0.00037 m, and 0.86, respectively, were obtained for the ANFIS model using all input variables, indicating a rather poor performance, (ii) metaheuristic algorithms were able to optimize the parameters of the ANFIS model in predicting GWL, (iii) the input pattern that included all input variables resulted in the most appropriate performance with RMSE, MAPE, and NSE of 0.28 m, 0.00019 m, and 0.97, respectively, using the ANIFS-ACOR hybrid model, (iv) results of Taylor’s diagram (CC = 0.98, STD = 0.2, and RMSD = 0.30), as well as the scatterplot (R2 = 0.97), showed that best prediction was achieved by ANFIS-ACOR, and (v) temperature and evaporation exerted stronger influence on GWL prediction than groundwater withdrawal and precipitation. The findings of this study reveal that metaheuristic algorithms can significantly improve the performance of the ANFIS model in predicting GWL.
1. Introduction
Groundwater resources are becoming increasingly important, especially in arid and semi-arid regions affected by climate change [1,2]. In many areas, surface water resources are rapidly decreasing, inducing larger pressure on groundwater [2]. Thus, the prediction of changes in groundwater level (GWL) is becoming increasingly essential for sustainable use [3,4,5,6,7]. Reliable prediction of GWL, however, requires extensive and labor-consuming observations. They involve climatic, hydrological, geological variables, and land use change. Furthermore, some of these variables (e.g., climate and land use change) change over time, which increases the model complexity [6,7]. Therefore, depending on the available information and uncertainties, different models have been developed to simulate the behavior of GWL changes. In general, three main model types are used to simulate and predict GWL: physical, numerical, and regression models.
Physical models are suitable for prediction but suffer from high cost of construction and require detailed physical information of the aquifer. Numerical models do not have the limitations of physical models but require information on the aquifer’s geology, such as hydraulic conductivity, storage coefficient, and aquifer thickness. Obtaining such information is still difficult, and in many areas, especially in Iran, it is either not available or associated with significant errors. As a result, numerical models are associated with weak performance. Some of these models are PMWIN, FFLOW, GMS, and Visual MODFLOW [8,9,10]. Regression models do not have the limitations of physical models and do not require the information needed by numerical models. They require time-dependent observations that affect GWL (e.g., precipitation, temperature, and aquifer withdrawal) [11]. However, these models have shown poor performance in complex situations, especially when the number of independent variables is high [11,12].
Machine learning (ML) and artificial intelligence (AI) models are sophisticated regression methods that compensate for the shortcomings of simple regression models. ML and AI models have been used in various disciplines showing a good performance compared to other regression models [13,14,15,16,17]. Among them, artificial neural networks (ANN), support vector machines (SVM), Bayesian network (BN), fuzzy inference system (FIS), and adaptive neuro-fuzzy inference systems (ANFIS) have attracted recent attention [18,19]. These models do not require structural and physical information of the system, instead time-dependent variables are considered. They have been used extensively by various researchers in groundwater management and GWL prediction [1,6,20,21].
ANFIS is a model developed from the combination of ANN and FIS [22]. This model has shown promising performance in many research fields [19,23,24,25]. In GWL simulations, ANFIS has been used by several researchers (Table 1). From 2009 to 2020, researchers compared the performance of ANFIS in predicting GWL with other machine learning models. In general, the capability of this model has revealed efficient performance in groundwater simulation. However, in some cases, it showed poor performance when trapped in local minima [26]. To improve the modeling quality, metaheuristic algorithms have been developed in the training of ANFIS [27]. These algorithms can use large amounts of data and are usually not trapped in local minima and show a good convergence rate.
According to Table 1, during the last ten years, only one study has used evolutionary algorithms to improve the performance of ANFIS. However, it is necessary to examine other algorithms to improve the performance of ANFIS. For example, Seifi et al. (2019) predicted GWL with lagged GWL values [28]. Variables such as temperature, precipitation, evaporation, and aquifer withdrawal, in addition to lagged GWL, have been used as input. Few studies have considered all these input variables simultaneously.

Table 1.
Summary of application of ANFIS models in GWL prediction.
Table 1.
Summary of application of ANFIS models in GWL prediction.
| No | Reference | Models Used | Input Variables * |
|---|---|---|---|
| 1 | [29] | ANFIS, Kriging | GWL |
| 2 | [30] | ANFIS, ANN | GWL, T, P |
| 3 | [31] | ANFIS, ANN | GWL, P, E, T, H |
| 4 | [32] | Wavelet-ANFIS, ANFIS | GWL |
| 5 | [33] | ANFIS | P |
| 6 | [34] | GP, ANN, ANFIS, SVM | GWL, P, E |
| 7 | [35] | GP, ANFIS | GWL, P, E |
| 8 | [36] | Wavelet-ANFIS, Wavelet, ANFIS, ANN | GWL, P, E, average Q |
| 9 | [37] | ANFIS, SVR | R, E, Q, W |
| 10 | [38] | ANFIS, SVM, ANN | GWL, SWL, P, T |
| 11 | [39] | Wavelet-ANFIS | GWL, P |
| 12 | [28] | Optimization of ANN, ANFIS, SVM, with GOA, PSO, WA, CSO, and KA | GWL |
| 13 | This study | Optimization of ANFIS with GA, PSO, ACOR, and DE | GWL, P, T, R, Q, E |
* GWL: groundwater level, T: temperature, E: evaporation, P: precipitation, Q: river flow, R: recharge, H: humidity, W: groundwater exploitation.
In recent years, several algorithms such as genetic algorithm (GA), particle swarm optimization (PSO), ant colony optimization for continuous domains (ACOR), and differential evolution (DE) have been used for better training of ANFIS. The results of these hybrid models are more accurate than that of the ANFIS itself. In a study, Azad et al. (2018) used GA, PSO, ACOR, and DE algorithms in ANFIS training to simulate the water quality of the Gorganrood River in Iran [40]. They showed that DE has the highest accuracy compared to other evolutionary algorithms in river quality simulation. In another study, they used the algorithms to model rainfall-runoff in Isfahan [41]. They reported that the ACOR algorithm provided the best accuracy among the investigated models. Yang et al. (2019) used ANFIS-GA and ANFIS-PSO hybrid models to predict landslides. The proposed models were capable of statistically predicting the landslides with an excellent level of accuracy [42].
Arya Azar et al. (2021) used ANFIS to predict the longitudinal dispersion coefficient of rivers. The Harris hawks optimization (HHO) algorithm was used to increase the model’s performance, and results were compared with experimental models and LSSVM in predicting the longitudinal dispersion coefficient of the river [43]. The results showed that the HHO-ANFIS hybrid model had a higher performance compared to other models. Ghordoyee Milan et al. (2021) used PSO, gray wolf optimization (GWO), and HHO algorithms to improve the results of ANFIS for optimal groundwater withdrawal. Results showed that HHO had the highest performance in improving the ANFIS model [19]. In another study, Kayhomayoon et al. (2021) evaluated the efficiency of ANFIS, ANFIS-HHO, and LSSVM models in predicting the shortage of groundwater reserves [1]. They reported that the optimized ANFIS with HHO had higher performance than other models.
Considering the importance of GWL prediction with the least possible information and a variety of machine learning models, along with the ability of metaheuristic algorithms to find optimal global solutions, GWL prediction was investigated in the present study using ANFIS. In other words, the ANFIS model sometimes does not correctly identify the behavior of the global minimum points and the model error increases due to the lack of proper prediction in these points [28]. Therefore, to improve the performance of the ANFIS model, it is necessary to use evolutionary algorithms that train the ANFIS model well. However, the main purpose of this study is to evaluate the efficiency of different ANFIS-metaheuristic hybrid models for GWL prediction in the Lake Urmia watershed. The performance of these models should be compared and, finally, the best model can be selected for forecasting.
The ANFIS was used together with several algorithms to find the best hybrid model in GWL prediction. For this purpose, GA, PSO, ACOR, and DE were used to improve the prediction performance of the ANFIS model. Since ANFIS-metaheuristic hybrid models have rarely been used in predicting GWL, investigating the performance of hybrid models with different algorithms is innovative. Since observation wells are close to the river, river flow can affect the GWL. Thus, river flow for wells close to rivers along with temperature, precipitation, and aquifer withdrawal were used to predict GWL. In total, 11 input patterns from various combinations of variables were used to develop ANFIS hybrid models to predict GWL. The results of the models, along with the input patterns, are provided using error evaluation criteria and graphs, and, finally, the most appropriate model and input pattern are proposed for GWL prediction.
2. Materials and Methods
2.1. Study Area
The Urmia aquifer (37°20′–37°50′ N, 44°50′–44°10′ E) is located in northwestern Iran along Lake Urmia, near the border of Turkey with an area of about 760 km2 (Figure 1). The aquifer is phreatic, with 64 observation wells and exploited by many production wells, which results in a 0.5-m drop in GWL every year. Thus, the storage of the alluvial aquifer of Urmia plain decreases by 15.1 million cubic meter (MCM) every year. The eastern part of the aquifer is of poor quality due to its border to Lake Urmia. About 70% of groundwater is used for agricultural purposes and the rest for drinking and industry. Due to the proximity of the GWL to the ground surface, groundwater evaporation is considerable, about 8 to 10 MCM per year. The average thickness of the aquifer is about 300 m in its center and 40 to 50 m at its margins. The climate of the area is cold and humid. Watersheds are fed by rivers, precipitation, and return water. The most important rivers in the area include Barandouz Chay, Nazlo Chay, Shahar Chay, and Roze Chay rivers. The general direction of groundwater flow is from west to east [44].
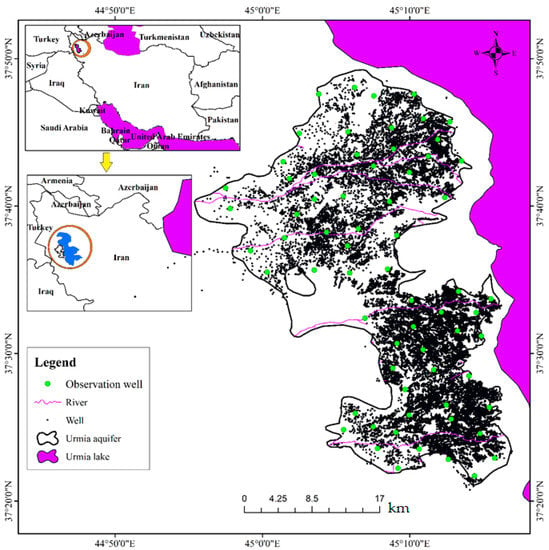
Figure 1.
Location of the study area in Iran.
2.2. Data and Research Input Patterns
To simulate the GWL, firstly, independent variables were specified. For this purpose, several effective variables, including precipitation, temperature, evaporation, groundwater exploitation, and river flow, were selected. This information was collected for a period of 16 years (2001 to 2017), with monthly time step. A summary of these data is shown in Table 2. The average precipitation (P) over the aquifer was about 18.8 mm/month. Due to many observation wells, two representative observation wells (P1 and P2) according to Table 2 were selected. One of these wells is affected by a river flow. The river flow was considered as an input variable for this observation well. The models that were developed for the two representative wells can be used for other observation wells of the aquifer. The monthly time series of input variables are depicted in Figure 2. The sinusoidal trend of the variables indicates strong seasonality. Figure 2 shows that the evaporation and precipitation increased and decreased, respectively, during the last year of the study period.

Table 2.
Summary of used variables for GWL modeling (monthly data) *.
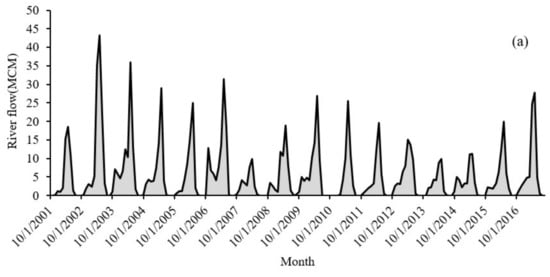
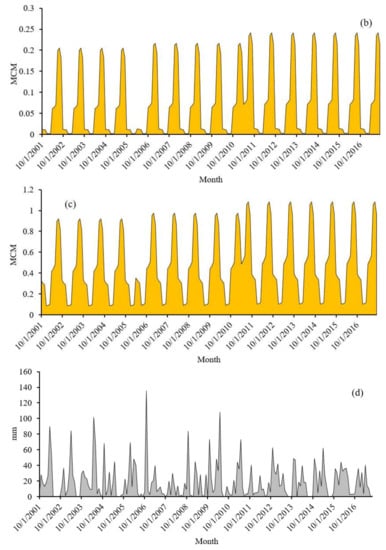
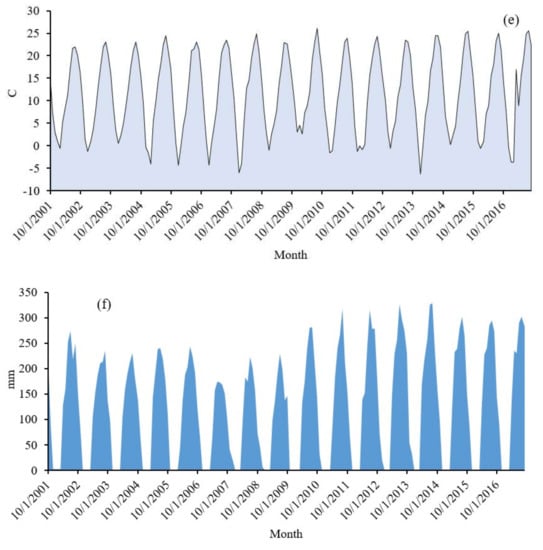
Figure 2.
Monthly time series of observed variables from 2001 to 2017, (a) river flow, (b) groundwater withdrawal of observation well P1, (c) groundwater withdrawal of observation well P2, (d) precipitation, (e) temperature, and (f) evaporation.
Input Data Patterns
Given the large number of wells in the aquifer, Thiessen polygons were used to determine the effects of the number of exploitation wells on observation wells P1 and P2. The wells within each polygon were considered to affect its GWL. Figure 3 shows the Thiessen polygons and observation wells P1, P2, and exploitation wells.
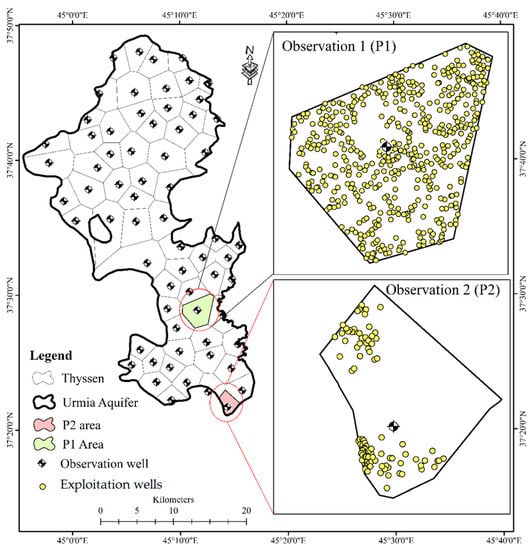
Figure 3.
Thiessen polygons for observation wells and the location of P1 and P2 wells.
Several input patterns, including different combinations of input parameters of GWL for the previous month, precipitation, evaporation, river flow, and monthly temperature, were defined to find the best combination of inputs [31,38,39]. According to Table 3 and Table 4, 11 and 16 input patterns were defined for observation wells P1 and P2, respectively, to investigate effects of input variables for model performance. These input patterns were used as input to the machine learning models to predict GWL. For observation well P2, the number of input patterns is higher than that of P1 because of also using river flow as input.

Table 3.
Input patterns for the prediction of GWL for observation well P1.

Table 4.
Input patterns for the prediction of GWL for observation well P2.
2.3. Adaptive Neuro-Fuzzy Inference System (ANFIS)
Jang (1993) introduced ANFIS by combining ANN and FIS. ANFIS does not have the limitations of ANN and FIS, such as overfitting and sensitivity to the definition of membership functions. Thus, it performs better in prediction problems [22]. The most common method for the training of ANFIS is the Sugeno-type FIS, which uses a robust learning algorithm to determine the parameters of the fuzzy system to train the model [19]. For two inputs (x1, x2) of the Sugeno-type FIS based on the {if-then} fuzzy rules, the output y of the ANFIS is
where A and B are fuzzy sets, and p, q, and r are model parameters that are determined in the training stage.
ANFIS architecture generally includes five layers (Figure 4) [22]. In the first layer, the input data pass through different membership functions, and the membership degree of input nodes to different fuzzy intervals is determined using membership functions. There are several types of membership functions, including triangular, trapezoid, Gaussian, and bell functions. Gaussian function was used in this study since it is defined by mean and standard deviation. In the second layer, which contains the rule nodes, fuzzy values are multiplied by each node, and the result is the weight of the rules. This layer uses the “AND” operator. The nodes of the third layer normalize the weight of the rules. The resultant nodes create the fuzzy-based rule outputs. The fifth layer is the last layer of the network, consisting of a single node that calculates the total output of the system. This layer transforms the results of each fuzzy rule into a non-fuzzy output using a defuzzification process.
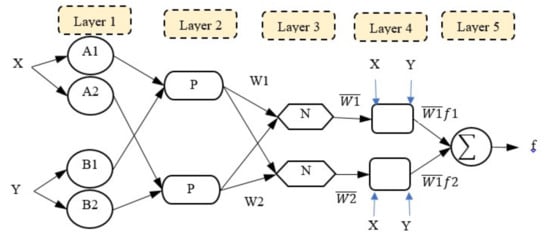
Figure 4.
Architecture of adaptive neuro-fuzzy inference system (ANFIS).
2.4. Development of the ANFIS Using Metaheuristic Optimization Algorithms
Along with the developed ANFIS model, several metaheuristic algorithms were used to train the ANFIS to develop hybrid models. According to the literature, each of these algorithms has unique features that can significantly improve the performance of the traditional ANFIS model [1,19,45,46]. The structure of ANFIS-metaheuristic algorithms hybrid models used in this study to predict GWL is depicted in Figure 5. Firstly, input patterns with different variables are given to the model, and then, the type of the fuzzy function and the ANFIS structure are determined. The developed ANFIS is trained with metaheuristic algorithms to improve results. Therefore, the objective function in this structure is to minimize the difference between the observed and predicted values. Finally, the GWL is predicted by the trained model. It should be noted that data were divided into two groups: about 70% of the data were used for training, and the rest were used for validation.
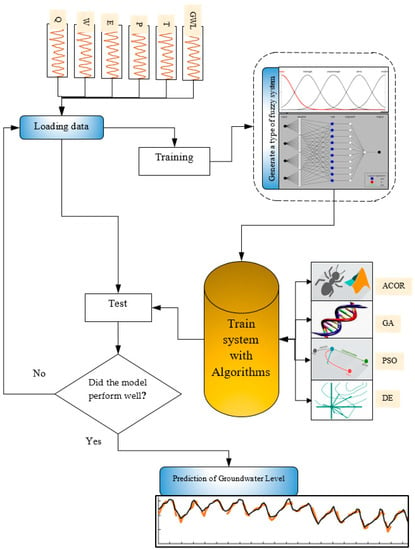
Figure 5.
Structure of ANFIS-metaheuristic algorithms hybrid models.
2.5. Particle Swarm Optimization (PSO)
PSO is a nature-inspired optimization method first introduced by Kennedy and Eberhart (1995) [47]. The PSO algorithm starts with creating a random population. Each component in nature is a different set of decision variables whose optimal values should be provided. Each component represents a vector in the problem-solving space. The algorithm includes a velocity vector in addition to the position vector, which forces the population to change their positions in the search space. The velocity consists of two vectors called p and pg. p is the best position that a particle has ever reached, and pg is the best position that another particle in its neighborhood has ever reached. In this algorithm, each particle provides a solution in each iteration. In the search for a d-dimensional space, the position of the particle i is represented by a D-dimensional vector called Xi = (Xi1, Xi2, …, XiD). The velocity of each particle is shown by a D-dimensional velocity vector called Vi = (Vi1, Vi2, …, ViD). Finally, the population moves to the optimum point using
where ω is the shrinkage factor used for convergence rate determination, r1 and r2 are random numbers between 0 and 1 with uniform distribution, N is the number of iterations, c1 is the best solution obtained by a particle, and c2 is the best solution identified by the whole population.
2.6. Genetic Algorithm (GA)
GA is a branch of AI that is based on the theory of evolution. Its theory was introduced by Rechenberg in the 1960s and developed by other researchers until 1975, when the GA was officially introduced by Holland and coworkers. GA optimization works based on considering an initial set of random solutions called populations [48]. Each individual in this population is called a chromosome, which represents a solution to the problem. This method is based on selecting individuals with higher eligibility that are more likely to survive and reproduce and reach better offspring after several generations. In the process of natural evolution, strong parents perform crossover to produce the next generation. By repeating this process and according to the principle of selecting strong parents, the next generations will result in a more favorable objective function. Decision-making variables are similar to genes, and a combination of them creates a chromosome-like string answer for the optimization problem [49].
2.7. Ant Colony Optimization for Continuous Domains (ACOR)
In the 1990s, Dorigo and coworkers introduced a new model called the ant-inspired algorithm to solve optimization problems [50]. Ants produce pheromone when they find food on their way back. Other ants follow the pheromone produced by the ants, eventually choosing a path including more pheromones, which indicates the shortest path between food and the nest. The more pheromones in a path, the more ants have selected that path for moving. The process of selecting a path by an ant is probabilistic. The ACOR algorithm uses a probability density function with a Gaussian kernel Gi (x) based on a weighted sum of several one-dimensional Gaussian functions
where , , , and are weight of the Gaussian function, standard deviation vector, mean vector, and the effective parameter, respectively. is calculated by
The higher the , the lower the rate of convergence of the algorithm. The continuous algorithm uses the concept of a solution archive: the solutions in the archive are ranked in the order of ascending error. The weight of a solution is defined as
where q is the specified parameter of the algorithm. When a new solution is added to the archive, the worst of the solutions is removed. In this study, the termination condition of the algorithm was considered to reach a certain number of iterations.
2.8. Differential Evolution (DE)
Storn (1995) introduced the DE algorithm to solve optimization problems [51]. The algorithm uses a differential operator to generate new answers exchanging information among the members of the population. All members of a population have an equal chance of being selected as a parent. The generation of the children is compared to the parent’s generation in terms of the objective function. Then, the best members enter the next generation. This method works by adjusting the mutation, crossover, and selection to reach the optimal point [52]. The most important advantages of this algorithm are its simplicity, high speed, and robustness.
2.9. Performance Evaluation Criteria
In this study, the ANFIS model itself, along with optimization methods, were used to model the GWL. Root mean square error (RMSE) (Equation (8)), mean absolute percentage error (MAPE) (Equation (9)), and Nash–Sutcliffe model efficiency coefficient (NSE) (Equation (10)) were used to evaluate the input patterns and machine learning methods as recommended in many machine leaning modeling studies.
where xo is the observed value, xp is the predicted value, and n is the number of samples. MAPE and RMSE values close to zero indicate perfect fit [53] and NSE ranges between −∞ and 1, where 1 is the optimal value, while values between 0 and 1 could be considered as acceptable [54].
3. Results
The ANFIS model was used together with the metaheuristic algorithms to improve its training performance in predicting the GWL of the two observation wells. Table 5 shows the parameters and specifications of the ANFIS and hybrid models, namely, ANFIS-GA, ANFIS-PSO, ANFIS-ACOR, and ANFIS-DE. The maximum number of iterations varied for each model, which was determined based on trial and error, and better results were not obtained for more iterations. To obtain appropriate values for each model, data were given in different ranges as initial values, and the best value for each parameter was determined. The Sugeno-type function was best for the ANFIS structure. In total, 10 rules were selected to predict GWL (8–12 were tested). Linear output function was selected as the best output function for ANFIS. The initial population for GA was selected to be 100 as the most suitable from the tested 50, 75, 100, and 125 populations. The value 0.7 was selected as the most appropriate for the mutation percentage; from a range between 0.2 and 0.6, the most appropriate value was 0.3 for the crossover percentage. After considering different ranges for other algorithms, the optimal values for the parameters of each model were selected according to Table 5. GA and PSO have the highest number of parameters, and ACOR and DE the lowest to achieve the optimal result. For example, except for the initial population selection, the ACOR algorithm can be adjusted with only two parameters of deviation distance rate and selection pressure (Table 5).

Table 5.
Used parameters of the ANFIS and ANFIS-metaheuristic algorithms hybrid models for the prediction of GWL.
3.1. Observation Well P1
The performance of the input patterns in the prediction of GWL is shown in Table 6. For the ANFIS model, there was a significant inconsistency for all input patterns. Therefore, the use of metaheuristic optimization algorithms was used to improve the ANFIS model. Input pattern L, in which all input variables were used, was the best input pattern. The ANFIS-PSO hybrid model showed best performance with MAPE, NSE, and RMSE criteria equal to 0.00019, 0.95, and 0.28 m for the test data, respectively. However, the DE and PSO algorithms were very close to each other. Regardless of the input pattern, the performance of the PSO algorithm in training the ANFIS model was the best compared to other algorithms. It can be concluded that the most suitable metaheuristic algorithms were PSO, DE, and GA, respectively, while the ACOR algorithm exerted the weakest prediction accuracy for most input patterns.

Table 6.
Evaluation criteria of studied input patterns using different models for the observation well P1.
The lowest performance was for input pattern E (temperature and evaporation). In general, the input patterns that included only two input variables had low simulation accuracy. Thus, few input variables are not capable of correctly identifying the nonlinear relationships. In contrast, input patterns with three or more variables showed good accuracy. This suggests that the participation of different input variables can correctly distinguish nonlinear relationships between the input variables and GWL. Input patterns that included lagged GWL resulted in higher prediction performance, which reveals its importance for prediction. Input patterns D, E, and G did not contain lagged GWL (previous month) as input, and, therefore, the performance of the models using these input patterns significantly decreased. For example, input pattern F, which included lagged GWL for the previous month compared to input pattern D, increased the prediction accuracy remarkably. The only difference between input patterns G and E was the presence of groundwater withdrawal. The presence of this input variable did not significantly improve the GWL prediction. Thus, it is necessary to consider input variables that have both proportional and inverse relations with the output variable. In other words, an input pattern that includes both increasing and decreasing effects on the output variable results in higher performance. In input patterns F, J, and H, temperature, evaporation, and precipitation were added to the input patterns, respectively, along with GWL and groundwater withdrawal. The results showed that evaporation, temperature, and precipitation are the most crucial input variables, respectively. For example, precipitation is essential in aquifer recharge and directly affects the GWL, while evaporation has indirect effects on GWL. As a result, the ANFIS-DE model resulted in the highest accuracy for input pattern J with MAPE, NSE, and RMSE values equal to 0.00027 m, 0.89, and 0.44 m, respectively, for the test data. Finally, the GWL for the previous month, evaporation, and temperature, were variables that improved the prediction accuracy of the models.
One of the best methods to interpret RMSE values and understand if they are acceptable for model evaluation is to evaluate them with standard deviation values (STD). It is known from previous studies that RMSE values less than half of the SD of the measured data might be considered low and acceptable [55,56]. Hence, considering the RMSE and STD values for both training and test data, the RMSE value is less than half the STD value in most scenarios. This indicates that the RMSE value for the second observation well is within the acceptable range.
Observed and predicted test data are depicted in Figure 6 for observation well P1. The results of ANFIS show that, in some months, there is a large prediction error, which can be seen for time steps 13, 37, and 49. However, improved ANFIS shows acceptable results. This be seen in the scatter plots of the hybrid models with R2 values higher than 0.9.
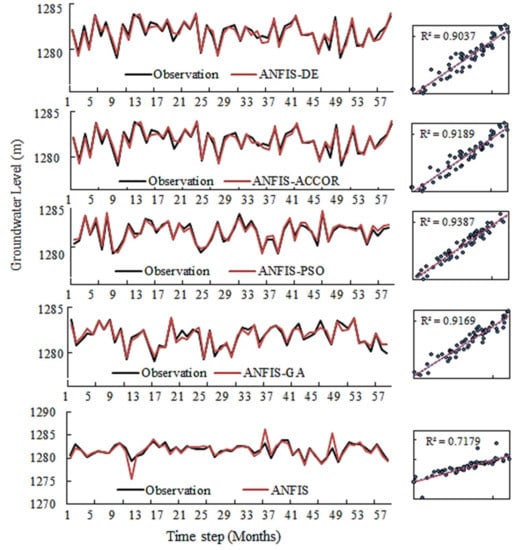
Figure 6.
Observations and predictions for well P1.
Taylor’s diagram of the selected input pattern of each model is depicted in Figure 7. The x and y axes indicate the standard deviation of the data. The quarter-circle arc shows the correlation coefficient of arbitrary and observation data, which varies from 0 to 1. The observation data lie on the x-axis, and predictions close to the x-axis indicate a strong correlation with observations. The green arcs indicate root mean square deviation (RMSD). The highest correlation with observations (>97%) was obtained using the ANFIS-PSO model. However, in other models, the correlation was lower than 95%. The standard deviation for the ANFIS-PSO model is equal to that of the observations. Results depicted in Figure 8, along with the previously obtained results, indicate that the ANFIS-PSO hybrid model leads to the best prediction performance compared to the other models.
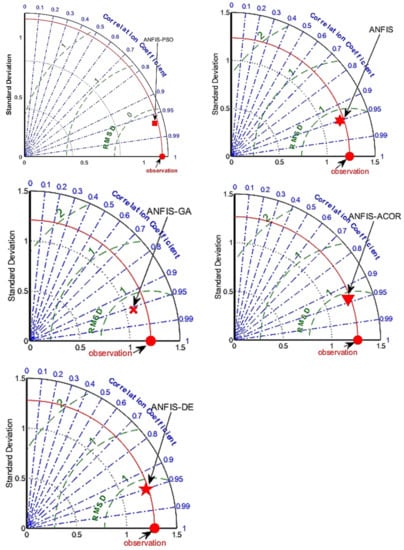
Figure 7.
Taylor’s diagram for the selected input pattern of each model for the observation well P1.
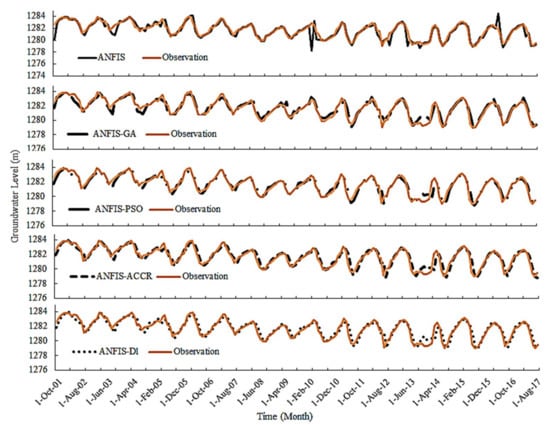
Figure 8.
Observations and predictions for well P1.
The time series prediction for the entire studied period is shown in Figure 8. The GWL has a sinusoidal trend because a large amount of groundwater is exploited in six months of the year. During the rest of the year, due to the lack of agricultural irrigation and reduced aquifer withdrawal, a rise in GWL can be observed. Since the temperature and evaporation are higher in the first half of the year, the pattern of changes in GWL, temperature, and evaporation are similar, and, therefore, the temperature and evaporation are considered as the effective variables in GWL prediction. However, given the changes in the trend of GWL throughout the study period, hybrid models gave accurate predictions. The simulation results show that for well P1 (observation well with no information on river flow), GWL dropped more than 2 m, i.e., about 0.12 m/year on average.
3.2. Observation Well P2
Observation well P2 was selected so that along with the effects of meteorological variables, the effects of the presence or absence of river flow can be investigated on GWL prediction. Therefore, the input patterns considered for this well included the river flow in addition to the same variables for well P1. The results of the evaluation criteria for the prediction of training and testing data for the ANFIS and hybrid models are given in Table 7. Unlike the results obtained from well P1, different input patterns were selected as the appropriate solution for each model. Input pattern L showed better performance for the ANFIS model. This input pattern included lagged GWL, groundwater withdrawal, river flow, precipitation, and temperature. Using this input pattern, MAPE, NSE, and RMSE were obtained equal to 0.00055 m, 0.86, and 0.79 m, respectively. Input pattern G was selected for the ANFIS-GA and ANFIS-DE hybrid models. Of the two, the DE algorithm performed better than the GA. The inputs of this input pattern included lagged GWL, evaporation, precipitation, groundwater withdrawal, and river flow. The only difference between this input pattern and the selected input pattern in the ANFIS (input pattern L) was evaporation instead of temperature. The values of MAPE, NSE, and RMSE for the test data were obtained: 0.00042 m, 0.95 , and 0.61 m for GA, respectively, as well as 0.00034 m, 0.96, and 0.53 m for DE. The input patterns N and Q were the best for the ANFIS-PSO and ANFIS-ACOR hybrid models, respectively. Input pattern N included all input variables except precipitation, while input pattern Q included all the input variables. Using the ANFIS-ACOR hybrid model, input pattern Q resulted in MAPE, NSE, and RMSE evaluation criteria equal to 0.0003 m, 0.97, and 0.45 m, respectively. The results for the observation well P2 show that for proper GWL simulation, it is necessary to consider input patterns with more than three variables. None of the input patterns with lower than four input variables resulted in proper accuracy in GWL prediction, which indicates the complex nonlinear relationships between the inputs and the output. As with the results obtained for P1, the GWL at the previous month had the highest impact on GWL prediction. In input pattern G, which was selected for the ANFIS-GA and ANFIS-DE hybrid models, the river flow was not used as input, but for other models, river flow was effective in improving the prediction accuracy.

Table 7.
Evaluation criteria of studied input patterns using different models for the observation well P2.
Input patterns E, F, J, and K did not include lagged GWL and they had the weakest prediction performance. Input pattern A, with only lagged GWL, provided a better result than input patterns E, F, J, and K.
Input patterns B and C included lagged GWL and aquifer withdrawal and either river flow or precipitation. The performance was better for input pattern B compared to input pattern C. It can be inferred that the river flow is more important than precipitation as an input. However, both variables bring similar information to the models. The best input pattern for the ANFIS-PSO model was input pattern N. Comparing the RMSE and STD values in most scenarios, especially in the selected scenario of each model, shows that RMSE values are always less than half of the STD values, which are within the acceptable range [55,56].
The time series for observations and predictions are shown in Figure 9. Similar to the results of observation well P1, the scatter plot of the ANFIS model indicated less accuracy (R2 = 0.71), while the hybrid models had an acceptable prediction performance, especially the ANFIS-ACOR hybrid model (R2 = 0.97). Therefore, input pattern Q, which includes all variables, is capable of predicting the GWL in the observation wells near the rivers with appropriate accuracy using the ANFIS-ACOR hybrid model.
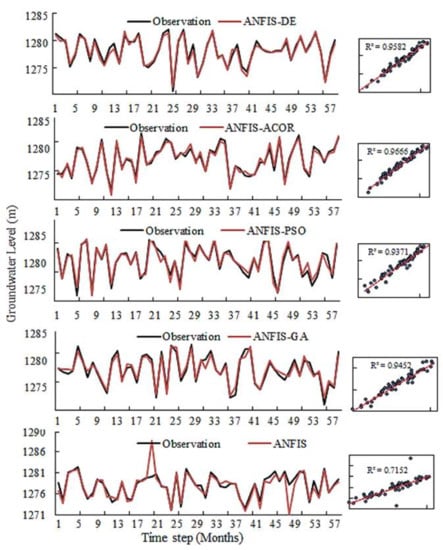
Figure 9.
Observations and predictions for well P2.
Taylor’s diagram for the selected input patterns for observation well P2 is shown in Figure 10. For the ANFIS-ACOR model, the correlation coefficient is about 0.98, which indicates efficient prediction. The standard deviation for both observations and predictions obtained by this model was similar and equal to 2.6 m. The correlation coefficient, standard deviation, and RMSD for other models were similar. The standard deviation of the ANFIS-PSO was close to that of the observation data.
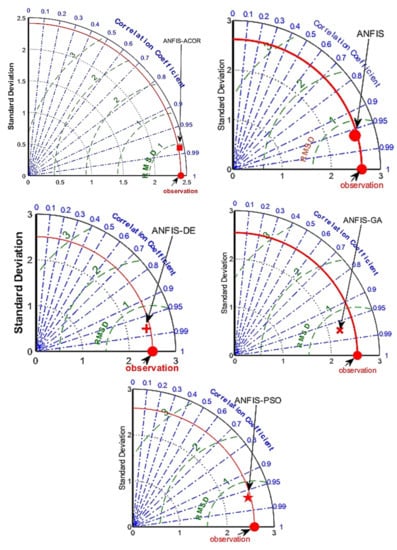
Figure 10.
Taylor’s diagram for the selected input pattern of each model for observation well P2.
The time input pattern prediction for the whole time period for all models is shown in Figure 11. Similar to the results obtained for observation well P1, hybrid models were able to recognize the trend in GWL. However, the ANFIS model resulted in high prediction errors for three time steps. As shown in the figure, these were December 2005, February 2011, and April 2014. Therefore, all models, except the ANFIS, are capable of a reliable GWL prediction in the study period. The simulation results show that for well P2 (observation well with river flow as an independent input variable), GWL dropped more than 8 m, i.e., ca. 0.57 m/year on average. Therefore, the annual drop in this area is more than that of the area of the observation well P1.
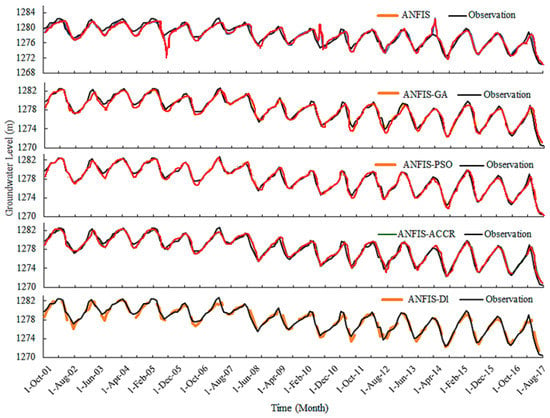
Figure 11.
Observation and prediction data of the studied period for the well P2.
4. Discussion
Accurate prediction of GWL is important to sustainably manage groundwater. Considering the river flow near the wells as an input parameter improved the prediction accuracy. This is consistent with the results of Moosavi et al. (2013) and Mirzavand et al. (2015). However, other studies have shown that the interaction between the surface water (stream flow) and aquifer improves the accuracy of groundwater simulation (Kim et al., 2020; Chunn et al., 2020; Tang et al., 2022) [57,58,59]. The findings of this study showed that although ANFIS was able to predict GWL values to some extent, it sometimes provided irrational values. The optimization algorithms used showed that the ANFIS hybrid models performed better than the ANFIS model. These results are consistent with the results of Ghordoyee Milan et al. (2021) and Kayhomayoon et al. (2021) who showed better performance using hybrid models to predict GWL. Additionally, the results are in line with the results of Seifi et al. (2019) who showed that ANFIS hybrid models had better performance in predicting GWL.
Among the studied models, the best model was the PSO algorithm. This is consistent with the results of Ghasemi et al. (2016) and Alarifi et al. (2019) [60,61]. It is necessary to evaluate various machine learning algorithms to determine the most appropriate one in specific research fields [62]. Applying such algorithms in other fields of science has shown that they can be considered an appropriate approach to improve many machine learning models such as ANN and ANFIS (e.g., Milan et al., 2021). Hybrid models result in reliable prediction performance of GWL. Moreover, the results showed that considering temperature and precipitation along with the river flow as input variables are effective in the performance of GWL prediction. In this situation, the changes in GWL can be predicted by studying climate change or changes in river flow.
5. Conclusions
Given the importance of GWL in assessing the quantitative status of aquifers for decision-making problems, from the perspective of water resources managers, it is essential to develop predictive models to investigate the status of groundwater resources for this purpose, ANFIS and hybrid ANFIS-metaheuristic algorithms were studied to simulate GWL in an aquifer. Several input variables, including the GWL at the previous month, precipitation, temperature, evaporation, and withdrawal, were considered using experimental input patterns. This approach was performed for two observation wells. For the observation well P1, an input pattern in which all input variables were used gave the best results using the ANFIS-PSO hybrid model with MAPE, RMSE, and NSE values equal to 0.00019, 0.95, and 0.28 m for the test data, respectively. For the observation well P2, river flow was added to the input patterns where the ANFIS-ACOR model showed the best performance with MAPE, NSE, and RMSE of 0.0003, 0.97, and 0.45 m for test data, respectively.
None of the input patterns with less than four input variables, showed acceptable performance in predicting the GWL. Results also showed that river flow generally can increase the prediction accuracy. Finally, results showed appropriate performance of the hybrid models for GWL prediction. This approach can be used in other areas with limited input data to predict GWL. The use of metaheuristic algorithms proposed in this study increased the prediction performance. Considering the uncertainty in input variables, evaluating new algorithms to improve the results, and investigating the effects of climate change on GWL are among the research topics that are suggested for future investigations.
Author Contributions
Conceptualization: Z.K., S.G.M. and F.B.; data collection: Z.K., S.G.M. and F.B.; formal analysis: Z.K., S.G.M., F.B. and N.A.A.; validation: Z.K., S.G.M. and F.B.; supervision: S.G.M. and R.B.; writing—original draft: All authors; funding acquisition: R.B. and S.G.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study will be available on interested request from the first corresponding author.
Acknowledgments
This study was supported by the MECW (Middle East in the Contemporary World) project at the Centre for Advanced Middle Eastern Studies, Lund University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kayhomayoon, Z.; Milan, S.G.; Azar, N.A.; Moghaddam, H.K. A New Approach for Regional Groundwater Level Simulation: Clustering, Simulation, and Optimization. Nat. Resour. Res. 2021, 30, 4165–4185. [Google Scholar] [CrossRef]
- Javadi, S.; Saatsaz, M.; Shahdany, S.M.H.; Neshat, A.; Milan, S.G.; Akbari, S. A new hybrid framework of site selection for groundwater recharge. Geosci. Front. 2021, 12, 101144. [Google Scholar] [CrossRef]
- Lee, S.; Lee, K.-K.; Yoon, H. Using artificial neural network models for groundwater level forecasting and assessment of the relative impacts of influencing factors. Appl. Hydrogeol. 2019, 27, 567–579. [Google Scholar] [CrossRef]
- Rajaee, T.; Ebrahimi, H.; Nourani, V. A review of the artificial intelligence methods in groundwater level modeling. J. Hydrol. 2019, 572, 336–351. [Google Scholar] [CrossRef]
- Butler, J.J., Jr.; Stotler, R.L.; Whittemore, D.O.; Reboulet, E.C. Interpretation of water level changes in the High Plains aquifer in western Kansas. Groundwater 2013, 51, 180–190. [Google Scholar] [CrossRef]
- Kardan Moghaddam, H.; Ghordoyee Milan, S.; Kayhomayoon, Z.; Arya Azar, N. The prediction of aquifer groundwater level based on spatial clustering approach using machine learning. Environ. Monit. Assess. 2021, 193, 173. [Google Scholar] [CrossRef] [PubMed]
- Kayhomayoon, Z.; Azar, N.A.; Milan, S.G.; Moghaddam, H.K.; Berndtsson, R. Novel approach for predicting groundwater storage loss using machine learning. J. Environ. Manag 2021, 296, 113237. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Lu, W.; Long, Y.; Li, P. Application and comparison of two prediction models for groundwater levels: A case study in Western Jilin Province, China. J. Arid Environ. 2009, 73, 487–492. [Google Scholar] [CrossRef]
- Brunner, P.A.; Simmons, C.T. HydroGeoSphere: A Fully Integrated, Physically Based Hydrological Model. Ground Water 2012, 50, 170–176. [Google Scholar] [CrossRef]
- Milan, S.G.; Roozbahani, A.; Banihabib, M.E. Fuzzy optimization model and fuzzy inference system for conjunctive use of surface and groundwater resources. J. Hydrol. 2018, 566, 421–434. [Google Scholar] [CrossRef]
- Mirarabi, A.; Nassery, H.R.; Nakhaei, M.; Adamowski, J.; Akbarzadeh, A.H.; Alijani, F. Evaluation of data-driven models (SVR and ANN) for groundwater-level prediction in confined and unconfined systems. Environ. Earth Sci. 2019, 78, 489. [Google Scholar] [CrossRef]
- Nadiri, A.A.; Naderi, K.; Khatibi, R.; Gharekhani, M. Modelling groundwater level variations by learning from multiple models using fuzzy logic. Hydrol. Sci. J. 2019, 64, 210–226. [Google Scholar] [CrossRef]
- Adamowski, J.; Chan, H.F.; Prasher, S.O.; Ozga-Zielinski, B.; Sliusarieva, A. Comparison of multiple linear and nonlinear regression, autoregressive integrated moving average, artificial neural network, and wavelet artificial neural network methods for urban water demand forecasting in Montreal, Canada. Water Resour. Res. 2012, 48, 1–14. [Google Scholar] [CrossRef]
- PPham, B.T.; Jaafari, A.; Avand, M.; Al-Ansari, N.; Dinh Du, T.; Yen, H.P.H.; Phong, T.V.; Nguyen, D.H.; Le, H.V.; Mafi-Gholami, D.; et al. Performance Evaluation of Machine Learning Methods for Forest Fire Modeling and Prediction. Symmetry 2020, 12, 1022. [Google Scholar] [CrossRef]
- Jaafari, A.; Pazhouhan, I.; Bettinger, P. Machine Learning Modeling of Forest Road Construction Costs. Forests 2021, 12, 1169. [Google Scholar] [CrossRef]
- Azar, N.A.; Kardan, N.; Ghordoyee Milan, S. Developing the artificial neural network–evolutionary algorithms hybrid models (ANN–EA) to predict the daily evaporation from dam reservoirs. Eng. Comput. 2021, 37, 1–9. [Google Scholar] [CrossRef]
- Asefpour Vakilian, K. Machine learning improves our knowledge about miRNA functions towards plant abiotic stresses. Sci. Rep. 2020, 10, 3041. [Google Scholar] [CrossRef]
- Vakilian, K.A.; Massah, J. A fuzzy-based decision making software for enzymatic electrochemical nitrate biosensors. Chemom. Intell. Lab. Syst. 2018, 177, 55–63. [Google Scholar] [CrossRef]
- Milan, S.G.; Roozbahani, A.; Azar, N.A.; Javadi, S. Development of adaptive neuro fuzzy inference system–evolutionary algo-rithms hybrid models (ANFIS-EA) for prediction of optimal groundwater exploitation. J. Hydrol. 2021, 598, 126258. [Google Scholar] [CrossRef]
- Roozbahani, A.; Ebrahimi, E.; Banihabib, M.E. A Framework for Ground Water Management Based on Bayesian Network and MCDM Techniques. Water Resour. Manag. 2018, 32, 4985–5005. [Google Scholar] [CrossRef]
- Nie, S.; Bian, J.; Wan, H.; Sun, X.; Zhang, B. Simulation and uncertainty analysis for groundwater levels using radial basis function neural network and support vector machine models. J. Water Supply Res. Technol. 2017, 66, 15–24. [Google Scholar] [CrossRef]
- Jang, J.-S.R. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Yan, H.; Zou, Z.; Wang, H. Adaptive neuro fuzzy inference system for classification of water quality status. J. Environ. Sci. 2010, 22, 1891–1896. [Google Scholar] [CrossRef]
- Keskin, M.E.; Taylan, D.; Terzi, O. Adaptive neural-based fuzzy inference system (ANFIS) approach for modelling hydrological time series. Hydrol. Sci. J. 2006, 51, 588–598. [Google Scholar] [CrossRef]
- Jaafari, A.; Termeh, S.V.R.; Bui, D.T. Genetic and firefly metaheuristic algorithms for an optimized neuro-fuzzy prediction modeling of wildfire probability. J. Environ. Manag. 2019, 243, 358–369. [Google Scholar] [CrossRef]
- Kisi, O.; Azad, A.; Kashi, H.; Saeedian, A.; Hashemi, S.A.A.; Ghorbani, S. Modeling Groundwater Quality Parameters Using Hybrid Neuro-Fuzzy Methods. Water Resour. Manag. 2019, 33, 847–861. [Google Scholar] [CrossRef]
- Peyghami, M.R.; Khanduzi, R. Novel MLP Neural Network with Hybrid Tabu Search Algorithm. Neural Netw. World 2013, 23, 255–270. [Google Scholar] [CrossRef][Green Version]
- Seifi, A.; Ehteram, M.; Singh, V.P.; Mosavi, A. Modeling and Uncertainty Analysis of Groundwater Level Using Six Evolutionary Optimization Algorithms Hybridized with ANFIS, SVM, and ANN. Sustainability 2020, 12, 4023. [Google Scholar] [CrossRef]
- Kholghi, M.; Hosseini, S.M. Comparison of Groundwater Level Estimation Using Neuro-fuzzy and Ordinary Kriging. Environ. Model. Assess. 2009, 14, 729–737. [Google Scholar] [CrossRef]
- Jalalkamali, A.; Sedghi, H.; Manshouri, M. Monthly groundwater level prediction using ANN and neuro-fuzzy models: A case study on Kerman plain, Iran. J. Hydroinformatics 2011, 13, 867–876. [Google Scholar] [CrossRef]
- Sreekanth, P.D.; Sreedevi, P.D.; Ahmed, S.; Geethanjali, N. Comparison of FFNN and ANFIS models for estimating groundwater level. Environ. Earth Sci. 2011, 62, 1301–1310. [Google Scholar] [CrossRef]
- Kisi, O.; Shiri, J. Wavelet and neuro-fuzzy conjunction model for predicting water table depth fluctuations. Hydrol. Res. 2012, 43, 286–300. [Google Scholar] [CrossRef]
- Shirmohammadi, B.; Vafakhah, M.; Moosavi, V.; Moghaddamnia, A. Application of Several Data-Driven Techniques for Predicting Groundwater Level. Water Resour. Manag. 2013, 27, 419–432. [Google Scholar] [CrossRef]
- Shiri, J.; Kisi, O.; Yoon, H.; Lee, K.K.; Nazemi, A.H. Predicting groundwater level fluctuations with meteorological effect implications—A comparative study among soft computing techniques. Comput. Geosci. 2013, 56, 32–44. [Google Scholar] [CrossRef]
- Fallah-Mehdipour, E.; Haddad, O.B.; Mariño, M.A. Prediction and simulation of monthly groundwater levels by genetic pro-gramming. J. Hydro-Environ. Res. 2013, 7, 253–260. [Google Scholar] [CrossRef]
- Moosavi, V.; Vafakhah, M.; Shirmohammadi, B.; Behnia, N. A Wavelet-ANFIS Hybrid Model for Groundwater Level Forecasting for Different Prediction Periods. Water Resour. Manag. 2013, 27, 1301–1321. [Google Scholar] [CrossRef]
- Mirzavand, M.; Khoshnevisan, B.; Shamshirband, S.; Kişi, O.; Ahmad, R.; Akib, S. Retracted Article: Evaluating groundwater level fluctuation by support vector regression and neuro-fuzzy methods: A comparative study. Nat. Hazards 2015, 102, 1611–1612. [Google Scholar] [CrossRef]
- Gong, Y.; Zhang, Y.; Lan, S.; Wang, H. A Comparative Study of Artificial Neural Networks, Support Vector Machines and Adaptive Neuro Fuzzy Inference System for Forecasting Groundwater Levels near Lake Okeechobee, Florida. Water Resour. Manag. 2016, 30, 375–391. [Google Scholar] [CrossRef]
- Zare, M.; Koch, M. Groundwater level fluctuations simulation and prediction by ANFIS- and hybrid Wavelet-ANFIS/Fuzzy C-Means (FCM) clustering models: Application to the Miandarband plain. J. Hydro-Environ. Res. 2018, 18, 63–76. [Google Scholar] [CrossRef]
- Azad, A.; Manoochehri, M.; Kashi, H.; Farzin, S.; Karami, H.; Nourani, V.; Shiri, J. Comparative evaluation of intelligent algorithms to improve adaptive neuro-fuzzy inference system performance in precipitation modelling. J. Hydrol. 2019, 571, 214–224. [Google Scholar] [CrossRef]
- Azad, A.; Karami, H.; Farzin, S.; Saeedian, A.; Kashi, H.; Sayyahi, F. Prediction of Water Quality Parameters Using ANFIS Optimized by Intelligence Algorithms (Case Study: Gorganrood River). KSCE J. Civ. Eng. 2018, 22, 2206–2213. [Google Scholar] [CrossRef]
- Yang, H.; Hasanipanah, M.; Tahir, M.M.; Bui, D.T. Intelligent prediction of blasting-induced ground vibration using ANFIS op-timized by GA and PSO. Nat. Resour. Res. 2020, 29, 739–750. [Google Scholar] [CrossRef]
- Arya Azar, N.; Ghordoyee Milan, S.; Kayhomayoon, Z. Predicting monthly evaporation from dam reservoirs using LS-SVR and ANFIS optimized by Harris hawks optimization algorithm. Environ. Monit. Assess. 2021, 193, 695. [Google Scholar] [CrossRef] [PubMed]
- Ministry of Energy. Iran Water Resources Management Reports; Ministry of Energy: Tehran, Iran, 2017. [Google Scholar]
- Paryani, S.; Neshat, A.; Javadi, S.; Pradhan, B. Comparative performance of new hybrid ANFIS models in landslide susceptibility mapping. Nat. Hazards 2020, 103, 1961–1988. [Google Scholar] [CrossRef]
- Ahmadlou, M.; Karimi, M.; Alizadeh, S.; Shirzadi, A.; Parvinnejhad, D.; Shahabi, H.; Panahi, M. Flood susceptibility assessment using integration of adaptive network-based fuzzy inference system (ANFIS) and biogeography-based optimization (BBO) and BAT algorithms (BA). Geocarto Int. 2019, 34, 1252–1272. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks 1995, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Banzhaf, W.; Nordin, P.; Keller, R.E.; Francone, F.D. Genetic Programming: An Introduction: On the Automatic Evolution of Computer Programs and Its Applications; Morgan Kaufmann Publishers Inc.: Burlington, MA, USA, 1998. [Google Scholar]
- Musharavati, F.; Hamouda, A.S. Modified genetic algorithms for manufacturing process planning in multiple parts manufacturing lines. Expert Syst. Appl. 2011, 38, 10770–10779. [Google Scholar] [CrossRef]
- Socha, K.; Dorigo, M. Ant colony optimization for continuous domains. Eur. J. Oper. Res. 2008, 185, 1155–1173. [Google Scholar] [CrossRef]
- Storn, R. Differrential Evolution—A Simple and Efficient Adaptive Scheme for Global Optimization over Continuous Spaces; Technical Report; International Computer Science Institute: Berkeley, CA, USA, 1995; Volume 11. [Google Scholar]
- D’Ambrosio, A.; Mazzeo, G.; Iorio, C.; Siciliano, R. A differential evolution algorithm for finding the median ranking under the Kemeny axiomatic approach. Comput. Oper. Res. 2017, 82, 126–138. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. Am. Soc. Agric. Biol. Eng. 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Singh, J.; Knapp, H.V.; Arnold, J.G.; Demissie, M. Hydrological modeling of the Iroquois river watershed using HSPF and SWAT. J. Am. Water Resour. Assoc. 2005, 41, 343–360. [Google Scholar] [CrossRef]
- Kastridis, A.; Theodosiou, G.; Fotiadis, G. Investigation of Flood Management and Mitigation Measures in Ungauged NATURA Protected Watersheds. Hydrology 2021, 8, 170. [Google Scholar] [CrossRef]
- Kim, N.W.; Chung, I.M.; Won, Y.S.; Arnold, J.G. Development and application of the integrated SWAT–MODFLOW model. J. Hydrol. 2008, 356, 1–16. [Google Scholar] [CrossRef]
- Chunn, D.; Faramarzi, M.; Smerdon, B.; Alessi, D.S. Application of an Integrated SWAT–MODFLOW Model to Evaluate Potential Impacts of Climate Change and Water Withdrawals on Groundwater–Surface Water Interactions in West-Central Alberta. Water 2019, 11, 110. [Google Scholar] [CrossRef]
- Tang, R.; Han, X.; Wang, X.; Huang, S.; Yan, Y.; Huang, J.; Shen, T.; Wang, Y.; Liu, J. Optimized Main Ditch Water Control for Agriculture in Northern Huaihe River Plain, Anhui Province, China, Using MODFLOW Groundwater Table Simulations. Water 2022, 14, 29. [Google Scholar] [CrossRef]
- Ghasemi, E.; Kalhori, H.; Bagherpour, R. A new hybrid ANFIS–PSO model for prediction of peak particle velocity due to bench blasting. Eng. Comput. 2016, 32, 607–614. [Google Scholar] [CrossRef]
- Alarifi, I.M.; Nguyen, H.M.; Bakhtiyari, A.N.; Asadi, A. Feasibility of ANFIS-PSO and ANFIS-GA Models in Predicting Thermophysical Properties of Al2O3-MWCNT/Oil Hybrid Nanofluid. Materials 2019, 12, 3628. [Google Scholar] [CrossRef] [PubMed]
- Karamoutsou, L.; Psilovikos, A. Deep Learning in Water Resources Management: The Case Study of Kastoria Lake in Greece. Water 2021, 13, 3364. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).