Flow Discharge Prediction Study Using a CFD-Based Numerical Model and Gene Expression Programming
Abstract
:1. Introduction
2. Materials and Methods Methods
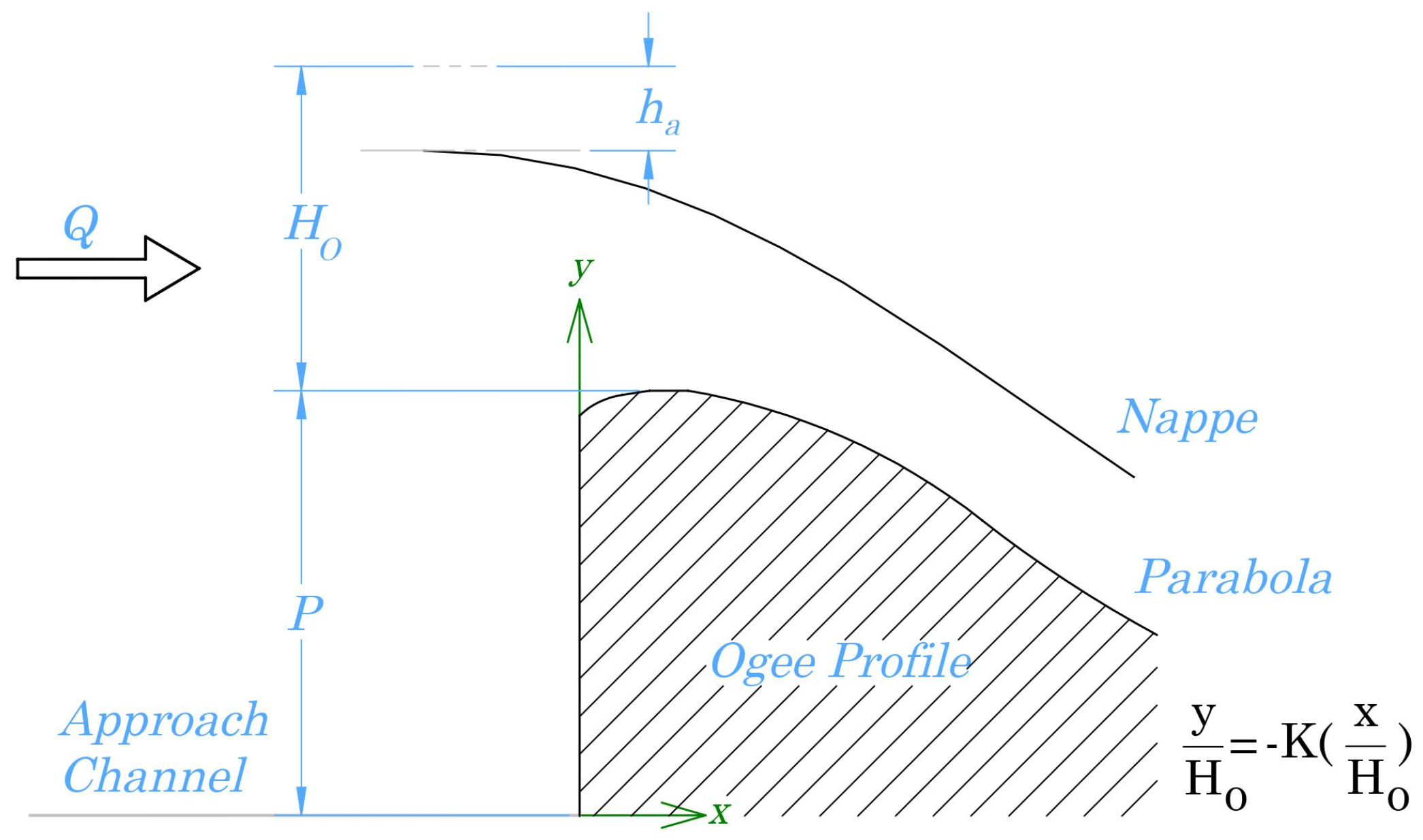
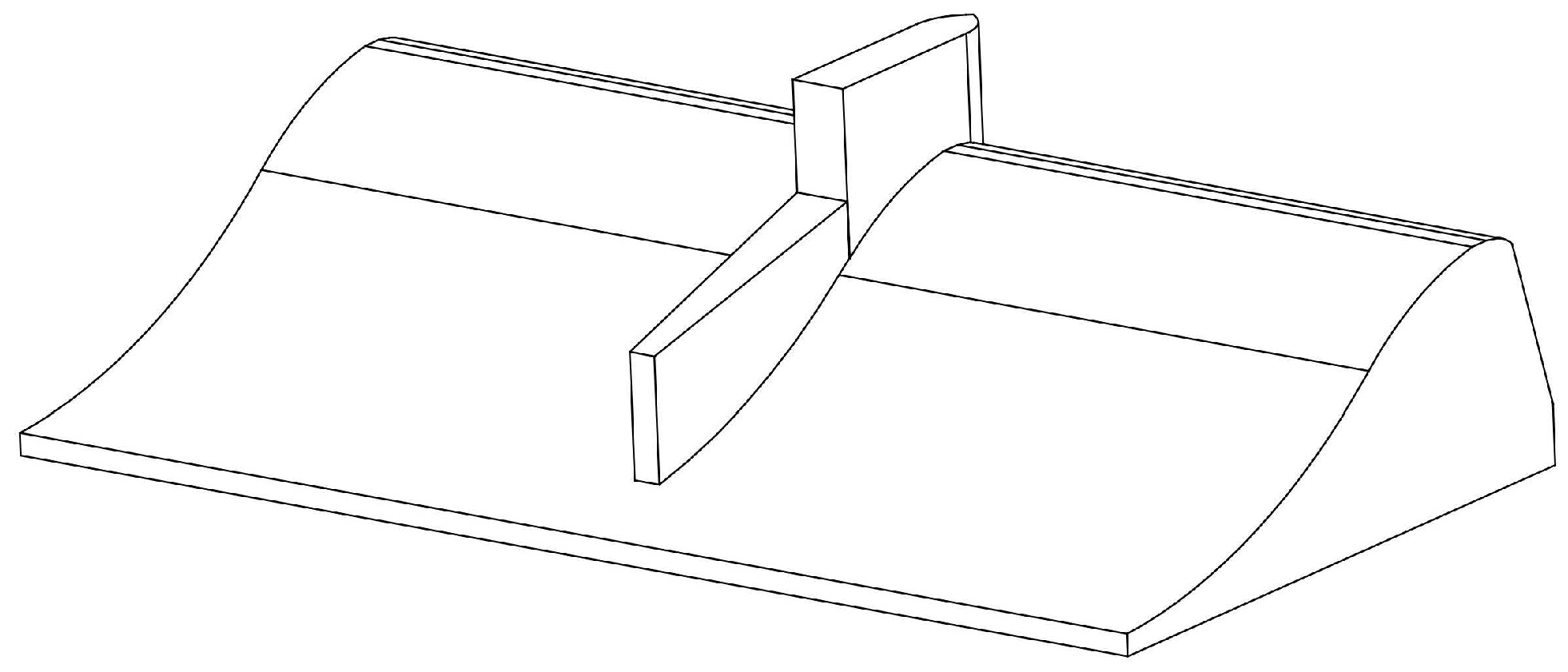
2.1. Flow-3D Numerical Modeling
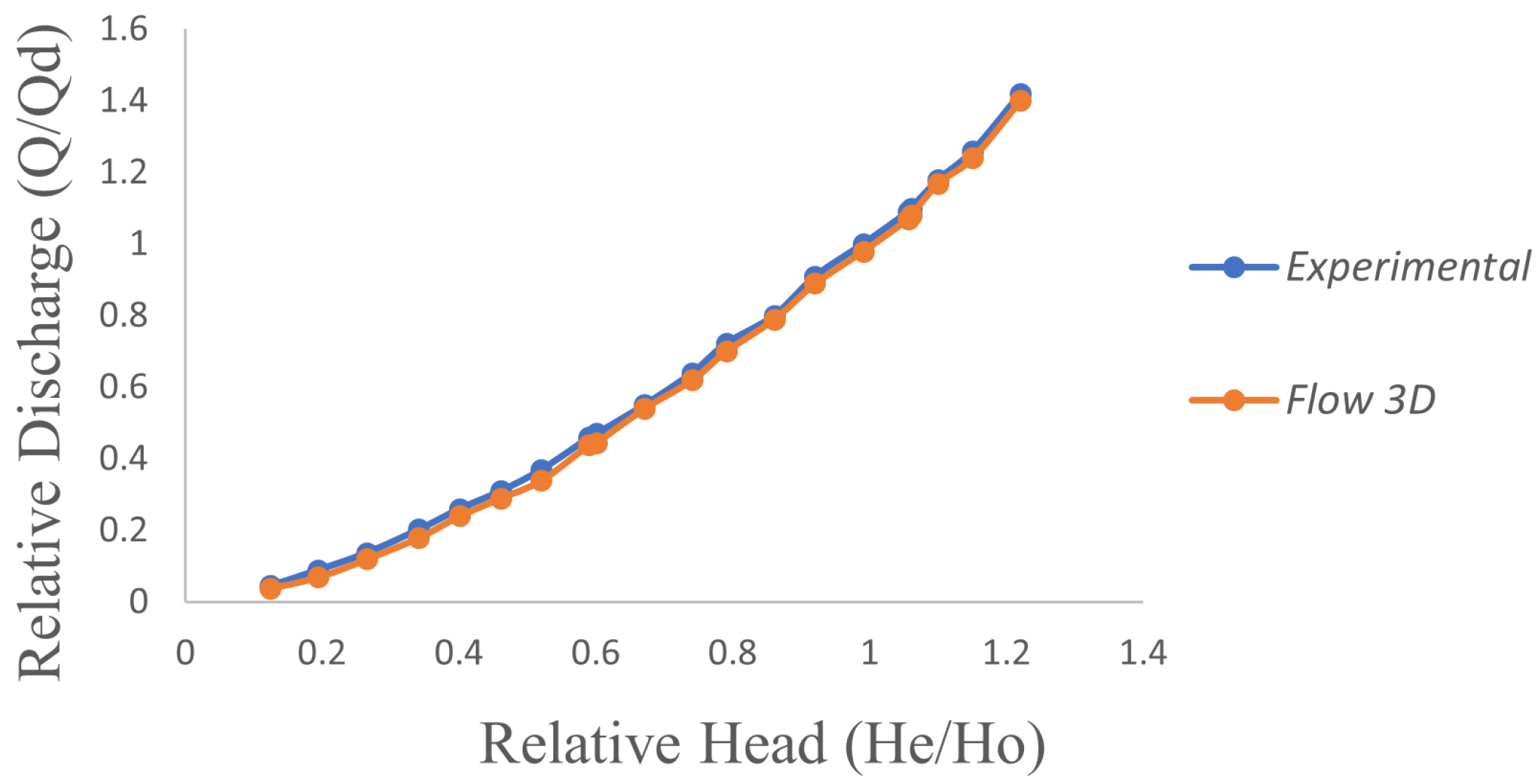
Estimation of Uncertainty in a CFD Application
2.2. Gene Expression Programming Approaches
Performance Criteria
3. Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| GEP | Gene expression Programming |
| RMSE | Root Mean Square Error |
| Coefficient of Determination | |
| MAE | Mean Absolute Error |
Appendix A
| Case Number | Equation |
|---|---|
| Case 1 | |
| Case 2 | |
| Case 3 | |
| Case 4 | |
| Case 5 | |
| Case 6 | |
| Case 7 | |
| Case 8 | |
| Case 9 | |
| Case 10 |
References
- Demeke, G.K.; Asfaw, D.H.; Shiferaw, Y.S. 3D hydrodynamic modelling enhances the design of Tendaho Dam Spillway, Ethiopia. Water 2019, 11, 82. [Google Scholar] [CrossRef] [Green Version]
- Heravi, G.; Salehi, M.M.; Rostami, M. Identifying cost-optimal options for a typical residential nearly zero energy building’s design in developing countries. Clean Technol. Environ. Policy 2020, 22, 2107–2128. [Google Scholar] [CrossRef]
- Korzeniowski, A.; Ghorbani, N. Put Options with Linear Investment for Hull-White Interest Rates. J. Math. Financ. 2021, 11, 152. [Google Scholar] [CrossRef]
- Amini, E.; Golbaz, D.; Asadi, R.; Nasiri, M.; Ceylan, O.; Majidi Nezhad, M.; Neshat, M. A Comparative Study of Metaheuristic Algorithms for Wave Energy Converter Power Take-Off Optimisation: A Case Study for Eastern Australia. J. Mar. Sci. Eng. 2021, 9, 490. [Google Scholar] [CrossRef]
- Boiten, W. Flow measurement structures. Flow Meas. Instrum. 2002, 13, 203–207. [Google Scholar] [CrossRef]
- Tafazzoli, S.; Shafaghat, R.; Alamian, R. Numerical investigation on the multi-body hydrodynamic interactions under Caspian Sea environmental conditions. Ocean. Eng. 2021, 232, 109048. [Google Scholar] [CrossRef]
- Mazaheri, P.; Asgarian, B.; Gholami, H. Assessment of strengthening, modification, and repair techniques for aging fixed offshore steel platforms. Appl. Ocean. Res. 2021, 110, 102612. [Google Scholar] [CrossRef]
- US Department of the Interior, Bureau of Reclamation. Design of Small Dams; US Department of the Interior: Washington, DC, USA, 1987. [Google Scholar]
- Ho, D.; Riddette, K. Application of computational fluid dynamics to evaluate hydraulic performance of spillways in Australia. Aust. J. Civ. Eng. 2010, 6, 81–104. [Google Scholar] [CrossRef]
- Tafazzoli, S.; Shafaghat, R.; Alamian, R. Optimization study of a catenary mooring system for a spar floating wind turbine based on its hydrodynamic responses. J. Eng. Marit. Environ. 2021, 235, 657–674. [Google Scholar] [CrossRef]
- Choupin, O.; Henriksen, M.; Etemad-Shahidi, A.; Tomlinson, R. Breaking-down and parameterising wave energy converter costs using the CapEx and similitude methods. Energies 2021, 14, 902. [Google Scholar] [CrossRef]
- Salazar, F.; San-Mauro, J.; Celigueta, M.Á.; Oñate, E. Shockwaves in spillways with the particle finite element method. Comput. Part. Mech. 2020, 7, 87–99. [Google Scholar] [CrossRef]
- Ghorbani, N.; Korzeniowski, A. Adaptive Risk Hedging for Call Options under Cox-Ingersoll- Ross Interest Rates. J. Math. Financ. 2020, 10, 697–704. [Google Scholar] [CrossRef]
- Choupin, O.; Andutta, F.P.; Etemad-Shahidi, A.; Tomlinson, R. A decision-making process for wave energy converter and location pairing. Renew. Sustain. Energy Rev. 2021, 147, 111225. [Google Scholar] [CrossRef]
- Savage, B.M.; Johnson, M.C. Flow over ogee spillway: Physical and numerical model case study. J. Hydraul. Eng. 2001, 127, 640–649. [Google Scholar] [CrossRef]
- Kim, D.G.; Park, J.H. Analysis of flow structure over ogee-spillway in consideration of scale and roughness effects by using CFD model. KSCE J. Civ. Eng. 2005, 9, 161–169. [Google Scholar] [CrossRef]
- Peltier, Y.; Dewals, B.; Archambeau, P.; Pirotton, M.; Erpicum, S. Pressure and velocity on an ogee spillway crest operating at high head ratio: Experimental measurements and validation. J. Hydro-Environ. Res. 2018, 19, 128–136. [Google Scholar] [CrossRef]
- Jahad, U.; Al-Ameri, R.; Chua, L.; Das, S. Investigating the Effects of Geometry on the Flow Characteristics and Energy Dissipation of Stepped Spillway Using Two-Dimensional Flow Modelling. In Proceedings of the International Association for Hydro-Environment Engineering and Research. Asia Pacific Division Congress, Yogyakarta, Indonesia, 2–5 September 2018; pp. 289–296. [Google Scholar]
- Aydin, M.C.; Isik, E.; Ulu, A.E. Numerical modeling of spillway aerators in high-head dams. Appl. Water Sci. 2020, 10, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Wan, W.; Liu, B.; Raza, A. Numerical prediction and risk analysis of hydraulic cavitation damage in a High-Speed-Flow spillway. Shock Vib. 2018, 2018, 1817307. [Google Scholar] [CrossRef]
- Ghanbari, R.; Heidarnejad, M. Experimental and numerical analysis of flow hydraulics in triangular and rectangular piano key weirs. Water Sci. 2020, 34, 32–38. [Google Scholar] [CrossRef] [Green Version]
- Bayon, A.; Valero, D.; García-Bartual, R.; López-Jiménez, P.A. Performance assessment of OpenFOAM and FLOW-3D in the numerical modeling of a low Reynolds number hydraulic jump. Environ. Model. Softw. 2016, 80, 322–335. [Google Scholar] [CrossRef]
- Valero, D.; Bung, D.B.; Crookston, B.M. Energy dissipation of a Type III basin under design and adverse conditions for stepped and smooth spillways. J. Hydraul. Eng. 2018, 144, 04018036. [Google Scholar] [CrossRef]
- Ferreira, C. Gene expression programming: A new adaptive algorithm for solving problems. arXiv 2001, arXiv:cs/0102027. [Google Scholar]
- Yildiz, A.; Yarar, A.; Kumcu, S.Y.; Marti, A.I. Numerical and ANFIS modeling of flow over an ogee-crested spillway. Appl. Water Sci. 2020, 10, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Ebtehaj, I.; Bonakdari, H.; Zaji, A.H.; Azimi, H.; Sharifi, A. Gene expression programming to predict the discharge coefficient in rectangular side weirs. Appl. Soft Comput. 2015, 35, 618–628. [Google Scholar] [CrossRef]
- Kisi, O.; Emiroglu, M.E.; Bilhan, O.; Guven, A. Prediction of lateral outflow over triangular labyrinth side weirs under subcritical conditions using soft computing approaches. Expert Syst. Appl. 2012, 39, 3454–3460. [Google Scholar] [CrossRef]
- Salmasi, F. Effect of downstream apron elevation and downstream submergence in discharge coefficient of ogee weir. ISH J. Hydraul. Eng. 2018, 27, 375–384. [Google Scholar] [CrossRef]
- Khan, M.; Azamathulla, H.M.; Tufail, M. Gene-expression programming to predict pier scour depth using laboratory data. J. Hydroinform. 2012, 14, 628–645. [Google Scholar] [CrossRef] [Green Version]
- Roushangar, K.; Akhgar, S.; Salmasi, F.; Shiri, J. Modeling energy dissipation over stepped spillways using machine learning approaches. J. Hydrol. 2014, 508, 254–265. [Google Scholar] [CrossRef]
- Bagatur, T.; Onen, F. Computation of design coefficients in ogee-crested spillway structure using GEP and regression models. KSCE J. Civ. Eng. 2016, 20, 951–959. [Google Scholar] [CrossRef]
- Bertone, E.; Stewart, R.A.; Zhang, H.; Veal, C. Data-driven recursive input–output multivariate statistical forecasting model: Case of DO concentration prediction in Advancetown Lake, Australia. J. Hydroinform. 2015, 17, 817–833. [Google Scholar] [CrossRef]
- Esmaeilpour, M.; Ghanbarian, B.; Liang, F.; Liu, H.H. Scale-dependent permeability and formation factor in porous media: Applications of percolation theory. Fuel 2021, 301, 121090. [Google Scholar] [CrossRef]
- Azita, M.; Mohammad, I. A Blockchain Information Management Framework for Construction Safety. In Proceedings of the International Conference on Computing in Civil Engineering, Orlando, FL, USA, 12–14 September 2021. [Google Scholar]
- Rahimi, Z.; Othman, F.; Shariff, A.R.M. Improving geometric construction of high resolution SAR images using Kriging-based surrogate modelling in mountainous terrain of Malaysia. Int. J. Remote Sens. 2021, 42, 8624–8639. [Google Scholar] [CrossRef]
- A GNSS-based weather forecasting approach using Nonlinear Auto Regressive Approach with Exogenous Input (NARX). J. Atmos. Sol. Terr. Phys. 2018, 178, 74–84. [CrossRef]
- Mohammadrezapour, O.; Piri, J.; Kisi, O. Comparison of SVM, ANFIS and GEP in modeling monthly potential evapotranspiration in an arid region (Case study: Sistan and Baluchestan Province, Iran). Water Supply 2019, 19, 392–403. [Google Scholar] [CrossRef] [Green Version]
- Roushangar, K.; Alami, M.T.; Saghebian, S.M. Modeling open channel flow resistance with dune bedform via heuristic and nonlinear approaches. J. Hydroinform. 2018, 20, 356–375. [Google Scholar] [CrossRef] [Green Version]
- Dindarloo, S.R.; Siami-Irdemoosa, E. Estimating the unconfined compressive strength of carbonate rocks using gene expression programming. arXiv 2016, arXiv:1602.03854. [Google Scholar]
- Amini, E.; Golbaz, D.; Amini, F.; Majidi Nezhad, M.; Neshat, M.; Astiaso Garcia, D. A parametric study of wave energy converter layouts in real wave models. Energies 2020, 13, 6095. [Google Scholar] [CrossRef]
- Neshat, M.; Mirjalili, S.; Sergiienko, N.Y.; Esmaeilzadeh, S.; Amini, E.; Heydari, A.; Garcia, D.A. Layout optimisation of offshore wave energy converters using a novel multi-swarm cooperative algorithm with backtracking strategy: A case study from coasts of Australia. Energy 2022, 239, 122463. [Google Scholar] [CrossRef]
- Venkata Raju Badanapuri, Design Principles that are involved in the Design of Flow over an Ogee Crest Spillway. Int. J. Sci. Res. 2019, 8, 245–254.
- Sarkardeh, H.; Marosi, M.; Roshan, R. Stepped spillway optimization through numerical and physical modeling. Int. J. Energy Environ. 2015, 6, 597. [Google Scholar]
- Matozinhos, C.F.; Campagnole dos Santos, A.A. Two-phase CFD simulation of research reactor siphon breakers: A verification, validation and applicability study. Nucl. Eng. Des. 2018, 326, 7–16. [Google Scholar] [CrossRef]
- Celik, I.; Ghia, U.; Roache, P.; Freitas, C.; Coloman, H.; Raad, P. Procedure of Estimation and Reporting of Uncertainty Due to Discretization in CFD Applications. J. Fluids Eng. 2008, 130, 078001. [Google Scholar] [CrossRef] [Green Version]
- Azimi, H.; Shabanlou, S.; Ebtehaj, I.; Bonakdari, H.; Kardar, S. Combination of computational fluid dynamics, adaptive neuro-fuzzy inference system, and genetic algorithm for predicting discharge coefficient of rectangular side orifices. J. Irrig. Drain. Eng. 2017, 143, 04017015. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J., Jr. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Morais, V.H.; Gireli, T.Z.; Vatavuk, P. Numerical and experimental models applied to an ogee crest spillway and roller bucket stilling basin. RBRH 2020, 25, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Ferreira, C. Gene Expression Programming: Mathematical Modeling by an Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2006; Volume 21. [Google Scholar]
- Lu, X.; Wang, X.; Zhang, L.; Zhang, T.; Yang, C.; Song, X.; Yang, Q. Improving forecasting accuracy of river flow using gene expression programming based on wavelet decomposition and de-noising. Hydrol. Res. 2018, 49, 711–723. [Google Scholar] [CrossRef] [Green Version]







| Values | Values | Values | |
|---|---|---|---|
| N, N, N | 1780000, 305212, 222500 | 1780000, 305212, 222500, | 1780000, 305212, 222500 |
| r | 1.72 | 1.72 | 1.72 |
| r | 1.56 | 1.56 | 1.56 |
| Q | 5.43 | 10.29 | 11.805 |
| Q | 5.51 | 10.2 | 11.69 |
| Q | 5.37 | 10.08 | 11.58 |
| P | 2.48 | 1.79 | 1.2 |
| Q | 5.38 | 10.34 | 11.93 |
| Q | 1.47% | 0.87% | 0.97% |
| Q | 0.5% | 0.48% | 1.04% |
| Q | 0.66% | 0.67% | 1.31% |
| Setting Parameters | Value |
|---|---|
| Functions set | +, −, /, x, exp, ln, cube root, Atan, Tanh |
| Chromosomes | 30 |
| Head size | 8 |
| Number of genes | 3 |
| Linking function | Addition |
| Fitness function error type | RMSE |
| Mutation rate | 0.044 |
| Inversion rate | 0.1 |
| One-point recombination rate | 0.3 |
| Two-point recombination rate | 0.3 |
| Gene recombination rate | 0.1 |
| Gene transposition rate | 0.1 |
| Type | Operator | Train Phasing | Test Phasing | ||||
|---|---|---|---|---|---|---|---|
| RMSE | MAE | RMSE | MAE | ||||
| Option 1 | +, −, *, / | 0.9 | 1.57 | 1.07 | 0.86 | 1.73 | 1.13 |
| Option 2 | +, −, *, /, x | 0.91 | 1.53 | 1.05 | 0.86 | 1.73 | 1.12 |
| Option 3 | +, −, *, /, x, exp | 0.9 | 1.65 | 1.03 | 0.86 | 1.59 | 1.01 |
| Option 4 | +, −, *, /, x, exp, ln, cube root | 0.9 | 1.59 | 1.06 | 0.87 | 1.61 | 1.06 |
| Option 5 | +, −, *, /, x, exp, ln, cube root, Atan, Tanh, min, max | 0.972 | 0.85 | 0.64 | 0.912 | 1.42 | 1.12 |
| Case Number | Train Phasing | Test Phasing | ||||
|---|---|---|---|---|---|---|
| RMSE | MAE | RMSE | MAE | |||
| Case 1 | 0.9 | 1.611 | 0.95 | 0.86 | 1.49 | 0.97 |
| Case 2 | 0.92 | 1.43 | 0.85 | 0.89 | 1.71 | 1.28 |
| Case 3 | 0.96 | 0.94 | 0.74 | 0.86 | 1.19 | 0.87 |
| Case 4 | 0.94 | 1.21 | 0.95 | 0.71 | 2.11 | 1.3 |
| Case 5 | 0.91 | 1.48 | 0.83 | 0.87 | 1.89 | 1.01 |
| Case 6 | 0.92 | 1.47 | 0.94 | 0.85 | 1.49 | 0.93 |
| Case 7 | 0.96 | 0.97 | 0.7 | 0.87 | 1.47 | 1.07 |
| Case 8 | 0.93 | 1.32 | 0.86 | 0.82 | 1.73 | 1.016 |
| Case 9 | 0.91 | 1.48 | 0.95 | 0.89 | 1.51 | 1.02 |
| Case 10 | 0.91 | 1.54 | 1.02 | 0.86 | 1.69 | 1.06 |
| Parameters | Value | Coefficients | Value |
|---|---|---|---|
| G1C1 | 2.02 | ||
| G3C6 | 0.06 | ||
| - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mozaffari, S.; Amini, E.; Mehdipour, H.; Neshat, M. Flow Discharge Prediction Study Using a CFD-Based Numerical Model and Gene Expression Programming. Water 2022, 14, 650. https://doi.org/10.3390/w14040650
Mozaffari S, Amini E, Mehdipour H, Neshat M. Flow Discharge Prediction Study Using a CFD-Based Numerical Model and Gene Expression Programming. Water. 2022; 14(4):650. https://doi.org/10.3390/w14040650
Chicago/Turabian StyleMozaffari, Sevda, Erfan Amini, Hossein Mehdipour, and Mehdi Neshat. 2022. "Flow Discharge Prediction Study Using a CFD-Based Numerical Model and Gene Expression Programming" Water 14, no. 4: 650. https://doi.org/10.3390/w14040650








