The Wave Climate of the Sea of Azov
Abstract
1. Introduction
2. Materials and Methods
2.1. Description of the Model
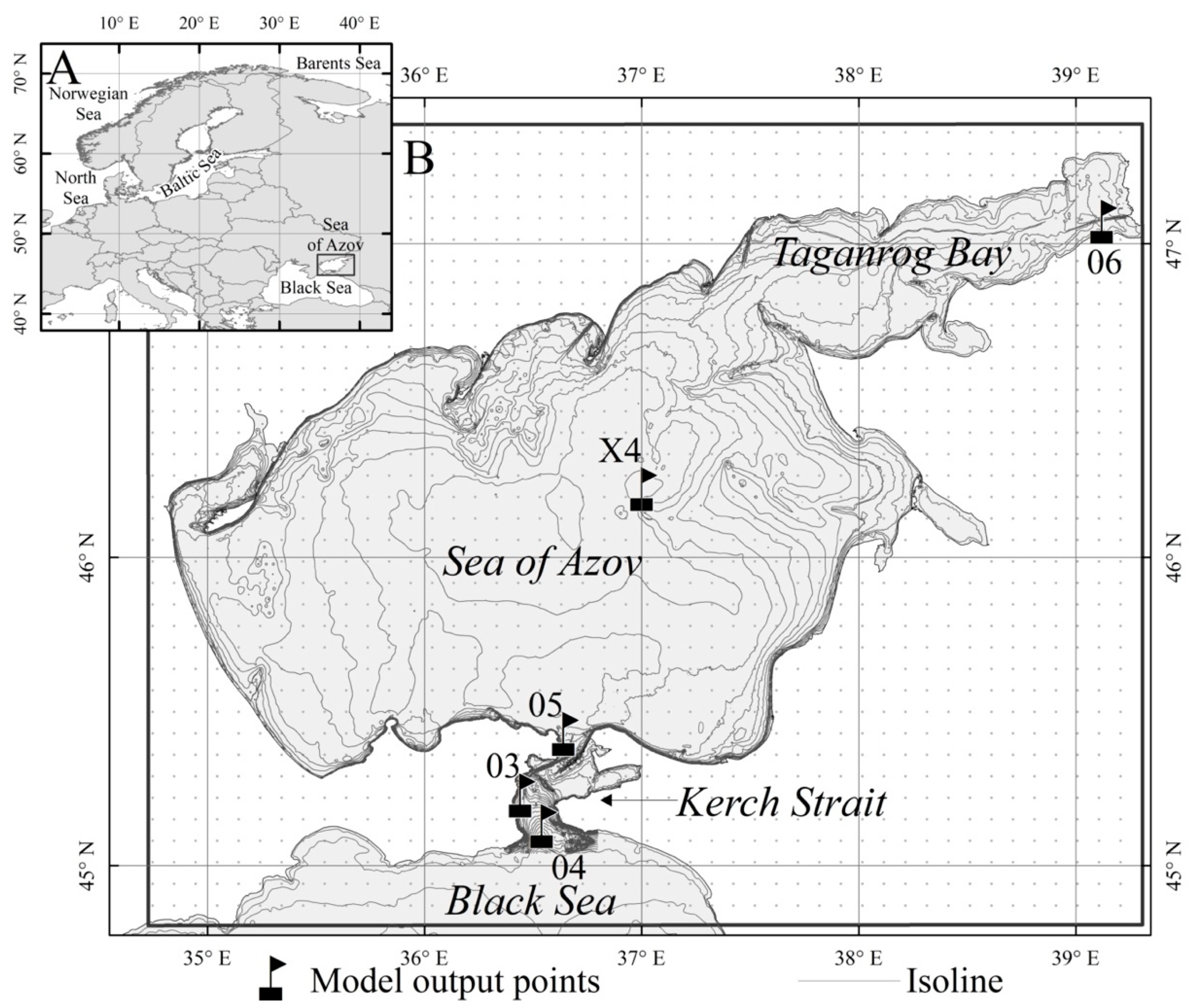
2.2. Study Area and Initial Data
2.3. Verification and Parameterization of the Model
3. Results
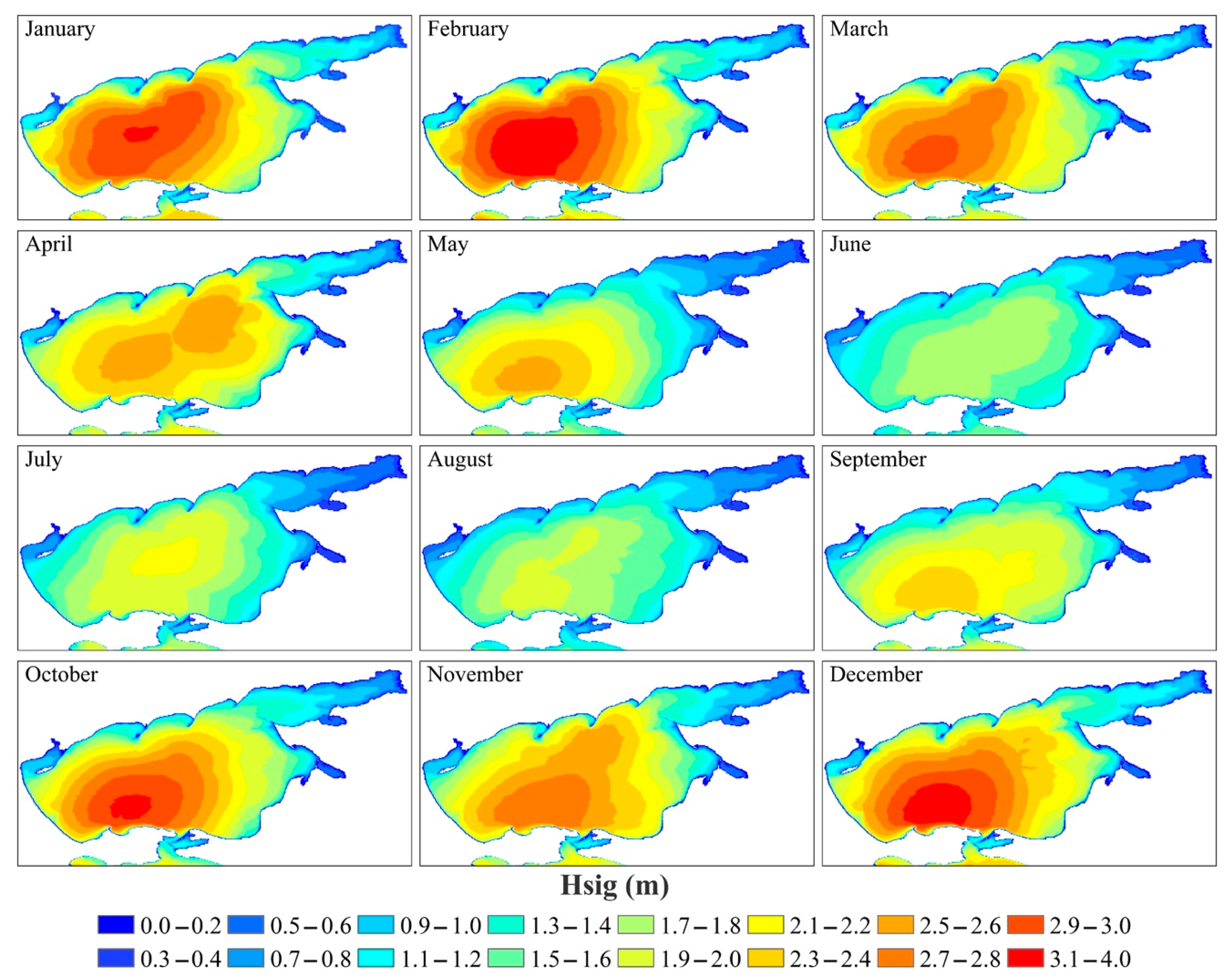
3.1. Average Long-Term Wind-Wave Pattern in the Sea of Azov
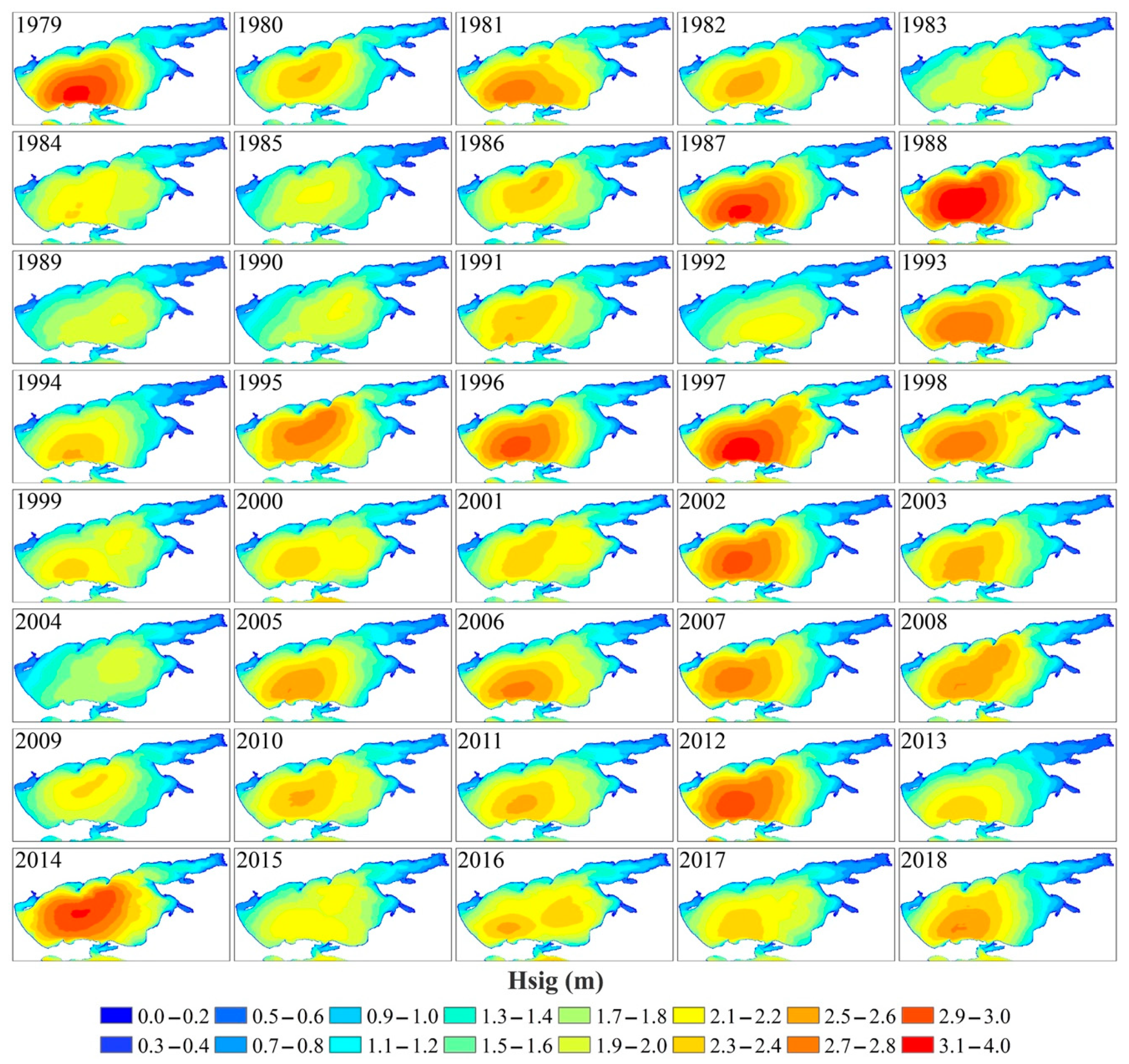
3.2. Interannual Dynamics of Wind Waves
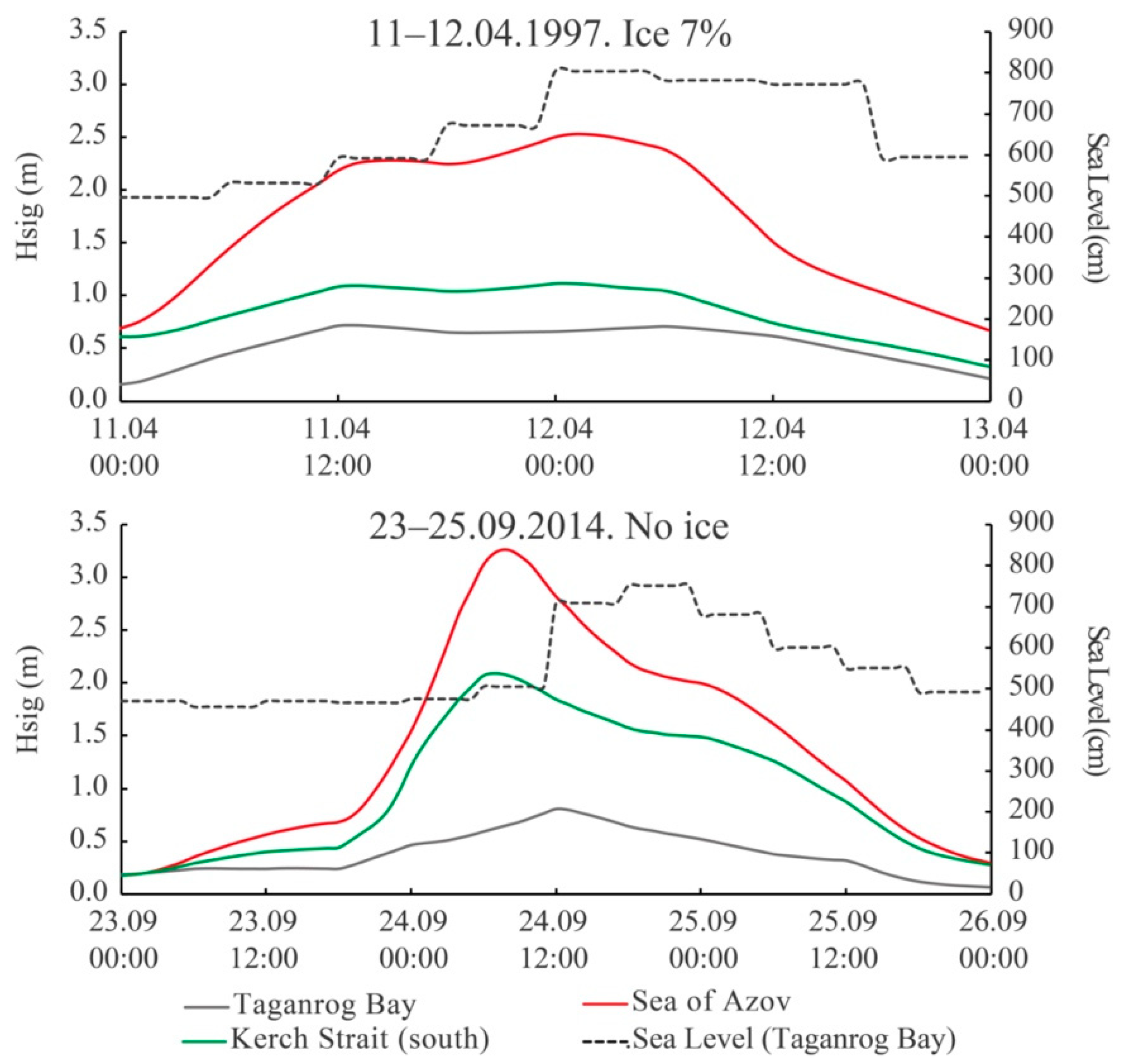
3.3. Storm and Its Combination with Surge and Dangerous Ice Phenomena
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Goryushina, E.M.; Yaitskaya, N.A. Dangerous Hydrometeorological Phenomena in the Azov-Black Sea Region. Eur. Proc. Soc. Behav. Sci. EpSBS 2019, 78, 1150–1154. [Google Scholar]
- Matishov, G.G.; Matishov, D.G. Current natural and social risks in the Azov-Black Sea region. Her. Russ. Acad. Sci. 2013, 83, 490–498. [Google Scholar] [CrossRef]
- Matishov, G.G.; Bespalova, L.A.; Ivlieva, O.V.; Tsygankova, A.E.; Kropyanko, L.V. The Sea of Azov: Recent abrasion processes and problems of coastal protection. Dokl. Earth Sci. 2016, 471, 1269–12721. [Google Scholar] [CrossRef]
- Cavaleri, L.; Abdallab, S.; Benetazzoa, A.; Bertottia, L.; Bidlotb, J.-R.; Breivikc, Ø.; Carniela, S.; Jensend, R.E.; Portilla-Yandune, J.; Rogersf, W.E.; et al. Wave modelling in coastal and inner seas. Prog. Oceanogr. 2018, 167, 164–233. [Google Scholar] [CrossRef]
- Rusu, E.; Soares, C.G. Wave modelling at the entrance of ports. Ocean. Eng. 2011, 38, 2089–2109. [Google Scholar] [CrossRef]
- Pallares, E.; Sánchez-Arcilla, A.; Espino, M. Wave energy balance in wave models (SWAN) for semi-enclosed domains–Application to the Catalan coast. Cont. Shelf Res. 2014, 87, 41–53. [Google Scholar] [CrossRef]
- Mao, M.; Van Der Westhuysen, A.J.; Xia, M.; Schwab, D.J.; Chawla, A. Modeling wind waves from deep to shallow waters in Lake Michigan using unstructured SWAN. J. Geophys. Res. Ocean. 2016, 121, 3836–3865. [Google Scholar] [CrossRef]
- Medvedeva, A.Y.; Arkhipkin, V.S.; Myslenkov, S.A.; Zilitinkevich, S.S. Wave climate of the Baltic Sea following the results of the swan spectral model application. Vestn. Mosk. Univ. Ser. 5 Geogr. 2015, 1, 12–22. [Google Scholar]
- Myslenkov, S.A.; Platonov, V.S.; Toropov, P.A.; Shestakova, A.A. Simulation of storm waves in the Barents Sea. Vestn. Mosk. Univ. Ser. 5 Geogr. 2015, 6, 65–75. [Google Scholar]
- Kislov, A.V.; Surkova, G.V.; Arkhipkin, V.S. Occurence frequency of storm wind waves in the Baltic, Black, and Caspian Seas under changing climate conditions. Russ. Meteorol. Hydrol. 2016, 41, 121–129. [Google Scholar] [CrossRef]
- Yaitskaya, N.A. Retrospective analysis of wind waves in the Caspian Sea in the second half of the XX-beginning of the XXI century and its connection with the regional climate changes. Geogr. Bull. 2017, 2, 57–70. [Google Scholar] [CrossRef]
- Akpınar, A.; Van Vledder, G.P.; Kömürcü, M.İ.; Özger, M. Evaluation of the numerical wave model (SWAN) for wave simulation in the Black Sea. Cont. Shelf Res. 2012, 50, 80–99. [Google Scholar] [CrossRef]
- Akpınar, A.; Bingölbalia, B.; Van Vledder, G.P. Wind and wave characteristics in the Black Sea based on the SWAN wave model forced with the CFSR winds. Ocean. Eng. 2016, 126, 276–298. [Google Scholar] [CrossRef]
- Van Vledder, G.P.; Akpınar, A. Wave model predictions in the Black Sea: Sensitivity to wind fields. Appl. Ocean. Res. 2015, 53, 161–178. [Google Scholar] [CrossRef]
- Bingölbali, B.; Akpınar, A.; Jafali, H.; Van Vledder, G.P. Downscaling of wave climate in the western Black Sea. Ocean. Eng. 2019, 172, 31–45. [Google Scholar] [CrossRef]
- Berdnikov, S.V.; Dashkevich, L.V.; Kulygin, V.V.; Sheverdyaev, I.V.; Tretyakova, I.A.; Yaitskaya, N.A. Ex-Mare-forecasting system of natural hazards in the Azov Sea region. Geogr. Environ. Sustain. 2018, 11, 29–45. [Google Scholar] [CrossRef][Green Version]
- Holthuijsen, L.H.; Booij, N.; Ris, R.C. A spectral wave model for the coastal zone. In Ocean Wave Measurement and Analysis; American Society of Civil Engineers: New York, NY, USA, 1993; pp. 630–641. [Google Scholar]
- Ris, R.C.; Holthuijsen, L.H.; Booij, N. A third-generation wave model for coastal regions: 2, verification. J. Geophys. Res. 1999, 104, 7667–7681. [Google Scholar] [CrossRef]
- Booij, N.; Holthuijsen, L.H.; Ris, R.C. A third-generation wave model for coastal regions. Model description and validation. J. Geophys. Res. 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- Zijlema, M.; Van der Westhuyse, A.J. On convergence behavior and numerical accuracy in stationary SWAN simulations of nearshore wind wave spectra. Coast. Eng. 2005, 52, 237–256. [Google Scholar] [CrossRef]
- Matishov, G. Bathymetry and patterns of formation of the bottom relief of the Sea of Azov. In Ecosystem Studies of the Azov, Black, Caspian Seas; Matishov, G., Ed.; Kola Scientific Centre of the Russian Academy of Sciences: Apatity, Russia, 2006; pp. 31–42. [Google Scholar]
- Matishov, G.; Levitus, S.; Matishov, D.; Gargopa, Y.; Dashkevich, L.; Berdnikov, S.; Kulygin, V.; Arkhipova, O.; Chikin, A.; Shabas, I.; et al. Climatic Atlas of the Sea of Azov 2008; NOAA/NESDIS: Washington, DC, USA, 2008; p. 103. [Google Scholar]
- Magaeva, A.A.; Tretyakova, I.A. Creation of a digital elevation model of the Sea of Azov bottom. In Ecology Economy Informatics; Matishov, G., Ed.; Southern Federal University: Rostov-on-Don, Russia, 2015; pp. 266–269. [Google Scholar]
- Yaitskaya, N.A. The results of hindcasting experiments of wind wave in the Sea of Azov (as illustrated by winters 2015-2017). Sci. South Russ. 2017, 13, 60–70. [Google Scholar] [CrossRef]
- Azov Research Institute of Fisheries. Available online: http://www.azniirkh.ru (accessed on 28 January 2021).
- The ERA-Interim Archive Version 2.0. Available online: http://www.ecmwf.int/node/8174 (accessed on 28 December 2021).
- Yaitskaya, N.; Tretyakova, I. Mathematical Modeling of Dangerous Storm and Surge Phenomena in the Basin of the Sea of Azov (24 March 2013). In Proceedings of the 16th International Multidisciplinary Scientific GeoConference SGEM 2016, Albena, Bulgaria, 28 June–7 July 2016; pp. 481–488. [Google Scholar] [CrossRef]
- The Unified State System of Information on the World Ocean. Available online: http://portal.esimo.ru/portal (accessed on 28 December 2021).
- Komen, G.; Hasselmann, S.; Hasselmann, K. On the existence of a fully developed wind sea spectrum. J. Phys. Oceanogr. 1984, 14, 1271–1285. [Google Scholar] [CrossRef]
- Hasselmann, K.; Barnett, T.P.; Bouws, E.; Carlson, H.; Cartwright, D.E.; Enke, K.; Ewing, J.A.; Gienapp, H.; Hasselmann, D.E.; Kruseman, P.; et al. Measurements of Wind-Wave Growth and Swell Decay during the Joint North Sea Wave Project (JONSWAP). Ergänzungsheft Zur Dtsch. Hydrogr. Z. 1973, 8, 1–95. [Google Scholar]
- Yaitskaya, N.A.; Magaeva, A.A. Dynamics of the ice regime of the Sea of Azov in the XX-XXI centuries. Led I Sneg 2018, 58, 373–386. [Google Scholar] [CrossRef]
- Matishov, G.G.; Grigorenko, K.S. Currents of the Azov Sea during the Don River Low-Water Period. Oceanology 2021, 61, 173–182. [Google Scholar] [CrossRef]
- Hydrometeorology and hydrochemistry of the USSR Seas. Vol. 5. The Sea of Azov; Goptarev, N.P., Simonova, A.I., Zatuchnaya, B.M., Gershanovich, D.E., Eds.; Gidrometeoizdat: St. Petersburg, Russia, 1991; p. 237. [Google Scholar]
- Reference Data on the Wind and Wave Regime of the Baltic, North, Black, Azov and Mediterranean Seas; Lopatoukhin, L.I., Bukhanovsky, A.V., Ivanov, S.V., Chernyshova, E.S., Eds.; Russian Maritime Register of Shipping: St. Petersburg, Russia, 2006; p. 452. [Google Scholar]
- Divinsky, B.V.; Kosyan, R.D.; Fomin, V.V. Climatic Fields of Sea Currents and Wind Waves of the Sea of Azov. Dokl. Earth Sci. 2021, 501, 976–988. [Google Scholar] [CrossRef]
- Dyakov, N.N.; Fomin, V.V.; Polozok, A.A. Climatic characteristics of waves in the Sea of Azov based on the observation data and reanalysis. Proc. State Oceanogr. Inst. 2015, 216, 60–78. [Google Scholar]
- Achite, M.; Ceribasi, G.; Ceyhunlu, A.I.; Wałęga, A.; Caloiero, T. The Innovative Polygon Trend Analysis (IPTA) as a Simple Qualitative Method to Detect Changes in Environment—Example Detecting Trends of the Total Monthly Precipitation in Semiarid Area. Sustainability 2021, 13, 12674. [Google Scholar] [CrossRef]
- Sen, Z.; Sisman, E.; Dabanli, I. Innovative Polygon Trend Analysis (IPTA) and applications. J. Hydrol. 2019, 575, 202–210. [Google Scholar] [CrossRef]
- Matishov, G.G.; Satitskiy, R.M.; Inzheneykin, Y.I. Conditions and consequences of shipwreck in the Kerch Strait in the storm on 11 November 2007. Sci. South Russ. 2008, 4, 54–63. [Google Scholar]
- Arkhipkin, V.S.; Gippius, F.N.; Koltermann, K.P.; Surkova, G.V. Wind waves in the Black Sea: Results of a hindcast study. Nat. Hazards Earth Syst. Sci. 2014, 14, 2883–2897. [Google Scholar] [CrossRef]

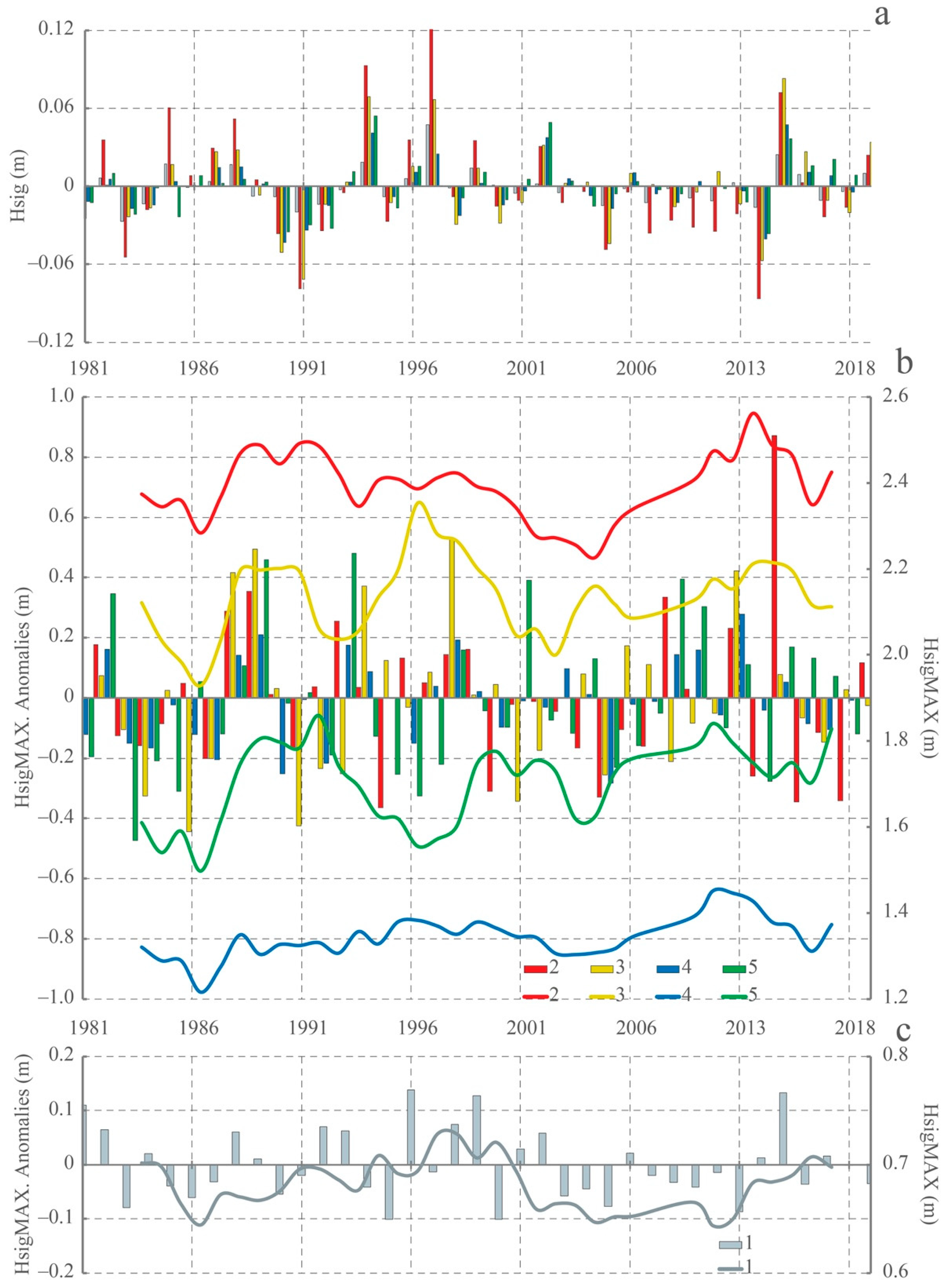
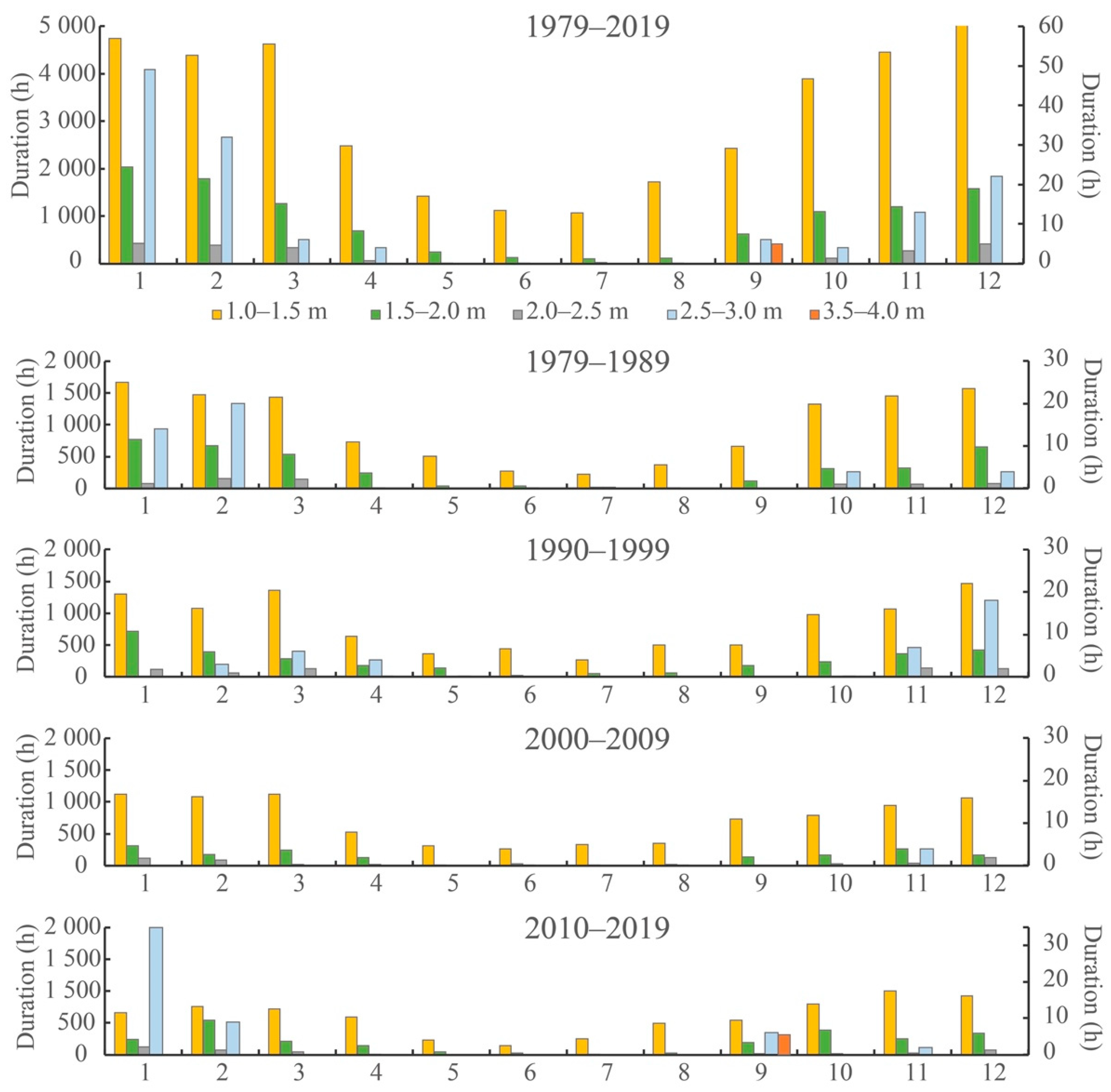
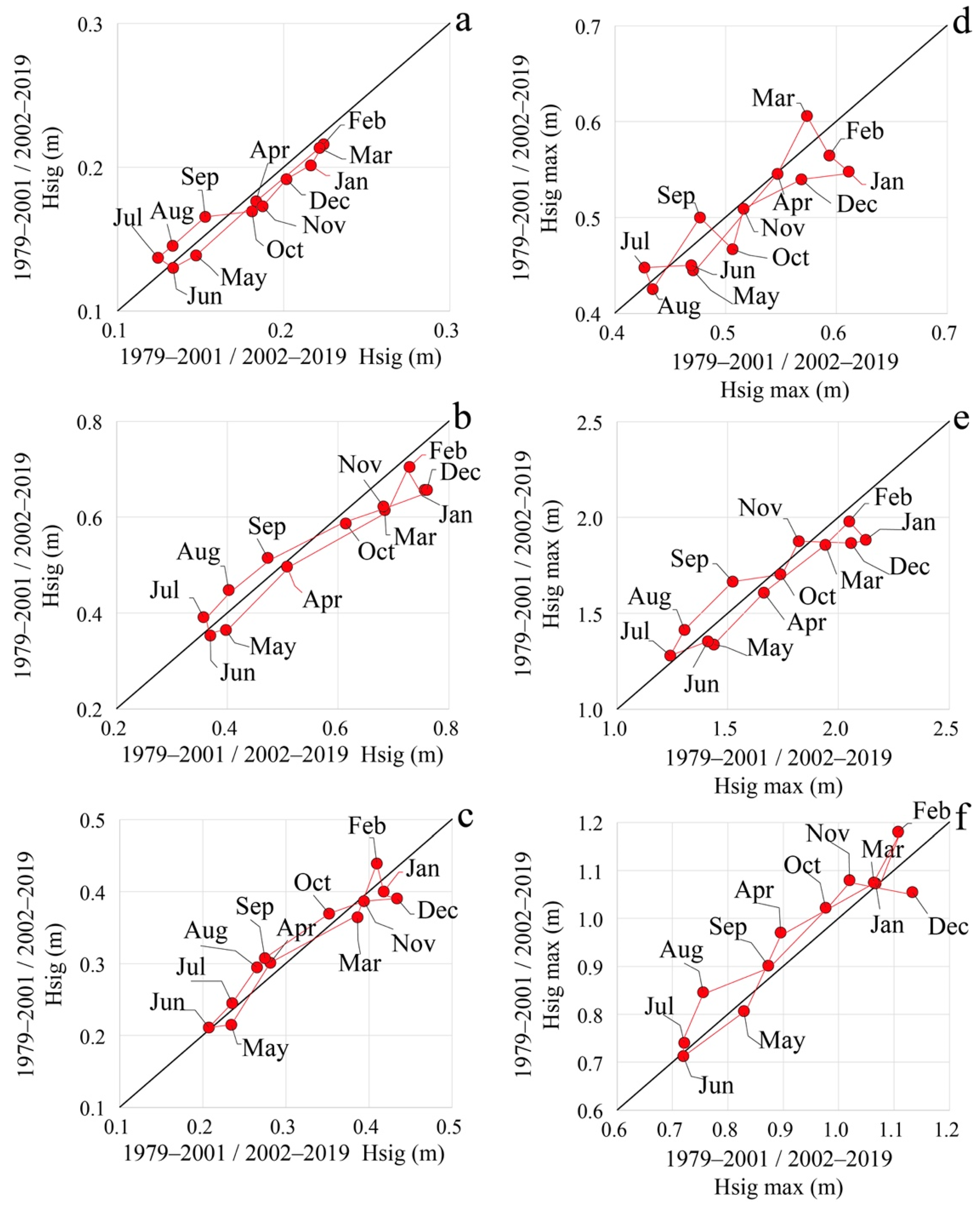
| Average | Maximum | Standard Deviation | Dispersion | Location | |
|---|---|---|---|---|---|
| Hsig (m) | 0.55 | 3.26 | 0.43 | 0.18 | Sea of Azov |
| Wlen (m) | 10.25 | 48.49 | 7.16 | 51.29 | |
| Tm (s.) | 2.89 | 6.78 | 0.95 | 0.91 | |
| Swell (m) | 0.00 | 0.48 | 0.00 | 0.00 | |
| Hsig (m) | 0.17 | 0.82 | 0.12 | 0.01 | Taganrog Bay |
| Wlen (m) | 2.71 | 10.97 | 1.84 | 3.40 | |
| Tm (s.) | 1.56 | 3.22 | 0.44 | 0.20 | |
| Swell (m) | 0.00 | 0.02 | 0.00 | 0.00 | |
| Hsig (m) | 0.37 | 2.19 | 0.28 | 0.08 | Kerch Strait (north) |
| Wlen (m) | 6.07 | 31.98 | 4.46 | 19.94 | |
| Tm (s.) | 2.23 | 5.40 | 0.78 | 0.61 | |
| Swell (m) | 0.00 | 0.09 | 0.00 | 0.00 | |
| Hsig (m) | 0.32 | 1.63 | 0.25 | 0.06 | Kerch Strait (center) |
| Wlen (m) | 5.13 | 23.27 | 3.76 | 14.12 | |
| Tm (s.) | 2.05 | 4.73 | 0.70 | 0.49 | |
| Swell (m) | 0.00 | 0.06 | 0.00 | 0.00 | |
| Hsig (m) | 0.47 | 2.67 | 0.36 | 0.13 | Kerch Strait (south) |
| Wlen (m) | 8.41 | 39.57 | 6.04 | 36.53 | |
| Tm (s.) | 2.73 | 6.41 | 0.92 | 0.84 | |
| Swell (m) | 0.00 | 0.26 | 0.01 | 0.00 |
| Winter | Spring | Summer | Autumn | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Hsig (m) | Wlen (m) | Tm (s) | Hsig (m) | Wlen (m) | Tm (s) | Hsig (m) | Wlen (m) | Tm (s) | Hsig (m) | Wlen (m) | Tm (s) | ||
| 1980–1989 | 0.22 | 3.33 | 1.70 | 0.18 | 2.81 | 1.58 | 0.12 | 1.87 | 1.37 | 0.18 | 2.80 | 1.58 | Taganrog Bay |
| 1990–1999 | 0.22 | 3.34 | 1.71 | 0.19 | 2.95 | 1.62 | 0.14 | 2.15 | 1.43 | 0.17 | 2.67 | 1.56 | |
| 2000–2009 | 0.20 | 3.06 | 1.65 | 0.17 | 2.71 | 1.57 | 0.14 | 2.20 | 1.44 | 0.17 | 2.60 | 1.53 | |
| 2010–2019 | 0.21 | 3.21 | 1.68 | 0.18 | 2.76 | 1.58 | 0.14 | 2.19 | 1.44 | 0.18 | 2.74 | 1.57 | |
| 1980–1989 | 0.76 | 13.80 | 3.35 | 0.53 | 9.97 | 2.84 | 0.34 | 6.49 | 2.36 | 0.61 | 11.22 | 3.02 | The Sea of Azov |
| 1990–1999 | 0.74 | 13.51 | 3.32 | 0.54 | 10.30 | 2.92 | 0.39 | 7.50 | 2.51 | 0.57 | 10.63 | 2.94 | |
| 2000–2009 | 0.67 | 12.38 | 3.19 | 0.49 | 9.44 | 2.80 | 0.41 | 7.74 | 2.56 | 0.57 | 10.55 | 2.94 | |
| 2010–2019 | 0.67 | 12.42 | 3.18 | 0.49 | 9.38 | 2.78 | 0.40 | 7.63 | 2.53 | 0.60 | 10.96 | 2.97 | |
| 1980–1989 | 0.60 | 10.34 | 3.03 | 0.43 | 7.72 | 2.60 | 0.32 | 5.92 | 2.33 | 0.52 | 9.24 | 2.88 | Kerch Strait (north) |
| 1990–1999 | 0.61 | 10.44 | 3.04 | 0.42 | 7.56 | 2.60 | 0.37 | 6.98 | 2.51 | 0.50 | 8.79 | 2.78 | |
| 2000–2009 | 0.57 | 9.85 | 2.94 | 0.41 | 7.41 | 2.57 | 0.39 | 7.36 | 2.58 | 0.51 | 9.02 | 2.83 | |
| 2010–2019 | 0.57 | 9.77 | 2.93 | 0.40 | 7.15 | 2.52 | 0.40 | 7.52 | 2.59 | 0.55 | 9.64 | 2.91 | |
| 1980–1989 | 0.42 | 6.54 | 2.32 | 0.30 | 4.87 | 2.00 | 0.22 | 3.45 | 1.72 | 0.34 | 5.43 | 2.10 | Kerch Strait (central part) |
| 1990–1999 | 0.42 | 6.49 | 2.31 | 0.30 | 4.84 | 2.01 | 0.24 | 3.87 | 1.80 | 0.33 | 5.25 | 2.06 | |
| 2000–2009 | 0.41 | 6.43 | 2.30 | 0.30 | 4.75 | 1.99 | 0.25 | 3.98 | 1.83 | 0.35 | 5.50 | 2.12 | |
| 2010–2019 | 0.41 | 6.33 | 2.28 | 0.29 | 4.62 | 1.95 | 0.26 | 4.14 | 1.85 | 0.37 | 5.77 | 2.15 | |
| 1980–1989 | 0.49 | 8.03 | 2.58 | 0.33 | 5.52 | 2.14 | 0.25 | 4.09 | 1.88 | 0.38 | 6.28 | 2.28 | Kerch Strait (south) |
| 1990–1999 | 0.49 | 8.06 | 2.58 | 0.34 | 5.73 | 2.19 | 0.27 | 4.40 | 1.93 | 0.37 | 6.12 | 2.24 | |
| 2000–2009 | 0.49 | 7.99 | 2.57 | 0.34 | 5.74 | 2.17 | 0.28 | 4.57 | 1.97 | 0.39 | 6.34 | 2.29 | |
| 2010–2019 | 0.47 | 7.79 | 2.54 | 0.34 | 5.68 | 2.15 | 0.28 | 4.56 | 1.97 | 0.40 | 6.54 | 2.32 | |
| January | February | March | April | May | June | July | August | September | October | November | December | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Hsig (m) |  |  |  |  |  |  |  |  |  |  |  |  | Taganrog Bay |
| Hsig max (m) |  |  |  |  |  |  |  |  |  |  |  |  | |
| Hsig (m) |  |  |  |  |  |  |  |  |  |  |  |  | Sea of Azov |
| Hsig max (m) |  |  |  |  |  |  |  |  |  |  |  |  | |
| Hsig (m) |  |  |  |  |  |  |  |  |  |  |  |  | Kerch Strait (center) |
| Hsig max (m) |  |  |  |  |  |  |  |  |  |  |  |  |
 Increasing Trend;
Increasing Trend;  Decreasing Trend;
Decreasing Trend;  No Trend.
No Trend.Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yaitskaya, N. The Wave Climate of the Sea of Azov. Water 2022, 14, 555. https://doi.org/10.3390/w14040555
Yaitskaya N. The Wave Climate of the Sea of Azov. Water. 2022; 14(4):555. https://doi.org/10.3390/w14040555
Chicago/Turabian StyleYaitskaya, Natalia. 2022. "The Wave Climate of the Sea of Azov" Water 14, no. 4: 555. https://doi.org/10.3390/w14040555
APA StyleYaitskaya, N. (2022). The Wave Climate of the Sea of Azov. Water, 14(4), 555. https://doi.org/10.3390/w14040555






