Solution of Shallow-Water Equations by a Layer-Integrated Hydrostatic Least-Squares Finite-Element Method
Abstract
:1. Introduction
2. The Governing Equations and Numerical Method
2.1. Shallow-Water Equations
2.2. θ Time Integration Method
2.3. Least-Squares Finite Element Method
3. Results and Discussions
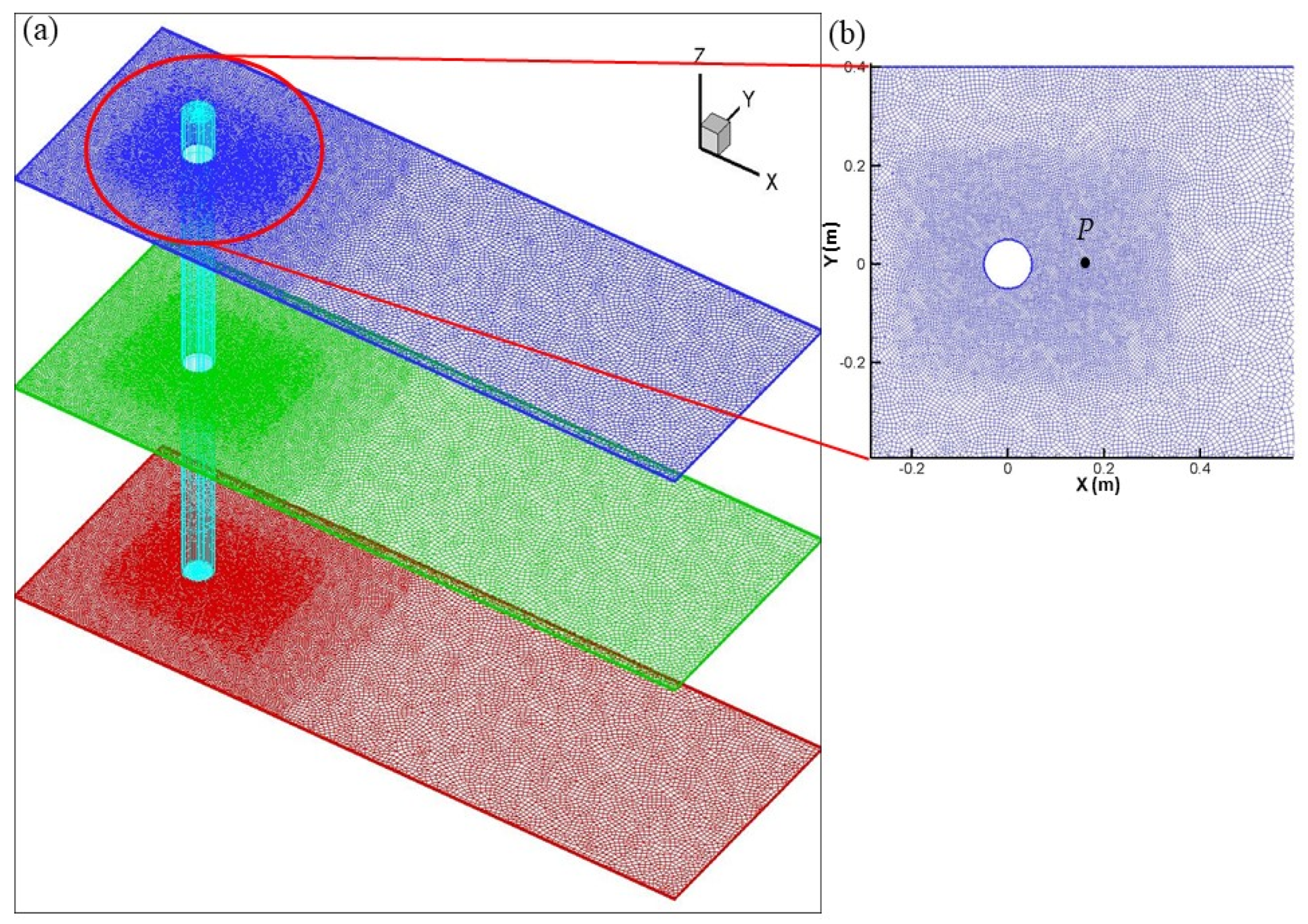
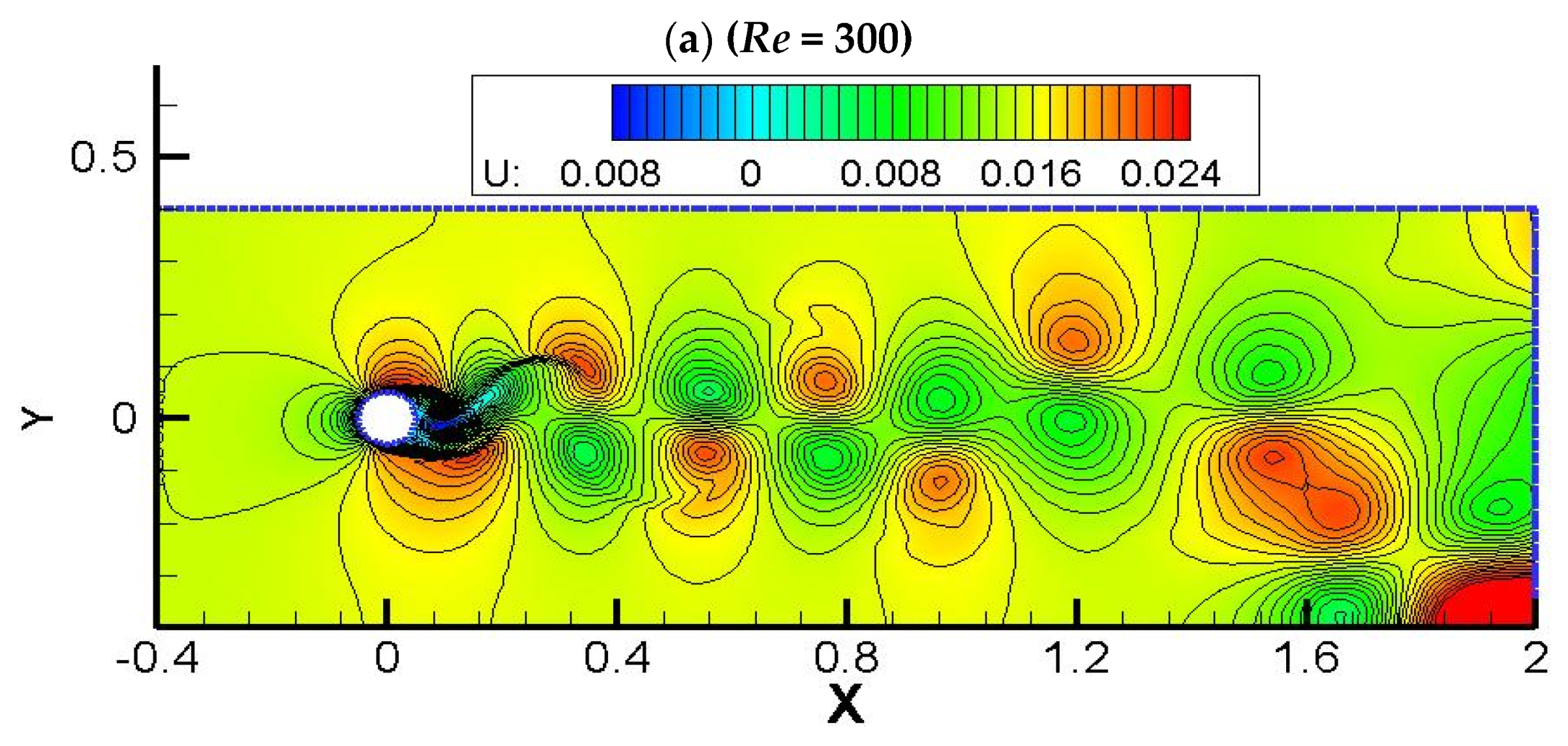
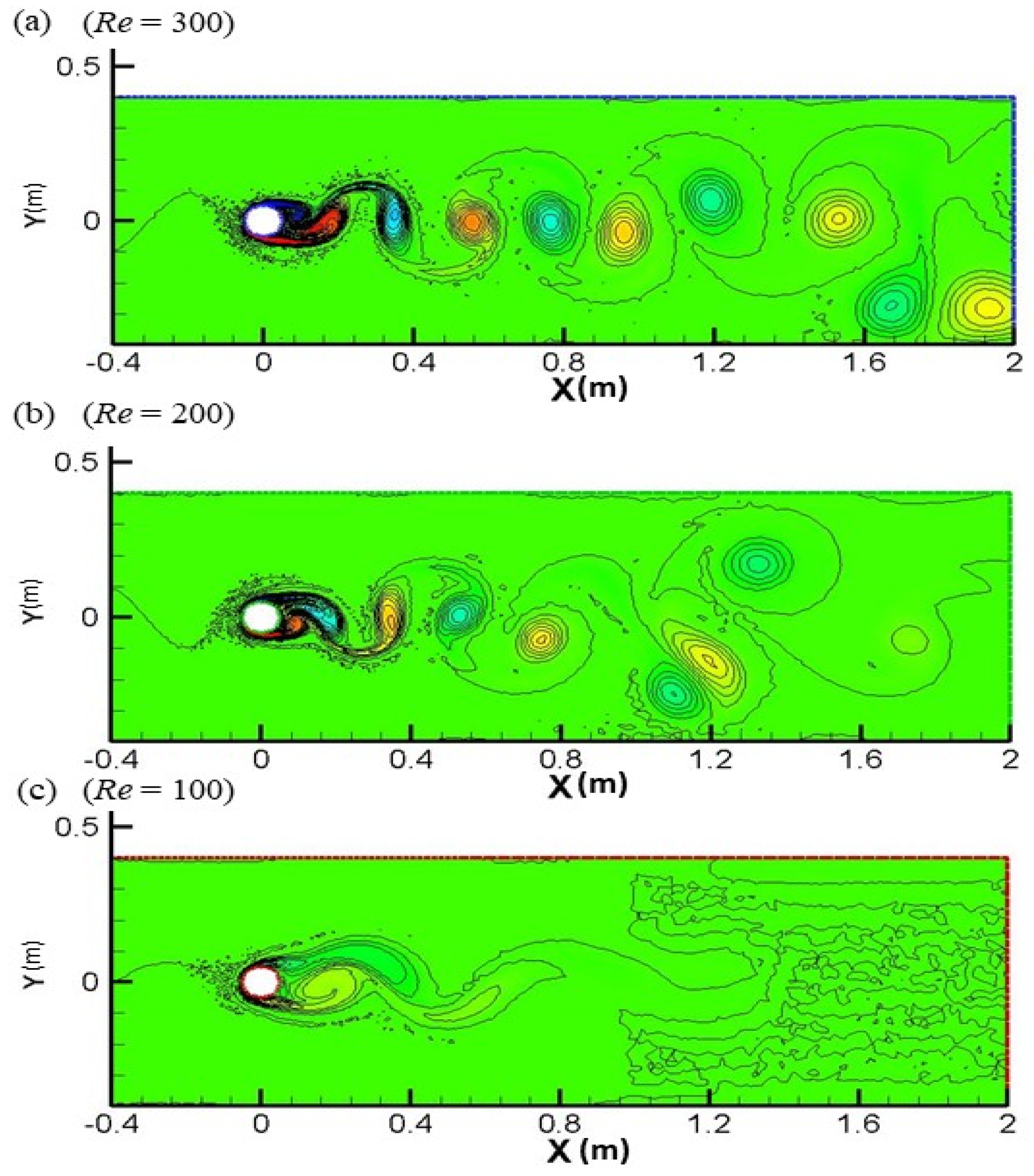
3.1. Von Karman Vortex Shedding
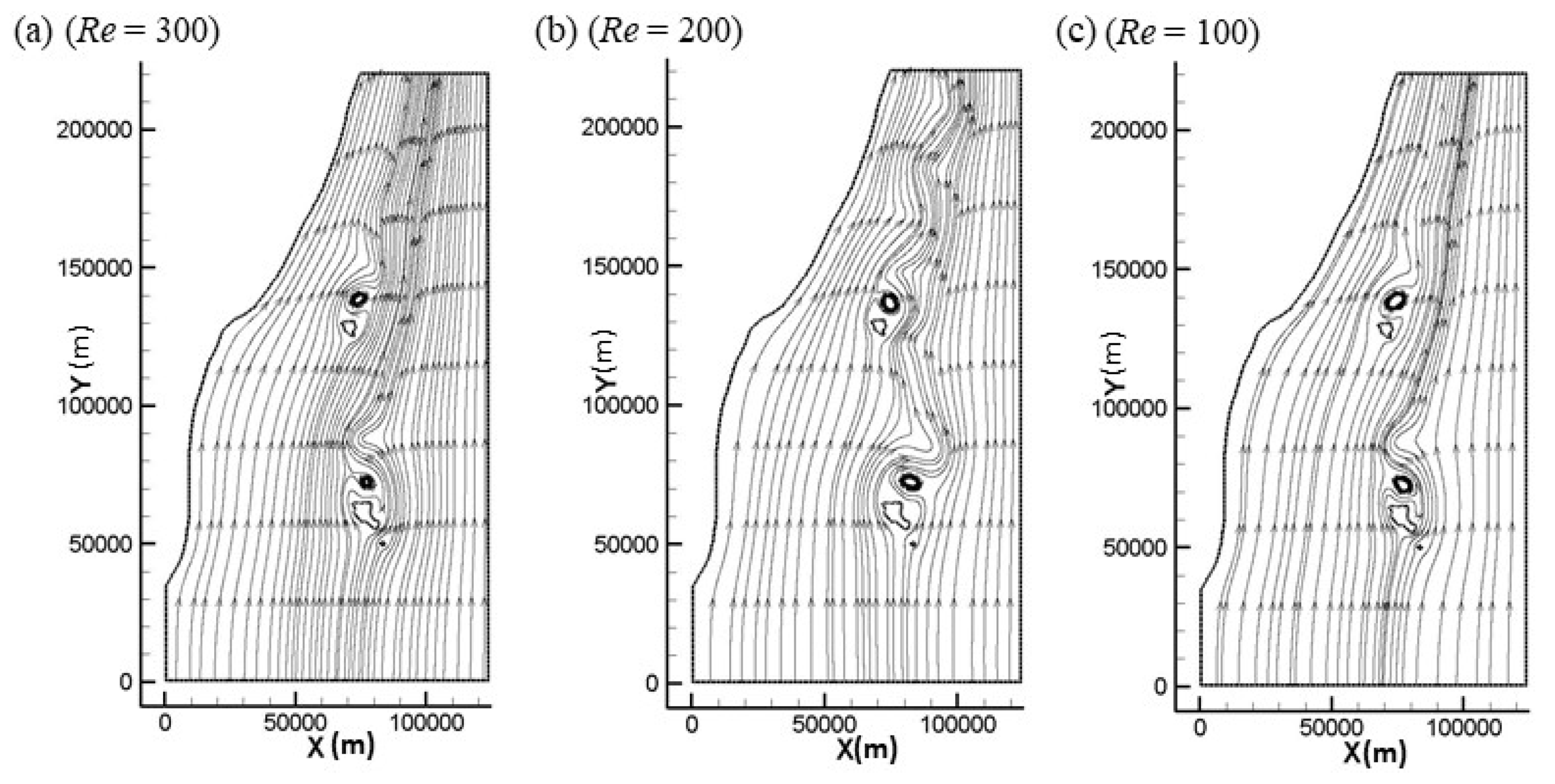
3.2. Green Island Vortex Shedding
3.3. Numerical Study
3.4. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Tritton, D.J. Experiments on the flow past a circular cylinder at low Reynolds numbers. J. Fluid Mech. 1959, 6, 547–567. [Google Scholar] [CrossRef]
- Williamson, C.H.K. Oblique and parallel modes of vortex shedding in the wake of a circular cylinder at low Reynolds numbers. J. Fluid Mech. 1989, 206, 579. [Google Scholar] [CrossRef] [Green Version]
- Williamson, C.H. Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 1996, 28, 477–539. [Google Scholar] [CrossRef]
- Zdravkovich, M.M. Flow around Circular Cylinders; Oxford University Press: Oxford, UK, 1997; ISBN 0198563965. [Google Scholar]
- Peter, A. Vortices and tall buildings: A recipe for resonance. Phys. Today 2010, 63, 9. [Google Scholar]
- Hubert, L.; Krueger, A. Satellite pictures of mesoscale eddies. Mon. Weather Rev. 1962, 90, 457–463. [Google Scholar] [CrossRef]
- Thomson, R.E.; Gower, J.F.; Bowker, N.W. Vortex streets in the wake of the Aleutian Islands. Mon. Weather Rev. 1977, 105, 873–884. [Google Scholar] [CrossRef] [Green Version]
- Li, X.F.; Clemente-Colon, P.; Pichel, W.G.; Vachon, P.W. Atmospheric vortex streets on a RADARSAT SAR image. Geophys. Res. Lett. 2000, 27, 1655–1658. [Google Scholar] [CrossRef]
- Young, G.S.; Zawislak, J. An observational study of vortex spacing in island wake vortex streets. Mon. Weather Rev. 2006, 134, 2285–2294. [Google Scholar] [CrossRef]
- Topouzelis, K.; Kitsiou, D. Detection and classification of mesoscale atmospheric phenomena above sea in SAR imagery. Remote Sens. Environ. 2015, 160, 263–272. [Google Scholar] [CrossRef]
- Barkley, R.A. Johnston atolls wake. J. Mar. Res. 1972, 30, 201–216. [Google Scholar]
- Wolanski, E.; Imberger, J.; Heron, M. Island wakes in shallow coastal waters. J. Geophys. Res. Ocean. 1984, 89, 10553–10569. [Google Scholar] [CrossRef]
- Heywood, K.J.; Stevens, D.P.; Bigg, G.R. Eddy formation behind the tropical island of Aldabra. Deep Sea Res. Part I 1996, 43, 555–578. [Google Scholar] [CrossRef] [Green Version]
- Dong, C.M.; McWilliams, J.C.; Shchepetkin, A.F. Island wakes in deep water. J. Phys. Oceanogr. 2007, 37, 962–981. [Google Scholar] [CrossRef]
- Zheng, Q.; Lin, H.; Meng, J.M.; Hu, X.M.; Song, Y.T.; Zhang, Y.Z.; Li, C.Y. Sub-mesoscale ocean vortex trains in the Luzon Strait. J. Geophys. Res. Ocean. 2008, 113, C04032. [Google Scholar] [CrossRef] [Green Version]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M. Global observations of nonlinear mesoscale eddies. Prog. Oceanogr. 2011, 91, 167–216. [Google Scholar] [CrossRef]
- Zheng, Q.; Holt, B.; Li, X.F.; Liu, X.N.; Zhao, Q.; Yuan, Y.L.; Yang, X.F. Deep-water seamount wakes on SEASAT SAR image in the Gulf stream region. Geophys. Res. Lett. 2012, 39, L16604. [Google Scholar] [CrossRef]
- Robinson, A.R.; McGillicuddy, D.J.; Calman, J.; Ducklow, H.W.; Fasham, M.J.R.; Hoge, F.E.; Leslie, W.G.; McCarthy, J.J.; Podewski, S.; Porter, D.L.; et al. Mesoscale and upper ocean variabilities during the 1989 JGOFS bloom study. Deep Sea Res. Part II Top. Stud. Oceanogr. 1993, 40, 9–35. [Google Scholar] [CrossRef]
- Faghmous, J.H.; Frenger, I.; Yao, Y.; Warmka, R.; Lindell, A.; Kumar, V. A daily global mesoscale ocean eddy dataset from satellite altimetry. Sci. Data 2015, 2, 150028. [Google Scholar] [CrossRef] [Green Version]
- Sorgente, R.; Olita1, A.; Oddo, P.; Fazioli1, L.; Ribotti, A. Numerical simulation and decomposition of kinetic energy in the Central Mediterranean: Insight on mesoscale circulation and energy conversion. Ocean Sci. 2011, 7, 503–519. [Google Scholar] [CrossRef] [Green Version]
- Dietze, H.; Matear, R.; Moore, T. Nutrient supply to anticyclonic meso-scale eddies off western Australia estimated with artificial tracers released in a circulation model. Deep-Sea Res. Pt. I 2009, 56, 1440–1448. [Google Scholar] [CrossRef]
- Chang, M.H.; Tang, T.Y.; Ho, C.R.; Chao, S.Y. Kuroshio-induced wake in the lee of Green Island of Taiwan. J. Geophys. Res. Ocean. Atmos. 2013, 118, 1508–1519. [Google Scholar] [CrossRef]
- Chang, M.H.; Jan, S.; Mensah, V.; Andres, M.; Rainville, L.; Yang, Y.J. Zonal migration and transport variations of the kuroshio east of Taiwan induced by eddy impingements. Deep Sea Res. Part I Oceanogr. Res. Pap. 2018, 131, 1–15. [Google Scholar] [CrossRef]
- Zheng, Z.W.; Zheng, Q. Variability of island-induced ocean vortex trains, in the Kuroshio region southeast of Taiwan Island. Cont. Shelf Res. 2014, 81, 1–6. [Google Scholar] [CrossRef]
- Hsu, P.C.; Chang, M.H.; Lin, C.C.; Huang, S.J.; Ho, C.R. Investigation of the island-induced ocean vortex train of the Kuroshio current using satellite imagery. Rem. Sens. Environ. 2017, 193, 54–64. [Google Scholar] [CrossRef]
- Hsu, P.C.; Cheng, K.H.; Jan, S.; Lee, H.J.; Ho, C.R. Vertical structure and surface patterns of green island wakes induced by the Kuroshio. Deep Sea Res. Part I Oceanogr. Res. Pap. 2019, 143, 1–16. [Google Scholar] [CrossRef]
- Hsu, P.C.; Ho, C.Y.; Lee, H.J.; Lu, C.Y.; Ho, C.R. Temporal variation and spatial structure of the Kuroshio-induced submesoscale island vortices observed from GCOM-C and Himawari-8 data. Rem. Sens. 2020, 12, 883. [Google Scholar] [CrossRef] [Green Version]
- Liang, S.J.; Lin, C.Y.; Hsu, T.W.; Ho, C.R.; Chang, M.H. Numerical study of vortex characteristics near Green Island, Taiwan. J. Coast. Res. 2013, 29, 1436–1444. [Google Scholar]
- Huang, S.J.; Ho, C.R.; Lin, S.L.; Liang, S.J. Spatial-temporal scales of Green Island wake due to passing of the Kuroshio current. Int. J. Rem. Sens. 2014, 35, 4484–4495. [Google Scholar] [CrossRef]
- Hsu, T.W.; Doong, D.J.; Hsieh, K.J.; Liang, S.J. Numerical study of Monsoon effecton Green Island Wake. J. Coast. Res. 2015, 31, 1141–1150. [Google Scholar] [CrossRef]
- Hou, T.H.; Chang, J.Y.; Tsai, C.C.; Hsu, T.W. 3D Numerical Simulation of Kuroshio-induced wake near Green Island, Taiwan. J. Mar. Sci. Tech. TAIW 2020, 29, 7. [Google Scholar] [CrossRef]
- Hou, T.H.; Chang, J.Y.; Tsai, C.C.; Hsu, T.W. Three-Dimensional Simulations of Wind Effects on Green Island Wake. Water 2020, 12, 3039. [Google Scholar] [CrossRef]
- Chen, F. The Kuroshio Power Plant; Springer: Cham, Switzerland, 2013. [Google Scholar]
- Hsu, T.W.; Liau, J.M.; Liang, S.J.; Tzang, S.Y.; Doong, D.J. Assessment of Kuroshio current power test site of Green Island, Taiwan. Renew. Energy 2015, 81, 853–863. [Google Scholar] [CrossRef]
- Phillips, O.M. The Dynamics of the Upper Ocean; Cambridge University Press: Cambridge, UK, 1977. [Google Scholar]
- Kinnmark, I. The Shallow-Water Wave Equations: Formulation, Analysis and Application; Springer: Berlin, Germany, 1986. [Google Scholar]
- Mei, C.C. The Applied Dynamics of Ocean Surface Waves; World Scientific: Singapore, 1989. [Google Scholar]
- Tan, W.Y. Shallow Water Hydrodynamics: Mathematical Theory and Numerical Solution fora Two-Dimensional System of Shallow-Water Equations; Elsevier: Singapore, 1992. [Google Scholar]
- Martin, J.L.; McCutcheon, S.C. Hydrodynamics and Transport for Water Quality Modeling; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Vreugdenhil, C.B. Numerical Methods for Shallow-Water Flow; Springer Science & BusinessMedia: Singapore, 2013. [Google Scholar]
- Peregrine, D.H. Long waves on a beach. J. Fluid Mech. 1967, 27, 815–827. [Google Scholar] [CrossRef]
- Nwogu, O. Alternative form of Boussinesq equations for nearshore wave propagation. J. Waterw. Port. Coast. Ocean. Eng. 1993, 119, 618–638. [Google Scholar] [CrossRef] [Green Version]
- Madsen, P.A.; Murray, R.; Sorensen, O.R. A new form of the Boussinesq equations with improved linear dispersion characteristics. Coast. Eng. 1991, 15, 371–388. [Google Scholar] [CrossRef]
- Casulli, V. Semi-implicit finite difference methods for two-dimensional shallow water equations. J. Comput. Phys. 1990, 86, 56–74. [Google Scholar] [CrossRef]
- Casulli, V.; Stalelling, G.S. Numerical simulation of 3D quasi-hydrostatic, free surface flows. J. Hydraul. Eng. 1998, 124, 678–686. [Google Scholar] [CrossRef]
- Casulli, V. A semi-implicit finite difference method for non-hydrostatic, free surface flows. Int. J. Numer. Methods Fluids 1999, 30, 425–440. [Google Scholar] [CrossRef]
- Namin, M.M.; Lin, B.; Falconer, R.A. An implicit numerical algorithm for solving non-hydrostatic free-surface flow problems. Int. J. Numer. Methods Fluids 2001, 35, 341–356. [Google Scholar] [CrossRef]
- Casulli, V.; Zanolli, P. Semi-implicit numerical modeling of nonhydrostatic free surface flows for environmental problems. Math. Comput. Model. 2002, 36, 1131–1149. [Google Scholar] [CrossRef]
- Lin, P.; Li, C.W. A σ-coordinate three-dimensional numerical model for surface wave propagation. Int. J. Numer. Meth. Fluids 2002, 38, 1045–1068. [Google Scholar] [CrossRef]
- Zijlema, M.; Stelling, G.S. Further experiences with computing non-hydrostatic free-surface flows involving water waves. Int. J. Numer. Methods Fluids 2005, 48, 169–197. [Google Scholar] [CrossRef]
- Waters, R.A. A semi-implicit finite element model for non-hydrostatic (dispersive) surface waves. Int. J. Numer. Methods Fluids 2005, 49, 721–737. [Google Scholar] [CrossRef]
- Fringer, O.B.; Gerritsen, M.; Street, R.L. An unstructured-grid, finite-volume, nonhydrostatic, parallel coastal ocean simulator. Ocean Model. 2006, 14, 139–173. [Google Scholar] [CrossRef]
- Yamazaki, Y.; Kowalik, Z.; Cheung, K.F. Depth-averaged non-hydrostatic model for wave breaking and run-up. Int. J. Numer. Methods Fluids 2009, 61, 473–497. [Google Scholar] [CrossRef]
- Wei, Z.P.; Jia, Y.F. Simulation of nearshore wave processes by a depth-integrated non-hydrostatic finite element model. Coast. Eng. 2014, 83, 93–107. [Google Scholar] [CrossRef]
- Lynett, P.; Liu, P.L.F. A two-layer approach to wave modeling. Proc. R. Soc. Lond. Ser. A 2004, 460, 2637–2669. [Google Scholar] [CrossRef]
- Pan, W.; Kramer, S.C.; Piggott, M.D. Multi-layer non-hydrostatic free surface modelling using the discontinuous Galerkin method. Ocean Model. 2019, 134, 68–83. [Google Scholar] [CrossRef]
- Pan, W.; Kramer, S.C.; Matthew, D.; Piggott, M.D. A σ-coordinate non-hydrostatic discontinuous finite element coastal ocean Model. Ocean Model. 2021, 157, 101732. [Google Scholar] [CrossRef]
- Liang, S.J.; Tang, J.H.; Wu, M.S. Solution of shallow-water equations using least-squares finite-element method. Acta Mech. Sin. 2008, 24, 523–532. [Google Scholar] [CrossRef]
- Liang, S.J.; Hsu, T.W. Least-Squares finite-element method for shallow-water equations with source terms. Acta Mech. Sin. 2009, 25, 597–610. [Google Scholar] [CrossRef]
- Gunzburger, M. Finite Element Methods for Viscous Incompressible Flows: A Guide to Theory, Practice and Algorithms; NASA STI/Recon Technical Report A; Academic Press: Cambridge, MA, USA, 1989; Volume 91, p. 30750. [Google Scholar]
- Laible, J.P.; Pinder, G.F. Solution of the shallow water equations by least squares collocation. Water Resour. Res. 1993, 29, 445–455. [Google Scholar] [CrossRef]
- Jiang, B.-N. The Least-Squares Finite Element Method—Theory and Applications in Computational Fluid Dynamics and Electromagnetics; Springer: Berlin, Germany, 1998. [Google Scholar]
- Caldeira, R.M.A.; Marchesiello, P.; Nezlin, N.P.; DiGiacomo, P.M.; McWilliams, J.C. Island wakes in the Southern California Bight. J. Geophys. Res. Ocean. Atmos. 2005, 110, C11012. [Google Scholar] [CrossRef]
- Doong, D.J.; Wu, L.C. Use of Microwave Radar Backscatter for Green Island Wake Observation and Analysis. In Ministry of Science and Technology (MOST) of Taiwan Project Report; Ministry of Science and Technology (MOST) of Taiwan: Taipei, Taiwan, 2016. (In Chinese) [Google Scholar]
- Borge, J.C.N.; Reichert, K.; Dittmer, J. Use of nautical radar as a wave monitoring instrument. Coast. Eng. 1999, 37, 331–342. [Google Scholar] [CrossRef]
- Saad, Y. Iterative Methods for Sparse Linear Systems; SIAM: Philadelphia, PA, USA, 2003. [Google Scholar]
- Liang, S.J.; Young, C.C.; Dai, C.; Wu, N.J.; Hsu, T.W. Simulation of ocean circulation of Dongsha water using non-hydrostatic shallow-water model. Water 2020, 12, 2832. [Google Scholar] [CrossRef]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, S.-J.; Doong, D.-J.; Chao, W.-T. Solution of Shallow-Water Equations by a Layer-Integrated Hydrostatic Least-Squares Finite-Element Method. Water 2022, 14, 530. https://doi.org/10.3390/w14040530
Liang S-J, Doong D-J, Chao W-T. Solution of Shallow-Water Equations by a Layer-Integrated Hydrostatic Least-Squares Finite-Element Method. Water. 2022; 14(4):530. https://doi.org/10.3390/w14040530
Chicago/Turabian StyleLiang, Shin-Jye, Dong-Jiing Doong, and Wei-Ting Chao. 2022. "Solution of Shallow-Water Equations by a Layer-Integrated Hydrostatic Least-Squares Finite-Element Method" Water 14, no. 4: 530. https://doi.org/10.3390/w14040530





