Hydro-Damage Properties of Red-Bed Mudstone Failures Induced by Nonlinear Seepage and Diffusion Effect
Abstract
:1. Introduction
2. Experimental Design on Liquid Flow Observation of Rocks Failure
2.1. Principles of Hydro-Damage Definition and Rock Mechanic Tests
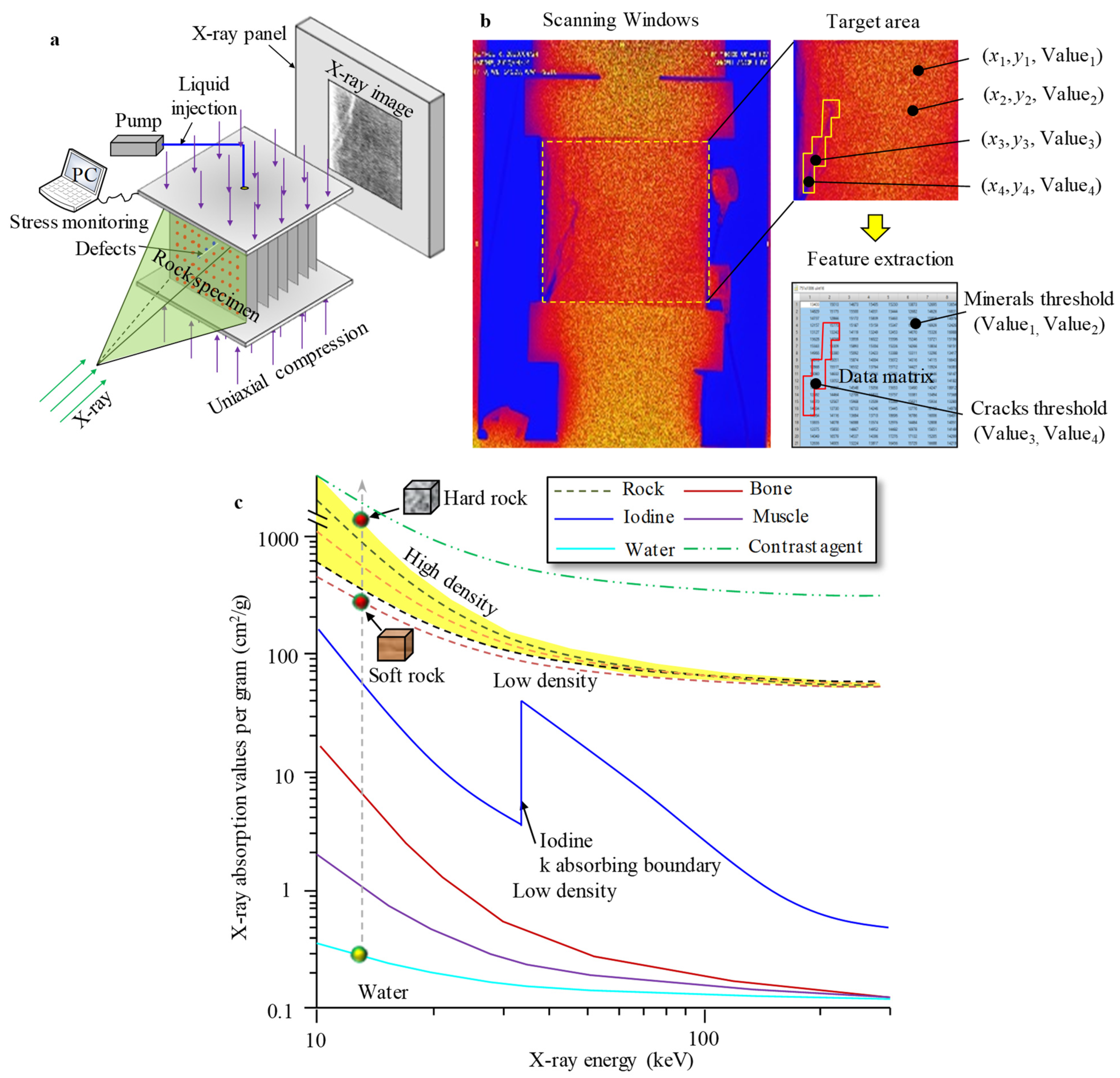
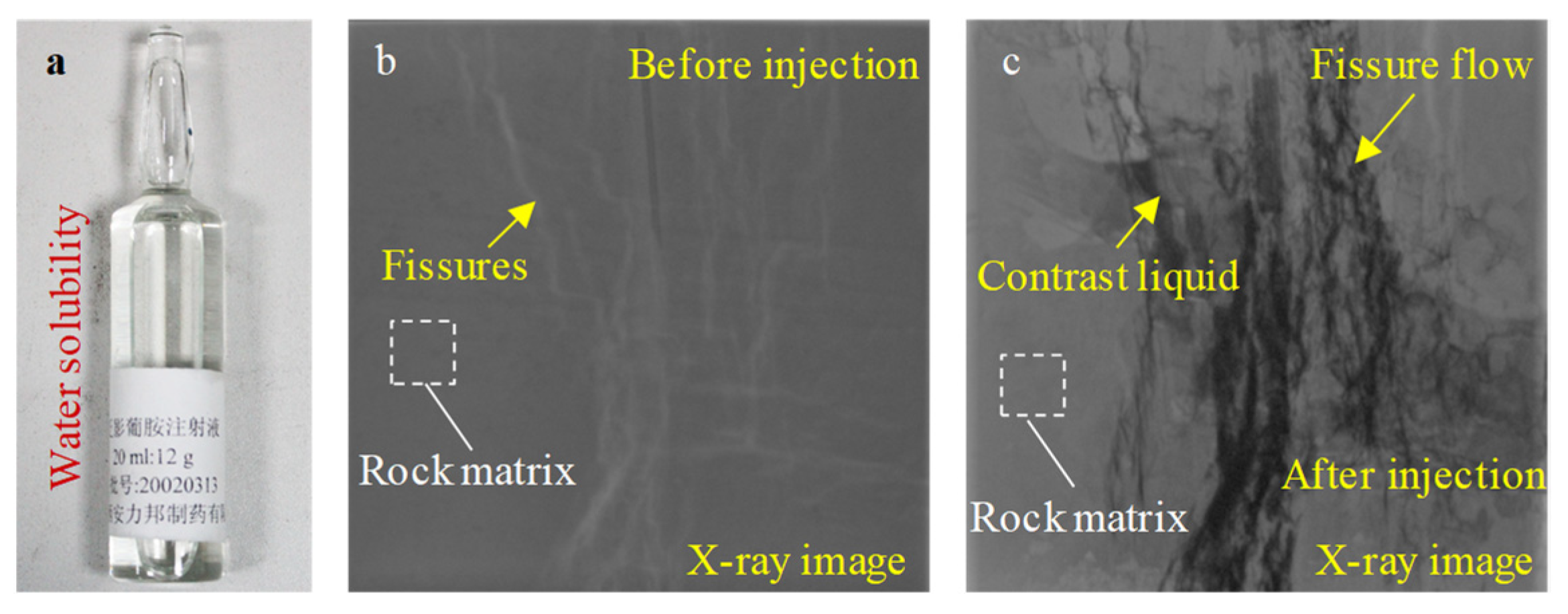
2.2. Enhanced X-ray Image Digital Radiology Techniques and Sample Preparation for Hydro-Rock Testing
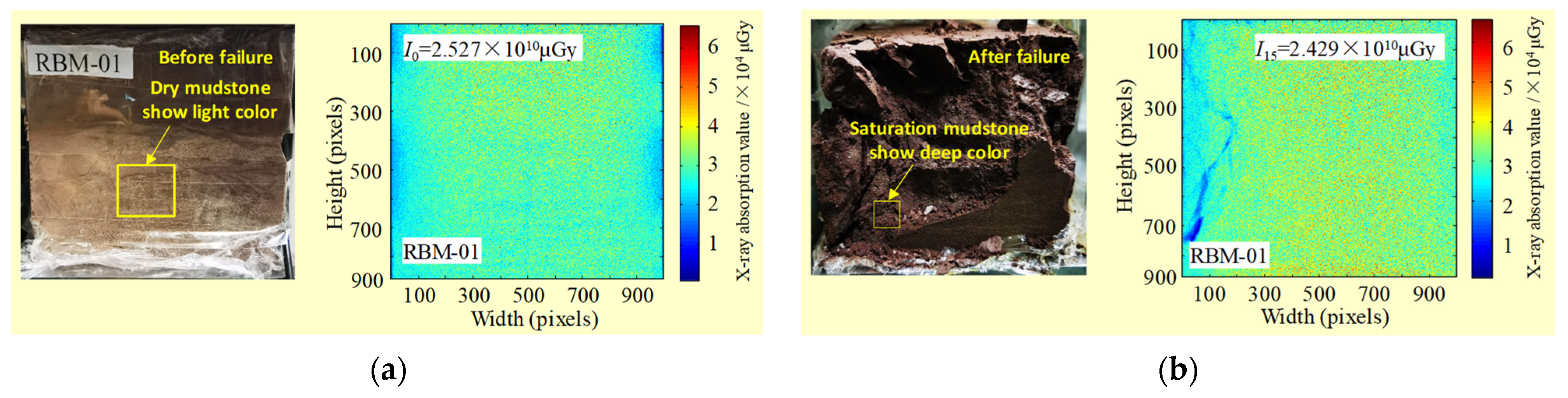
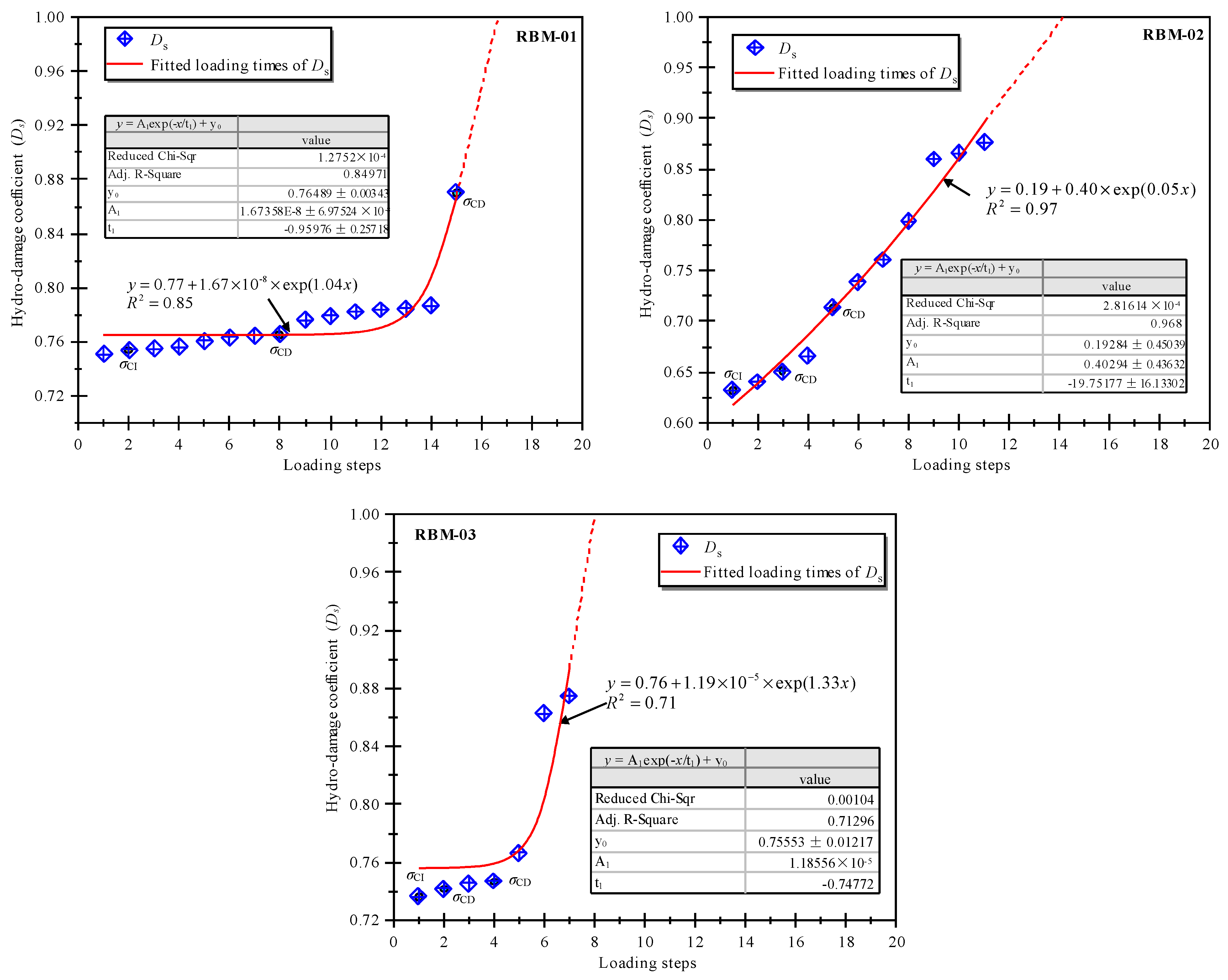
3. Hydro-Damage Evolution with Red-Bed Mudstone Failures
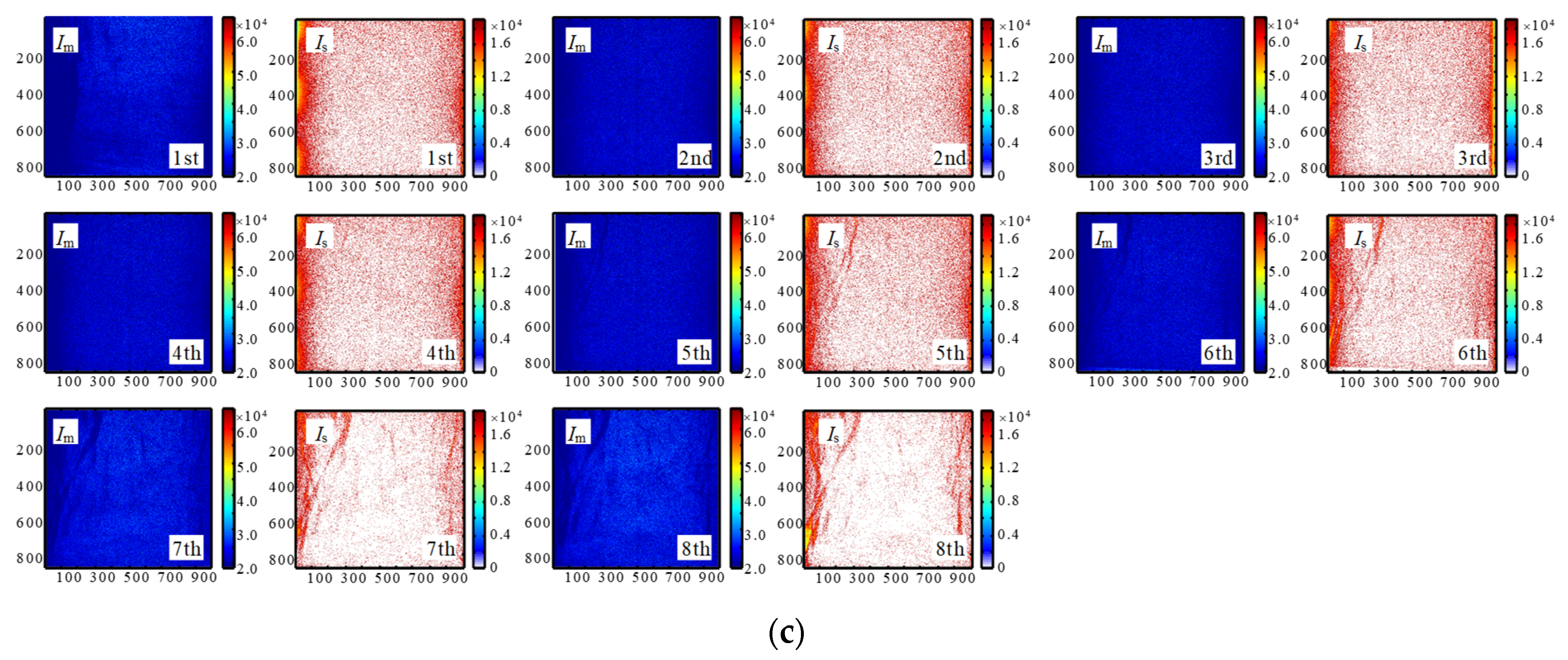
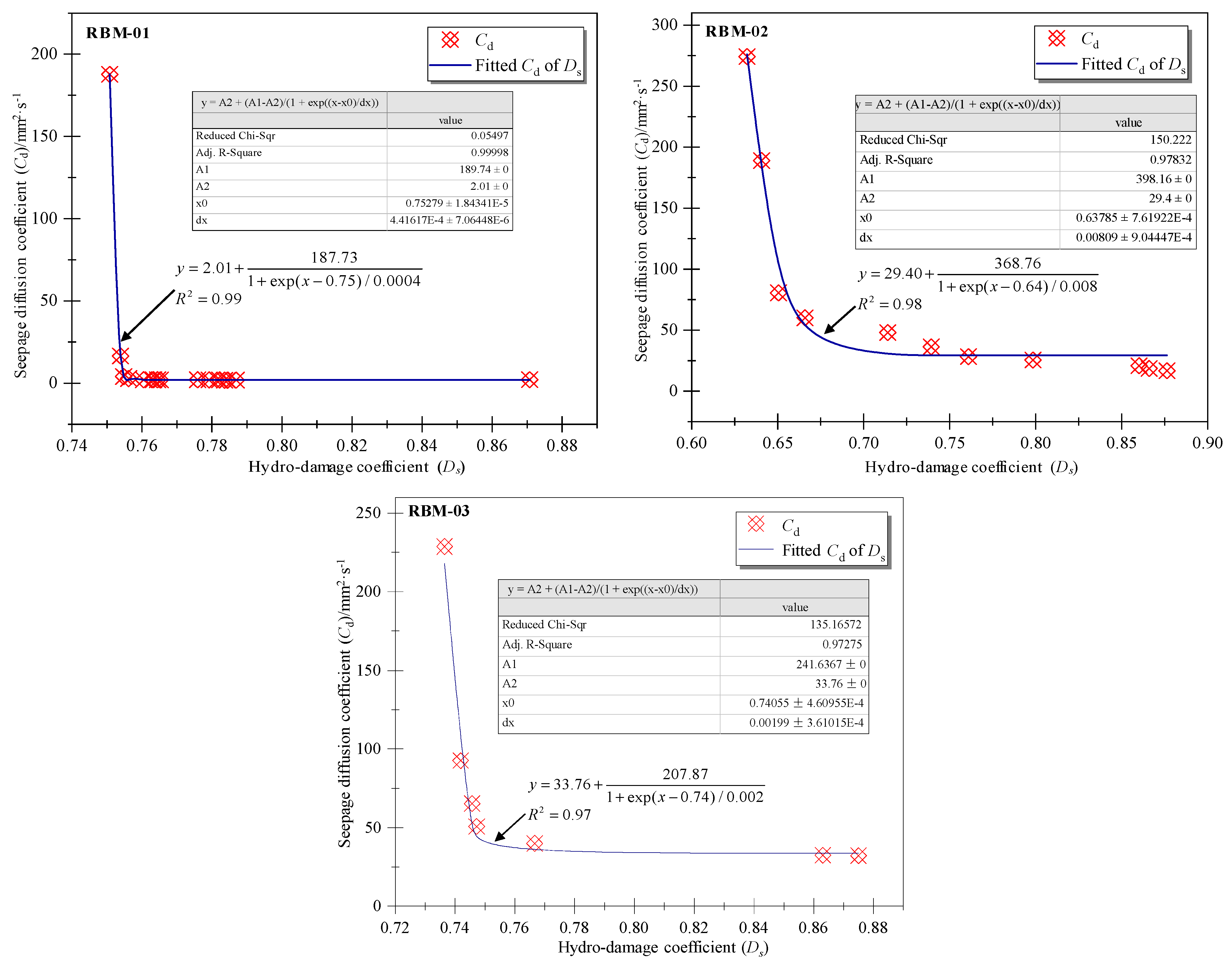
4. Seepage and Diffusion Coefficient Evolution with Rock Failures
5. Conclusions
- (1)
- During the failure of red-bed mudstone specimens, hydrodynamic force intensifies the fluid-filled fissure, and the interaction between the fissure flow and solid matrix introduces the dispersion and attenuation of an elastic wave. Furthermore, the fluid-filled fissure undergoes a stable development process with the crack growth.
- (2)
- The X-ray image analysis of the red-bed mudstone specimen failure indicates that the spatial morphology distribution of the pipeline fluid transition to fissure flow showed the physical phenomena of nonlinear seepage and abnormal diffusion. Therefore, the red-bed mudstone pipeline fluid fissure induces a dual mechanical behavior of nonlinear seepage and diffusion with significant seepage–diffusion effects under hydrodynamic force.
- (3)
- The statistical analysis of the relationship between the mudstone hydro-damage factor and seepage–diffusion coefficient indicates that the seepage–diffusion coefficient of the mudstone shows a nonlinear decreasing trend under hydrodynamic force with the increase in water damage aggravation of mudstone specimens; the analysis also indicates that the initial seepage–diffusion coefficient was large under the initial rupture state of the mudstone specimens. The saturation degree of the mudstone specimen increases gradually against the gradual decrease in the saturated seepage velocity and diffusion flux. These results support a reasonable explanation for the seepage catastrophes of red-bed mudstone masses from the material scale.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, M.; Yin, Y.P.; Huang, B.L. Mechanisms of rainfall-induced landslides in gently inclined red beds in the eastern Sichuan Basin, SW China. Landslides 2015, 12, 973–983. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, Q.; Hu, Z.M. Effects of rainwater softening on red mudstone of deep-seated landslide, Southwest China. Eng. Geol. 2016, 204, 1–13. [Google Scholar] [CrossRef]
- Yu, Y.; Shen, M.F.; Sun, H.Y.; Shan, Y.Q. Robust design of siphon drainage method for stabilizing rainfall-induced landslides. Eng. Geol. 2019, 249, 186–197. [Google Scholar] [CrossRef]
- Chen, J.; Dai, F.C.; Xu, L.; Chen, S.; Wang, P.F.; Long, W.; Shen, N.Q. Properties and microstructure of a natural slip zone in loose deposits of red beds, southwestern China. Eng. Geol. 2014, 183, 53–64. [Google Scholar] [CrossRef]
- Zhou, C.Y.; Yu, L.; You, F.F.; Liu, Z.; Liang, Y.H.; Zhang, L.H. Coupled seepage and stress model and experiment verification for creep behavior of soft rock. Int. J. Geomech. 2020, 9, 20. [Google Scholar] [CrossRef]
- Ma, J.J.; Wang, J. A stress-induced permeability evolution model for fissured porous media. Rock Mech. Rock Eng. 2016, 49, 477–485. [Google Scholar] [CrossRef]
- Zhu, Y.J.; Liu, X.L.; Wang, E.Z. Influence of impoundment gravity and pore pressure on reactivation of faults. Geomech. Geophys. Geo-Energy Geo-Resour. 2020, 6, 64. [Google Scholar] [CrossRef]
- Yang, S.Q.; Tian, W.L.; Jing, H.W.; Huang, Y.H.; Yang, X.X.; Meng, B. Deformation and damage failure behavior of mudstone specimens under single-stage and multi-stage triaxial compression. Rock Mech. Rock Eng. 2019, 52, 673–689. [Google Scholar] [CrossRef]
- Wen, T.; Tang, H.M.; Huang, L.; Wang, Y.K.; Ma, J.W. Energy evolution: A new perspective on the failure mechanism of purplish-red mudstones from the Three Gorges Reservoir area, China. Eng. Geol. 2020, 264, 105350. [Google Scholar] [CrossRef]
- Lu, Y.; Wu, B.; He, M.Q.; Wang, L.G.; Ma, D.; Huang, Z. Prediction of fracture evolution and groundwater inrush from karst collapse pillars in coal seam floors: A micromechanics-based stress-seepage-damage coupled modeling approach. Geofluids 2020, 2020, 8830304. [Google Scholar] [CrossRef]
- Zhu, C.; Xu, X.D.; Wang, X.T.; Xiong, F.; Tao, Z.G.; Lin, Y.; Chen, J. Experimental investigation on nonlinear flow anisotropy behavior in fracture media. Geofluids 2019, 2019, 5874849. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Khorshidian, H.; Mohammadi, M.; Sanati-Nezhad, A.; Hejazi, S.H. Functionalized multiscale visual models to unravel flow and transport physics in porous structures. Water Res. 2020, 175, 115676. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Liu, X.; Ye, Z.; Wang, E. Experimental investigation of the nonlinear evolution from pipe flow to fissure flow during carbonate rock failures. Bull. Eng. Geol. Environ. 2021, 80, 4459–4470. [Google Scholar] [CrossRef]
- Sun, H.; Liu, X.; Ye, Z.; Wang, E. A new proposed method for observing fluid in rock fractures using enhanced x-ray images from digital radiography. Geomech. Geophys. Geo-Energy Geo-Resour. 2021, 8, 10. [Google Scholar] [CrossRef]
- Sun, H.; Liu, X.L.; Zhu, J.B. Correlational fractal characterisation of stress and acoustic emission during coal and rock failure under multilevel dynamic loading. Int. J. Rock Mech. Min. Sci. 2019, 117, 1–10. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Zhao, G.F.; Li, Q. Acoustic emission uncovers thermal damage evolution of rock. Int. J. Rock Mech. Min. Sci. 2020, 132, 104388. [Google Scholar] [CrossRef]
- Zimmerman, R.W.; Al-Yaarubi, A.; Pain, C.C.; Grattoni, C.A. Non-linear regimes of fluid flow in rock fractures. Int. J. Rock Mech. Min. Sci. 2004, 41, 384. [Google Scholar] [CrossRef]
- Rong, G.; Cheng, L.; He, R.H.; Quan, J.S.; Tan, J. Investigation of critical non-linear flow behavior for fractures with different degrees of fractal roughness. Comput. Geotech. 2021, 133, 104065. [Google Scholar] [CrossRef]
- Xiong, F.; Wei, W.; Xu, C.; Jiang, Q. Experimental and numerical investigation on nonlinear flow behaviour through three dimensional fracture intersections and fracture networks. Comput. Geotech. 2020, 121, 103446. [Google Scholar] [CrossRef]
- Xiong, F.; Jiang, Q.; Xu, C. Fast Equivalent Micro-Scale Pipe Network Representation of Rock Fractures Obtained by Computed Tomography for Fluid Flow Simulations. Rock Mech. Rock Eng. 2021, 54, 937–953. [Google Scholar] [CrossRef]
- Wang, L.Q.; Yin, Y.P.; Huang, B.L.; Dai, Z.W. Damage evolution and stability analysis of the Jianchuandong Dangerous Rock Mass in the Three Gorges Reservoir Area. Eng. Geol. 2020, 265, 105439. [Google Scholar] [CrossRef]
- Sun, H.; Du, W.; Liu, C. Uniaxial Compressive Strength Determination of Rocks Using X-ray Computed Tomography and Convolutional Neural Networks. Rock Mech. Rock Eng. 2021, 54, 4225–4237. [Google Scholar] [CrossRef]
- Raghavan, R. Fractional derivatives: Application to transient flow. J. Pet. Sci. Eng. 2011, 80, 7–13. [Google Scholar] [CrossRef]





| Model | Rated Voltage | Initial Flow | Motor Speed | Maximum Lift |
|---|---|---|---|---|
| LS-0412 | 1.2 A | 2.0 L/min | 2200 r/min | 30 m |
| Gauge Diameter (mm) | Normal Flow Range (m3/h) | Expand Flow Range (m3/h) | Typical Withstand Pressure (MPa) |
|---|---|---|---|
| DN4 | 0.04–0.25 | 0.04–0.25 | 6.30 |
| Number | Peak Loading of Multilevel Stress (Mpa) and Hydro-Damage Coefficients | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| σ1 | σ2 | σ3 | σ4 | σ5 | σ6 | σ7 | σ8 | σ9 | σ10 | σ11 | σ12 | σ13 | σ14 | σ15 | |
| Ds1 | Ds2 | Ds3 | Ds4 | Ds5 | Ds6 | Ds7 | Ds8 | Ds9 | Ds10 | Ds11 | Ds12 | Ds13 | Ds14 | Ds15 | |
| RBM-01 | 3.82 | 5.56 | 7.66 | 10.12 | 12.76 | 15.58 | 18.20 | 20.74 | 22.32 | 24.16 | 26.44 | 28.52 | 30.96 | 33.30 | 36.76 |
| 0.354 | 0.364 | 0.372 | 0.391 | 0.408 | 0.405 | 0.413 | 0.413 | 0.518 | 0.622 | 0.625 | 0.629 | 0.731 | 0.843 | 0.907 | |
| RBM-02 | 3.32 | 4.60 | 7.14 | 9.90 | 11.72 | 10.48 | 3.02 | 3.34 | 3.34 | 3.20 | 2.58 | N/A | N/A | N/A | N/A |
| 0.724 | 0.701 | 0.707 | 0.713 | 0.725 | 0.753 | 0.772 | 0.789 | 0.820 | 0.870 | 0.923 | N/A | N/A | N/A | N/A | |
| RBM-03 | 3.72 | 5.68 | 8.16 | 9.02 | 6.16 | 2.24 | 0.92 | N/A | N/A | N/A | N/A | N/A | N/A | N/A | N/A |
| 0.444 | 0.448 | 0.714 | 0.811 | 0.942 | 0.948 | 0.972 | N/A | N/A | N/A | N/A | N/A | N/A | N/A | N/A | |
| Loading Steps | RBM-01 | RBM-02 | RNM-03 | |||
|---|---|---|---|---|---|---|
| Thresholds(μGy) | Seepage–Diffusion Coefficient (mm2/s) | Thresholds (μGy) | Seepage–Diffusion Coefficient (mm2/s) | Thresholds (μGy) | Seepage–Diffusion Coefficient (mm2/s) | |
| 1st | 26,000 | 187.69 | 19,000 | 274.28 | 19,000 | 409.95 |
| 2nd | 26,000 | 16.45 | 19,000 | 188.97 | 19,000 | 228.74 |
| 3rd | 26,000 | 4.02 | 19,000 | 80.51 | 19,000 | 92.63 |
| 4th | 26,000 | 2.84 | 19,000 | 60.03 | 19,000 | 65.33 |
| 5th | 26,000 | 2.01 | 19,000 | 48.00 | 19,000 | 50.73 |
| 6th | 26,000 | 2.04 | 19,000 | 36.33 | 19,000 | 39.95 |
| 7th | 26,000 | 2.01 | 19,000 | 28.33 | 19,000 | 32.40 |
| 8th | 26,000 | 1.96 | 19,000 | 25.43 | N/A | N/A |
| 9th | 26,000 | 1.99 | 19,000 | 20.82 | N/A | N/A |
| 10th | 26,000 | 1.99 | 19,000 | 18.48 | N/A | N/A |
| 11th | 26,000 | 1.99 | 19,000 | 16.70 | N/A | N/A |
| 12th | 26,000 | 1.77 | N/A | N/A | N/A | N/A |
| 13th | 26,000 | 1.77 | N/A | N/A | N/A | N/A |
| 14th | 26,000 | 1.81 | N/A | N/A | N/A | N/A |
| 15th | 26,000 | 2.07 | N/A | N/A | N/A | N/A |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, Z.; Liu, X.; Dong, Q.; Wang, E.; Sun, H. Hydro-Damage Properties of Red-Bed Mudstone Failures Induced by Nonlinear Seepage and Diffusion Effect. Water 2022, 14, 351. https://doi.org/10.3390/w14030351
Ye Z, Liu X, Dong Q, Wang E, Sun H. Hydro-Damage Properties of Red-Bed Mudstone Failures Induced by Nonlinear Seepage and Diffusion Effect. Water. 2022; 14(3):351. https://doi.org/10.3390/w14030351
Chicago/Turabian StyleYe, Zhenni, Xiaoli Liu, Qinxi Dong, Enzhi Wang, and Huan Sun. 2022. "Hydro-Damage Properties of Red-Bed Mudstone Failures Induced by Nonlinear Seepage and Diffusion Effect" Water 14, no. 3: 351. https://doi.org/10.3390/w14030351
APA StyleYe, Z., Liu, X., Dong, Q., Wang, E., & Sun, H. (2022). Hydro-Damage Properties of Red-Bed Mudstone Failures Induced by Nonlinear Seepage and Diffusion Effect. Water, 14(3), 351. https://doi.org/10.3390/w14030351







