A Short Cost-Effective Methodology for Tracing the Temporal and Spatial Anthropogenic Inputs of Micropollutants into Ecosystems: Verified Mass-Balance Approach Applied to River Confluence and WWTP Release
Abstract
:1. Introduction
2. Sample Collection and Analytical Methods
3. Materials and Methods Developed
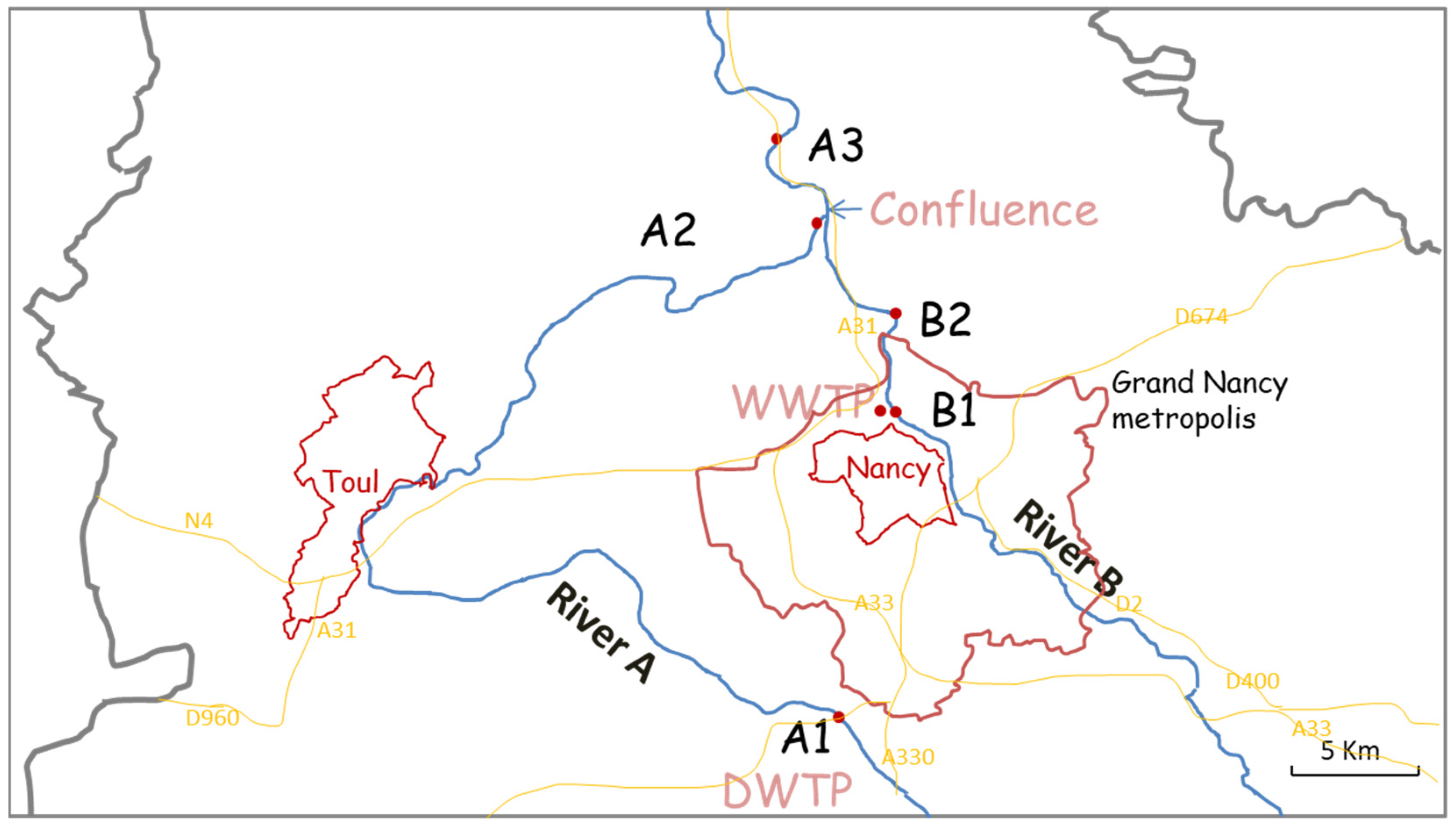
3.1. Objective and Constraints of the Sampling Zones
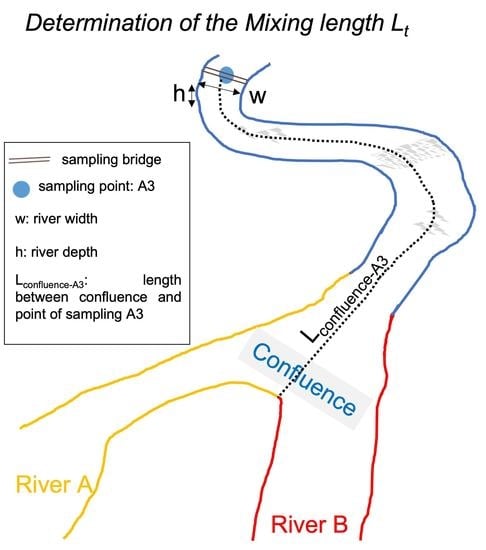
3.2. Mixing Length
| Coef | Coef′ | Coef″ | Model Equation | Lt (Confluence) (km) | Lt (WWTP) (km) | References |
|---|---|---|---|---|---|---|
| 0.4 | 0.6 | 0.667 | 4.3 | 2.1 | [30,31] | |
| 0.125 | 0.16 | 0.78 | 5.0 | 2.5 | [29,32,33] | |
| 0.075 | 0.23 | 0.33 | 2.2 | 1.1 | [34,35,36,37] | |
| 0.0759 | 0.6 | 0.133 | 0.9 | 0.4 | [38] |
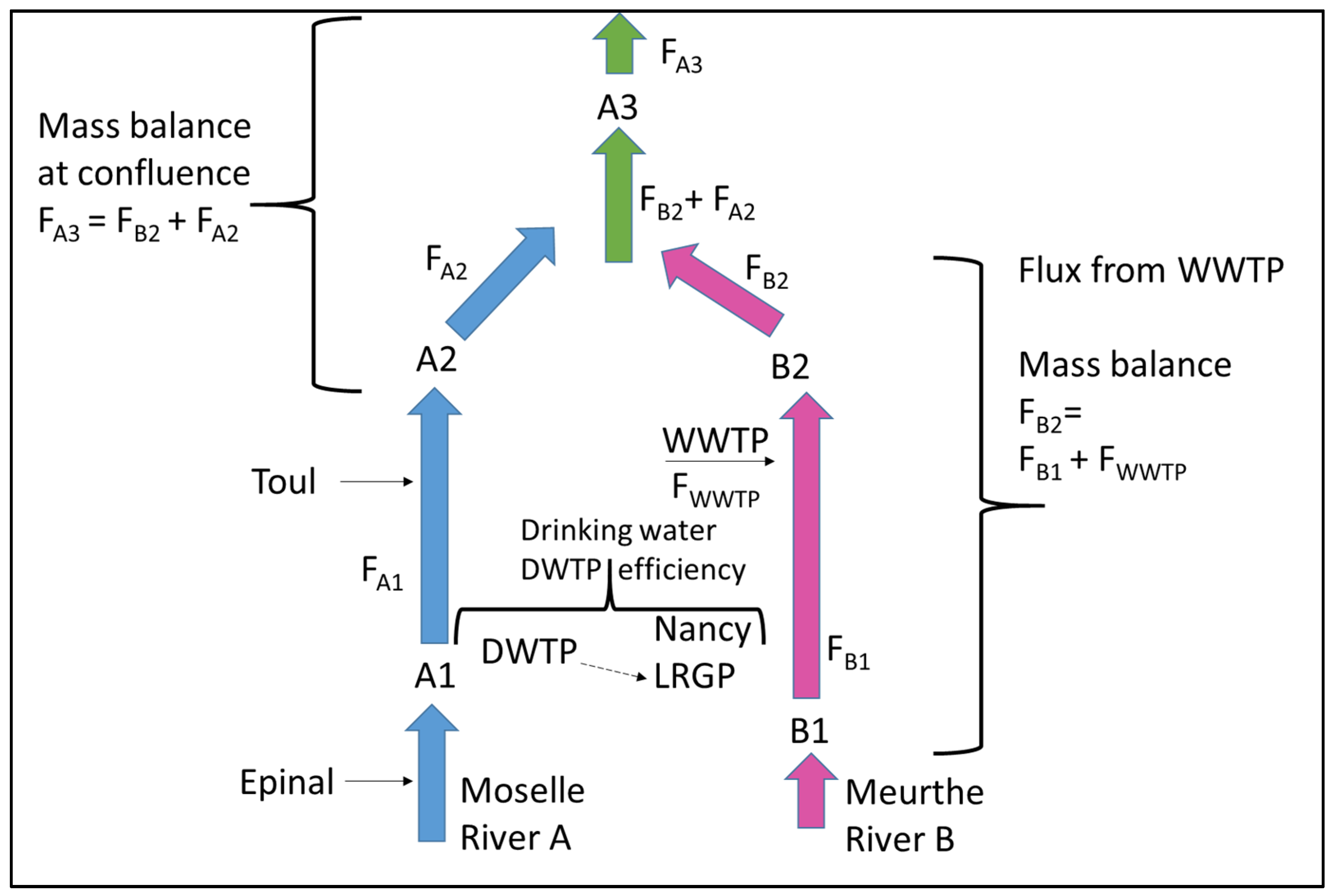
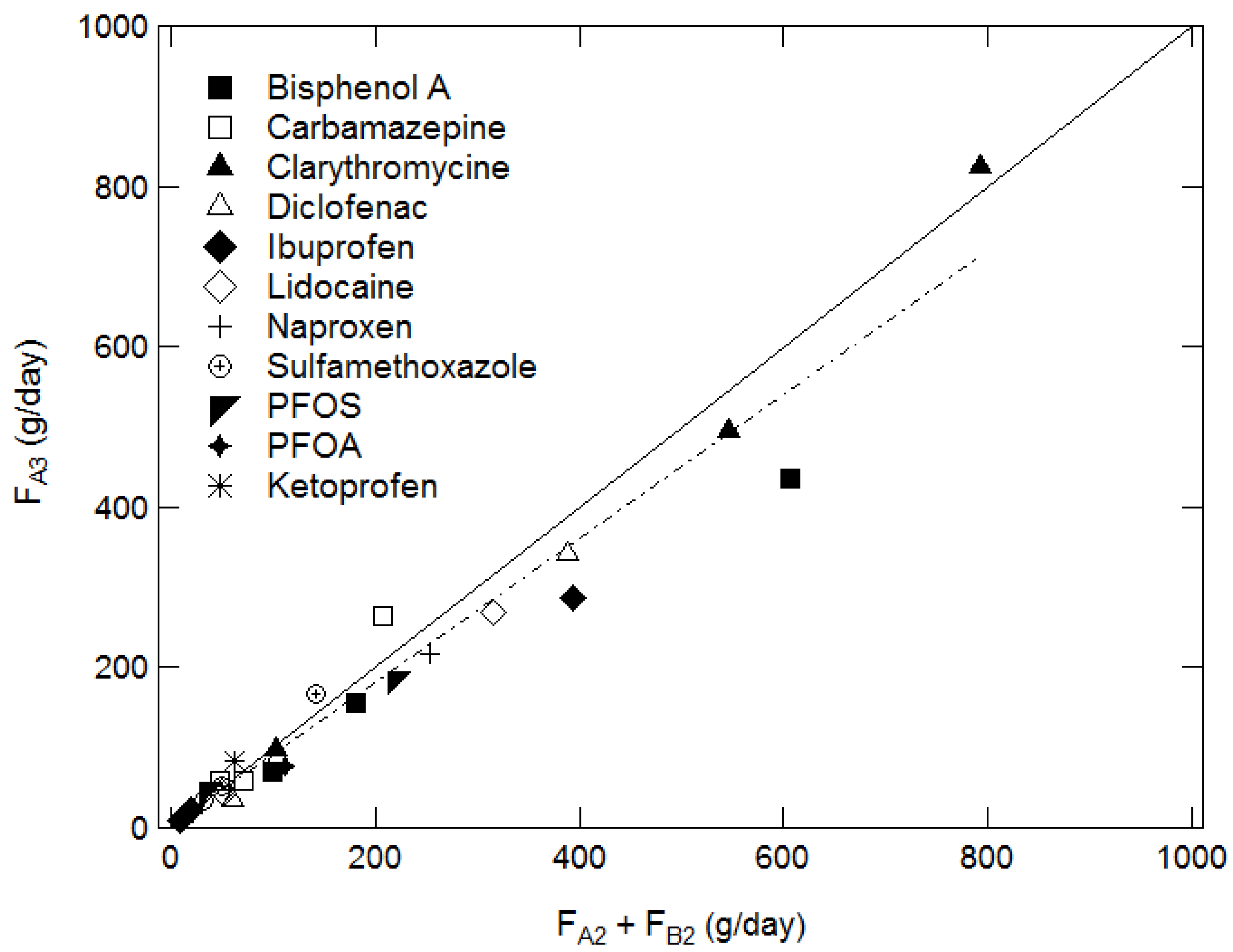
3.3. Verification of the Mixing Length Method by Using Mass Balance at a River Confluence
4. Results and Discussions
4.1. Overall Study of the Results
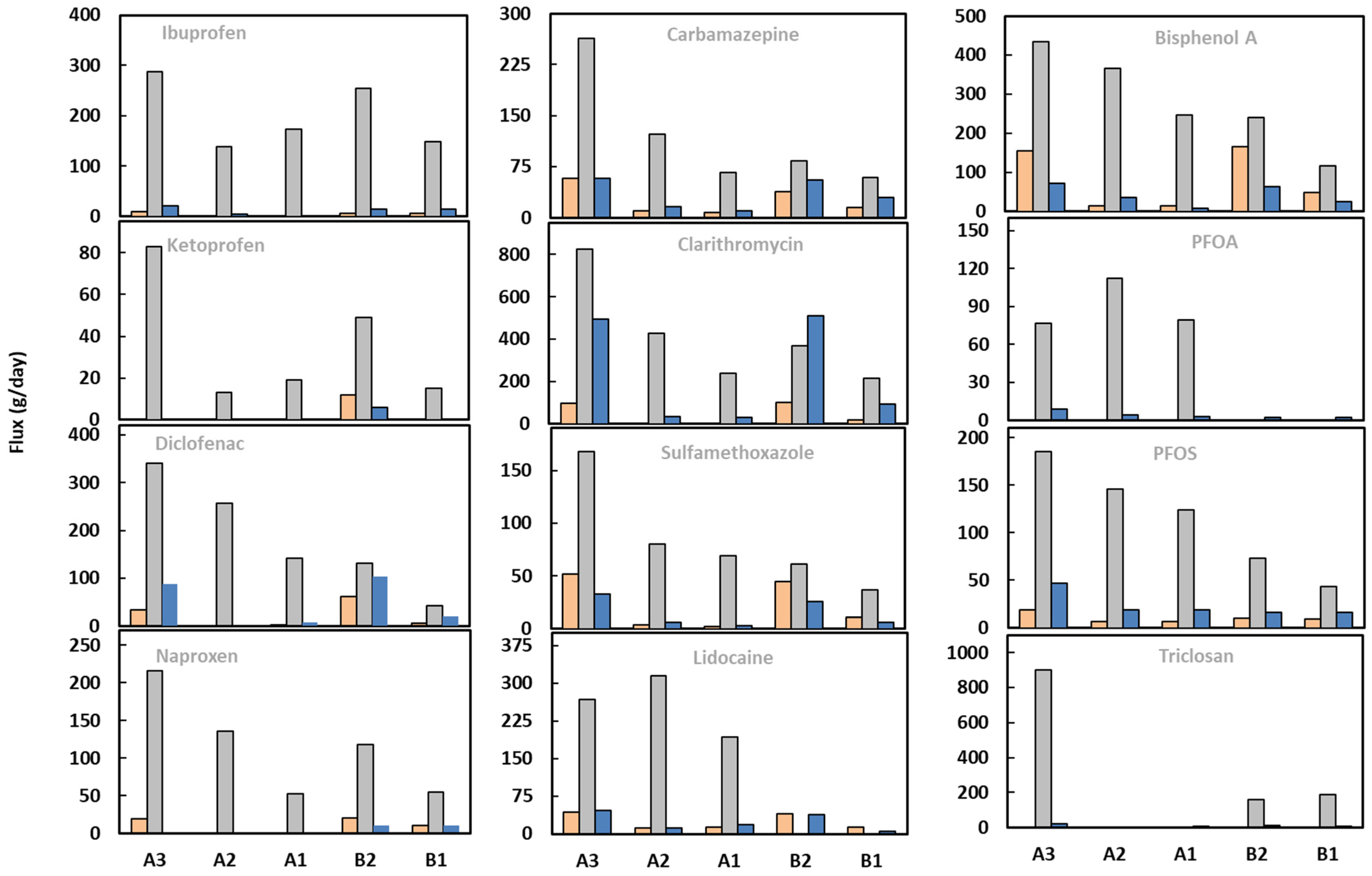
4.2. Release of Micropollutants from WWTP
4.3. Drinking Water Assessment
4.4. Spatial Variations of Micropollutants in Rivers: Effect of Hydrological and Anthropogenic Factors
4.5. Temporal Variations of Micropollutants in Rivers
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liu, H.; Nkundabose, J.P.; Chen, H.; Yang, L.; Meng, C.; Ding, N. Decontamination of ibuprofen micropollutants from water based on visible-light-responsive hybrid photocatalyst. J. Environ. Chem. Eng. 2022, 10, 107154. [Google Scholar] [CrossRef]
- Gomes, I.B.; Simões, L.C.; Simões, M. The effects of emerging environmental contaminants on Stenotrophomonas maltophilia isolated from drinking water in planktonic and sessile states. Sci. Total Environ. 2018, 643, 1348–1356. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kumar, R.; Vuppaladadiyam, A.K.; Antunes, E.; Whelan, A.; Fearon, R.; Sheehan, M.; Reeves, L. Emerging contaminants in biosolids: Presence, fate and analytical techniques. Emerg. Contam. 2022, 8, 162–194. [Google Scholar] [CrossRef]
- Richardson, S.D. Water Analysis: Emerging Contaminants and Current Issues. Anal. Chem. 2003, 75, 4943. [Google Scholar] [CrossRef] [Green Version]
- Stamm, C.; Räsänen, K.; Burdon, F.; Altermatt, F.; Jokela, J.; Joss, A.; Ackermann, M.; Eggen, R. Unravelling the Impacts of Micropollutants in Aquatic Ecosystems. In Advances in Ecological Research; Elsevier: Amsterdam, The Netherlands, 2016; Volume 55, pp. 183–223. [Google Scholar] [CrossRef]
- Gallé, T.; Pittois, D.; Bayerle, M.; Braun, C. An immission perspective of emerging micropollutant pressure in Luxembourgish surface waters: A simple evaluation scheme for wastewater impact assessment. Environ. Pollut. 2019, 253, 992–999. [Google Scholar] [CrossRef]
- Yang, L.; Xu, L.; Bai, X.; Jin, P. Enhanced visible-light activation of persulfate by Ti3+ self-doped TiO2/graphene nanocomposite for the rapid and efficient degradation of micropollutants in water. J. Hazard. Mater. 2019, 365, 107–117. [Google Scholar] [CrossRef]
- Liu, J.; Lu, G.; Yang, H.; Dang, T.; Yan, Z. Ecological impact assessment of 110 micropollutants in the Yarlung Tsangpo River on the Tibetan Plateau. J. Environ. Manag. 2020, 262, 110291. [Google Scholar] [CrossRef]
- Castiglioni, S.; Davoli, E.; Riva, F.; Palmiotto, M.; Camporini, P.; Manenti, A.; Zuccato, E. Mass balance of emerging contaminants in the water cycle of a highly urbanized and industrialized area of Italy. Water Res. 2018, 131, 287–298. [Google Scholar] [CrossRef]
- Boxall, A.B.A.; Rudd, M.A.; Brooks, B.W.; Caldwell, D.J.; Choi, K.; Hickmann, S.; Innes, E.; Ostapyk, K.; Staveley, J.P.; Verslycke, T.; et al. Pharmaceuticals and Personal Care Products in the Environment: What Are the Big Questions? Environ. Health Perspect. 2012, 120, 1221–1229. [Google Scholar] [CrossRef]
- Richardson, S.D.; Kimura, S.Y. Water Analysis: Emerging Contaminants and Current Issues. Anal Chem. 2020, 92, 473–505. [Google Scholar] [CrossRef]
- Salvestrini, S.; Fenti, A.; Chianese, S.; Iovino, P.; Musmarra, D. Diclofenac sorption from synthetic water: Kinetic and thermodynamic analysis. J. Environ. Chem. Eng. 2020, 8, 104105. [Google Scholar] [CrossRef]
- Trapido, M.; Epold, I.; Bolobajev, J.; Dulova, N. Emerging micropollutants in water/wastewater: Growing demand on removal technologies. Environ. Sci. Pollut. Res. 2014, 21, 12217–12222. [Google Scholar] [CrossRef] [PubMed]
- Reinstorf, F.; Strauch, G.; Schirmer, K.; Gläser, H.-R.; Möder, M.; Wennrich, R.; Osenbrück, K. Mass fluxes and spatial trends of xenobiotics in the waters of the city of Halle, Germany. Environ. Pollut. 2008, 152, 452–460. [Google Scholar] [CrossRef]
- Feitosa-Felizzola, J.; Chiron, S. Occurrence and distribution of selected antibiotics in a small Mediterranean stream (Arc River, Southern France). J. Hydrol. 2009, 364, 50–57. [Google Scholar] [CrossRef]
- Liu, W.-R.; Yang, Y.-Y.; Liu, Y.-S.; Zhang, L.-J.; Zhao, J.-L.; Zhang, Q.-Q.; Zhang, M.; Zhang, J.-N.; Jiang, Y.-X.; Ying, G.-G. Biocides in wastewater treatment plants: Mass balance analysis and pollution load estimation. J. Hazard. Mater. 2017, 329, 310–320. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Spina, F.; Gea, M.; Bicchi, C.; Cordero, C.; Schilirò, T.; Varese, G.C. Ecofriendly laccases treatment to challenge micropollutants issue in municipal wastewaters. Environ. Pollut. 2020, 257, 113579. [Google Scholar] [CrossRef] [PubMed]
- Barceló, D.; Žonja, B.; Ginebreda, A. Toxicity tests in wastewater and drinking water treatment processes: A complementary assessment tool to be on your radar. J. Environ. Chem. Eng. 2020, 8, 104262. [Google Scholar] [CrossRef]
- Sabri, N.A.; Schmitt, H.; Van Der Zaan, B.; Gerritsen, H.W.; Zuidema, T.; Rijnaarts, H.H.M.; Langenhoff, A.A.M. Prevalence of antibiotics and antibiotic resistance genes in a wastewater effluent-receiving river in the Netherlands. J. Environ. Chem. Eng. 2020, 8, 102245. [Google Scholar] [CrossRef]
- Luo, Y.L.; Guo, W.S.; Ngo, H.H.; Nghiem, L.D.; Hai, F.I.; Zhang, J.; Liang, S.; Wang, X.C. A review on the occurrence of micropollutants in the aquatic environment and their fate and removal during wastewater treatment. Sci. Total Environ. 2014, 473–474, 619–641. [Google Scholar] [CrossRef]
- Hatoum, R.; Potier, O.; Roques-Carmes, T.; Lemaitre, C.; Hamieh, T.; Toufaily, J.; Horn, H.; Borowska, E. Elimination of Micropollutants in Activated Sludge Reactors with a Special Focus on the Effect of Biomass Concentration. Water 2019, 11, 2217. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez Narvaez, O.M.; Peralta-Hernandez, J.M.; Goonetilleke, A.; Bandala, E.R. Treatment technologies for emerging contaminants in water: A review. Chem. Eng. J. 2017, 323, 361–380. [Google Scholar] [CrossRef] [Green Version]
- Gimeno, P.; Severyns, J.; Acuña, V.; Comas, J.; Corominas, L. Balancing environmental quality standards and infrastructure upgrade costs for the reduction of microcontaminant loads in rivers. Water Res. 2018, 143, 632–641. [Google Scholar] [CrossRef] [PubMed]
- Das, S.; Ray, N.M.; Wan, J.; Khan, A.; Chakraborty, T.; Ray, M.B. Micropollutants in Wastewater: Fate and Removal Processes. In Physico-Chemical Wastewater Treatment and Resource Recovery; BoD—Books on Demand: London, UK, 2017. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Gao, W.; Wang, Y.; Jiang, G. Suspect screening analysis of the occurrence and removal of micropollutants by GC-QTOF MS during wastewater treatment processes. J. Hazard. Mater. 2019, 376, 153–159. [Google Scholar] [CrossRef] [PubMed]
- Schwientek, M.; Guillet, G.; Rügner, H.; Kuch, B.; Grathwohl, P. A high-precision sampling scheme to assess persistence and transport characteristics of micropollutants in rivers. Sci. Total Environ. 2016, 540, 444–454. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ayoub, H.; Roques-Carmes, T.; Potier, O.; Koubaissy, B.; Pontvianne, S.; Lenouvel, A.; Guignard, C.; Mousset, E.; Poirot, H.; Toufaily, J.; et al. Iron-impregnated zeolite catalyst for efficient removal of micropollutants at very low concentration from Meurthe river. Environ. Sci. Pollut. Res. 2018, 25, 34950–34967. [Google Scholar] [CrossRef]
- Ayoub, H.; Roques-Carmes, T.; Potier, O.; Koubaissy, B.; Pontvianne, S.; Lenouvel, A.; Guignard, C.; Mousset, E.; Poirot, H.; Toufaily, J.; et al. Comparison of the removal of 21 micropollutants at actual concentration from river water using photocatalysis and photo-Fenton. SN Appl. Sci. 2019, 1, 836. [Google Scholar] [CrossRef] [Green Version]
- Elhadi, N.; Harrington, A.; Hill, I.; Lau, Y.L.; Krishnappan, B.G. River mixing—A state-of-the-art report. Can. J. Civ. Eng. 1984, 11, 585–609. [Google Scholar] [CrossRef]
- United States Environmental Protection Agency. Mixing Zone for River Confluence; United States Environmental Protection Agency: Washington, DC, USA, 2013.
- Katopodes, N.D. Free-Surface Flow: Environmental Fluid Mechanics; Butterworth-Heinemann: Ann Arbor, MI, USA, 2019. [Google Scholar] [CrossRef]
- Sayre, W.W. Natural mixing processes in rivers. In Environmental Impact on Rivers; Chapter 6; Hsieh Wen Shen: Fort Collins, CO, USA, 1973. [Google Scholar]
- Elder, J.W. The dispersion of marked fluid in turbulent shear flow. J. Fluid Mech. 1959, 5, 544–560. [Google Scholar] [CrossRef]
- Sanders, T.G.; Adrian, D.D.; Joyce, J.M. Mixing length for representative water quality sampling. Water. Pollut. Control. Fed. 1977, 49, 2467–2478. [Google Scholar]
- Ruthven, D. The dispersion of a decaying effluent discharged continuously into a uniformly flowing stream. Water Res. 1971, 5, 343–352. [Google Scholar] [CrossRef]
- Fischer, H.B. Discussion of “Time of travel of soluble contaminants in streams”. J. San. Eng. Div. 1964, 90, 124. [Google Scholar] [CrossRef]
- Fischer, H.B. Dispersion predictions in natural streams. J. San. Eng. Div. 1968, 94, 927. [Google Scholar] [CrossRef]
- Socolofsky, S.; Jirka, G.H. Special Topics in Mixing and Transport Processes in the Environment. Coastal and Ocean Engineering Division. 2004, Texas A&M University, M.S. 3136 College Station, TX 77843-3136. Available online: https://docplayer.net/54848090-Special-topics-in-mixing-and-transport-processes-in-the-environment.html (accessed on 21 September 2020).
- Brisaert, M.; Heylen, M.; Plaizier-Vercammen, J. Investigation on the chemical stability of erythromycin in solutions using an optimization system. Pharm. Weekbl. Sci. Ed. 1996, 18, 182–186. [Google Scholar] [CrossRef] [PubMed]
- Fairbairn, D.J.; Arnold, W.A.; Barber, B.L.; Kaufenberg, E.F.; Koskinen, W.C.; Novak, P.J.; Rice, P.J.; Swackhamer, D.L. Contaminants of Emerging Concern: Mass Balance and Comparison of Wastewater Effluent and Upstream Sources in a Mixed-Use Watershed. Environ. Sci. Technol. 2015, 50, 36–45. [Google Scholar] [CrossRef]
- Musolff, A.; Leschik, S.; Möder, M.; Strauch, G.; Reinstorf, F.; Schirmer, M. Temporal and spatial patterns of micropollutants in urban receiving waters. Environ. Pollut. 2009, 157, 3069–3077. [Google Scholar] [CrossRef]
- Castiglioni, S.; Valsecchi, S.; Polesello, S.; Rusconi, M.; Melis, M.; Palmiotto, M.; Manenti, A.; Davoli, E.; Zuccato, E. Sources and fate of perfluorinated compounds in the aqueous environment and in drinking water of a highly urbanized and industrialized area in Italy. J. Hazard. Mater. 2015, 282, 51–60. [Google Scholar] [CrossRef]
| Codes | Meaning |
|---|---|
| River A | Moselle River |
| River B | Meurthe River |
| Location A1 | Messein: on the Moselle River, place of water catchment (to produce drinking water) |
| Location A2 | Pompey: on the Moselle River, upstream of the confluence |
| Location A3 | Belleville: on the Moselle River, downstream of the confluence of the Meurthe River and the Moselle River |
| Location B1 | Malzéville: on the Meurthe River, upstream of the wastewater treatment plant |
| Location B2 | Moulin Noir: on the Meurthe River, downstream of the wastewater treatment plant and upstream of the confluence |
| FiA1t | Mass flux of micropollutant i at location A1 on the Moselle River and time t (add for all) |
| FiA2t | Mass flux of micropollutant i at location A2 on the Moselle River and time t |
| FiA3t | Mass flux of micropollutant i at location A3 on the Moselle River and time t |
| FiB1t | Mass flux of micropollutant i at location B1 on the Meurthe River and time t |
| FiB2t | Mass flux of micropollutant i at location B2 on the Meurthe River and time t |
| CiA1t | Concentration of micropollutant i at location A1 on the Moselle River and time t |
| CiA2t | Concentration of micropollutant i at location A2 on the Moselle River and time t |
| CiA3t | Concentration of micropollutant i at location A3 on the Moselle River and time t |
| CiB1t | Concentration of micropollutant i at location B1 on the Meurthe River and time t |
| CiB2t | Concentration of micropollutant i at location B2 on the Meurthe River and time t |
| FiWWTPt | Mass flux of micropollutant i released from WWTP and time t |
| CiDWt | Concentration of micropollutant i in the drinking water and time t |
| Family | Class | Compound | LoQ (ng/L) | SPE Recovery % | IM | IS |
|---|---|---|---|---|---|---|
| Addit. | Plastic additive | Bisphenol A | 21.1 | 30 | - | BPA-d16 |
| EDCs and Phs | Hormone | Estrone | 3.14 | 20 | - | Estrone-d4 |
| Hormone | 17β-Estradiol | 12.8 | 20 | - | Estrone-d4 | |
| Hormone | Ethynylestradiol | 20.6 | 9 | - | Estrone-d4 | |
| Anti-epileptic | Carbamazepine | 7.72 | 47 | + | Carbamazepine-d10 | |
| Anti-epileptic | Carbamazepine-10,11-epoxide | 2.80 | 105 | + | Carbamazepine-d10 | |
| Antibiotic | Clarithromycin | 31.3 | 11 | + | Sulfadimethoxine-d6 | |
| Chemotherapy Drug | Cyclophosphamide | 1.21 | 47 | + | Sulfadimethoxine-d6 | |
| Anti-inflammatory and pain killer | Diclofenac | 5.09 | 60 | + | Diclofenac-d4 | |
| Antibiotic | Erythromycin | 18.4 | 17 | + | Carbamazepine-d10 | |
| Anti-inflammatory | Ibuprofen | 0.92 | 75 | - | Ibuprofen-d3 | |
| Anti-inflammatory | Ketoprofen | 0.72 | 84 | + | Carbamazepine-d10 | |
| Anesthetic | Lidocaine | 18.0 | 39 | + | Sulfadimethoxine-d6 | |
| Anti-inflammatory | Naproxen | 4.00 | 66 | + | Diclofenac-d4 | |
| Antibiotic | Sulfadimethoxine | 9.50 | 72 | + | Sulfadimethoxine-d6 | |
| Antibiotic | Sulfadimidine | 9.00 | 65 | + | Sulfadimethoxine-d6 | |
| Antibiotic | Sulfamethoxazole | 1.50 | 64 | + | Sulfadimethoxine-d6 | |
| Antibiotic | Sulfathiazole | 1.20 | 61 | + | Sulfadimethoxine-d6 | |
| PCP | Antiseptic | Triclosan | 39.0 | 8 | - | Estrone-d4 |
| PFCs | PFC | PFOA | 6.54 | 74 | - | Ibuprofen-d3 |
| PFC | PFOS | 4.29 | 35 | - | Ibuprofen-d3 |
| Date Micropollutant (i) | September fit% | January fit% | October fit% | Average fit% |
|---|---|---|---|---|
| Clarithromycin | 6 | −4 | 9 | 6.3 |
| Sulfamethoxazole | −6 | −20 | −6 | 10.7 |
| Lidocaine | 15 | 15 | 8 | 12.6 |
| Ibuprofen | −13 | 27 | −10 | 16.7 |
| PFOS | −12 | 16 | −34 | 20.7 |
| Carbamazepine | −19 | −28 | 18 | 21.7 |
| Bisphenol A | 14 | 28 | 28 | 23.3 |
| Diclofenac | 46 | 12 | 15 | 24.3 |
| Date Micropollutant (i) | September FiWWTPt (g/day) | January FiWWTPt (g/day) | October FiWWTPt (g/day) | Average FiWWTPt (g/day) |
|---|---|---|---|---|
| Estrone | - | 13 | 5 | 6 |
| PFOS | 1 | 30 | 0 | 10 |
| Ketoprofen | 12 | 34 | 6 | 17 |
| Lidocaine | 27 | - | 33 | 20 |
| Naproxen | 10 | 63 | 0 | 24 |
| Carbamazepine | 23 | 25 | 25 | 24 |
| Sulfamethoxazole | 34 | 24 | 20 | 26 |
| Ibuprofen | 1 | 107 | 1 | 36 |
| Diclofenac | 56 | 88 | 85 | 76 |
| Bisphenol A | 117 | 124 | 39 | 93 |
| Clarithromycin | 84 | 153 | 417 | 218 |
| Date | September | January | October | March |
|---|---|---|---|---|
| Micropollutant (i) | C (ng/L) | C (ng/L) | C (ng/L) | C (ng/L) |
| Sulfamethoxazole | 64 | 32 | 23 | 6 |
| Bisphenol A | 236 | 92 | 80 | 54 |
| Ibuprofen | 9 | 97 | 18 | 22 |
| Naproxen | 30 | 45 | 13 | 20 |
| Ketoprofen | 17 | 18 | 7 | 7 |
| Triclosan | - | 60 | 13 | 13 |
| Estrone | - | 7 | 6 | - |
| Clarithromycin | 148 | 140 | 639 | 16 |
| Diclofenac | 87 | 50 | 120 | 51 |
| Carbamazepine | 54 | 32 | 68 | 19 |
| Lidocaine | 57 | - | 47 | - |
| Carbamazepine-10,11-epoxide | 3 | - | 3 | - |
| PFOS | 14 | 27 | 20 | 6 |
| PFOA | - | - | 3 | 0.8 |
| Estrone | - | 7 | 6 | 4 |
| Erythromycin | - | 914 | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ayoub, H.; Potier, O.; Koubaissy, B.; Pontvianne, S.; Lenouvel, A.; Guignard, C.; Poirot, H.; Toufaily, J.; Hamieh, T.; Roques-Carmes, T. A Short Cost-Effective Methodology for Tracing the Temporal and Spatial Anthropogenic Inputs of Micropollutants into Ecosystems: Verified Mass-Balance Approach Applied to River Confluence and WWTP Release. Water 2022, 14, 4100. https://doi.org/10.3390/w14244100
Ayoub H, Potier O, Koubaissy B, Pontvianne S, Lenouvel A, Guignard C, Poirot H, Toufaily J, Hamieh T, Roques-Carmes T. A Short Cost-Effective Methodology for Tracing the Temporal and Spatial Anthropogenic Inputs of Micropollutants into Ecosystems: Verified Mass-Balance Approach Applied to River Confluence and WWTP Release. Water. 2022; 14(24):4100. https://doi.org/10.3390/w14244100
Chicago/Turabian StyleAyoub, Hawraa, Olivier Potier, Bachar Koubaissy, Steve Pontvianne, Audrey Lenouvel, Cédric Guignard, Hélène Poirot, Joumana Toufaily, Tayssir Hamieh, and Thibault Roques-Carmes. 2022. "A Short Cost-Effective Methodology for Tracing the Temporal and Spatial Anthropogenic Inputs of Micropollutants into Ecosystems: Verified Mass-Balance Approach Applied to River Confluence and WWTP Release" Water 14, no. 24: 4100. https://doi.org/10.3390/w14244100
APA StyleAyoub, H., Potier, O., Koubaissy, B., Pontvianne, S., Lenouvel, A., Guignard, C., Poirot, H., Toufaily, J., Hamieh, T., & Roques-Carmes, T. (2022). A Short Cost-Effective Methodology for Tracing the Temporal and Spatial Anthropogenic Inputs of Micropollutants into Ecosystems: Verified Mass-Balance Approach Applied to River Confluence and WWTP Release. Water, 14(24), 4100. https://doi.org/10.3390/w14244100