Nonstationary Annual Maximum Flood Frequency Analysis Using a Conceptual Hydrologic Model with Time-Varying Parameters
Abstract
:1. Introduction
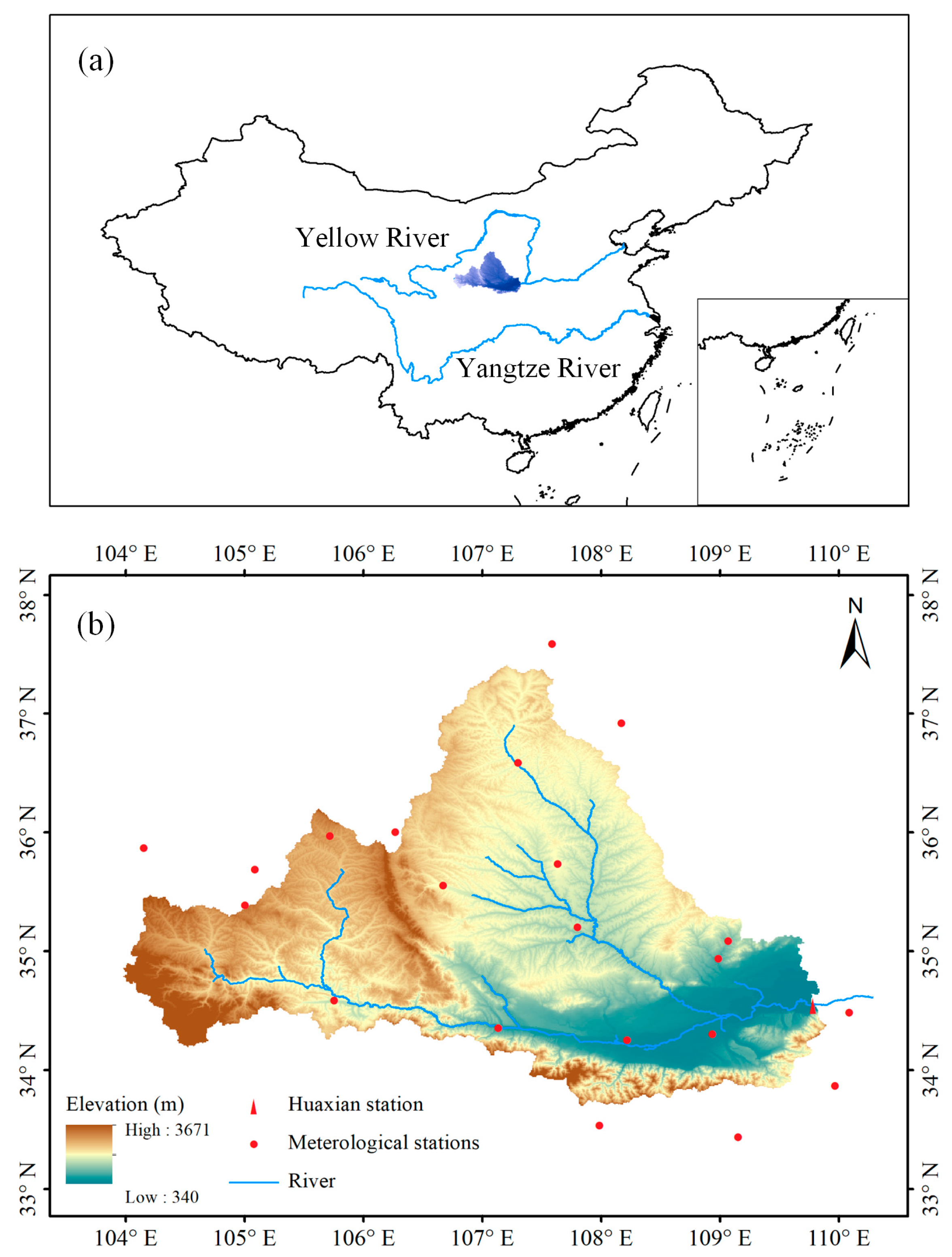
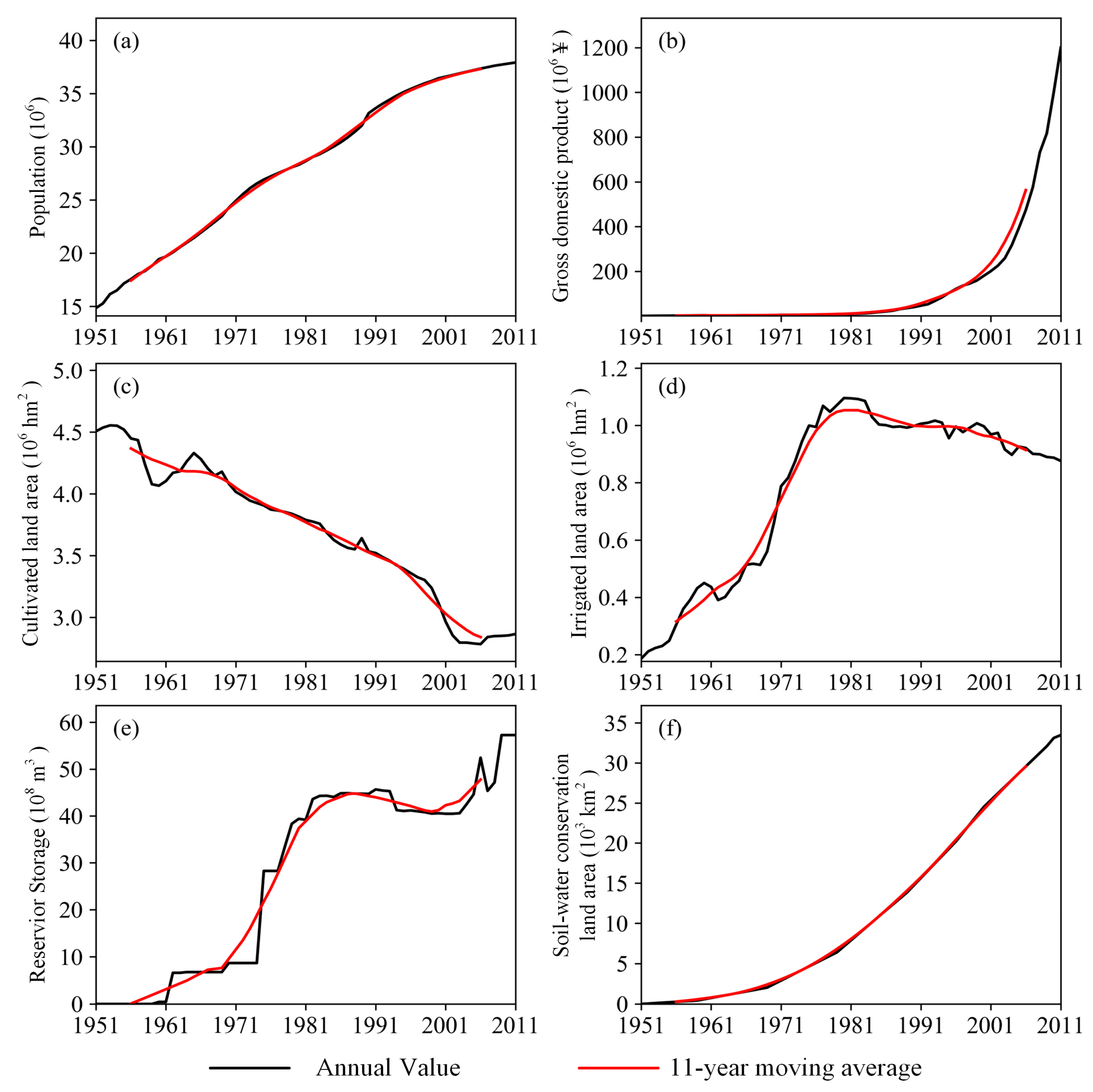
2. Study Area and Data
3. Methodology
3.1. GR4J Model: Stationary and Nonstationary
3.2. Parameter Estimation and Model Selection
3.3. Deriving Flood Frequency Distribution through Monte Carlo Simulation
4. Results
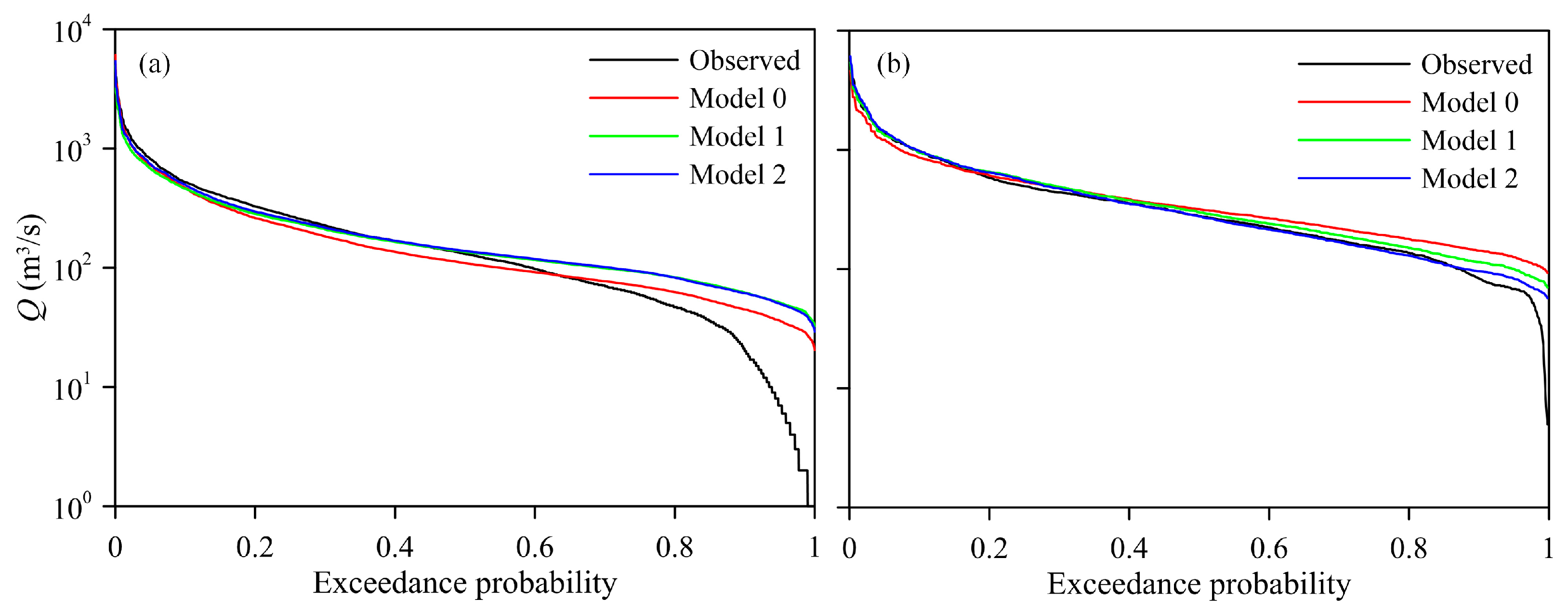
4.1. Simulation Performance of the Stationary and Nonstationary GR4J Models
4.2. Dynamic Variation of Time-Varying Parameter
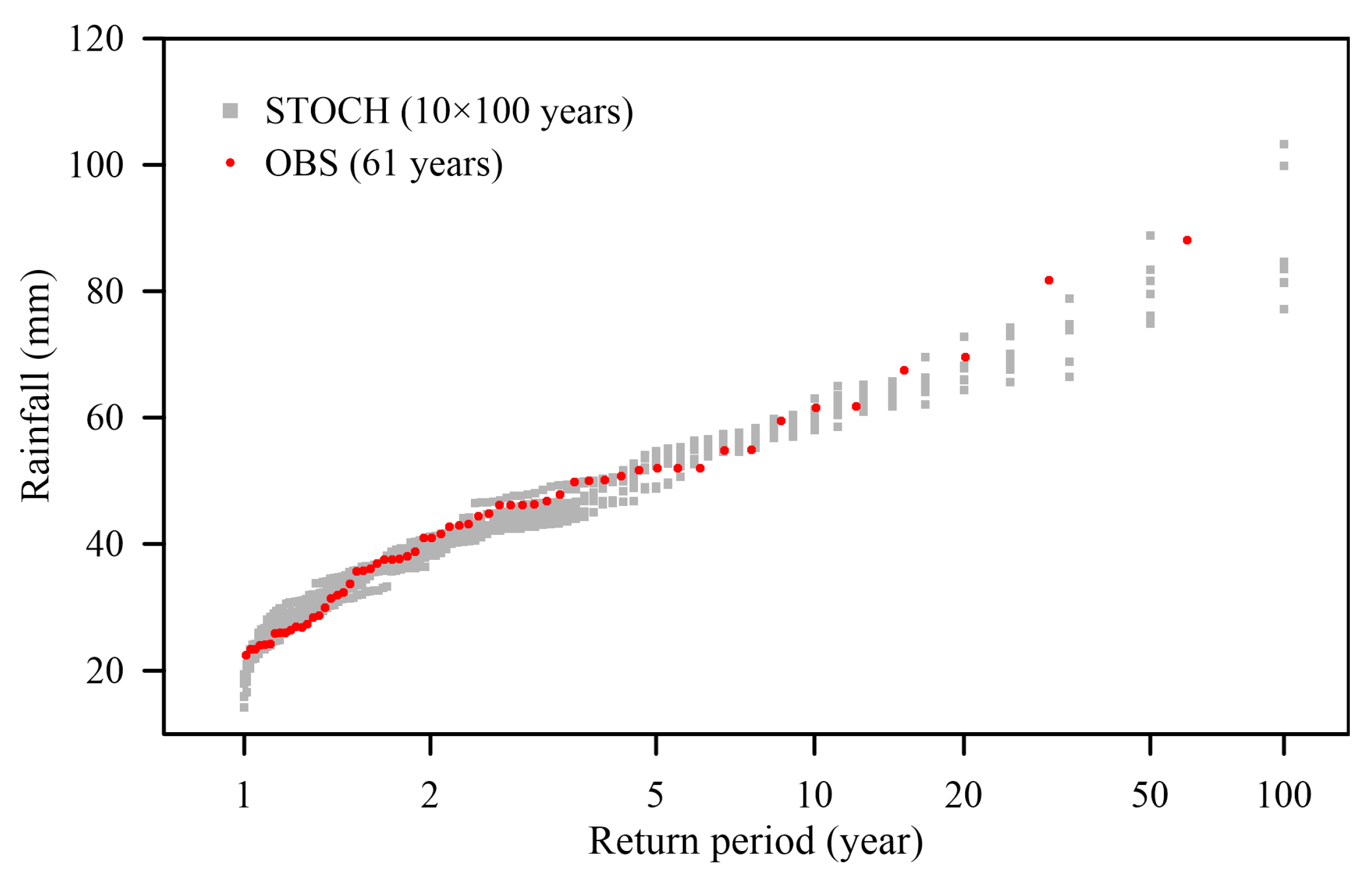
4.3. Performance of the Stochastic Rainfall Model
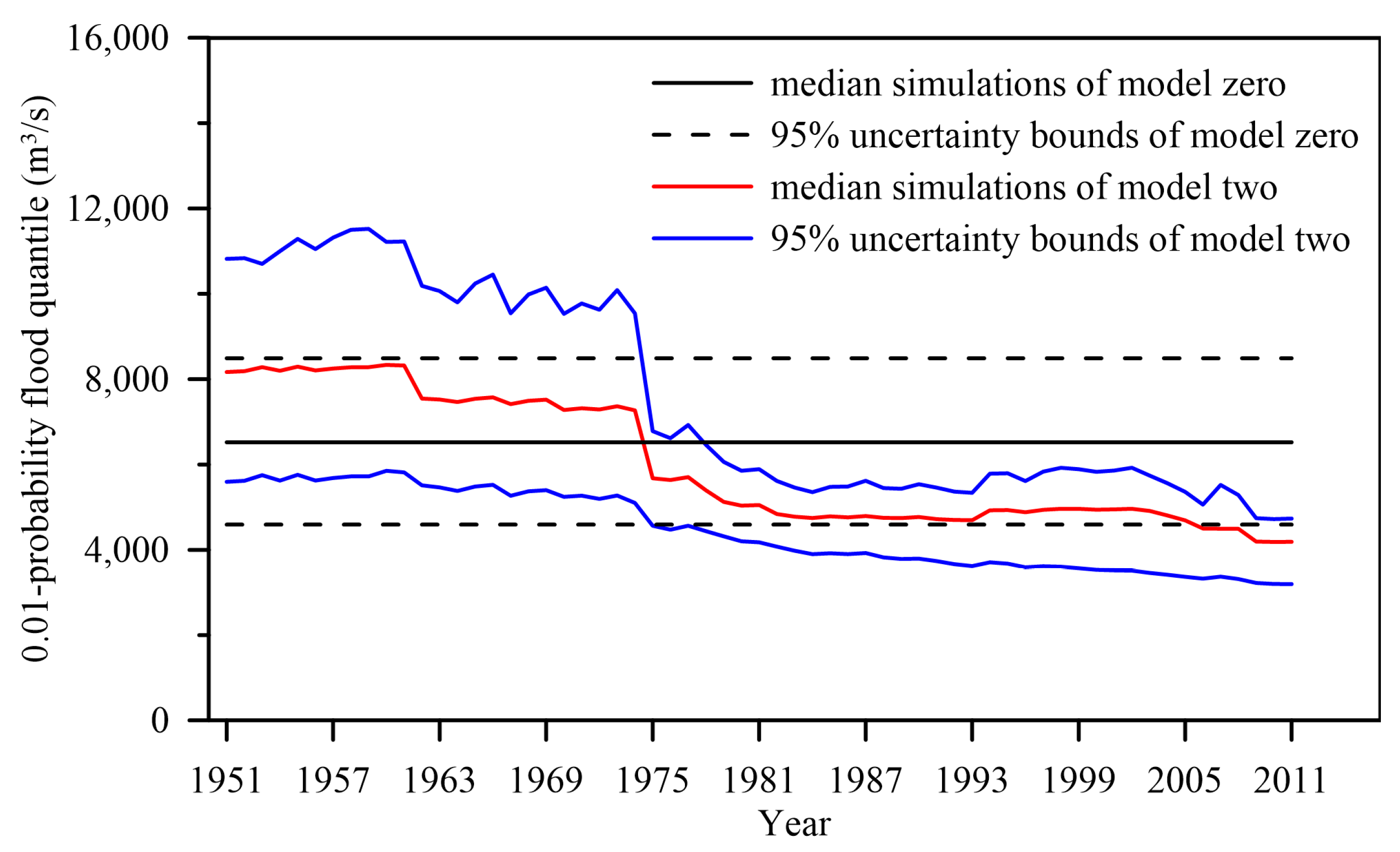
4.4. Flood Frequency Derivation Using the Stationary and Nonstationary Model
5. Discussion
6. Conclusions
- Improved model performance can be achieved when the parameter (representing the production storage capacity) is treated as time-dependent or as a function of external variables that reflect changes in the hydrological responses within WRB;
- Incorporating the watershed conditions as covariates for the model parameter (model two) can better describe nonstationarity in the flood frequency and magnitude in WRB than the over-simplified time-dependent model (model one);
- The nonstationary model can achieve a more rational description of variations in the frequency and magnitude of floods over time, which reveals the deficiency when applying a stationary model under changing watershed conditions.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Stefanidis, S.; Alexandridis, V.; Theodoridou, T. Flood Exposure of Residential Areas and Infrastructure in Greece. Hydrology 2022, 9, 145. [Google Scholar] [CrossRef]
- Tate, E.; Rahman, M.A.; Emrich, C.T.; Sampson, C.C. Flood Exposure and Social Vulnerability in the United States. Nat. Hazards 2021, 106, 435–457. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2022: Impacts, Adaptation, and Vulnerability. In Contribution of Working Group II to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Milly, P.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.; Stouffer, R.J. Stationarity id Dead: Whither Water Management. Science 2008, 319, 573–574. [Google Scholar] [CrossRef] [PubMed]
- Westra, S.; Sisson, S.A. Detection of non-stationarity in precipitation extremes using a max-stable process model. J. Hydrol. 2011, 406, 119–128. [Google Scholar] [CrossRef] [Green Version]
- Biondi, D.; De Luca, D.L. Process-based design flood estimation in ungauged basins by conditioning model parameters on regional hydrological signatures. Nat. Hazards 2015, 79, 1015–1038. [Google Scholar] [CrossRef]
- Qu, C.; Li, J.; Yan, L.; Yan, P.; Cheng, F.; Lu, D. Non-Stationary Flood Frequency Analysis Using Cubic B-Spline-Based GAMLSS Model. Water 2020, 12, 1867. [Google Scholar] [CrossRef]
- Liu, M.; Ma, X.; Yin, Y.; Zhang, Z.; Yin, J.; Ullah, I.; Arshad, M. Non-stationary Frequency Analysis of Extreme Streamflow Disturbance in a Typical Ecological Function Reserve of China under a Changing Climate. Ecohydrology 2021, 14, e2323. [Google Scholar] [CrossRef]
- Su, C.; Chen, X. Assessing the Effects of Reservoirs on Extreme Flows Using Nonstationary Flood Frequency Models with the Modified Reservoir Index as a Covariate. Adv. Water Resour. 2019, 124, 29–40. [Google Scholar] [CrossRef]
- Zhou, Y.; Guo, S.; Xu, C.-Y.; Xiong, L.; Chen, H.; Ngongondo, C.; Li, L. Probabilistic Interval Estimation of Design Floods under Non-Stationary Conditions by an Integrated Approach. Hydrol. Res. 2022, 53, 259–278. [Google Scholar] [CrossRef]
- Li, S.; Qin, Y. Frequency Analysis of the Nonstationary Annual Runoff Series Using the Mechanism-Based Reconstruction Method. Water 2022, 14, 76. [Google Scholar] [CrossRef]
- Sen, S.; He, J.; Kasiviswanathan, K.S. Uncertainty Quantification Using the Particle Filter for Non-Stationary Hydrological Frequency Analysis. J. Hydrol. 2020, 584, 124666. [Google Scholar] [CrossRef]
- He, C.; Chen, F.; Wang, Y.; Long, A.; He, X. Flood Frequency Analysis of Manas River Basin in China under Non-stationary Condition. J. Flood Risk Manag. 2021, 14, e12745. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, Y.; Wang, B.; Tan, S.; Feng, P. Nonstationary Flood Frequency Analysis Using Univariate and Bivariate Time-Varying Models Based on GAMLSS. Water 2018, 10, 819. [Google Scholar] [CrossRef] [Green Version]
- Dong, Q.; Zhang, X.; Lall, U.; Sang, Y.-F.; Xie, P. An Improved Nonstationary Model for Flood Frequency Analysis and Its Implication for the Three Gorges Dam, China. Hydrol. Sci. J. 2019, 64, 845–855. [Google Scholar] [CrossRef]
- Khaliq, M.N.; Ouarda, T.; Ondo, J.; Gachon, P.; Bobée, B. Frequency analysis of a sequence of dependent and/or non-stationary hydro-meteorological observations: A review. J. Hydrol. 2006, 329, 534–552. [Google Scholar] [CrossRef]
- Olsen, J.R.; Lambert, J.H.; Haimes, Y.Y. Risk of extreme events under nonstationary conditions. Risk Anal. 1998, 18, 497–510. [Google Scholar] [CrossRef]
- Renard, B.; Lang, M.; Bois, P. Statistical analysis of extreme events in a non-stationary context via a Bayesian framework: Case study with peak-over-threshold data. Stoch. Environ. Res. Risk Assess. 2006, 21, 97–112. [Google Scholar] [CrossRef] [Green Version]
- Leclerc, M.; Ouarda, T.B. Non-stationary regional flood frequency analysis at ungauged sites. J. Hydrol. 2007, 343, 254–265. [Google Scholar] [CrossRef]
- Delgado, J.M.; Apel, H.; Merz, B. Flood trends and variability in the Mekong river. Hydrol. Earth Syst. Sci. 2010, 14, 407–418. [Google Scholar] [CrossRef] [Green Version]
- Katz, R.W.; Parlange, M.B.; Naveau, P. Statistics of extremes in hydrology. Adv. Water Resour. 2002, 25, 1287–1304. [Google Scholar] [CrossRef]
- El Adlouni, S.; Ouarda, T.; Zhang, X.; Roy, R.; Bobée, B. Generalized maximum likelihood estimators for the nonstationary generalized extreme value model. Water Resour. Res. 2007, 43, W03410. [Google Scholar] [CrossRef]
- López, J.; Francés, F. Non-stationary flood frequency analysis in continental Spanish rivers, using climate and reservoir indices as external covariates. Hydrol. Earth Syst. Sci. 2013, 17, 3189–3203. [Google Scholar] [CrossRef] [Green Version]
- Xiong, L.; Du, T.; Xu, C.; Guo, S.; Jiang, C.; Gippel, C.J. Non-Stationary Annual Maximum Flood Frequency Analysis Using the Norming Constants Method to Consider Non-Stationarity in the Annual Daily Flow Series. Water Resour. Manag. 2015, 29, 3615–3633. [Google Scholar] [CrossRef]
- Xiong, L.; Jiang, C. Designing flood hydrograph of the Weihe River considering nonstationarity. J. Water Resour. Res. 2015, 4, 109–119. [Google Scholar] [CrossRef]
- Vasiliades, L.; Galiatsatou, P.; Loukas, A. Nonstationary frequency analysis of annual maximum rainfall using climate covariates. Water Resour. Manag. 2015, 29, 339–358. [Google Scholar] [CrossRef]
- Haberlandt, U.; Radtke, I. Hydrological model calibration for derived flood frequency analysis using stochastic rainfall and probability distributions of peak flows. Hydrol. Earth Syst. Sci. 2014, 18, 353–365. [Google Scholar] [CrossRef] [Green Version]
- Winter, B.; Schneeberger, K.; Dung, N.V.; Huttenlau, M.; Achleitner, S.; Stötter, J.; Merz, B.; Vorogushyn, S. A Continuous Modelling Approach for Design Flood Estimation on Sub-Daily Time Scale. Hydrol. Sci. J. 2019, 64, 539–554. [Google Scholar] [CrossRef] [Green Version]
- Grimaldi, S.; Nardi, F.; Piscopia, R.; Petroselli, A.; Apollonio, C. Continuous Hydrologic Modelling for Design Simulation in Small and Ungauged Basins: A Step Forward and Some Tests for Its Practical Use. J. Hydrol. 2021, 595, 125664. [Google Scholar] [CrossRef]
- Fleischmann, A.S.; Collischonn, W.; Paiva, R.C.D.D. Estimating Design Hydrographs at the Basin Scale: From Event-Based to Continuous Hydrological Simulation. RBRH 2019, 24, e4. [Google Scholar] [CrossRef] [Green Version]
- Rowe, T.; Smithers, J. Review: Continuous Simulation Modelling for Design Flood Estimation—A South African Perspective and Recommendations. Water SA 2018, 44, 691–705. [Google Scholar] [CrossRef]
- Huang, X.; Wang, L.; Han, P.; Wang, W. Spatial and Temporal Patterns in Nonstationary Flood Frequency across a Forest Watershed: Linkage with Rainfall and Land Use Types. Forests 2018, 9, 339. [Google Scholar] [CrossRef] [Green Version]
- Falter, D.; Schröter, K.; Dung, N.V.; Vorogushyn, S.; Kreibich, H.; Hundecha, Y.; Apel, H.; Merz, B. Spatially Coherent Flood Risk Assessment Based on Long-Term Continuous Simulation with a Coupled Model Chain. J. Hydrol. 2015, 524, 182–193. [Google Scholar] [CrossRef] [Green Version]
- Yu, G.; Wright, D.B.; Zhu, Z.; Smith, C.; Holman, K.D. Process-Based Flood Frequency Analysis in an Agricultural Watershed Exhibiting Nonstationary Flood Seasonality. Hydrol. Earth Syst. Sci. 2019, 23, 2225–2243. [Google Scholar] [CrossRef] [Green Version]
- Boughton, W.; Droop, O. Continuous simulation for design flood estimation-a review. Environ. Modell. Softw. 2003, 18, 309–318. [Google Scholar] [CrossRef]
- Cameron, D.S.; Beven, K.J.; Tawn, J.; Blazkova, S.; Naden, P. Flood frequency estimation by continuous simulation for a gauged upland catchment (with uncertainty). J. Hydrol. 1999, 219, 169–187. [Google Scholar] [CrossRef]
- Blazkova, S.; Beven, K. Flood frequency estimation by continuous simulation of subcatchment rainfalls and discharges with the aim of improving dam safety assessment in a large basin in the Czech Republic. J. Hydrol. 2004, 292, 153–172. [Google Scholar] [CrossRef]
- Aronica, G.T.; Candela, A. Derivation of flood frequency curves in poorly gauged Mediterranean catchments using a simple stochastic hydrological rainfall-runoff model. J. Hydrol. 2007, 347, 132–142. [Google Scholar] [CrossRef]
- Moretti, G.; Montanari, A. Inferring the flood frequency distribution for an ungauged basin using a spatially distributed rainfall-runoff model. Hydrol. Earth Syst. Sci. 2008, 12, 1141–1152. [Google Scholar] [CrossRef] [Green Version]
- Haberlandt, U.; Ebner Von Eschenbach, A.; Buchwald, I. A space-time hybrid hourly rainfall model for derived flood frequency analysis. Hydrol. Earth Syst. Sci. 2008, 12, 1353–1367. [Google Scholar] [CrossRef] [Green Version]
- Courty, L.G.; Wilby, R.L.; Hillier, J.K.; Slater, L.J. Intensity-duration-frequency curves at the global scale. Environ. Res. Lett. 2019, 14, 084045. [Google Scholar] [CrossRef]
- Venkatesh, K.; Maheswaran, R.; Devacharan, J. Framework for Developing IDF Curves Using Satellite Precipitation: A Case Study Using GPM-IMERG V6 Data. Earth Sci. Inform. 2022, 15, 671–687. [Google Scholar] [CrossRef]
- Westra, S.; Thyer, M.; Leonard, M.; Kavetski, D.; Lambert, M. A strategy for diagnosing and interpreting hydrological model nonstationarity. Water Resour. Res. 2014, 50, 5090–5113. [Google Scholar] [CrossRef] [Green Version]
- Wallner, M.; Haberlandt, U. Non-stationary hydrological model parameters: A framework based on SOM-B. Hydrol. Process. 2015, 29, 3145–3161. [Google Scholar] [CrossRef]
- Deng, C.; Liu, P.; Wang, W.; Shao, Q.; Wang, D. Modelling time-variant parameters of a two-parameter monthly water balance model. J. Hydrol. 2019, 573, 918–936. [Google Scholar] [CrossRef]
- Song, J.X.; Xu, Z.X.; Liu, C.M.; Li, H.E. Ecological and environmental instream flow requirements for the Wei River-the largest tributary of the Yellow River. Hydrol. Process. 2007, 21, 1066–1073. [Google Scholar] [CrossRef]
- Wei, H.; Li, J.; Wang, J.; Tian, P. Analysis on runoff trend and influence factors in Weihe River basin. Bull. Soil Water Conserv. 2008, 28, 76–80. [Google Scholar]
- Li, S.; Xiong, L.; Li, H.; Leung, L.R.; Demissie, Y. Attributing runoff changes to climate variability and human activities: Uncertainty analysis using four monthly water balance models. Stoch. Environ. Res. Risk Assess. 2016, 30, 251–269. [Google Scholar] [CrossRef]
- Zhao, G.; Mu, X.; Tian, P.; Wang, F.; Gao, P. Climate changes and their impacts on water resources in semiarid regions: A case study of the Wei River basin, China. Hydrol. Process. 2013, 27, 3852–3863. [Google Scholar] [CrossRef]
- Gao, Z.; Long, D.; Tang, G.; Zeng, C.; Huang, J.; Hong, Y. Assessing the Potential of Satellite-Based Precipitation Estimates for Flood Frequency Analysis in Ungauged or Poorly Gauged Tributaries of China’s Yangtze River Basin. J. Hydrol. 2017, 550, 478–496. [Google Scholar] [CrossRef]
- Gao, P.; Geissen, V.; Ritsema, C.J.; Mu, X.; Wang, F. Impact of climate change and anthropogenic activities on stream flow and sediment discharge in the Wei River basin, China. Hydrol. Earth. Syst. Sci. 2013, 17, 961–972. [Google Scholar] [CrossRef] [Green Version]
- Su, X.L.; Kang, S.Z.; Wei, X.M.; Xing, D.W.; Cao, H. Impact of climate change and human activity on the runoff of Wei River basin to the Yellow River. J. Northwest A F Univ. (Nat. Sci. Ed.) 2007, 35, 153–159. [Google Scholar]
- Liu, Q.; Li, S.; Zhou, G.; Feng, Z.; Wang, G.; Qiu, Q. Attribution of Nonstationary Changes in the Annual Runoff of the Weihe River Using the De-Nonstationarity Method. Hydrol. Res. 2022, 53, 407–418. [Google Scholar] [CrossRef]
- Yan, L.; Xiong, L.; Luan, Q.; Jiang, C.; Yu, K.; Xu, C.-Y. On the Applicability of the Expected Waiting Time Method in Nonstationary Flood Design. Water Resour. Manag. 2020, 34, 2585–2601. [Google Scholar] [CrossRef]
- Jiang, C.; Xiong, L.; Wang, D.; Liu, P.; Guo, S.; Xu, C. Separating the impacts of climate change and human activities on runoff using the Budyko-type equations with time-varying parameters. J. Hydrol. 2015, 522, 326–338. [Google Scholar] [CrossRef]
- Adam, J.C.; Clark, E.A.; Lettenmaier, D.P.; Wood, E.F. Correction of global precipitation products for orographic effects. J. Clim. 2006, 19, 15–38. [Google Scholar] [CrossRef]
- Wang, D.; Hejazi, M. Quantifying the relative contribution of the climate and direct human impacts on mean annual streamflow in the contiguous United States. Water Resour. Res. 2011, 47, W00J12. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Wu, X.; Finlayson, B.L.; Webber, M.; Wei, T.; Li, M.; Chen, Z. Variability and trend in the hydrology of the Yangtze River, China: Annual precipitation and runoff. J. Hydrol. 2014, 513, 403–412. [Google Scholar] [CrossRef]
- Yang, T. Shaanxi Statistical Yearbook; China Statistics Press: Beijing, China, 2009. [Google Scholar]
- Shao, H. Simulation of Soil and Water Loss Variation toward Terrace Practice in the Weihe River Basin; Northwest A & F University: Xi’an, China, 2005. [Google Scholar]
- Perrin, C.; Michel, C.; Andréassian, V. Improvement of a parsimonious model for streamflow simulation. J. Hydrol. 2003, 279, 275–289. [Google Scholar] [CrossRef]
- Kuczera, G.; Kavetski, D.; Franks, S.; Thyer, M. Towards a Bayesian total error analysis of conceptual rainfall-runoff models: Characterising model error using storm-dependent parameters. J. Hydrol. 2006, 331, 161–177. [Google Scholar] [CrossRef]
- Renard, B.; Kavetski, D.; Leblois, E.; Thyer, M.; Kuczera, G.; Franks, S.W. Toward a reliable decomposition of predictive uncertainty in hydrological modeling: Characterizing rainfall errors using conditional simulation. Water Resour. Res. 2011, 47, W11516. [Google Scholar] [CrossRef]
- Zeng, L.; Xiong, L.; Liu, D.; Chen, J.; Kim, J.S. Improving Parameter Transferability of GR4J Model under Changing Environments Considering Nonstationarity. Water 2019, 11, 2029. [Google Scholar] [CrossRef] [Green Version]
- Vrugt, J.A.; Gupta, H.V.; Bouten, W.; Sorooshian, S. A Shuffled Complex Evolution Metropolis algorithm for optimization and uncertainty assessment of hydrologic model parameters. Water Resour. Res. 2003, 39, 1201. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Gupta, H.V.; Dekker, S.C.; Sorooshian, S.; Wagener, T.; Bouten, W. Application of stochastic parameter optimization to the Sacramento soil moisture accounting model. J. Hydrol. 2006, 325, 288–307. [Google Scholar] [CrossRef] [Green Version]
- Feyen, L.; Vrugt, J.A.; Nualláin, B.Ó.; van der Knijff, J.; De Roo, A. Parameter optimisation and uncertainty assessment for large-scale streamflow simulation with the LISFLOOD model. J. Hydrol. 2007, 332, 276–289. [Google Scholar] [CrossRef] [Green Version]
- Ajami, N.K.; Duan, Q.; Sorooshian, S. An integrated hydrologic Bayesian multimodel combination framework: Confronting input, parameter, and model structural uncertainty in hydrologic prediction. Water Resour. Res. 2007, 43, W01403. [Google Scholar] [CrossRef]
- Gelman, A.; Rubin, D.B. Inference from iterative simulation using multiple sequences. Stat. Sci. 1992, 7, 457–472. [Google Scholar] [CrossRef]
- Smith, T.; Sharma, A.; Marshall, L.; Mehrotra, R.; Sisson, S. Development of a formal likelihood function for improved Bayesian inference of ephemeral catchments. Water Resour. Res. 2010, 46, W12551. [Google Scholar] [CrossRef]
- Liao, Y.; Zhang, Q.; Chen, D. Stochastic modeling of daily precipitation in China. J. Geogr. Sci. 2004, 14, 417–426. [Google Scholar]
- Knighton, J.O.; Walter, M.T. Critical Rainfall Statistics for Predicting Watershed Flood Responses: Rethinking the Design Storm Concept. Hydrol. Process. 2016, 30, 3788–3803. [Google Scholar] [CrossRef]
- Liao, Y.; Chen, D.; Gao, G.; Xie, Y. Impacts of climate changes on parameters of a weather generator for daily precipitation in China. Acta Geogr. Sin. 2009, 7, 871–878. [Google Scholar]
- Hesarkazzazi, S.; Arabzadeh, R.; Hajibabaei, M.; Rauch, W.; Kjeldsen, T.R.; Prosdocimi, I.; Castellarin, A.; Sitzenfrei, R. Stationary vs Non-Stationary Modelling of Flood Frequency Distribution across Northwest England. Hydrol. Sci. J. 2021, 66, 729–744. [Google Scholar] [CrossRef]



| Parameter | Description | Unit | Feasible Range |
|---|---|---|---|
| production storage capacity | mm | 20–1200 | |
| groundwater exchange coefficient | mm | −5–3 | |
| one day ahead maximum capacity of the routing store | mm | 20–500 | |
| time base of unit hydrograph | days | 1–5 |
| Case | Covariate | Equation for the Time-Varying Parameter | NSE [-] | KGE [-] | RE [%] | |
|---|---|---|---|---|---|---|
| RS | SWC | |||||
| C0 | 0.711 | 0.801 | 11.5 | |||
| C1 | ✓ | 0.753 | 0.845 | 8.9 | ||
| C2 | ✓ | 0.748 | 0.839 | 9.4 | ||
| C3 | ✓ | ✓ | 0.765 | 0.853 | 8.5 | |
| Model | Covariates | Calibration Period (1951–1990) | Validation Period (1991–2011) | ||||
|---|---|---|---|---|---|---|---|
| NSE [-] | KGE [-] | RE [%] | NSE [-] | KGE [-] | RE [%] | ||
| Model zero | none | 0.711 | 0.801 | 11.5 | 0.692 | 0.791 | 13.5 |
| Model one | time | 0.743 | 0.832 | 9.8 | 0.714 | 0.812 | 10.1 |
| Model two | RS, SWC | 0.765 | 0.853 | 8.5 | 0.716 | 0.818 | 9.8 |
| Event Characteristics | Unit | OBS | STOCH |
|---|---|---|---|
| Number of rainfall events per year | - | 54 | 48 |
| Mean of event volume | mm | 9.54 | 10.08 |
| Standard deviation of event volume | mm | 14.76 | 13.58 |
| Skewness of event volume | - | 3.24 | 3.52 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, L.; Bi, H.; Li, Y.; Liu, X.; Li, S.; Chen, J. Nonstationary Annual Maximum Flood Frequency Analysis Using a Conceptual Hydrologic Model with Time-Varying Parameters. Water 2022, 14, 3959. https://doi.org/10.3390/w14233959
Zeng L, Bi H, Li Y, Liu X, Li S, Chen J. Nonstationary Annual Maximum Flood Frequency Analysis Using a Conceptual Hydrologic Model with Time-Varying Parameters. Water. 2022; 14(23):3959. https://doi.org/10.3390/w14233959
Chicago/Turabian StyleZeng, Ling, Hongwei Bi, Yu Li, Xiulin Liu, Shuai Li, and Jinfeng Chen. 2022. "Nonstationary Annual Maximum Flood Frequency Analysis Using a Conceptual Hydrologic Model with Time-Varying Parameters" Water 14, no. 23: 3959. https://doi.org/10.3390/w14233959









