Large Eddy Simulation of Compound Open Channel Flows with Floodplain Vegetation
Abstract
1. Introduction
2. Mathematical Model
2.1. Governing Equations
2.2. Boundary Condition and Numerical Algorithm
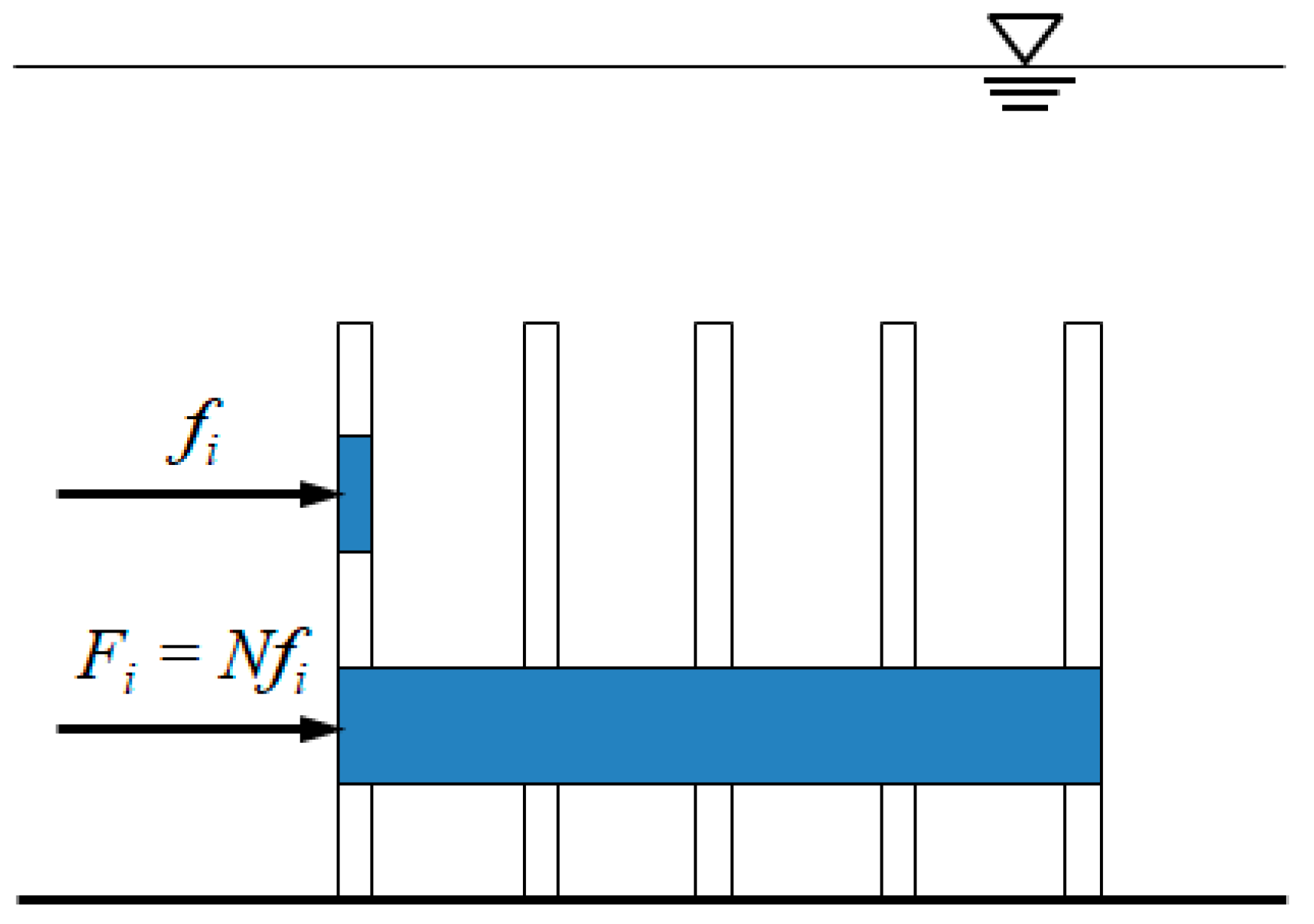
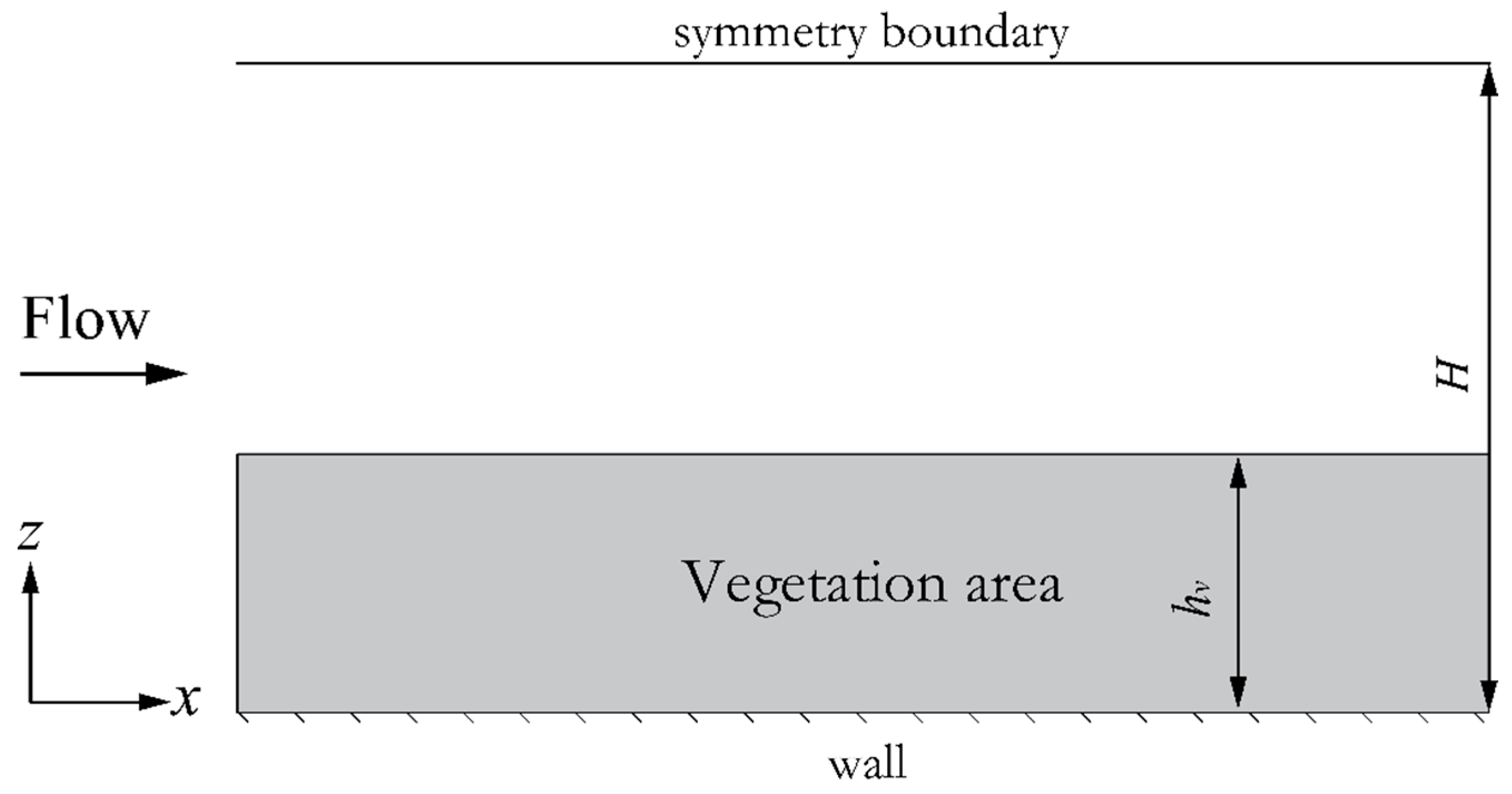
3. Verification of Drag Force Method
3.1. Simulation Implementation
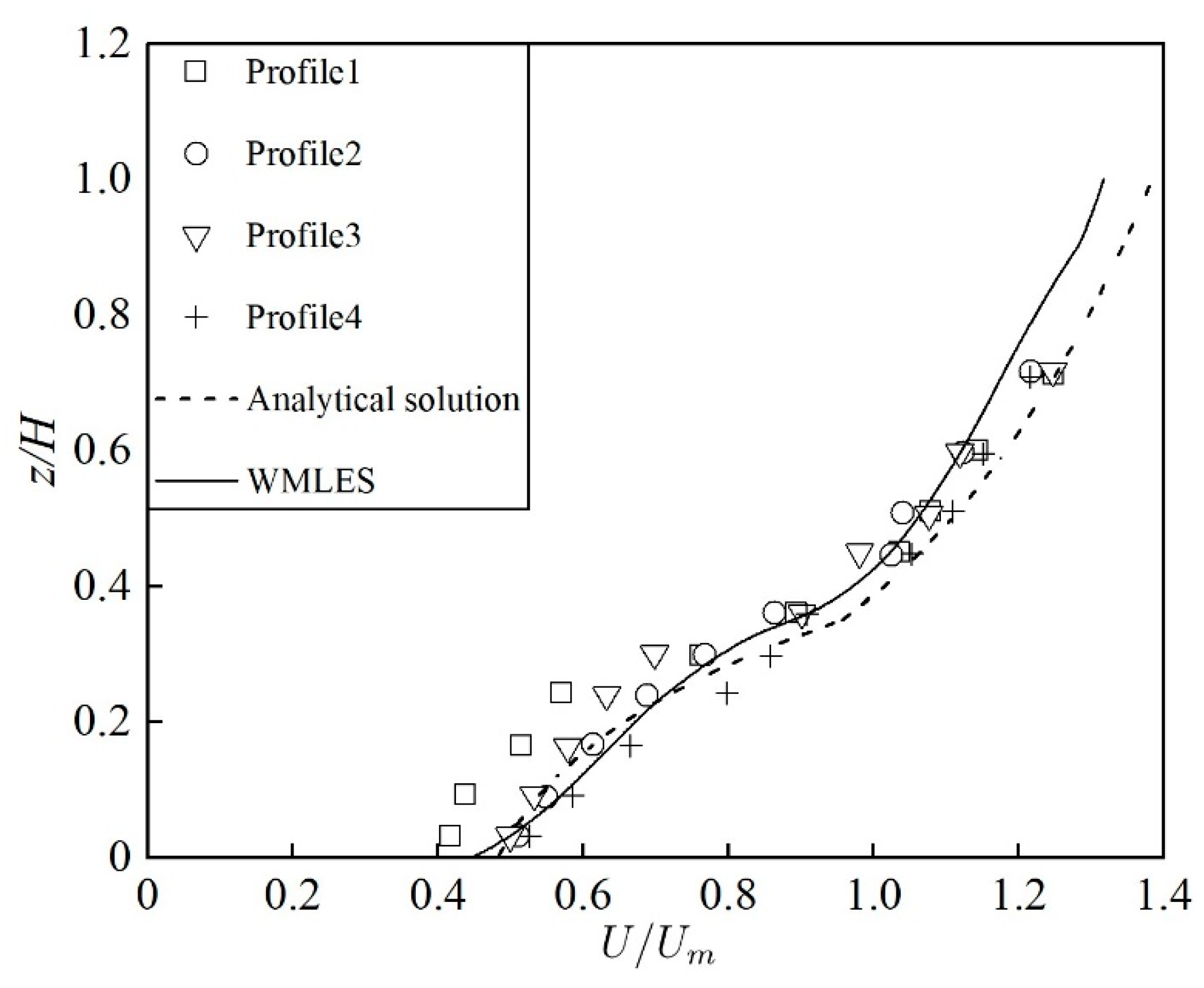
3.2. Case Verification
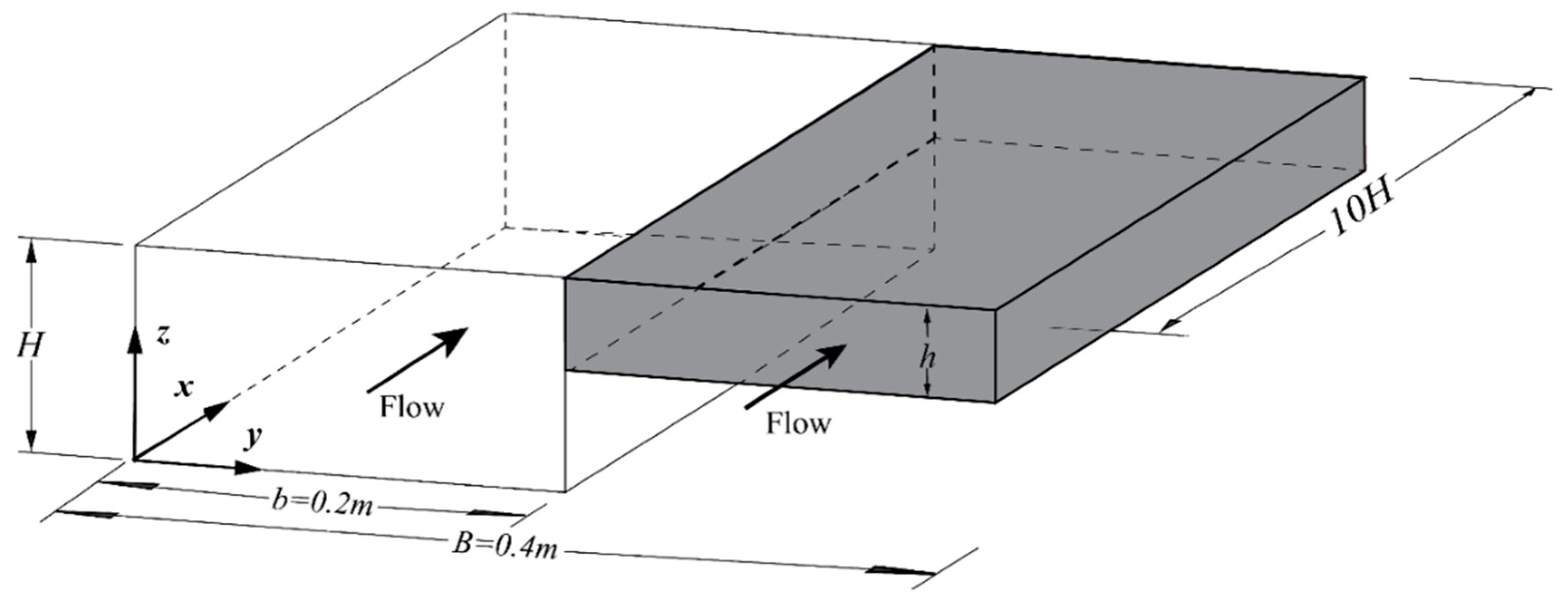
4. Computational Cases
5. Results
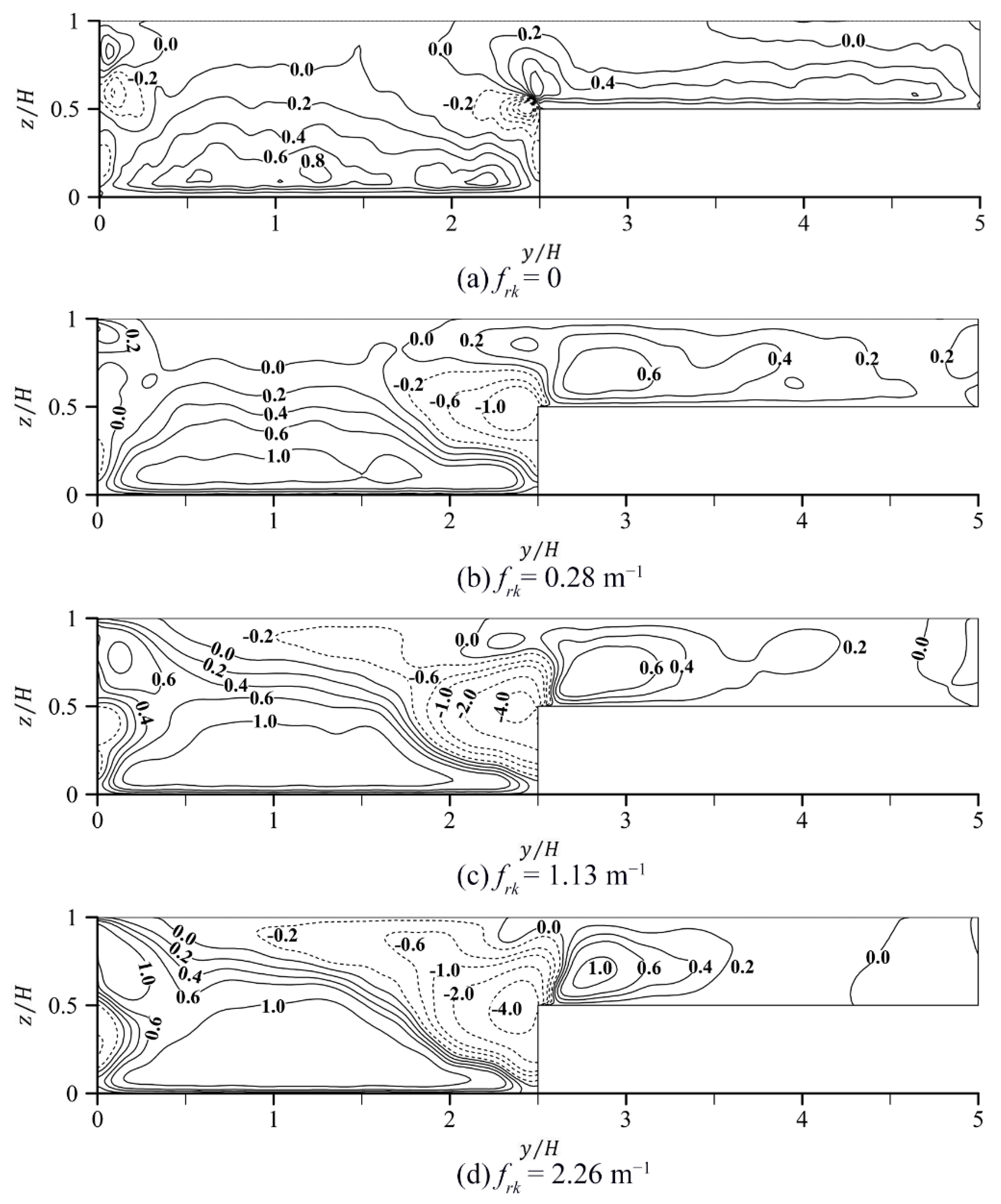
5.1. Flow Field and Secondary Flow
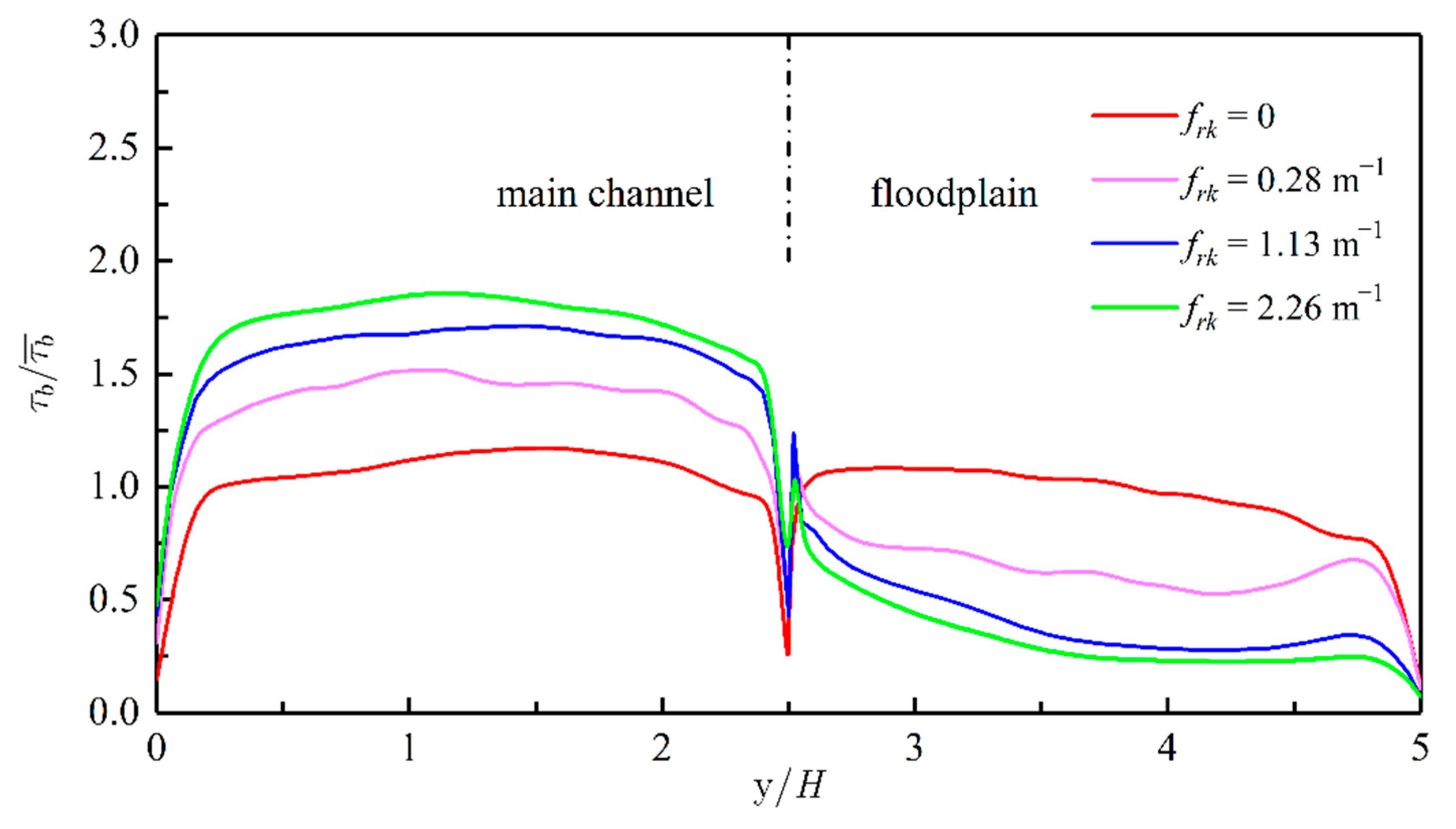
5.2. Bed Shear Stress
5.3. Reynolds Stress
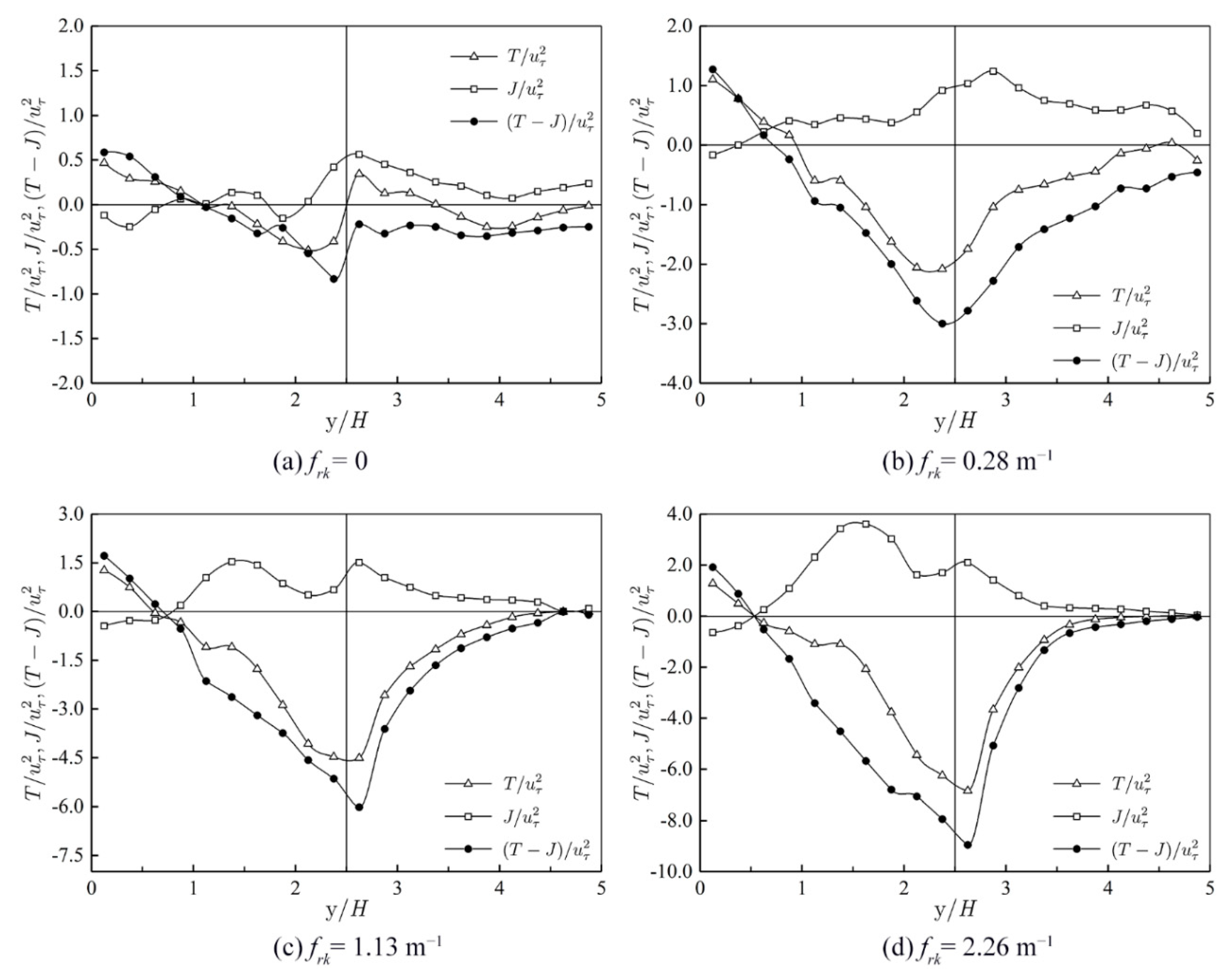
5.4. Lateral Momentum Exchange
5.5. Vertical Structures
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yuan, S.; Xu, L.; Tang, H.; Xiao, Y.; Gualtieri, C. The dynamics of river confluences and their effects on the ecology of aquatic environment: A review. J. Hydrodyn. 2022, 34, 1–14. [Google Scholar] [CrossRef]
- Salauddin, M.; O’Sullivan, J.J.; Abolfathi, S.; Pearson, J.M. Eco-engineering of seawalls-an opportunity for enhanced climate resilience from increased topographic complexity. Front. Mar. Sci. 2021, 8, 674630. [Google Scholar] [CrossRef]
- O’Sullivan, J.; Salauddin, M.; Abolfathi, S.; Pearson, J.M. Effectiveness of eco-retrofits in reducing wave overtopping on seawalls. Coast. Eng. Proc. 2020, 36v, 13. [Google Scholar] [CrossRef]
- Liu, N.; Salauddin, M.; Yeganeh-Bakhtiari, A.; Pearson, J.; Abolfathi, S. The impact of eco-retrofitting on coastal resilience enhancement—A physical modelling study. IOP Conf. Ser. Earth Environ. Sci. 2022, 1072, 012005. [Google Scholar] [CrossRef]
- Naot, D.; Nezu, I.; Nakagawa, H. Hydrodynamic behavior of partly vegetated open channels. J. Hydraul. Eng. 1996, 122, 625–633. [Google Scholar] [CrossRef]
- Kang, H.; Choi, S.U. Turbulence modeling of compound open-channel flows with and without vegetation on the floodplain using the Reynolds stress model. Adv. Water. Resour. 2006, 29, 1650–1664. [Google Scholar] [CrossRef]
- Yang, K.J.; Liu, X.N.; Cao, S.Y.; Zhang, Z.X. Turbulence characteristics of overbank flow in compound river channel with vegetated floodplain. J. Theor. Appl. Mech. 2006, 38, 246–250. (In Chinese) [Google Scholar]
- Zhang, M.L.; Shen, Y.M.; Zhu, L.Y. Depth-averaged two-dimensional numerical simulation for curved open channels with vegetation. J. Hydraul. Eng. 2008, 39, 794–800. (In Chinese) [Google Scholar]
- Cui, J.; Neary, V.S. LES study of turbulent flows with submerged vegetation. J. Hydraul. Res. 2008, 46, 307–316. [Google Scholar] [CrossRef]
- Sun, X.; Shiono, K. Flow resistance of one-line emergent vegetation along the floodplain edge of a compound open channel. Adv. Water Resour. 2009, 32, 430–438. [Google Scholar] [CrossRef]
- Huai, W.X.; Gao, M.; Zeng, Y.H.; Li, D. Two-dimensional analytical solution for compound channel flows with vegetated floodplains. Appl. Math. Mech. 2009, 30, 1049–1056. [Google Scholar] [CrossRef]
- Zhang, M.L.; Li, C.W.; Shen, Y.M. A 3D non-linear k-ε turbulent model for prediction of flow and mass transport in channel with vegetation. Appl. Math. Model. 2010, 34, 1021–1031. [Google Scholar] [CrossRef]
- Zhang, M.W. Research on Flow Characteristics in Compound Channels with Vegetated Floodplains. Ph.D. Thesis, Tsinghua University, Beijing, China, 2011. (In Chinese). [Google Scholar]
- Zeng, C.; Li, C.W. Measurements and modeling of open-channel flows with finite semi-rigid vegetation patches. Environ. Fluid Mech. 2014, 14, 113–134. [Google Scholar] [CrossRef]
- Zeng, Y.H.; Huai, W.X.; Zhao, M.D. Flow characteristics of rectangular open channels with compound vegetation roughness. Appl. Math. Mech. 2016, 37, 341–348. [Google Scholar] [CrossRef]
- Dupuis, V.; Proust, S.; Berni, C.; Paquier, A. Mixing layer development in compound channel flows with submerged and emergent rigid vegetation over the floodplains. Exp. Fluids 2017, 58, 30. [Google Scholar] [CrossRef]
- Barman, J.; Kumar, B. Flow behaviour in a multi-layered vegetated floodplain region of a compound channel. Ecohydrology 2022, 15, e2427. [Google Scholar] [CrossRef]
- Paquier, A.; Oudart, T.; Bouteiller, C.L.; Meulé, S.; Larroudé, P.; Dalrymple, R.A. 3D numerical simulation of seagrass movement under waves and currents with GPUSPH. Int. J. Sediment Res. 2021, 36, 711–722. [Google Scholar] [CrossRef]
- Kazemi, E.; Koll, K.; Tait, S.; Shao, S.D. SPH modelling of turbulent open channel flow over and within natural gravel beds with rough interfacial boundaries. Adv. Water Resour. 2020, 140, 103557. [Google Scholar] [CrossRef]
- Donnelly, J.; Abolfathi, S.; Pearson, J.; Chatrabgoun, O.; Daneshkhah, A. Gaussian process emulation of spatio-temporal outputs of 2D inland flood model. Water Res. 2022, 225, 119100. [Google Scholar] [CrossRef]
- Goodarzi, D.; Lari, K.S.; Khavasi, E.; Abolfathi, S. Large eddy simulation of turbidity currents in a narrow channel with different obstacle configurations. Sci. Rep. 2020, 10, 12814. [Google Scholar] [CrossRef]
- Zeng, C.; Ding, S.W.; Zhou, J.; Wang, L.L.; Chen, C. A three-dimensional numerical simulation based on WMLES for compound open-channel turbulent flows. Adv. Sci. Technol. Water Resour. 2020, 40, 17–22. (In Chinese) [Google Scholar]
- Cater, J.E.; Williams, J.J.R. Large eddy simulation of a long asymmetric compound open channel. J. Hydraul. Res. 2008, 46, 445–453. [Google Scholar] [CrossRef]
- Xie, Z.H.; Lin, B.L.; Falconer, R.A. Large-eddy simulation of the turbulent structure in compound open-channel flows. Adv. Water Resour. 2013, 53, 66–75. [Google Scholar] [CrossRef]
- Ding, S.W.; Zeng, C.; Zhou, J.; Wang, L.L.; Chen, C. Impact of the depth ratio on the flow structure and turbulence characteristics of the compound open-channel flows. Water Sci. Eng. 2022, 15, 265–272. [Google Scholar] [CrossRef]
- Zeng, C.; Qiu, F.; Ding, S.; Zhou, J.; Xu, J.; Wang, L.; Yin, Y. Study on energy and momentum correction coefficients in compound open-channel flows. Hydro-Sci. Eng. 2022, 46–54. (In Chinese) [Google Scholar] [CrossRef]
- Dunn, C.; Lopez, F.; Garcia, M.H. Mean Flow and Turbulence in a Laboratory Channel with Simulated Vegetation. Available online: https://www.ideals.illinois.edu/items/12292 (accessed on 1 October 1996).
- Thomas, T.G.; Williams, J.J.R. Large eddy simulation of turbulent flow in an asymmetric compound channel. J. Hydraul. Res. 1995, 33, 27–41. [Google Scholar] [CrossRef]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Zang, T. Spectral Methods in Fluid Dynamics; Springer: Amsterdam, The Netherlands, 1987. [Google Scholar]
- Shishkin, A.; Wagner, C. Direct Numerical Simulation of a Turbulent Flow Using a Spectral/hp Element Method. In New Results in Numerical and Experimental Fluid Mechanics V. Notes on Numerical Fluid Mechanics and Multidisciplinary Design (NNFM); Rath, H.J., Holze, C., Heinemann, H.J., Henke, R., Hönlinger, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar] [CrossRef]
- Rai, N.; Mondal, S. Spectral methods to solve nonlinear problems: A review. Partial. Differ. Equ. Appl. Math. 2021, 4, 100043. [Google Scholar] [CrossRef]
- Armanini, A. Roughness in fixed-bed streams. In Principles of River Hydraulics; Springer: Cham, Switzerland, 2018; pp. 1–31. [Google Scholar] [CrossRef]
- Kouwen, N. Modern approach to design of grassed channels. J. Irrig. Drain. Eng. 1992, 118, 733–743. [Google Scholar] [CrossRef]
- Huai, W.X.; Zeng, Y.H.; Xu, Z.G.; Yang, Z.H. Three-layer model for vertical velocity distribution in open channel flow with submerged rigid vegetation. Adv. Water Resour. 2009, 32, 487–492. [Google Scholar] [CrossRef]
- Righetti, M.; Armanini, A. Flow resistance in open channel flows with sparsely distributed bushes. J. Hydrol. 2002, 269, 55–64. [Google Scholar] [CrossRef]
- Nezu, I.; Onisuka, K. Turbulent structures in partly vegetated open-channel flows with LDA and PI V measurements. J. Hydraul. Res. 2001, 39, 629–642. [Google Scholar] [CrossRef]
- Hunt, J.C.R.; Wray, A.A.; Moin, P. Eddies, Stream, and Convergence Zones in Turbulent Flows; Center for Turbulence Research Report: Stanford, CA, USA, 1988; pp. 193–208. [Google Scholar]





| Q (m3/s) | H (m) | hv (m) | bv (m) | S0 | frk (m−1) |
|---|---|---|---|---|---|
| 0.179 | 0.335 | 0.1175 | 0.0064 | 0.0036 | 1.23 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, C.; Bai, Y.; Zhou, J.; Qiu, F.; Ding, S.; Hu, Y.; Wang, L. Large Eddy Simulation of Compound Open Channel Flows with Floodplain Vegetation. Water 2022, 14, 3951. https://doi.org/10.3390/w14233951
Zeng C, Bai Y, Zhou J, Qiu F, Ding S, Hu Y, Wang L. Large Eddy Simulation of Compound Open Channel Flows with Floodplain Vegetation. Water. 2022; 14(23):3951. https://doi.org/10.3390/w14233951
Chicago/Turabian StyleZeng, Cheng, Yimo Bai, Jie Zhou, Fei Qiu, Shaowei Ding, Yudie Hu, and Lingling Wang. 2022. "Large Eddy Simulation of Compound Open Channel Flows with Floodplain Vegetation" Water 14, no. 23: 3951. https://doi.org/10.3390/w14233951
APA StyleZeng, C., Bai, Y., Zhou, J., Qiu, F., Ding, S., Hu, Y., & Wang, L. (2022). Large Eddy Simulation of Compound Open Channel Flows with Floodplain Vegetation. Water, 14(23), 3951. https://doi.org/10.3390/w14233951





