Comparative Study on Water Temperature Stratified Flow under Different Vertical Coordinate Systems in Delft3D
Abstract
:1. Introduction
2. Materials and Methods
3. Results
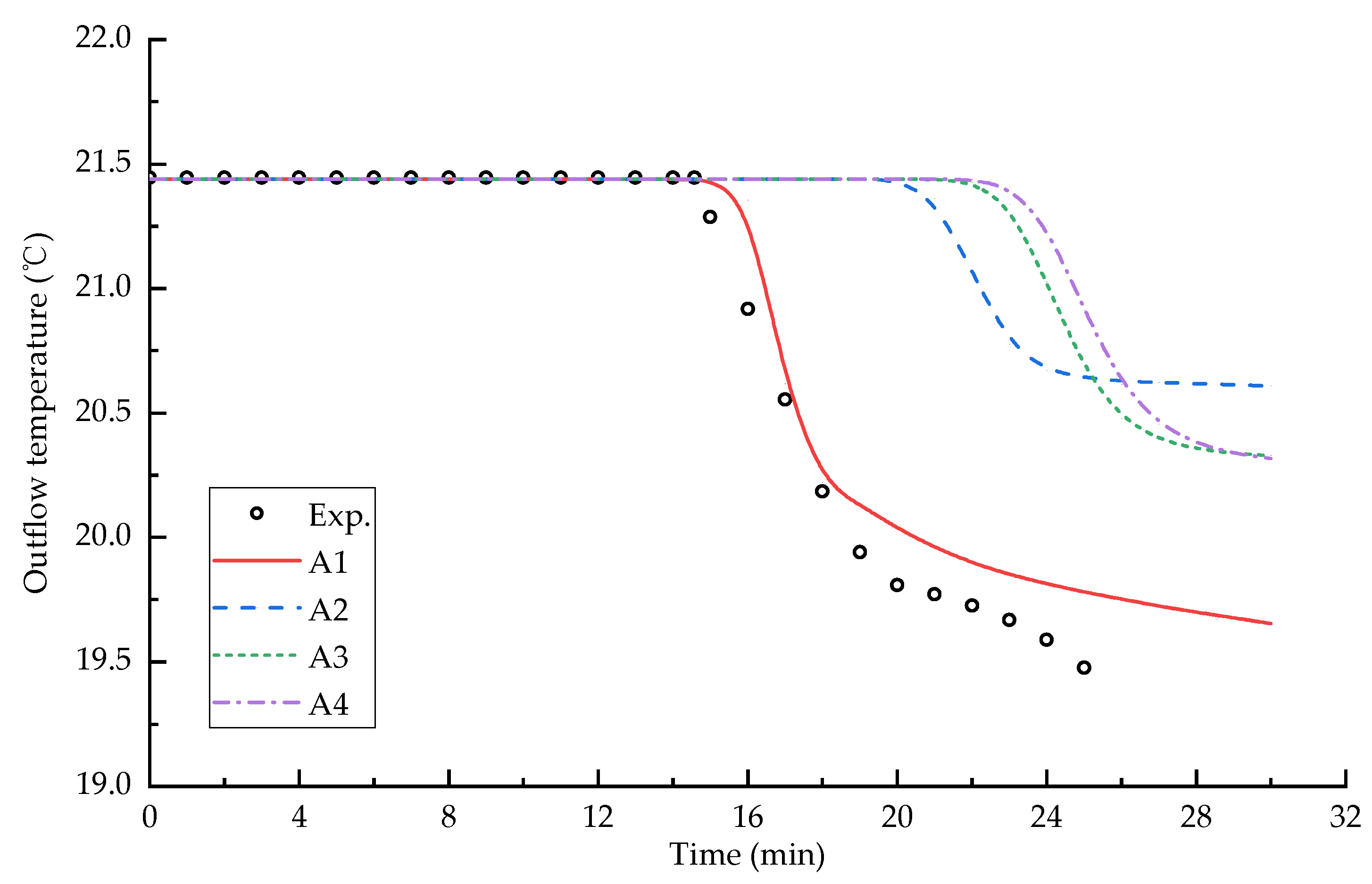
3.1. Comparison of the σ-Coordinate System and the z-Coordinate System Model
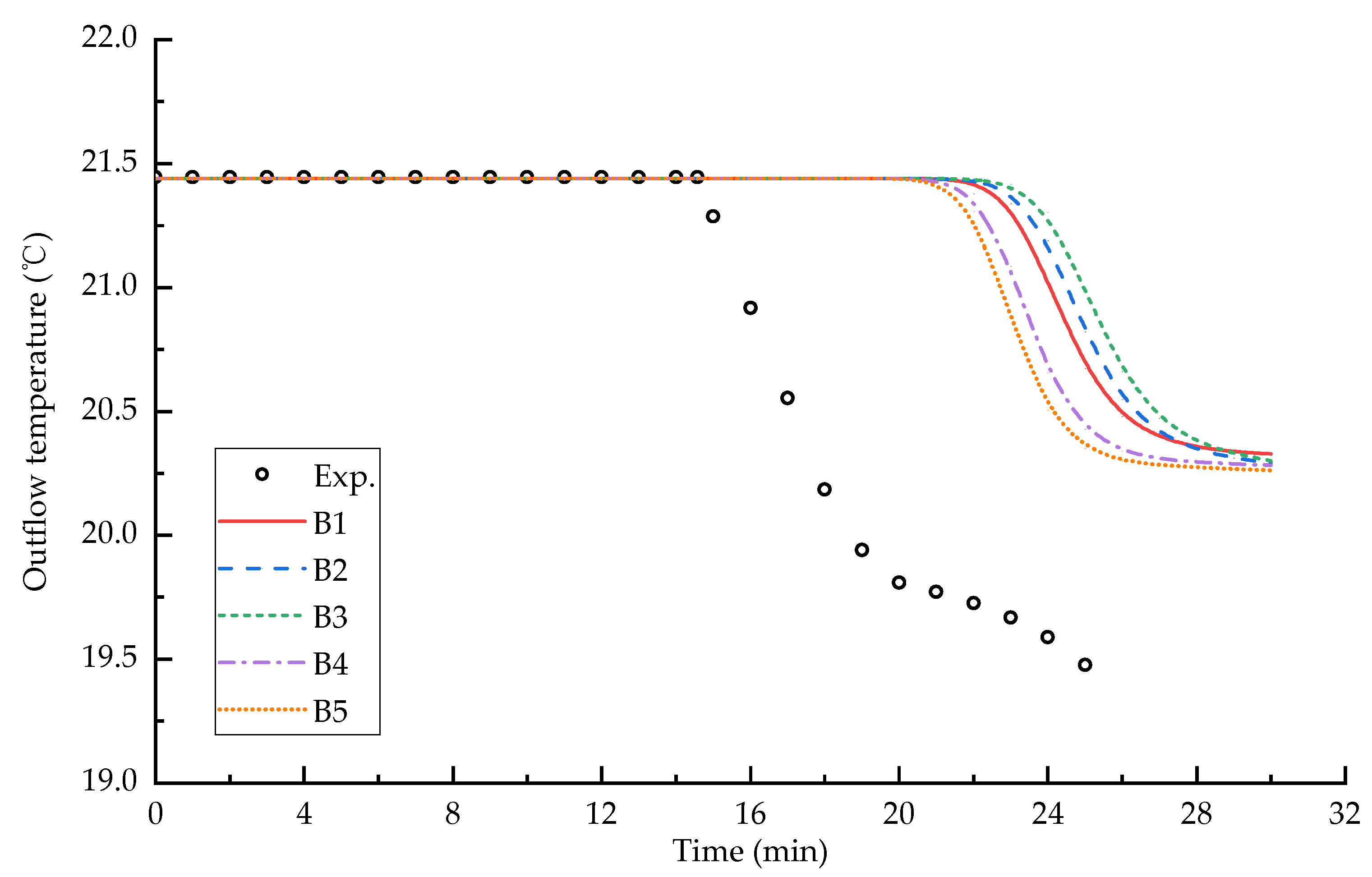
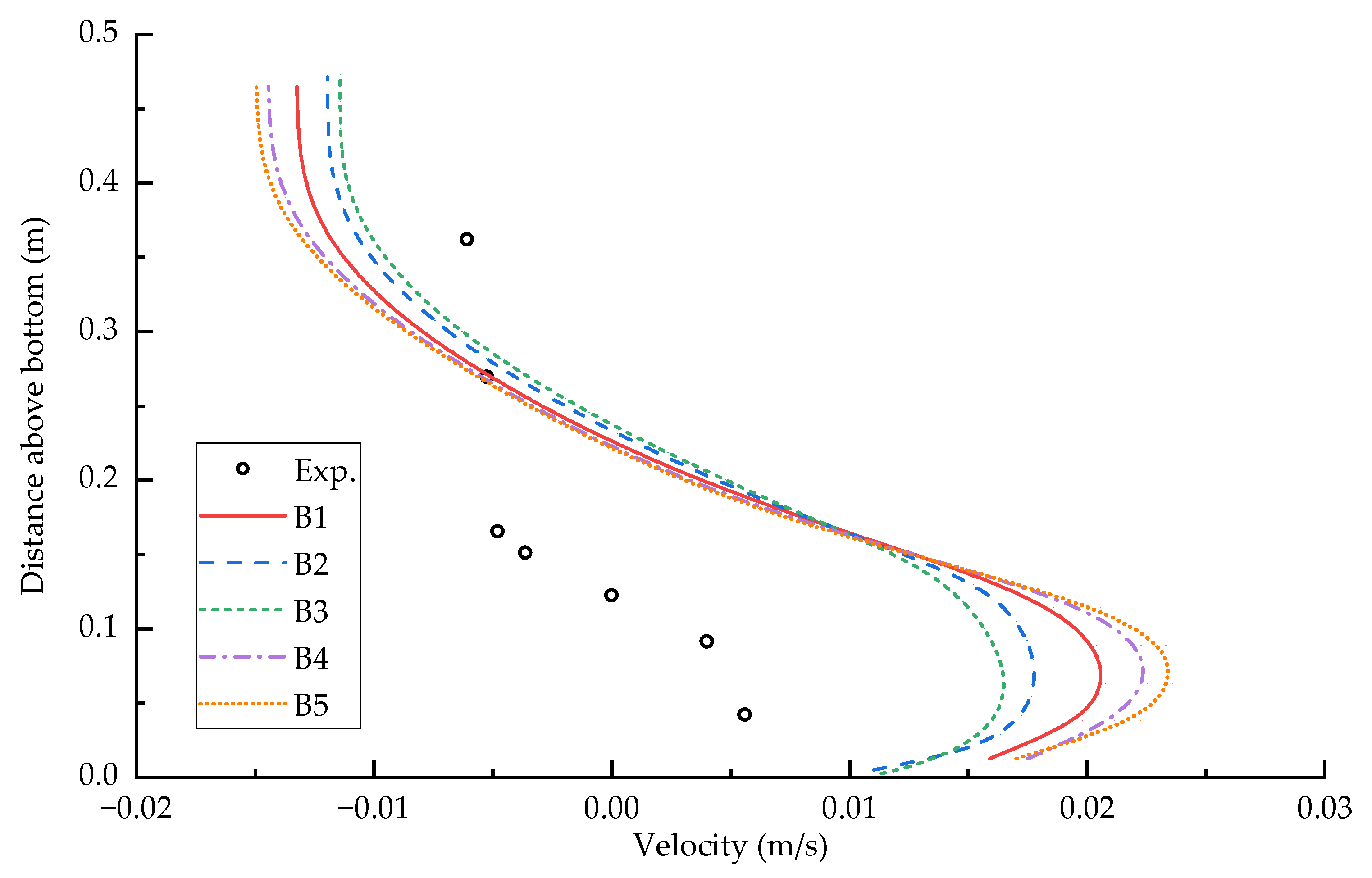
3.2. Effect of Grid Resolution on the z-Coordinate System Model
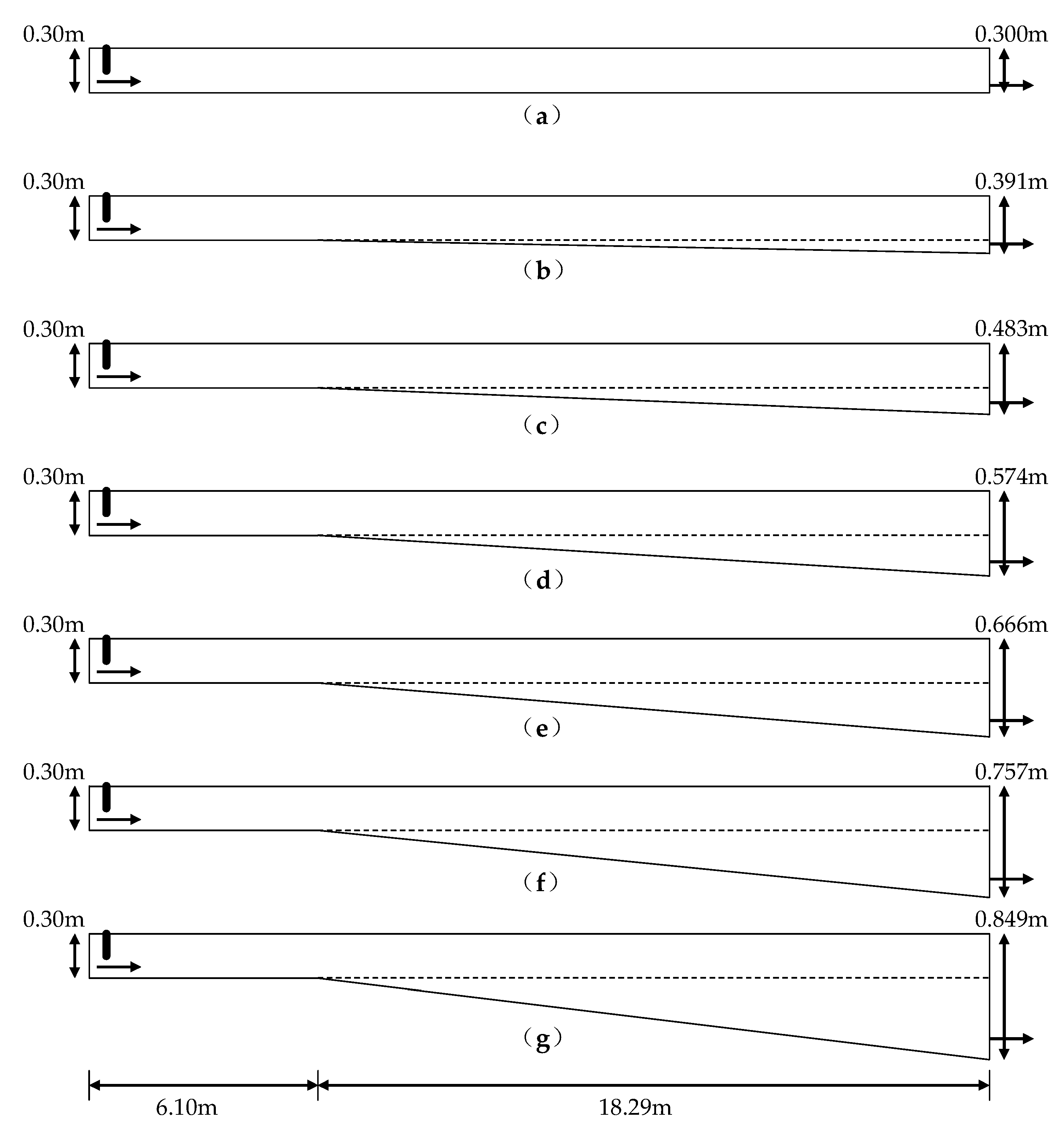
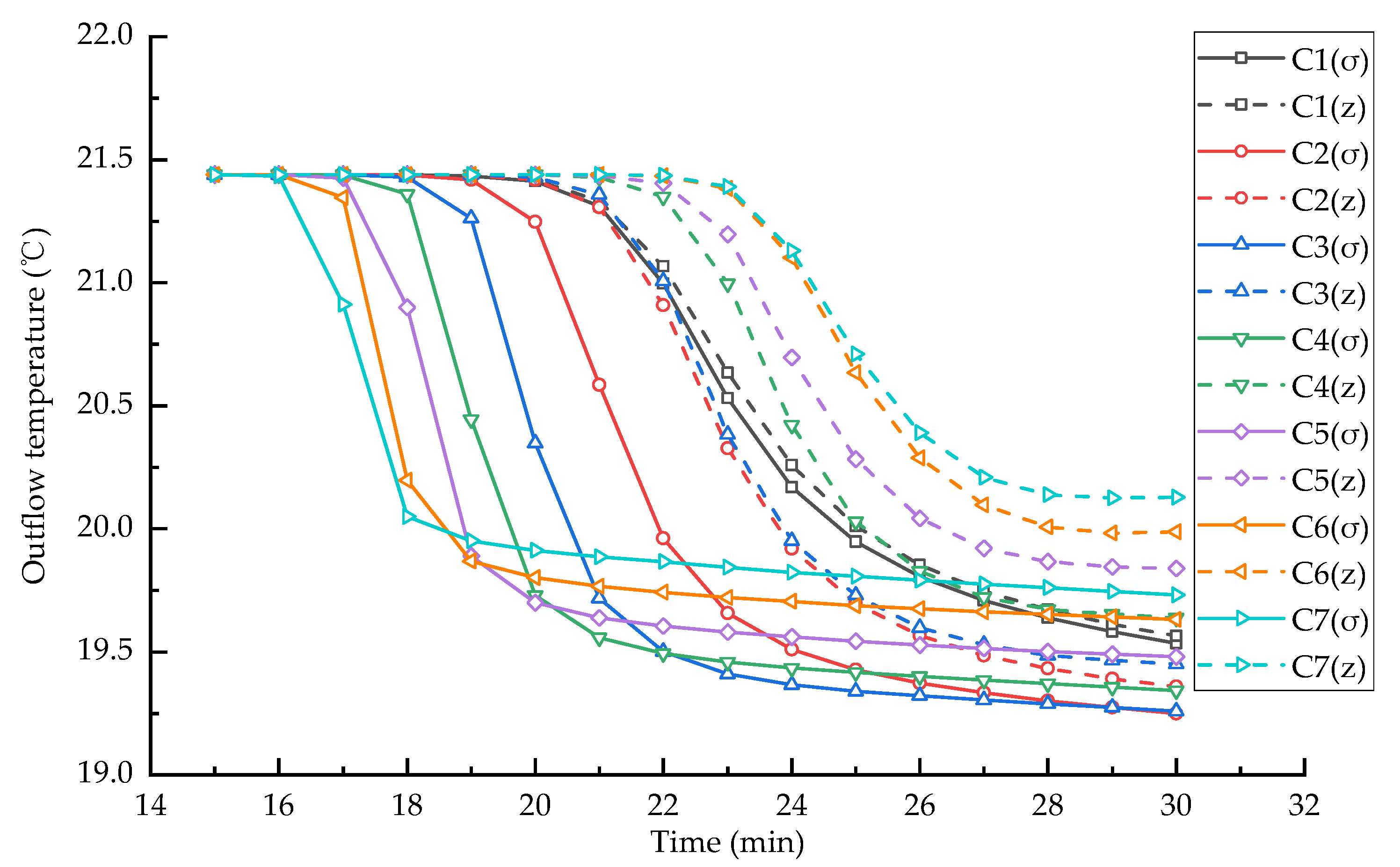
3.3. Effect of Bottom Slope on Simulation Accuracy
- When the bottom slope is the same, the outlet water temperature of the σ-coordinate system model is always lower than that of the z-coordinate system model. This means that the z-coordinate system model causes more vertical diffusion and leads to a higher water temperature of the outlet;
- In the σ-coordinate system model, with the increase in the bottom slope, the arrival time of cold water at the outlet is gradually advanced. This suggests that the larger the bottom slope of a reservoir, the higher the velocity of the cold-water underflow. When the bottom slope is more than 10‰ (conditions C4~C7), the outlet water temperature at the end time increases with the increasing bottom slope. This can be explained by the larger bottom slope, which contains more static water with a temperature of 21.44 °C. Compared to a large amount of initial hot water, the cold-water underflow is relatively small, which means that the outlet water temperature is more difficult to decrease;
- In the z-coordinate system model, for condition C2, as the bottom slope increases, the arrival time of cold water at the outlet is advanced; for condition C3, the simulation result is similar to condition C2; for conditions C4~C7, the arrival time of cold water at the outlet is gradually delayed with the increasing bottom slope. This suggests that when the bottom slope is more than 10‰ (conditions C4~C7), the simulation result of the z-coordinate system model may be incorrect;
- Since the σ-coordinate system model can simulate the formation process of cold-water underflow in the reservoir accurately, the simulation result of the σ-coordinate system model can be regarded as a reference to study the effect of bottom slopes on the simulation accuracy of the z-coordinate system model. As shown in Figure 8, when the bottom slope increases, the simulation deviation between the σ-coordinate system model and the z-coordinate system model also increases, which means that the numerical errors caused by the z-coordinate system model continue to increase. It can be concluded that the simulation accuracy of the z-coordinate system model decreases with the increasing bottom slope.
4. Discussion
5. Conclusions
- When simulating cold water flowing into a reservoir, the σ-coordinate system model has high simulation accuracy and is not affected by the truncation errors of the horizontal baroclinic gradient force. In contrast, the z-coordinate system model is inaccurate due to artificial vertical diffusion;
- The numerical errors in the z-coordinate system cold-water underflow reservoir model mainly consist of the following two parts: one is caused by the staircase representation of the bottom boundary, and one is caused by artificial vertical diffusion as the vertical grid lines are not parallel with the flow direction;
- To reduce the numerical error caused by the staircase representation of boundaries in the z-coordinate system model, the methods of remapping of near-bottom layers and increasing the vertical grid resolution have little influence on the simulation results. However, the method of increasing the horizontal grid resolution can decrease this numerical error, although there is still a large deviation from the observed data;
- To reduce artificial vertical diffusion in the z-coordinate system cold-water underflow reservoir model, the vertical grid lines should be parallel with the flow direction. The F-test shows that when the bottom slope is less than 18‰, the z-coordinate system model can simulate cold water flowing into a reservoir accurately.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, Z.; Liu, D.; Ji, D.; Xiao, S. Influence of the Impounding Process of the Three Gorges Reservoir up to Water Level 172.5 M on Water Eutrophication in the Xiangxi Bay. Sci. China Technol. Sci. 2010, 53, 1114–1125. [Google Scholar] [CrossRef]
- Fu, B.; Wu, B.; Lue, Y.; Xu, Z.; Cao, J.; Niu, D.; Yang, G.; Zhou, Y. Three Gorges Project: Efforts and Challenges for the Environment. Prog. Phys. Geogr. 2010, 34, 741–754. [Google Scholar] [CrossRef]
- Xu, X.; Tan, Y.; Yang, G. Environmental Impact Assessments of the Three Gorges Project in China: Issues and Interventions. Earth-Sci. Rev. 2013, 124, 115–125. [Google Scholar] [CrossRef]
- Gao, Q.; He, G.; Fang, H.; Bai, S.; Huang, L. Numerical Simulation of Water Age and Its Potential Effects on the Water Quality in Xiangxi Bay of Three Gorges Reservoir. J. Hydrol. 2018, 566, 484–499. [Google Scholar] [CrossRef]
- Zhang, M.; Niu, Z.; Cai, Q.; Xu, Y.; Qu, X. Effect of Water Column Stability on Surface Chlorophyll and Time Lags Under Different Nutrient Backgrounds in a Deep Reservoir. Water 2019, 11, 1504. [Google Scholar] [CrossRef]
- Zhang, L.; Xia, Z.; Zhou, C.; Fu, L.; Yu, J.; Taylor, W.D.; Hamilton, P.B.; Cappellen, P.V.; Ji, D.; Liu, D. Unique Surface Density Layers Promote Formation of Harmful Algal Blooms in the Pengxi River, Three Gorges Reservoir. Freshw. Sci. 2020, 39, 722–734. [Google Scholar] [CrossRef]
- Li, Y.; Sun, J.; Lin, B.; Liu, Z. Thermal-hydrodynamic Circulations and Water Fluxes in a Tributary Bay of the Three Gorges Reservoir. J. Hydrol. 2020, 585, 124319. [Google Scholar] [CrossRef]
- Li, P.; Yao, Y.; Lian, J.; Ma, C. Effect of Thermal Stratified Flow on Algal Blooms in a Tributary Bay of the Three Gorges Reservoir. J. Hydrol. 2021, 601, 126648. [Google Scholar] [CrossRef]
- Liu, L.; Liu, D.; Johnson, D.M.; Yi, Z.; Huang, Y. Effects of Vertical Mixing on Phytoplankton Blooms in Xiangxi Bay of Three Gorges Reservoir: Implications for Management. Water Res. 2012, 46, 2121–2130. [Google Scholar] [CrossRef]
- Holbach, A.; Norra, S.; Wang, L.; Yijun, Y.; Hu, W.; Zheng, B.; Bi, Y. Three Gorges Reservoir: Density Pump Amplification of Pollutant Transport into Tributaries. Environ. Sci. Technol. 2014, 48, 7798–7806. [Google Scholar] [CrossRef]
- Zhao, Y.; Zheng, B.; Wang, L.; Qin, Y.; Li, H.; Cao, W. Characterization of Mixing Processes in the Confluence Zone Between the Three Gorges Reservoir Mainstream and the Daning River Using Stable Isotope Analysis. Environ. Sci. Technol. 2016, 50, 9907–9914. [Google Scholar] [CrossRef]
- Yang, Z.; Cheng, B.; Xu, Y.; Liu, D.; Ma, J.; Ji, D. Stable Isotopes in Water Indicate Sources of Nutrients that Drive Algal Blooms in the Tributary Bay of a Subtropical Reservoir. Sci. Total Environ. 2018, 634, 205–213. [Google Scholar] [CrossRef]
- Cheng, Y.; Mu, Z.; Wang, H.; Zhao, F.; Li, Y.; Lin, L. Water Residence Time in a Typical Tributary Bay of the Three Gorges Reservoir. Water 2019, 11, 1585. [Google Scholar] [CrossRef]
- Song, Y.; Shen, L.; Zhang, L.; Li, J.; Chen, M. Study of a Hydrodynamic Threshold System for Controlling Dinoflagellate Blooms in Reservoirs. Environ. Pollut. 2021, 278, 116822. [Google Scholar] [CrossRef]
- Cornelissen, S. Numerical Modelling of Stratified Flows: Comparison of the Sigma and Z Coordinate Systems; Tu Delft: Delft, The Netherlands, 2004. [Google Scholar]
- Haney, R.L. On the Pressure Gradient Force Over Steep Topography in Sigma Coordinate Ocean Models. J. Phys. Oceanogr. 1991, 21, 610–619. [Google Scholar] [CrossRef]
- Mellor, G.L.; Ezer, T.; Oey, L. The Pressure Gradient Conundrum of Sigma Coordinate Ocean Models. J. Atmos. Ocean. Technol. 1994, 11, 1126–1134. [Google Scholar] [CrossRef]
- Zamani, B.; Koch, M. Comparison between Two Hydrodynamic Models in Simulating Physical Processes of a Reservoir with Complex Morphology: Maroon Reservoir. Water 2020, 12, 814. [Google Scholar] [CrossRef]
- Stelling, G.S.; Van kester, J.A.T.M. On the Approximation of Horizontal Gradients in Sigma Co-ordinates for Bathymetry with Steep Bottom Slopes. Int. J. Numer. Methods Fluids 1994, 18, 915–935. [Google Scholar] [CrossRef]
- Platzek, F.; Stelling, G.; Jankowski, J.; Patzwahl, R. On the Representation of Bottom Shear Stress in Z-layer Models. In Proceedings of the 10th International Conference on Hydroinformatics: Hic 2012, Hamburg, Germany, 14–18 July 2012. [Google Scholar]
- Johnson, B.H. A Review of Numerical Reservoir Hydrodynamic Modeling: Us Army Engineer Waterways Experiment Station. 1981. Available online: https://apps.dtic.mil/sti/pdfs/ADA097823.pdf (accessed on 1 February 1981).
- Sarker, S. Essence of Mike 21C (FDM Numerical Scheme): Application on the River Morphology of Bangladesh. Open J. Model. Simul. 2022, 10, 88–117. [Google Scholar] [CrossRef]
- Sarker, S. A Short Review on Computational Hydraulics in the Context of Water Resources Engineering. Open J. Model. Simul. 2021, 10, 1–31. [Google Scholar] [CrossRef]
- Deltares. Delft3d-Flow User Manual; Deltares: Delft, The Netherlands, 2020. [Google Scholar]
- Postma, L.; Stelling, G.; Boon, J. Three-dimensional Water Quality and Hydrodynamic Modelling in Hong Kong, III. Stratification and Water Quality. In Proceedings of the 2nd International Symposium on Environmental Hydraulics, Hong Kong, China, 16–18 December 1998. [Google Scholar]
- Burchard, H.; Baumert, H. On the Performance of a Mixed-layer Model Based on the K-epsilon Closure. J. Geophys. Res.-Ocean. 1995, 100, 8523–8540. [Google Scholar] [CrossRef]
- Winton, M.; Hallberg, R.; Gnanadesikan, A. Simulation of Density-driven Frictional Downslope Flow in Z-coordinate Ocean Models. J. Phys. Oceanogr. 1998, 28, 2163–2174. [Google Scholar] [CrossRef]
- Wang, C.; Huang, B.; Xu, T.; Zhu, D.Z.; Wang, L.; Wang, Y. Numerical Modeling of Energy Dissipation of Internal Solitary Waves Encountering Step Topography. Ocean. Eng. 2022, 259, 111853. [Google Scholar] [CrossRef]
- Xia, M.; Jiang, L. Application of an Unstructured Grid-based Water Quality Model to Chesapeake Bay and Its Adjacent Coastal Ocean. J. Mar. Sci. Eng. 2016, 4, 52. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Ateljevich, E.; Yu, H.; Wu, C.H.; Yu, J.C. A New Vertical Coordinate System for a 3d Unstructured-grid Model. Ocean. Model. 2015, 85, 16–31. [Google Scholar] [CrossRef]
- Chen, C.; Qi, J.; Liu, H.; Beardsley, R.C.; Lin, H.; Cowles, G. A Wet/dry Point Treatment Method of Fvcom, Part I: Stability Experiments. J. Mar. Sci. Eng. 2022, 10, 896. [Google Scholar] [CrossRef]
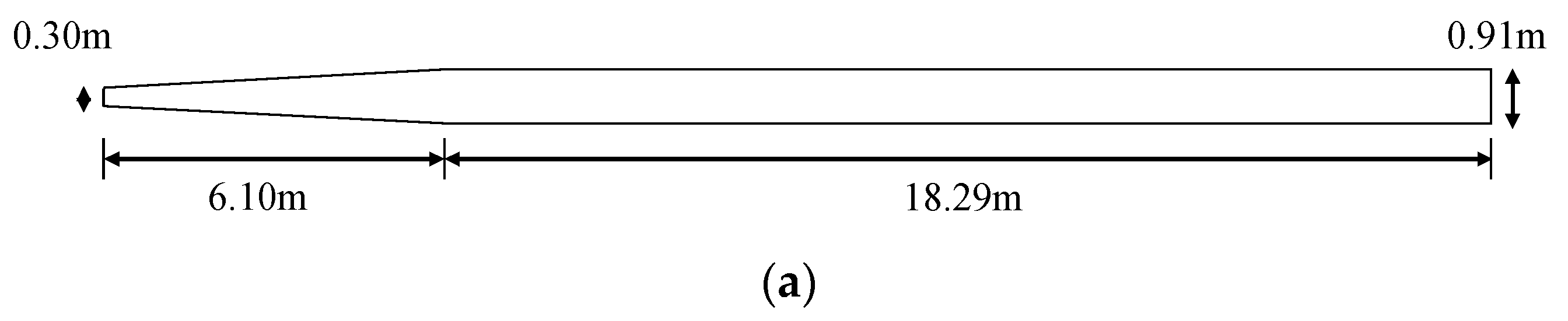
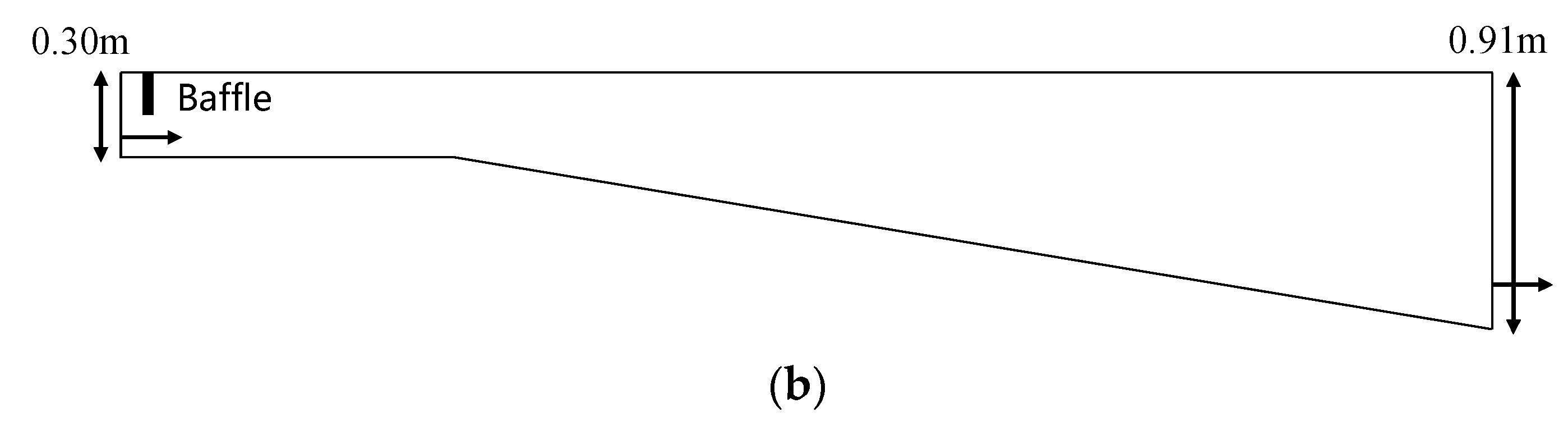


| Simulation Conditions | Vertical Coordinate System | Horizontal Grid | Vertical Grid Number | |
|---|---|---|---|---|
| Longitudinal Grid Number | Lateral Grid Number | |||
| A1 | σ-coordinate | 80 | 9 | 36 |
| A2 | σ-coordinate (anti-creep) | 80 | 9 | 36 |
| A3 | z-coordinate | 80 | 9 | 36 |
| A4 | z-coordinate (remapping) | 80 | 9 | 36 |
| Simulation Conditions | Time Step (min) | Manning Number (m−1/3s) | Background Horizontal Eddy Viscosity Coefficient (m2/s) | Background Horizontal Eddy Diffusion Coefficient (m2/s) | Turbulence Model |
|---|---|---|---|---|---|
| A1~A4 | 0.01 | 0.009 | 0.01 | 0.01 | k-ε model |
| Simulation Conditions | Vertical Coordinate System | Horizontal Grid | Vertical Grid Number | |
|---|---|---|---|---|
| Longitudinal Grid Number | Lateral Grid Number | |||
| B1 | z-coordinate | 80 | 9 | 36 |
| B2 | z-coordinate | 80 | 9 | 72 |
| B3 | z-coordinate | 80 | 9 | 100 |
| B4 | z-coordinate | 160 | 9 | 36 |
| B5 | z-coordinate | 240 | 9 | 36 |
| Simulation Conditions | C1 | C2 | C3 | C4 | C5 | C6 | C7 |
|---|---|---|---|---|---|---|---|
| Bottom slope | 0‰ | 5‰ | 10‰ | 15‰ | 20‰ | 25‰ | 30‰ |
| Depth of the downstream section (m) | 0.300 | 0.391 | 0.483 | 0.574 | 0.666 | 0.757 | 0.849 |
| Height of the outlet hole (m) | 0.050 | 0.065 | 0.080 | 0.096 | 0.111 | 0.126 | 0.141 |
| Simulation Conditions | C1 | C2 | C3 | C4 | C5 | C6 | C7 |
|---|---|---|---|---|---|---|---|
| α | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 |
| F | 1.02 | 1.04 | 1.30 | 1.91 | 3.62 | 19.12 | 43.26 |
| P(F < = f) | 0.48 | 0.48 | 0.33 | 0.14 | 0.02 | 0.00 | 0.00 |
| F critical value | 2.69 | 2.69 | 2.69 | 2.69 | 2.69 | 2.69 | 2.69 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lang, Y.; Hu, Z.; Hao, R.; Li, Y.; Han, L. Comparative Study on Water Temperature Stratified Flow under Different Vertical Coordinate Systems in Delft3D. Water 2022, 14, 2737. https://doi.org/10.3390/w14172737
Lang Y, Hu Z, Hao R, Li Y, Han L. Comparative Study on Water Temperature Stratified Flow under Different Vertical Coordinate Systems in Delft3D. Water. 2022; 14(17):2737. https://doi.org/10.3390/w14172737
Chicago/Turabian StyleLang, Yun, Zijun Hu, Ruixia Hao, Yafei Li, and Lijuan Han. 2022. "Comparative Study on Water Temperature Stratified Flow under Different Vertical Coordinate Systems in Delft3D" Water 14, no. 17: 2737. https://doi.org/10.3390/w14172737
APA StyleLang, Y., Hu, Z., Hao, R., Li, Y., & Han, L. (2022). Comparative Study on Water Temperature Stratified Flow under Different Vertical Coordinate Systems in Delft3D. Water, 14(17), 2737. https://doi.org/10.3390/w14172737






