Model and Experimental Studies of the Seepage Failure of Damaged Geotextile at the Joint between Tubes in a Geotextile Tube Dam
Abstract
:1. Introduction
2. Critical Gradient Theoretical Model
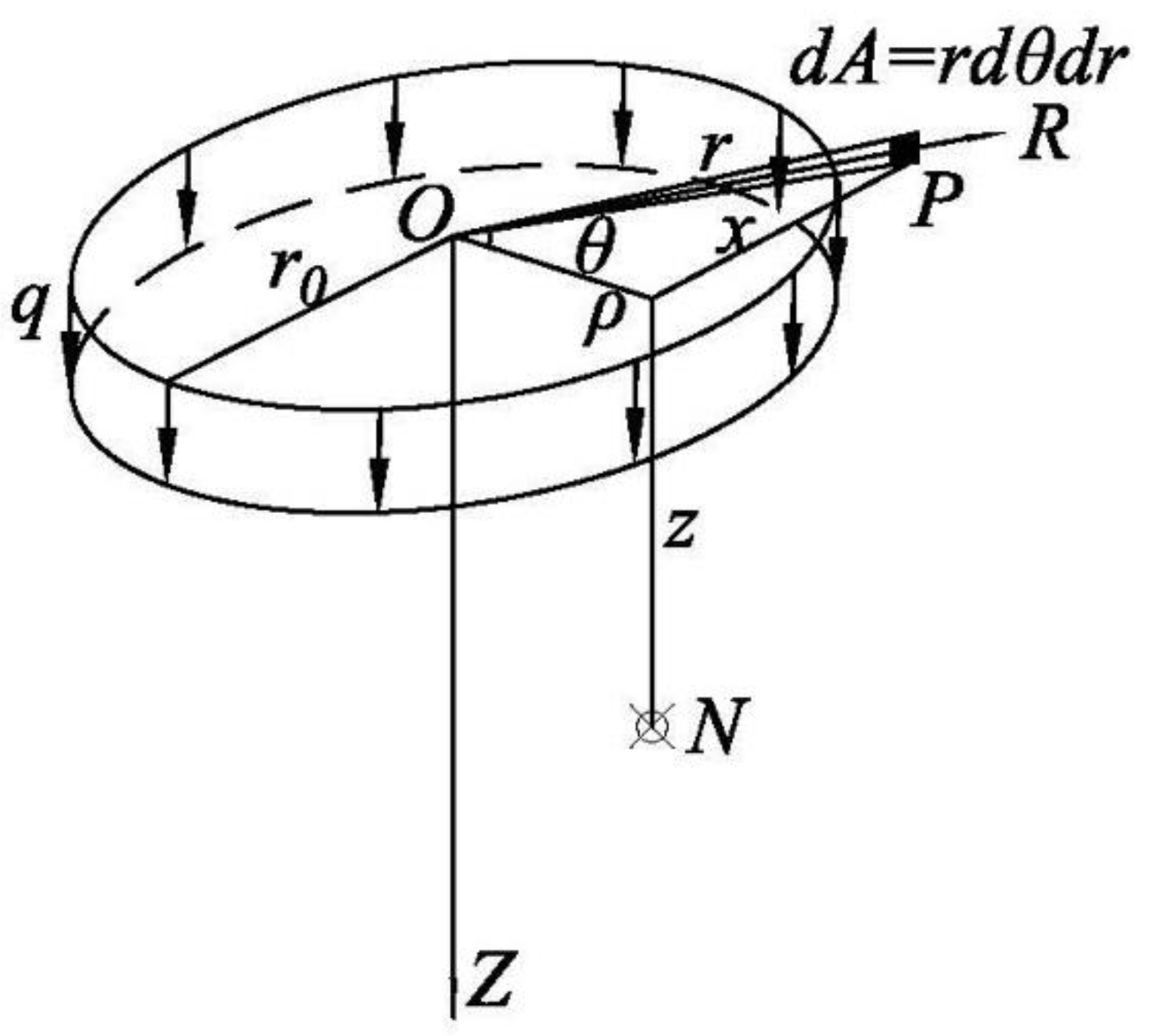
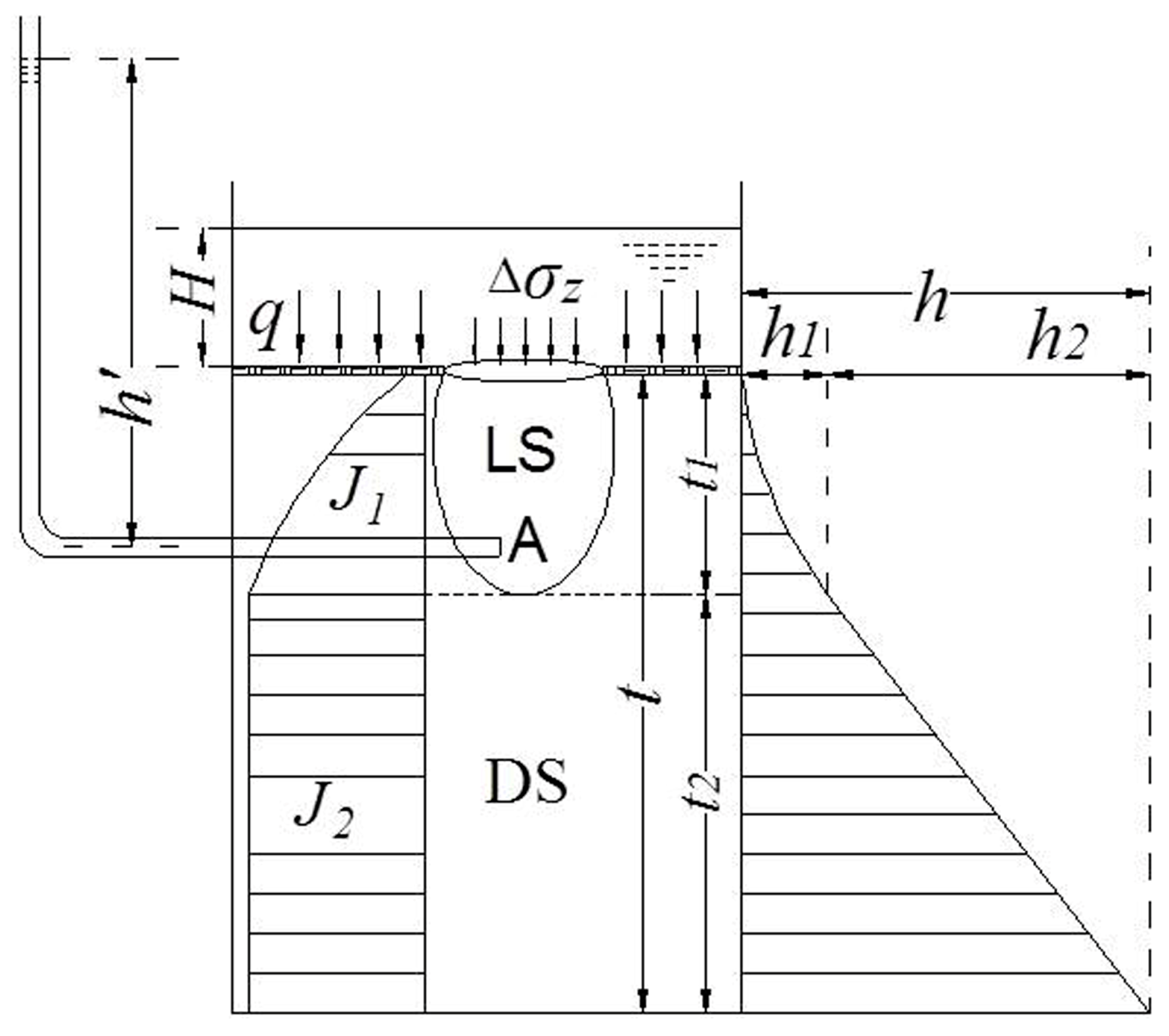
2.1. Vertical Stress Calculation
2.2. Force Analysis of Seepage Failure
3. Sand Erosion Tests by Upward Seepage Flow
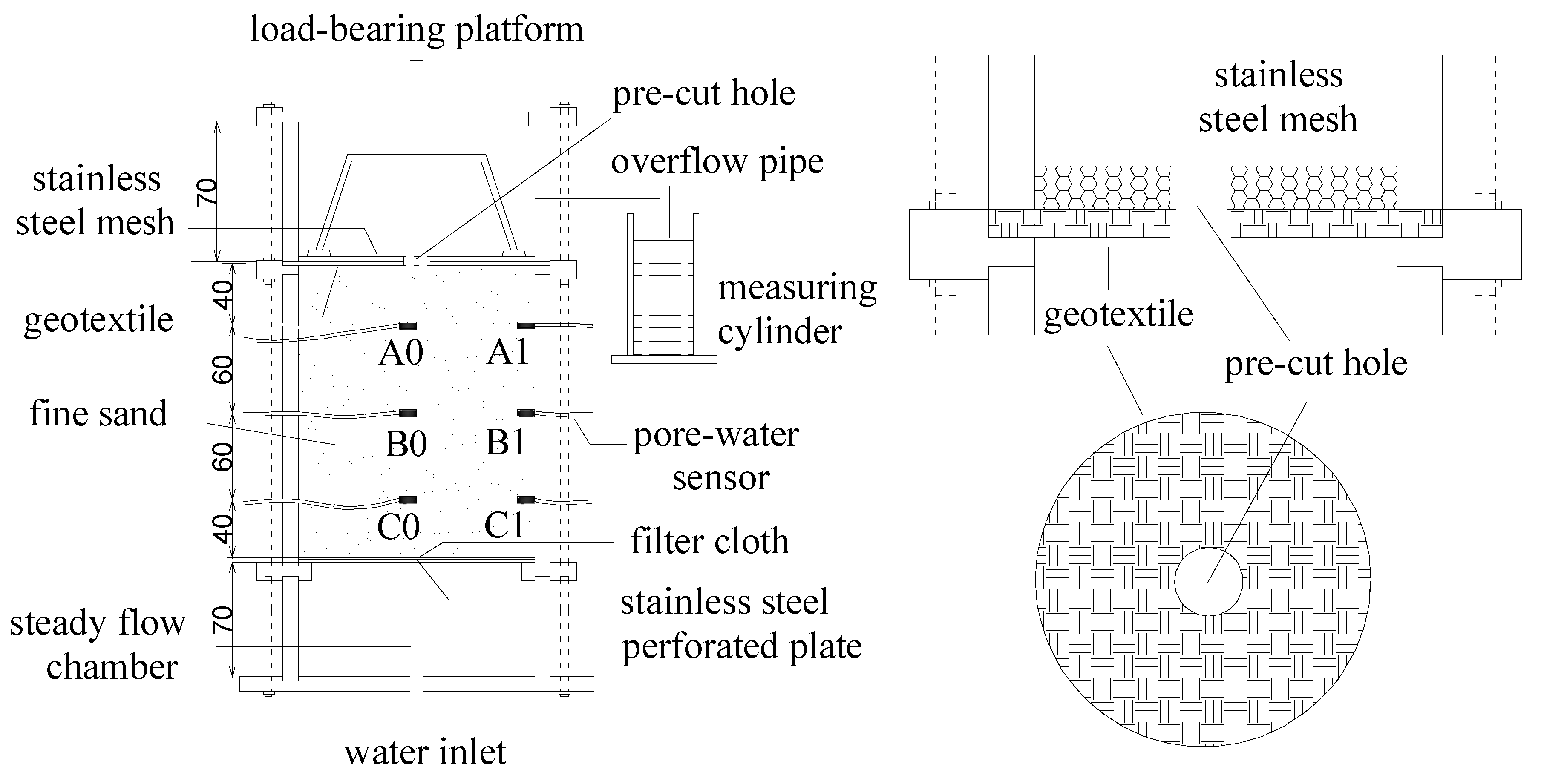
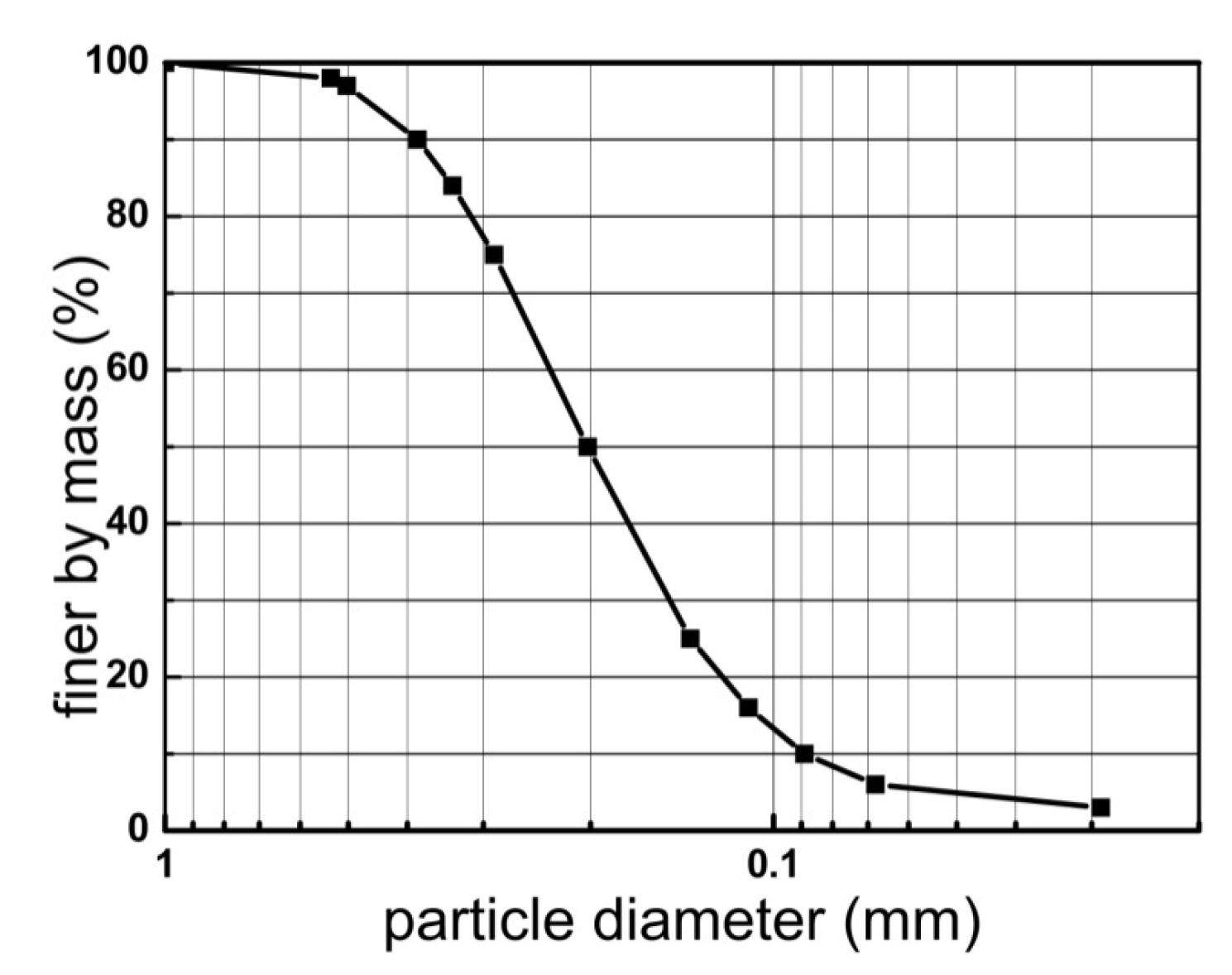
3.1. Test Apparatus and Materials
3.2. Testing Program and Procedures
- Before the sand seepage erosion tests, the steady-flow chamber, sand chamber, stainless-steel perforated plate, and filter cloth were assembled successively, as shown in Figure 5. To ensure the homogeneity of the sand sample, the sand was compacted layer by layer with a thickness of 4 cm per layer. Each layer was compacted with a metal rod several times to the target relative density. This process was repeated until the sand was filled to the top of the sand chamber. During sand filling, pore-water sensors were placed at predetermined positions.
- The geotextile with the hole and the acrylic cylinder of the overflow chamber were placed successively after the surface of the sand sample was flattened. Then, the hard stainless-steel mesh and the load-bearing platform were installed. In the end, the overflow chamber was secured by bolting the cover plate and flange.
- In the process of specimen saturation, the required overburden load was first applied through the loading device. Second, water from the external tank was slowly introduced into the specimen through the steady-flow chamber. To avoid sand particle disturbance, the saturation process must be slow. Then, the sand was soaked for 12 h under a static head to ensure a high degree of saturation.
- Starting with zero differential head, the water tank was first raised by 3 cm (hydraulic gradient = 0.15). During this period, the pore-water pressure and the seepage rate were recorded using a measuring cylinder under the overflow pipe every 2 min, and the corresponding hydraulic conductivity was calculated. If there is no change in the water pressure and seepage rate for two consecutive times and no notable seepage channel is observed, then the sand sample is considered to be stable. After another 20 min under this hydraulic gradient, the hydraulic gradient was increased by raising the tank another 3 cm. This process was repeated until hydraulic conductivity changed by more than 20%. For the remainder of the test, the differential head was increased in small increments of 1 cm (hydraulic gradient = 0.05). The test progressed until the sand sample completely failed.
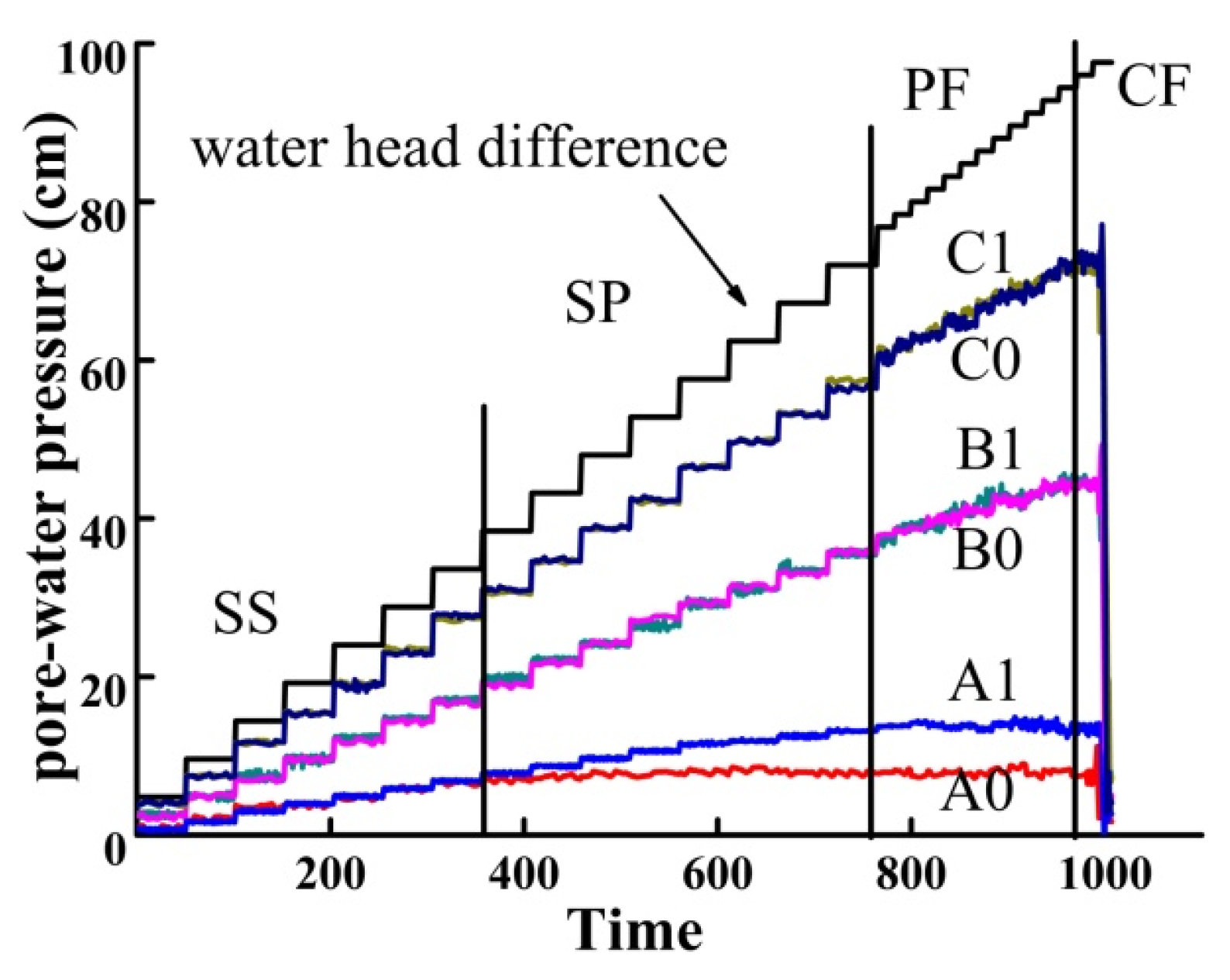
4. Test Results and Analysis
Seepage Failure Progression
5. Discussion
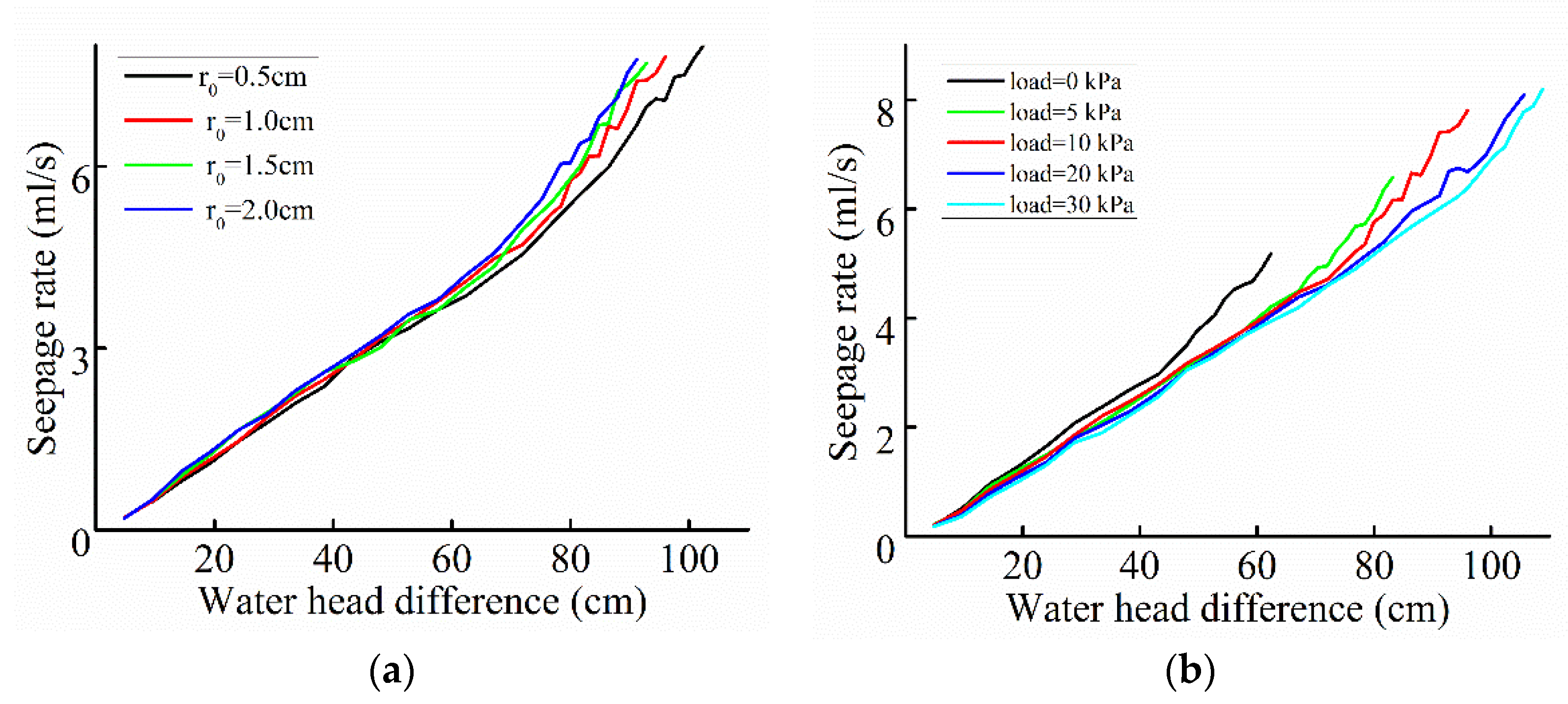
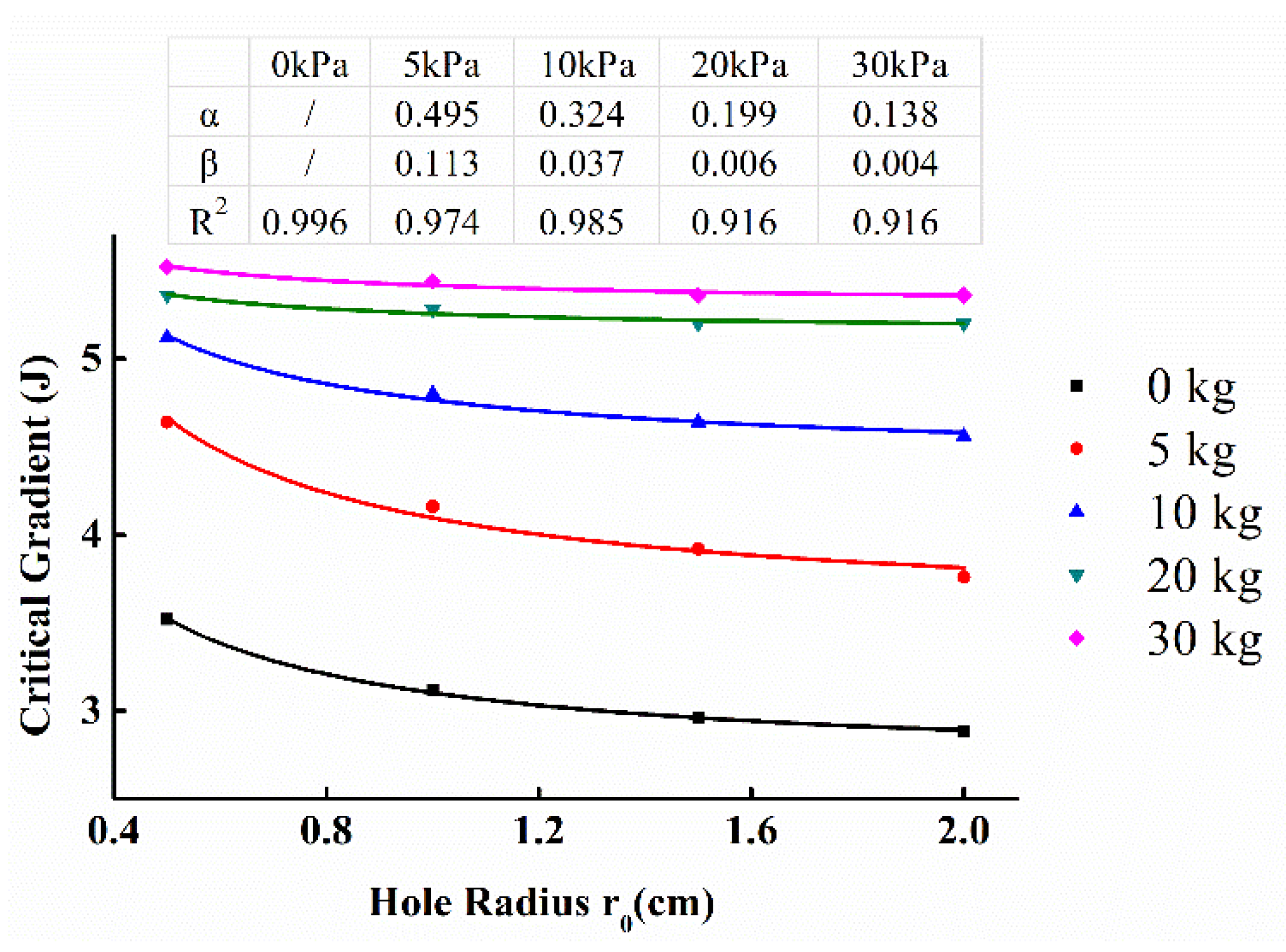
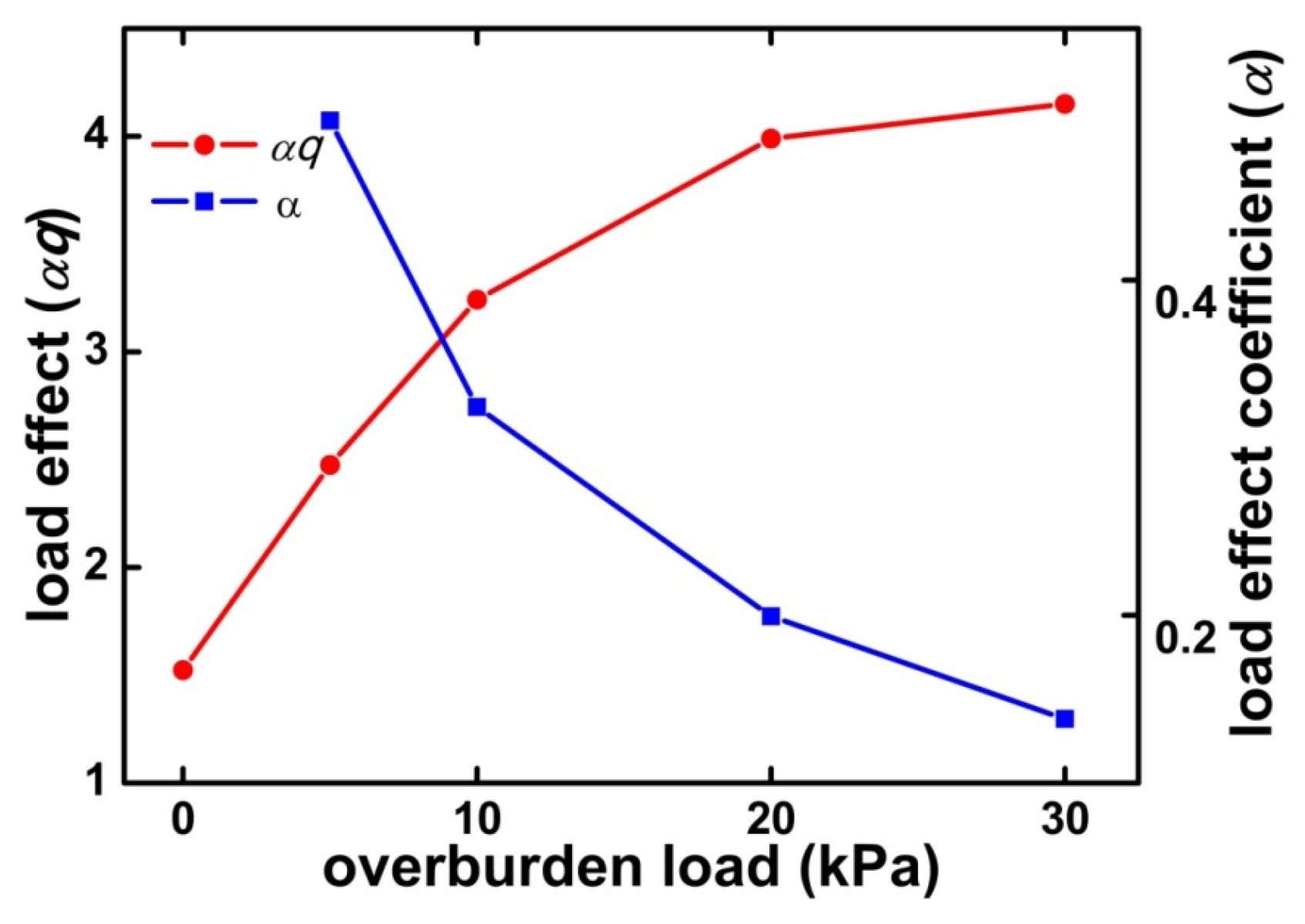
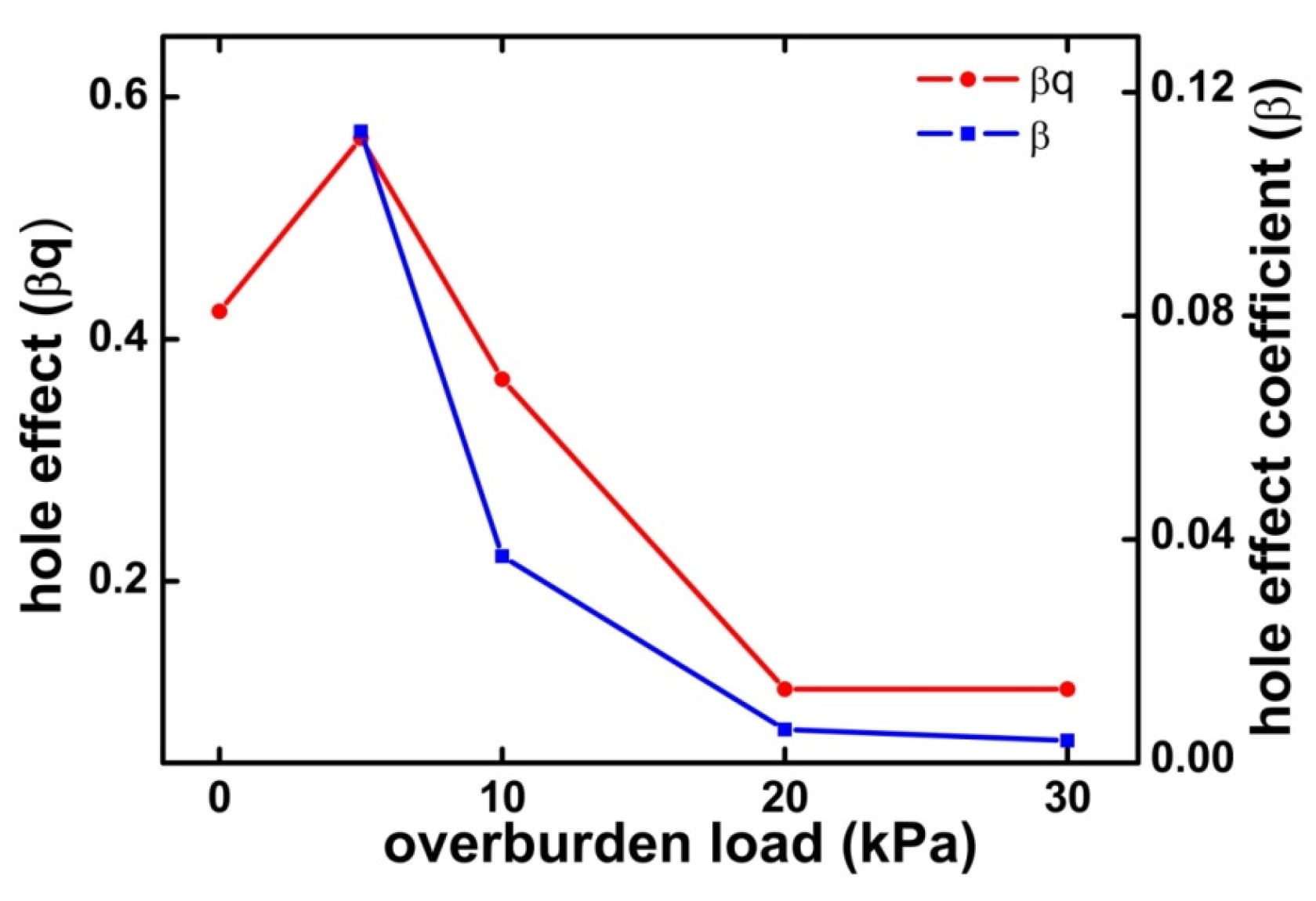
5.1. Effect of the Overburden Load
5.2. Effect of the Hole
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Guo, W.; Chu, J.; Nie, W. Analysis of geosynthetic tubes inflated by liquid and consolidated soil. Geotext. Geomembr. 2014, 42, 277–283. [Google Scholar] [CrossRef]
- Kiran, A.S. Stability of Upper Geotextile Tube in a Stacked Formation Under Wave Loading. Int. J. Geosynth. Ground Eng. 2022, 8, 32. [Google Scholar] [CrossRef]
- Kim, H.-J.; Won, M.-S.; Jamin, J.C. Finite-element analysis on the stability of geotextile tube–reinforced embankments under scouring. Int. J. Geomech. 2015, 15, 06014019. [Google Scholar] [CrossRef]
- Chang, Y.; Chu, K.-W.; Chuang, L.Z.-H. Sustainable coastal zone planning based on historical coastline changes: A model from case study in Tainan, Taiwan. Landsc. Urban Plan. 2018, 174, 24–32. [Google Scholar] [CrossRef]
- Yang, Y.; Wei, Z.; Cao, G.; Yang, Y.; Wang, H.; Zhuang, S.; Lu, T. A case study on utilizing geotextile tubes for tailings dams construction in China. Geotext. Geomembr. 2019, 47, 187–192. [Google Scholar] [CrossRef]
- Carlos, D.; Carneiro, J.R.; Pinho-Lopes, M.; Lopes, M. Effect of soil grain size distribution on the mechanical damage of nonwoven geotextiles under repeated loading. Int. J. Geosynth. Ground Eng. 2015, 1, 9. [Google Scholar] [CrossRef] [Green Version]
- Lopes, M.; Paula, A.M. Long-term response and design of two geosynthetics: Effect of field installation damage. Geosynth. Int. 2018, 25, 98–117. [Google Scholar] [CrossRef]
- Huang, C.-C. Comparative study on performance and index tests simulating abrasion damage of a woven geotextile. Geosynth. Int. 2008, 15, 358–368. [Google Scholar] [CrossRef]
- Lu, Z.-M.; Wu, C.-E. Key techniques and practices of dyke engineering design of qingcaosha reservoir. Yangtze River 2013, 44, 28–32. (In Chinese) [Google Scholar] [CrossRef]
- Lv, Z.J. Application of technology of geotextile tubes in Sizhaopu reclamation project. Zhejiang Hydrotech. 2002, 4, 27–30. (In Chinese) [Google Scholar] [CrossRef]
- Huang, C.-C.; Tzeng, Y.-S. Abrasion damage of a woven geotextile due to various gravelly flows. Geosynth. Int. 2007, 14, 277–286. [Google Scholar] [CrossRef]
- Huang, C.; Tzeng, Y.; Liao, C. Laboratory tests for simulating abrasion damage of a woven geotextile. Geotext. Geomembr. 2007, 25, 293–301. [Google Scholar] [CrossRef]
- Pinho-Lopes, M.; Lopes, M.D.L. Influence of mechanical damage induced in laboratory on the soil-geosynthetic interaction in inclined-plane shear. Constr. Build. Mater. 2018, 185, 468–480. [Google Scholar] [CrossRef] [Green Version]
- Rosete, A.; Lopes, P.M.; Pinho-Lopes, M. Tensile and hydraulic properties of geosynthetics after mechanical damage and abrasion laboratory tests. Geosynth. Int. 2013, 20, 358–374. [Google Scholar] [CrossRef] [Green Version]
- Cheah, C.; Gallage, C.; Dawes, L.; Kendall, P. Measuring hydraulic properties of geotextiles after installation damage. Geotext. Geomembr. 2017, 45, 462–470. [Google Scholar] [CrossRef] [Green Version]
- Miszkowska, A.; Lenart, S.; Koda, E. Changes of Permeability of Nonwoven Geotextiles due to Clogging and Cyclic Water Flow in Laboratory Conditions. Water 2017, 9, 660. [Google Scholar] [CrossRef]
- Shao, J.; Zhang, Q.; Wu, X.; Lei, Y.; Wu, X.; Wang, Z. Investigation on the Water Flow Evolution in a Filled Fracture under Seepage-Induced Erosion. Water 2020, 12, 3188. [Google Scholar] [CrossRef]
- Huang, Z.; Bai, Y.; Xu, H.; Cao, Y.; Hu, X. A Theoretical Model to Predict the Critical Hydraulic Gradient for Soil Particle Movement under Two-Dimensional Seepage Flow. Water 2017, 9, 828. [Google Scholar] [CrossRef] [Green Version]
- Tomlinson, S.S.; Vaid, Y.P. Seepage forces and confining pressure effects on piping erosion. Can. Geotech. J. 2000, 37, 1–13. [Google Scholar] [CrossRef]
- Suits, L.D.; Sheahan, T.C.; Chang, D.S.; Zhang, L.M. A stress-controlled erosion apparatus for studying internal erosion in soils. Geotech. Test. J. 2011, 34, 579–589. [Google Scholar] [CrossRef]
- Wang, S.; Chen, J.-S.; Luo, Y.-L.; Sheng, J.-C. Experiments on internal erosion in sandy gravel foundations containing a suspended cutoff wall under complex stress states. Nat. Hazards 2014, 74, 1163–1178. [Google Scholar] [CrossRef]
- Liang, Y.; Yeh, T.-C.J.; Wang, J.; Liu, M.; Zha, Y.; Hao, Y. Onset of suffusion in upward seepage under isotropic and anisotropic stress conditions. Eur. J. Environ. Civ. Eng. 2017, 23, 1520–1534. [Google Scholar] [CrossRef]
- Robbins, B.A.; Stephens, I.J.; Leavell, D.A.; Lopez-Soto, J.; Montalvo-Bartolomei, A.M. Laboratory piping tests on fine gravel. Can. Geotech. J. 2018, 55, 1552–1563. [Google Scholar] [CrossRef]
- Chew, S.H.; Tian, H.; Tan, S.A.; Karunaratne, G.P. Erosion stability of punctured geotextile filters subjected to cyclic wave loadings—A laboratory study. Geotext. Geomembr. 2003, 21, 221–239. [Google Scholar] [CrossRef]
- Bolt, A.F.; Sterpejkowicz-Wersocki, W. Test of Soil-Geotextile System under Changable Hydrclic Head Conditions; ICGGE: Bombay, India, 2004. [Google Scholar]
- Terzaghi, K. Theoretical Soil Mechanics; Wiley and Sons, Inc.: New York, NY, USA, 1943. [Google Scholar]
- Israr, J.; Indraratna, B. Study of critical hydraulic gradients for seepage-induced failures in granular soils. J. Geotech. Geoenviron. Eng. 2019, 145, 04019025. [Google Scholar] [CrossRef]
- Chang, K.-T.; Lee, K.Z.-Z.; Wu, H.-Y. Internal Erosion Failure of Uniform Sands under Confinement and Constricted Seepage Exit. Water 2020, 12, 2417. [Google Scholar] [CrossRef]
- Finno, R.J.; Zhang, Y.; Buscarnera, G. Experimental validation of terzaghi’s effective stress principle for gassy sand. J. Geotech. Geoenviron. Eng. 2017, 143, 04017092. [Google Scholar] [CrossRef]
- Wang, J.; Liu, X.; Xiang, J.; Jiang, Y.; Feng, B. Laboratory model tests on water inrush in foundation pit bottom. Environ. Earth Sci. 2016, 75, 1072. [Google Scholar] [CrossRef]
- Chang, D.S.; Zhang, L.M. Critical hydraulic gradients of internal erosion under complex stress states. J. Geotech. Geoenviron. Eng. 2013, 139, 1454–1467. [Google Scholar] [CrossRef]
- Xie, Q.; Liu, J.; Han, B.; Li, H.; Li, Y.; Li, X. Critical hydraulic gradient of internal erosion at the soil-structure interface. Fluid Flow Fract. Porous Media 2018, 6, 92. [Google Scholar] [CrossRef]
- Indraratna, B.; Radampola, S. Analysis of Critical Hydraulic Gradient for Particle Movement in Filtration. J. Geotech. Geoenviron. Eng. 2002, 4, 128. [Google Scholar] [CrossRef]
- Allaire, S.E.; Roulier, S.; Cessna, A.J. Quantifying preferential flow in soils: A review of different techniques. J. Hydrol. 2009, 378, 179–204. [Google Scholar] [CrossRef]
- Lu, D.; Wang, H.; Geng, N.; Xia, Y.; Xu, C.; Hua, E. Imaging and characterization of the preferential flow process in agricultural land by using electrical resistivity tomography and dual-porosity model. Ecol. Indic. 2022, 134, 108498. [Google Scholar] [CrossRef]
- Parekh, M.L.; Kanning, W.; Bocovich, C.; Mooney, M.A.; Koelewijn, A.R. Backward erosion monitored by spatial-temporal pore pressure changes during field experiments. J. Geotech. Geoenviron. Eng. 2016, 142, 04016050. [Google Scholar] [CrossRef]
- Shao, W.; Bogaard, T.; Bakker, M.; Berti, M. The influence of preferential flow on pressure propagation and landslide triggering of the Rocca Pitigliana landslide. J. Hydrol. 2016, 543, 360–372. [Google Scholar] [CrossRef]
- Zhu, X.; Peng, J.; Jiang, C.; Guo, W. A Preliminary Study of the Failure Modes and Process of Landslide Dams Due to Upstream Flow. Water 2019, 11, 1115. [Google Scholar] [CrossRef] [Green Version]
- Zhou, H.X.; Cao, H.; Zhang, W. Experimental studies on seepage failure of the top stratum at a weak spot in double-layer dike foundations. Adv. Mater. Res. 2011, 368, 2387–2393. [Google Scholar] [CrossRef]




| Geotextile Type | Ma | Tgt | kn | n | O90 | Ts | εu | Tc |
|---|---|---|---|---|---|---|---|---|
| Woven polypropylene | 170 | 0.68 | 6.7 × 10−3 | 85 | 0.12 | 75 × 75 | 17.8 × 17.8 | 3.4 |
| Soil Type | Cu | Cc | Gs | k | e0 | φ | Jt |
|---|---|---|---|---|---|---|---|
| Quartz sand | 2.6 | 1.1 | 2.65 | 3.5 × 10−3 | 42.8 | 30° | 1.155 |
| Load (kPa) | 0 | 5 | 10 | 20 | 30 | |
|---|---|---|---|---|---|---|
| Radius (cm) | ||||||
| 0.5 | 3.52 | 4.64 | 5.12 | 5.36 | 5.52 | |
| 1 | 3.12 | 4.16 | 4.8 | 5.28 | 5.44 | |
| 1.5 | 2.96 | 3.92 | 4.64 | 5.2 | 5.36 | |
| 2 | 2.88 | 3.76 | 4.56 | 5.2 | 5.36 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, W.; Wang, T.; Shu, Y. Model and Experimental Studies of the Seepage Failure of Damaged Geotextile at the Joint between Tubes in a Geotextile Tube Dam. Water 2022, 14, 3934. https://doi.org/10.3390/w14233934
Mao W, Wang T, Shu Y. Model and Experimental Studies of the Seepage Failure of Damaged Geotextile at the Joint between Tubes in a Geotextile Tube Dam. Water. 2022; 14(23):3934. https://doi.org/10.3390/w14233934
Chicago/Turabian StyleMao, Wenlong, Tianwen Wang, and Yiming Shu. 2022. "Model and Experimental Studies of the Seepage Failure of Damaged Geotextile at the Joint between Tubes in a Geotextile Tube Dam" Water 14, no. 23: 3934. https://doi.org/10.3390/w14233934






