Seismic Safety Assessment of Arch Dams Using an ETA-Based Method with Control of Tensile and Compressive Damage
Abstract
:1. Introduction
1.1. Framework and Motivation
1.2. Objetives and Contributions
2. On the Seismic Safety of Concrete Dams
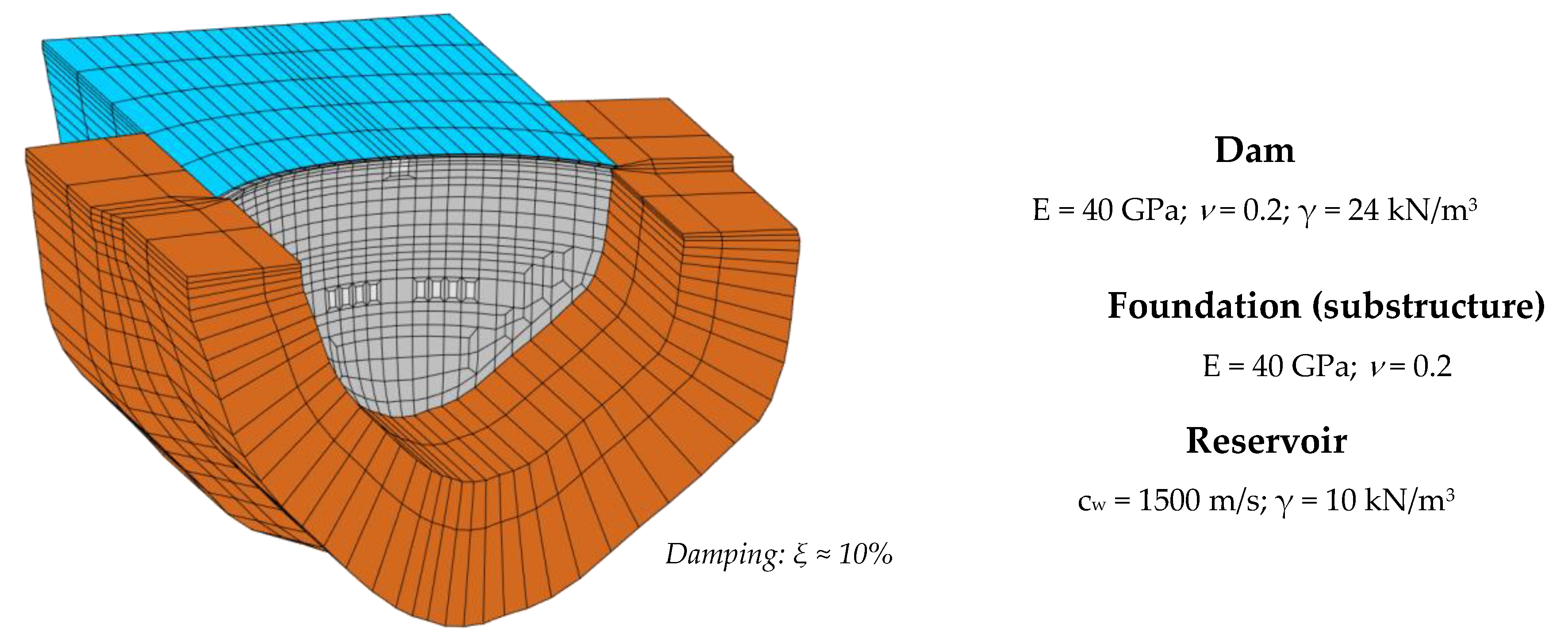
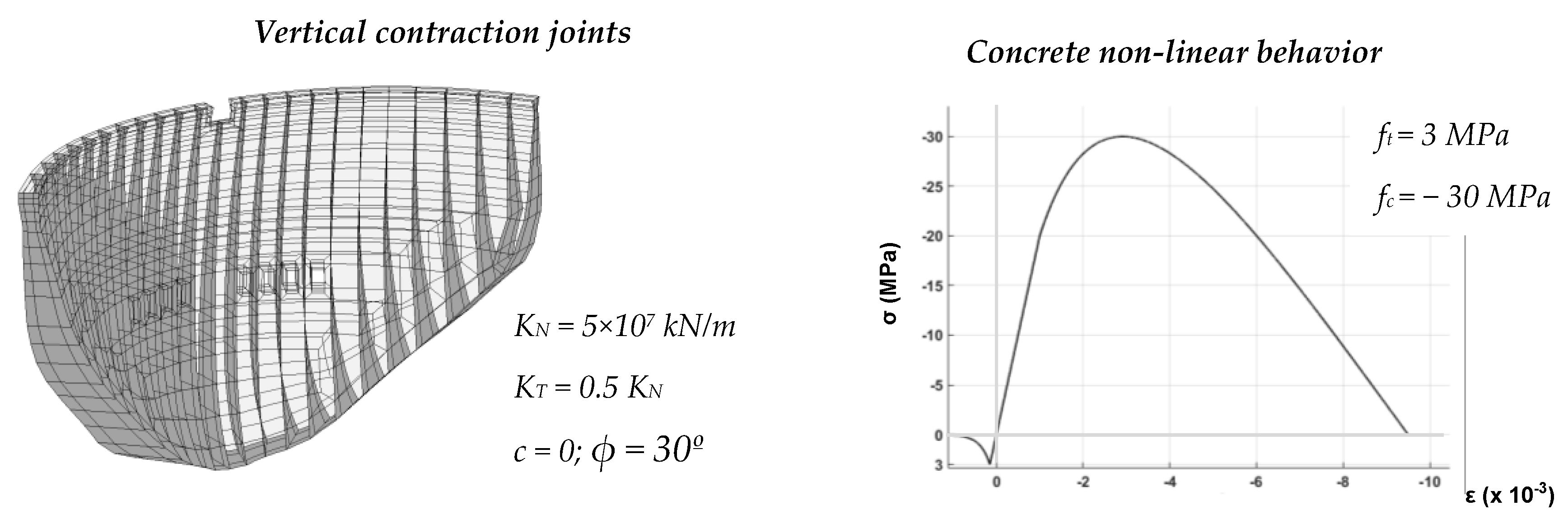
2.1. Models for Non-Linear Dynamic Analysis of Dam–Reservoir-Foundation Systems

2.2. Ground Motion
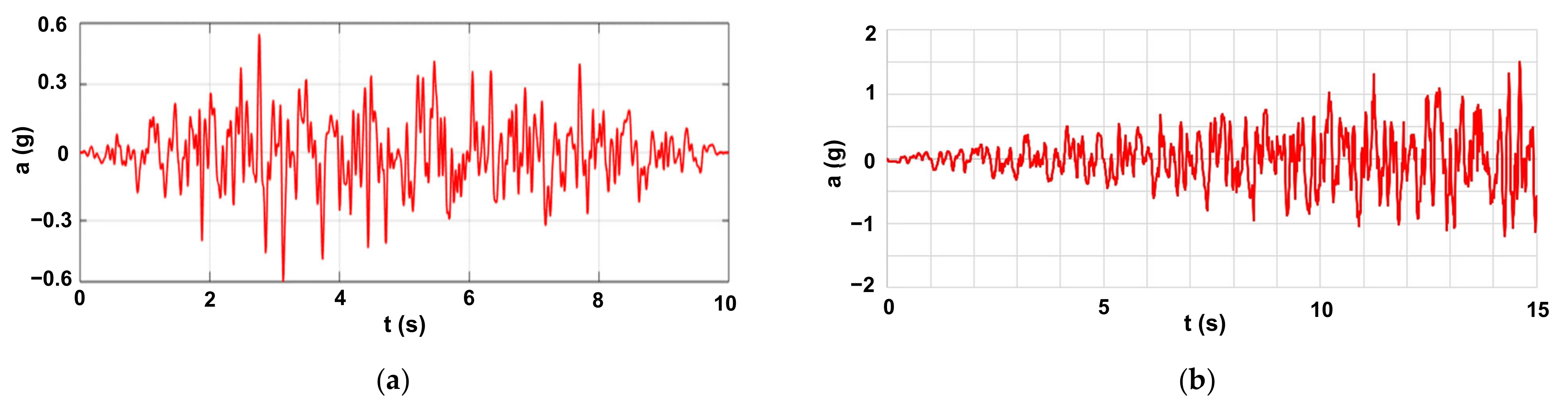
2.3. Methods of Analysis
2.4. Seismic Design and Performance Criteria
3. ETA-Based Method for Seismic Safety Assessment of Arch Dams
- Phase 1: Development of the 3D finite element model of the dam–reservoir–foundation system and generation the intensifying seismic load.
- Phase 2: Perform the non-linear seismic calculations and output the non-linear response results in multiple time steps (response time histories, deformed shapes with joint movements, principal stresses fields, tensile and compressive damage).
- Phase 3: Estimation of the performance endurance limits and comparison with reference ground motion parameters (OBE and SEE) for the seismic safety assessment.

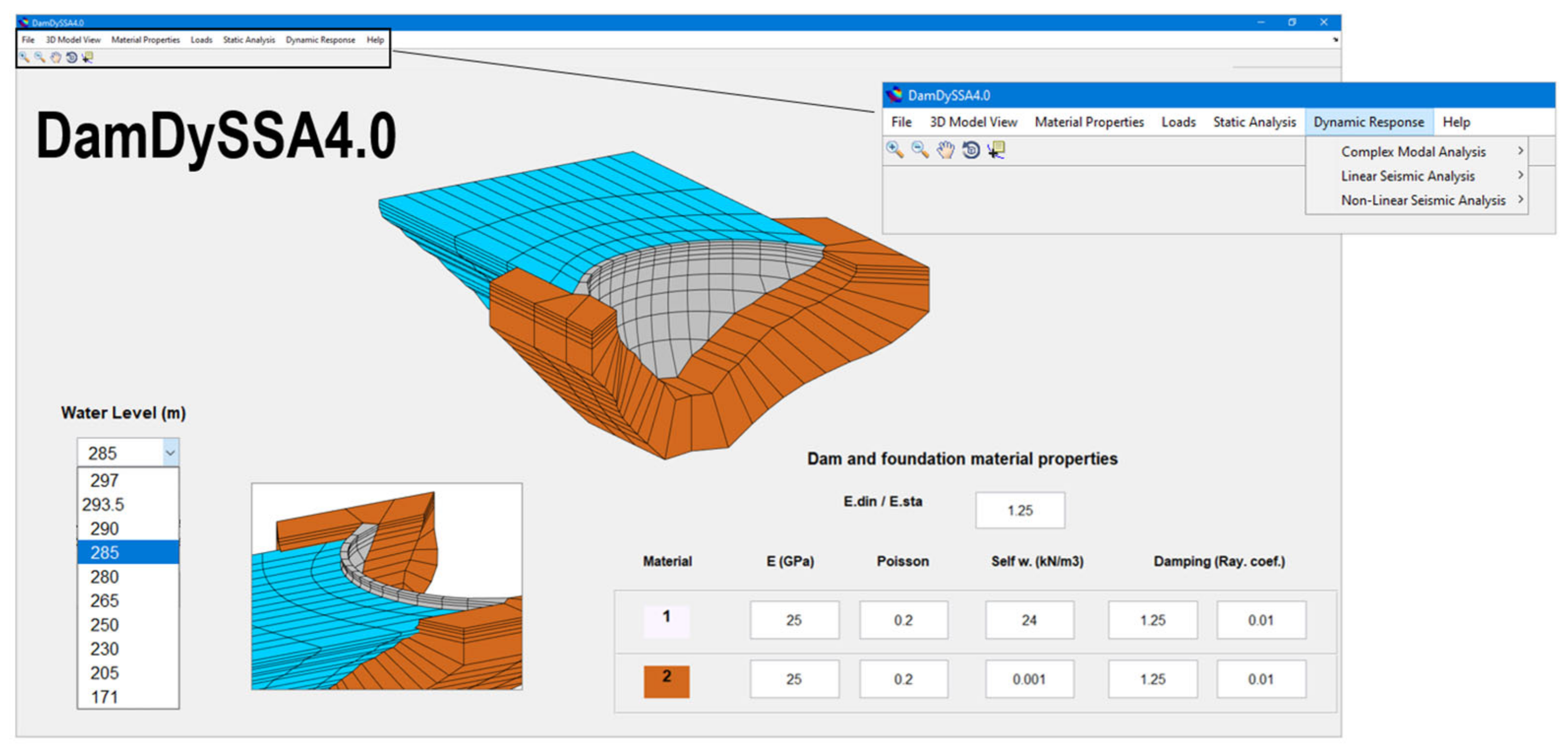
4. Used Finite Element Program (DamDySSA)
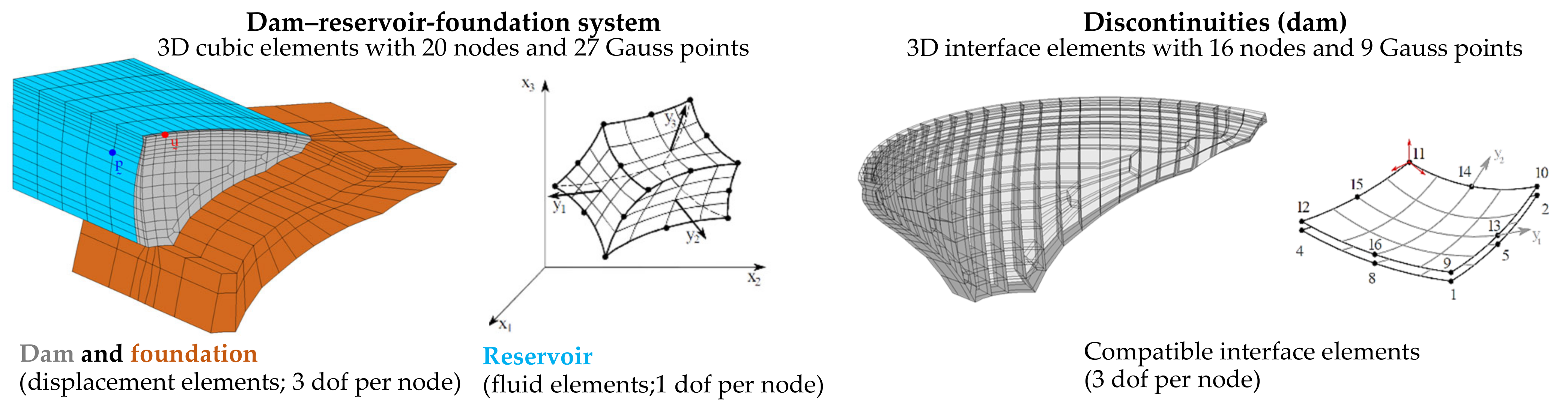
4.1. Dynamic Behavior of the Dam–Reservoir-Foundation System: Finite Element Formulation
4.2. Non-Linear Time-Stepping Method for Non-Linear Seismic Analysis
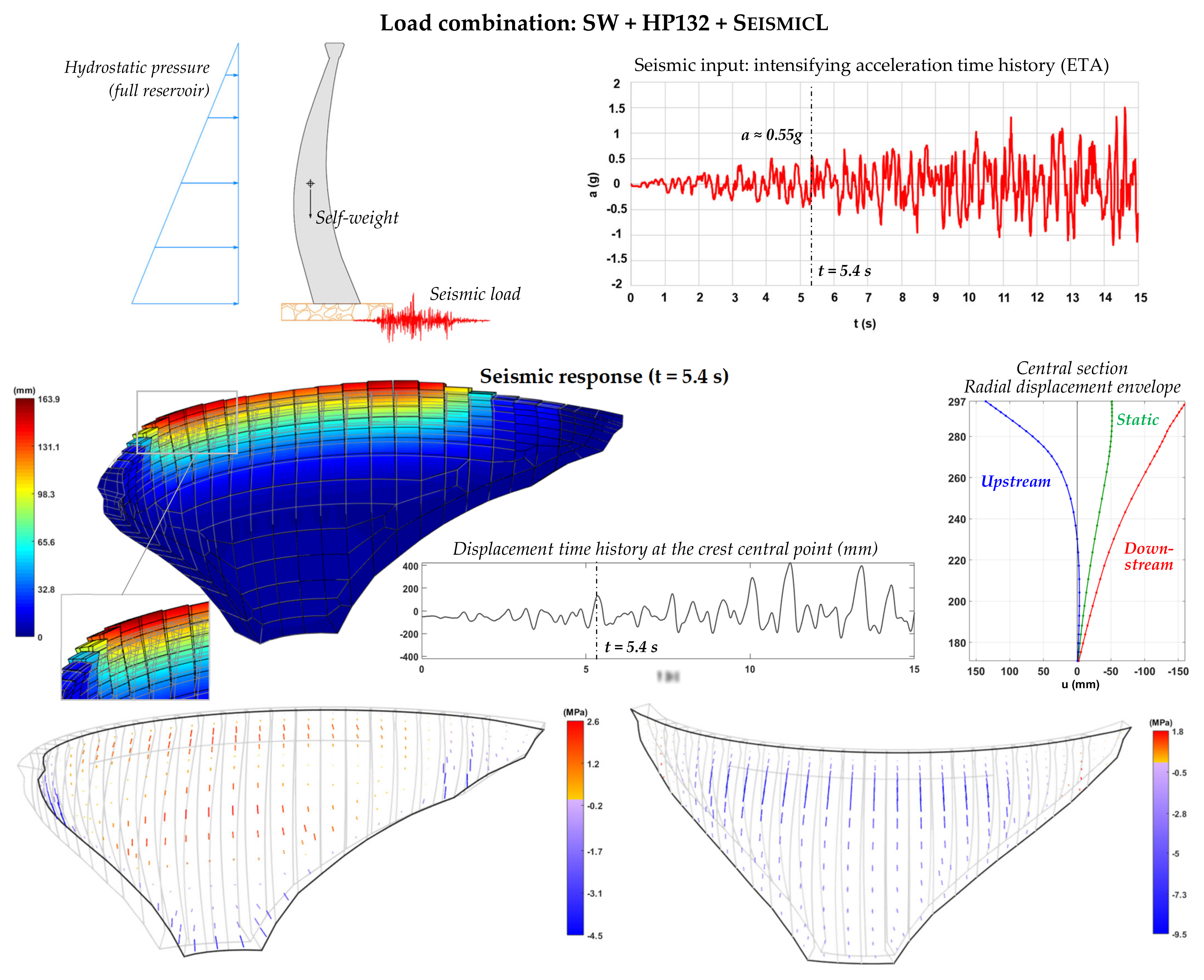
5. Results: Seismic Safety Assessment of Arch Dams
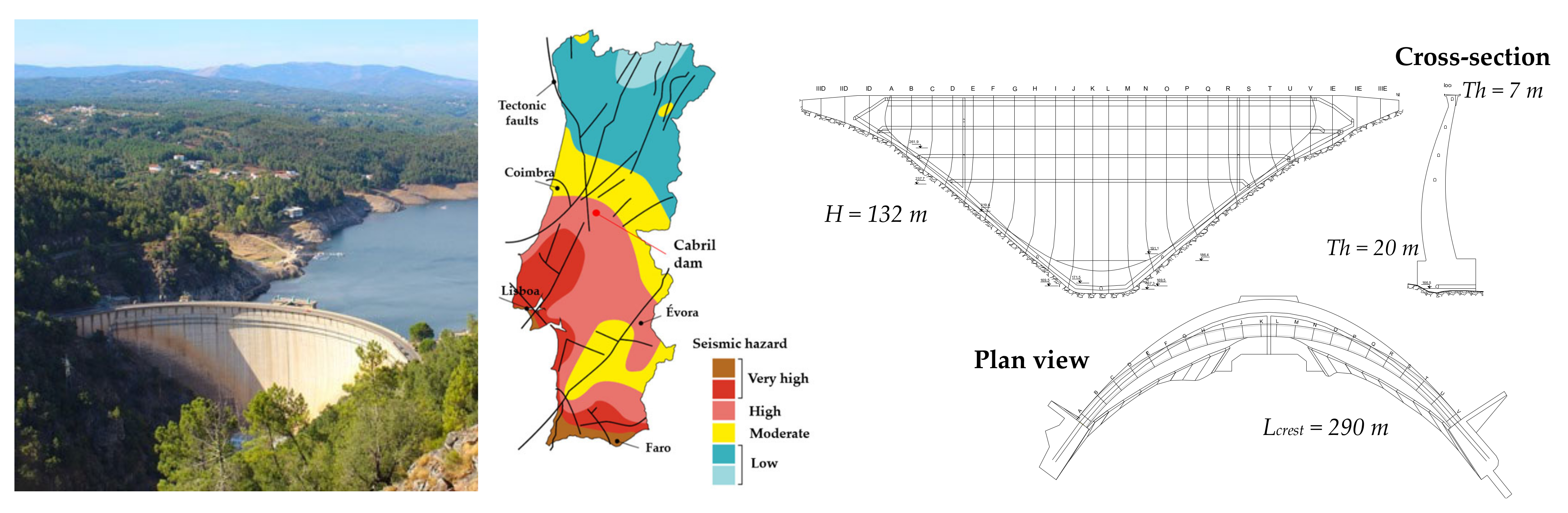
5.1. Case Study I: Cabril Dam (130 m-High)
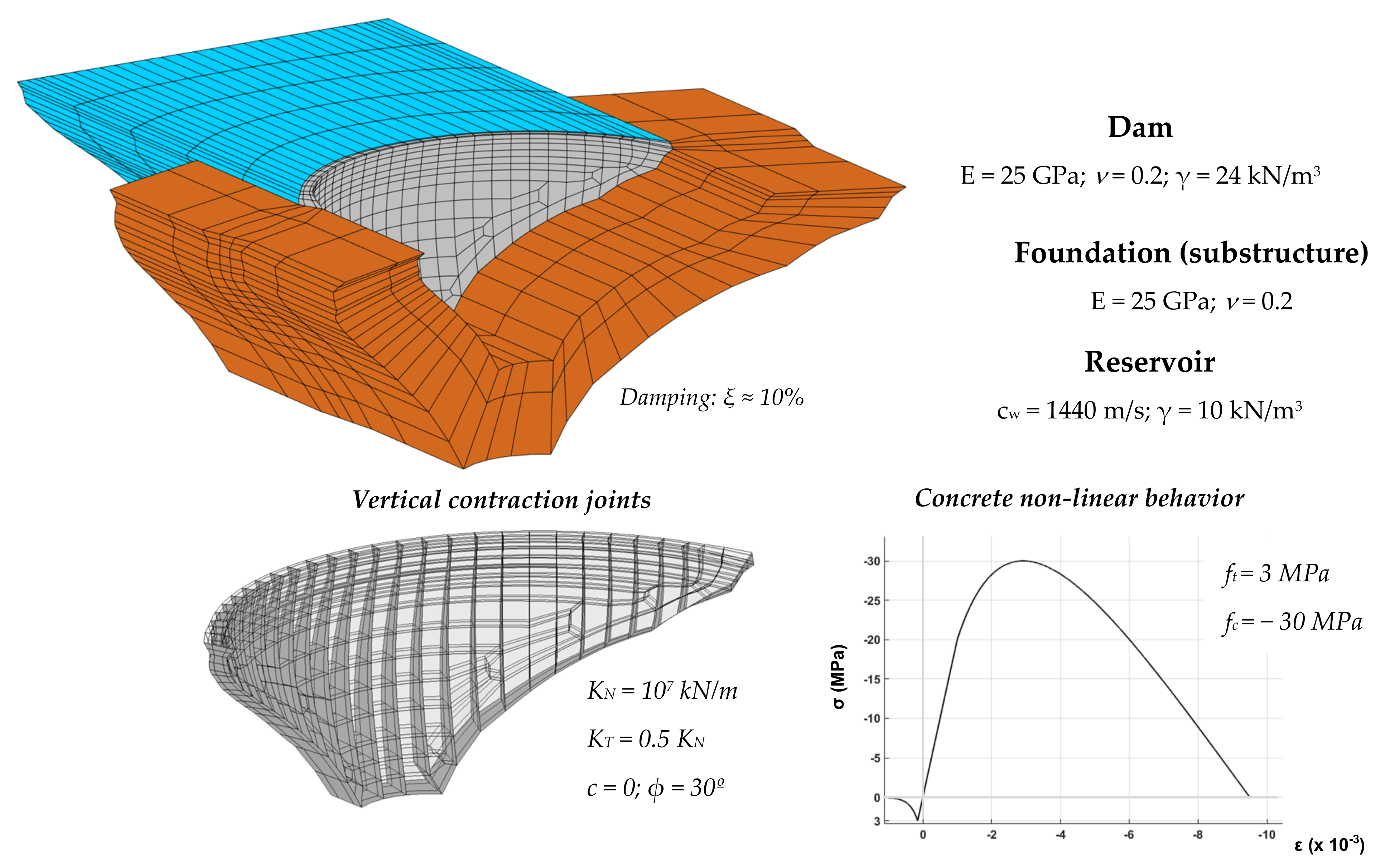
5.1.1. Dam Description and Finite Element Mesh
5.1.2. Non-Linear Seismic Analysis and Seismic Safety Assessment
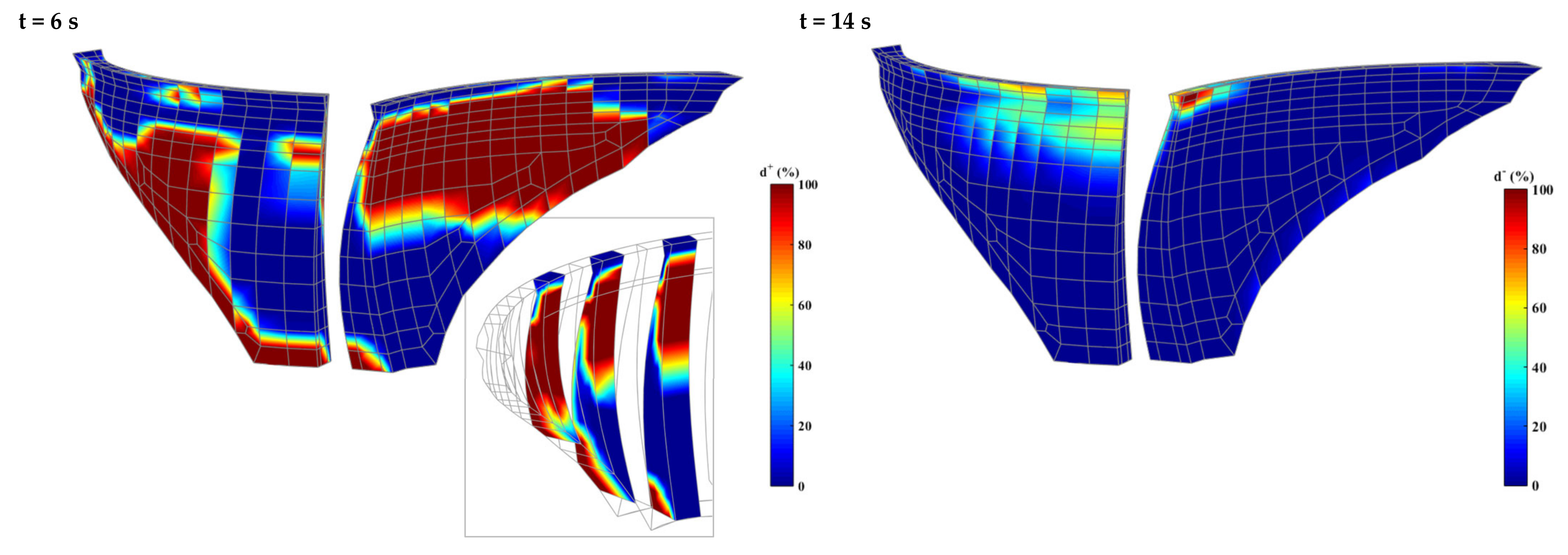
5.2. Case Study II: Cahora Bassa Dam (170 m-High)
5.2.1. Dam Description and Finite Element Mesh

5.2.2. Non-Linear Seismic Analysis and Seismic Safety Assessment
5.3. Discussion
6. Conclusions and Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- ICOLD Bulletin 169: Global Climate Change, Dams, Reservoirs and Related Water Sources; Technical Committee Y, International Commission on Large Dams: Paris, France, 2016.
- ICOLD Bulletin Preprint 185: Challenges and Needs for Dams in the 21st Century. In Technical Committee on Global Climate Change and Dams, Reservoirs and the Associated Water Resources; International Commission on Large Dams: Paris, France, 2019.
- UNESCO. UN-Water United Nations World Water Development Report 2020: Water and Climate Change; United Nations Educational, Scientific, and Cultural Organization: Paris, France, 2020. [Google Scholar]
- ICOLD World Declaration on Dam Safety; International Commission on Large Dams: Porto, Portugal, 2019; pp. 36–40.
- IJHD World Atlas & Industry Guide; Aqua Media Int. Ltd.: Wallington, UK, 2021.
- Wieland, M.; Chen, H. Leassons Learnt from the Wenchuan Earthquake. Int. Water Power Dam Constr. 2009.
- Wieland, M. Features of Seismic Hazard in Large Dam Projects and Strong Motion Monitoring of Large Dams. Front. Archit. Civ. Eng. China 2010, 4, 56–64. [Google Scholar] [CrossRef]
- Wieland, M. Seismic Hazard and Seismic Design and Safety Aspects of Large Dam Projects. In Perspectives on European Earthquake Engineering and Seismology; Geotechnical, Geological and Earthquake Engineering; Ansal, A., Ed.; Springer: Cham, Switzerland, 2014; pp. 627–650. [Google Scholar]
- Wieland, M. Safety Aspects of Sustainable Storage Dams and Earthquake Safety of Existing Dams. Engineering 2016, 2, 325–331. [Google Scholar] [CrossRef] [Green Version]
- Wang, R.; Chen, L.; Zhang, C. Seismic Design of Xiluodu Ultra-High Arch Dam. Water Sci. Eng. 2018, 11, 288–301. [Google Scholar] [CrossRef]
- Wang, R. Key Technologies in the Design and Construction of 300 M Ultra-High Arch Dams. Engineering 2016, 2, 350–359. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Xu, Y.; Wang, G.; Jin, F. Non-Linear Seismic Response of Arch Dams with Contraction Joint Opening and Joint Reinforcements. Earthq. Eng. Struct. Dyn. 2000, 29, 1546–1566. [Google Scholar] [CrossRef]
- Zhang, C.; Xu, Y.; Jin, F.; Wang, G. Studies on Seismic Behaviour of Xiaowan Arch Dam and Earthquake Resistance Measures. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Darbre, G.R.; Schwager, M.V.; Panduri, R. Seismic Safety Evaluation of Large Dams in Switzerland: Lessons Learned. Int. Water Power Dam Constr. 2019, 70, 22–27. [Google Scholar]
- Alegre, A.; Carvalho, E.; Matsinhe, B.; Mendes, P.; Oliveira, S.; Proença, J. Monitoring Vibrations in Large Dams. In Proceedings of the HYDRO 2019—Concept to closure: Practical Steps, Porto, Portugal, 16–19 October 2019. [Google Scholar]
- Alegre, A.; Oliveira, S.; Carvalho, E.; Mendes, P.; Proença, J.; Matsinhe, B. Continuous Dynamic Monitoring of Large Arch Dams and Vibration-Based Damage Detection. In Proceedings of the HYDRO 2022—Roles of Hydro in the Global Recovery, Strasbourg, France, 25–27 April 2022. [Google Scholar]
- Oliveira, S.; Alegre, A.; Carvalho, E.; Mendes, P.; Proença, J. Seismic and Structural Health Monitoring Systems for Large Dams: Theoretical, Computational and Practical Innovations. Bull. Earthq. Eng. 2022, 20, 4483–4512. [Google Scholar] [CrossRef]
- Chopra, A.K. Earthquake Analysis of Arch Dams: Factors to Be Considered. J. Struct. Eng. 2012, 138, 205–214. [Google Scholar] [CrossRef] [Green Version]
- Chen, H. Seismic Safety of High Concrete Dams. Earthq. Eng. Eng. Vib. 2014, 13, 1–16. [Google Scholar] [CrossRef]
- ICOLD Bulletin 148: Selecting Seismic Parameters for Large Dams—Guidelines (Revision of Bulletin 72); Committee on Seismic Aspects of Dam Design, International Commission on Large Dams: Paris, France, 2016.
- ICOLD Bulletin 168: Recommendations for Operation, Maintenance and Rehabilitation; International Comission on Large Dams: Paris, France, 2017.
- ICOLD Bulletin 158: Dam Surveillance Guide; International Comission on Large Dams: Paris, France, 2018.
- Valamanesh, V.; Estekanchi, H.E.; Vafai, A.; Ghaemian, M. Application of the Endurance Time Method in Seismic Analysis of Concrete Gravity Dams. Sci. Iran. 2011, 18, 326–337. [Google Scholar] [CrossRef] [Green Version]
- Hariri-Ardebili, M.A.; Saouma, V.E.; Porter, K.A. Quantification of Seismic Potential Failure Modes in Concrete Dams. Earthq. Eng. Struct. Dyn. 2016, 45, 979–997. [Google Scholar] [CrossRef]
- Meghella, M.; Furgani, L. Application of Endurance Time Analysis Method to the NonLinear Seismic Analysis of Dams: Potentialities and Limitations. In Proceedings of the ICOLD 82nd Annual Meeting, Banff, AB, Canada, 4–5 October 2014. [Google Scholar]
- Hariri-Ardebili, M.A.; Mirzabozorg, H. Estimation of Probable Damages in Arch Dams Subjected to Strong Ground Motions Using Endurance Time Acceleration Functions. KSCE J. Civ. Eng. 2014, 18, 574–586. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Mirzabozorg, H.; Estekanchi, H.E. Nonlinear Seismic Assessment of Arch Dams and Investigation of Joint Behavior Using Endurance Time Analysis Method. Arab. J. Sci. Eng. 2014, 39, 3599–3615. [Google Scholar] [CrossRef]
- Abdollahi, A.; Amini, A.; Hariri-Ardebili, M.A. An Uncertainty-Aware Dynamic Shape Optimization Framework: Gravity Dam Design. Reliab. Eng. Syst. Saf. 2022, 222, 108402. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Furgani, L.; Meghella, M.; Saouma, V.E. A New Class of Seismic Damage and Performance Indices for Arch Dams via ETA Method. Eng. Struct. 2016, 110, 145–160. [Google Scholar] [CrossRef]
- Furgani, L.; Hariri-Ardebili, M.A.; Meghella, M.; Seyed-Kolbadi, S.M. On the Dynamic Capacity of Concrete Dams. Infrastructures 2019, 4, 57. [Google Scholar] [CrossRef] [Green Version]
- Hariri-Ardebili, M.; Mahdavi, G.; Abdollahi, A.; Amini, A. An RF-PCE Hybrid Surrogate Model for Sensitivity Analysis of Dams. Water 2021, 13, 302. [Google Scholar] [CrossRef]
- Segura, R.L.; Miquel, B.; Paultre, P.; Padgett, J.E. Accounting for Uncertainties in the Safety Assessment of Concrete Gravity Dams: A Probabilistic Approach with Sample Optimization. Water 2021, 13, 855. [Google Scholar] [CrossRef]
- Pedro, J.O.; Câmara, R. Coupled Models for Dynamic Analysis of Arch Dams. In Proceedings of the 8th European Conference on Earthquake Engineering, Lisbon, Portugal, 7–12 September 1986. [Google Scholar]
- Chopra, A.K.; Tan, H. Modelling Dam-Foundation Interaction in Analysis of Arch Dams. In Proceedings of the 10th World Conference on Earthquake Engineering, Madrid, Spain, 19–24 July 1992. [Google Scholar]
- Westergaard, H.M. Water Pressures on Dams during Earthquakes. Trans. Am. Soc. Civ. Eng. 1933, 98, 418–472. [Google Scholar] [CrossRef]
- Tiliouine, B.; Seghir, A. Fluid-Structure Models for Dynamic Studies of Dam-Water Systems. In Proceedings of the 11th European Conference on Earthquake Engineering, Paris, France, 6–11 September 1998. [Google Scholar]
- Fok, K.L.; Chopra, A.K. Hydrodynamic and Foundation Flexibility Effects in Earthquake Response of Arch Dams. J. Struct. Eng. 1986, 112, 1810–1828. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Bettess, P. Fluid-Structure Dynamic Interaction and Wave Forces. An Introduction to Numerical Treatment. An Introduction to Numerical Treatment. Int. J. Numer. Methods Eng. 1978, 13, 1–16. [Google Scholar] [CrossRef]
- Bouaanani, N.; Lu, F.Y. Assessment of Potential-Based Fluid Finite Elements for Seismic Analysis of Dam-Reservoir Systems. Comput. Struct. 2009, 87, 206–224. [Google Scholar] [CrossRef]
- Lokke, A.; Chopra, A.K. Direct Finite Element Method for Nonlinear Earthquake Analysis of 3-Dimensional Semi-Unbounded Dam–water-Foundation Rock Systems. Earthq. Eng. Struct. Dyn. 2018, 47, 1309–1328. [Google Scholar] [CrossRef] [Green Version]
- Clough, R.W. Non-Linear Mechanisms in the Seismic Response of Arch Dams. In Proceedings of the International Research Conference on Earthquake Engineering, Skopje, Yugoslavia, 30 June–3 July 1980. [Google Scholar]
- Fok, K.L.; Chopra, A.K. Earthquake Analysis of Arch Dams Including Dam-Water Interaction, Reservoir Boundary Absorption and Foundation Flexibility. Earthq. Eng. Struct. Dyn. 1986, 14, 155–184. [Google Scholar] [CrossRef]
- Wang, J.-T.; Chopra, A.K. Linear Analysis of Concrete Arch Dams Including Dam-Water-Foundation Rock Interaction Considering Spatially Varying Ground Motions. Earthq. Eng. Struct. Dyn. 2010, 39, 731–750. [Google Scholar] [CrossRef]
- Alves, S.W.; Hall, J.F. Generation of Spatially Nonuniform Ground Motion for Nonlinear Analysis of a Concrete Arch Dam. Earthq. Eng. Struct. Dyn. 2006, 35, 1139–1357. [Google Scholar] [CrossRef]
- Zhang, C.; Pan, J.; Wang, J.-T. Influence of Seismic Input Mechanisms and Radiation Damping on Arch Dam Response. Soil Dyn. Earthq. Eng. 2009, 29, 1282–1293. [Google Scholar]
- Dominguez, J.; Maeso, O. Model for the Seismic Analysis of Arch Dams Including Interaction Effects. In Proceedings of the 10th World Conference on Earthquake Engineering, Madrid, Spain, 19–24 July 1992. [Google Scholar]
- Alves, S.W. Nonlinear Analysis of Pacoima Dam with Spatially Non-Uniform Ground Motion. Ph.D. Thesis, California Institute of Technology, Pasadena, California, 2004. [Google Scholar]
- Wang, J.-T.; Lv, D.-D.; Jin, F.; Zhang, C. Earthquake Damage Analysis of Arch Dams Considering Dam–water–foundation Interaction. Soil Dyn. Earthq. Eng. 2013, 49, 64–74. [Google Scholar] [CrossRef]
- Mirzabozorg, H.; Kordzadeh, A.; Hariri-Ardebili, M.A. Seismic Response of Concrete Arch Dams Including Dam-Reservoir-Foundation Interaction Using Infinite Elements. Electron. J. Struct. Eng. 2012, 12, 63–73. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Mirzabozorg, H. A Comparative Study of Seismic Stability of Coupled Arch Dam-Foundation-Reservoir Systems Using Infinite Elements and Viscous Boundary Models. Int. J. Struct. Stab. Dyn. 2013, 13, 1350032. [Google Scholar] [CrossRef]
- Chen, D.-H.; Du, C.-B.; Yuan, J.-W.; Hong, Y.-W. An Investigation into the Influence of Damping on the Earthquake Response Analysis of a High Arch Dam. J. Earthq. Eng. 2012, 16, 329–349. [Google Scholar] [CrossRef]
- Robbe, E.; Kashiwayanagi, M.; Yamane, Y. Seismic Analyses of Concrete Dam, Comparison between Finite-Element Analyses and Seismic Records. In Proceedings of the 16th World Conference on Earthquake Engineering, Santiago, Chile, 9–13 January 2017. [Google Scholar]
- Chopra, A.K.; Wang, J.-T. Earthquake Response of Arch Dams to Spatially Varying Ground Motion. Earthq. Eng. Struct. Dyn. 2010, 39, 887–906. [Google Scholar] [CrossRef]
- Proulx, J.; Darbre, G.R. Earthquake Response of Large Arch Dams Observational Evidence and Numerical Modelling. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Fenves, G.L.; Mojtahedi, S.; Reimer, R.B. Effect of Contraction Joints on Earthquake Response of an Arch Dam. J. Struct. Eng. 1992, 118, 1039–1055. [Google Scholar] [CrossRef]
- Niwa, A.; Clough, R.W. Non-Linear Seismic Response of Arch Dams. Earthq. Eng. Struct. Dyn. 1982, 10, 267–281. [Google Scholar] [CrossRef]
- Cervera, M.; Oliver, J.; Faria, R. Seismic Evaluation of Concrete Dams via Continuum Damage Models. Earthq. Eng. Struct. Dyn. 1995, 24, 1225–1245. [Google Scholar] [CrossRef]
- Valliappan, S.; Yazdchi, M.; Khalili, N. Seismic Analysis of Arch Dams—A Continuum Damage Mechanics Approach. Int. J. Numer. Methods Eng. 1999, 45, 1695–1724. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Mirzabozorg, H. Seismic Performance Evaluation and Analysis of Major Arch Dams Considering Material and Joint Nonlinearity Effects. ISRN Civ. Eng. 2012, 2012, 681350. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.-T.; Zhang, C.; Jin, F. Nonlinear Earthquake Analysis of High Arch Dam-Water-Foundation Rock Systems. Earthq. Eng. Struct. Dyn. 2012, 41, 1157–1176. [Google Scholar] [CrossRef]
- Pan, J.; Xu, Y.; Jin, F. Seismic Performance Assessment of Arch Dams Using Incremental Nonlinear Dynamic Analysis. Eur. J. Environ. Civ. Eng. 2015, 19, 305–326. [Google Scholar] [CrossRef]
- Alegre, A. Modelling and Monitoring the Dynamic Behaviour of Concrete Dams. Modal Analysis and Seismic Response. Ph.D. Thesis, Instituto Superior Técnico, University of Lisbon, Lisboa, Portugal, 2021. [Google Scholar]
- Goldgruber, M. Non-Linear Seismic Modelling of Concrete Dams. Ph.D. Thesis, Graz University of Technology, Graz, Austria, 2015. [Google Scholar]
- Bommer, J.; Acevedo, A.B. The Use of Real Earthquake Accelerograms as Input to Dynamic Analysis. J. Earthq. Eng. 2004, 8, 43–91. [Google Scholar] [CrossRef]
- Clough, R.W.; Penzien, J. Dynamics of Structures, 3rd ed.; Computers & Structures, Inc.: Berkeley, CA, USA, 2003. [Google Scholar]
- Gasparini, D.A.; Vanmarcke, E.H. Simulated Earthquake Motions Compatible with Prescribed Response Spectra. Research Report R76-4; Dept. of Civil Engineering, Massachusetts Institute of Technology: Cambridge, MA, USA, 1976. [Google Scholar]
- Boore, D.M. Simulation of Ground Motion Using the Stochastic Method. Pure Appl. Geophys. 2003, 160, 636–676. [Google Scholar] [CrossRef] [Green Version]
- Carvalho, A. Modelação Estocástica Da Acção Sísmica Em Portugal Continental [Stochastic Modelling of the Seismic Action in Continental Portugal]. Ph.D. Thesis, Instituto Superior Técnico, University of Lisbon, Lisbon, Portugal, 2007. [Google Scholar]
- Estekanchi, H.E.; Vafai, H.; Sadeghazar, M. Endurance Time Method for Seismic Analysis and Design of Structures. Sci. Iran. 2004, 11, 361–370. [Google Scholar]
- Mashayekhi, M.; Estekanchi, H.E.; Vafai, H.; Ahmadi, G. An Evolutionary Optimization-Based Approach for Simulation of Endurance Time Load Functions. Eng. Optim. 2019, 51, 2069–2088. [Google Scholar] [CrossRef]
- Nozari, A.; Estekanchi, H.E. Optimization of Endurance Time Acceleration Functions for Seismic Assessment of Structures. Int. J. Optim. Civ. Eng. 2011, 1, 257–277. [Google Scholar]
- Wieland, M. Models of Earthquake Ground Shaking Used in Seismic Design and Safety Checks of Large Dams. Int. J. Civ. Eng. 2019, 17, 515–522. [Google Scholar] [CrossRef]
- Vamvatsikos, D.; Cornell, C.A. Incremental Dynamic Analysis. Earthq. Eng. Struct. Dyn. 2002, 31, 491–514. [Google Scholar] [CrossRef]
- Alembagheri, M.; Ghaemian, M. Damage Assessment of a Concrete Arch Dam through Nonlinear Incremental Dynamic Analysis. Soil Dyn. Earthq. Eng. 2013, 44, 127–137. [Google Scholar] [CrossRef]
- Oliveira, S.; Silvestre, A.; Câmara, R. Barragem de Ribeiradio. Obra Constrúida. Verificação Da Segurança Estrutural Para Ações Estáticas E Dinâmicas. Cenários Correntes E de Rotura [Ribeiradio Dam. Built Structure. Structural Safety Verification under Static and Dynamic Loads. Current and Fail]; Report; Concrete Dams Department, LNEC: Lisboa, Portugal, 2014. [Google Scholar]
- LNEC. Cahora Bassa Hydroelectric Scheme. Analysis of the Seismic Dam Behaviour; Concrete Dams Department, National Laboratory for Civil Engineering: Lisboa, Portugal, 2009. [Google Scholar]
- Oliveira, S.; Alegre, A.; Silvestre, A.; Espada, M.; Câmara, R. Seismic Safety Evaluation of Luzzone Dam. Use of a 3DFEM State Formulation in Pressures and Displacements. In Proceedings of the 13th ICOLD International Benchmark Workshop on Numerical Analysis of Dams, EPFL, Lausanne, Switzerland, 9–11 September 2015. [Google Scholar]
- Gunn, R.M.; Balissat, M.; Manso, P.; Mouvet, L.; Schleiss, A. (Eds.) Proceedings of the 13th ICOLD International Benchmark Workshop on the Numerical Analysis of Dams; Swiss Committee on Dams: Luzern, Switzerland, 2016. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method: Its Basis and Fundamentals, 7th ed.; Elsevier Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Newmark, N. A Method of Computation for Structural Dynamics. J. Eng. Mech. Div. 1959, 85, 67–94. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L.; Fox, D.D. The Finite Element Method for Solid and Structural Mechanics, 7th ed.; Butt, Ed.; Elsevier: Amsterdam, The Netherlands, 2014; ISBN 9781856176347. [Google Scholar]
- Oliveira, S. Continuous Monitoring Systems for the Dynamic Performance Assessment of Arch Dams. In Sub-Program D, in Study of Evolutive Deterioration Processes in Concrete Dams. Safety Control over Time; Aqua~Media International Ltd.: Wallington, UK, 2002. [Google Scholar]
- Oliveira, S.; Faria, R. Numerical Simulation of Collapse Scenarios in Reduced Scale Tests of Arch Dams. Eng. Struct. 2006, 28, 1430–1439. [Google Scholar] [CrossRef]
- Planning and Infrastructure Ministry. Regulamento de Segurança de Barragens [Dam Safety Regulation]; Decree-law No. 21/2018 of March 28; Portuguese Republic Diary No. 62, Series I; 2018. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alegre, A.; Oliveira, S.; Mendes, P.; Proença, J.; Ramos, R.; Carvalho, E. Seismic Safety Assessment of Arch Dams Using an ETA-Based Method with Control of Tensile and Compressive Damage. Water 2022, 14, 3835. https://doi.org/10.3390/w14233835
Alegre A, Oliveira S, Mendes P, Proença J, Ramos R, Carvalho E. Seismic Safety Assessment of Arch Dams Using an ETA-Based Method with Control of Tensile and Compressive Damage. Water. 2022; 14(23):3835. https://doi.org/10.3390/w14233835
Chicago/Turabian StyleAlegre, André, Sérgio Oliveira, Paulo Mendes, Jorge Proença, Rafael Ramos, and Ezequiel Carvalho. 2022. "Seismic Safety Assessment of Arch Dams Using an ETA-Based Method with Control of Tensile and Compressive Damage" Water 14, no. 23: 3835. https://doi.org/10.3390/w14233835




