Research on Sea Spray Distribution of Marine Vessels Based on SPH-FEM Coupling Numerical Simulation Method
Abstract
:1. Introduction
2. Theoretical Methods
2.1. Governing Equations
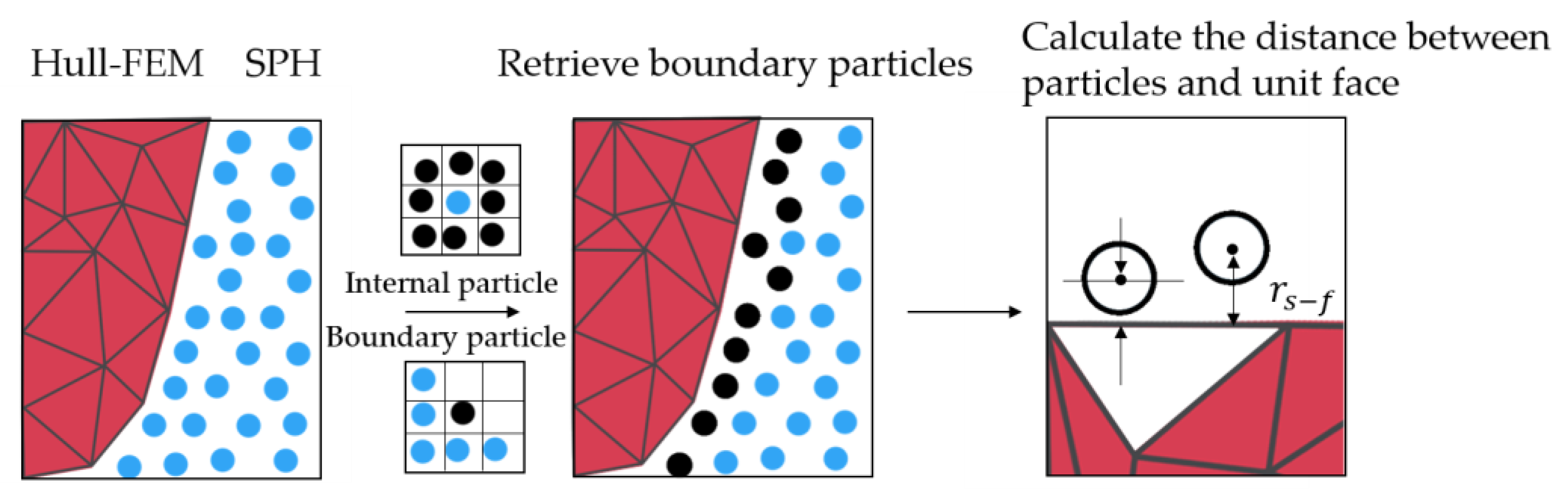
2.2. Coupling Wall Boundary Treatment
3. Method Validation Analysis
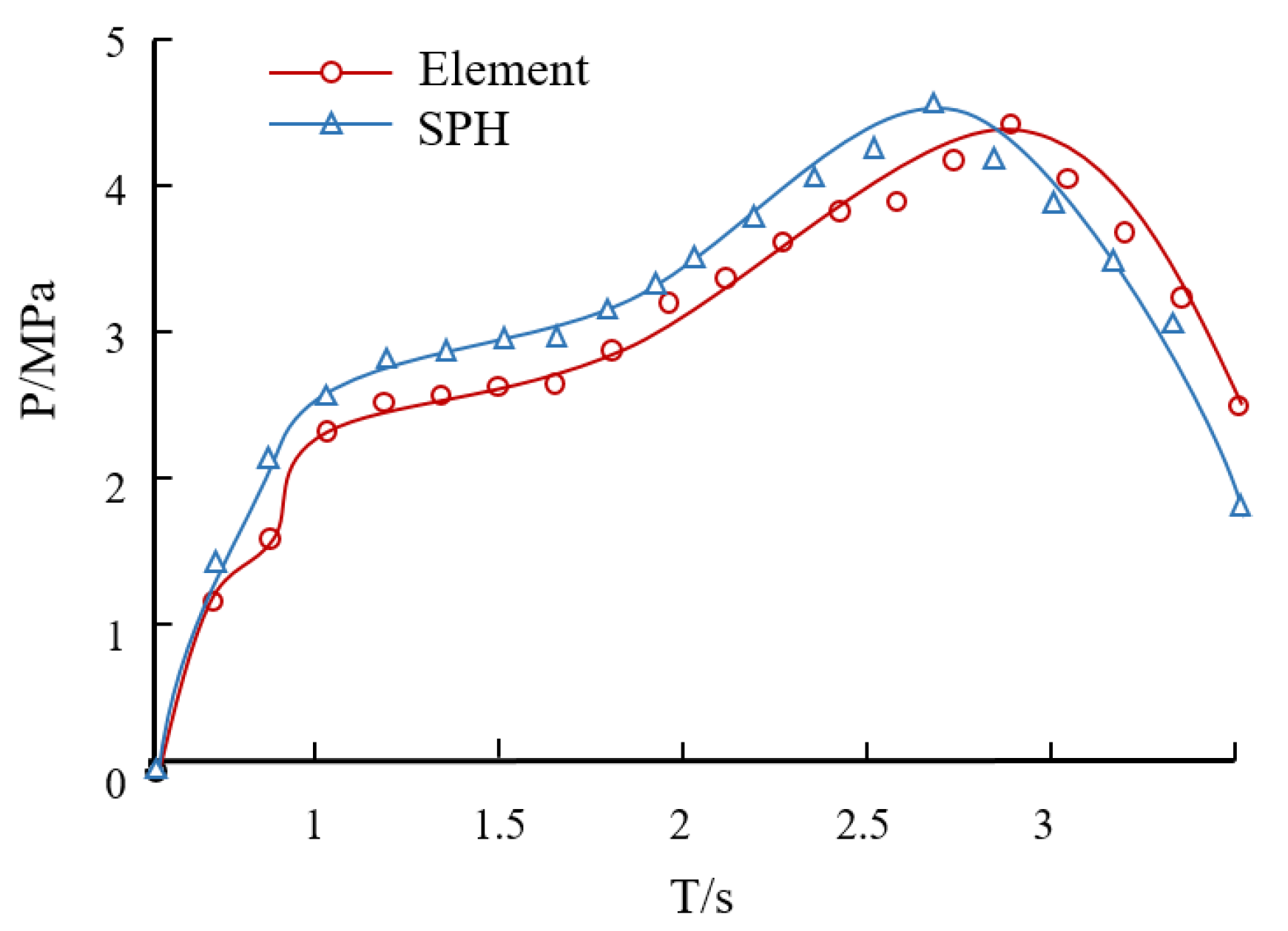
3.1. Methods Analysis
3.2. Method Validation
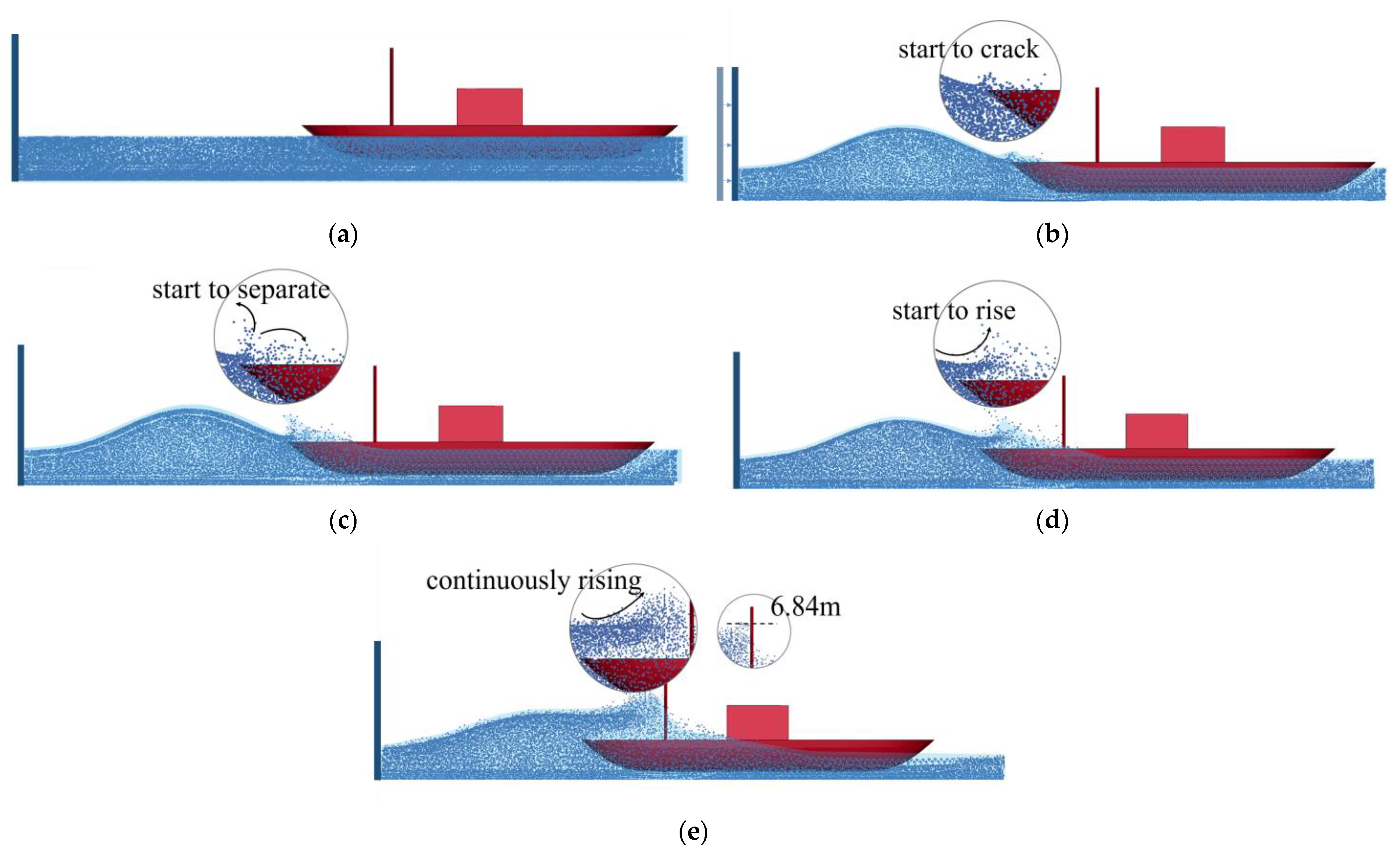
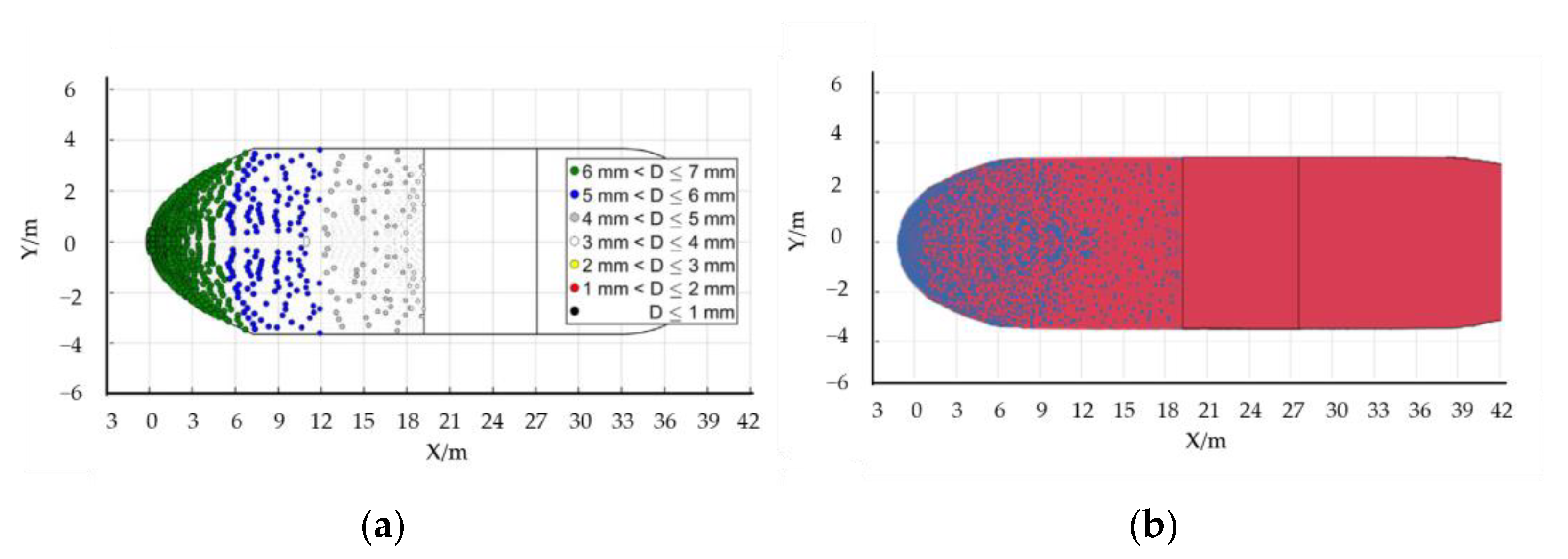
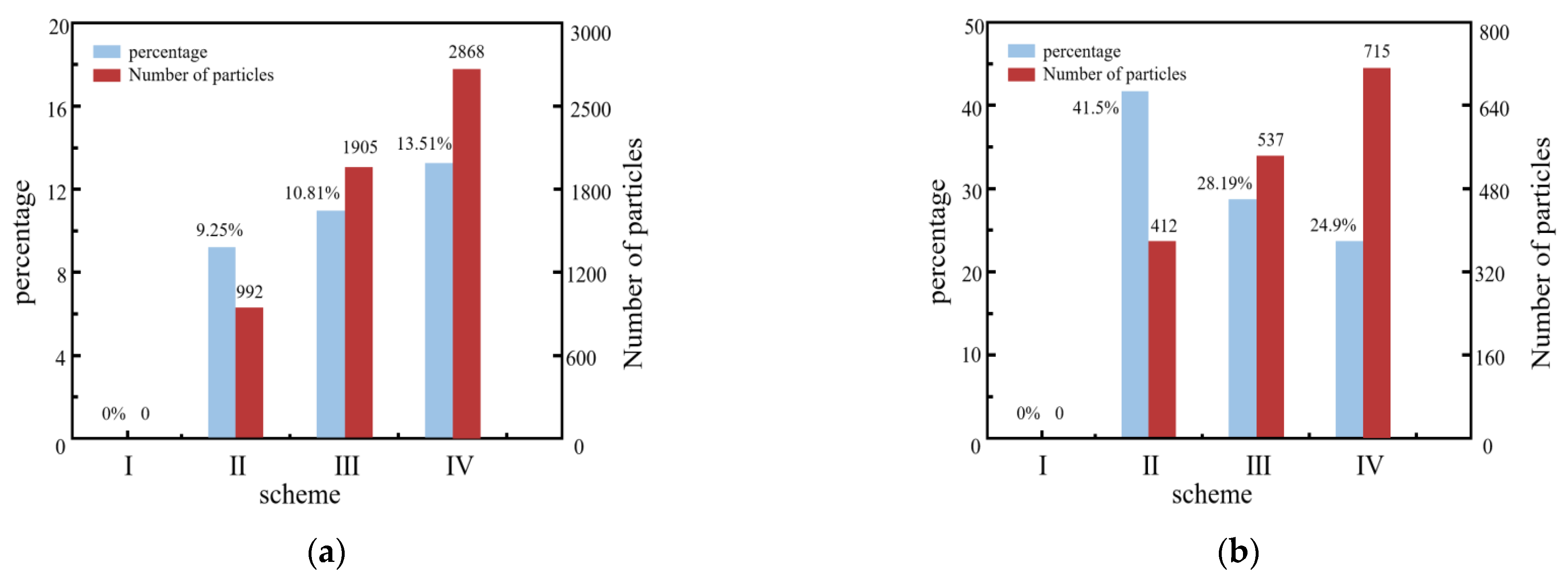
4. Case and Analysis of Calculation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, L.; Liu, R.; Yi, X. Research and Development of Anti-Icing/Deicing Techniques for Vessels: Review. Ocean. Eng. 2022, 260, 112008. [Google Scholar] [CrossRef]
- Lozowski, E.P.; Stallabrass, J.R.; Hearty, P.F. The icing of an Unheated, Nonrotating Cylinder. Part I: A Simulation Model. J. Appl. Meteorol. Climatol. 2017, 22, 2053–2062. [Google Scholar] [CrossRef]
- Mintu, S.; Molyneux, D. Ice Accretion for Ships and Offshore Structures. Part 1—State of the Art Review. Ocean Eng. 2022, 258, 111501. [Google Scholar] [CrossRef]
- Wang, Y.; Ju, L.; Han, D.; Wang, Q. Numerical Investigation of the Impacting and Freezing Process of a Single Supercooled Water Droplet. Phys. Fluids 2021, 33, 042114. [Google Scholar] [CrossRef]
- Veron, F. Ocean Spray. Annu. Rev. Fluid Mech. 2015, 47, 507–538. [Google Scholar] [CrossRef]
- Ryerson, C.C. Ice Protection of Offshore Platforms. Cold Reg. Sci. Technol. 2011, 65, 97–110. [Google Scholar] [CrossRef]
- Lozowski, E.P.; Szilder, K.; Makkonen, L. Computer Simulation of Marine Ice Accretion. Philos. Trans. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 2000, 358, 2811–2845. [Google Scholar] [CrossRef]
- Kulyakhtin, A.; Tsarau, A. A Time-Dependent Model of Marine Icing with Application of Computational Fluid Dynamics. Cold Reg. Sci. Technol. 2014, 104–105, 33–44. [Google Scholar] [CrossRef] [Green Version]
- Samuelsen, E.M.; Edvardsen, K.; Graversen, R.G. Modelled and Observed Sea-Spray Icing in Arctic-Norwegian Waters. Cold Reg. Sci. Technol. 2017, 134, 54–81. [Google Scholar] [CrossRef] [Green Version]
- Shojaei Barjouei, A.; Naseri, M. A Comparative Study of Statistical Techniques for Prediction of Meteorological and Oceanographic Conditions: An Application in Sea Spray Icing. JMSE 2021, 9, 539. [Google Scholar] [CrossRef]
- Naseri. Samuelsen Unprecedented Vessel-Icing Climatology Based on Spray-Icing Modelling and Reanalysis Data: A Risk-Based Decision-Making Input for Arctic Offshore Industries. Atmosphere 2019, 10, 197. [Google Scholar] [CrossRef] [Green Version]
- Jones, K.F.; Andreas, E.L. Sea Spray Concentrations and the Icing of Fixed Offshore Structures. Q. J. R. Meteorol. Soc. 2012, 138, 131–144. [Google Scholar] [CrossRef]
- Samuelsen, E.M. Prediction of Ship Icing in Arctic Waters-Observations and Modelling for Application in Operational Weather Forecasting. Ph.D. Thesis, UiT The Arctic University of Norway, Tromsø, Norway, 2017. [Google Scholar]
- Moore, G.W.K. A Climatology of Vessel Icing for the Subpolar North Atlantic Ocean. Int. J. Climatol. 2013, 33, 2495–2507. [Google Scholar] [CrossRef]
- Fairall, C.W.; Banner, M.L.; Peirson, W.L.; Asher, W.; Morison, R.P. Investigation of the Physical Scaling of Sea Spray Spume Droplet Production. J. Geophys. Res. Ocean. 2009, 114, C10. [Google Scholar] [CrossRef]
- Mintu, S.; Molyneux, D.; Colbourne, B. A Theoretical Model for Ship–Wave Impact Generated Sea Spray. J. Offshore Mech. Arct. Eng. 2021, 143, 041201. [Google Scholar] [CrossRef]
- Bodaghkhani, A.; Dehghani, S.R.; Muzychka, Y.S.; Colbourne, B. Understanding spray cloud formation by wave impact on marine objects. Cold Reg. Sci. Technol. 2016, 129, 114–136. [Google Scholar] [CrossRef]
- Young, F.R. Fizzics: The Science of Bubbles, Droplets, and Foams; The Johns Hopkins University Press: Baltimore, MD, USA, 2011; pp. 4–19. [Google Scholar]
- Horjen, I. Offshore Drilling Rig Ice Accretion Modeling Including a Surficial Brine Film. Cold Reg. Sci. Technol. 2015, 119, 84–110. [Google Scholar] [CrossRef]
- Kulyakhtin, A.; Kulyakhtin, S.; Løset, S. The Role of the Ice Heat Conduction in the Ice Growth Caused by Periodic Sea Spray. Cold Reg. Sci. Technol. 2016, 127, 93–108. [Google Scholar] [CrossRef]
- Haukebø, A.R. Modelling of Marine Icing with Close Range Photogrammetry. Master’s Thesis, UiT The Arctic University of Norway, Tromsø, Norway, 2015. [Google Scholar]
- Banari, A. Lattice Boltzmann Simulation of Multiphase Flows; Application to Wave Breaking and Sea Spray Generation, University of Rhode Island: Kingston, RI, USA, 2014. [Google Scholar]
- Tang, S.; Yang, Z.; Liu, C.; Dong, Y.-H.; Shen, L. Numerical Study on the Generation and Transport of Spume Droplets in Wind over Breaking Waves. Atmosphere 2017, 8, 248. [Google Scholar] [CrossRef] [Green Version]
- Kees, C.E.; Akkerman, I.; Farthing, M.W.; Bazilevs, Y. A Conservative Level Set Method Suitable for Variable-Order Approximations and Unstructured Meshes. J. Comput. Phys. 2011, 230, 4536–4558. [Google Scholar] [CrossRef]
- Watanabe, Y.; Ingram, D.M. Size Distributions of Sprays Produced by Violent Wave Impacts on Vertical Sea Walls. Proc. R. Soc. A 2016, 472, 20160423. [Google Scholar] [CrossRef] [Green Version]
- Ding, Z.; Ren, B.; Wang, Y.; Ren, X. Experimental Study of Unidirectional Irregular Wave Slamming on the Three-Dimensional Structure in the Splash Zone. Ocean. Eng. 2008, 35, 1637–1646. [Google Scholar] [CrossRef]
- Greco, M.; Lugni, C. 3-D Seakeeping Analysis with Water on Deck and Slamming. Part 1: Numerical Solver. J. Fluids Struct. 2012, 33, 127–147. [Google Scholar] [CrossRef]
- Dehghani-Sanij, A.R.; Dehghani, S.R.; Naterer, G.F.; Muzychka, Y.S. Sea Spray Icing Phenomena on Marine Vessels and Offshore Structures: Review and Formulation. Ocean. Eng. 2017, 132, 25–39. [Google Scholar] [CrossRef]
- Shipilova, O.; Kulyakhtin, A.; Tsarau, A.; Libby, B.; Moslet, P.O.; Loset, S. Mechanism and Dynamics of Marine Ice Accretion on Vessel Archetypes. In Proceedings of the OTC Arctic Technology Conference, Houston, TX, USA, 3–5 December 2012; p. OTC-23762-MS. [Google Scholar]
- Zakrzewski, W.P. Splashing a Ship with Collision-Generated Spray. Cold Reg. Sci. Technol. 1987, 14, 65–83. [Google Scholar] [CrossRef]
- Kulyakhtin, A.; Shipilova, O.; Libby, B.; Løset, S. Full-Scale 3D CFD Simulation of Spray Impingement on a Vessel Produced by Ship-Wave Interaction. In Proceedings of the The 21st IAHR International Symposium on Ice, Dalian, China, 11–15 June 2012; p. 11291141. [Google Scholar]
- Kulyakhtin, A. Numerical Modelling and Experiments on Sea Spray Icing. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2014. [Google Scholar]
- Mintu, M.; Azam, S. Theoretical and Numerical Methods for Predicting Ship-Wave Impact Generated Sea Spray. Ph.D. Thesis, Memorial University of Newfoundland, St. John’s, NL, Canada, 2021. [Google Scholar]
- Fragassa, C.; Topalovic, M.; Pavlovic, A.; Vulovic, S. Dealing with the Effect of Air in Fluid Structure Interaction by Coupled SPH-FEM Methods. Materials 2019, 12, 1162. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Korzilius, S.P.; Schilders, W.H.; Anthonissen, M.J. An Improved CSPM Approach for Accurate Second-Derivative Approximations with SPH. J. Appl. Math. Phys. 2016, 5, 168–184. [Google Scholar] [CrossRef] [Green Version]
- Gomez-Gesteira, M.; Rogers, B.D.; Dalrymple, R.A.; Crespo, A.J. State-of-the-Art of Classical SPH for Free-Surface Flows. J. Hydraul. Res. 2010, 48, 6–27. [Google Scholar] [CrossRef]
- Ben Belgacem, I.; Khochtali, H.; Cheikh, L.; Barhoumi, E.M.; Ben Salem, W. Comparison between Two Numerical Methods SPH/FEM and CEL by Numerical Simulation of an Impacting Water Jet. In Advances in Materials, Mechanics and Manufacturing; Springer: Berlin/Heidelberg, Germany, 2020; pp. 50–60. [Google Scholar]
- Stasch, J.; Avci, B.; Wriggers, P. Numerical Simulation of Fluid-structure Interaction Problems by a Coupled SPH-FEM Approach. Pamm 2016, 16, 491–492. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Wu, Y.; Wu, H.; Yang, C.; Feng, Q. Numerical Analysis of Dynamic Compaction Using FEM-SPH Coupling Method. Soil Dyn. Earthq. Eng. 2021, 140, 106420. (In Chinese) [Google Scholar] [CrossRef]
- Dehghani, S.R.; Naterer, G.F.; Muzychka, Y.S. 3-D Trajectory Analysis of Wave-Impact Sea Spray over a Marine Vessel. Cold Reg. Sci. Technol. 2018, 146, 72–80. [Google Scholar] [CrossRef]
- Dehghani, S.R.; Muzychka, Y.S.; Naterer, G.F. Droplet trajectories of wave-impact sea spray on a marine vessel. Cold Reg. Sci. Technol. 2016, 127, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Yang, Y. Simulation of Ship Pitch and Heave Motion in Regular Waves. J. Dalian Marit. Univ. 2002, 28, 13–16. (In Chinese) [Google Scholar] [CrossRef]







| FEM (Hull) Parameters | Value | SPH Parameters | Value |
|---|---|---|---|
| Material density/(kg/m3) | 7850 | Fluid particle density(kg/m3) | 998 |
| Grid spacing/m | 0 | Initial spacing of fluid particles/m | 0.01 |
| Number of grids | 1067 | Number of fluid particles | 26,570 |
| Modulus of elasticity/MPa | 2.06 × 105 | Smooth kernel functions | Wendland |
| Poisson’s ratio | 0.25 | Smooth length/m | 0.015 |
| Global damping factor | 0.00 | Pressure correction algorithm | CSPM algorithm |
| FEM Time step/s | 1.0 × 10−4 | Viscosity coefficient | 0.3 |
| Sound velocity coefficient | 10 | ||
| Fluid dynamic viscosity/(Pa·s) | 1.0 × 10−3 | ||
| SPH Time step/s | 1.0 × 10−4 |
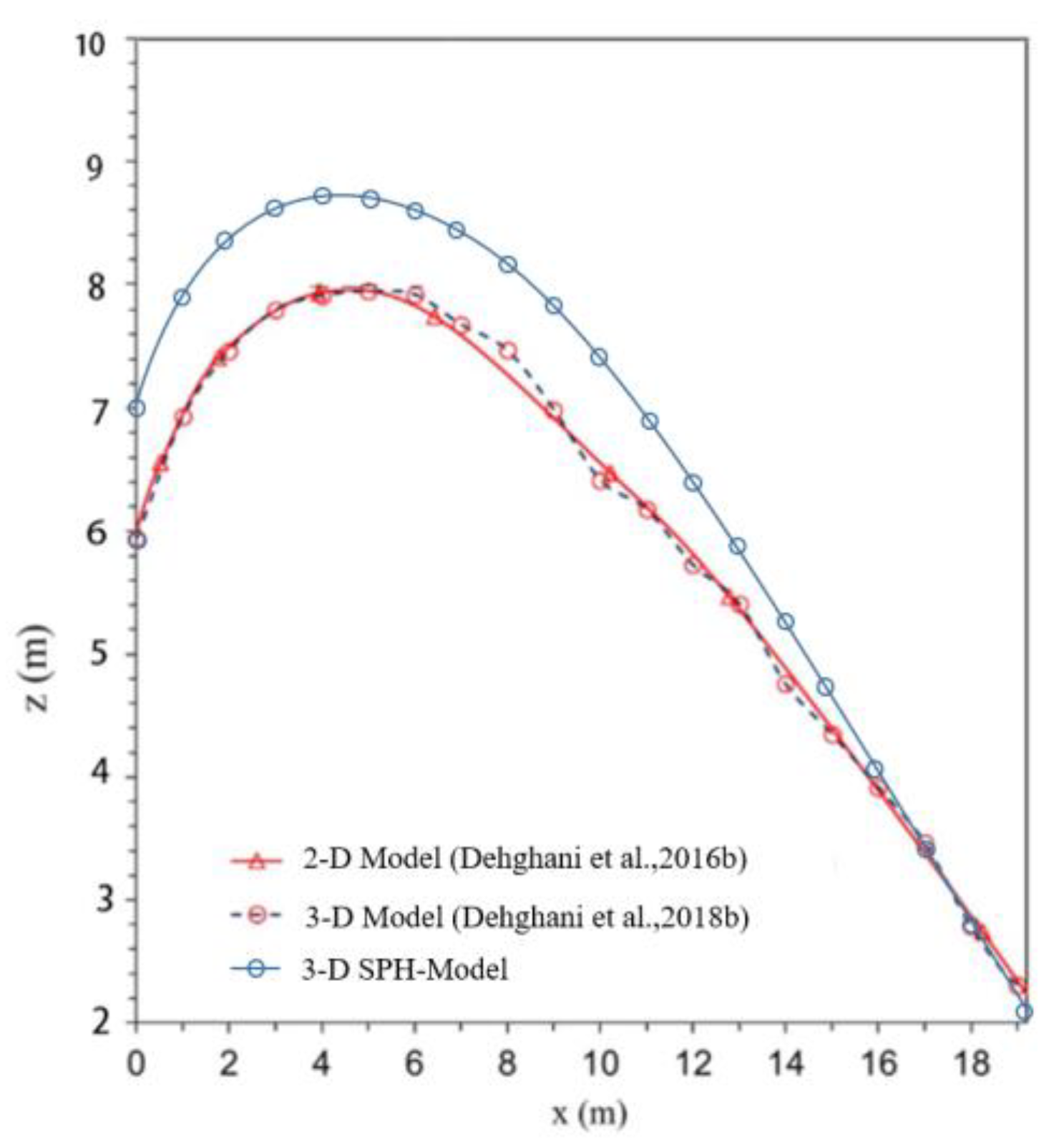
| Positions on the Vessel | Result | |||
|---|---|---|---|---|
| Zakrzewski et al. (1988) [30] | Dehghani et al. 2-D (2016b) [41] | Dehghani et al. 3-D (2018b) [40] | SPH-Model | |
| Wet height of the foremast | 5.85 m | 6.28 m | 6.25 m | 6.84 m |
| Front side of the superstructure | 2.07 m | 2.33 m | 2.6–3.5 m | 3.1 m |
| Roof of the superstructure | No spray | No spray | No spray | No spray |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Bai, X.; Wang, J.; Chen, G.; Zhang, T. Research on Sea Spray Distribution of Marine Vessels Based on SPH-FEM Coupling Numerical Simulation Method. Water 2022, 14, 3834. https://doi.org/10.3390/w14233834
Chen J, Bai X, Wang J, Chen G, Zhang T. Research on Sea Spray Distribution of Marine Vessels Based on SPH-FEM Coupling Numerical Simulation Method. Water. 2022; 14(23):3834. https://doi.org/10.3390/w14233834
Chicago/Turabian StyleChen, Jiajing, Xu Bai, Jialu Wang, Guanyu Chen, and Tao Zhang. 2022. "Research on Sea Spray Distribution of Marine Vessels Based on SPH-FEM Coupling Numerical Simulation Method" Water 14, no. 23: 3834. https://doi.org/10.3390/w14233834
APA StyleChen, J., Bai, X., Wang, J., Chen, G., & Zhang, T. (2022). Research on Sea Spray Distribution of Marine Vessels Based on SPH-FEM Coupling Numerical Simulation Method. Water, 14(23), 3834. https://doi.org/10.3390/w14233834





