Extreme Rainfall Indices in Southern Levant and Related Large-Scale Atmospheric Circulation Patterns: A Spatial and Temporal Analysis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data and Quality Control
2.3. Methods
2.3.1. Indices of Extreme Precipitation
2.3.2. Trend Detection
2.3.3. Teleconnection Indices
3. Results
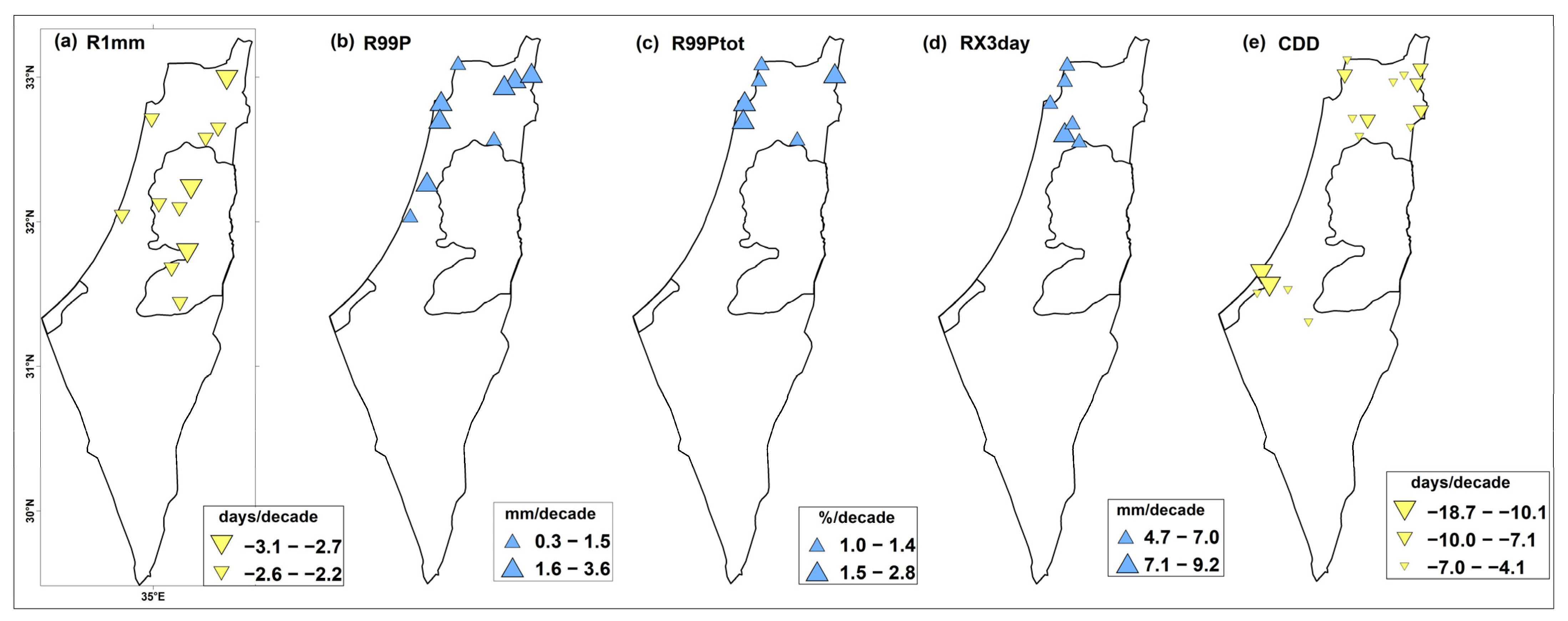
3.1. Annual Trends of Extreme Precipitation Indices
3.2. Seasonal Trends of the Extreme Precipitation Indices
3.2.1. Winter Trends

3.2.2. Spring Trends
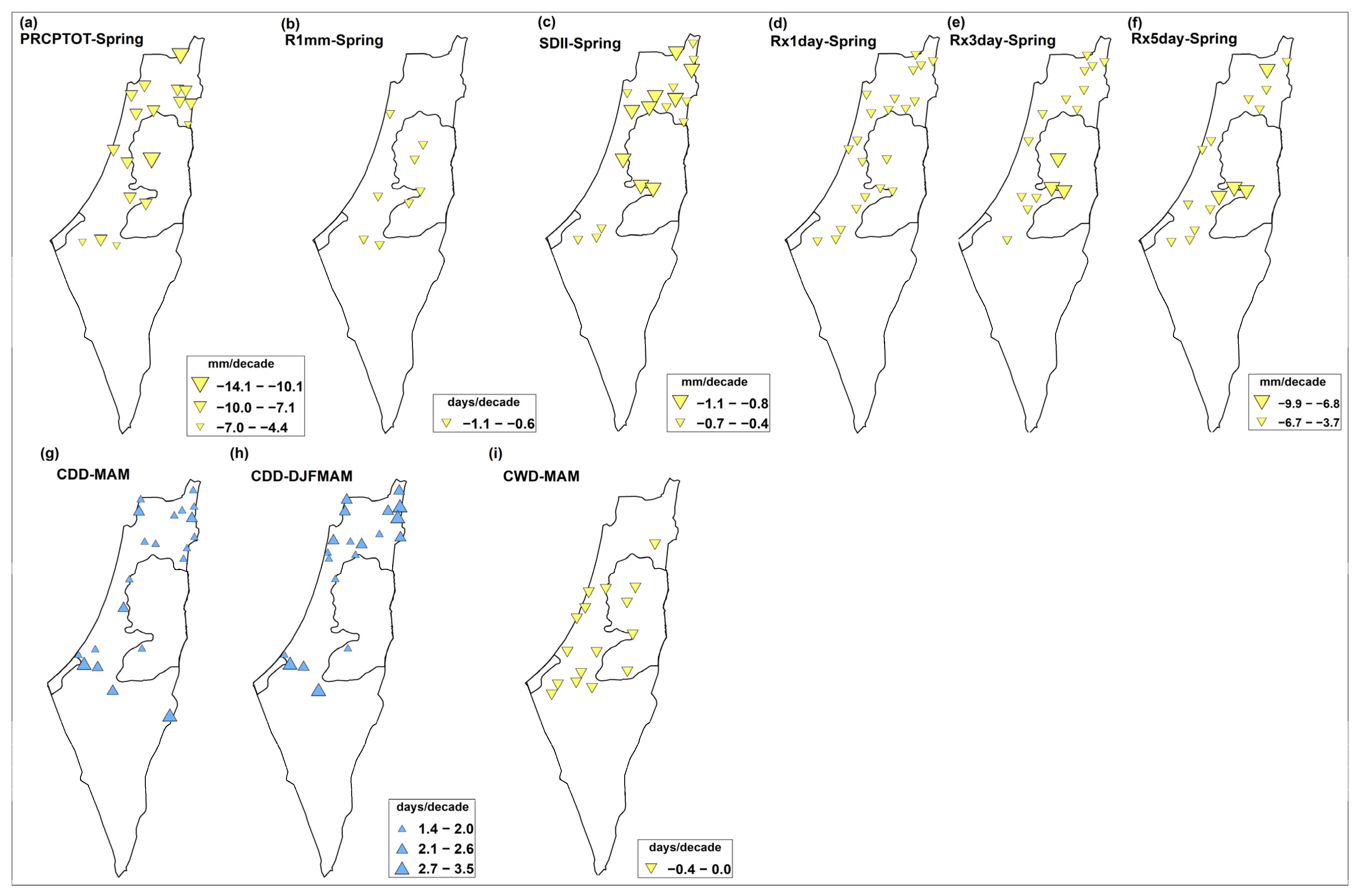
3.2.3. Autumn Trends
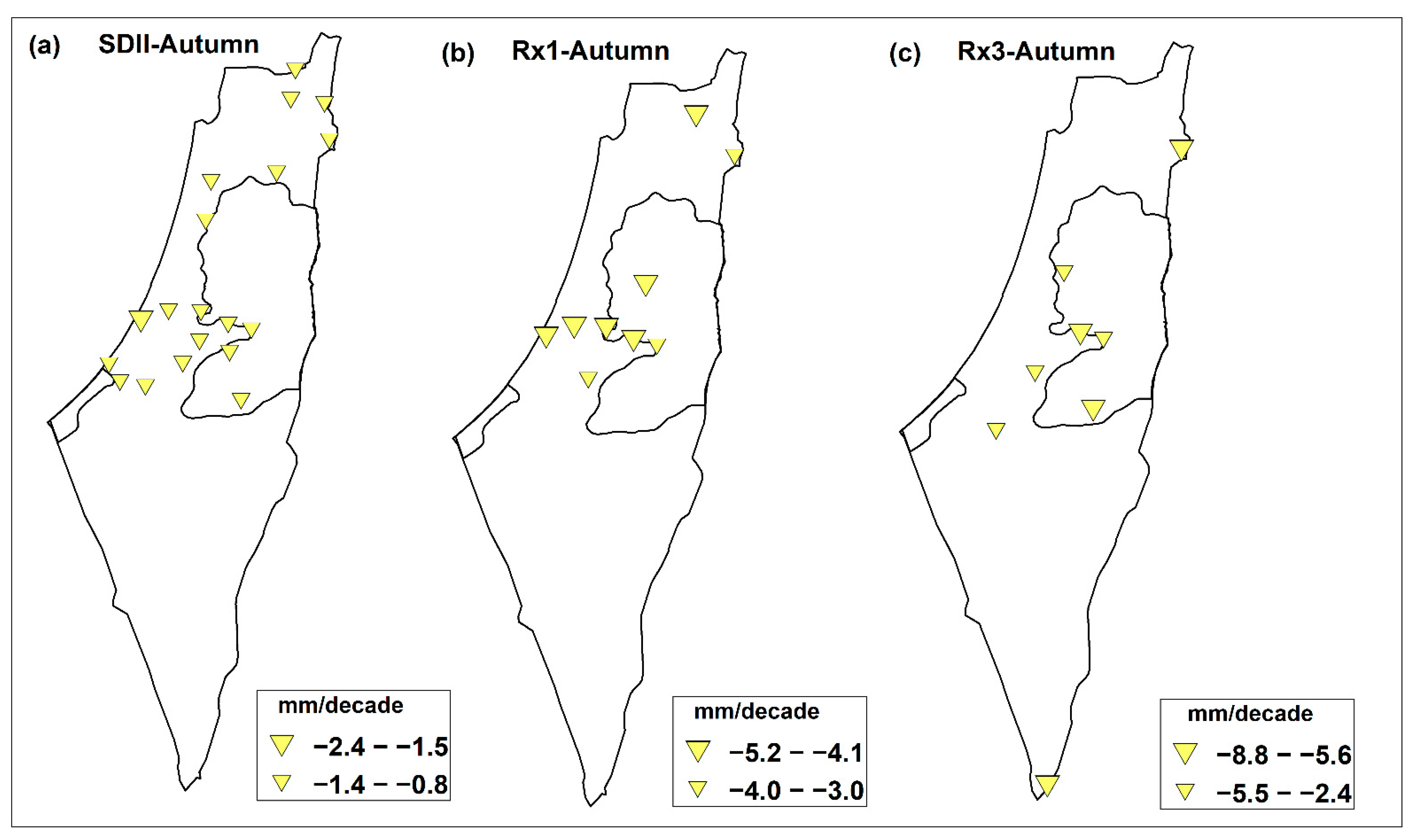
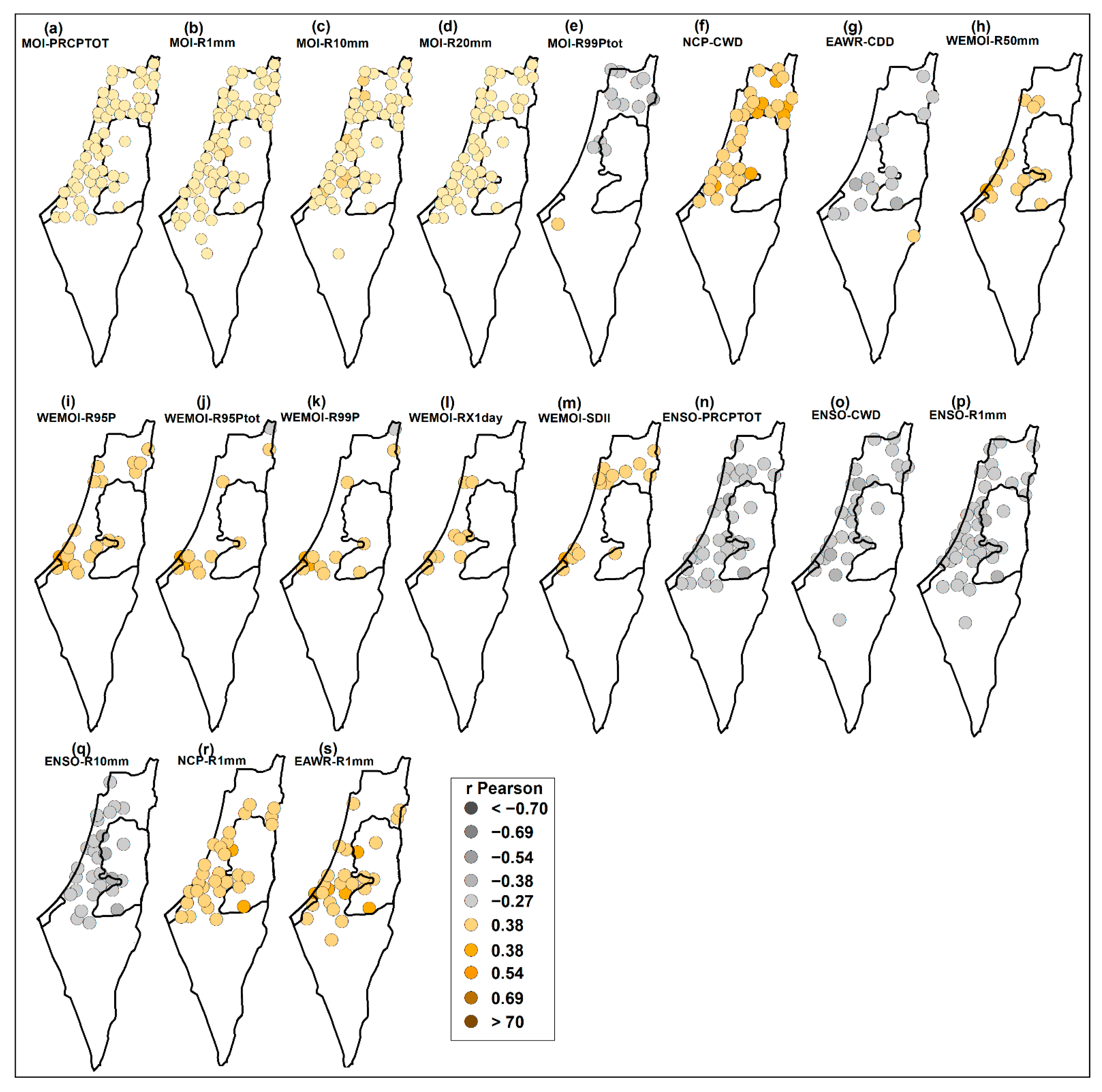
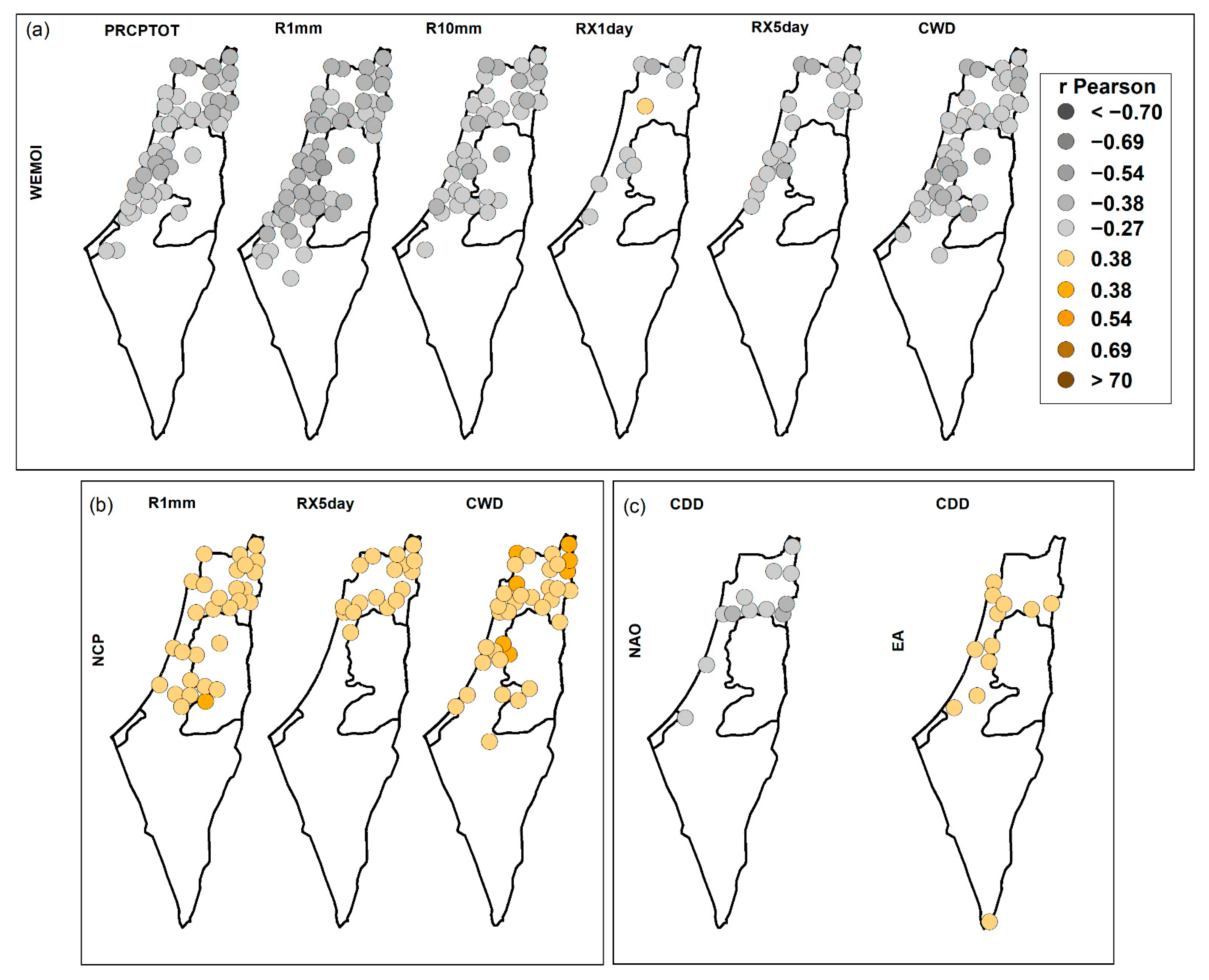
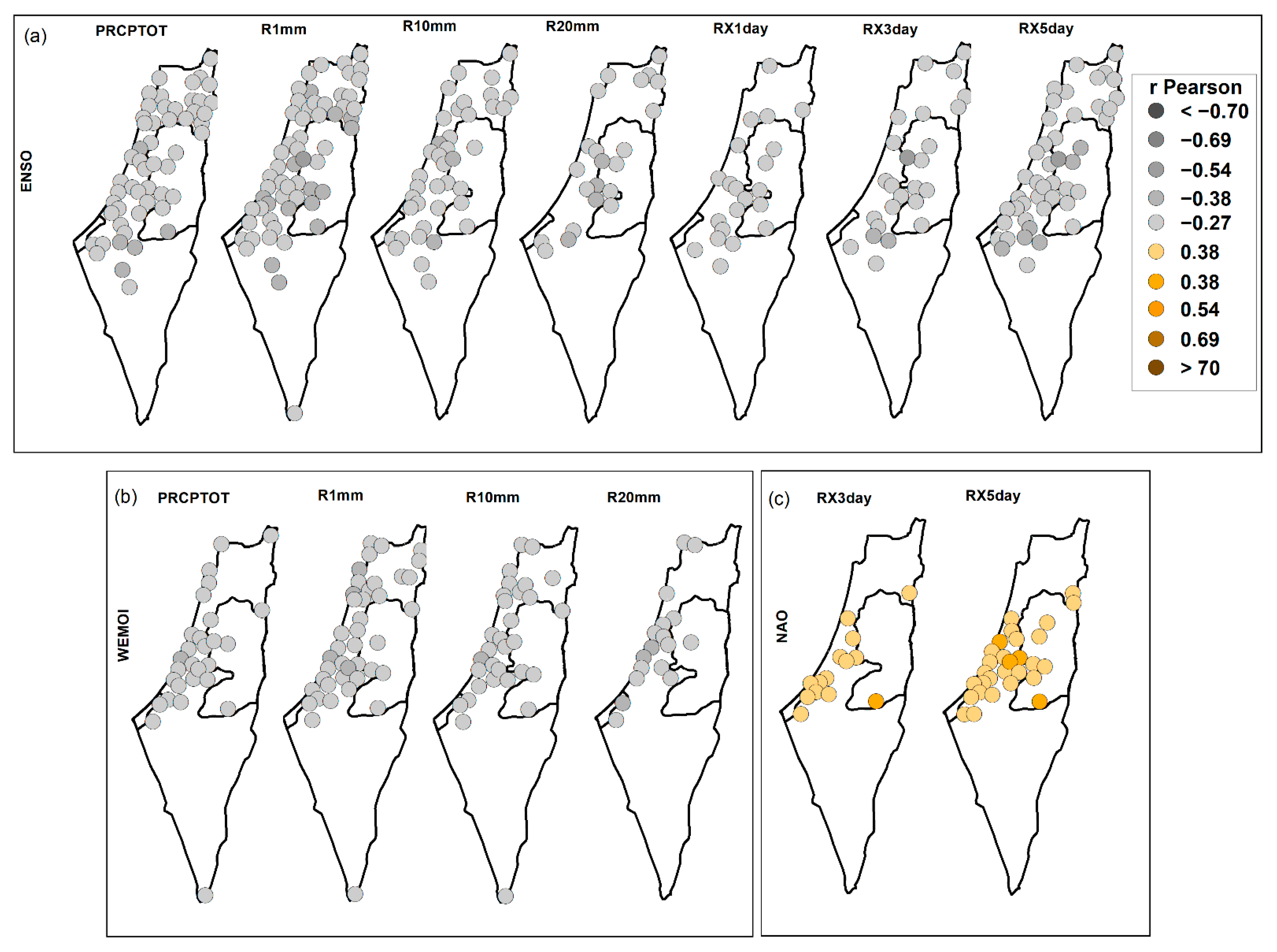
3.3. Extreme Rainfall Indices and Teleconnection Patterns
3.3.1. Annual Scale
| Index | WEMO | EAWR | NAO | EA | MO | NCP | ENSO | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| + | − | + | − | + | − | + | − | + | − | + | − | + | − | |
| PRCPTOT | 3 | 0 | 0 | 2 | 10 | 0 | 0 | 0 | 39 | 0 | 3 | 0 | 0 | 33 |
| R1mm | 0 | 0 | 26 | 0 | 8 | 0 | 0 | 0 | 43 | 0 | 31 | 0 | 0 | 39 |
| R10mm | 3 | 0 | 5 | 0 | 6 | 0 | 2 | 0 | 40 | 0 | 6 | 0 | 0 | 28 |
| R20mm | 15 | 0 | 5 | 0 | 8 | 0 | 1 | 0 | 28 | 0 | 2 | 0 | 0 | 8 |
| R50mm | 14 | 0 | 2 | 0 | 2 | 3 | 0 | 0 | 3 | 0 | 4 | 0 | 0 | 8 |
| R95P | 19 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 3 | 0 | 2 | 0 | 0 | 1 |
| R95Ptot | 10 | 1 | 0 | 0 | 0 | 8 | 2 | 1 | 2 | 2 | 2 | 0 | 0 | 0 |
| R99P | 11 | 1 | 0 | 0 | 0 | 8 | 2 | 1 | 2 | 0 | 2 | 0 | 0 | 0 |
| R99Ptot | 2 | 0 | 5 | 0 | 0 | 8 | 0 | 0 | 1 | 12 | 5 | 0 | 0 | 0 |
| RX1day | 9 | 0 | 1 | 0 | 0 | 2 | 2 | 1 | 3 | 2 | 2 | 0 | 0 | 3 |
| RX3day | 6 | 5 | 2 | 0 | 6 | 5 | 1 | 0 | 0 | 2 | 0 | 0 | 0 | 1 |
| RX5day | 2 | 0 | 2 | 0 | 2 | 2 | 1 | 0 | 2 | 1 | 0 | 0 | 0 | 0 |
| SDII | 15 | 0 | 0 | 0 | 1 | 3 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| CDD | 0 | 0 | 1 | 14 | 1 | 6 | 9 | 0 | 3 | 0 | 8 | 0 | 0 | 5 |
| CWD | 2 | 0 | 8 | 0 | 0 | 0 | 3 | 0 | 5 | 0 | 31 | 0 | 0 | 28 |
3.3.2. Seasonal Scale
| Index | Season | WEMO | EA/WR | NAO | EA | MO | NCP | ENSO | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| + | − | + | − | + | − | + | − | + | − | + | − | + | − | ||
| PRCPTOT | Winter | 0 | 0 | 20 | 0 | 0 | 0 | 0 | 0 | 43 | 0 | 51 | 0 | 0 | 2 |
| Spring | 0 | 37 | 0 | 0 | 0 | 1 | 0 | 0 | 5 | 0 | 8 | 0 | 0 | 1 | |
| Autumn | 0 | 20 | 4 | 0 | 9 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 48 | |
| R1mm | Winter | 0 | 7 | 41 | 0 | 0 | 0 | 0 | 0 | 53 | 0 | 58 | 0 | 0 | 1 |
| Spring | 0 | 57 | 0 | 0 | 3 | 0 | 0 | 2 | 3 | 0 | 27 | 0 | 0 | 5 | |
| Autumn | 0 | 35 | 7 | 0 | 14 | 0 | 0 | 0 | 6 | 0 | 0 | 0 | 0 | 56 | |
| R10mm | Winter | 0 | 0 | 30 | 0 | 1 | 0 | 1 | 0 | 58 | 0 | 55 | 0 | 0 | 5 |
| Spring | 0 | 37 | 1 | 1 | 0 | 1 | 0 | 0 | 9 | 1 | 9 | 1 | 0 | 1 | |
| Autumn | 0 | 26 | 5 | 0 | 6 | 0 | 1 | 0 | 4 | 0 | 0 | 0 | 0 | 33 | |
| R20mm | Winter | 0 | 0 | 6 | 0 | 2 | 0 | 0 | 0 | 32 | 0 | 30 | 0 | 0 | 6 |
| Spring | 0 | 4 | 0 | 4 | 0 | 0 | 1 | 0 | 4 | 0 | 2 | 0 | 2 | 4 | |
| Autumn | 0 | 15 | 3 | 0 | 2 | 0 | 1 | 0 | 2 | 0 | 0 | 0 | 0 | 20 | |
| RX1day | Winter | 1 | 2 | 3 | 1 | 1 | 2 | 1 | 0 | 2 | 1 | 4 | 0 | 0 | 5 |
| Spring | 1 | 9 | 1 | 1 | 0 | 1 | 2 | 1 | 2 | 0 | 0 | 0 | 2 | 2 | |
| Autumn | 0 | 8 | 4 | 0 | 3 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 15 | |
| RX3day | Winter | 0 | 3 | 7 | 0 | 0 | 9 | 2 | 0 | 6 | 0 | 15 | 0 | 0 | 7 |
| Spring | 0 | 8 | 0 | 0 | 0 | 0 | 0 | 1 | 4 | 0 | 3 | 0 | 0 | 2 | |
| Autumn | 0 | 9 | 0 | 0 | 13 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 19 | |
| RX5day | Winter | 0 | 2 | 7 | 0 | 3 | 5 | 1 | 0 | 9 | 0 | 20 | 0 | 0 | 3 |
| Spring | 0 | 16 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 16 | 0 | 0 | 1 | |
| Autumn | 0 | 5 | 0 | 0 | 28 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 38 | |
| SDII | Winter | 0 | 0 | 0 | 0 | 0 | 1 | 3 | 0 | 1 | 0 | 1 | 0 | 0 | 4 |
| Spring | 0 | 0 | 0 | 1 | 1 | 0 | 3 | 0 | 2 | 0 | 1 | 0 | 1 | 1 | |
| Autumn | 0 | 2 | 1 | 0 | 0 | 0 | 0 | 2 | 1 | 0 | 0 | 0 | 0 | 5 | |
| CDD | Winter | 0 | 1 | 0 | 2 | 0 | 32 | 1 | 0 | 0 | 14 | 0 | 15 | 0 | 1 |
| Spring | 7 | 0 | 1 | 3 | 0 | 12 | 12 | 0 | 1 | 0 | 0 | 9 | 1 | 3 | |
| CWD | Winter | 0 | 1 | 50 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 48 | 0 | 1 | 25 |
| Spring | 0 | 37 | 0 | 0 | 2 | 0 | 0 | 10 | 4 | 0 | 33 | 0 | 0 | 2 | |

4. Discussion
5. Conclusions
- -
- Substantial decreasing trends were found for extreme rainfall indices at an annual scale, and for spring and autumn seasons, mainly for the PRCPTOT, R1mm, R10mm, and R20mm indices.
- -
- At an annual scale, southern Levant tends to have more intense rainy days, showing increased trends for all the heavy precipitation indices.
- -
- Seasonally, winter PRCPTOT, RX1day, RX3day, RX5day, and SDII indices showed increasing trends, significant for SDII index in the northwestern locations in the area, related with the PRCPTOT increasing and the R1mm decreasing.
- -
- In spring and autumn, most extreme indices showed decreasing trends, these being the seasons mostly contributing to the annual declines in the PRCPTOT, RX1day, RX3day, RX5day, R1mm, R10mm, R20mm, and CDD indices.
- -
- Southern Levant had experienced longer periods of extreme dry spells (CDD) in spring and consistently shorter extreme wet spells (CWD) for winter, spring, and the combined winter–spring season.
- -
- The NCP, WEMO, and ENSO atmospheric circulation patterns are the main regulators for the extreme rainfall indices in winter, spring, and autumn, respectively.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Najafi, M.R.; Moradkhani, H. A Hierarchical Bayesian Approach for the Analysis of Climate Change Impact on Runoff Extremes. Hydrol. Process. 2014, 28, 6292–6308. [Google Scholar] [CrossRef]
- Abiodun, B.J.; Mogebisa, T.O.; Petja, B.; Abatan, A.A.; Roland, T.R. Potential Impacts of Specific Global Warming Levels on Extreme Rainfall Events over Southern Africa in CORDEX and NEX-GDDP Ensembles. Int. J. Climatol. 2020, 40, 3118–3141. [Google Scholar] [CrossRef]
- Ellwanger, J.H.; Kulmann-Leal, B.; Kaminski, V.L.; Valverde-Villegas, J.M.; da VEIGA, A.B.G.; Spilki, F.R.; Fearnside, P.M.; Caesar, L.; Giatti, L.L.; Wallau, G.L.; et al. Beyond Diversity Loss and Climate Change: Impacts of Amazon Deforestation on Infectious Diseases and Public Health. An Acad Bras Cienc. 2020, 92, e20191375. [Google Scholar] [CrossRef] [PubMed]
- Lima, A.O.; Lyra, G.B.; Abreu, M.C.; Oliveira-Júnior, J.F.; Zeri, M.; Cunha-Zeri, G. Extreme Rainfall Events over Rio de Janeiro State, Brazil: Characterization Using Probability Distribution Functions and Clustering Analysis. Atmos. Res. 2021, 247, 105221. [Google Scholar] [CrossRef]
- Easterling, D.R.; Evans, J.L.; Groisman, P.Y.; Karl, T.R.; Kunkel, K.E.; Ambenje, P. Observed Variability and Trends in Extreme Climate Events: A Brief Review. Bull. Am. Meteorol. Soc. 2000, 81, 417–425. [Google Scholar] [CrossRef]
- Trenberth, K.E. Changes in Precipitation with Climate Change. Clim. Res. 2011, 47, 123–138. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Q.; Yang, X.; Ji, F.; Liu, D.L.; Yu, Q. Extreme Rainfall, Rainfall Erosivity, and Hillslope Erosion in Australian Alpine Region and Their Future Changes. Int. J. Climatol. 2020, 40, 1213–1227. [Google Scholar] [CrossRef]
- Towfiqul Islam, A.R.M.; Rahman, M.S.; Khatun, R.; Hu, Z. Spatiotemporal Trends in the Frequency of Daily Rainfall in Bangladesh during 1975–2017. Theor. Appl. Climatol. 2020, 141, 869–887. [Google Scholar] [CrossRef]
- Katz, R.W.; Brown, B.G. Extreme Events in a Changing Climate: Variability Is More Important than Averages. Clim. Change 1992, 21, 289–302. [Google Scholar] [CrossRef]
- de Lima, M.I.P.; Santo, F.E.; Ramos, A.M.; de Lima, J.L.M.P. Recent Changes in Daily Precipitation and Surface Air Temperature Extremes in Mainland Portugal, in the Period 1941-2007. Atmos. Res. 2013, 127, 195–209. [Google Scholar] [CrossRef]
- Solomon, S.D.; Qin, M.; Manning, Z.; Chen, M.; Marquis, K.B.; Averyt, M.T.; Miller, H.L.; Solomon, S.; Qin, D.; Manning, M.; et al. Summary for Policymakers. In Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K., Tignor, M., Miller, H.L., Eds.; Cambridge University Press: New York, NY, USA; Geneva, Switzerland, 2007. [Google Scholar] [CrossRef]
- Zhang, X.; Alexander, L.; Hegerl, G.C.; Jones, P.; Tank, A.K.; Peterson, T.C.; Trewin, B.; Zwiers, F.W. Indices for Monitoring Changes in Extremes Based on Daily Temperature and Precipitation Data. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 851–870. [Google Scholar] [CrossRef]
- Şensoy, S.; Türkoğlu, N.; Akçakaya, A.; Ekici, M.; Demircan, M.; Ulupınar, Y.; Atay, H.; Tüvan, A.; Demirbaş, H. Trends in Turkey Climate Indices from 1960 To 2010. Meteoroloji. Gov. Tr. 2013. Available online: https://www.researchgate.net/publication/289520845_Trends_in_Turkey_Climate_Indices_from_1960_to_2010 (accessed on 26 October 2022).
- Yilmaz, A.G. The Effects of Climate Change on Historical and Future Extreme Rainfall in Antalya, Turkey. Hydrol. Sci. J. 2015, 60, 2148–2162. [Google Scholar] [CrossRef] [Green Version]
- Almazroui, M. Rainfall Trends and Extremes in Saudi Arabia in Recent Decades. Atmosphere 2020, 11, 964. [Google Scholar] [CrossRef]
- Nastos, P.T.; Zerefos, C.S. On Extreme Daily Precipitation Totals at Athens, Greece. Adv. Geosci. 2007, 10, 59–66. [Google Scholar] [CrossRef] [Green Version]
- Deshpande, N.R.; Kulkarni, A.; Krishna Kumar, K. Characteristic Features of Hourly Rainfall in India. Int. J. Climatol. 2012, 32, 1730–1744. [Google Scholar] [CrossRef]
- Alpert, P.; Ben-Gai, T.; Baharad, A.; Benjamini, Y.; Yekutieli, D.; Colacino, M.; Diodato, L.; Ramis, C.; Homar, V.; Romero, R.; et al. The Paradoxical Increase of Mediterranean Extreme Daily Rainfall in Spite of Decrease in Total Values. Geophys. Res. Lett. 2002, 29, 31-1–31-4. [Google Scholar] [CrossRef] [Green Version]
- Goodess, C.M.; Jones, P.D. Links between Circulation and Changes in the Characteristics of Iberian Rainfall. Int. J. Climatol. 2002, 22, 1593–1615. [Google Scholar] [CrossRef]
- Alexander, L.v.; Zhang, X.; Peterson, T.C.; Caesar, J.; Gleason, B.; Klein Tank, A.M.G.; Haylock, M.; Collins, D.; Trewin, B.; Rahimzadeh, F.; et al. Global Observed Changes in Daily Climate Extremes of Temperature and Precipitation. J. Geophys. Res. Atmos. 2006, 111, 1042–1063. [Google Scholar] [CrossRef] [Green Version]
- Donat, M.G.; Alexander, L.V.; Yang, H.; Durre, I.; Vose, R.; Caesar, J. Global Land-Based Datasets for Monitoring Climatic Extremes. Bull. Am. Meteorol. Soc. 2013, 94, 997–1006. [Google Scholar] [CrossRef]
- Westra, S.; Alexander, L.V.; Zwiers, F.W. Global Increasing Trends in Annual Maximum Daily Precipitation. J. Clim. 2013, 26, 3904–3918. [Google Scholar] [CrossRef] [Green Version]
- Acar, Z.; Gönençgil, B. Investigation of Extreme Precipitation Indices in Turkey. Theor. Appl. Climatol. 2022, 148, 679–691. [Google Scholar] [CrossRef]
- Haylock, M.; Nicholls, N. Trends in Extreme Rainfall Indices for an Updated High Quality Data Set for Australia, 1910–1998. Int. J. Climatol. 2000, 20, 1533–1541. [Google Scholar] [CrossRef]
- Basher, M.A.; Stiller-Reeve, M.A.; Saiful Islam, A.K.M.; Bremer, S. Assessing Climatic Trends of Extreme Rainfall Indices over Northeast Bangladesh. Theor. Appl. Climatol. 2018, 134, 441–452. [Google Scholar] [CrossRef]
- Tong, S.; Li, X.; Zhang, J.; Bao, Y.; Bao, Y.; Na, L.; Si, A. Spatial and temporal variability in extreme temperature and precipitation events in Inner Mongolia (China) during 1960–2017. Sci. Total. Environ. 2019, 649, 75–89. [Google Scholar] [CrossRef] [PubMed]
- Larbi, I.; Hountondji, F.C.C.; Annor, T.; Agyare, W.A.; Gathenya, J.M.; Amuzu, J. Spatio-Temporal Trend Analysis of Rainfall and Temperature Extremes in the Vea Catchment, Ghana. Climate 2018, 6, 87. [Google Scholar] [CrossRef] [Green Version]
- Xoplaki Climate Variability over the Mediterranean; University of Bern: Bern, Switzerland, 2002.
- Black, E. The impact of climate change on daily precipitation statistics in Jordan and Israel. Atmospheric Sci. Lett. 2009, 10, 192–200. [Google Scholar] [CrossRef]
- Lelieveld, J.; Hadjinicolaou, P.; Kostopoulou, E.; Chenoweth, J.; El Maayar, M.; Giannakopoulos, C.; Hannides, C.; Lange, M.A.; Tanarhte, M.; Tyrlis, E.; et al. Climate change and impacts in the Eastern Mediterranean and the Middle East. Clim. Change 2012, 114, 667–687. [Google Scholar] [CrossRef] [Green Version]
- Mayewski, P.A.; Rohling, E.; Stager, J.C.; Karlén, W.; Maasch, K.A.; Meeker, L.D.; Meyerson, E.A.; Gasse, F.; Van Kreveld, S.; Holmgren, K.; et al. Holocene climate variability. Quat. Res. 2004, 62, 243–255. [Google Scholar] [CrossRef]
- Orland, I.J.; Bar-Matthews, M.; Kita, N.T.; Ayalon, A.; Matthews, A.; Valley, J.W. Climate deterioration in the Eastern Mediterranean as revealed by ion microprobe analysis of a speleothem that grew from 2.2 to 0.9 ka in Soreq Cave, Israel. Quat. Res. 2009, 71, 27–35. [Google Scholar] [CrossRef]
- Frumkin, A.; Magaritz, M.; Carmi, I.; Zak, I. The Holocene climatic record of the salt caves of Mount Sedom Israel. Holocene 1991, 1, 191–200. [Google Scholar] [CrossRef]
- Giorgi, F. Climate Change Hot-Spots. Geophys. Res. Lett. 2006, 33, 101029. [Google Scholar] [CrossRef]
- Lu, J.; Vecchi, G.A.; Reichler, T. Expansion of the Hadley cell under global warming. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef] [Green Version]
- Zittis, G.; Almazroui, M.; Alpert, P.; Ciais, P.; Cramer, W.; Dahdal, Y.; Fnais, M.; Francis, D.; Hadjinicolaou, P.; Howari, F.; et al. Climate Change and Weather Extremes in the Eastern Mediterranean and Middle East. Rev. Geophys. 2022, 60, e2021RG000762. [Google Scholar] [CrossRef]
- Al-Qinna, M.I.; Hammouri, N.A.; Obeidat, M.M.; Ahmad, F.Y. Drought analysis in Jordan under current and future climates. Clim. Chang. 2011, 106, 421–440. [Google Scholar] [CrossRef]
- Shadeed, S. Spatio-temporal Drought Analysis in Arid and Semi-arid Regions: A Case Study from Palestine. Arab. J. Sci. Eng. 2013, 38, 2303–2313. [Google Scholar] [CrossRef]
- Mathbout, S.; Lopez-Bustins, J.A.; Martin-Vide, J.; Bech, J.; Rodrigo, F.S. Spatial and temporal analysis of drought variability at several time scales in Syria during 1961–2012. Atmospheric Res. 2018, 200, 153–168. [Google Scholar] [CrossRef]
- Lange, M.A. Impacts of Climate Change on the Eastern Mediterranean and the Middle East and North Africa Region and the Water–Energy Nexus. Atmosphere 2019, 10, 455. [Google Scholar] [CrossRef] [Green Version]
- Ben-Gai, T.; Bitan, A.; Manes, A.; Alpert, P. Long-term changes in annual rainfall patterns in southern Israel. Theor. Appl. Clim. 1994, 49, 59–67. [Google Scholar] [CrossRef]
- Ben-Gai, T.; Bitan, A.; Manes, A.; Alpert, P.; Rubin, S. Spatial and Temporal Changes in Rainfall Frequency Distribution Patterns in Israel. Arch. Meteorol. Geophys. Bioclimatol. Ser. B 1998, 61, 177–190. [Google Scholar] [CrossRef]
- Freiwan, M.; Kadioglu, M. Spatial and temporal analysis of climatological data in Jordan. Int. J. Clim. 2008, 28, 521–535. [Google Scholar] [CrossRef]
- Ghanem, A.A. Climatology of the areal precipitation in Amman/Jordan. Int. J. Clim. 2011, 31, 1328–1333. [Google Scholar] [CrossRef]
- Ziv, B.; Saaroni, H.; Pargament, R.; Harpaz, T.; Alpert, P. Trends in rainfall regime over Israel, 1975–2010, and their relationship to large-scale variability. Reg. Environ. Chang. 2014, 14, 1751–1764. [Google Scholar] [CrossRef]
- Yosef, Y.; Aguilar, E.; Alpert, P. Changes in extreme temperature and precipitation indices: Using an innovative daily homogenized database in Israel. Int. J. Clim. 2019, 39, 5022–5045. [Google Scholar] [CrossRef]
- Zhang, X.; Aguilar, E.; Sensoy, S.; Melkonyan, H.; Tagiyeva, U.; Ahmed, N.; Kutaladze, N.; Rahimzadeh, F.; Taghipour, A.; Hantosh, T.H.; et al. Trends in Middle East climate extreme indices from 1950 to 2003. J. Geophys. Res. Earth Surf. 2005, 110. [Google Scholar] [CrossRef]
- Donat, M.G.; Peterson, T.C.; Brunet, M.; King, A.D.; Almazroui, M.; Kolli, R.K.; Boucherf, D.; Al-Mulla, A.Y.; Nour, A.Y.; Aly, A.A.; et al. Changes in extreme temperature and precipitation in the Arab region: Long-term trends and variability related to ENSO and NAO. Int. J. Climatol. 2014, 34, 581–592. [Google Scholar] [CrossRef]
- Salameh, A.A.M.; Gámiz-Fortis, S.R.; Castro-Díez, Y.; Abu Hammad, A.; Esteban-Parra, M.J. Spatio-temporal analysis for extreme temperature indices over the Levant region. Int. J. Clim. 2019, 39, 5556–5582. [Google Scholar] [CrossRef]
- Kutiel, H.; Benaroch, Y. North Sea-Caspian Pattern (NCP)—An upper level atmospheric teleconnection affecting the Eastern Mediterranean: Identification and definition. Theor. Appl. Clim. 2002, 71, 17–28. [Google Scholar] [CrossRef]
- Price, C.; Stone, L.; Huppert, A.; Rajagopalan, B.; Alpert, P. A possible link between El Niño and precipitation in Israel. Geophys. Res. Lett. 1998, 25, 3963–3966. [Google Scholar] [CrossRef]
- Kelley, C.; Ting, M.; Seager, R.; Kushnir, Y. Mediterranean precipitation climatology, seasonal cycle, and trend as simulated by CMIP5. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Ziv, B.; Dayan, U.; Kushnir, Y.; Roth, C.; Enzel, Y. Regional and global atmospheric patterns governing rainfall in the southern Levant. Int. J. Clim. 2006, 26, 55–73. [Google Scholar] [CrossRef]
- Yosef, Y.; Saaroni, H.; Alpert, P. Trends in Daily Rainfall Intensity Over Israel 1950/1-2003/4. Open Atmos. Sci. J. 2009, 3, 196–203. [Google Scholar] [CrossRef] [Green Version]
- Ávila, A.; Justino, F.; Wilson, A.; Bromwich, D.; Amorim, M. Recent precipitation trends, flash floods and landslides in southern Brazil. Environ. Res. Lett. 2016, 11, 114029. [Google Scholar] [CrossRef]
- Spinoni, J.; Barbosa, P.; Bucchignani, E.; Cassano, J.; Cavazos, T.; Christensen, J.H.; Christensen, O.B.; Coppola, E.; Evans, J.; Geyer, B.; et al. Future Global Meteorological Drought Hot Spots: A Study Based on CORDEX Data. J. Clim. 2020, 33, 3635–3661. [Google Scholar] [CrossRef]
- Garnaut, R. The Garnaut Climate Change Review: Final Report; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Trewin, B. A daily homogenized temperature data set for Australia. Int. J. Clim. 2013, 33, 1510–1529. [Google Scholar] [CrossRef]
- Sibson, R. A Brief Description of Natural Neighbour Interpolation. In Interpreting Multivariate Data; John Wiley & Sons: New York, NY, USA, 1981. [Google Scholar]
- Wang, X.L.; Feng, Y. RHtestsV4 User Manual; Climate Research Division, Atmospheric Science and Technology Directorate, Science and Technology Branch, Environment Canada: Toronto, ON, Canada, 2013. [Google Scholar]
- Wang, X.L.; Chen, H.; Wu, Y.; Feng, Y.; Pu, Q. New Techniques for the Detection and Adjustment of Shifts in Daily Precipitation Data Series. J. Appl. Meteorol. Clim. 2010, 49, 2416–2436. [Google Scholar] [CrossRef]
- Villafuerte, M.Q.; Matsumoto, J.; Kubota, H. Changes in extreme rainfall in the Philippines (1911-2010) linked to global mean temperature and ENSO. Int. J. Clim. 2015, 35, 2033–2044. [Google Scholar] [CrossRef]
- Wang, S.; Jiang, F.; Ding, Y. Spatial coherence of variations in seasonal extreme precipitation events over Northwest Arid Region, China. Int. J. Clim. 2015, 35, 4642–4654. [Google Scholar] [CrossRef]
- Wu, C.; Huang, G. Projection of climate extremes in the Zhujiang River basin using a regional climate model. Int. J. Clim. 2016, 36, 1184–1196. [Google Scholar] [CrossRef] [Green Version]
- Klein Tank, A.B.G.; Zwiers, F.W. Guidelines on Analysis of Extremes in a Changing Climate in Support of Informed Decisions for Adaptation; World Meteorological Organization (WMO): Geneva, Switzerland, 2009. [Google Scholar]
- Ajjur, S.B.; Riffi, M.I. Analysis of the observed trends in daily extreme precipitation indices in Gaza Strip during 1974–2016. Int. J. Clim. 2020, 40, 6189–6200. [Google Scholar] [CrossRef]
- Zhang, X.B.F.Y. R ClimDex 1.0 User Mannual; Climate research branch environment Canada: Downsview, ON, Canada, 2004. [Google Scholar]
- Mann, H.B. Non-Parametric Test Against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods. Biometrika 1957, 44, 298. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Zhang, X.; Vincent, L.A.; Hogg, W.D.; Niitsoo, A. Temperature and precipitation trends in Canada during the 20th century. Atmos.-Ocean 2000, 38, 395–429. [Google Scholar] [CrossRef]
- New, M.; Hewitson, B.; Stephenson, D.B.; Tsiga, A.; Kruger, A.; Manhique, A.; Gomez, B.; Coelho, C.A.S.; Masisi, D.N.; Kululanga, E.; et al. Evidence of trends in daily climate extremes over southern and west Africa. J. Geophys. Res. Atmos. 2006, 111, D14102. [Google Scholar] [CrossRef]
- Demir, V.; Keskin, A. Water level change of lakes and sinkholes in Central Turkey under anthropogenic effects. Arch. Meteorol. Geophys. Bioclimatol. Ser. B 2020, 142, 929–943. [Google Scholar] [CrossRef]
- Citakoglu, H.; Minarecioglu, N. Trend analysis and change point determination for hydro-meteorological and groundwater data of Kizilirmak basin. Arch. Meteorol. Geophys. Bioclimatol. Ser. B 2021, 145, 1275–1292. [Google Scholar] [CrossRef]
- Wang, X.L.; Swail, V.R. Changes of Extreme Wave Heights in Northern Hemisphere Oceans and Related Atmospheric Cir-culation Regimes. J. Clim. 2001, 14. [Google Scholar] [CrossRef]
- Patakamuri, S.K.; O’Brien, N. Package ‘Modifiedmk’ (Version 1.4.0): Modified Versions of Mann Kendall and Spearman’s Rho Trend Tests. CRAN 2021. Available online: https://cran.r-project.org/web/packages/modifiedmk/modifiedmk.pdf (accessed on 1 September 2021).
- Efthymiadis, D.; Goodess, C.; Jones, P. Trends in Mediterranean gridded temperature extremes and large-scale circulation influences. Nat. Hazards Earth Syst. Sci. 2011, 11, 2199–2214. [Google Scholar] [CrossRef]
- Popov, T.; Gnjato, S.; Trbić, G.; Ivanišević, M. Recent Trends in Extreme Temperature Indices in Bosnia and Herzegovina. Carpathian J. Earth Environ. Sci. 2018, 13, 211–224. [Google Scholar] [CrossRef]
- Yenigun, K.; Ibrahim, W.A. Investigation of drought in the northern Iraq region. Meteorol. Appl. 2019, 26, 490–499. [Google Scholar] [CrossRef] [Green Version]
- Nouri, M.; Homaee, M. Drought trend, frequency and extremity across a wide range of climates over Iran. Meteorol. Appl. 2020, 27, e1899. [Google Scholar] [CrossRef]
- Hameed, M.; Ahmadalipour, A.; Moradkhani, H. Drought and food security in the middle east: An analytical framework. Agric. For. Meteorol. 2020, 281, 107816. [Google Scholar] [CrossRef]
- AlSarmi, S.; Washington, R. Recent observed climate change over the Arabian Peninsula. J. Geophys. Res. Earth Surf. 2011, 116. [Google Scholar] [CrossRef]
- Shohami, D.; Dayan, U.; Morin, E. Warming and drying of the eastern Mediterranean: Additional evidence from trend analysis. J. Geophys. Res. Earth Surf. 2011, 116. [Google Scholar] [CrossRef]
- Hochman, A.; Mercogliano, P.; Alpert, P.; Saaroni, H.; Bucchignani, E. High-resolution projection of climate change and extremity over Israel using COSMO-CLM. Int. J. Clim. 2018, 38, 5095–5106. [Google Scholar] [CrossRef]
- Luong, T.M.; Dasari, H.P.; Hoteit, I. Extreme precipitation events are becoming less frequent but more intense over Jeddah, Saudi Arabia. Are shifting weather regimes the cause? Atmos. Sci. Lett. 2020, 21, e981. [Google Scholar] [CrossRef]
- Cheng, C.S.; Auld, H.; Li, Q.; Li, G. Possible impacts of climate change on extreme weather events at local scale in south–central Canada. Clim. Change 2012, 112, 963–979. [Google Scholar] [CrossRef] [Green Version]
- Papalexiou, S.M.; Montanari, A. Global and Regional Increase of Precipitation Extremes Under Global Warming. Water Resour. Res. 2019, 55, 4901–4914. [Google Scholar] [CrossRef]
- Seidel, D.J.; Fu, Q.; Randel, W.J.; Reichler, T.J. Widening of the tropical belt in a changing climate. Nat. Geosci. 2008, 1, 21–24. [Google Scholar] [CrossRef]
- Hertig, E.; Seubert, S.; Paxian, A.; Vogt, G.; Paeth, H.; Jacobeit, J. Changes of total versus extreme precipitation and dry periods until the end of the twenty-first century: Statistical assessments for the Mediterranean area. Arch. Meteorol. Geophys. Bioclimatol. Ser. B 2013, 111, 1–20. [Google Scholar] [CrossRef]
- Sillmann, J.; Roeckner, E. Indices for extreme events in projections of anthropogenic climate change. Clim. Change 2008, 86, 83–104. [Google Scholar] [CrossRef] [Green Version]
- Tebaldi, C.; Hayhoe, K.; Arblaster, J.M.; Meehl, G.A. Going to the Extremes: An Intercomparison of Model-Simulated Historical and Future Changes in Extreme Events. Clim. Change 2006, 79, 185–211. [Google Scholar] [CrossRef]
- Saaroni, H.; Ziv, B.; Lempert, J.; Gazit, Y.; Morin, E. Prolonged dry spells in the Levant region: Climatologic-synoptic analysis. Int. J. Clim. 2015, 35, 2223–2236. [Google Scholar] [CrossRef]
- Kutiel, H.; Paz, S. Sea Level Pressure Departures in the Mediterranean and their Relationship with Monthly Rainfall Conditions in Israel. Arch. Meteorol. Geophys. Bioclimatol. Ser. B 1998, 60, 93–109. [Google Scholar] [CrossRef]
- Törnros, T. On the relationship between the Mediterranean Oscillation and winter precipitation in the Southern Levant. Atmos. Sci. Lett. 2013, 14, 287–293. [Google Scholar] [CrossRef]
- Baltacı, H.; Akkoyunlu, B.O.; Tayanç, M. Relationships between teleconnection patterns and Turkish climatic extremes. Arch. Meteorol. Geophys. Bioclimatol. Ser. B 2018, 134, 1365–1386. [Google Scholar] [CrossRef]
- Redolat, D.; Monjo, R.; Lopez-Bustins, J.A.; Martin-Vide, J. Upper-Level Mediterranean Oscillation index and seasonal variability of rainfall and temperature. Theor. Appl. Clim. 2019, 135, 1059–1077. [Google Scholar] [CrossRef]
- Müller-Plath, G.; Lüdecke, H.-J.; Lüning, S. Long-distance air pressure differences correlate with European rain. Sci. Rep. 2022, 12, 10191. [Google Scholar] [CrossRef]
- Martin-Vide, J.; Lopez-Bustins, J.-A. The Western Mediterranean Oscillation and rainfall in the Iberian Peninsula. Int. J. Clim. 2006, 26, 1455–1475. [Google Scholar] [CrossRef]
- Krichak, S.O.; Alpert, P. Decadal trends in the east Atlantic-west Russia pattern and Mediterranean precipitation. Int. J. Clim. 2005, 25, 183–192. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, Y.; Fang, G.; Li, Y.; Li, Z.; Wang, F.; Xia, Z. Observed changes in extreme precipitation over the Tienshan Mountains and associated large-scale climate teleconnections. J. Hydrol. 2022, 606, 127457. [Google Scholar] [CrossRef]
- Zhu, J.; Zhou, H.; Xiao, H.; Wang, X. Singular value decomposition (SVD) based correlation analysis of climatic factors and extreme precipitation in Hunan Province, China, during 1960–2009. J. Water Clim. Change 2021, 12, 3602–3616. [Google Scholar] [CrossRef]
- Quishpe-Vásquez, C.; Gámiz-Fortis, S.R.; García-Valdecasas-Ojeda, M.; Castro-Díez, Y.; Esteban-Parra, M.J. Tropical Pacific sea surface temperature influence on seasonal streamflow variability in Ecuador. Int. J. Clim. 2019, 39, 3895–3914. [Google Scholar] [CrossRef]

| No. | Index | Indicator Name | Definition | Unit |
|---|---|---|---|---|
| 1 | PRCPTOT | Annual total wet day precipitation | Annual total precipitation from days ≥1 mm | mm |
| 2 | R1mm | Number of wet days | Annual count of days when precipitation ≥1 mm | Days |
| 3 | R10mm | Number of heavy precipitation days | Annual count of days when precipitation ≥10 mm | Days |
| 4 | R20mm | Number of very heavy precipitation days | Annual count of days when precipitation ≥20 mm | Days |
| 5 | R50mm | Number of days above 50 mm | Annual count of days when precipitation ≥50 mm | Days |
| 6 | R95P | Very wet days | Annual total precipitation when daily precipitation amount >95th percentile | mm |
| 7 | R99P | Extremely wet days | Annual total precipitation when daily precipitation amount >99th percentile | mm |
| 8 | R95Ptot | Contribution from very wet days | 100*R95P/PRCPTOT | % |
| 9 | R99Ptot | Contribution from extremely wet days | 100*R99P/PRCPTOT | % |
| 10 | RX1day | Max 1-day precipitation amount | Monthly maximum 1-day precipitation | mm |
| 11 | RX3day | Max 3-day precipitation amount | Monthly maximum consecutive 3-day precipitation | mm |
| 12 | RX5day | Max 5-day precipitation amount | Monthly maximum consecutive 5-day precipitation | mm |
| 13 | SDII | Simple daily intensity index | Annual total precipitation divided by the number of wet days (defined as precipitation ≥1 mm) in the year | mm/day |
| 14 | CWD | Consecutive wet days | Maximum number of consecutive days when precipitation ≥1 mm | Days |
| 15 | CWD-DJF | Consecutive wet days in winter | Maximum number of consecutive days when precipitation ≥1 mm, between December to February | Days |
| 16 | CWD-MAM | Consecutive wet days in spring | Maximum number of consecutive days when precipitation ≥1 mm, between March to May | Days |
| 17 | CWD-DJFMAM | Consecutive wet days in winter and spring | Maximum number of consecutive days when precipitation ≥1 mm between December to March | Days |
| 18 | CDD | Consecutive dry days | Maximum number of consecutive days when precipitation <1 mm | Days |
| 19 | CDD-DJF | Consecutive dry days in winter | Maximum number of consecutive days when precipitation <1 mm, between December to February | Days |
| 20 | CDD-MAM | Consecutive dry days in spring | Maximum number of consecutive days when precipitation <1 mm, between March to May | Days |
| 21 | CDD-DJFMAM | Consecutive dry days in winter and spring | Maximum number of consecutive days when precipitation <1 mm between December to March | Days |
| No. | Index | Total (+) Trends (Sig.) | Total (−) Trends (Sig.) | No Trend | Trend for Averaged Time Series |
|---|---|---|---|---|---|
| 1 | PRCPTOT | 25 (0) | 41 (1) | 0 | −2.9 (mm/decade) |
| 2 | R1mm | 3 (0) | 63 (11) | 0 | −1.1 (days/decade) |
| 3 | R10mm | 15 (0) | 51 (3) | 2 | −0.2 (days/decade) |
| 4 | R20mm | 5 (0) | 27 (2) | 27 | 0.0 (days/decade) |
| 5 | R50mm | 17 (0) | 3 (0) | 46 | 0.07 (days/decade) |
| 6 | R95P | 48 (4) | 14 (0) | 4 | 5.3 (mm/decade) |
| 7 | R99P | 9 (9) | 0 (0) | 57 | 4.4 ** (mm/decade) |
| 8 | R95Ptot | 52 (2) | 10 (0) | 4 | 0.8 (%/decade) |
| 9 | R99Ptot | 9 (6) | 0 (0) | 57 | 0.78 ** (%/decade) |
| 10 | RX1day | 51 (3) | 15 (0) | 0 | 1.7 ** (mm/decade) |
| 11 | RX3day | 48 (6) | 18 (0) | 0 | 2.1 ** (mm/decade) |
| 12 | RX5day | 48 (1) | 18 (0) | 0 | 1.2 (mm/decade) |
| 13 | SDII | 50 (4) | 16 (0) | 0 | 0.19 (mm/decade) |
| 14 | CWD | 48 (0) | 18 (0) | 25 | 0.04 (days/decade) |
| 15 | CDD | 9 (0) | 57 (16) | 0 | −2.7 ** (days/decade) |
| Index | Season | Tot. (+) Trends (Sig.) | Tot. (−) Trends (Sig.) | No Trend | Trend for Averaged Time Series |
|---|---|---|---|---|---|
| PRCPTOT | Winter | 48 (0) | 18 (0) | 0 | 8.8 mm/decade |
| Spring | 2 (0) | 64 (18) | 0 | −5.8 mm/decade | |
| Autumn | 12 (0) | 54 (0) | 0 | −1.9 mm/decade | |
| R1mm | Winter | 6 (0) | 60 (3) | 0 | −0.6 days/decade |
| Spring | 7 (0) | 59 (8) | 0 | −0.3 days/decade | |
| Autumn | 20 (0) | 37 (0) | 9 | −0.08 days/decade | |
| R10mm | Winter | 27 (0) | 33 (0) | 6 | −0.05 days/decade |
| Spring | 4 (0) | 62 (7) | 0 | −0.02 days/decade | |
| Autumn | 12 (0) | 28 (0) | 26 | 0 | |
| R20mm | Winter | 46 (0) | 9 (0) | 11 | 0.1 days/decade |
| Spring | 0 (0) | 22 (5) | 44 | −0.09 days/decade | |
| Autumn | 3 (0) | 25 (4) | 38 | 0.04 days/decade | |
| RX1day | Winter | 53 (6) | 13 (0) | 0 | 2.2 * mm/decade |
| Spring | 2 (0) | 64 (21) | 0 | −2.1 * mm/decade | |
| Autumn | 6 (0) | 60 (9) | 0 | −1.8 mm/decade | |
| RX3day | Winter | 52 (7) | 14 (0) | 0 | 3.3 mm/decade |
| Spring | 1 (0) | 65 (20) | 0 | −3.6 * mm/decade | |
| Autumn | 7 (0) | 59 (8) | 0 | −2.5 mm/decade | |
| RX5day | Winter | 46 (2) | 20 (0) | 0 | 1.7 mm/decade |
| Spring | 2 (0) | 64 (15) | 0 | −3.7 mm/decade | |
| Autumn | 11 (0) | 55 (3) | 0 | −2.4 mm/decade | |
| SDII | Winter | 55 (11) | 11 (0) | 0 | 0.25 mm/decade |
| Spring | 6 (0) | 60 (19) | 0 | −0.52 * mm/decade | |
| Autumn | 3 (0) | 63 (19) | 0 | −0.75 * mm/decade | |
| CDD | Winter | 22 (0) | 44 (0) | 0 | −0.03 days/decade |
| Spring | 59 (21) | 5 (0) | 0 | 1.5 ** days/decade | |
| Winter-spring | 59 (20) | 7 (0) | 0 | 1.7 * days/decade | |
| CWD | Winter | 15 (0) | 25 (0) | 26 | −0.05 days/decade |
| Spring | 3 (0) | 53 (16) | 10 | −0.2 days/decade | |
| Winter-spring | 22 (0) | 21 (0) | 23 | −0.01 days/decade |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salameh, A.A.M.; Ojeda, M.G.-V.; Esteban-Parra, M.J.; Castro-Díez, Y.; Gámiz-Fortis, S.R. Extreme Rainfall Indices in Southern Levant and Related Large-Scale Atmospheric Circulation Patterns: A Spatial and Temporal Analysis. Water 2022, 14, 3799. https://doi.org/10.3390/w14233799
Salameh AAM, Ojeda MG-V, Esteban-Parra MJ, Castro-Díez Y, Gámiz-Fortis SR. Extreme Rainfall Indices in Southern Levant and Related Large-Scale Atmospheric Circulation Patterns: A Spatial and Temporal Analysis. Water. 2022; 14(23):3799. https://doi.org/10.3390/w14233799
Chicago/Turabian StyleSalameh, Ala A. M., Matilde García-Valdecasas Ojeda, María Jesús Esteban-Parra, Yolanda Castro-Díez, and Sonia R. Gámiz-Fortis. 2022. "Extreme Rainfall Indices in Southern Levant and Related Large-Scale Atmospheric Circulation Patterns: A Spatial and Temporal Analysis" Water 14, no. 23: 3799. https://doi.org/10.3390/w14233799
APA StyleSalameh, A. A. M., Ojeda, M. G.-V., Esteban-Parra, M. J., Castro-Díez, Y., & Gámiz-Fortis, S. R. (2022). Extreme Rainfall Indices in Southern Levant and Related Large-Scale Atmospheric Circulation Patterns: A Spatial and Temporal Analysis. Water, 14(23), 3799. https://doi.org/10.3390/w14233799






