Deep Learning Methods for Predicting Tap-Water Quality Time Series in South Korea
Abstract
:1. Introduction
2. Related Literature
2.1. Deep Learning-Based Methods
2.2. Statistical Methods
2.3. Comparison of Methods
2.4. Drinking Water Quality Standards
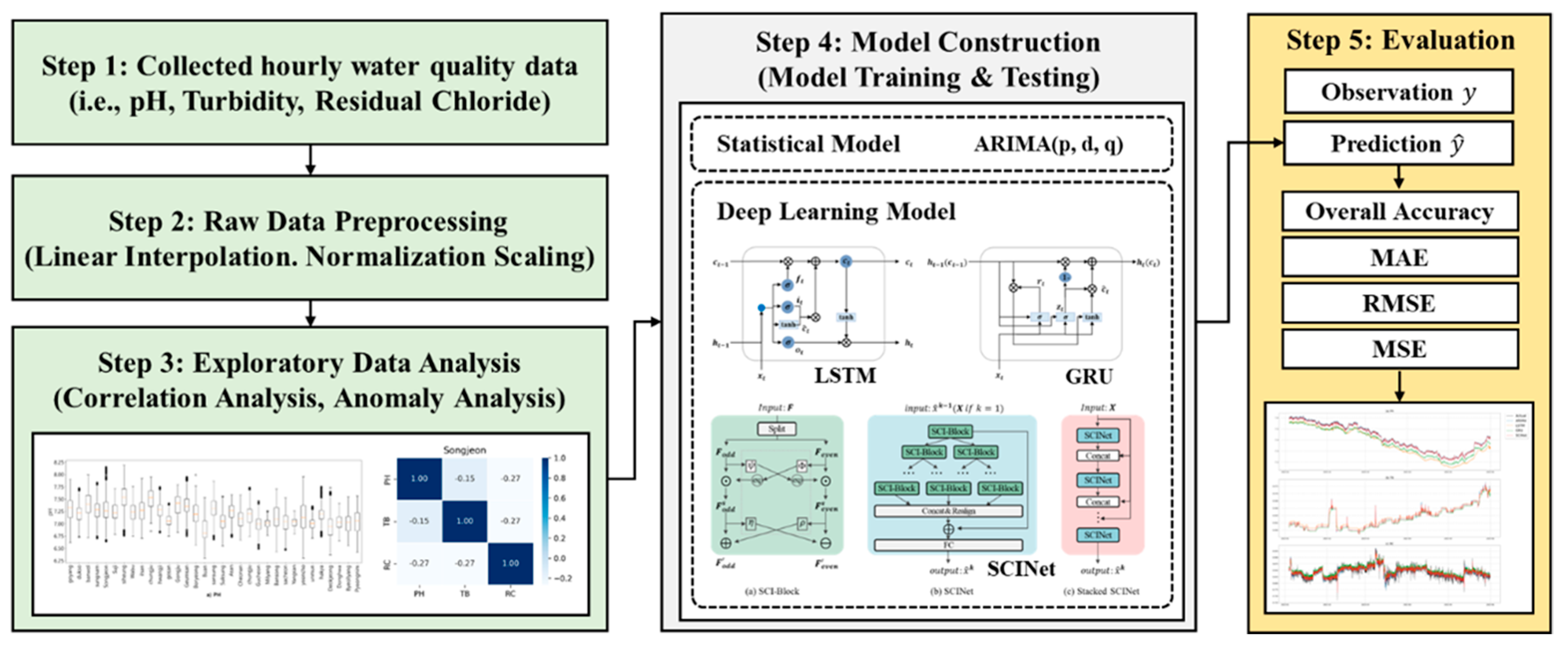
3. Methodology
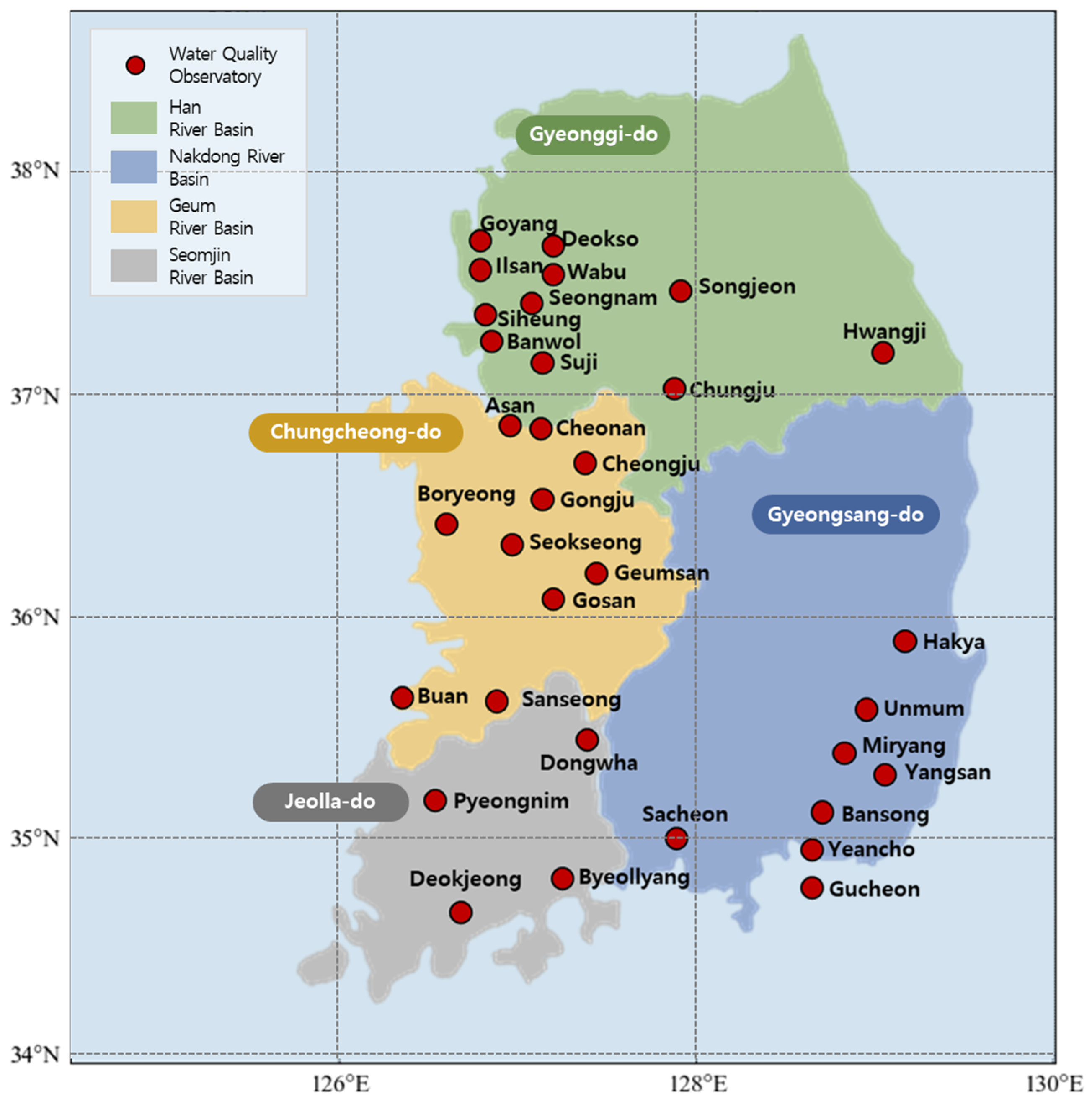
3.1. Scope of Study
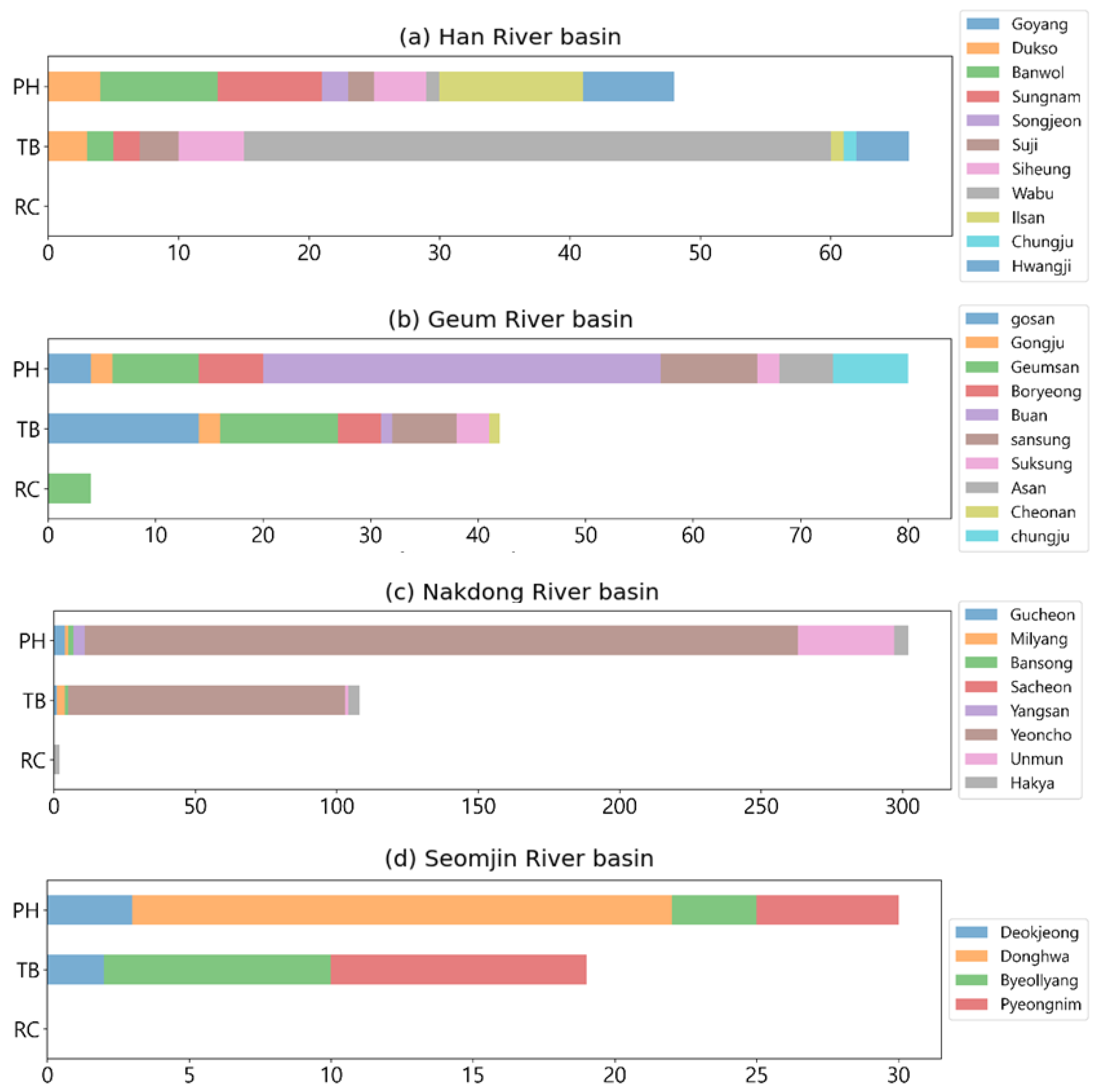
3.2. Spatial Range
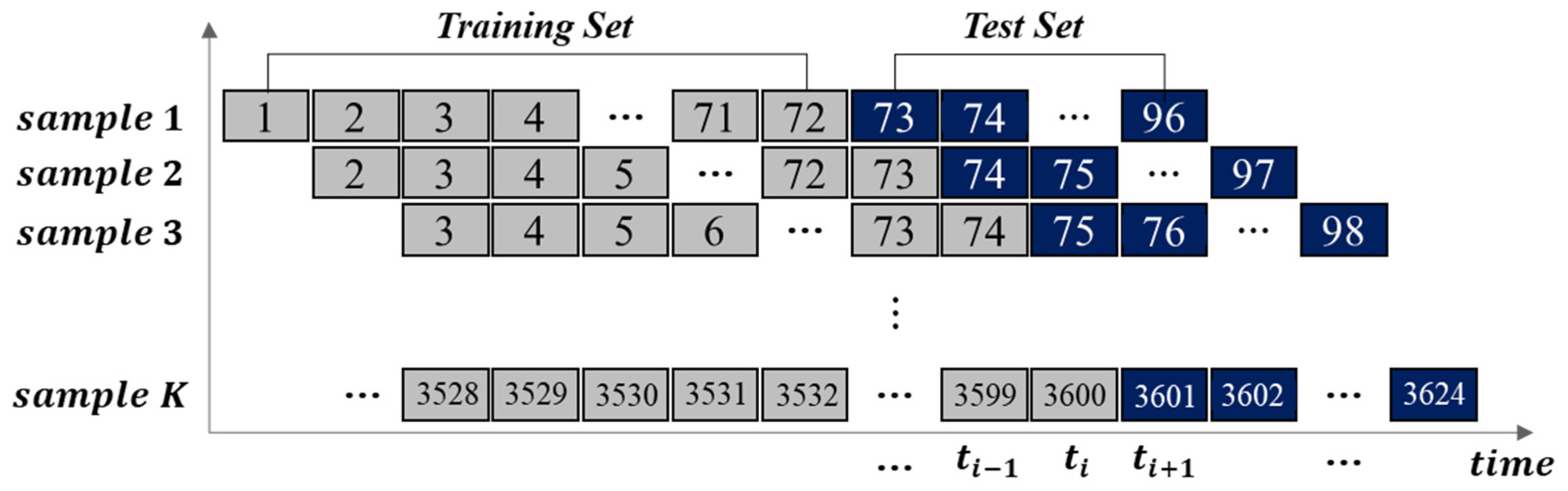
3.3. Temporal Range
3.4. Data Preprocessing
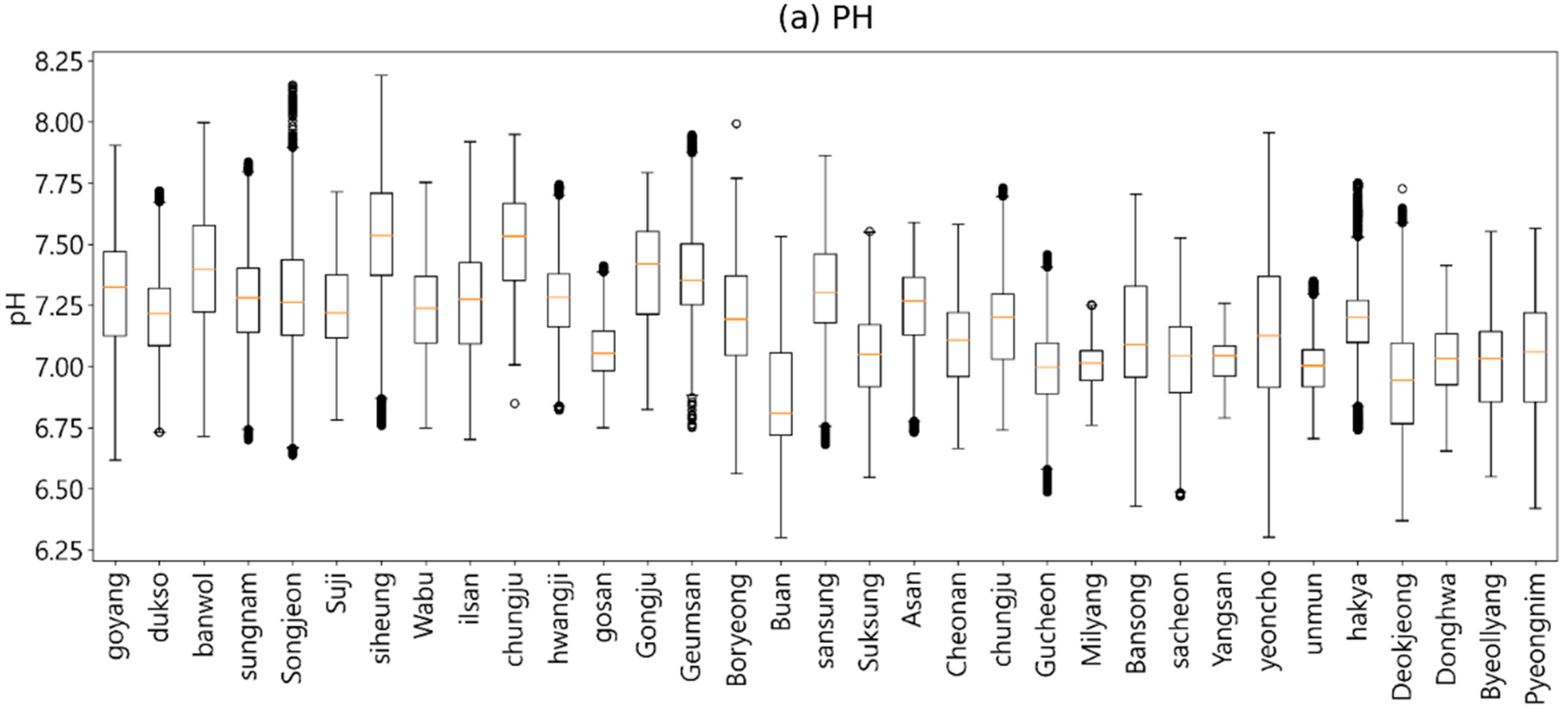
4. Exploratory Data Analysis
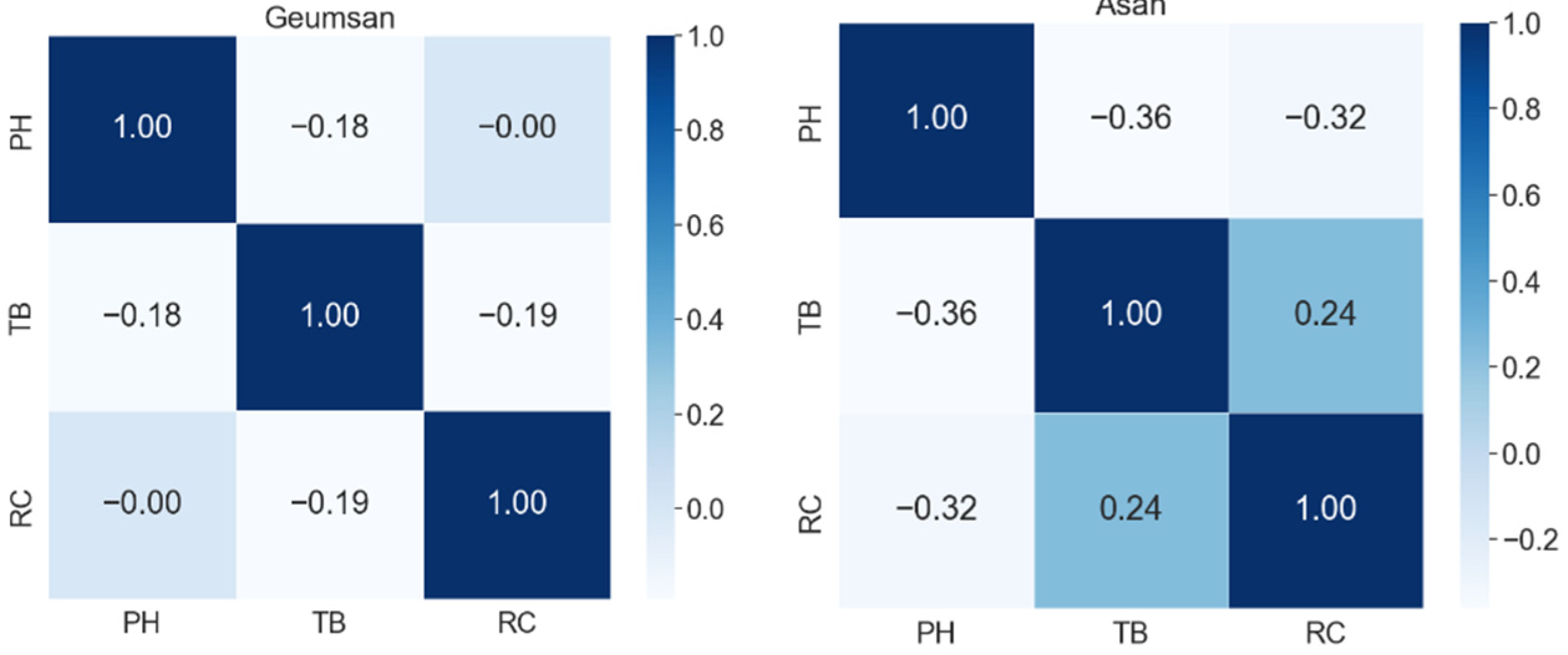
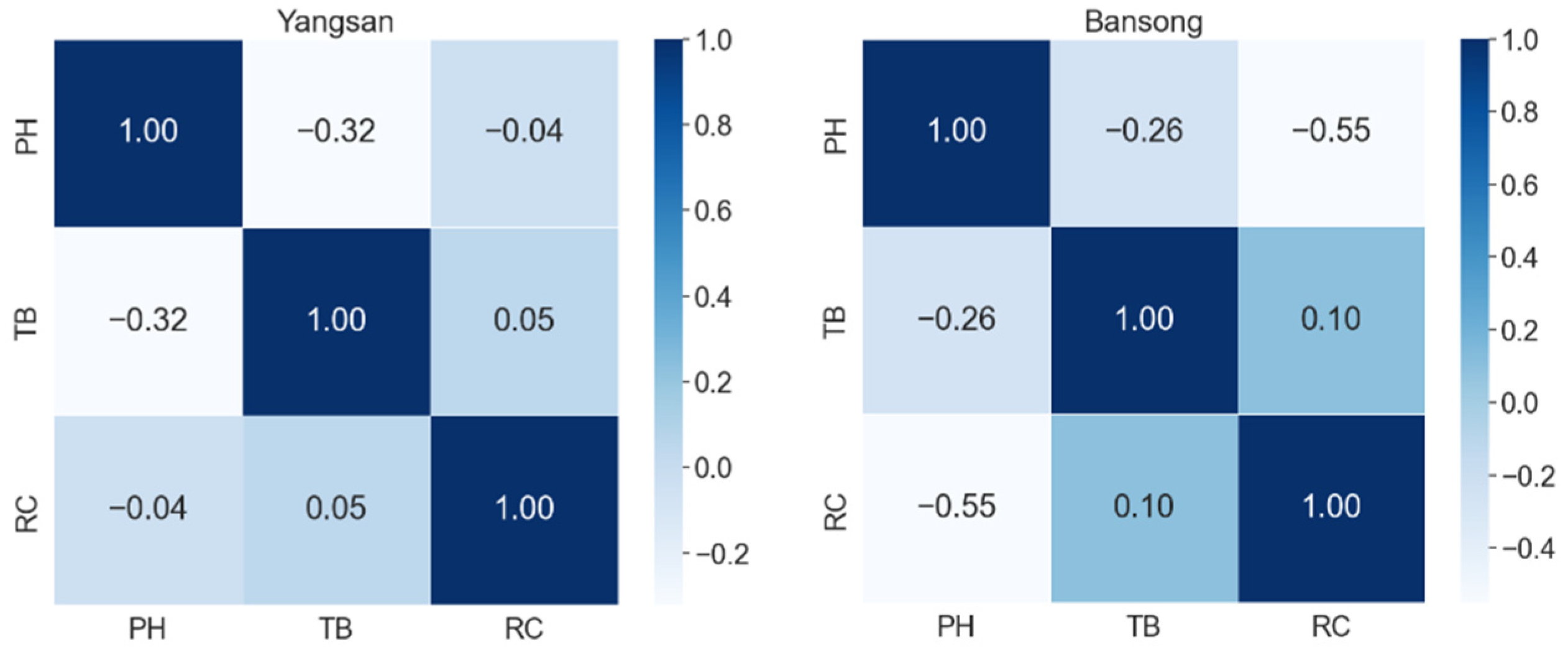
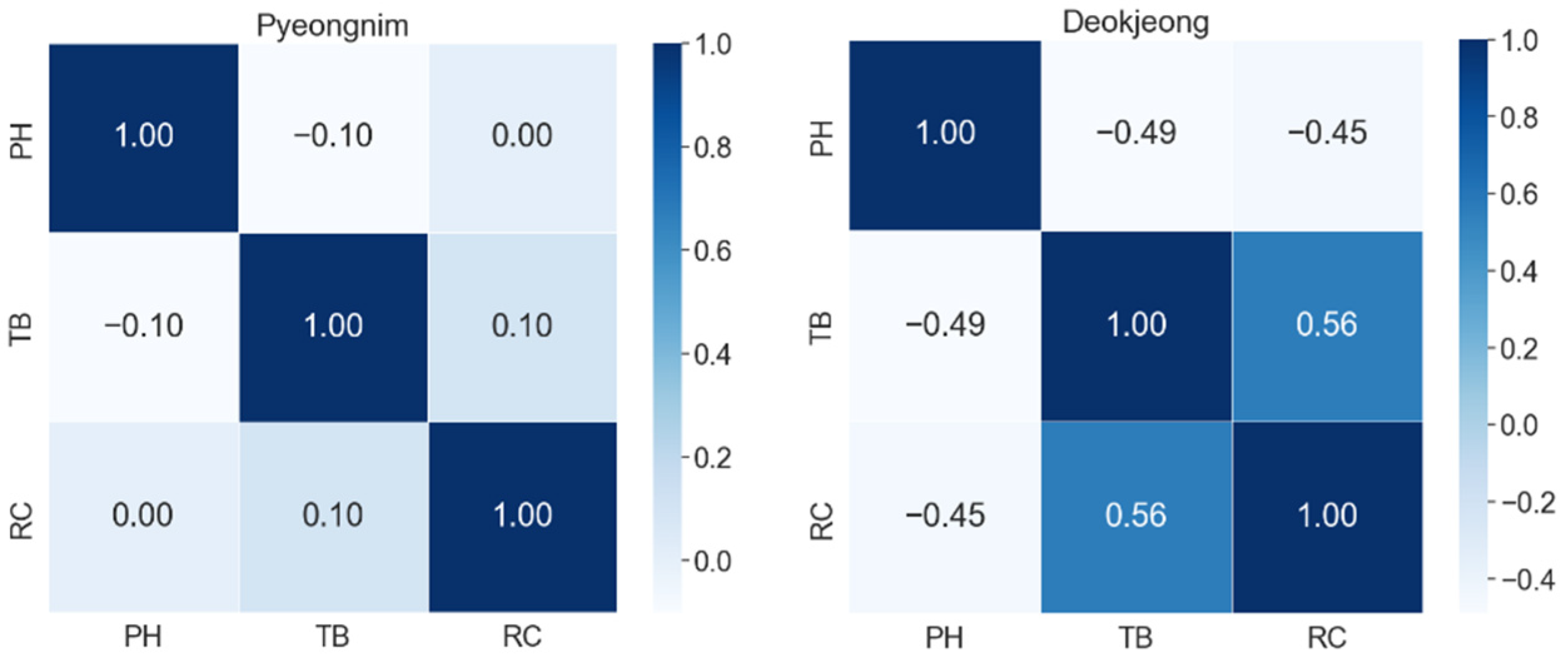
4.1. Correlation Analysis
4.2. Anomaly Analysis
5. Development of Tap Water Quality Prediction Models
5.1. Deep Learning-Based Methods
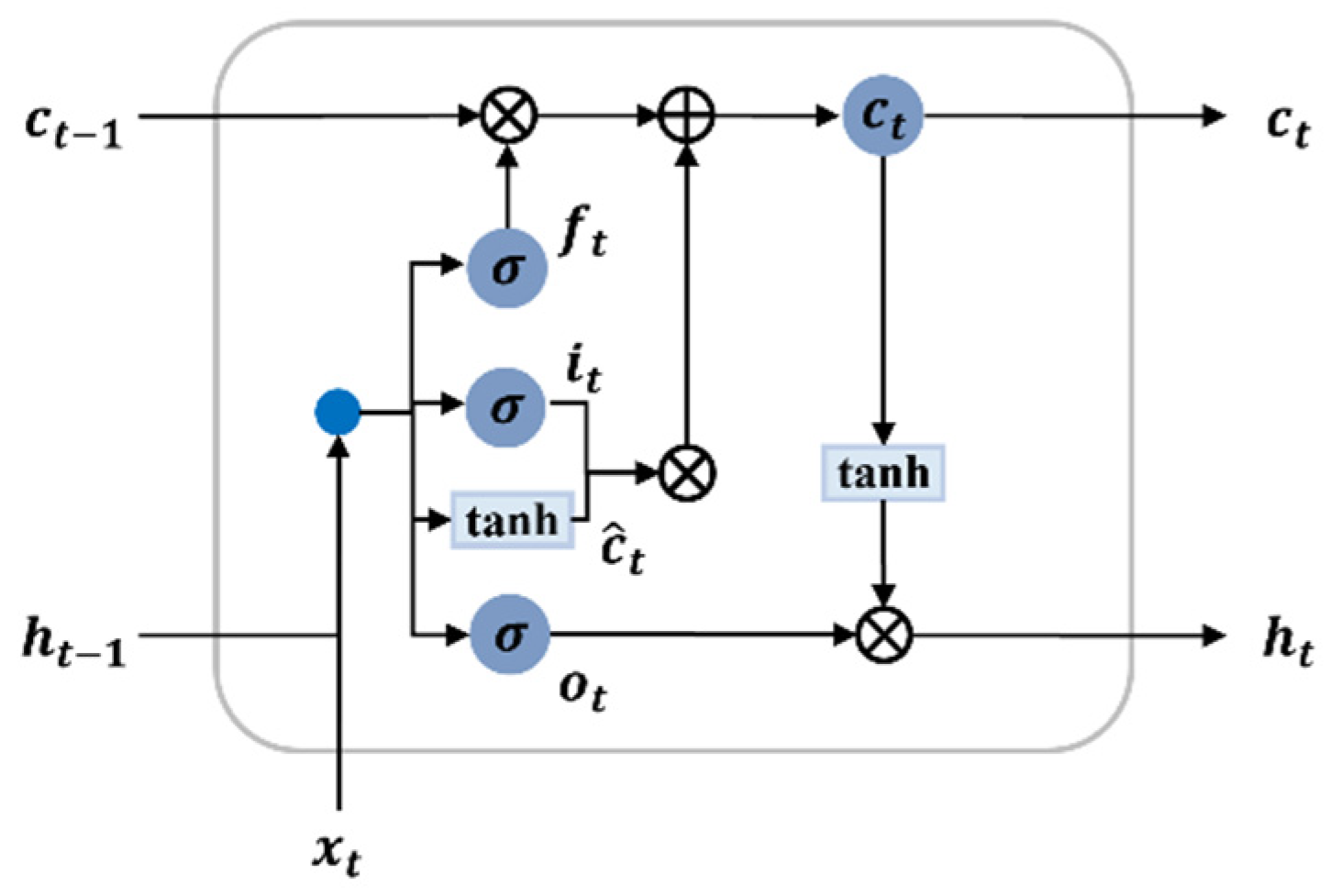
5.1.1. LSTM
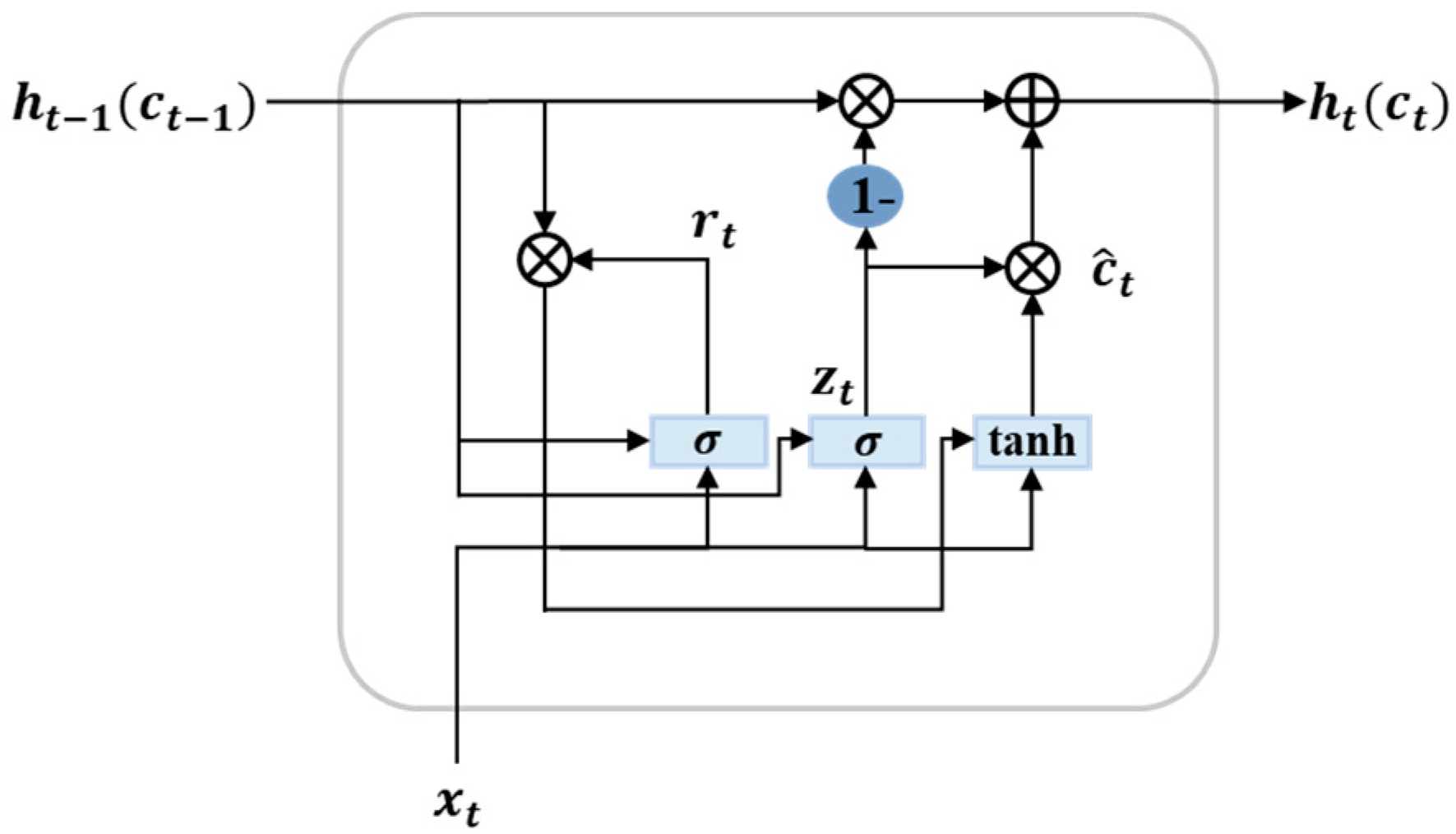
5.1.2. GRU
5.1.3. SCINet
5.2. Classical Statistical Methods
5.3. Tap Water Quality Prediction Models
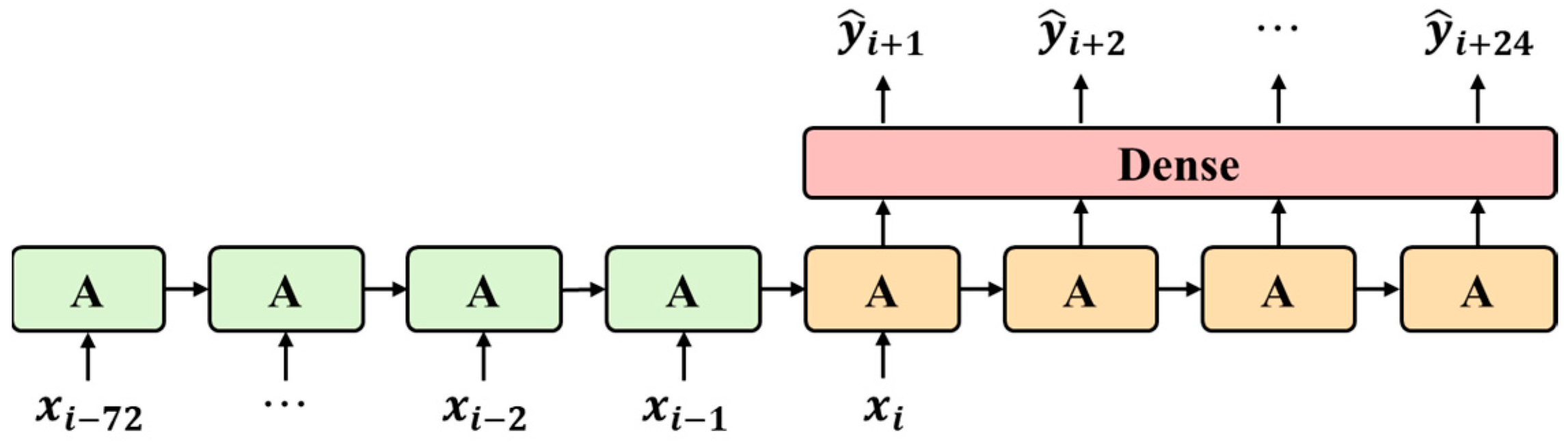
5.3.1. Architecture of LSTM, GRU, and SCINet Models
5.3.2. Performance Comparison with the ARIMA Model
6. Model Performance Evaluation
6.1. Evaluation Method
6.2. Evaluation Metrics
6.3. Cross-Validation
6.4. Model Construction and Running Time
6.5. Overall Prediction Accuracy in Major River Basins
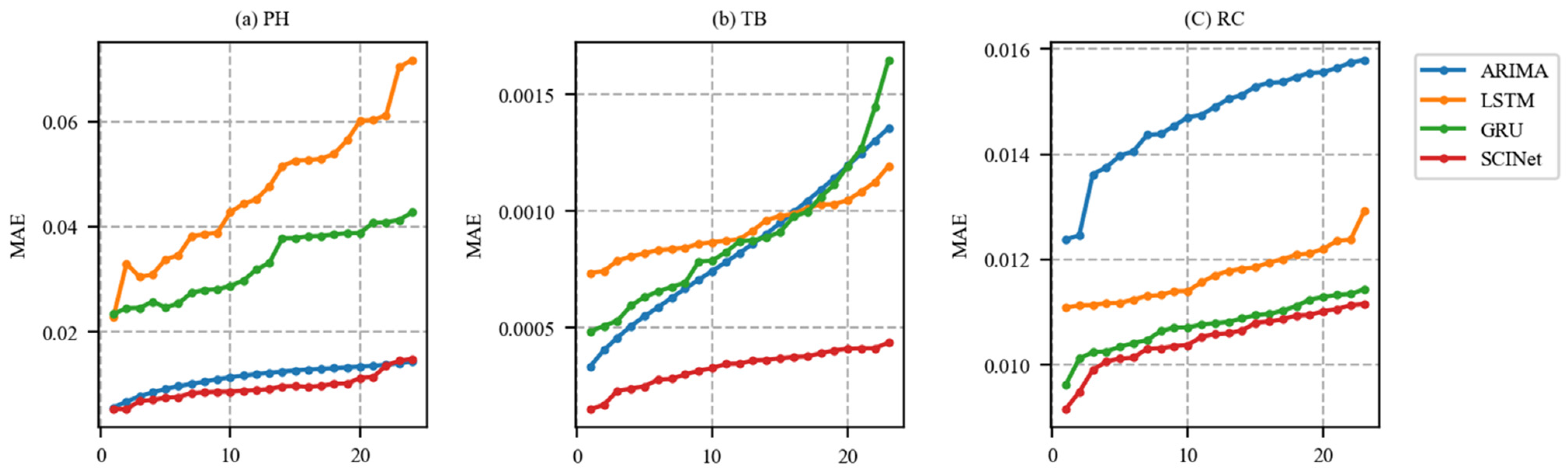
6.6. Long-Term Forecasting Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- National Waterworks Information System. Statistics of Waterworks 2020. Available online: https://www.waternow.go.kr/web/ssdoData?pMENUID=8 (accessed on 10 October 2022).
- Lee, C.W.; Lee, Y.J.; Park, J.S. Determination of the sensor placement for detection water quality problems in water supply systems. J. Korean Soc. Hazard Mitig. 2020, 20, 299–306. [Google Scholar] [CrossRef] [Green Version]
- Ryu, D.; Choi, T. Development of the Smart Device for Real Time Water Quality Monitoring. J. KIECS 2019, 14, 723–728. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, L.; Zhang, W.; Wang, X. Reliable model of reservoir water quality prediction based on improved ARIMA method. Environ. Eng. Sci. 2019, 36, 1041–1048. [Google Scholar] [CrossRef]
- Desye, B.; Belete, B.; Asfaw Gebrezgi, Z.; Terefe Reda, T. Efficiency of treatment plant and drinking water quality assessment from source to household, gondar city, Northwest Ethiopia. J. Environ. Public Health 2021, 2021, 9974064. [Google Scholar] [CrossRef] [PubMed]
- Yi, S.; Ryu, M.; Suh, J.; Kim, S.; Seo, S.; Kim, S.; Jang, S. K-water’s integrated water resources management system (K-HIT, K-water Hydro Intelligent Toolkit). Water Int. 2020, 45, 552–573. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, Y.; Xiao, F.; Wang, Y.; Sun, L. Water quality prediction method based on IGRA and LSTM. Water 2018, 10, 1148. [Google Scholar] [CrossRef] [Green Version]
- Dong, Q.; Lin, Y.; Bi, J.; Yuan, H. An integrated deep neural network approach for large-scale water quality time series prediction. In Proceedings of the 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC), Bari, Italy, 6–9 October 2019; pp. 3537–3542. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar] [CrossRef]
- Liu, M.; Zeng, A.; Xu, Z.; Lai, Q.; Xu, Q. Time series is a special sequence: Forecasting with sample convolution and interaction. arXiv 2021, arXiv:2106.09305. [Google Scholar] [CrossRef]
- Ahmed, U.; Mumtaz, R.; Anwar, H.; Shah, A.A.; Irfan, R.; García-Nieto, J. Efficient water quality prediction using supervised machine learning. Water 2019, 11, 2210. [Google Scholar] [CrossRef]
- Chen, K.; Chen, H.; Zhou, C.; Huang, Y.; Qi, X.; Shen, R.; Liu, F.; Zuo, M.; Zou, X.; Wang, J. Comparative analysis of surface water quality prediction performance and identification of key water parameters using different machine learning models based on big data. Water Res. 2020, 171, 115454. [Google Scholar] [CrossRef] [PubMed]
- El Bilali, A.; Taleb, A. Prediction of irrigation water quality parameters using machine learning models in a semi-arid environment. J. Saudi Soc. Agric. Sci. 2020, 19, 439–451. [Google Scholar] [CrossRef]
- Loos, S.; Shin, C.M.; Sumihar, J.; Kim, K.; Cho, J.; Weerts, A.H. Ensemble data assimilation methods for improving river water quality forecasting accuracy. Water Res. 2020, 171, 115343. [Google Scholar] [CrossRef] [PubMed]
- Solanki, A.; Agrawal, H.; Khare, K. Predictive analysis of water quality parameters using deep learning. Int. J. Comput. Appl. 2015, 125, 0975–8887. [Google Scholar] [CrossRef] [Green Version]
- Singha, S.; Pasupuleti, S.; Singha, S.S.; Singh, R.; Kumar, S. Prediction of groundwater quality using efficient machine learning technique. Chemosphere 2021, 276, 130265. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, X.; Smith, K.; Inial, G.; Liu, S.; Conil, L.B.; Pan, B. Integrating water quality and operation into prediction of water production in drinking water treatment plants by genetic algorithm enhanced artificial neural network. Water Res. 2019, 164, 114888. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.; Wang, J.; Sangaiah, A.K.; Xie, Y.; Yin, X. Analysis and prediction of water quality using LSTM deep neural networks in IoT environment. Sustainability 2019, 11, 2058. [Google Scholar] [CrossRef] [Green Version]
- Vadiati, M.; Rajabi Yami, Z.; Eskandari, E.; Nakhaei, M.; Kisi, O. Application of artificial intelligence models for prediction of groundwater level fluctuations: Case study (Tehran-Karaj alluvial aquifer). Environ. Monit. Assess. 2022, 194, 619. [Google Scholar] [CrossRef]
- Samani, S.; Vadiati, M.; Azizi, F.; Zamani, E.; Kisi, O. Groundwater Level Simulation Using Soft Computing Methods with Emphasis on Major Meteorological Components. Water Resour. Manag. 2022, 36, 3627–3647. [Google Scholar] [CrossRef]
- Peng, L.; Wu, H.; Gao, M.; Yi, H.; Xiong, Q.; Yang, L.; Cheng, S. TLT: Recurrent fine-tuning transfer learning for water quality long-term prediction. Water Res. 2022, 225, 119171. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, J.; Tan, W.; Sheng, Y.; Zhang, S.; Meng, L.; Zou, X.; Lin, H.; Sun, G.; Guo, P. Prediction of the Total Phosphorus Index Based on ARIMA. In Proceedings of the International Conference on Artificial Intelligence and Security, Qinghai, China, 15–20 July 2022; pp. 333–347. [Google Scholar]
- Zhang, L.; Xin, F. Prediction model of river water quality time series based on ARIMA model. In Proceedings of the International Conference on Geo-Informatics in Sustainable Ecosystem and Society, Handan, China, 21–25 November 2018; pp. 127–133. [Google Scholar]
- Chen, Y.; Zheng, B. What happens after the rare earth crisis: A systematic literature review. Sustainability 2019, 11, 1288. [Google Scholar] [CrossRef] [Green Version]
- Abbas, F.; Feng, D.; Habib, S.; Rahman, U.; Rasool, A.; Yan, Z. Short term residential load forecasting: An improved optimal nonlinear auto regressive (NARX) method with exponential weight decay function. Electronics 2018, 7, 432. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.H.; Song, G.W.; Im, Y.J.; Cho, M.S. Development of Predictive Time-Series Models for Anomaly Detection of Tap-Water Quality. KIISE Trans. Comput. Pract. 2022, 28, 465–473. [Google Scholar] [CrossRef]
- Fischer, T.; Krauss, C. Deep learning with long short-term memory networks for financial market predictions. Eur. J. Oper. Res. 2018, 270, 654–669. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Z.; Chen, W.; Wu, X.; Chen, P.C.; Liu, J. LSTM network: A deep learning approach for short-term traffic forecast. IET Intell. Transp. Syst. 2017, 11, 68–75. [Google Scholar] [CrossRef] [Green Version]
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar] [CrossRef]
- Shojaei, A.; Flood, I. Univariate modeling of the timings and costs of unknown future project streams: A case study. Int. J. Adv. Syst. Meas. 2018, 11, 36–46. [Google Scholar]





| Methods | Advantages | Disadvantages | Ref. |
|---|---|---|---|
| ARIMA 1 |
|
| [4,23,25,26] |
| LSTM 2 |
|
| [9,19] |
| GRU 3 |
|
| [10] |
| SCINet 4 |
|
| [11] |
| Dataset | Period | Observed Data |
|---|---|---|
| Modeling (training) | 1 January 2017–31 December 2021 | 4,338,576 |
| Model validation (out of sample) | 1 January 2022–31 May 2022 | 358,776 |
| Model Configuration | Han River | Geum River | Nakdong River | Seomjin River | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PH | TB | RC | PH | TB | RC | PH | TB | RC | PH | TB | RC | ||
| LSTM | Other parameter | Input node: 128; activation: ReLU; dropout rate: 0.2; loss: mean squared error; optimizer: Adam; learning rate: 0.001; epoch: 200 | |||||||||||
| Batch size | 34 | 24 | 39 | 58 | 47 | 32 | 34 | 47 | 39 | 34 | 36 | 39 | |
| GRU | Other parameter | Input node: 128; activation: ReLU; dropout rate: 0.2; loss: mean squared error; optimizer: Adam; learning rate: 0.001; epoch: 200 | |||||||||||
| Batch size | 21 | 56 | 37 | 21 | 56 | 55 | 21 | 39 | 37 | 21 | 39 | 53 | |
| SCINet | Other parameter | Hidden size: 8; stacks: 1; levels: 3; learning rate: 0.007; batch size: 64; dropout: 0.25 | |||||||||||
| Location | pH | Turbidity | Residual Chloride |
|---|---|---|---|
| Han River | ARIMA(2,1,2) | ARIMA(1,1,2) | ARIMA(2,1,1) |
| Geum River | ARIMA(1,1,3) | ARIMA(1,1,1) | ARIMA(1,1,3) |
| Nakdong River | ARIMA(0,1,2) | ARIMA(2,1,4) | ARIMA(1,1,2) |
| Seomjin River | ARIMA(0,1,2) | ARIMA(2,1,1) | ARIMA(1,1,2) |
| Parameters | LSTM | GRU | SCINet |
|---|---|---|---|
| Epochs | 100 | 100 | - |
| 200 | 200 | ||
| Batch size = 64, optimizer = Adam, learning rate = 0.001 | |||
| Accuracy (%) Time (min) | 98.75 | 98.75 | 99.58 |
| 98.71 | 98.73 | 99.55 | |
| 35 | 27 | 05 | |
| 27 | 25 | 05 | |
| Batch size = 128, optimizer = Adam, learning rate = 0.001 | |||
| Accuracy (%) Time (min) | 98.73 | 98.79 | 98.77 |
| 98.72 | 98.76 | 98.89 | |
| 33 | 23 | 08 | |
| 24 | 20 | 07 | |
| Dataset | Indicator | pH | Turbidity | Residual Chloride | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Method | ARIMA | LSTM | GRU | SCINet | ARIMA | LSTM | GRU | SCINet | ARIMA | LSTM | GRU | SCINet | |
| Han River | |||||||||||||
| Goyang | 0.99715 | 0.99281 | 0.99677 | 0.99719 | 0.98477 | 0.98042 | 0.98434 | 0.98719 | 0.98175 | 0.98174 | 0.98398 | 0.98592 | |
| Deokso | 0.99735 | 0.99408 | 0.99487 | 0.99728 | 0.96943 | 0.96656 | 0.96879 | 0.97133 | 0.97699 | 0.98065 | 0.98131 | 0.98096 | |
| Banwol | 0.98855 | 0.98508 | 0.98725 | 0.99021 | 0.97448 | 0.96857 | 0.97648 | 0.97183 | 0.88134 | 0.89947 | 0.91617 | 0.91870 | |
| Seongnam | 0.99795 | 0.98195 | 0.99649 | 0.99795 | 0.90435 | 0.89575 | 0.90255 | 0.91811 | 0.97942 | 0.97722 | 0.98173 | 0.98351 | |
| Songjeon | 0.99630 | 0.99501 | 0.99621 | 0.99658 | 0.93905 | 0.94128 | 0.92918 | 0.95416 | 0.95604 | 0.95201 | 0.84342 | 0.95865 | |
| Suji | 0.99739 | 0.97795 | 0.97802 | 0.99748 | 0.90199 | 0.90542 | 0.90691 | 0.92447 | 0.94664 | 0.96040 | 0.96033 | 0.96149 | |
| Siheung | 0.99712 | 0.98176 | 0.98499 | 0.99727 | 0.95739 | 0.90197 | 0.91485 | 0.96032 | 0.97480 | 0.95683 | 0.97566 | 0.98025 | |
| Wabu | 0.99421 | 0.99378 | 0.99430 | 0.99501 | 0.94281 | 0.92375 | 0.93642 | 0.94623 | 0.97491 | 0.98067 | 0.97963 | 0.98131 | |
| Ilsan | 0.99732 | 0.99161 | 0.99609 | 0.99717 | 0.97388 | 0.96456 | 0.97542 | 0.98011 | 0.97823 | 0.97697 | 0.97912 | 0.98051 | |
| Chungju | 0.99231 | 0.98184 | 0.99282 | 0.99364 | 0.94169 | 0.93293 | 0.92548 | 0.95039 | 0.94928 | 0.95354 | 0.95295 | 0.95361 | |
| Hwangji | 0.99660 | 0.99095 | 0.99424 | 0.99702 | 0.99336 | 0.96186 | 0.96387 | 0.98478 | 0.98226 | 0.96071 | 0.97667 | 0.98412 | |
| Geum River | |||||||||||||
| Gosan | 0.99752 | 0.98970 | 0.99637 | 0.99771 | 0.98707 | 0.96847 | 0.97202 | 0.98703 | 0.97598 | 0.98069 | 0.98072 | 0.98108 | |
| Gongju | 0.99886 | 0.98308 | 0.99877 | 0.99894 | 0.97053 | 0.96019 | 0.96550 | 0.97792 | 0.97619 | 0.97714 | 0.97672 | 0.98282 | |
| Geumsan | 0.99811 | 0.99553 | 0.99622 | 0.99809 | 0.98579 | 0.98648 | 0.98689 | 0.99071 | 0.96873 | 0.97041 | 0.97156 | 0.97236 | |
| Boryeong | 0.99211 | 0.99040 | 0.99352 | 0.99591 | 0.96668 | 0.97149 | 0.97171 | 0.97644 | 0.97996 | 0.98066 | 0.98293 | 0.98338 | |
| Buan | 0.99720 | 0.99646 | 0.99663 | 0.99693 | 0.91718 | 0.87630 | 0.86198 | 0.93233 | 0.96897 | 0.98066 | 0.97166 | 0.97172 | |
| Sanseong | 0.99481 | 0.99389 | 0.99558 | 0.99581 | 0.94637 | 0.94994 | 0.95021 | 0.95995 | 0.95793 | 0.95959 | 0.95926 | 0.96423 | |
| Seokseong | 0.98705 | 0.98603 | 0.98459 | 0.99352 | 0.95065 | 0.95701 | 0.95791 | 0.97192 | 0.94903 | 0.95834 | 0.95849 | 0.96211 | |
| Asan | 0.99718 | 0.98874 | 0.99658 | 0.99838 | 0.96649 | 0.96965 | 0.97130 | 0.97317 | 0.97105 | 0.97485 | 0.97517 | 0.97603 | |
| Cheonan | 0.99743 | 0.99676 | 0.99740 | 0.99851 | 0.98124 | 0.98108 | 0.98116 | 0.98317 | 0.98004 | 0.97380 | 0.97796 | 0.98036 | |
| Cheongju | 0.99855 | 0.98836 | 0.99090 | 0.99797 | 0.90400 | 0.93815 | 0.93884 | 0.93990 | 0.91801 | 0.94180 | 0.94242 | 0.95701 | |
| Nakdong River | |||||||||||||
| Gucheon | 0.99538 | 0.99373 | 0.99362 | 0.99479 | 0.96746 | 0.97397 | 0.95964 | 0.98098 | 0.93704 | 0.94804 | 0.94934 | 0.95019 | |
| Miryang | 0.99810 | 0.99443 | 0.99571 | 0.99810 | 0.96307 | 0.96014 | 0.96695 | 0.97329 | 0.97659 | 0.97299 | 0.97553 | 0.97674 | |
| Bansong | 0.99788 | 0.99710 | 0.99469 | 0.99815 | 0.95958 | 0.95697 | 0.94961 | 0.95831 | 0.95668 | 0.95346 | 0.96087 | 0.95867 | |
| Sacheon | 0.99497 | 0.99483 | 0.98901 | 0.99638 | 0.94955 | 0.94778 | 0.93498 | 0.96190 | 0.96047 | 0.96836 | 0.96693 | 0.97061 | |
| Yangsan | 0.99707 | 0.99387 | 0.99123 | 0.99697 | 0.97905 | 0.95178 | 0.96784 | 0.98221 | 0.97156 | 0.97288 | 0.97249 | 0.97368 | |
| Yeoncho | 0.99884 | 0.99774 | 0.99667 | 0.99876 | 0.89065 | 0.66796 | 0.66542 | 0.91065 | 0.97453 | 0.97500 | 0.97446 | 0.97658 | |
| Unmun | 0.99754 | 0.99688 | 0.99441 | 0.99780 | 0.97116 | 0.97312 | 0.97816 | 0.98062 | 0.95991 | 0.96270 | 0.96112 | 0.96670 | |
| Hakya | 0.99805 | 0.97437 | 0.99602 | 0.99769 | 0.95385 | 0.96060 | 0.95747 | 0.96079 | 0.95745 | 0.95546 | 0.96005 | 0.96117 | |
| Seomjin River | |||||||||||||
| Deokjeong | 0.99812 | 0.99071 | 0.99716 | 0.99792 | 0.97053 | 0.96247 | 0.97088 | 0.97457 | 0.96917 | 0.97497 | 0.97555 | 0.97590 | |
| Donghwa | 0.99604 | 0.98659 | 0.99198 | 0.99614 | 0.99537 | 0.98720 | 0.99090 | 0.99476 | 0.98204 | 0.98277 | 0.98280 | 0.98437 | |
| Byeollyang | 0.99886 | 0.99211 | 0.99878 | 0.99868 | 0.96725 | 0.97020 | 0.97592 | 0.97834 | 0.98765 | 0.98611 | 0.98749 | 0.98752 | |
| Pyeongnim | 0.99720 | 0.99581 | 0.99261 | 0.99710 | 0.96929 | 0.97500 | 0.97294 | 0.98278 | 0.95703 | 0.95713 | 0.96111 | 0.96322 | |
| Methods | Metrics | pH | Turbidity | Residual Chloride | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Horizon | Horizon | Horizon | ||||||||
| 6 | 12 | 24 | 6 | 12 | 24 | 6 | 12 | 24 | ||
| ARIMA | MAE | 0.0079 | 0.0095 | 0.0113 | 0.0004 | 0.0005 | 0.0008 | 0.0130 | 0.0137 | 0.0146 |
| RMSE | 0.0060 | 0.0073 | 0.0086 | 0.0001 | 0.0002 | 0.0003 | 0.0095 | 0.0099 | 0.0104 | |
| NSE | 0.9957 | 0.9937 | 0.9909 | 0.9783 | 0.9612 | 0.9124 | 0.6236 | 0.5801 | 0.5276 | |
| LSTM | MAE | 0.0490 | 0.0424 | 0.0469 | 0.0008 | 0.0008 | 0.0009 | 0.0113 | 0.0113 | 0.0117 |
| RMSE | 0.0505 | 0.0445 | 0.0493 | 0.0009 | 0.0010 | 0.0011 | 0.0151 | 0.0152 | 0.0158 | |
| NSE | 0.6895 | 0.6203 | 0.6255 | 0.9549 | 0.9371 | 0.9076 | 0.6015 | 0.5731 | 0.5343 | |
| GRU | MAE | 0.0272 | 0.0271 | 0.0329 | 0.0007 | 0.0007 | 0.0009 | 0.0099 | 0.0102 | 0.0107 |
| RMSE | 0.0285 | 0.0288 | 0.0348 | 0.0008 | 0.0009 | 0.0011 | 0.0134 | 0.0139 | 0.0146 | |
| NSE | 0.8758 | 0.8731 | 0.8657 | 0.9443 | 0.9450 | 0.8808 | 0.5099 | 0.4604 | 0.4069 | |
| SCINet | MAE | 0.0068 | 0.0077 | 0.0094 | 0.0002 | 0.0002 | 0.0003 | 0.0095 | 0.0099 | 0.0104 |
| RMSE | 0.0087 | 0.0099 | 0.0122 | 0.0004 | 0.0005 | 0.0006 | 0.0130 | 0.0136 | 0.0144 | |
| NSE | 0.9948 | 0.9932 | 0.9894 | 0.9801 | 0.9679 | 0.9485 | 0.6254 | 0.5884 | 0.5394 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Im, Y.; Song, G.; Lee, J.; Cho, M. Deep Learning Methods for Predicting Tap-Water Quality Time Series in South Korea. Water 2022, 14, 3766. https://doi.org/10.3390/w14223766
Im Y, Song G, Lee J, Cho M. Deep Learning Methods for Predicting Tap-Water Quality Time Series in South Korea. Water. 2022; 14(22):3766. https://doi.org/10.3390/w14223766
Chicago/Turabian StyleIm, Yunjeong, Gyuwon Song, Junghyun Lee, and Minsang Cho. 2022. "Deep Learning Methods for Predicting Tap-Water Quality Time Series in South Korea" Water 14, no. 22: 3766. https://doi.org/10.3390/w14223766








