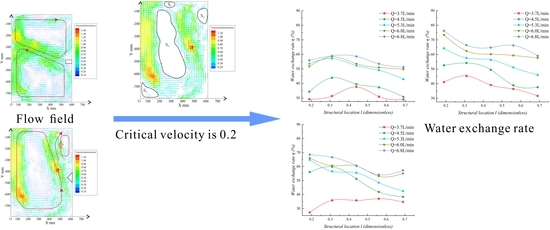
Experimental Study on the Influence of Barrier Structures on Water Renewal Capacity in Slow-Flow Water Bodies
Abstract
:1. Introduction
2. Experimental Methods
2.1. Experimental Facility and Instrumentation
2.2. Experimental Similarity Rule and Data Processing
2.3. Experimental Conditions
3. Experimental Results
3.1. Flow Field Distribution
3.2. Velocity Variation
3.3. Water Exchange Rate and Average Velocity
3.4. Information Entropy Analysis
4. Discussion
5. Conclusions
- There is a good positive correlation between η and average velocity (R2 = 0.94). Compared with η of 21.61–44.43% of water with no structures, placing barrier structures in the water can significantly improve the water exchange rate (up to twice its value). The results are of practical significance for designing and adjusting structures in water to improve water quality.
- The location parameter l changes the deflection mainstream velocity and direction, and its influence on η is non-monotonic. With the increase in l, circulation gradually appears and the area gradually expands. The deflection angle and the ratio of lateral velocity to streamwise velocity decrease, and the deflection effect of the structure weakens. The flow field for a large l (0.69) is similar to that with no structures. To achieve a higher η by placing structures in the water, the optimal l that corresponds to the triangular prism, rectangular column, and semi-cylinder is 0.2–0.3, 0.2–0.3, and 0.3–0.55, respectively.
- Structures have different effects on the flow field due to the different interaction surfaces, and the resistance effect of the rectangular column is the strongest. The deflection angles for the triangular prism and semi-cylinder are about 30°–45° at various flow rates, and these will be smaller for a larger l. The deflection angle of the rectangular column can be 90° for a smaller l, and the influence on the flow field is more obvious. In all cases, η for the rectangular column is relatively large, while that for the semi-cylinder is relatively small. A larger interaction area between the flow and structures generally results in a higher η.
- The flow rate Q is an important factor that affects water renewal capacity, changing the interaction intensity between the flow and structures. The average velocity and η increase with the increase in Q, and the flow rate that corresponds to the maximum η is generally 6.8 L/min.
- The information entropy H varies positively with the average velocity (R2 = 0.68). H for the rectangular column is larger, indicating that the rectangular column plays a more obvious role in adjusting the velocity composition, while H for the semi-cylinder is relatively smaller.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, N.; Cao, Y.Q.; Huang, L.Y. Repairing Technology and Protection Countermeasures for Slow-Flow Water Bodies Pollution. S. North Water Transf. Water Sci. Technol. 2008, 6, 101–103. (In Chinese) [Google Scholar] [CrossRef]
- Gao, J.; Dang, H.; Liu, L.; Kong, S. Pollution survey and countermeasures of urban slow-flow water body. Appl. Mech. Mater. 2012, 178–181, 661–665. [Google Scholar] [CrossRef]
- Olsen, Y.S.; Fraser, M.W.; Martin, B.C.; Pomeroy, A.; Lowe, R.; Pedersen, O.; Kendrick, G.A. In situ oxygen dynamics in rhizomes of the seagrass Posidonia sinuosa: Impact of light, water column oxygen, current speed and wave velocity. Mar. Ecol. Prog. Ser. 2018, 590, 67–77. [Google Scholar] [CrossRef] [Green Version]
- Peralta, G.; Brun, F.G.; Perez-Llorens, J.L.; Bouma, T.J. Direct effects of current velocity on the growth, morphometry and architecture of seagrasses: A case study on Zostera noltii. Mar. Ecol. Prog. Ser. 2006, 327, 135–142. [Google Scholar] [CrossRef] [Green Version]
- Ke, X.; Li, W. Hormonal correlates of seedling growth of two Vallisneria species growth at different current velocities. Hydrobiologia 2006, 556, 243–249. [Google Scholar] [CrossRef]
- Wu, C.Y.; Chen, W. Indicator system construction and health assessment of wetland ecosystem—Taking Hongze Lake Wetland, China as an example. Ecol. Indic. 2020, 112, 106164. [Google Scholar] [CrossRef]
- Chang, N.N.; Zhang, Q.H.; Wang, Q.; Luo, L.; Wang, X.C.C.; Xiong, J.Q.; Han, J.X. Current status and characteristics of urban landscape lakes in China. Sci. Total Environ. 2020, 712, 135669. [Google Scholar] [CrossRef]
- Ao, D.; Luo, L.; Dzakpase, M.; Chen, R.; Xue, T.; Wang, X.C.C. Replenishment of landscape water with reclaimed water: Optimization of supply scheme using transparency as an indicator. Ecol. Indic. 2018, 88, 503–511. [Google Scholar] [CrossRef]
- Hu, S.J.; Niu, Z.G.; Chen, Y.F.; Li, L.F.; Zhang, H.Y. Global wetlands: Potential distribution, wetland loss, and status. Sci. Total Environ. 2017, 586, 319–327. [Google Scholar] [CrossRef]
- Yuan, D.; Meng, X.; Duan, C.; Wei, Z.; Gao, W.; Chang, J.; Lv, X.; Pan, Y. Effects of water exchange rate on morphological and physiological characteristics of two submerged macrophytes from Erhai Lake. Ecol. Evol. 2018, 8, 12750–12760. [Google Scholar] [CrossRef]
- Wu, B.B.; Wang, G.Q.; Wang, Z.W.; Liu, C.M.; Ma, J.M. Integrated hydrologic and hydrodynamic modeling to assess water exchange in a data-scarce reservoir. J. Hydrol. 2017, 555, 15–30. [Google Scholar] [CrossRef]
- Gao, Q.F.; He, G.J.; Fang, H.W.; Bai, S.; Huang, L. Numerical simulation of water age and its potential effects on the water quality in Xiangxi Bay of Three Gorges Reservoir. J. Hydrol. 2018, 566, 484–499. [Google Scholar] [CrossRef]
- Pilotti, M.; Simoncelli, S.; Valerio, G. A simple approach to the evaluation of the actual water renewal time of natural stratified lakes. Water Resour. Res. 2014, 50, 2830–2849. [Google Scholar] [CrossRef]
- Huang, L.; Fang, H.W.; He, G.J.; Jiang, H.L.; Wang, C.H. Effects of internal loading on phosphorus distribution in the Taihu Lake driven by wind waves and lake currents. Environ. Pollut. 2016, 219, 760–773. [Google Scholar] [CrossRef]
- Huang, A.P.; Liu, X.B.; Peng, W.Q.; Dong, F.; Wang, W.J. Spatiotemporal Characteristics of Water Age in the Largest Freshwater Lake in China. In World Environmental and Water Resources Congress 2019: Hydraulics, Waterways, and Water Distribution System Analysis; American Society of Civil Engineers: Pittsburgh, PA, USA, 2019; pp. 376–381. [Google Scholar]
- Amorim, L.F.; Martins, J.R.S.; Nogueira, F.F.; Silva, F.P.; Duarte, B.P.S.; Magalhaes, A.A.B.; Vincon-Leite, B. Hydrodynamic and ecological 3D modeling in tropical lakes. SN Appl. Sci. 2021, 3, 444. [Google Scholar] [CrossRef]
- Peng, F.J.; Li, K.F.; Liang, R.F.; Li, X.T.; Zhang, P.; Yuan, Q.; Ji, Q.F.; Zhu, Z.X.; Wang, Y.M. Shallow lake water exchange process before and after water diversion projects as affected by wind field. J. Hydrol. 2021, 592, 125785. [Google Scholar] [CrossRef]
- Li, Y.P.; Archarya, K.; Yu, Z.B. Modeling impacts of Yangtze River water transfer on water ages in Lake Taihu, China. Ecol. Eng. 2011, 37, 325–334. [Google Scholar] [CrossRef]
- Djihouessi, M.B.; Aina, M.P. A review of hydrodynamics and water quality of Lake Nokoué: Current state of knowledge and prospects for further research. Reg. Stud. Mar. Sci. 2018, 18, 57–67. [Google Scholar] [CrossRef]
- Li, Y.P.; Tang, C.Y.; Zhu, J.T.; Pan, B.Z.; Anim, D.O.; Ji, Y.; Yu, Z.B.; Acharya, K. Parametric uncertainty and sensitivity analysis of hydrodynamic processes for a large shallow freshwater lake. Hydrol. Sci. J. 2015, 60, 1078–1095. [Google Scholar] [CrossRef]
- Huang, M.T.; Tian, Y. An Integrated Graphic Modeling System for Three-Dimensional Hydrodynamic and Water Quality Simulation in Lakes. Int. J. Geo-Inf. 2019, 8, 18. [Google Scholar] [CrossRef]
- You, X.Y.; Zhang, C.X. On improvement of water quality of a reservoir by optimizing water exchange. Environ. Prog. Sustain. 2017, 37, 399–409. [Google Scholar] [CrossRef]
- Luyiga, S.; Haande, S.; Semyalo, R.P.; Kizito, Y.S.; Miyingo-Kezimbira, A.; Brettum, P.; Solheim, A.L.; Odong, R.; Asio, S.M.; Jensen, K.H.; et al. How water exchange and seasonality affect the eutrophication of Murchison Bay, Lake Victoria. Limnologica 2015, 53, 60–73. [Google Scholar] [CrossRef]
- Zhu, W.; Wan, L.; Zhao, L.F. Effect of nutrient level on phytoplankton community structure in different water bodies. J. Environ. Sci. 2010, 22, 32–39. [Google Scholar] [CrossRef]
- Wu, Y.; Dai, R.; Xu, Y.F.; Han, J.G.; Li, P.P. Statistical assessment of water quality issues in Hongze Lake, China, related to the operation of a water diversion project. Sustainability 2018, 10, 1885. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R.Y.; Wu, B.S. Environmental Impacts of High Water Turbidity of the Niulan River to Dianchi Lake Water Diversion Project. J. Environ. Eng. 2020, 146, 05019006. [Google Scholar] [CrossRef]
- Min, P.; Song, W.W.; Zhang, P.; Shao, Y.X.; Li, L.; Pang, Y.; Wang, J.J.; Xu, Q. Research into the Eutrophication of an Artificial Playground Lake near the Yangtze River. Sustainability 2018, 10, 867. [Google Scholar] [CrossRef] [Green Version]
- Fomarelli, R.; Galelli, S.; Castelletti, A.; Antenucci, J.P.; Marti, C.L. An empirical modeling approach to predict and understand phytoplankton dynamics in a reservoir affected by interbasin water transfers. Water Resour. Res. 2013, 49, 3626–3641. [Google Scholar] [CrossRef]
- Gohari, A.; Eslamian, S.; Mirchi, A.; Abedi-Koupaei, J.; Bavani, A.M.; Madani, K. Water transfer as a solution to water shortage: A fix that can Backfire. J. Hydrol. 2013, 491, 23–39. [Google Scholar] [CrossRef]
- Tang, C.H.; Yi, Y.J.; Yang, Z.F.; Sun, J. Risk forecasting of pollution accidents based on an integrated Bayesian Network and water quality model for the South to North Water Transfer Project. Ecol. Eng. 2016, 96, 109–116. [Google Scholar] [CrossRef]
- Tang, C.Y.; He, C.; Li, Y.P.; Acharya, K. Diverse responses of hydrodynamics, nutrients and algal biomass to water diversion in a eutrophic shallow lake. J. Hydrol. 2021, 593, 125933. [Google Scholar] [CrossRef]
- Gao, X.P.; Xu, L.P.; Zhang, C. Estimating renewal timescales with residence time and connectivity in an urban man-made lake in China. Environ. Sci. Pollut. Res. Int. 2016, 23, 13973–13983. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.M.; Wang, S.; Fu, B.J.; Gao, G.Y.; Shen, Q. Ecological effects and potential risks of the water diversion project in the Heihe River Basin. Sci. Total Environ. 2018, 619–620, 794–803. [Google Scholar] [CrossRef] [PubMed]
- Kang, M.X.; Tian, Y.M.; Zhang, H.Y.; Wang, D.H. Relationship between Hydrodynamic Conditions and Water Quality in Landscape Water Body. IOP Conf. Ser. Earth Environ. Sci. 2018, 112, 012001. [Google Scholar] [CrossRef]
- Li, D.F.; He, W.X.; Lin, B.; Bai, F.Q.; Xie, F. Study and Analysis on Strengthening Hydrodynamic of Guazhuhu Lake Based on 2D-Numerical Simulation. In Proceedings of the 2017 6th International Conference on Energy and Environmental Protection (ICEEP 2017), Zhuhai, China, 29–30 June 2017. [Google Scholar] [CrossRef] [Green Version]
- Yan, L.I.; Guan, H.L.; Wang, Y. Effect of water diversion from the Yangtze River to Chang Lake on hydrodynamic characteristics and water quality of Chang Lake. IOP Conf. Ser. Earth Environ. Sci. 2018, 153, 062060. [Google Scholar] [CrossRef]
- Huang, J.C.; Yan, R.H.; Gao, J.F.; Zhang, Z.M.; Qi, L.Y. Modeling the impacts of water transfer on water transport pattern in Lake Chao, China. Ecol. Eng. 2016, 95, 271–279. [Google Scholar] [CrossRef]
- Dai, C.; Tan, Q.; Lu, W.T.; Liu, Y.; Guo, H.C. Identification of optimal water transfer schemes for restoration of a eutrophic lake: An integrated simulation-optimization method. Ecol. Eng. 2016, 95, 409–421. [Google Scholar] [CrossRef]
- Li, Y.P.; Tang, C.Y.; Wang, C.; Tian, W.; Pan, B.Z.; Hua, L.; Lau, J.; Yu, Z.B.; Archarya, K. Assessing and modeling impacts of different inter-basin water transfer routes on Lake Taihu and the Yangtze River, China. Ecol. Eng. 2013, 60, 399–413. [Google Scholar] [CrossRef]
- Xu, R.C.; Pang, Y.; Hu, Z.B.; Kaisam, J.P. Dual-Source Optimization of the “Diverting Water from the Yangtze River to Tai Lake (DWYRTL)” Project Based on the Euler Method. Complexity 2020, 2020, 3256596. [Google Scholar] [CrossRef]
- Song, W.W.; Xu, Q.; Fu, X.Q.; Zhang, P.; Pang, Y.; Song, D.H. Research on the Relationship between Water Diversion and Water Quality of Xuanwu Lake, China. Int. J. Environ. Res. Public Health 2018, 15, 1262. [Google Scholar] [CrossRef]
- You, A.J.; Hua, L. Optimization and Effect of Inner Water Diversion and Distribution in the West Lake of Hangzhou. IOP Conf. Ser. Earth Environ. Sci. 2019, 264, 012018. [Google Scholar] [CrossRef] [Green Version]
- Song, W.W.; Fu, X.Q.; Pang, Y.; Song, D.H.; Xu, Q.; Zhang, P. Research on Water Environment Regulation of Artificial Playground Lake Interconnected Yangtze River. Int. J. Environ. Res. Public Health 2018, 15, 2110. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, M.X.; Dolatshah, A.; Zhu, W.L.; Yu, G.L. Case Study on Water Quality Improvement in Xihu Lake through Diversion and Water Distribution. Water 2018, 10, 333. [Google Scholar] [CrossRef] [Green Version]
- Jensen, B.; Carstensen, S.; Christensen, E.D. Mixing of stratified flow around bridge piers in steady current. J. Hydraul. Eng. 2018, 144, 04018041. [Google Scholar] [CrossRef] [Green Version]
- Leli, I.T.; Stevaux, J.C. Lake-islands: A distinct morphology of river systems. J. S. Am. Earth Sci. 2021, 111, 103424. [Google Scholar] [CrossRef]
- Pandey, M.; Sharma, P.K.; Ahmad, Z.; Singh, U.K.; Karna, N. Three Dimensional Velocity Measurements around Bridge Piers in Gravel Bed. Mar. Georesour. Geotechnol. 2017, 36, 663–676. [Google Scholar] [CrossRef]
- Gautam, P.; Eldho, T.I.; Mazumder, B.S.; Behera, M.R. Experimental Study of Flow and Turbulence characteristics around Simple and Complex Piers using PIV. Exp. Therm. Fluid Sci. 2018, 100, 193–206. [Google Scholar] [CrossRef]
- Namaee, M.R.; Sui, J. Velocity profiles and turbulence intensities around side-by-side bridge piers under ice-covered flow condition. J. Hydrol. Hydromech. 2020, 68, 70–82. [Google Scholar] [CrossRef] [Green Version]
- Izadinia, E.; Heidarpour, M.; Schleiss, A.J. Investigation of turbulence flow and sediment entrainment around a bridge pier. Stoch. Environ. Res. Risk Asses. 2013, 27, 1303–1314. [Google Scholar] [CrossRef] [Green Version]
- Guo, X.F.; Chen, C.H.; Tang, J.J. Numerical simulation of the hydrodynamic effects of an artificial island. Fresenius Environ. Bull. 2018, 27, 2671–2682. [Google Scholar]
- Yan, H.K.; Wang, N.; Yu, T.L.; Song, N.Q. Hydrodynamic behavior and the effects of water pollution from Dalian’s large-scale offshore airport island in Jinzhou Bay, China. J. Waterw. Port Coast. Ocean Eng. 2015, 141, 05014003. [Google Scholar] [CrossRef]
- Liu, T.; Liu, Y.H.; Hou, Z.Q. Numerical Study on Influence of Water Exchange for Artificial Island Group. IOP Conf. Ser. Earth Environ. Sci. 2018, 171, 012016. [Google Scholar] [CrossRef]
- Branson, P.M.; Ghisalberti, M.; Ivey, G.N. Three-dimensionality of shallow island wakes. Environ. Fluid Mech. 2019, 19, 1393–1416. [Google Scholar] [CrossRef] [Green Version]
- Carnacina, I.; Leonardi, N.; Pagliara, S. Characteristics of Flow Structure around Cylindrical Bridge Piers in Pressure-Flow Conditions. Water 2019, 11, 2240. [Google Scholar] [CrossRef] [Green Version]
- Hou, L.; Wang, J.X.; Liang, Y. Study on the application of distortion similarity theory to fishway model test. Eng. J. Wuhan Unv. 2021, 54, 298–306. [Google Scholar] [CrossRef]
- Zhang, B.M. Distorted scale model and scale effects. In Proceedings of the International Symposium on Hydraulic Research in Nature and Laboratory Proceedings, Wuhan, China, 17–20 November 1992; pp. 7–10. [Google Scholar]
- Bansal, M.K. Dispersion in Natural Streams. J. Hydraul. Div. 1971, 97, 1867–1886. [Google Scholar] [CrossRef]
- Rulli, M.C.; Rosso, R. Modeling catchment erosion after wildfires in the San Gabriel Mountains of southern California. Geophys. Res. Lett. 2005, 32, 312–321. [Google Scholar] [CrossRef]
- Seo, H.; Kim, K.C. Experimental study on flow and turbulence characteristics of bubbly jet with low void fraction. Int. J. Multiph. Flow 2021, 142, 103738. [Google Scholar] [CrossRef]
- Yang, P.; Zhang, H.; Wang, Y.; Wang, Y.; Wang, Y. Overland flow velocities measured using a high-resolution particle image velocimetry system. J. Hydrol. 2020, 590, 125225. [Google Scholar] [CrossRef]
- Liu, D.M.; Ma, L.B.; Li, N.; Zhao, Y.Z.; Cheng, H. Experimental research on flow field of high head pump turbine based on PIV test. IOP Conf. Ser. Earth Environ. Sci. 2021, 627, 012016. [Google Scholar] [CrossRef]
- Bai, R.N.; Zhu, D.J.; Chen, H.; Li, D.X. Laboratory Study of Secondary Flow in an Open Channel Bend by Using PIV. Water 2019, 11, 659. [Google Scholar] [CrossRef]
- Xiong, J.L.; Shen, J.; Qin, Q.B.; Du, J.B. Water exchange and its relationships with external forcings and residence time in Chesapeake Bay. J. Mar. Syst. 2020, 215, 103497. [Google Scholar] [CrossRef]
- Qi, H.D.; Lu, J.Z.; Chen, X.L.; Sauvage, S.; Sanchez-Perez, J.M. Water age prediction and its potential impacts on water quality using a hydrodynamic model for Poyang Lake, China. Environ. Sci. Pollut. Res. 2016, 23, 13327–13341. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.P.; Xu, L.P.; Zhang, C. Modelling the effect of water diversion projects on renewal capacity in an urban artificial lake in China. J. Hydroinform. 2015, 17, 990–1002. [Google Scholar] [CrossRef]
- Jiang, X.H.; Liu, C.M. Water renewal time of the Yellow River mainstream based on reservoir action. J. Geogr. Sci. 2013, 23, 113–122. [Google Scholar] [CrossRef]
- Hua, Z.L.; Gu, L.; Liu, X.D. Improving water exchange rate of shallow lakes through water diversion works. Water Resour. Protect. 2009, 25, 9–17. (In Chinese) [Google Scholar]
- Yao, Y.M.; Peng, H.; Du, Y.J.; Liu, L. Numerical Study on water exchange in Xiangshangang Bay. Acta Ocean. Sin. 2014, 36, 126–130. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, W.X. Study on Hydrodynamic and Water Exchange Characteristics of Caofeidian Wetland. Shijiazhuang Tiedao Univ. 2019. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, Y.M.; Zhang, Y.C.; Zhang, L.J.; Gao, Y.X.; Zhao, Y. The influence of lake hydrodynamics on blue algal growth. China Environ. Sci. 2007, 27, 707–711. (In Chinese) [Google Scholar]
- Mitrovic, S.M.; Hardwick, L.; Dorani, F. Use of flow management to mitigate cyanobacterial blooms in the Lower Darling River, Australia. J. Plankton Res. 2011, 33, 229–241. [Google Scholar] [CrossRef]
- Yan, B.L.; Lin, H.J. Research on Diversion Water Scheme of Improving Environmental Water Quality in the Hangjiahu Area. China Rural. Water Hydropower 2008, 9, 33–35. (In Chinese) [Google Scholar]
- Yan, Y.X.; Jiang, X.X.; Ruan, X.H.; Li, Y.; Zhao, Z.H.; Ni, L.X.; Zhang, Y. Water pollution characteristics and control measures in cities of plain river network area. Water Resour. Prot. 2008, 25, 1–3. (In Chinese) [Google Scholar]
- Engelmann, L.; Ihme, M.; Wlokas, I.; Kempf, A. Towards the Suitability of Information Entropy as an LES Quality Indicator. Flow Turbul. Combust. 2021, 108, 353–385. [Google Scholar] [CrossRef]
- Engelmann, L.; Wlokas, I.; Kempf, A.M. What can we learn from information-entropy about turbulence and Large-Eddy-Simulation? PAMM 2019, 19, e201900253. [Google Scholar] [CrossRef]
- Yan, Y.; Wang, J. Information Entropy Embedded Back Propagation Neural Network Approach for Debris Flows Hazard Assessment. IOP Conf. Ser. Earth Environ. Sci. 2020, 453, 012015. [Google Scholar] [CrossRef]
- Akundi, A.; Smith, E.; Tseng, T.L. Information entropy applied to software based control flow graphs. Int. J. Syst. Assur. Eng. Manag. 2018, 9, 1080–1091. [Google Scholar] [CrossRef]
- Shannon, C.E.; Weaver, W.; Burks, A.W. The Mathematical Theory of Communication; Wiley: New York, NY, USA, 1951. [Google Scholar]
- Murtaza, G.; Hashmi, H.M.; Naeem, U.A.; Khan, D.; Ahmad, N. Effect of bridge pier shape on scour depth at uniform single bridge pier. Mehran Univ. Res. J. Eng. Technol. 2018, 37, 539–544. [Google Scholar] [CrossRef]
- Zhang, X.Q.; Wang, T.; Lu, X.B. Influence of bridge piers shapes on the flow of the lower Yellow River. Water Pract. Technol. 2021, 16, 661–680. [Google Scholar] [CrossRef]













| Experiment Conditions | Q (L/min) | l | Structural Shape | Experiment Conditions | Q (L/min) | l | Structural Shape |
|---|---|---|---|---|---|---|---|
| R1-0-0 | 3.7 | — | — | R3-3-2 | T | ||
| R1-1-1 | 0.19 | R | R3-3-3 | C | |||
| R1-1-2 | T | R3-4-1 | 0.56 | R | |||
| R1-1-3 | C | R3-4-2 | T | ||||
| R1-2-1 | 0.31 | R | R3-4-3 | C | |||
| R1-2-2 | T | R3-5-1 | 0.69 | R | |||
| R1-2-3 | C | R3-5-2 | T | ||||
| R1-3-1 | 0.44 | R | R3-5-3 | C | |||
| R1-3-2 | T | R4-0-0 | 6.0 | — | — | ||
| R1-3-3 | C | R4-1-1 | 0.19 | R | |||
| R1-4-1 | 0.56 | R | R4-1-2 | T | |||
| R1-4-2 | T | R4-1-3 | C | ||||
| R1-4-3 | C | R4-2-1 | 0.31 | R | |||
| R1-5-1 | 0.69 | R | R4-2-2 | T | |||
| R1-5-2 | T | R4-2-3 | C | ||||
| R1-5-3 | C | R4-3-1 | 0.44 | R | |||
| R2-0-0 | 4.5 | — | — | R4-3-2 | T | ||
| R2-1-1 | 0.19 | R | R4-3-3 | C | |||
| R2-1-2 | T | R4-4-1 | 0.56 | R | |||
| R2-1-3 | C | R4-4-2 | T | ||||
| R2-2-1 | 0.31 | R | R4-4-3 | C | |||
| R2-2-2 | T | R4-5-1 | 0.69 | R | |||
| R2-2-3 | C | R4-5-2 | T | ||||
| R2-3-1 | 0.44 | R | R4-5-3 | C | |||
| R2-3-2 | T | R5-0-0 | 6.8 | — | — | ||
| R2-3-3 | C | R5-1-1 | 0.19 | R | |||
| R2-4-1 | 0.56 | R | R5-1-2 | T | |||
| R2-4-2 | T | R5-1-3 | C | ||||
| R2-4-3 | C | R5-2-1 | 0.31 | R | |||
| R2-5-1 | 0.69 | R | R5-2-2 | T | |||
| R2-5-2 | T | R5-2-3 | C | ||||
| R2-5-3 | C | R5-3-1 | 0.44 | R | |||
| R3-0-0 | 5.3 | — | — | R5-3-2 | T | ||
| R3-1-1 | 0.19 | R | R5-3-3 | C | |||
| R3-1-2 | T | R5-4-1 | 0.56 | R | |||
| R3-1-3 | C | R5-4-2 | T | ||||
| R3-2-1 | 0.31 | R | R5-4-3 | C | |||
| R3-2-2 | T | R5-5-1 | 0.69 | R | |||
| R3-2-3 | C | R5-5-2 | T | ||||
| R3-3-1 | 0.44 | R | R5-5-3 | C |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, L.; Yang, X.; Yang, Y.-b.; Zhou, H.; Jiang, R.; Cai, J.; Li, N.; Wang, J. Experimental Study on the Influence of Barrier Structures on Water Renewal Capacity in Slow-Flow Water Bodies. Water 2022, 14, 3757. https://doi.org/10.3390/w14223757
Pan L, Yang X, Yang Y-b, Zhou H, Jiang R, Cai J, Li N, Wang J. Experimental Study on the Influence of Barrier Structures on Water Renewal Capacity in Slow-Flow Water Bodies. Water. 2022; 14(22):3757. https://doi.org/10.3390/w14223757
Chicago/Turabian StylePan, Longyang, Xingguo Yang, Yeong-bin Yang, Hongwei Zhou, Rui Jiang, Junyi Cai, Niannian Li, and Jiamei Wang. 2022. "Experimental Study on the Influence of Barrier Structures on Water Renewal Capacity in Slow-Flow Water Bodies" Water 14, no. 22: 3757. https://doi.org/10.3390/w14223757
APA StylePan, L., Yang, X., Yang, Y.-b., Zhou, H., Jiang, R., Cai, J., Li, N., & Wang, J. (2022). Experimental Study on the Influence of Barrier Structures on Water Renewal Capacity in Slow-Flow Water Bodies. Water, 14(22), 3757. https://doi.org/10.3390/w14223757