Daily Rhythms and Oxygen Balance in the Hypersaline Lake Moynaki (Crimea)
Abstract
:1. Introduction
2. Materials and Methods
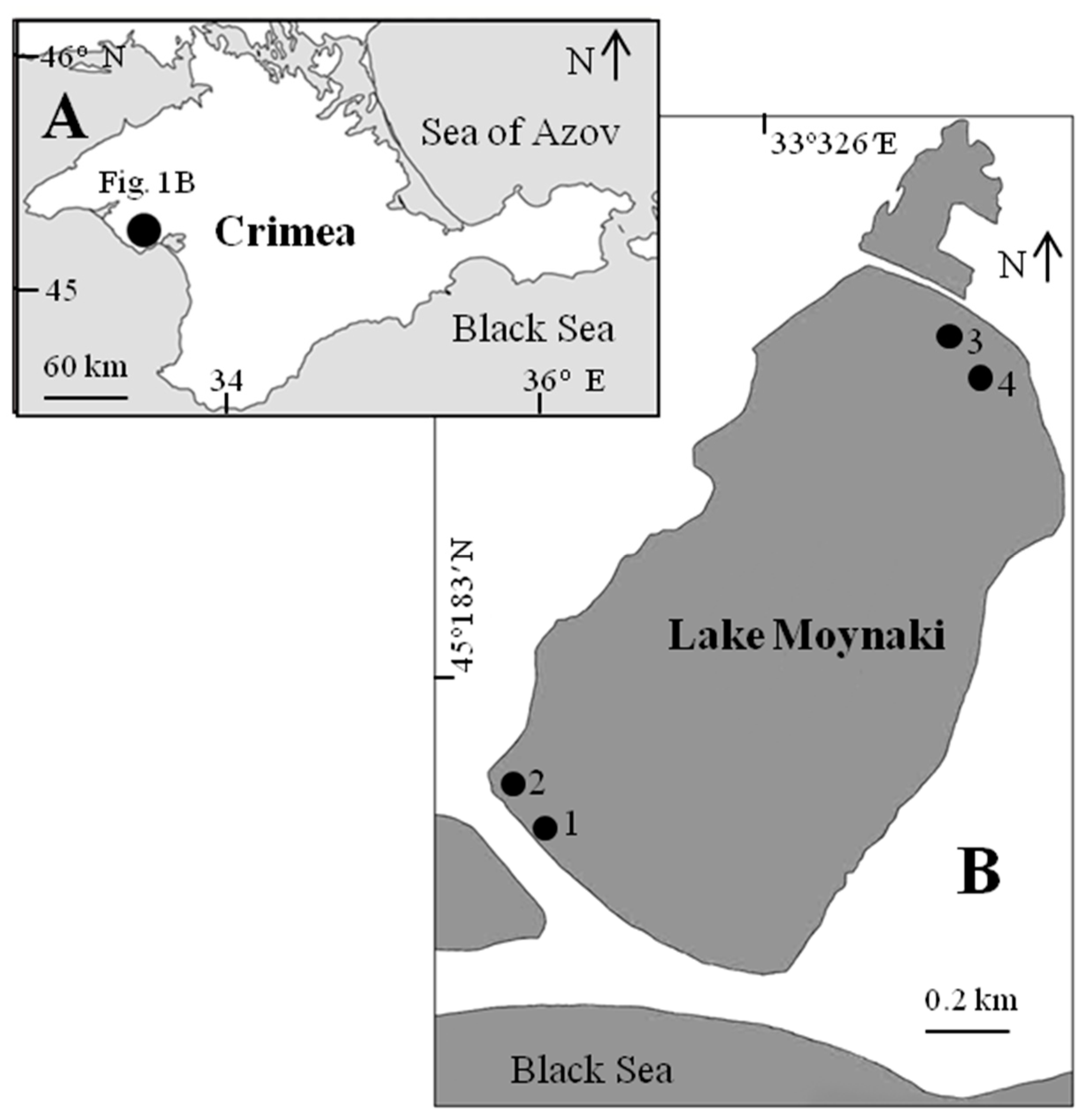
2.1. Study Area
2.2. Methods
2.3. Data Processing
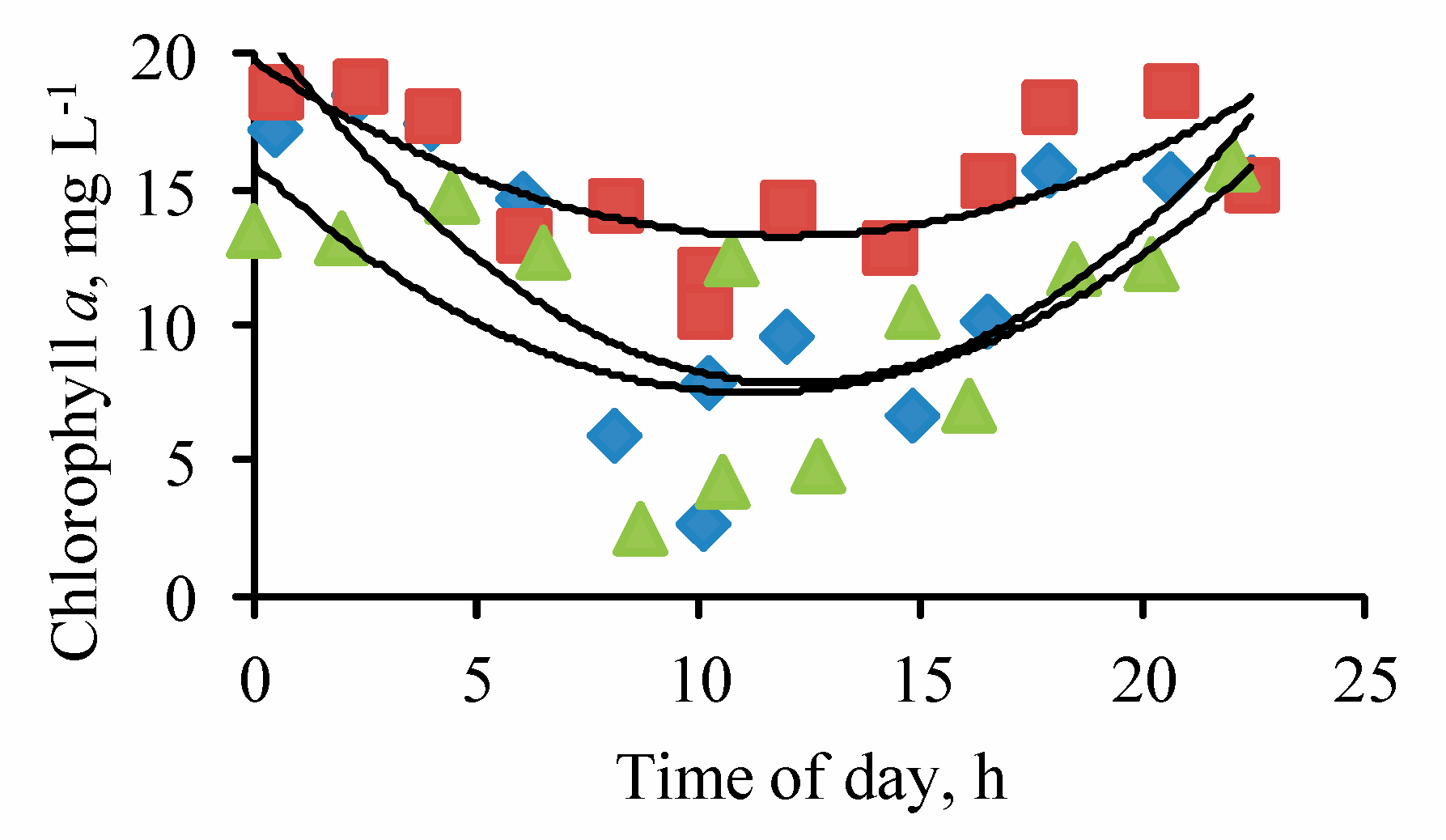
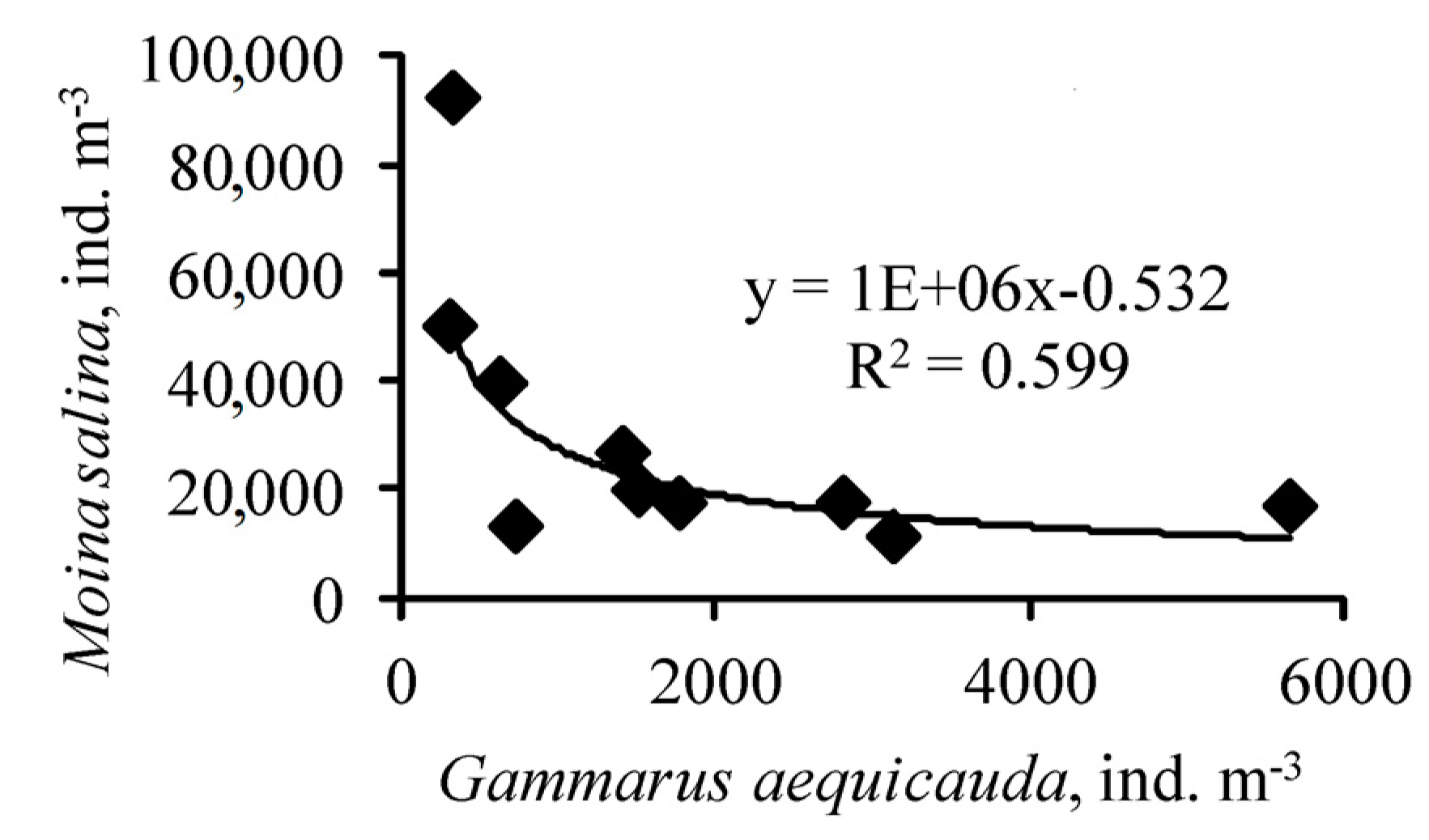
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Holling, C.S. Understanding the complexity of economic, ecological, and social systems. Ecosystems 2001, 4, 390–405. [Google Scholar] [CrossRef]
- Green, D.G.; Sadedin, S. Interactions matter—Complexity in landscapes and ecosystems. Ecol. Complex. 2005, 2, 117–130. [Google Scholar] [CrossRef]
- Allen, C.R.; Angeler, D.G.; Garmestani, A.S.; Gunderson, L.H.; Holling, C.S. Panarchy: Theory and application. Ecosystems 2014, 17, 578–589. [Google Scholar] [CrossRef] [Green Version]
- Shadrin, N.V. The alternative saline lake ecosystem states and adaptive environmental management. J. Oceanol. Limnol. 2018, 36, 2010–2017. [Google Scholar] [CrossRef]
- Stross, R.G.; Chisholm, S.W.; Downing, T.A. Causes of daily rhythms in photosynthetic rates of phytoplankton. Biol. Bull. 1973, 145, 200–209. [Google Scholar] [CrossRef]
- Andrew, T.E.; Cabrera, S.; Montecino, V. Diurnal changes in zooplankton respiration rates and the phytoplankton activity in two Chilean lakes. Hydrobiologia 1989, 175, 121–135. [Google Scholar] [CrossRef]
- Forsberg, B.R.; Melack, J.M.; Richey, J.E.; Pimentel, T.P. Regional and seasonal variability in planktonic photosynthesis and planktonic community respiration in Amazon floodplain lakes. Hydrobiologia 2017, 800, 187–206. [Google Scholar] [CrossRef]
- Baxa, M.; Musil, M.; Kummel, M.; Hanzlík, P.; Tesařová, B.; Pechar, L. Dissolved oxygen deficits in a shallow eutrophic aquatic ecosystem (fishpond)–Sediment oxygen demand and water column respiration alternately drive the oxygen regime. Sci. Total Environ. 2021, 766, 142647. [Google Scholar] [CrossRef]
- Winberg, G.G.; Yarovitsina, L.I. Daily fluctuations in the amount of dissolved oxygen as a method for measuring the value of the primary production of water bodies. Tr. Limnol. Stantsii V Kosine 1939, 22, 128–143. (In Russian) [Google Scholar]
- Winberg, G.G. On the measurement of the rate of exchange of oxygen between a water basin and atmosphere. CR Acad. Sci. URSS 1940, 26, 666–669. [Google Scholar]
- Staehr, P.A.; Bade, D.; Van de Bogert, M.C.; Koch, G.R.; Williamson, C.; Hanson, P.; Cole, J.J.; Kratz, T. Lake metabolism and the diel oxygen technique: State of the science. Limnol. Oceanogr. Methods 2010, 8, 628–644. [Google Scholar] [CrossRef]
- Lovett, G.M.; Cole, J.J.; Pace, M.L. Is net ecosystem production equal to ecosystem carbon accumulation? Ecosystems 2006, 9, 152–155. [Google Scholar] [CrossRef]
- Hall, R.O., Jr.; Beaulieu, J.J. Estimating autotrophic respiration in streams using daily metabolism data. Freshw. Sci. 2013, 32, 507–516. [Google Scholar] [CrossRef]
- Bas-Silvestre, M.; Quintana, X.D.; Compte, J.; Gascón, S.; Boix, D.; Antón-Pardo, M.; Obrador, B. Ecosystem metabolism dynamics and environmental drivers in Mediterranean confined coastal lagoons. Estuar. Coast. Shelf Sci. 2020, 245, 106989. [Google Scholar] [CrossRef]
- Tolkamp, H.H.; Van Vierssen, W.; Knoben, R.A. Oxygen variation in Dutch water types in relation to biological water quality criteria. Int. Ver. Theor. Angew. Limnol. Verh. 1991, 24, 2095–2099. [Google Scholar] [CrossRef]
- Witek, Z.; Jarosiewicz, A.; Cyra, M. Peculiarities of pelagic community metabolism in small dimictic lakes as demonstrated by daily changes of oxygen vertical distribution. Pol. J. Environ. Stud. 2013, 22, 933–943. [Google Scholar]
- Kragh, T.; Andersen, M.R.; Sand-Jensen, K. Profound afternoon depression of ecosystem production and nighttime decline of respiration in a macrophyte-rich, shallow lake. Oecologia 2017, 185, 157–170. [Google Scholar] [CrossRef]
- Palshin, N.I.; Efremova, T.V.; Zdorovennova, G.E.; Gavrilenko, G.G.; Zdorovennov, R.E.; Terzhevik, A.Y.; Volkov, S.Y.; Bogdanov, S.R. Diurnal dynamics of dissolved oxygen in a small mesotrophic lake during spring under-ice warming. Izv. Rus. Geogr. Obs. 2019, 151, 27–39. (In Russian) [Google Scholar] [CrossRef]
- Sand-Jensen, K.; Andersen, M.R.; Martinsen, K.T.; Borum, J.; Kristensen, E.; Kragh, T. Shallow plant-dominated lakes–extreme environmental variability, carbon cycling and ecological species challenges. Ann. Bot. 2019, 124, 355–366. [Google Scholar] [CrossRef] [Green Version]
- Duarte, C.M.; Prairie, Y.T.; Montes, C.; Cole, J.J.; Striegl, R.; Melack, J.; Downing, J.A. CO2 emissions from saline lakes: A global estimate of a surprisingly large flux. J. Geophys. Res. Biogeosci. 2008, 113, G04041. [Google Scholar] [CrossRef] [Green Version]
- Yan, F.; Sillanpää, M.; Kang, S.; Aho, K.S.; Qu, B.; Wei, D.; Li, X.; Li, C.; Raymond, P.A. Lakes on the Tibetan Plateau as conduits of greenhouse gases to the atmosphere. J. Geophys. Res. Biogeosci. 2018, 123, 2091–2103. [Google Scholar] [CrossRef]
- Jellison, R.; Anderson, R.F.; Melack, J.M.; Heil, D. Organic matter accumulation in sediments of hypersaline Mono Lake during a period of changing salinity. Limnol. Oceanogr. 1996, 41, 1539–1544. [Google Scholar] [CrossRef]
- Shadrin, N.; Zheng, M.; Oren, A. Past, present and future of saline lakes: Research for global sustainable development. Chin. J. Oceanol. Limnol. 2015, 33, 1349–1353. [Google Scholar] [CrossRef]
- Prazukin, A.V.; Anufriieva, E.V.; Shadrin, N.V. Photosynthetic activity of filamentous green algae mats hypersaline lake Chersonesskoye (Crimea). Vestn. TVER Univ. Ser. Biol. I Ecol. 2019, 2, 87–102. (In Russian) [Google Scholar]
- Shadrin, N.; Anufriieva, E. Ecosystems of hypersaline waters: Structure and trophic relations. Zhurnal Obs. Biol. 2018, 79, 418–427. [Google Scholar]
- Saccò, M.; White, N.E.; Harrod, C.; Salazar, G.; Aguilar, P.; Cubillos, C.F.; Meredith, K.; Baxter, B.K.; Oren, A.; Anufriieva, E.; et al. Salt to conserve: A review on the ecology and preservation of hypersaline ecosystems. Biol. Rev. 2021, 96, 2828–2850. [Google Scholar] [CrossRef] [PubMed]
- Gat, J.R.; Shatkay, M. Gas exchange with saline waters. Limnol. Oceanogr. 1991, 36, 988–997. [Google Scholar] [CrossRef]
- Sherwood, J.E.; Stagnitti, F.; Kokkinn, M.J.; Williams, W.D. Dissolved oxygen concentrations in hypersaline waters. Limnol. Oceanogr. 1991, 36, 235–250. [Google Scholar] [CrossRef]
- Debelius, B.; Gomez-Parra, A.; Forja, J.M. Oxygen solubility in evaporated seawater as a function of temperature and salinity. Hydrobiologia 2009, 632, 157–165. [Google Scholar] [CrossRef]
- Shadrin, N.V. Hypersaline lakes as polyextreme habitats for life. In Introduction to Salt Lake Sciences; Zheng, M., Deng, T., Oren, A., Eds.; Science Press: Beijing, China, 2018; pp. 180–187. [Google Scholar]
- Anufriieva, E.; Hołyńska, M.; Shadrin, N. Current invasions of Asian Cyclopid species (Copepoda: Cyclopidae) in Crimea, with taxonomical and zoogeographical remarks on the hypersaline and freshwater fauna. Ann. Zool. 2014, 64, 109–130. [Google Scholar] [CrossRef]
- Soulié, T.; Mas, S.; Parin, D.; Vidussi, F.; Mostajir, B. A new method to estimate planktonic oxygen metabolism using high-frequency sensor measurements in mesocosm experiments and considering daytime and nighttime respirations. Limnol. Oceanogr. Methods 2021, 19, 303–316. [Google Scholar] [CrossRef]
- Shadrin, N.; Yakovenko, V.; Anufriieva, E. Suppression of Artemia spp. (Crustacea, Anostraca) populations by predators in the Crimean hypersaline lakes: A review of the evidence. Int. Rev. Hydrobiol. 2019, 104, 5–13. [Google Scholar] [CrossRef] [Green Version]
- Shadrin, N.; Yakovenko, V.; Anufriieva, E. Gammarus aequicauda and Moina salina in the Crimean saline waters: New experimental and field data on their trophic relation. Aquac. Res. 2020, 51, 3091–3099. [Google Scholar] [CrossRef]
- Shadrin, N.V.; Yakovenko, V.A.; Anufriieva, E.V. Appearance of a new species of Cladocera (Anomopoda, Chydoridae, Bosminidae) in the hypersaline Moynaki Lake, Crimea. Biol. Bull. 2021, 48, 934–937. [Google Scholar] [CrossRef]
- Müller, P.H.; Neuman, P.; Storm, R. Tafeln der Mathematischen Statistik; VEB Fachbuchverlag: Leipzig, Germany, 1979; 276p. [Google Scholar]
- Thode, H.C. Testing for Normality; Marcel Dekker Inc.: New York, NY, USA, 2002; 368p. [Google Scholar]
- Cole, J.J.; Bade, D.L.; Bastviken, D.; Pace, M.L.; Van de Bogert, M. Multiple approaches to estimating air-water gas exchange in small lakes. Limnol. Oceanogr. Methods 2010, 8, 285–293. [Google Scholar] [CrossRef]
- Geider, R.J.; Osborne, B.A. Respiration and microalgal growth: A review of the quantitative relationship between dark respiration and growth. New Phytol. 1989, 112, 327–341. [Google Scholar] [CrossRef]
- Ivleva, I.I. The Temperature of the Environment and the Rate of Energy Metabolism Aquatic Animals; Naukova Dumka: Kiyev, Ukraine, 1981; 231p. (In Russian) [Google Scholar]
- Rasmusson, L.M.; Gullström, M.; Gunnarsson, P.C.; George, R.; Björk, M. Estimation of a whole plant Q10 to assess seagrass productivity during temperature shifts. Sci. Rep. 2019, 9, 12667. [Google Scholar] [CrossRef] [Green Version]
- Gudasz, C.; Karlsson, J.; Bastviken, D. When does temperature matter for ecosystem respiration? Environ. Res. Commun. 2021, 3, 121001. [Google Scholar] [CrossRef]
- Sushchenya, L.M. Intensity of Respiration of Crustaceans; Naukova Dumka: Kyiv, Ukraine, 1972; 196p. (In Russian) [Google Scholar]
- Balushkina, E.V. The Functional Significance of Chironomid Larvae in Continental Reservoirs; Nauka: Leningrad, Russia, 1987; 179p. (In Russian) [Google Scholar]
- Alimov, A.F. An Introduction to Production Hydrobiology; Gidrometeoizdat: Leningrad, Russia, 1989; 152p. (In Russian) [Google Scholar]
- Yakovenko, V.; Shadrin, N.; Anufriieva, E. The prawn Palaemon adspersus in the hypersaline Lake Moynaki (Crimea): Ecology, long-term changes, and prospects for aquaculture. Water 2022, 14, 2786. [Google Scholar] [CrossRef]
- Anufriieva, E.; Shadrin, N. The long-term changes in plankton composition: Is Bay Sivash transforming back into one of the world’s largest habitats of Artemia sp. (Crustacea, Anostraca)? Aquac. Res. 2020, 51, 341–350. [Google Scholar] [CrossRef]
- Horppila, J.; Nurminen, L. Effects of submerged macrophytes on sediment resuspension and internal phosphorus loading in Lake Hiidenvesi (southern Finland). Water Res. 2003, 37, 4468–4474. [Google Scholar] [CrossRef]
- Widdows, J.; Pope, N.D.; Brinsley, M.D.; Asmus, H.; Asmus, R.M. Effects of seagrass beds (Zostera noltii and Z. marina) on near-bed hydrodynamics and sediment resuspension. Mar. Ecol. Prog. Ser. 2008, 358, 125–136. [Google Scholar] [CrossRef] [Green Version]
- Zheng, X.; Zhang, K.; Yang, T.; He, Z.; Shu, L.; Xiao, F.; Wu, Y.; Wang, B.; Yu, H.; Yan, Q. Sediment resuspension drives protist metacommunity structure and assembly in grass carp (Ctenopharyngodon idella) aquaculture ponds. Sci. Total Environ. 2021, 764, 142840. [Google Scholar] [CrossRef] [PubMed]
- Anufriieva, E.; Kolesnikova, E.; Revkova, T.; Latushkin, A.; Shadrin, N. Human-induced sharp salinity changes in the world’s largest hypersaline lagoon Bay Sivash (Crimea) and their effects on the ecosystem. Water 2022, 14, 403. [Google Scholar] [CrossRef]
- Alimov, A.F. Elements of aquatic ecosystem function theory. Proc. Zool. Inst. Russ. Acad. Sci. 2000, 283, 2–147. [Google Scholar]
- Shadrin, N.V.; Anufriieva, E.V. Climate change impact on the marine lakes and their Crustaceans: The case of marine hypersaline Lake Bakalskoye (Ukraine). Turk. J. Fish. Aquat. Sci. 2013, 13, 603–611. [Google Scholar] [CrossRef]
- Middelburg, J.J.; Levin, L.A. Coastal hypoxia and sediment biogeochemistry. Biogeosciences 2009, 6, 1273–1293. [Google Scholar] [CrossRef] [Green Version]
- Jessen, G.L.; Lichtschlag, A.; Ramette, A.; Pantoja, S.; Rossel, P.E.; Schubert, C.J.; Struck, U.; Boetius, A. Hypoxia causes preservation of labile organic matter and changes seafloor microbial community composition (Black Sea). Sci. Adv. 2017, 3, e1601897. [Google Scholar] [CrossRef]


| Date, Time | Oxygen Consumption, mg O2 h−1 m−3 | ||||||
|---|---|---|---|---|---|---|---|
| Gammarus aequicauda | Moina salina | Eucypris mareotica | Total Zooplankton | Chironomid Larvae | Total Zoocenosis | Total Zooplankton/Total Zoocenosis | |
| Outside Ruppia thickets | |||||||
| Station 1 | |||||||
| 14 September 2021 13:00 | 3.14 | 2.33 | 0.08 | 5.55 | 14.14 | 19.69 | 0.28 |
| 15 September 2021 12:00 | 6.58 | 1.07 | 0.01 | 7.66 | 14.14 | 21.80 | 0.35 |
| 15 September 2021 17:53 | 5.57 | 1.00 | 0.08 | 6.65 | 14.14 | 20.79 | 0.32 |
| 16 September 2021 00:30 | 1.19 | 2.70 | <0.01 | 4.60 | 14.14 | 18.74 | 0.25 |
| 16 September 2021 04:00 | 2.56 | 0.73 | 0 | 3.29 | 14.14 | 17.43 | 0.19 |
| 16 September 2021 06:04 | 5.08 | 1.00 | 0.05 | 6.85 | 14.14 | 20.99 | 0.33 |
| Average | 4.02 | 1.47 | 0.04 | 5.77 | 14.14 | 19.91 | 0.26 |
| CV | 0.510 | 0.560 | 1.025 | 0.280 | - | 0.081 | 0.208 |
| Station 3 | |||||||
| 14 September 2021 14:00 | 2.93 | 5.84 | 0.05 | 8.82 | 14.14 | 22.96 | 0.38 |
| 15 September 2021 12:43 | 2.46 | 1.76 | 0.01 | 4.23 | 14.14 | 18.37 | 0.23 |
| 15 September 2021 18:27 | 3.96 | 1.01 | 0.02 | 4.99 | 14.14 | 19.13 | 0.26 |
| 16 September 2021 00:01 | 0.90 | 7.00 | 0 | 7.9 | 14.14 | 22.04 | 0.36 |
| 16 September 2021 04:28 | 1.21 | 3.71 | 0 | 4.92 | 14.14 | 19.06 | 0.26 |
| 16 September 2021 06:32 | 1.61 | 1.56 | 0.12 | 3.29 | 14.14 | 17.43 | 0.19 |
| Average | 2.18 | 3.48 | 0.03 | 5.69 | 14.14 | 19.83 | 0.28 |
| CV | 0.532 | 0.713 | 1.390 | 0.382 | - | 0.110 | 0.266 |
| Inside Ruppia thickets | |||||||
| Station 2 | |||||||
| 14 September 2021 13:10 | 66.40 | 0.64 | 0.56 | 67.60 | 10.52 | 78.12 | 0.87 |
| Station 4 | |||||||
| 14 September 2021 14:10 | 30.26 | 0.74 | 0.09 | 31.09 | 10.52 | 41.61 | 0.75 |
| Average | 48.33 | 0.69 | 0.33 | 49.35 | 10.52 | 59.87 | 0.81 |
| CV | 0.529 | 0.102 | 1.023 | 0.523 | - | 0.431 | 0.105 |
| GPP | R | Ra | Ra/R | Fla | Fal | Fla − Fal | Fla/GPP | R/GPP | |
|---|---|---|---|---|---|---|---|---|---|
| Day time | |||||||||
| Station 1 | 37.9 | 9.7 | 0.24 | 0.03 | 17.6 | 0 | 0.48 | 0.25 | |
| Station 2 | 25 | 10.7 | 0.72 | 0.07 | 1.9 | 0 | 0.08 | 0.43 | |
| Station 3 | 19.0 | 10.1 | 0.21 | 0.04 | 0.7 | 0 | 0.04 | 0.53 | |
| Average/CV | 27.3/ 0.354 | 10.1/ 0.054 | 0.39/ 0.735 | 0.04/ 0.496 | 6.7/ 1.398 | 0.40/ 0.352 | |||
| Dark time (night) | |||||||||
| Station 1 | 0 | 5.6 | 0.24 | 0.04 | 0 | 1.2 | −1.2 | ||
| Station 2 | 0 | 5.9 | 0.72 | 0.12 | 0 | 0.96 | −0.96 | ||
| Station 3 | 0 | 5.5 | 0.21 | 0.04 | 0 | 0.72 | −0.72 | ||
| Average/CV | 0 | 5.7/ 0.037 | 0.39/ 0.735 | 0.07/ 0.693 | 0 | 0.96/ 0.250 | −0.96/ 0.250 | ||
| Day and night | |||||||||
| Station 1 | 37.9 | 15.2 | 0.4778 | 0.03 | 17.6 | 1.2 | 16.4 | 0.46 | 0.40 |
| Station 2 | 25 | 16.6 | 1.4368 | 0.09 | 1.9 | 1.0 | 1.8 | 0.08 | 0.66 |
| Station 3 | 19.0 | 15.6 | 0.4184 | 0.03 | 0.8 | 0.7 | 0.1 | 0.04 | 0.82 |
| Average/CV | 27.3/ 0.354 | 15.9/ 0.041 | 0.78/ 0.735 | 0.05/ 0.693 | 6.7/ 1.398 | 1.00/ 0.250 | 6.1/ 1.483 | 0.19/ 1.199 | 0.63/ 0.338 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shadrin, N.; Anufriieva, E.; Latushkin, A.; Prazukin, A.; Yakovenko, V. Daily Rhythms and Oxygen Balance in the Hypersaline Lake Moynaki (Crimea). Water 2022, 14, 3753. https://doi.org/10.3390/w14223753
Shadrin N, Anufriieva E, Latushkin A, Prazukin A, Yakovenko V. Daily Rhythms and Oxygen Balance in the Hypersaline Lake Moynaki (Crimea). Water. 2022; 14(22):3753. https://doi.org/10.3390/w14223753
Chicago/Turabian StyleShadrin, Nickolai, Elena Anufriieva, Alexander Latushkin, Alexander Prazukin, and Vladimir Yakovenko. 2022. "Daily Rhythms and Oxygen Balance in the Hypersaline Lake Moynaki (Crimea)" Water 14, no. 22: 3753. https://doi.org/10.3390/w14223753





