Analysis of the Invasion of Acetes into the Water Intake of the Daya Bay Nuclear Power Base
Abstract
:1. Introduction
2. Methods
2.1. Numerical Model
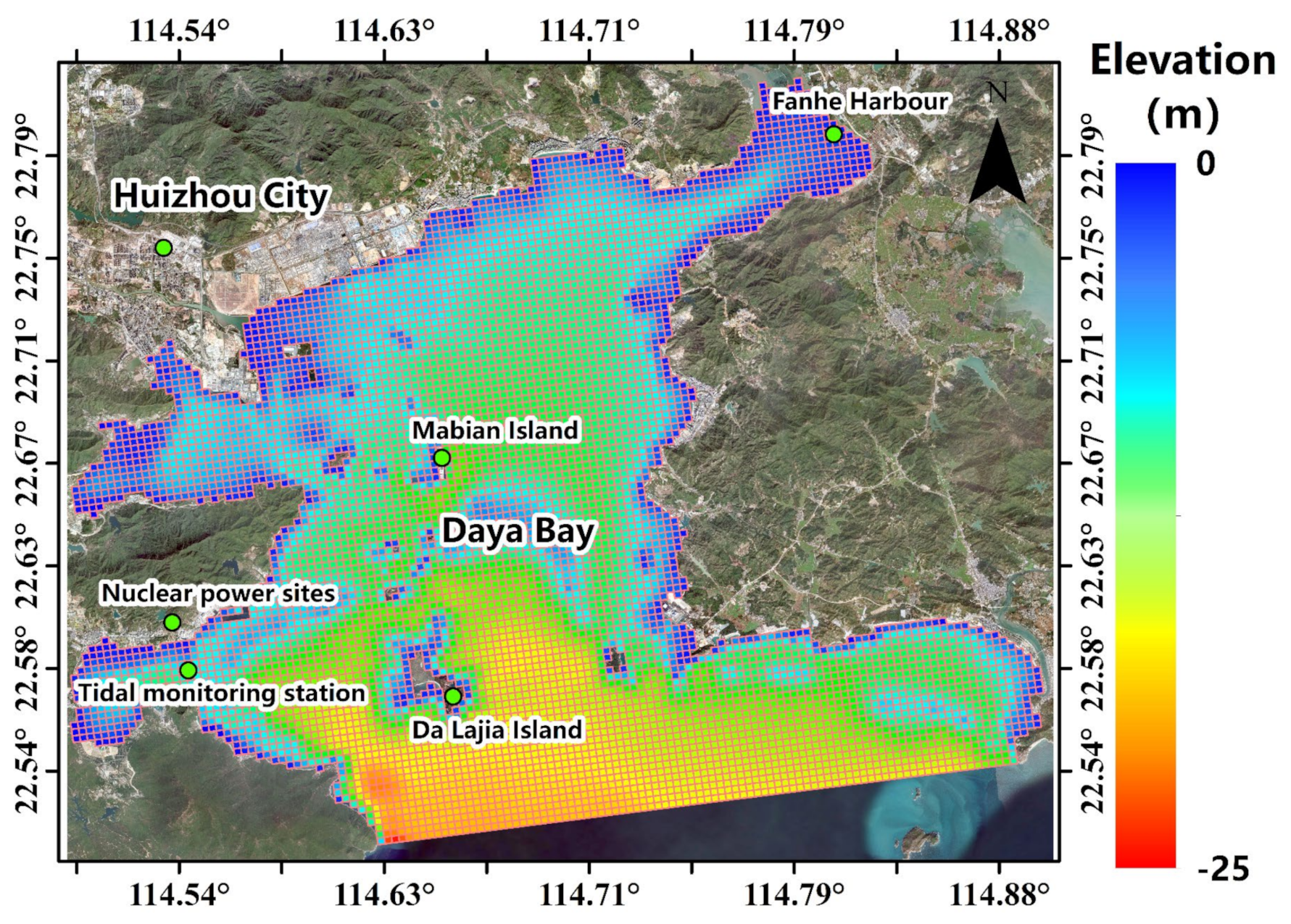
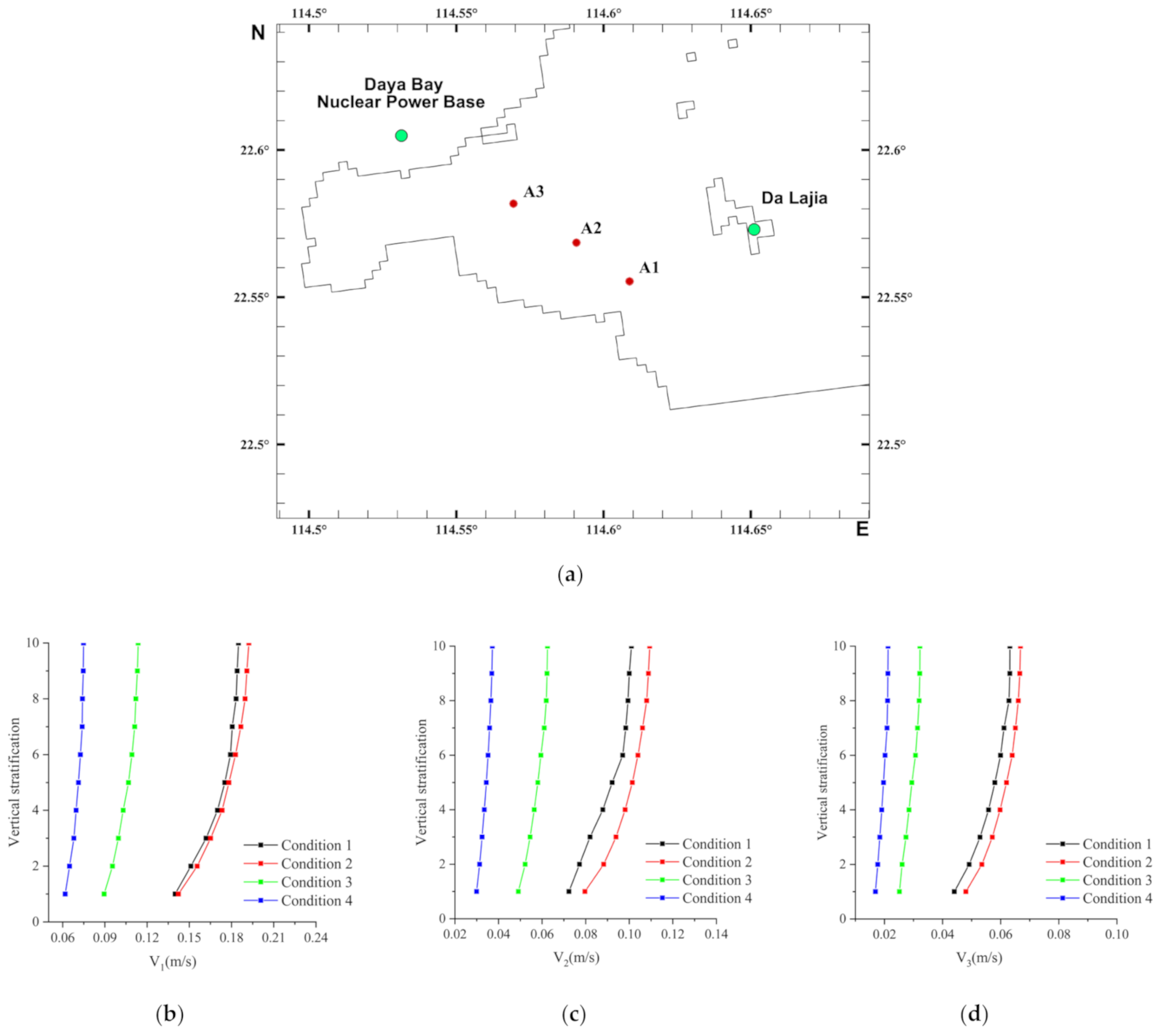
2.2. Computational Domain, Boundary Conditions and Cases
2.3. Acetes Migration
2.4. Biological Residual Current
2.5. Lagrange Particle-Tracking Method
2.6. Validation of Hydrodynamic Property
2.6.1. Hydrodynamic Property
2.6.2. Acetes Invasion
3. Results and Discussion
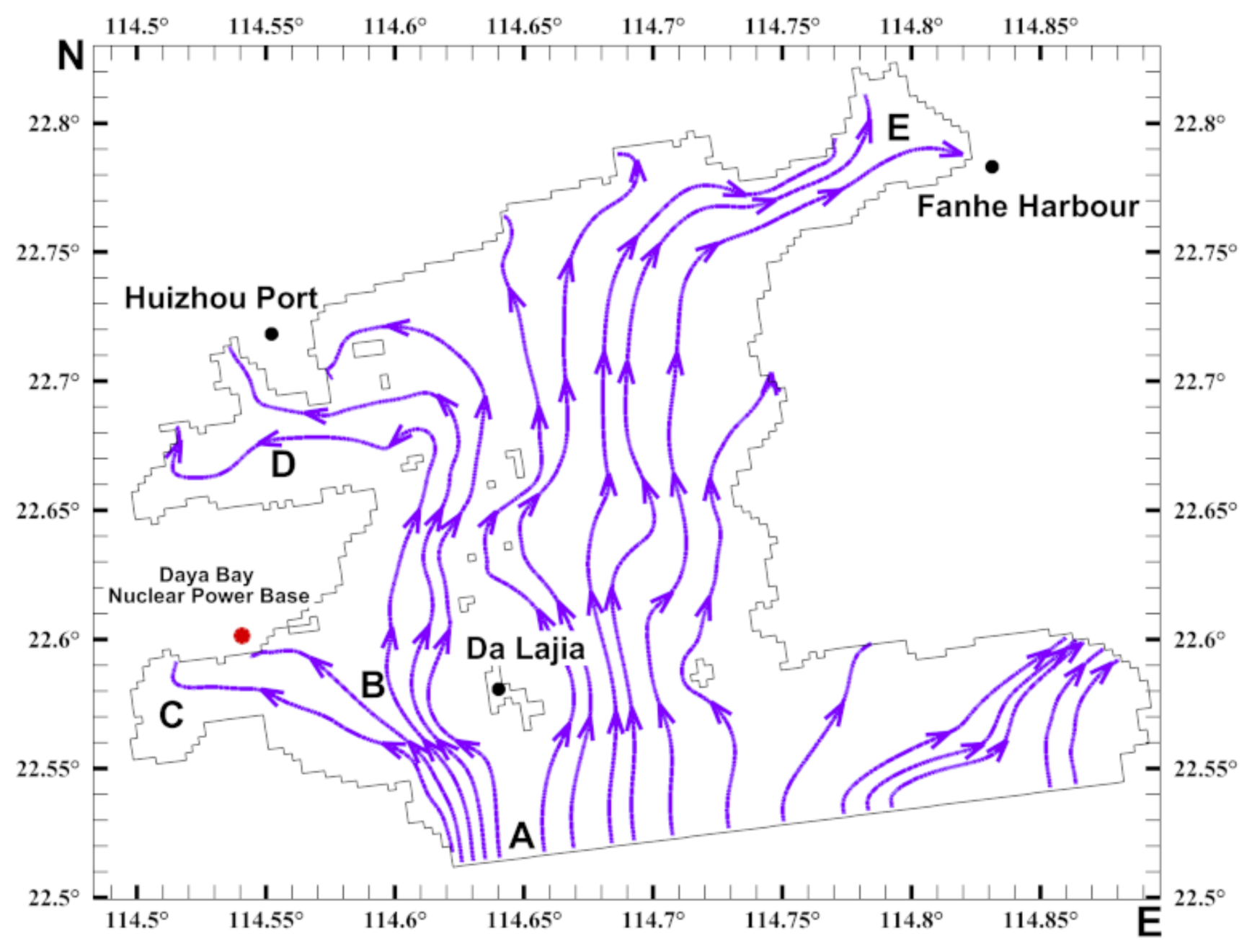
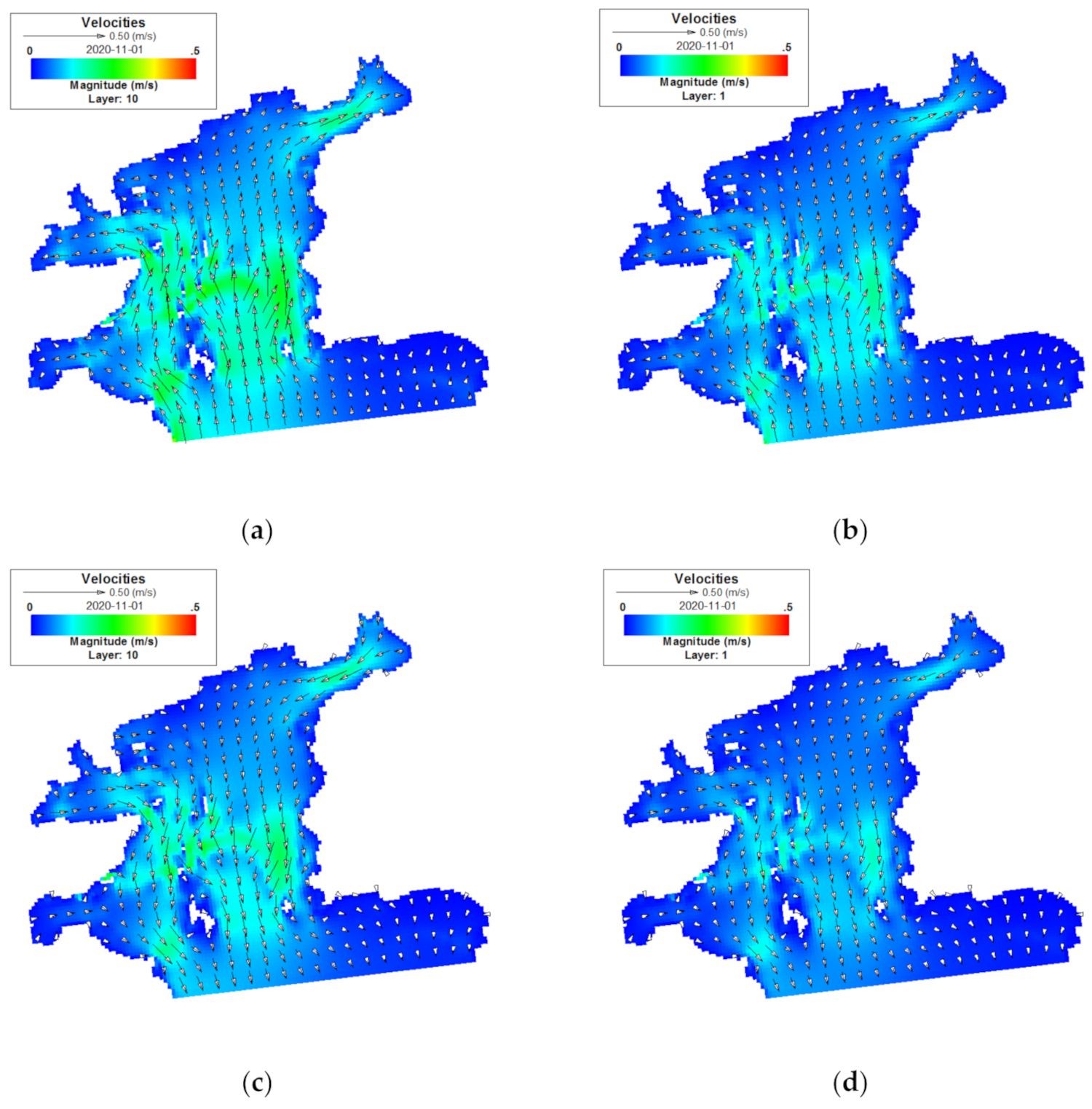
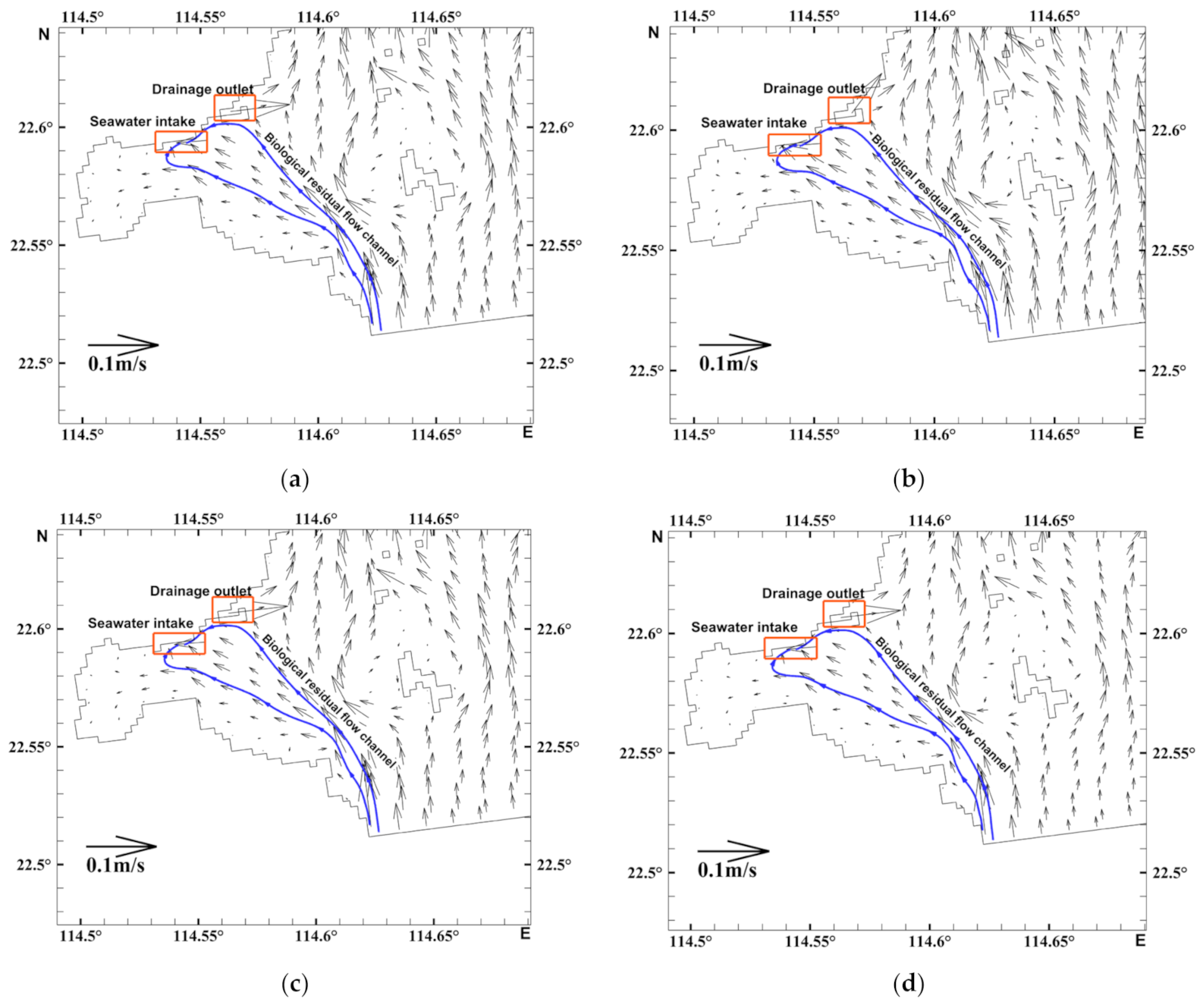
3.1. Flow Field Characteristics
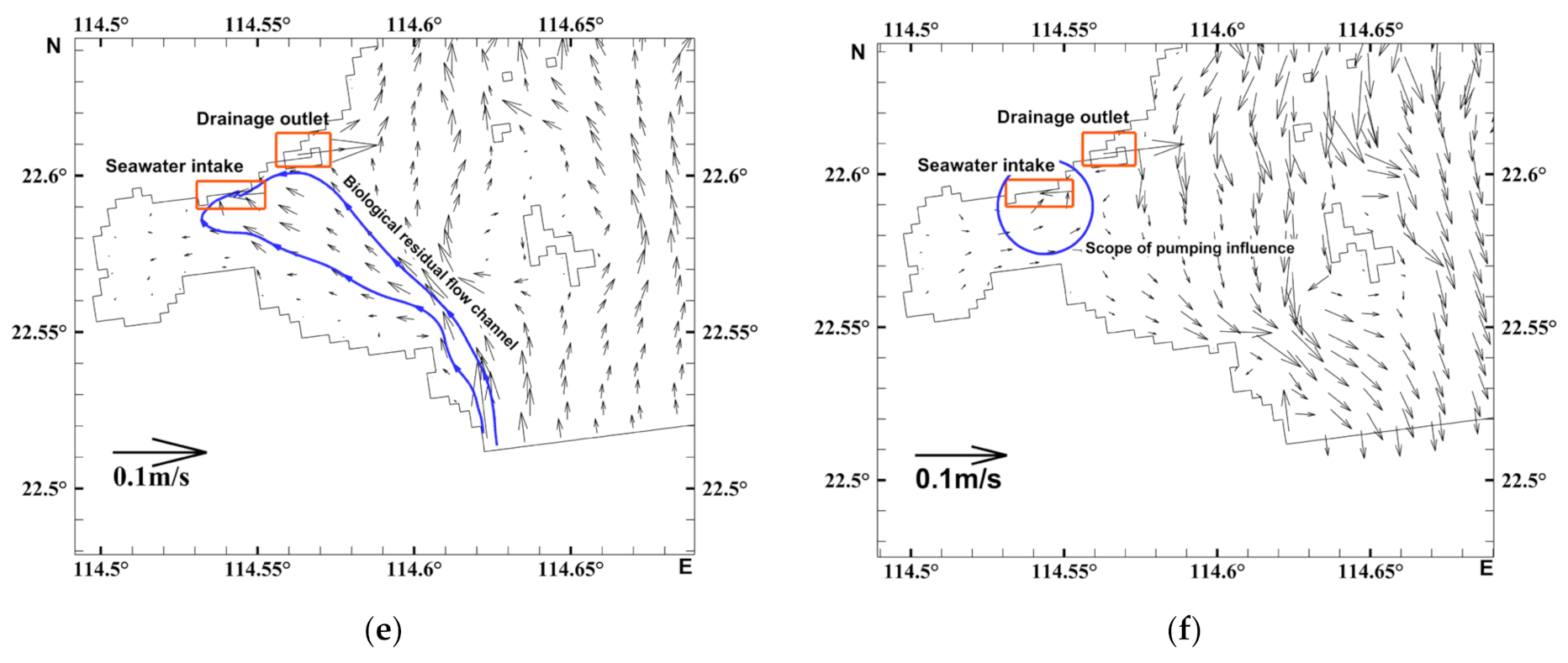
3.2. Characteristics of the Biological Residual Current of Acetes
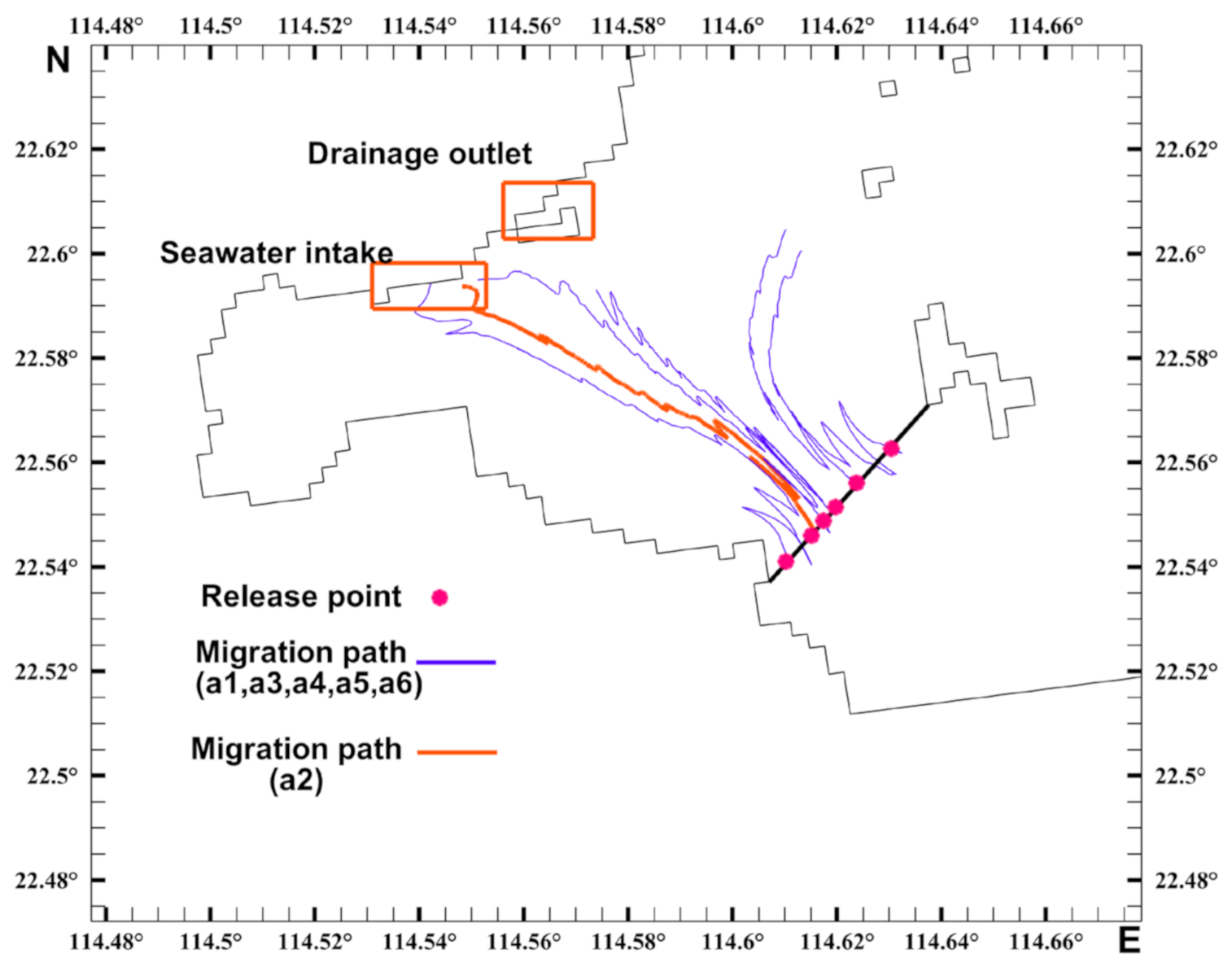
3.3. Analysis of the Migration Pathways of Invasive Acetes
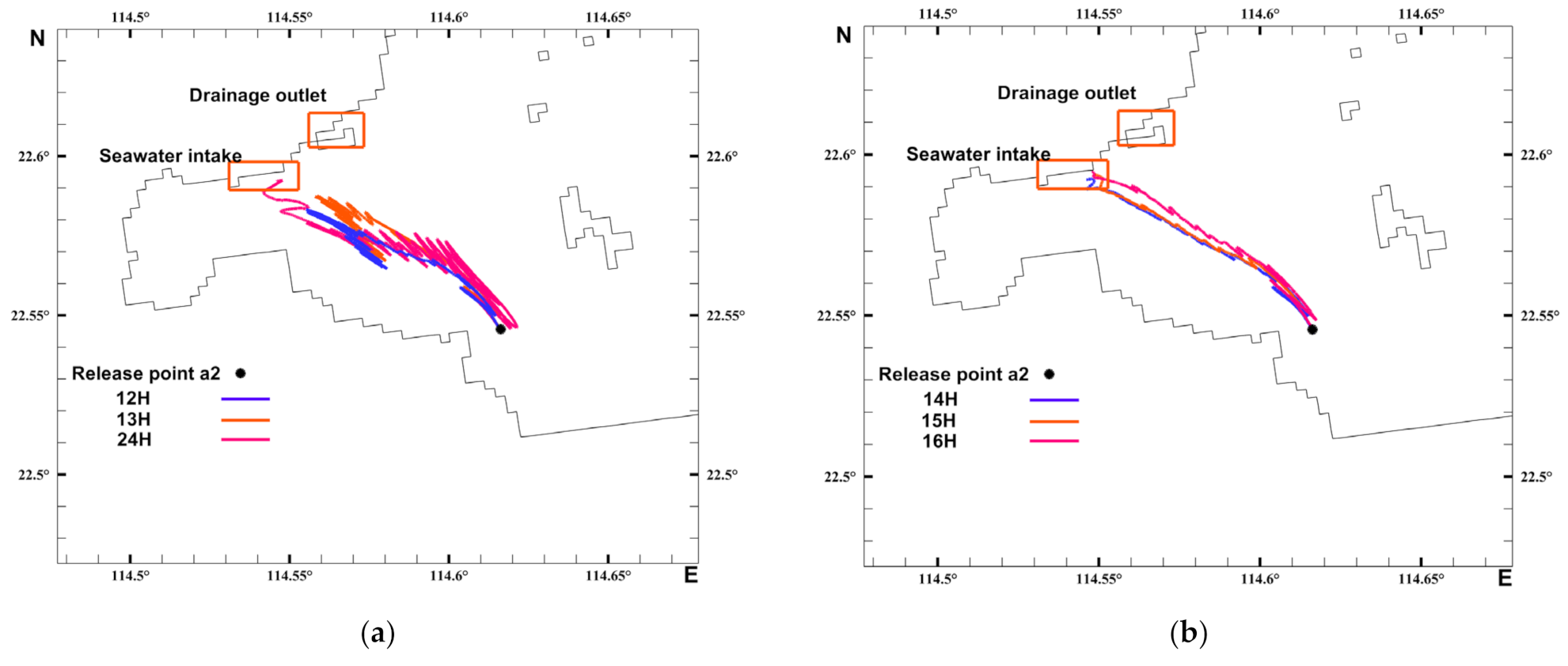
3.4. Timing Analysis of the Acetes Invasion
3.5. Lagrangian Particle Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fu, X.C.; Du, F.L.; Pu, X.; Wang, X.; Han, F. Analysis on Critical Factors of Marine Organism Impacts on Water Intake Safety at Nuclear Power Plants. J. Nucl. Eng. Radiat. Sci. 2020, 6, 041101. [Google Scholar] [CrossRef]
- Guoping, R. Analysis of the causes of water intake blockage in nuclear power plants and strategies to cope with it. Nucl. Power Eng. 2015, 36, 151–154. (In Chinese) [Google Scholar]
- Sha, C.; Yang, J.; Zhang, W.J.; Zhang, R.Y.; Bai, W. Investigation and analysis of sea life monitoring technology for nuclear power plant intake in China. Water Supply Drain. 2020, 56, 13–16. (In Chinese) [Google Scholar]
- Zeng, L.; Chen, G.; Wang, T.; Yang, B.; Yu, J.; Liao, X.; Huang, H. Acoustic detection and analysis of Acetes chinensis in the adjacent waters of the Daya Bay Nuclear Power Plant. J. Fish. Sci. China 2019, 6, 1029–1039. (In Chinese) [Google Scholar]
- Shih, R. The migratory distribution and generation alternation of the Acetes chinensis Hansen in the coastal waters of southern Zhejiang. East China Sea Mar. 1986, 4, 56–61. (In Chinese) [Google Scholar]
- Ejigu, M.T. Overview of water quality modeling. Cogent Eng. 2021, 8, 1891711. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Li, F.Q.; Chen, C.J. Water quality analysis and prediction of the Qiantang River water diversion project. J. Hydropower 2005, 4, 47–51. (In Chinese) [Google Scholar]
- Lopes, J.F.; Silva, C.I.; Cardoso, A.C. Validation of a water quality model for the Ria de Aveiro lagoon, Portugal. Environ. Modell. Softw. 2008, 23, 479–494. [Google Scholar] [CrossRef]
- Martin; J. L. Application of Two-Dimensional Water Quality Model. J. Environ. Eng. 1988, 114, 317–336. [Google Scholar] [CrossRef]
- Zheng, L.; Chen, C.; Merryl, A.; Liu, H. A modeling study of the Satilla River estuary, Georgia. II: Suspended sediment. Estuaries Coasts 2003, 26, 670–679. [Google Scholar] [CrossRef]
- Mellor, G.L.; Yamada, T. Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. 1982, 20, 851–875. [Google Scholar] [CrossRef] [Green Version]
- Hamrick, J.M. A Three-Dimensional Environmental Fluid Dynamics Computer Code: Theoretical and Computational Aspect; The College of William and Mary, Virginia Institute of Marine Science: Gloucester Point, VA, USA, 1992. [Google Scholar]
- Alarcon, V.J.; Linhoss, A.C.; Kelble, C.R.; Mickle, P.F.; Sanchez-Banda, G.F.; Mardonez-Meza, F.E.; Bishop, J.; Ashby, S.L. Coastal inundation under concurrent mean and extreme sea-level rise in Coral Gables, Florida, USA. Nat. Hazards 2022, 111, 2933–2962. [Google Scholar] [CrossRef]
- Chen, X.; Zhu, L.; Zhang, H. Numerical simulation of summer circulation in the East China Sea and its application in estimating the sources of red tides in the Yangtze River estuary and adjacent sea areas. J. Hydrodyn. Ser. B 2007, 19, 272–281. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, D.; Abbasbandy, S.; Rashidi, M.M. Analytical solution of fractional Navier-Stokes equation byusing modifed Laplace decomposition method. Ain Shams Eng. J. 2014, 5, 569–574. [Google Scholar] [CrossRef] [Green Version]
- Johnson, D.R.; Perry, H.M.; Burke, W.D. Developing jellyfish strategy hypotheses using circulation models. Hydrobiologia 2001, 451, 213–221. [Google Scholar] [CrossRef]
- North, E.W.; Schlag, Z.; Hood, R.R.; Li, M.; Zhong, L.; Gross, T.; Kennedy, V.S. Vertical swimming behavior influences the dispersal of simulated oyster larvae in a coupled particle-tracking and hydrodynamic model of Chesapeake Bay. Mar. Ecol. Prog. Ser. 2008, 359, 99–115. [Google Scholar] [CrossRef]
- Hofmann, E.E.; Klinck, J.M.; Locarnini, R.A.; Fach, B.; Murphy, E. Krill transport in the Scotia Sea and environs. Antarct. Sci. 1998, 10, 406–415. [Google Scholar] [CrossRef] [Green Version]
- Fach, B.A.; Hofmann, E.E.; Murphy, E.J. Transport of Antarctic krill (Euphausia superba) across the Scotia Sea. Part II: Krill growth and survival. Deep. Sea Res. Part I 2006, 53, 1011–1043. [Google Scholar] [CrossRef] [Green Version]
- Wu, W.; Yan, I.H.; Song, D.H. Study of tidal dynamics in Daya Bay—I. Observational analysis and numerical simulation of the tidal wave system. J. Trop. Oceanogr. 2017, 36, 34–45. (In Chinese) [Google Scholar]
- Jiang, R.; Guo, B.T. Relationship between variability of coastal shrimp production and meteorological factors in Fujian. Mar. Bull. 1983, 2, 69–74. (In Chinese) [Google Scholar]
- Wu, Y.; Wang, Y.; Hou, Q.; Jiao, F.; Sun, G. Empirical feedback on incidents of blockage of water intake systems in nuclear power plants by marine foreign bodies. Nucl. Saf. 2017, 16, 26–32. (In Chinese) [Google Scholar]
- Li, Y.; Acharya, K.; Yu, Z. Modeling impacts of Yangtze River water transfer on water ages in Lake Taihu, China. Ecol. Eng. 2011, 37, 325–334. [Google Scholar] [CrossRef]
- Li, Y.; Wang, J.; Hua, L. Response of algae growth to pollution reduction of drainage basin based on EFDC model for channel reservoirs: A case of Changtan Reservoir, Guangdong Province. J. Lake Sci. 2015, 27, 811–818. [Google Scholar]
- Kim, N.S.; Kang, H.; Kwon, M.S.; Jang, H.-S.; Kim, J.G. Comparison of Seawater Exchange Rate of Small Scale Inner Bays within Jinhae Bay. J. Korean Soc. Mar. Environ. Energy 2016, 19, 74–85. [Google Scholar] [CrossRef]
- Hongzhou, X.U.; Lin, J.; Shen, J.; Dynamics, W.D. Wind impact on pollutant transport in a shallow estuary. Acta Oceanol. Sin. 2008, 3, 147–160. [Google Scholar]
- Jung, J.; Nam, J.; Kim, J.; Bae, Y.H.; Kim, H.S. Estimation of Temperature Recovery Distance and the Influence of Heat Pump Discharge on Fluvial Ecosystems. Water 2020, 12, 949. [Google Scholar] [CrossRef] [Green Version]
- Shin, B.S.; Kim, K.H.; Kim, J.H.; Baek, S.-H. Feasibility Study for Tidal Power Plant Site in Garolim Bay Using EFDC Model. J. Korean Soc. Coast. Ocean. Eng. 2011, 23, 489–495. [Google Scholar] [CrossRef]
- Chen, L.J.; Yang, F.; Zhong, X.M.; Song, D.D.; Li, G.D.; Kang, C.J.; Xiong, E. Advances in the life history of the Chinese shrimp, Myrmecophthalmus chinensis. J. Shanghai Ocean. Univ. 2022, 31, 1032–1040. (In Chinese) [Google Scholar]
- Sun, Z.Y.; Chen, Z.Z.; Yang, L.Q.; Zhu, J. Seasonal variation of tidal currents and residual currents in Daya Bay and surrounding sea areas. J. Xiamen Univ. (Nat. Sci. Ed.) 2020, 59, 278–286. [Google Scholar]
- Yang, G.B. Characteristics of tidal movement in the Daya Bay marine area. People’s Pearl River 2001, 22, 30–32. (In Chinese) [Google Scholar]
- Jiang, W.; Feng, S. 3D analytical solution to the tidally induced Lagrangian residual current equations in a narrow bay. Ocean Dyn. 2014, 64, 1073–1091. [Google Scholar] [CrossRef]



| Date | Description of the Event |
|---|---|
| 10 January 2015 | In this accident, works cleaned approximate 1.3 tonnes of Acetes in the drum net backwash drain at the nuclear power site’s Ling’ao 2 unit. Units 1 and 2 had to operate with lower power. |
| 9 January 2016 | In the circulating water filtration system, the number of Acetes detected was much higher than the tolerance level of safety design. Units 1 and 2 had to be shut down. |
| 12 h | 13 h | 14 h | 15 h | 16 h | |
|---|---|---|---|---|---|
| Calculation time/h | 18:00–6:00 (The following day) | 18:00–7:00 (The following day) | 17:00–7:00 (The following day) | 16:00–7:00 (The following day) | 16:00–8:00 (The following day) |
| Date of entry into the stream | 4–14 November | 5–14 November | 5–15 November | 5–14 November | 5–14 November |
| Duration of inflow days/d | 10 | 9 | 10 | 9 | 9 |
| Date of departure | 11.14–11.20 | 11.14–11.20 | 11.15–11.20 | 11.14–11.20 | 11.14–11.20 |
| Duration of outflow days/d | 6 | 6 | 5 | 6 | 6 |
| Date of peak residual flow rate | 11.09 | 11.10 | 11.09 | 11.09 | 11.10 |
| L0 | L1 | L2 | L3 | L4 | L5 | L6 | L7 | L8 | L9 | L10 | L11 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Average biological residual current rate/cm·s−1 | 12 h | 2.89 | 2.80 | 2.46 | 1.86 | 1.40 | 1.10 | 0.95 | 1.09 | 1.46 | 1.64 | 1.90 | 3.44 |
| 13 h | 2.92 | 2.74 | 2.31 | 1.76 | 1.35 | 1.08 | 0.93 | 1.05 | 1.39 | 1.58 | 1.97 | 3.50 | |
| 14 h | 3.51 | 3.39 | 2.83 | 2.15 | 1.66 | 1.33 | 1.13 | 1.28 | 1.68 | 1.75 | 2.47 | 3.53 | |
| 15 h | 3.57 | 3.35 | 2.72 | 2.09 | 1.63 | 1.31 | 1.12 | 1.26 | 1.62 | 1.70 | 1.95 | 3.50 | |
| 16 h | 3.54 | 3.28 | 2.62 | 2.02 | 1.59 | 1.29 | 1.10 | 1.24 | 1.58 | 1.67 | 1.93 | 3.49 | |
| Nocturnal Migration Hours | Average Migration Speed through the Segments/km·d−1 | Duration of the Inflow Cycle/d | Determining Whether an Incoming Flow Period Can Reach Section C(Y/N) | Through Various Periods/d | Time of Arrival at the Water Intake/d | ||||
|---|---|---|---|---|---|---|---|---|---|
| A | B | C | A | B | C | ||||
| 12 h | 0.91 | 0.52 | 0.99 | 10 | N | 2.6 | >15 | 4.1 | >20 |
| 13 h | 0.99 | 0.54 | 1.03 | 9 | N | 2.4 | >15 | 3.0 | >20 |
| 14 h | 1.18 | 0.71 | 1.37 | 10 | Y | 1.9 | 5.8 | 3.0 | 10.7 |
| 15 h | 1.18 | 0.75 | 1.44 | 9 | Y | 2.0 | 5.5 | 2.9 | 10.4 |
| 16 h | 1.24 | 0.78 | 1.50 | 9 | Y | 1.9 | 5.3 | 2.8 | 9.9 |
| 12 h | 13 h | 14 h | 15 h | 16 h | 24 h | |
|---|---|---|---|---|---|---|
| Acetes invasion time/d | >15 | >15 | 8 | 7 | 6.5 | 12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Yang, L.; Ren, H.; Liu, Z.; Jia, Z. Analysis of the Invasion of Acetes into the Water Intake of the Daya Bay Nuclear Power Base. Water 2022, 14, 3741. https://doi.org/10.3390/w14223741
Li X, Yang L, Ren H, Liu Z, Jia Z. Analysis of the Invasion of Acetes into the Water Intake of the Daya Bay Nuclear Power Base. Water. 2022; 14(22):3741. https://doi.org/10.3390/w14223741
Chicago/Turabian StyleLi, Xinghao, Lin Yang, Huatang Ren, Zhaowei Liu, and Zeyu Jia. 2022. "Analysis of the Invasion of Acetes into the Water Intake of the Daya Bay Nuclear Power Base" Water 14, no. 22: 3741. https://doi.org/10.3390/w14223741





